Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Latin American applied research
versión impresa ISSN 0327-0793versión On-line ISSN 1851-8796
Lat. Am. appl. res. vol.43 no.3 Bahía Blanca jul. 2013
Adaptive blind interference cancellation and spatial scheduling schemes for closed loop multiuser mimo systems
H. Mendoza†‡ and G. Corral-Briones†
† LCD-Laboratorio de Comunicaciones Digitales-Universidad Nacional de Córdoba-Argentina
‡ GID-IE Grupo de investigación y Desarrollo en Ingeniería Electrónica - Universidad Nacional de Misiones-Argentina-
Email: mendoza@fio.unam.edu.ar - gcorral@efn.unc.edu.ar
Abstract — To improve the spectrum efficiency in wireless communication, two techniques are commonly used: adaptive digital signal processing and resource allocation. The aim of both techniques is to reduce the interference level. In this paper we study the performance improvement of using jointly these techniques for closed loop multiuser MIMO systems. We propose a closed loop spatial multiuser scheduling scheme that enables code-reuse without significantly degrading the performance of an Adaptive Blind Receiver (ABR).
Keywords — Blind; MIMO; Interference; Schedule.
I. INTRODUCTION
Closed loop transmit diversity (CL-TD) technique, applied on MIMO broadcasting channel, improves the system capacity in both, the single user scenario and the multiuser case (Caire and Shamai, 2003). However, in order to improve the spectrum efficiency of practical schemes while keeping small performance degradation, it is necessary a joint signal processing at both side of the radio link.
At the receiver, several algorithms have been proposed with the aim to reduce the interference level efficiently (Wrulich et al., 2008; Mehlfuhrer et al., 2008). On MIMO channels, the use of low complexity receivers that improve the performance of conventional scheme (that treats interference as white Gaussian noise), is of fundamental importance (Lupas and Verdu, 1990). In particular, blind adaptive receiver results attractive for high data rate packet communication because on such dynamic environment is difficult for a mobile user to get precise information about the rest of active users. Closed loop multiuser MIMO is a promising technique for achieving high spectrum efficiency needed for the higher data rate of future wireless system. The standard WCDMA 3GPP (2006); Hottinen et al. (2003) allocates a limited feedback channel that can be used for sending back to the Base Station information about the channel back to the Base Station (BS). This information is used to support two closed loop transmit diversity modes, and can also enable spatial multiplexing techniques that increase the system’s capacity and potentially simplify the receiver architecture (Haikola et al., 2006).
Due to practical considerations, the most widely analyzed scenery for the down link broadcast channel considers a BS equipped with two antennas and single- antenna mobile users (Love et al., 2008). Schemes that schedule multiple users prefiltering them at the transmission by a matriz with channel information weights reported by these users, have been extensively studied in terms of capacity gain (Corral-Briones et al., 2005; Dowhuszko et al., 2007; Shenoy et al., 2009). Although achievable system capacity is important to study, the potential of those schemes does not give practical information about the type of transceiver that enable high spectrum efficiency with affordable complexity.
In this paper we analyze the performance in terms of Bit Error Rate (BER) of different user scheduling methods that use space signal processing at the BS (to reduce interference) and adaptive blind interference cancellation at the mobilw stations. A new spatial Multiuser Scheduler (MS) is proposed based on the observation that a blind detector cancels the interference that belongs to a subspace orthogonal to the desired signal. The proposed scheme enables code-reuse doubling the number of users that can coexist without significant performance degradation. The results presented are for WCDMA closed loop transmit diversity mode 1 (Yoo et al., 2007).
The following notation is used in the paper. ℜ, C, (.)*, (.)T, (.)H, <.>, ||.||, denote real part, complex number, complex conjugate, transpose, hermitian, correlation and norm, respectively. Scalars are written in lowercase, vectors in bold lowercase and matrices with bold uppercase letters. The system model is presented in Section II. Adaptive blind receiver is analyzed in Section III, followed by scheduling schemes presented in Section IV. Simulation results are presented in Section V, followed by paper conclusions.
II. SYSTEM MODEL
The system model for the downlink of a wireless communication system is illustrated in Fig. 1. The system consist of a single BS with 2 Tx antennas j=1, 2 and K≥2 active user equipments (UEs) with single-elements antennas.

Figure 1: MIMO-BC system with Kusers.
In case of flat fading and rich scattering, the channel gain from a jth Tx antenna to a kth User (UE) is described by a zero-mean circularly symmetric complex Gausssian Random Variable (RV) gjk, for j=1,2 and k=1,...,K. For simplicity we assume that all UE´s are homogeneous and experience independent fading. We also assume that each UE has a low-rate, reliable, and delay-free feedback channel to the BS.
For convenience, we will assume that the user of interest is k=1. The signal received by user 1, in a single symbol interval [0,T], can be written as
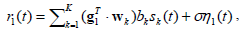 | (1) |
where g1=[g11 g12]T is the channel gain vector from the BS to the desired user with unit variance entries. w1=[w11 w12]T is the Tx weight vector that maximizes the received energy for the desired user.  represents the identical and independent distribuited (iid) users data stream with zero mean and unit variance. sk(t) is the unit-energy signature waveform of the kthuser. η1(t) is Additive White Gaussian Noise (AWGN) component with unit variance and σ is a scalar factor that affects the variance level of the AWGN component.
represents the identical and independent distribuited (iid) users data stream with zero mean and unit variance. sk(t) is the unit-energy signature waveform of the kthuser. η1(t) is Additive White Gaussian Noise (AWGN) component with unit variance and σ is a scalar factor that affects the variance level of the AWGN component.
Let 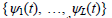 be a set of L orthonormal signals defined on ith [iT,iT+T] time interval. The received signal vector r1∈CL×1of the desired user is the L-dimensional representation of r1(t) on the basis
be a set of L orthonormal signals defined on ith [iT,iT+T] time interval. The received signal vector r1∈CL×1of the desired user is the L-dimensional representation of r1(t) on the basis 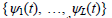 , that is, the l component of the column vector r1 is
, that is, the l component of the column vector r1 is
 | (2) |
Furthermore, we define the componens of the signature vector  as
as
 | (3) |
and the component of the L-dimensional Gaussian vector n1∈CL’1 as
 | (4) |
For convenience, the received signal (2) is expressed in vector form:
 | (5) |
 | (6) |
where
 | (7) |
 | (8) |
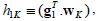 | (9) |
 | (10) |
 | (11) |
The autocorrelation matrix of the received signal r1[i] is given by
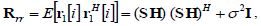 | (12) |
 | (13) |
where  with akk=|h1k|2 k=1,..., K and I is the L×L identity matrix. The system model adopted is illustrated in Fig. 2.
with akk=|h1k|2 k=1,..., K and I is the L×L identity matrix. The system model adopted is illustrated in Fig. 2.

Figure 2: System Model Scheme.
III. BLIND ADAPTIVE RECEIVER
The adaptive Minimum Output Energy detector (MOE) was first proposed by Honig et al. (1995) and is blind to some extent because a training sequence is not required. It is therefore commonly known as the adaptive blind receiver. The adaptive MOE algorithm is implemented by a transversal FIR filter which converges to the MMSE detector to within a scaling factor (Verdu, 1998). Figure 3 shows the implementation structure.
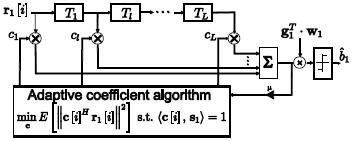
Figure 3: Blind Adaptive Receiver Structure.
A key property of every linear multiuser receiver is that the impulse response can be decomposed as a sum of two orthogonal components. One of those components is equal to the signature waveform of the desired user which is assumed known and fixed throughout this section. That is, c[i]=s1+ x1[i], where x1Hs1=0. The cost function is the variance of the filter output, known as Output Energy (OE), and minimized over the adaptive component x1[i] subject to the constraint <c[i], s1>=1 (Honig et al., 1995).
The OE is given by
 | (14) |
where i is the time index interval and the MOE may be written as
 | (15) |
The decision on b1, for the desired user, is
 | (16) |
where we use the actual adjusted channel coefficient h11.
In order to apply the gradient descent algorithm to the cost function (14), we must take into account that, at every iteration, x1[i] must be orthogonal to s1 because we are following (on average) the steepest descent line along the subspace orthogonal to s1. The unconstrained gradient of (14) is
 | (17) |
where the component orthogonal to s1 results in a scaled version of the component of r1 orthogonal to s1, that is
 | (18) |
Therefore, the projected gradient (in the subspace orthogonal to s1) is
 | (19) |
where z[i]=c[i]H r1[i] is the filter output. According to (19) the stochastic gradient adaptation rule is
 | (20) |
where  is the matrix that projects vectors, pre-multiplies it, onto the space orthogonal to s1 and μ∈ℜ1×1is the step-size.
is the matrix that projects vectors, pre-multiplies it, onto the space orthogonal to s1 and μ∈ℜ1×1is the step-size.
A. Trajectory of the Tap-Weight Vector
The trajectory of the vector coefficients is analyzed in similar way to that given in Honig et al. (1995) but is re-stated here fof convenience. Adding s1 to both sides of (20) gives
 | (21) |
where  The MOE vector is
The MOE vector is
 | (22) |
where 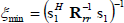 is the MOE generated with copt and Rrr is the autocorrelation matrix (13). By substracting copt to both sides of (21), we have
is the MOE generated with copt and Rrr is the autocorrelation matrix (13). By substracting copt to both sides of (21), we have
 | (23) |
replacing (23) in (21), and taking expectation, we have
 | (24) |
where 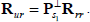 From (24) the equivalent correlation matrix which determines the transient behavior of tap is Rur (Gong et al., 2000). Since Rur can not be symmetric, eigenvalues can be complex and the analysis becomes quite difficult to carry out. However, if we consider the fact that
From (24) the equivalent correlation matrix which determines the transient behavior of tap is Rur (Gong et al., 2000). Since Rur can not be symmetric, eigenvalues can be complex and the analysis becomes quite difficult to carry out. However, if we consider the fact that
 | (25) |
since x1H[i] s1=0, for all i, the filter output can be re-stated as
 | (26) |
where the fact that  has been used. Now, replacing (26) in (20) and taking into account (22), we have
has been used. Now, replacing (26) in (20) and taking into account (22), we have
 | (27) |
then, taking expectation at both sides of (27) and assuming that x1[i] and r1[i] are independent, we have
 | (28) |
where  and
and  . Upon convergence, we can consider
. Upon convergence, we can consider 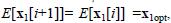 , therefore, (28) can be written as
, therefore, (28) can be written as
 | (29) |
 | (30) |
From (30), x1opt could not be calculated because, as will show later, Ruu is singular, but could be calculated from copt (22), that is
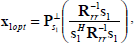 | (31) |
i.e., the projection of copt into subspace orthogonal to s1. Therefore the expression for the trajectory of the tap as a function of the adaptive component is given by
 | (32) |
where 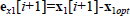 and for convergence stability we must have
and for convergence stability we must have  From (32) the matrix
From (32) the matrix  may be seen as the equivalent correlation matrix for the adaptive part in (24) in performance analysis, since is similar to Rur but Hermitian, Gong et al. (2001). Deeping in the eigen-analysis of both matrix Rur and Ruu (based on Gong et al., 2001), it can be verified that s1 is an eigenvector of Ruu with zero eigenvalue
may be seen as the equivalent correlation matrix for the adaptive part in (24) in performance analysis, since is similar to Rur but Hermitian, Gong et al. (2001). Deeping in the eigen-analysis of both matrix Rur and Ruu (based on Gong et al., 2001), it can be verified that s1 is an eigenvector of Ruu with zero eigenvalue 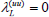 , where the superscript denotes the matrix correspondence. Since s1 is a eigenvector, Ruu is singular and the corresponding eigenvalue plays no role in the convergence of the blind detector because the tap-weight vector is never adapted in the direction of s1.
, where the superscript denotes the matrix correspondence. Since s1 is a eigenvector, Ruu is singular and the corresponding eigenvalue plays no role in the convergence of the blind detector because the tap-weight vector is never adapted in the direction of s1.
To gain more insight into the convergence of the mean tap vector, it is necessary to study the eigenvalues of Ruu. It can be done by applying the Minimax theorem (Simon, 1996) which state
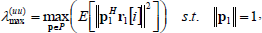 | (33) |
where P is the orthonormal vector set with pn, n=1, ..., L. Similarly, the other eigenvalues in descendent order, can be obtained by
 | (34) |
Descomposing  , where pn| is the projection of pn into s1 direction and pn⊥ is the projection of pn in the orthogonal subspace of s1, we have
, where pn| is the projection of pn into s1 direction and pn⊥ is the projection of pn in the orthogonal subspace of s1, we have
 | (35) |
Taking into account (35) the argument can be written as
 | (36) |
then, using Ruu in place of Rrr, we have
 | (37) |
with
 | (38) |
Maximizing (33) with respect to pn requires to make pn⊥ as large as possible, while keeping pn|=1. Consequently pn⊥ must be set to 0, that is
 | (39) |
Takin into account (39) and (13), we arrive at the following result
 | (40) |
We therefore conclude that x1[i] converges to x1opt along L-1 modes, each of which decays exponentially with parameter  , where
, where 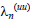 is the nth eigenvalue of the Ruu.
is the nth eigenvalue of the Ruu.
B. Learning Curve of MOE
The OE at the filter output is given by
 | (41) |
where the expectation value is taken over the received signal. The MOE is
 | (42) |
where we use (28). Substracting (42) from (41), we have
 | |
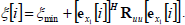 | (43) |
Making a similar derivation with (43) as described in Farhang-Boroujeny (1999), the expression (43) can be written as
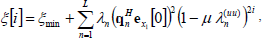 | (44) |
where qn is the normalize eigenvector of Ruu with corresponding eigenvalue λn(uu) . Since s1 is an eigenvector of Ruu, we can assign q1, q2, ..., qK-1, qK= s1 to the eigenvectors associated with the K-1 largest eigenvalues; and qL+1, qL+2, ..., qL to the eigenvectors spanning the noise subspace. It can be shown that qn, n=1, ..., K-1 span the same subspace as 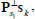 k=2, ..., K, and all these subspace are orthogonal to s1. Parallel to this, copt is known to belongs to the subspace generated by sk, k=1, ..., K. It is clear to see that x1opt=copt-s1, also lies in the same subspace, but it is orthogonal to s1. Then, x1opt must lie in span
k=2, ..., K, and all these subspace are orthogonal to s1. Parallel to this, copt is known to belongs to the subspace generated by sk, k=1, ..., K. It is clear to see that x1opt=copt-s1, also lies in the same subspace, but it is orthogonal to s1. Then, x1opt must lie in span  k=2, ..., K. Consequently this implies that x1opt ∈ (q1, ..., qK-1). From this property of x1opt, it may be seen that when x1[0]=0, (44) can be simplified to
k=2, ..., K. Consequently this implies that x1opt ∈ (q1, ..., qK-1). From this property of x1opt, it may be seen that when x1[0]=0, (44) can be simplified to
 | (45) |
where is clear that only the K-1 largest eigenvalues of Ruu affect the transient behavior of the algorithm when the adaptive component is initialized in x1[0]=0.
C. Probability of Error
To analyze the bit error-rate of the blind adaptive receiver P1b(σ), we can consider K-users case. In first place we treat the channel coefficient as a constant value (block fading) to derive a first expression. Then, the result is averaged over the pdf of the adjusted channel gain.
The probability of error is
 | (46) |
with
 | (47) |
where  belong to a set of 2(K-1) vectors that contains all the data combination of the interferent users.
belong to a set of 2(K-1) vectors that contains all the data combination of the interferent users.
With focus on one term of the (47) and taking into account that if b1=-1 in (16), the filter output is
 | (48) |
where m1 is another zero-mean circularly symmetric complex Gausssian random variable and
 |
Considering (48), one term of (47) is given by
 | (49) |
Proceeding in similar way with the other terms of (47) and replacing in (46), we have P1(σ) in (50). Then we must take expectation value over the pdf of h11 and h1k in order to get P1b(σ).
In (50) the phase term  just affect the phase distribution of the random variable h1k inside of the Q(.) function, which statistic is uniform over [0, 2π], so can be dropped. The expression of P1b(σ) can be re-written as in (51) where the expectation value is taken over each h1k.
just affect the phase distribution of the random variable h1k inside of the Q(.) function, which statistic is uniform over [0, 2π], so can be dropped. The expression of P1b(σ) can be re-written as in (51) where the expectation value is taken over each h1k.
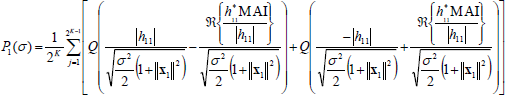 | (50) |
 | (51) |
IV. SCHEDULING SCHEMES
From (51) we can observe that error probability depends of the two term of MAI. One of them is function of the blind adaptive algorithm and the other one depends directly of the beam weights. In order to minimize the interference level experienced by the receiver, the first idea is to schedule users with orthogonal beam weights Haikola et al. (2006). That is
 | (52) |
where only two users can be used because the number of transmit antennas defines the number of orthogonal users that can be served simultaneously. Equation (52) can be interpreted in a different way, noting that the two scheduled users should be collinear and opposite in phase at the receiver
Another scheduling strategy follows from the observation that the impact of interference on the performance of blind adaptive receivers is through the real term of the argument of Q(.) function. Due to the fact that the blind adaptive algorithm decodes the desired user in a direction orthogonal to interference and noise, we can project some part of the interference in a subspace orthogonal to the desired data by selecting users with proper beamforming weights that result in a π/2 relative rotation. In the case of K=2 the scheduler selects two user that report orthogonal beam weights, in the same fashion as Scheduler A, but instead of prefiltering the transmit signal with those reported weights, one weight is rotated by π/2 before used it in the prefiltering matrix. That is, if w´1 and w2 are the orthogonal weights reported by the scheduled users, then a rotation is applied to w´1. That is
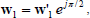 | (53) |
and then prefiltering with w1 and w2 is used at BS. The condition imposed by (53) doesn't change the correlation between the beam weights and the purpose of beamforming, which is the energy maximization at the receiver side of each user. In the case of an even number of users, K≥2, the BS can schedule 2N users distributed in N groups of two users with orthogonal beam weights, where N represents the total set number of spreading code available. The received signal in the time interval or user one can be written as
 | (54) |
with  The condition imposed by (53) minimizes the interference caused by user 2 because its real component is almost cancelled.
The condition imposed by (53) minimizes the interference caused by user 2 because its real component is almost cancelled.
V. SIMULATION RESULT
In this section we investigate the system performance under scheduling schemes (52) and (53), using two type of detection: matched filtering and adaptive blind interference cancelation. Three scenarios are considered: one with two users with different signature codes, other with twelve users with six signature sequence (code-reuse), and the other one similar to the previous scenery except that a pair of them, the ones whose performance is analyzed, does not share the same signature code. A Gold sequence of length 7 and quantized weights for HSDPA mode 1 are used for all the cases 3GPP (2006).
Figure 4 shows that signature code-reuse lead to a full performance degradation for both detection schemes when scheduling (52) is used. This behavior can be explained taking into account that both interference and desired signals are collinear with this scheduling strategy. In this case, the use of different signature sequences is essential to recover performance degradation. For comparison, the two user scenary are plotted in the figure in order to evaluate the performance degradation with higher multiuser interference.

Figure 4: Blind Adaptive Receiver performance with Scheduler A. Cross-correlation of the Gold spreading code is -0.1429
Figure 5 shows the performance of the adaptive blind receiver in the same three scenarios, mentioned earlier, but now the scheduling scheme uses π/2 rotation. In the 10 interference users scenario, a performance improvement of about 3 dB in the high SNR zone can be achieved with Scheduler B. This scheduler enable the code-reuse. It is easy to note that in the case of 12 users the BER of the blind adaptive schemes is almost the same as that of the blind scheme with Scheduler A and different signature codes. On the other hand, the matched filter does not show any performances change due to the particular interference treatment given by Scheduler B.

Figure 5: Blind Adaptive Receiver performance with Scheduler B.
The different behavior of the ABR is due to fact that Scheduler A force data user 1 and user 2 to travel collinear and with opposite phase, so the ABR algorithm cannot separate efficiently the users because they are collinear. On the other hand, Scheduler B adjusts the data of the scheduled users to arrive with π/2 rotation, so the ABR algorithm can work properly.
VI. CONCLUSIONS
We have studied the performance of the adaptive blind MOE receiver in a 2x1 MIMO scenario with practical MS schemes for taking advantage of multiuser diversity in a multiple antenna broadcasting channel with limited feedback.
A new scheduling scheme that tried to reduce interference while keeping the not cancelled interference in a subspace orthogonal to the desired signal at the receiver is proposed in this paper for closed loop MIMO system. The combination of the proposed scheduler with an adaptive blind receiver enables code reuse making possible to achieve higher spectrum efficiency with low complexity receivers. The proposed scheduler is analyzed for the practical case when the amount of feedback channel is compatible with mode 1 of the HSDPA technology.
REFERENCES
1. 3GPP, physical layer procedures(fdd), 3gpp technical speciffication ts 25.214 ver. 7.3 (2006 ). [ Links ]
2. Caire, G. and S. Shamai, "On the achievable throughput of a multiantenna gaussian broadcast channel," IEEE Trans. Information theory, 49, 1691-1706 (2003). [ Links ]
3. Corral-Briones, G., A.A. Dowhuszko, J. Hamalainen and R. Wichman, "Achievable data rates for two transmit antenna broadcast channels with WCDMA HSDPA feedback information," IEEE Int. Conf. on Communications, 2722-2727 (2005). [ Links ]
4. Dowhuszko, A.A., G. Corral-Briones, J. Hamalainen and R. Wichman, "Achievable sum-rate analysis of practical multiuser scheduling schemes with limited feedback," IEEE Int. Conf. on Communications, 4381-4386 (2007). [ Links ]
5. Farhang-Boroujeny, B., Adaptive filters: theory and applications. John Wiley & Sons, San Francisco U.S.A. (1999). [ Links ]
6. Gong, Y., T.J. Lim and B. Farhang-Boroujeny, "Performance analysis of the LMS blind minimum-output-energy CDMA detector," IEEE Int. Conf. Acoustics, speech, and signal processing (2000). [ Links ]
7. Gong, Y., B. Farhang-Boroujeny and T.J. Lim, "Variable step-size LMS blind CDMA multiuser detector," IEEE Int. Conf. Acoustics, speech, and signal processing (2001). [ Links ]
8. Haikola, V., M. Lampinen and V.M. Kuusela, "Practical multiuser beamforming in WCDMA," Vehicular technology conference (2006). [ Links ]
9. Honig, M., U. Madhow and S. Verdu, "Blind adaptive multiuser detection," IEEE Trans. Information theory, 41, 944-960 (1995). [ Links ]
10. Hottinen, A., O. Tirkkonen and R. Wichman, Multi-antenna transceiver techniques for 3G and beyond, John Wiley & Sons, West Sussex, England (2003). [ Links ]
11. Love, D.J., R.W, Heath, V.K.N. Lau, D. Gesbert, B.D. Rao and M. Andrews, "An overview of limited feedback in wireless communication systems," IEEE Trans. on Selected areas in communications, 26, 1341-1365 (2008). [ Links ]
12. Lupas, R. and S. Verdu, "Near-far resistance of multiuser detectors in asynchronous channels," IEEE Trans. Communications, 38, 496-508 (1990). [ Links ]
13. Mehlfuhrer, C., M. Wrulich and M. Rupp, "Intra-cell interference aware equalization for TXAA HSDPA," 3rd international symposium on wireless pervasive computing, 406-409 (2008). [ Links ]
14. Shenoy, S.P., I. Ghauri and D.T.M. Slock, "Multiuser extensions for closed loop transmit diversity in HSDPA," IEEE Int. Conf. on Communications (2009). [ Links ]
15. Simon, H., Adaptive filter theory, Prentice-Hall inc., New Jersey (1996). [ Links ]
16. Verdu, S., Multiuser detection, Cambridge Univ. Pr., Cambridge (1998). [ Links ]
17. Wrulich, M., C. Mehlfuhrer and M. Rupp, "Interference aware MMSE equalization for MIMO TXAA," Int. conf. communications, control and signal processing, 1585-1589 (2008). [ Links ]
18. Yoo, T., N. Jindal and A. Goldsmith, "Multi-antenna downlink channels with limited feedback and user selectionm," IEEE Trans. on Selected areas in communications, 25, 1478-1491 (2007). [ Links ]
Received: May 8, 2012
Accepted: October 20, 2012
Recommended by Subject Editor: Gastón Schlotthauer, Marí Eugenia Torres and José Luis Figueroa.














