MHD free convection and mass transfer flow past an accelerated vertical plate with chemical reaction in presence of radiation

D. Sarma^†, N. Ahmed^‡ and   H. Deka^†

^† Department of Mathematics, Cotton College, Guwahati – 781001, Assam, India E
Email: dipaksarma11@yahoo.com, dekahiren@yahoo.com
^‡ Department of Mathematics, Gauhati University, Guwahati – 781014, Assam, India
Email: saheel_nazib@yahoo.com

Abstract — This paper deals with the study of the thermal radiation and chemical reaction effects on an unsteady MHD free convective mass transfer flow past an accelerated infinite vertical plate embedded in a porous medium. The Rosseland approximation is used to describe the radiative heat flux in the energy equation. The dimensionless governing equations of motion are solved by using Laplace transform technique in closed form. Expressions for the velocity, temperature and concentration are obtained. The resulting velocity and temperature profiles as well as the skin-friction, rate of heat and mass transfer are shown graphically for different values of  the physical parameters viz., Grashof number, Prandtl number, Schmidt number, Chemical reaction parameter, Radiation parameter,  Magnetic parameter and Porosity parameter.

Keywords — MHD; Thermal Radiation; Chemical Reaction; and Electrically Conducting Fluid.

I. INTRODUCTION

Magnetohydrodynamic flows find its applications in meteorology, solar physics, cosmic fluid dynamics, astrophysics, geophysics and in the motion of earth's core. MHD free convection flows have also significant applications in the field of stellar and planetary magnetospheres, aeronautical plasma flows, chemical engineering and electronics. The principle of MHD is also utilized in stabilizing a flow against the transition from laminar to turbulent flow and in reduction of turbulent drag and suppression of flow separation. The application of MHD principle in medicine and biology are of paramount interest owing to their significance in bio-medical engineering in general and in the treatment of various pathological states in particular. The biomedical engineering includes cardiac MRI, ECG etc. Raptis and Soundalgekar (1984), Agrawal et al. (1989) and Soundalgekar et al. (1995) have paid attention to the study of MHD free convection and mass transfer flows. Chaudhary and Jain (2008) presented an analytical study of magnetohydrodynamic transient convection flow past a vertical surface embedded in a porous medium with an oscillating temperature. Chemical reactions usually accompany a large amount of exothermic and endothermic reactions. These characteristic can be easily seen in a lot of industrial processes. It has been realized that it is not always permissible to neglect the convection effects in porous constructed chemical reactors. A large amount of research work has been reported in this field. Particularly, the study of heat and mass transfer with chemical reactions is of considerable importance in the free convection flows (Rubin and Atkinson, 2001; Middleman, 1998). It is known that buoyancy induced flow within fluid-saturated porous media is encountered in a wide range of thermal engineering applications such as in geothermal systems, oil extraction, ground water pollution, heat exchangers, storage of nuclear wastes, packed bed catalytic reactors, atmospheric and oceanic circulation. Comprehensive discussions and reviews are found in literature (Niel and Bejan, 1992; Cheng, 1985; Cheng and Minkowycz, 1977; Ghoshdastidar, 2004). Radiation is a process of heat transfer through electromagnetic waves. Radiative convective flows are encountered in countless industrial and environment process viz., heating and cooling chambers, fossil fuel combustion energy processes, evaporation from large open water reservoirs, astrophysical flows and solar power technology and space vehicle re-entry. Radiative heat and mass transfer play an important role in manufacturing industries for the design of reliable equipment. Nuclear power plants, gas turbines and various propulsion devices for aircraft, missiles, satellites and space vehicles are examples of such engineering applications. If the temperature of the surrounding fluid is rather high, radiation effects play an important role in space related technology. Hossain and Takhar (1996) analyzed the effect of radiation using the Rosseland diffusion approximation which leads to non-similar solutions for the forced and free convection flow of an optically dense fluid from vertical surfaces with constant free stream velocity and surface temperature. Hossain et al. (1999) studied the effect of radiation on free convection heat transfer from a porous vertical plate. Raptis et al. (2004) presented the effect of thermal radiation on MHD flow. In recent years, Kandasamy and Prabhu (2005) studied the heat and mass transfer under a chemical reaction with a heat source. The effect of thermal radiation on a three dimensional free convective flow with mass transfer past a porous vertical plate has been recently studied by Sarma and Deka (2012). Tak et al. (2010) presented MHD mixed convection boundary layer flow with double diffusion and thermal radiation adjacent to a vertical permeable surface embedded in porous medium.

The study of flow for an electrically conducting fluid has many applications in engineering problems such as magnetohydrodynamics (MHD) generators plasma studies, nuclear reactors, geothermal energy extraction, and the boundary layer control in the field of aerodynamics (Branover, 1985). An excellent summary of applications is given by Huges and Young (1966). Raptis (1986) studied mathematically the case of time varying two dimensional natural convective flow of an incompressible, electrically conducting fluid along an infinite vertical porous plate embedded in a porous medium. Ahmed and Sarmah (2009) studied a transient radiative MHD free and forced convection flow with mass transfer past an impulsively fixed infinite vertical plate. Ahmed and Sengupta (2011) presented an analytical solution to the problem of a three dimensional MHD mixed convection flow past an infinite vertical porous plate with thermal radiation (Rosseland model) taking into account the effects of thermo-diffusion and diffusion-thermo. Uddin and Kumar (2011) studied the effect of MHD heat and mass transfer free convection flow near the lower stagnation point of an isothermal cylinder imbedded in porous domain with the presence of radiation. Vasu et al. (2011) studied the radiation and mass transfer effects on transient free convection flow a dissipative fluid past semi-infinite vertical plate with uniform heat and mass flux. Vyas and Srivastava (2010) investigated the problem of Radiative MHD flow over a non-isothermal stretching sheet in porous medium. Recently, Ahmed et al. (2012) have studied the problem of MHD convective mass transfer flow of an electrically conducting incompressible viscous past an infinite vertical porous plate with constant heat and chemical reaction in presence of a heat source. Very recently, Reddy (2012) has investigated magnetohydrodynamics and radiation effects on unsteady convection flow of micropolar fluid past a vertical porous plate with variable wall heat flux.

The object of the present work is to investigate the thermal radiation and chemical reaction effects on an unsteady MHD free convective mass transfer flow past an accelerated infinite vertical plate embedded in a porous medium. This work is an extension of the problem studied by Jha and Sharma (2011) to the case when there is an imposed thermal radiation.

II. GOVERNING EQUATIONS

We consider a one dimensional flow of an MHD incompressible viscous and electrically conducting fluid with radiation along an infinite vertical plate embedded in porous medium. The -axis is taken along the infinite plate and - axis perpendicular to it. Initially, at all points the plate and the fluid are at same temperature  with concentration level . When time > 0, the temperature and concentration level at the plate are raised to 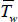 and  respectively. A magnetic field of uniform strength is applied perpendicular to the plate. Assume that the plate is accelerating with a velocity  in its own plane at time > 0. Under these conditions and Boussinesq's approximation, the governing equations of the problem are

Momentum equation:

(1)

Energy equation:

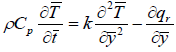(2)

Species continuity equation

(3)

where B₀ is the magnetic induction /strength of applied field, υ is the kinematic viscosity, σ is the electrical conductivity, β is the coefficient of volume expansion for heat transfer, U is the acceleration of the plate, β^* is the coefficient of volume expansion for mass transfer, D is the coefficient of chemical molecular diffusivity, C_p is the specific heat at constant pressure,  is the species concentration,  is the species concentration in the free stream, K^* is the permeability of porous medium, is the rate of first order chemical reaction, k is the thermal conductivity, q_r is the radiative heat flux along y-direction .

The relevant initial and boundary conditions are

	(4)
	(5)

The radiative heat flux q_r under Rosseland approximation by Brewster (1992) has the form

(6)

where σ₁ is the Stefan –Boltzmann constant and k₁ is the mean absorption coefficient.

We assume that the temperature differences within the flow are sufficiently small so that can be expressed as a linear function. By using Taylor's, we expand about the free stream temperature  and neglecting higher order terms. This result of the following approximation:

(7)

Using equations (6) and (7), we have

(8)

Then (2) becomes

(9)

III.  MATHEMATICAL FORMULATIONS

We introduce the following non-dimensional quantities

where Gr is the Grashof number for heat transfer, Gc is the Grashof number for mass transfer, N is the radiation parameter, M is the Hartmann number α is the porosity parameter and

Using non-dimensional quantities in the Eqs. (1), (9) and (3), we get

	(10)
	(11)
	(12)

The relevant initial and boundary conditions are

	(13)
	(14)

Taking Laplace transform on both sides of (10), (11) and (12) subject to the relevant initial and boundary conditions (13) and (14), we get

	(15)
	(16)
	(17)

where s is the Laplace parameter.

The analytic solutions of (10), (11) and (12) can be obtained by taking the inverse Laplace transforms of (15), (16) and (17) subject to the relevant initial and boundary conditions (13) and (14). So, the solutions of the problem for the velocity u, temperature  and concentration C for t> 0 are as follows:

	(18)
	(19)
	(20)

Skin Friction

The skin friction co-efficient at the plate is given by

(21)

Heat Transfer Coefficient  

The rate of heat transfer in terms of Nusselt number at the plate is given by

(22)

Mass Transfer Coefficient

The rate of mass transfer in terms Sherwood number at the plate is given by

(23)

IV. RESULTS AND DISCUSSION

In order to get physical insight into the problem, the numerical calculations are carried out for the velocity field, temperature field, skin friction, rate of heat and mass transfer by assigning some selected values to the parameters involved in the problem. These numerical results have been displayed in figures. In most of the cases of our investigation, the values of the parameter Pr is chosen to be 0.71 which corresponds to air at 25⁰C and Sc is considered to be 0.60 which represents water vapor diffused in air. The thermal Grashof number Gr is taken to be 4,5,6 [externally cool], the values of the radiation parameter N are considered positive for considering  radiation not absorption and the other parameters are arbitrarily positive.

Figures 1, 2 and 3 represent the temperature profiles against y for different values of time t, radiation parameter N and Prandtl number Pr, respectively. In all three figures, the magnitude of temperature is maximum at the plate and then tends to zero asymptotically as y → ∞. It is marked in Fig. 1 that the temperature profile increases with the increasing time t. Figure 2 represents the temperature profile for different values of radiation parameter N. It is observed from this figure that the radiation parameter decreases the temperature distribution. That is, the thickness of the thermal boundary layer decreases. The temperature profile under the effect of Prandtl number is given in Fig. 3 which shows that, increasing values of Prandtl number implies the decrease in temperature profile. This leads to decrease the thermal boundary layer thickness.

Fig.1. Temperature profile   against y for different values of t with Pr=0.71, N=3.

Fig. 2. Temperature profile q  against y for different values of N with Pr=0.71, t=1.

Fig. 3. Temperature profile q  against y for different values of Pr with N=3, t=1.

Figures 4, 5, 6 and 7 display velocity profile versus y for different values of thermal Grashof number Gr, porosity parameter α, solutal Grashof number Gc and time t. From these figures, it is observed that velocity increases sharply and attains its maximum value near the plate at y=1 and then leads to zero as y → ∞. Figure 4 depicts that velocity increases owing to an increase in the value of Gr. The thermal Grashof number Gr signifies the relative effects of the thermal buoyancy force to the viscous hydrodynamic force in the boundary layer. As expected, it is observed that there is a rise in the velocity due to the enhancement of thermal buoyancy force. Here, the positive values of Gr correspond to cooling of the plate. Figure 5 shows that the velocity decreases with the decreasing α. Thus, the presence of a porous medium increases the resistance to flow which results in decrease in the flow velocity. From Fig. 6, it is observed that an increase in Gc leads to rise in the velocity. This means that an increase in the value of Gc has a tendency to increase the mass buoyancy effect. That is, mass buoyancy force accelerates flow. From Fig. 7, it is seen that velocity increases with the increase of time t.

Fig. 4. Velocity profile u against y for different values of Gr with Pr=0.71, N=3, M=1, α=1, Sc=0.6, K=1, Gc =4, t=1.

Fig. 5. Velocity profile u against y for different values of α with Pr=0.71, N=3, M=1, Sc=0.6, K=1, Gr=4, Gc=4, t=1.

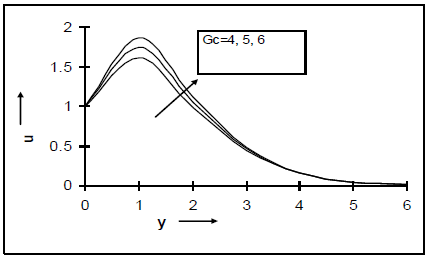
Fig. 6. Velocity profile u against y for different values of Gc with Pr=0.71, N=3, M=1, α=1, Sc=0.6, K=1, Gr=4, t=1.

Fig. 7. Velocity profile u against y for different values of t with Pr=0.71, N=3, M=1, α=1, Sc=0.6, K=1, Gr=4, Gc=4.

Figures 8, 9, 10, 11 and 12 exhibit the effects of radiation parameter N, magnetic parameter M, rate of  chemical reaction parameter K, Schmidt number Sc and Prandtl number Pr on velocity profile against y, respectively. From all these figures, it is seen that the maximum velocity attains in the vicinity of the plate and then decreases to zero as y → ∞.

Fig. 8. Velocity profile u against y for different values of N with Pr=0.71, M=1, α=1, Sc=0.6, K=1, Gr=4, Gc=4, t=1.

Fig. 9. Velocity profile u against y for different values of M with Pr=0.71, N=3, α=1, Sc=0.6, K=1, Gr=4, Gc=4, t=1.

Fig. 10.  Velocity profile u against y for different values of K with Pr=0.71, N=3, M=1, α=1, Sc=0.6, Gr=4, Gc=4, t=1.

Fig. 11.  Velocity profile u against y for different values of Sc with Pr=0.71, N=3, M=1, α=1, K=1, Gr=4, Gc=4, t=1.

Fig. 12. Velocity profile u against y for different values of Pr with N=3, M=1, α=1, Sc=0.6, K=1,Gr=4,Gc=4, t=1.

Figure 8 illustrates the effect of radiation parameter on the velocity and it is seen that there is a decrease in the velocity with the increase in radiation parameter. An increase in N leads to a decrease in the boundary layer thickness and to enhance the heat transfer rate in the presence of thermal buoyancy force. In Fig. 9, we notice that an increase in M causes the velocity to fall. It is because that the application of transverse magnetic field will result a resistive type force (Lorentz's force), similar to drag force. The velocity decreases owing to an increase in the value of rate of chemical reaction parameter K as shown in Fig. 10. Figure 11 portrays the effect of Schmidt number Sc on the velocity which shows that as the Schmidt number increases, the velocity decreases. It is well supported from physical reality because Schmidt number increases means mass diffusion decreases and mass diffusivity generally increases fluid velocity. Physically, fluids with higher Prandtl number have high viscosity and hence move slowly. This behaviour is evident from Fig. 12 as expected.  

Variations of skin friction (viscous drag) against M for various values of N, t, Pr, K, Sc, Gr, Gc and α are plotted through Figs. 13 to 20. From Figs. 13 to 17, it is observed that the magnitude of skin friction is decreased by N, t, Pr, K and Sc up to certain values of M and then increases. Figures 18, 19 and 20 show that the viscous drag is increased by thermal buoyancy force, mass buoyancy force and porosity parameter up to certain values of Hartmann number M and then decreases.

Fig. 13.  Skin friction t against M for different values of N with Pr=0.71, α=1, Sc=0.6, K=1, Gr=4, Gc=4, t=1.

Fig.14- Skin friction t against M for different values of t with Pr=0.71, N=3, α=1, Sc=0.6, K=1, Gr=4, Gc=4.

Fig. 15. Skin friction t against M for different values of Pr with N=3, α=1, Sc=0.6, K=1, Gr=4, Gc=4, t=1.

Fig. 16. Skin friction t  against M for different values of K with N=3, α=1, Sc=0.6, Pr=0.71, Gr=4,Gc=4, t=1.

Fig. 17.  Skin friction t  against M for different values of Sc with N=3, α=1, K=1, Pr=0.71, Gr=4, Gc=4, t=1.

Fig. 18.  Skin friction t against M for different values of Gr with N=3, α=1, Sc=0.6, K=1, Pr=0.71, Gc=4, t=1.

Fig. 19.  Skin friction t against M for different values of Gc with N=3, α=1, Sc=0.6, K=1, Pr=0.71, Gr=4, t=1.

Fig. 20.  Skin friction t against M for different values of α with N=3, Sc=0.6, K=1, Pr=0.71, Gr=4, Gc=4, t=1.

Figures 21 and 22 deal with the effects of rate of chemical reaction parameter K and Schmidt number Sc over the Sherwood number (rate of mass transfer) Sh. From these figures, it is clear that the rate at which the mass gets transferred is increased by Sc and K.

Fig. 21.  Sherwood number Sh at the plate y=0 against t for different values of K with Sc=0.6.

Fig. 22.  Sherwood number Sh at the plate y=0 against t for different values of Sc with K=1.

Figures 23 and 24 exhibit how the Nusselt number (rate of heat transfer) is affected under radiation parameter N and Prandtl number Pr, respectively. Figure 23 depicts that the rate of heat transfer increases with the increasing values of radiation parameter. Figure 24 shows that the Nusselt number increases with the increasing values of Prandtl number.

Fig. 23.  Nusselt number Nu at the plate y=0 against t for different values of N with Pr=0.71.

Fig. 24.  Nusselt number Nu at the plate y=0 against t for different values of Pr with N=3.

V. CONCLUSIONS

1. The radiation parameter N decreases the temperature distribution in the thermal boundary layer.

2. The presence of a porous medium retards the fluid motion and it is in an excellent agreement with the physical reality.

3. The increase in radiation parameter N leads to decrease the boundary layer thickness and to enhance the heat transfer rate in the presence of thermal buoyancy force.

4. An increase in value of magnetic parameter M leads to fall in the velocity which is consistent with the law of Physics.

5. The rate at which the mass gets transfered is increased by Schmidt number Sc and rate of chemical reaction parameter K.

6. The rate of heat transfer from the plate to the fluid gets increased due to radiation effect.

APPENDIX

REFERENCES
1. Agrawal, A.K., B. Kishor, and A. Raptis, "Effects of MHD free convection and mass transfer on the flow past a vibrating infinite vertical cylinder," Warme und Stoffubertragung, 24,243-250 (1989).         [ Links ]
2. Ahmed, N., D. Sarma and H. Deka, "MHD convective mass transfer flow of an electrically conducting incompressible viscous past an infinite vertical porous plate with constant heat and chemical reaction in presence of a heat source," Appl. Math. Sci., 6, 1011-1020 (2012).         [ Links ]
3. Ahmed, N. and H.K. Sarmah, "A transient radiative MHD free and forced convection flow with mass transfer past an impulsively fixed infinite vertical plate," Int. J. of Appl. Math. and Mech., 5, 87-98 (2009).         [ Links ]
4. Ahmed, N. and S. Sengupta, "Thermo-Diffusion and Diffusion- Thermo effects on a three dimensional MHD convection flow past an infinite vertical porous plate with thermal radiation," Megnetohydrodynamics, 47, 41-60 (2011).         [ Links ]
5. Branover, H., Magnetohydrodyamic Flow in Ducts, John Wiley and Sons Ltd. (1985).         [ Links ]
6. Brewster, Q., Thermal Radiative Transfer and Properties, John Wiley and Sons. Inc., New York (1992).         [ Links ]
7. Cheng, P., NATO Advanced Study in Natural Convection, Izmir, Turkey (1985).         [ Links ]
8. Cheng, P. and W.J. Minkowycz, "Free convection about a vertical flat plate embedded in a porous medium with application to heat transfer from a dike," J. Geophys. Res., 82, 2040–2044 (1977).         [ Links ]
9. Chaudhary, R.C. and A. Jain, "Magnetohydrodynamic Transient Convection Flow past a Vertical Surface Embedded in a Porous Medium with Oscillating Temperature," Turkish J. Eng. Env. Sci., 32, 13–22 (2008).         [ Links ]
10. Ghoshdastidar, P.S., Heat Transfer, Oxford University Press, UK (2004).         [ Links ]
11. Hossain, M.A. and H.S. Takhar, "Radiation effects on mixed convection along a vertical plate with uniform surface temperature," Heat Mass Transfer, 31, 243–248 (1996).         [ Links ]
12. Hossain, M.A., M.A. Alim and R. Das, "The effect of radiation on free convection from a porous vertical plate," Int. J. Heat Mass Transfer, 42, 181–191(1999).         [ Links ]
13. Huges, W.F. and F.J. Young, The Electro-Magneto Dynamics of fluids, John Wiley and sons, New York, (1966).         [ Links ]
14. Jha, A.K. and R. Sharma, "Mass transfer with chemical reaction effects on MHD free convective flow past an accelerated vertical plate," Int. Conf. on Fluid Dynamics and its applications, 648-655 (2011).         [ Links ]
15. Kandasamy, R.K.P. and K.K.S. Prabhu, "Chemical reaction, heat and mass transfer on MHD flow over a vertical stretching surface with heat source and thermal stratification effects," Int. J. of Heat and Mass Transfer, 48, 4557-4561 (2005).         [ Links ]
16. Middleman, S., An Introduction to Mass and Heat Transfer, John Wiley & Sons, Inc. (1998).         [ Links ]
17. Nield, D.A. and A. Bejan, Convection in Porous Media, Springer, Berlin (1992).         [ Links ]
18. Raptis, A. and V.M. Soundalgekar, "MHD Flow past a Steadily Moving Infinite Vertical Plate with Mass Transfer and Constant Heat Flux," ZAMM, 64, 127–130 (1984).         [ Links ]
19. Raptis, A., A.C. Perdikis and H.S. Takhar, "Effect of thermal radiation on MHD flow," Appl. Math. and Comp., 153, 645-649 (2004).         [ Links ]
20. Raptis, A., "Flow through a porous medium in the presence of magnetic field," Int. J. Energy Res., 10, 97-101 (1986).         [ Links ]
21. Reddy, G.M., "Magnetohydrodynamics and radiation effects on unsteady convection flow of micropolar fluid past a vertical porous plate with variable wall heat flux," Int. S. Res. Network ISRN Thermodynamics, ID 146263, 1-8 (2012).         [ Links ]
22. Rubin, H. and J. Atkinson, Environmental Fluid Mechanics, Marcel Dekker, Inc, New York (2001).         [ Links ]
23. Sarma, D. and H. Deka, "Effect of thermal radiation on a three dimensional free convective flow with mass transfer past a porous vertical plate," Int. J. of Math. Sci. & Engg. Appls, 6, 135-151 (2012).         [ Links ]
24. Soundalgekar, V.M., S.N. Ray and U.N. Das, "MHD flow past an infinite vertical oscillating plate with mass transfer and constant heat flux," Proc. Math. Soc., 11, 95-98 (1995).         [ Links ]
25. Tak, S.S., A. Khan and R. Mathur, "MHD mixed convection boundary layer flow with double diffusion and thermal radiation adjacent to a vertical permeable surface embedded in porous medium," African J. of Math. Phy., 8, 67-77 (2010).         [ Links ]
26. Uddin, Z. and M. Kumar, "MHD heat and mass transfer free convection flow near the lower stagnation point of an isothermal cylinder imbedded  in porous domain with the presence of radiation," Jordan J. of Mech. and Industrial Engg., 5, 419-423 (2011).         [ Links ]
27. Vasu, B., V.R. Prasad and B.N. Reddy, "Radiation and mass transfer effects on transient free convection flow a dissipative fluid  past semi-infinite vertical plate with uniform heat and mass flux," J. of Appl. Fluid Mechanics, 4, 15-26 (2011).         [ Links ]
28. Vyas, P. and N. Srivastava, "Radiative MHD flow over a non-isothermal stretching sheet in porous medium," Appl. Mathematical Sciences, 4, 2475-2484 (2010).         [ Links ]

Received: August 22, 2012
Accepted: April 1, 2013
Recommended by Subject Editor: Walter Ambrosini