Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Latin American applied research
Print version ISSN 0327-0793On-line version ISSN 1851-8796
Lat. Am. appl. res. vol.44 no.1 Bahía Blanca Jan. 2014
Magnetohydrodynamic heat and mass transfer flow with induced magnetic filed and viscous dissipative effects
S. Ahmed† and A. Batin‡
† Fluid Dynamics Research, Department of Mathematics, Goalpara College, Goalpara 783101, Assam, India. heat_mass@yahoo.in
‡ Department of Mathematics, Indira Gandhi College, Boitamari, Bongaigaon 783389, Assam, India. abdulbatin@yahoo.in
Abstract — An approximate solution to the problem of steady free convective MHD flow of an incompressible viscous electrically-conducting fluid over an infinite vertical isothermal porous plate with mass convection is presented here. A uniform magnetic field is assumed to be applied transversely to the direction of the flow, taking into account the induced magnetic field with viscous and magnetic dissipations of energy. The dimensionless governing equations are solved by using the series solution method. The induced magnetic field, current density, temperature gradient and flow velocity are studied for magnetohydrodynamic body force, magnetic Prandtl number, Schmidt number and Eckert number. It is observed that the induced magnetic field is found to increase with a rise in magnetic Prandtl number. Current density is strongly reduced with increasing magnetic Prandtl number, but enhanced with Schmidt number. The acquired knowledge in our study can be used by designers to control MHD flow as suitable for a certain applications such as laminar magneto-aerodynamics, and MHD propulsion thermo-fluid dynamics.
Keywords — Newtonian Fluid; Thermo-Fluid Dynamics; Heat Transfer Control; MHD Energy Generators; Viscous and Magnetic Dissipative Heat.
I. INTRODUCTION
The study of magneto-hydrodynamic flow for an electrically conducting fluid past a porous vertical surface has attracted the interest of many researchers in view of its important applications in many engineering problems such as plasma studies, petroleum industries, MHD power generators, cooling of nuclear reactors, the boundary layer control in aerodynamics, and crystal growth. In all these applications understanding the behaviour of MHD convective flow and the various problem parameters that influence is a very important asset to designers developing applications that aim to control this flow. In view of these applications, several investigators have made model studies on the effect of magnetic field free convection flows. Some of them are Georgantopoulos (1979), Nanousis et al. (1980) and Raptis and Singh (1983). Along with the effects of magnetic field as well as transpiration parameter, being an effective method of controlling the boundary layer has been considered by Kafoussias et al. (1979). Raptis and Soundalgekar (1984) investigated the steady laminar free convection flow of an electrically conducting fluid along a porous hot vertical plate in presence of heat source/sink. The combined heat and mass transfer of an electrically conducting fluid in MHD natural convection adjacent to a vertical surface was analyzed by Chen (2004). The study of heat and mass transfer on the free convective oscillatory flow of a viscous incompressible fluid past an infinite vertical porous plate in presence of transverse sinusoidal suction velocity and a constant free stream velocity was presented by Ahmed (2009). Seddeek (2004) investigated the effects of heat source in the presence of suction and blowing on mixed free-forced convective flow and mass transfer over an accelerating surface in the case of variable viscosity. Zueco et al. (2009) studied the problem of thermophoretic hydromagnetic dissipative heat and mass transfer by network simulation numerical technique. Steven et. al. (2012) studied the magnetic hydrodynamic free convective flow past an infinite vertical porous plate with the effect of viscous dissipation subject to a constant suction velocity.
The effects of external temperature-dependent sources on the unsteady free convective flows past an infinite vertical porous plate were presented by Pop and Soundalgekar (1979). Zueco Jordán (2006) presented a numerical analysis of an unsteady free convective MHD flow of a dissipative fluid along a vertical plate subject to a constant heat flux. Ahmed and Liu (2010) analyzed the effects of mixed convection and mass transfer of three-dimensional oscillatory flow of a viscous incompressible fluid past an infinite vertical porous plate in presence of transverse sinusoidal suction velocity oscillating with time and a constant free stream velocity. Chamkha and Camille (2000) investigated the effects of heat generation/absorption and thermophoresis on hydromagnetic flow with heat and mass transfer over a flat surface. Free convection flow past a vertical plate with surface temperature oscillations was considered by Li et al. (1982). Ahmed (2010) investigated the effect of periodic heat transfer on unsteady MHD mixed convection flow past a vertical porous flat plate with constant suction and heat sink when the free stream velocity oscillates in about a non-zero constant mean. Chamkha (2003) investigated the chemical reaction effects on heat and mass transfer laminar boundary layer flow in presence of heat generation/absorption. The effect of the local acceleration term on the MHD transient free convection flow over a vertical plate was studied by Aldoss and Al-Nimir (2005). Muthucumaraswamy et al. (2001) studied the heat and mass transfer effects on flow past an impulsively started infinite vertical plate. Asghar et al. (2005) investigated the effects of Hall current and heat transfer on the steady flow of an electrically conducting, Oldroyd- B and incompressible fluid. The fluid is between two electrically insulating disks maintained at two constant but different temperatures. The flow is due to a pull with constant velocities of eccentric rotating infinite disks and an external uniform magnetic field is applied perpendicular to the disks. The magnetic Reynolds number is assumed small so that the induced magnetic field is neglected.
The above studies have generally been confined to very small magnetic Reynolds numbers, allowing magnetic induction effects to be neglected. Such effects must be considered for larger values of magnetic Reynolds number. Glauert (1962) presented a seminal analysis for hydromagnetic flat plate boundary layers along a magnetized plate with uniform magnetic field in the streamwise direction at the plate. He obtained series expansion solutions (for both large and small values of the electrical conductivity parameter) for the velocity and a magnetic field, indicating that for a critical value of applied magnetic field, boundary-layer separation arises. Dorrepaal and Moosavizadeh (1998) studied the oblique stagnation-point magnetohydrodynamic flow in the vicinity of a location where a separation vortex reattaches itself to a rigid boundary, obtaining a similarity solution for the velocity and induced magnetic field distributions near the point of reattachment. Raptis and Massalas (1998) investigated the effects of radiation on the oscillatory flow of a gray gas, absorbing-emitting in presence of induced magnetic field and analytical solutions were obtained with the help of perturbation technique. The hydrodynamic free convective flow of an optically thin gray gas in the presence of radiation, when the induced magnetic field is taken into account was studied by Raptis et al. (2003) using perturbation technique. More recently Bég et al. (2009) obtained local non-similarity numerical solutions for the velocity, temperature and induced magnetic field distributions in forced convection hydromagnetic boundary layers, over an extensive range of magnetic Prandtl numbers and Hartmann numbers. Bég et al. (2009) have also derived closed-form solutions for the velocity, temperature and magnetic induction functions in Rayleigh free convection hydromagnetic flow. Alom et al. (2008) investigated the steady MHD heat and mass transfer by mixed convection flow from a moving vertical porous plate with induced magnetic, thermal diffusion, constant heat and mass fluxes, and the non-linear coupled equations are solved by shooting iteration technique. Ahmed and Zueco (2010) studied the effect of the transverse magnetic field on a steady mixed convective heat and mass transfer flow of an incompressible viscous electrically conducting fluid past an infinite vertical isothermal porous plate taking into account the induced magnetic field, viscous and magnetic dissipations of energy in presence of chemical reaction of first order and heat generation/absorption, and the non-linear coupled equations are solved by network simulation technique. Ahmed and Chamkha (2010) investigated the effects of radiation and chemical reaction on steady mixed convective heat and mass transfer flow of an optically thin gray gas over an infinite vertical porous plate with constant suction taking into account the induced magnetic field, and viscous dissipation of energy, and the non-linear coupled equations are solved by series solution method. The steady magnetohydrodynamic (MHD) mixed convection stagnation point flow over a vertical flat plate is investigated by Ali et al. (2011). Ahmed et al. (2012) investigated the effect of the transverse magnetic field on a transient free and forced convective flow over an infinite vertical plate impulsively held fixed in free stream taking into account the induced magnetic field.
The present paper aims to study the problem of a steady magnetohydrodynamic free convective boundary layer flow over a porous vertical isothermal flat plate with constant suction where the effects of the induced magnetic field as well as viscous and magnetic dissipations of energy has been considered. The present study may have useful applications to several transport processes as well as magnetic materials processing. The analytical results for some particular cases are matched with Raptis et al. (2003) and found them in excellent agreement.
II. MATHEMATICAL ANALYSIS
The steady MHD mixed convective heat and mass transfer flow of an electrically conducting, viscous incompressible fluid over a porous vertical infinite isothermal plate with viscous dissipative heat and magnetic dissipation of energy has been considered (Fig. 1) by making the following assumptions:
- All the fluid properties except the density in the buoyancy force term are constant;
- The Eckert number Ec is small;
- The plate is subjected to a constant suction velocity;
- A magnetic field of uniform strength (H0) is applied transversely to the direction of the main stream taking into account the induced magnetic field;
- The magnetic Prandtl number is so chosen in comparison to the Hartmann number such that the induced magnetic is not negligible;
- The concentration of the diffusing species in the binary mixture is assumed to be very small in comparison with the other chemical species, which are present, and hence the Soret and Dufour effects are negligible;
- The equation of conservation of electric charge is ∇ · J=0 where J=(Jx,Jy,Yz). The direction of propagation is considered only along the y-axis and does not have any variation along the y-axis and so ∂Jy/∂y=0 which gives Jy=constant. Since the plate is electrically non-conducting, this constant is zero and hence Jy=0 everywhere in the flow;
- The wall is maintained at constant temperature
 and concentration
and concentration  higher than the ambient temperature
higher than the ambient temperature  and concentration
and concentration  respectively;
respectively; - The fluid is non-magnetic, neglecting the thermoelectric effect together with the short circuit condition.

Fig. 1: Physical configuration.
In case of electrically conducting fluid, the flow and heat transfer are induced by an imposed magnetic field. An e.m.f. is produced in the fluid flowing across the transverse magnetic field. The resultant effect of current and magnetic field produces a force, resisting the fluid motion. The fluid velocity also affects the magnetic field by producing an induced magnetic field which perturbs the original field.
We introduce a coordinate system  with
with  -axis vertically upwards along the plate,
-axis vertically upwards along the plate,  -axis normal to the plate into the fluid region and
-axis normal to the plate into the fluid region and  -axis along the width of the plate. Let the plate be long enough in
-axis along the width of the plate. Let the plate be long enough in  -direction for the flow to be parallel. Let
-direction for the flow to be parallel. Let  be the fluid velocity and
be the fluid velocity and  be the magnetic induction vector at a point
be the magnetic induction vector at a point  in the fluid. Since the plate is infinite in length in
in the fluid. Since the plate is infinite in length in  -direction, therefore all the physical quantities except possibly the pressure are assumed to be independent of
-direction, therefore all the physical quantities except possibly the pressure are assumed to be independent of  .
.
Within the frame of such assumptions and under the Boussinesq's approximation and in consistency with boundary layer theory, the governing equations relevant to the problem are:
 | (1) |
which is satisfied with  constant.
constant.
 | (2) |
which holds for 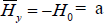 constant=strength from applied magnetic field.
constant=strength from applied magnetic field.
 | (3) |
 | (4) |
 | (5) |
 | (6) |
Since there is no large velocity gradient here, the viscous term in the Eq. (3) vanishes for small m and hence for the outer flow, beside there is no induced magnetic field along x-direction gradient, so we have
 | (7) |
By eliminating the pressure term from the Eqs. (3) and (7), we obtain
 | (8) |
The Boussinesq approximation gives
 | (9) |
On using (1) and (9) in the Eq. (8) and noting that ρ∞ is approximately equal to 1, the momentum equation reduces to
 | (10) |
The boundary conditions are:
 | (11) |
The non-dimensional quantities are:

The non-dimensional forms of (4) to (6) and (10) are
 | (12) |
 | (13) |
 | (14) |
 | (15) |
The corresponding boundary conditions are:
 | (16) |
III. METHOD OF SOLUTION
Perturbation theory leads to an expression for the desired solution in terms of a power series in some "small" parameter that quantifies the deviation from the exactly solvable problem. The leading term in this power series is the solution of the exactly solvable problem, while further terms describe the deviation in the solution, due to the deviation from the initial problem. Perturbation theory is applicable if the problem at hand can be formulated by adding a "small" term (Eckert number "Ec" in this work) to the mathematical description of the exactly solvable problem.
The solution of the Eq. (14) subject to the boundary condition (16) is
 | (17) |
Now, in order to solve the Eqs. (12), (13) and (15) under the boundary condition (16), we note that EC << 1 for all the incompressible fluids and it is assumed the solutions of the equations to be of the form
f(y) = f0(y) + Ec f1(y) + O(Ec2) (18)
where f stands for u, θ or Hx.
Substituting (18) into the Eqs. (12), (13) and (15) and equating the coefficients of the same degree terms and neglecting terms of O(Ec2), the following differential equations are obtained:
 | (19) |
 | (20) |
 | (21) |
 | (22) |
 | (23) |
 | (24) |
The boundary conditions (16) reduce to
 | (15) |
The solutions of the Eqs. (19) to (24) subject to the boundary conditions (25) are:
 | (26) |
 | (27) |
 | (28) |
 | (29) |
 | (30) |
 | (31) |
These analytical approximate solutions under perturbation technique give a wider applicability in understanding the basic physics and chemistry of the problem, which are particularly important in industrial and technological fields.
IV. RATE OF HEAT TRANSFER
The Nusselt number is often used to determine heat transfer. The non-dimensional heat flux at the plate y=0 in terms of Nusselt number Nu is given by
 | (32) |
where  and
and

V. CURRENT DENSITY
The non-dimensional current density at the plate y=0 is given by
 | (33) |
where

VI. VALIDATION
The method is validated by directly comparing its results with those of Raptis et al. (2003) without radiation, for Prm=3, M=4, Ec=0=Grm as shown in Table 1, where Prm=3>1 which implies that viscous diffusion rate is dominant over the magnetic diffusion rate. From Table 1, it is seen that the results for flow velocity are in excellent agreement. Therefore, this leads to confidence in the numerical results. In Table 1, it is observed that the flow velocity is accelerated when free convection parameter increases from 2.0 through 5.0 to 10.0.
Table 1: Comparison of values of the flow velocity (u) with those obtained by Raptis et al. (2003) for Prm=3, M=4, Ec=0=Grm:

VII. RESULTS AND DISCUSSION
In order to get physical insight into the problem, we have carried out the numerical calculations for the velocity field, induced magnetic field, temperature gradient and current density at the plate and the values are demonstrated in graphs and Tables. The Prandtl number Pr is taken for air (Pr=0.71) at 20oC, water (Pr=7.0) and water at 4oC (Pr=11.4). The thermal Grashof number Gr and the Eckert number (Ec) take positive values corresponds to cooling of the plate by free convection currents. Also the values of the Schmidt number (Sc), so chosen to represent the presence of various species Hydrogen (Sc=0.20), Helium (Sc=0.30), Steam (Sc=0.60) and Oxygen (Sc=0.66).
Figure 2 illustrates the response of induced magnetic field to Hartmann number and magnetic Prandtl number for conducting air (Pr = 0.71) and diffusing species helium (Sc = 0.30). Increase in Hartmann number clearly reduces the induced magnetic field magnitudes, whereas increasing in Prm boosts the values of Hx through the boundary layer when y>1. In this figure, Prm is set as greater than 1.0 and implies that the viscous diffusion rate exceeds the magnetic diffusion. In the vicinity of the plate, the values of Hx remains negative for all values of M and Prm, i.e., the induced magnetic flux reversal arises for y→0 into the boundary layer, and transverse to the plate. In all the cases, Hx peaks a short distance from the plate, and then decays to be zero in the free stream.

Fig. 2: Induced magnetic field distribution with Hartmann number and Magnetic Prandtl number
Figure 3 shows the distribution of current density at the plate for various magnetic Prandtl number and Schmidt number over Hartmann number. A rise in Prm from 4.0 through 5.0 to 6.0 serves to depress strongly current density magnitudes throughout the regime, but the current density rises with Schmidt number. These effects are very useful for small Hartmann numbers and insignificant in the free stream. It is also found that the current density has a large negative value throughout the flow field. Thus it is concluded that the magnetic Prandtl number or Schmidt number has a strong role on the current density.

Fig. 3: Current density distribution with Magnetic Prandtl number and Schmidt number.
In Fig. 4, the distribution of temperature gradient distribution (∂q/∂y) with Hartmann, magnetic Prandtl and Prandtl number, is presented for diffusing species helium. An increase in M, Prm and Pr leads to reduce sharply ∂q/∂y and these results are very much effective near the plate, but insignificant far away from the plate.

Fig. 4: Temperature gradient distribution with Hartmann, Magnetic Prandtl and Prandtl number.
In Fig. 5, the influence of Hartmann number and magnetic Prandtl number on the flow velocity distributions is shown for conducting air and diffusing species helium. With an increase in M from 0.5 through 1.0 to 3.0, there is clear decrease in flow velocity i.e. flow is strongly decelerated. It is evident that the presence of the transverse magnetic field produces a resistive force on the flow velocity. This force is called the Lorentz force acting on the flow velocity, which leads to slow down the motion of electrically conducting fluid. In no case however, there is a flow reversal i.e. velocity remains positive through the boundary layer. On the other hand, the flow velocity is accelerated when magnetic Prandtl number rises from 2.0 through 3.5 to 4.0.

Fig. 5: Flow velocity distribution with Magnetic Prandtl number and Schmidt number
The effects of Hartmann number M, and magnetic Prandtl number Prm on the fluid temperature for the mercury flow are illustrated in Fig. 6. The trend is very consistent for all M (or Prm) i.e. a monotonic decay from a maximum value (q = 1) at the wall (y=0) to the free stream. Temperatures are strongly enhanced with increasing transverse magnetic field (or Magnetic Prandtl number). The presence of transverse magnetic field produces a resistive force on the fluid flow. This force is called the Lorentz force, which leads to slow down of the motion of electrically conducting fluid and therefore, this leads to decrease in the thickness of boundary layer and hence to increase in the temperature of fluid flow.

Fig. 6: Temperature distribution with Magnetic Prandtl number and Hartmann number
The response of induced magnetic field (Hx) to viscous dissipative heat (Ec) as well as Schmidt number (Sc) is shown in Table 2 for Gr=2, Grm=2, Pr=0.71, Prm=5 and M=6. Here magnetic Prandtl number, Prm, is set as 5 and implies the ratio of momentum diffusivity (viscosity) is five times the magnetic diffusivity i.e. the viscous diffusion rate is five times the magnetic diffusion rate. Increasing Eckert number clearly increases the induced magnetic field magnitudes when y>1, but this trend is reversed in the vicinity of the wall. Also it is found that, the induced magnetic field decrease strongly with an increase in Schmidt number for y>1. Also for different values of Ec and Sc, the induced magnetic flux reversal arises for the region 0<y<1 due to the negative values of Hx.
Table 2: Induced Magnetic distribution for different values of Sc and Ec over y, for Gr=2=Grm, Pr=0.71, Prm=5 and M=6.

The numerical values of current density for Eckert number and Prandtl number over Hartmann number are presented in Table 3 for Gr==5, Grm=5, Pr=0.71, Prm=5 and Sc=0.30. An increase in viscous dissipative heat reduces the current density, whereas current density rises with the increase of Prandtl number. It is observed that, when Hartmann number, M→1, maximum effects on current density occurred, but these effects are insignificant for large values of Hartmann number.
Table 3: Current density distribution for different values of Ec and Pr over M, for Gr=2=Grm, Pr=0.71, Prm=5 and Sc=0.30

VIII. CONCLUSIONS
In this paper, it was demonstrated that the perturbation technique can be extended and applied to obtain a closed form expression for the problem of a steady mixed convective MHD flow of an incompressible viscous electrically conducting fluid past an infinite vertical porous plate in presence of transverse magnetic field with combined heat and mass transfer, taking into account the induced magnetic field with viscous and magnetic dissipations of energy. The present analysis brings out the following results of physical parameters of the flow field:
- A velocity overshoot is observed with lower values of magnetic field effects but vanishes for very high values of the Hartmann number in the flow regime;
- Increasing magnetic Prandtl number (Prm) or magnetic field (M) serves to decelerates the flow velocity significantly for the case of conducting air.
- With an increase in Prm, the induced magnetic field along x-direction is progressively accelerated, but the magnetic field depress the Hx.
- Increasing Schmidt number (Sc) serves to escalate the Current density at the plate, but the current density decreases for the effect of Prm.
- The temperature component (θ) increases with an increase of Magnetic field or Magnetic Prandtl number.
- The induced magnetic flux reversal arises for both the effects of Ec and Sc.
- All the temperature gradients (∂q/∂y) have maximum values in the neighbourhood of y=1 comparison to the other values of distance and it is observed to decrease ∂q/∂y for M or Prm or Pr.
The study has important applications in nuclear heat transfer control, and MHD energy generators. Currently the authors are exploring extensions of this work to study rheological (non-Newtonian) working fluid effects, the results of which will be reported in the near future.
NOMENCLATURE
| H0 | Uniform magnetic field |
| Hx | Induced magnetic field along x-direction |
 | Species concentration (Kg. m-3) |
| CP | Specific heat at constant pressure (J. kg-1. K) |
 | Species concentration in the free stream (Kg. m-3) |
 | Species concentration at the surface (Kg. m-3) |
| D | Chemical molecular diffusivity (m2.s-1) |
| Ec | Eckert number/dissipative heat |
| g | Acceleration due to gravity (m.s-2) |
| Gr | Thermal Grashof number |
| Grm | Mass Grashof number |
| M | Hartmann number/Magnetic parameter |
 | Mass flux per unit area |
| Nu | Nusselt number |
 | Pressure (Pa) |
| Prm | Magnetic Prandtl number |
| Pr | Prandtl number |
 | Heat flux per unit area |
| Sc | Schmidt number |
 | Dimensional Temperature |
 | Dimensional Fluid temperature at the surface |
 | Dimensional Fluid temperature in the free stream |
| u | Dimensionless velocity component in x-direction (m. s-1) |
| v0 | Dimensionless suction velocity (m. s-1) |
| J | Current density |
Greek symbols
| β | Coefficient of volume expansion for heat transfer (K-1), |
 | Coefficient of volume expansion for mass transfer (K-1) |
| η | Magnetic diffusivity |
| θ | Dimensionless fluid temperature (K), |
| λ | Thermal conductivity (W. m-1. K-1), |
| μ | Coefficient of viscosity (kg. m-3) |
| ν | Kinematic viscosity (m2.s-1), |
| ρ | Density (kg. m-3), |
| σ | Electrical conductivity |
| τ | Shearing stress (N. m-2) |
 | Dimensionless species concentration (Kg. m-3) |
Subscripts
| w | Conditions on the wall |
| ∞ | Free stream conditions |
APPENDIX



ACKNOWLEDGEMENTS
The authors acknowledge the important comments of the reviewers which have helped to improve the present article.
REFERENCES
1. Ahmed, S., "The study of heat and mass transfer on free convective three-dimensional unsteady flows over a porous vertical plate," J. Energy, Heat and Mass Transfer, 31, 89-110 (2009). [ Links ]
2. Ahmed, S., "Free and forced convective MHD oscillatory flows over an infinite porous surface in an oscillating free stream," Latin American Applied Research, 40, 167-173 (2010). [ Links ]
3. Ahmed, S. and A.J. Chamkha, "Effects of chemical reaction, heat and mass transfer and radiation on MHD flow along a vertical porous wall in the presence of induced magnetic field," Int. Journal of Industrial Mathematics, 2, 245-261 (2010). [ Links ]
4. Ahmed, S. and Liu, I-C., "Mixed convective three-dimensional heat and mass transfer flow with transversely periodic suction velocity," Int. J. Appl. Math. and Mech., 6, 58-73 (2010). [ Links ]
5. Ahmed, S. and J. Zueco, "Combined heat and mass transfer by mixed convection MHD flow along a porous plate with chemical reaction in presence of heat source," Appl. Math. and Mech., 31, 1217-1230 (2010). [ Links ]
6. Ahmed, S., O.A. Bég, S. Vedad, M. Zeinalkhani and A. Heidari, "Mathematical modelling of magnetohydrodynamic transient free and forced convective flow with induced magnetic field effects," Int. Pure and Appl. Sci. and Tech., 11, 109-125 (2012). [ Links ]
7. Aldoss, T.K. and M.A. Al-Nimir, "Effect of the local acceleration term on the MHD transient free convection flow over a vertical plate," Int. J. Numer. Methods Heat Fluid Flow, 15, 296-305 (2005). [ Links ]
8. Ali, F.M., R. Nazar, N.M. Arifin and I. Pop, "MHD Mixed Convection Boundary Layer Flow Toward a Stagnation Point on a Vertical Surface With Induced Magnetic Field," Trans. ASME Journal of Heat Transfer, 133, 1-6 (2011). [ Links ]
9. Alom, M.M., I.M. Rafiqul and F. Rahman, "Steady heat and mass transfer by mixed convection flow from a vertical porous plate with induced magnetic field, constant heat and mass fluxes," Thammasat Int. J. Sc. Tech., 13, 1-13 (2008). [ Links ]
10. Asghar, S., M.R. Mohyuddin and T. Hayat, "Effects of Hall current & heat transfer on flow due to a pull of eccentric rotating disks," Int. J. Heat and Mass Transfer, 48, 599-607 (2005). [ Links ]
11. Bég, O.A., A.Y. Bakier, V.R. Prasad, J. Zueco and S.K. Ghosh, "Nonsimilar, laminar, steady, electrically-conducting forced convection liquid metal boundary layer flow with induced magnetic field effects," Int. J. Thermal Sciences, 48, 1596-1606 (2009). [ Links ]
12. Chamkha, A.J. and I. Camille, "Effects of heat generation/absorption and thermophoresis on hydromagnetic flow with heat and mass transfer over a flat surface," Int. J. Numer. Methods Heat Fluid Flow, 10, 432-448 (2000). [ Links ]
13. Chamkha, A.J., "MHD flow of a uniformly stretched vertical permeable surface in the presence of heat generation/absorption and a chemical reaction," Int. Comm. in Heat and Mass Transfer, 30, 413-422 (2003). [ Links ]
14. Chen, C.H., "Combined heat and mass transfer in MHD free convection from a vertical surface with Ohmic heating and viscous dissipation," Int. J. of Eng. Sc., 42, 699-713 (2004). [ Links ]
15. Dorrepaal, J.M. and S. Moosavizadeh, "Steady incompressible magneto-hydrodynamic flow near a point of reattachment," Physics of Fluids, 10, 1512-1516 (1998). [ Links ]
16. Glauert, M.B., "The boundary layer on a magnetized plate," J. Fluid Mechanics, 12, 625-638 (1962). [ Links ]
17. Georgantopoulos, G.A., "Effects of free convection on the Hydromagnetic accelerated flow past a vertical porous limiting surface," Astrop. and Space Science, 65, 433-441 (1979). [ Links ]
18. Kafousias, N.G., N. Nanousis and G.A. Georgantopoulos, "Free convection effects on the Stokes problem for an infinite vertical limiting surface with constant suction," Astrop. and Space Science, 64, 391-399 (1979). [ Links ]
19. Li, J., D.B. Ingham and I. Pop, "Natural convection from a vertical flat late with a surface temperature oscillation," Int. J. of Heat and Mass Transfer, 44, 2311-2322 (1982). [ Links ]
20. Muthucumaraswamy, R., P. Ganesan and V.M. Soundalgekar, "Heat and mass transfer effects on flow past an impulsively started vertical plate," Acta Mechanica, 146, 1-8 (2001). [ Links ]
21. Nanousis, N., G.A. Georgantopoulos and A. Papaioannou, "Hydromagnetic free convection flow in the Stokes problem for a porous vertical limiting surface with constant suction," Astrop. and Space Science, 70, 377-383 (1980). [ Links ]
22. Pop, I., and V.M. Soundalgekar, "Unsteady free convection flow past an infinite plate with constant suction and heat sources," Astrop. and Space Science, 62, 389-396 (1979). [ Links ]
23. Raptis, A., and A.K. Singh, "MHD free convection flow past an accelerated vertical plate," Int. Comm. in Heat and Mass Transfer, 10, 313-321 (1983). [ Links ]
24. Raptis, A.A., and V. M. Soundalgekar, "Steady laminar free convection flow of an electrically conducting fluid along a porous hot vertical plate in presence of heat source/sink," ZAMM, 64, 127-130 (1984). [ Links ]
25. Raptis, A., and C.V. Massalas, "Magnetohydrodynamic flow past a plate by the presence of radiation," Heat and Mass transfer, 34, 107-109 (1998). [ Links ]
26. Raptis, A.A., C. Perdikis and A. Leontitsis, "Effects of radiation in an optically thin gray gas flowing past a vertical infinite plate in the presence of a magnetic field," Heat and Mass Transfer, 39, 771-773 (2003). [ Links ]
27. Seddeek, M.A., "Thermal-diffusion and diffusion-thermo effects on mixed free-forced convective flow and mass transfer over an accelerating surface with a heat source in the presence of suction and blowing in the case of variable viscosity," Acta Mechanica, 172, 83-94 (2004). [ Links ]
28. Steven, N., G.K. Francis and S.K. Johana, "Magnetic hydrodynamic free convective flow past an infinite vertical porous plate," Appl. Math., 3, 1-6 (2012). [ Links ]
29. Zueco, J., O.A. Bég, H.S. Takhar and V.R. Prasad, "Thermophoretic hydromagnetic dissipative heat and mass transfer with lateral mass flux, heat source, Ohmic heating and thermal conductivity effects: network simulation numerical study," Appl. Thermal Eng., 29, 2808-2815 (2009). [ Links ]
30. Zueco Jordán, J., "Numerical study of a unsteady free convective MHD flow of a dissipative fluid along a vertical plate subject to a constant heat flux," Int. J. of Eng. Sci., 44, 1380-1393 (2006). [ Links ]
Received: September 30, 2012
Accepted: April 4, 2013
Recommended by Subject Editor: Walter Ambrosini














