Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Anales de la Asociación Química Argentina
Print version ISSN 0365-0375
An. Asoc. Quím. Argent. vol.94 no.1-3 Buenos Aires Jan./July 2006
REGULAR PAPERS
Peptide potencial energy surfaces and protein folding
1Torrens*, F.; 2Castellano, G.
1 Institut Universitari de Ciència Molecular, Universitat de València, Edifici d'Instituts de Paterna, P. O. Box 22085, E-46071 València, Spain.
FAX: +34-963543274, E-Mail: Francisco.Torrens@uv.es
2 Departamento de Ciencias Experimentales, Facultad de Ciencias Experimentales, Universidad Católica de Valencia San Vicente Mártir, Guillem de Castro 106, E 46003 València, Spain.
Received February 10th, 2006. In final form March 14th, 2006
Dedicated to Prof. Imre G. Csizmadia on the occasion of his 75th birthday
Abstract
This report outlines the utility of a 3D —> 1D transformation of peptide conformation, which leads to a linearized notation of protein secondary and tertiary structures that may be used for an objective description of protein folding. The method is intended to be descriptive and not to be predictive. It is established from first principles that the idealized 2D-y–f map must have nine minima. It is obvious to ask whether all these nine conformations are actually occurring in proteins. The objective is to repeat a previous analysis of 258 proteins determined using program ECEPP2, with the improved ECEPP2 + polarization. An analysis is performed on 258 proteins with known X-ray structure. The proteins contain 56 495 amino-acid residues with well-defined f and y angles. The minima are identified with the aid of the nine ECEPP2 minima of Ac–Ala–NHMe with f and y ± 40° tolerance. ECEPP2 is improved with the inclusion of the interacting induced-dipole polarization model, SIMPLEX-MS 3 geometry optimization and the calculation of the dipole moment from the point distribution of net charges. The analysis of 258 proteins determined using ECEPP2 is repeated with the improved ECEPP2 + polarization. The relative frequency of occurrence of those conformations energetically favoured for enantioners g–g–, etc. in the y–f map of the backbone conformations of amino acids decreases as: g–a/g+a > g–g+/g+g– > g–g–/g+g+ >> ag+/ag– > aa. For the amino acids, the same preference diminishes as: Pro >> Ile > Val > Leu > Thr > Met > Ala > Glu > Phe > Trp > Tyr > Gln > Lys > Ser > Cys > Arg > Asp > His > Asn > Gly. The strong preference of Pro is in agreement with its character of a-helix and b sheet breaker, and b turn and random-coil former. The analysis of 258 proteins determined using ECEPP2 is repeated with the improved ECEPP2 + polarization and there is a good agreement between the two. Achiral Gly relative frequencies of occurrence are close to one. Pro is the amino acid with the greatest (g–g–, etc.)/(g+g+, etc.) preference and with the greatest influence on protein conformation. Pro is the amino acid with the largest Pglobal conformational parameter. The original software used in the investigation is available from the author.
Resumen
Este reporte reseña la utilidad de una transformación de conformación de péptido 3D —>1D, que conduce a una notación linealizada de estructuras de proteínas secundarias y terciarias la cual puede ser usada para una descripción objetiva del plegamiento de proteínas. El método tiene la intención de ser descriptivo y no predictivo. Desde los primeros principios se ha establecido que el mapa 2D-y–f idealizado debe tener nueve mínimos. Es obvia la pregunta, entonces, si todas las nueve conformaciones ocurren realmente en proteínas. El objetivo es repetir un análisis previo, realizado con el programa ECEPP2 en 258 proteínas, con estructura de Rayos-X conocida, utilizando el mejorado ECEPP2 + polarización. Estas proteínas contienen 56496 residuos amino ácidos con ángulos f y y bien definidos. Los mínimos son identificados con la ayuda de los nueve mínimos obtenidos para Ac–Ala–NHMe por ECEPP2 con tolerancia ± 40° para f y y. ECEPP2 es mejorado con la inclusión del modelo de polarización de dipolo inducido SIMPLEX-MS 3en la optimización de geometrías y el cálculo del momento dipolar a partir de la distribución puntual de cargas netas. La frecuencia relativa de ocurrencia de aquellas conformaciones energéticamente favorecidas por los enantiómeros g–g–, etc. en el mapa y–f de las conformaciones del esqueleto de amino ácidos decrece como: g–a/g+a > g–g+/g+g– > g–g–/g+g+ >> ag+/ag– > aa. Para los amino ácidos, la misma preferencia disminuye en el sentido: Pro >> Ile > Val > Leu > Thr > Met > Ala > Glu > Phe > Trp > Tyr > Gln > Lys > Ser > Cys > Arg > Asp > His > Asn > Gly. La fuerte preferencia de Pro está de acuerdo con su carácter rompedor de a-hélices y b-hojas, y formador de b-giros y ovillos aleatorios. El análisis de 258 proteínas determinadas utilizando ECPP2 se repitió utilizando el mejorado ECEPP2 + polarización y hay buen acuerdo entre los dos métodos. Las frecuencias relativas de ocurrencia de Gly aquiral son próximas a uno. Pro es el amino ácido con la mayor preferencia (g–g–, etc.)/(g+g+, etc.) y con mayor influencia en la conformación de proteínas. Pro es el amino ácido con el mayor parámetro conformacional Pglobal. El software original utilizado en la investigación está disponible por parte del autor.
Introduction and Notation
Multidimensional conformational analysis (MCA) allows predicting, from the topology of the potential energy curves (PEC), the topology of the potential energy surface (PES) if the molecular system is ideal [1–3]. In the case of three-fold periodicity the 3x3 = 9 minima are energetically degenerate. This case is operative for two –CH3 rotors as may be occurring in propane, and in molecules with two equivalent –CH3 groups. If the component PECs continue to have three minima, but these minima are energetically non degenerate, the resultant PES will have nine non equivalent minima. In the case of the ideal PES, it was possible to make a statement that all nine minima have the same energy value; in the non ideal case, it is possible to make an analogous statement that all nine minima have different energy values. However, it is not possible to predict what the energy spectrum of these nine minima might be, and what the relative stability of these minima could be. Nevertheless, by making an intuitive guess, it is suggested an order for the relative stabilities of the diagonal elements:
E(O2) > E(O1) > E(O0) (1)
where E is the energy. What is important to note is that PES for a single peptide unit (cf. scheme 1)
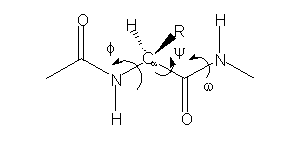
Scheme 1
may be represented as:
E = E( f, y ) (2)
if w is constant (usually w = 180º). Nevertheless, taken into account that, from the viewpoint of the torsional potential, the f and y rotations are demonstrated to be practically free, the corresponding Ramachandran (y - f) maps are determined by the non bonding and hydrogen bonding (H bonding) interactions, for each amino acid in a specific way.
Nine minima are expected to be present on the surface (cf. figure 1). However, only five out of the nine minima have been recognized earlier in the literature, which are labelled as left-handed helix, right-handed helix, extended like conformation, g-turn and inverse g-turn.
In figure 1 both f and y vary between zero and 360°. However, protein chemists adopted a range for both f and y that runs between –180° and 180°, covering both clockwise and counter-clockwise rotations, which may be labelled as standard (STD):
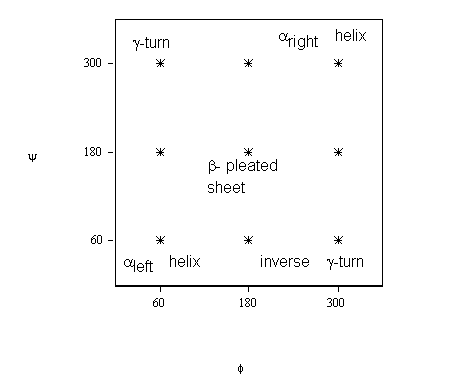
Figure 1. Idealized PES topology for a single amino-acid residue indicating the five minima already identified in the protein literature.
(The idealized location of the minima is specified by stars.)
-180° < f STD< 180
-180° < y STD < 180° (3)
The representation is more useful, as topological (TOP) relationships can be recognized with a greater ease:
0° < f TOP < 360°
0° < y TOP < 360° (4)
More important is the fact that, apart from the central minimum (b-pleated sheet), the minima occur in pairs. Thus, the remaining unassigned four minima (figure 1) could be regarded as two pairs of minima. Apart from the aa conformation, the most important, that is the energetically most favoured, conformations for the L enantiomer are at the extreme and lower right of scheme 2 (g, gauche, a, anti), and for the D enantiomer the most favoured conformations are at the upper and extreme left. The topological relationship of the two families of conformations ({g–g–, g–g+, ag+, g–a} and {g+g+, g+g–, ag–, g+a}) is illustrated (scheme 2).

Scheme 2
In order to refer to the as of yet unassigned conformations, the midpoint at the top is labelled as ag– and the midpoint at the bottom is labelled as ag+. The midpoint at the left is labelled as g+a and the midpoint at the right is labelled as g–a. Utilizing the labels used previously to denote the location of the minima, the following arrangement is obtained. For glycine (Gly) where no chiral centre exists, the aa conformation is to be located at the geometric centre [4]. For L amino acids, the position of the aa conformation is shifted towards the lower-right hand corner. Similarly, for D amino acids the position of the aa conformation is shifted towards the upper-left hand corner of the idealized topological scheme (scheme 2) which represents only a different cut of the PES as illustrated by the broken lines in figure 2.

Figure 2. Idealized PES topology for a single amino-acid residue involving two complete cycles of rotation in both f and y (g, gauche, a, anti).
For certain molecular residues, molecular computations established the actual location of the nine minima (scheme 2). The values of f and y deviate somewhat from the ideal values. table 1 lists these numerical values for N formylalaninamide (For–Ala–NH2) [3]. Typical absolute errors for folded gauche–gauche g–g– – g+g+ – g–g+ – g+g–, completely-extended fully-planar anti–anti aa and semifolded gauche–anti ag+– ag– – g–a – g+a are 15.9, 11.3 and 17.1º, respectively (14.8º on average). In particular, the extended aa conformation shows a smaller error, the semifolded ag conformations, a greater error, and the folded gg conformations, an intermediate error. Therefore, the error is smaller for extended and folded structures and greater for semifolded structures.
Table 1. Optimized f, y Torsional Angle Pairs for For–Ala–NH2 and the Idealized Torsional Angle Pairs

In a PES associated with an ideal molecular system, minima, saddle points and maxima occur in a predictable regular pattern. It is customary to denote these critical points with the number of negative eigenvalues of the Hessian matrix, with elements:
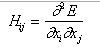
where [xi, xj] are any pair of the total of n variables including [ f , y]. The number of negative eigenvalues of the Hessian is usually referred to by the index l of the critical point. For ordinary surfaces n varies between zero and two (0 < l < 2):
l = 0 for minima
l = 1 for saddle points
l = 2 for maxima (6)
For potential energy hypersurfaces (PEHS):
0 < λ < 2 (7)
for minima l = 0, for maxima l = n, and in between are located the transition-state points with a variety of indices ranging from one to n – 1. figure 3 again shows an ideal surface as applied to a single peptide residue.

Figure 3. The topology of an idealized two-dimensional (2D)-y–f map containing the a priori predicted nine minima for a single amino-acid residue (…–CONH–CHR–CONH–…). The horizontal and vertical dashed lines represent low lying mountain ridges that separate the nine distinctly different catchment regions (g, gauche, a, anti). [Notice that the topologically (TOP) useful regions of f and y are given in a 0–360° range.] Numerals indicate the expected location of saddle points (l = 1) and maxima (l = 2).
In figure 3 the minima are not labelled by 0 but by the letters introduced earlier g–g–, aa, g–g+, etc., but critical points of higher indices are denoted by their l values, viz. 1, and 2. There are two points to note about figure 3. (1) The minima are separated from each other by mountain ridges containing maxima and saddle points. Each valley contains a single minimum and these valleys are normally referred to, after Mezey [5], as catchment regions. (2) In figure 3, the indices of the PES may be calculated from the indices of the appropriate PEC if Mezey's criteria are fulfilled:
λ (χ1,χ2) = λ(χ1) + λ(χ2) (8)
It was established from first principles that the idealized 2D-ψ-f PES ( table 1 and figure 3) must have nine minima. It is, therefore, an obvious question to ask whether all these conformations are actually occurring in proteins. Perczel et al. [6] analyzed 258 proteins with known X-ray structure [7,8], which contained 56 495 amino-acid residues with well-defined f and y angles. They identified the minima with the aid of those of N acetyl N' methylalaninamide (Ac–Ala–NHMe) determined with the ECEPP2 method [9,10], allowing a ±40° tolerance in the f and y values. Perczel et al. [11] concluded the following. (1) The non assigned conformations are quite large, indicating that Ac–Ala–NHMe may not be as good a model to mimic a single amino-acid residue in a protein than hitherto might have been believed. (2) Gly has the greatest number of non assigned cases implying that the alanine (Ala) derivative, which has a side chain, may be a much better model to all amino-acid residues with side chains than Gly, which has no side chain. (3) Since Gly is achiral, instead of nine only five unique conformations occur (g–g– = g+g+, g–g+ = g+g–, ag+ = ag–, g–a = g+a). The actual finding is not all that far from expectation: g–g– = 850, g+g+ = 631, g–g+ = 79, g+g– = 160, ag+ = 62, ag– = 45, g–a = 388 and g+a = 324. The actual degeneracy is lost in the 1799 non assigned conformations. (4) Phenylalanine (Phe) has no g+g– conformation, and proline (Pro) has no g+a and g+g– conformations. All other amino-acid residues do occur in all the possible nine conformations. One of the authors, F.T., met Prof. Csizmadia during his postdoctoral stage on protein modelling, working for the Centre National de la Recherche Scientifique (CNRS) Molecular Modelling Scientific Group, IBM–CNRS–Université de Nancy I (1991-1992). In our joint collaboration with Prof. Rivail to molecular modelling, he always advised with good courage and mood, constantly trying to extend the ab initio quantum chemical picture of the subject. In earlier publications, the dipeptide model N formylglycinamide (For–Gly–NH2) was studied with molecular mechanic polarizing force fields implemented in MM2 [12,13] and ECEPP2 [14]. The aim of the present study is to repeat a previous analysis of 258 proteins determined using ECEPP2, with the improved ECEPP2 + polarization. Section 2 describes the computational method. Section 3 present and discusses the calculation results. Section 4 summarizes the conclusions.
Computational Method
A frequently used molecular mechanics method for peptides is the empirical conformational energy program for peptides version 2 (ECEPP2) [9,10]. The force field describes the molecular steric energy as a sum of the electrostatic, non bonded, torsional, cystine torsional and loop-closing energy components. ECEPP2 provides the following functionalities: (1) study of linear polypeptides and those polypeptides that include intramolecular disulphide bonds, (2) calculation of the conformational energy for any sequence of residues and any set of dihedral angles, (3) comparison of the relative energies of the different conformations of a given polypeptide; (4) a standard file of residues is provided, which includes 26 amino acid residues and 20 terminal groups; (5) the user can eventually provide complementary residues or replace the standard residues by its own. The auxiliary program chemical modelling application platform (CMAP, B. T. Luke, IBM) can serve as an access platform to ECEPP2, for which it offers the following functionalities: (1) aid in the preparation of the data and job-command-language needed for the submission of an ECEPP2 work, (2) gateway with all the other programs to which CMAP gives access and (3) visualization of the studied polypeptide. CMAP integrates ECEPP2 as calculation program: ECEPP2 calculations of reasonable size can then be interactively executed under CMAP. The following improvements have been implemented in ECEPP2 [14]: (1) inclusion of the interacting induced-dipole polarization model by the method of Applequist [15], (2) geometry optimization by SIMPLEX-MS 3 algorithm [16] and (3) calculation of the dipole moment from the point distribution of atomic net charges. The modifications have been also implemented in programs molecular mechanics (MM2) [17] and molecular mechanics extended for coordination complexes of transition metals (MMX) [18–21].
Two methods for the calculation of the effect of the induced dipole moments on the polarization energy term have been proposed, viz. the polarization procedure by non interacting induced dipoles (NID), and the polarization scheme by interacting induced dipoles (ID) [12–14]. NID assumes scalar isotropic atomic polarizabilities. ID allows the interaction of the induced dipole moments by means of tensor effective anisotropic atomic polarizabilities. The atomic polarizabilities used (NID) and obtained (ID) for For–Gly–NH2 (cf. table 2) show that for ECEPP2, the total molecular polarizabilities are greater with ID than with NID. The atomic polarizabilities of the H, C and N atoms are greater with ID; however, the atomic contributions from the O atom are greater with NID. For the five ID minima, similar atomic and total molecular polarizabilities are obtained. For MM2, the total molecular polarizabilities are greater for NID than for ID. The atomic polarizabilities of the N and O atoms are greater with NID; however, the atomic contributions from the H and C atoms are greater with ID. For aa and g–g+, similar ID total molecular polarizabilities are obtained. Effective atomic and total molecular polarizabilities increase in the order gg < ag < aa, i.e. folded < semifolded < extended conformation.
A previous analysis of 258 proteins determined using ECEPP2 has been repeated with ECEPP2 + polarization. The set of Protein Data Bank (PDB) structures is the same used by Perczel et al. [6,11]. The use of ECEPP2 + polarization followed two strategies: (1) double scan of the idealized 2D-y–f maps (just as Perczel et al. used ECEPP2) and (2) geometry optimization of the f–y angles with SIMPLEX–MS–3. Both plans reached the same set of minima.
Table 2. Atomic Polarizabilities (in Å3) Used (ECEPP2+NID)a and Obtained (ECEPP2+ID)b in the Calculation of the
Polarization Energy for For–Gly–NH2 conformations

a NID: polarization by non interacting induced dipoles.
b ID: polarization by interacting induced dipoles.
c g, gauche, a, anti, g–g– = g+g+, g+g+ = g+g–, ag+ = ag–, g–a = g+a.
Calculation Results and Discussion
ECEPP2 + polarization has been applied to the calculation of the five minima of the conformational PES of For–Gly–NH2. The minima were described by Perczel et al. [3] with ECEPP2 (grid geometry optimization) and ab initio (second-derivatives optimization). The g–g–, g–g+, ag+ and g–a minima are folded conformations while the fully-planar aa minimum is all-trans extended. The ECEPP2 + polarization calculations have been optimized with SIMPLEX MS 3. The total energy differences (cf. table 3) are compared with MM2 and ab initio SCF 3 21G references [3]. Five structures are found with the ECEPP2 methods, two with the MM2 methods and four with ab initio. The three types of methods show only aa and g–g+ structures at the same time. These are the only minima with MM2, as well as the two main minima with ECEPP2 and ab initio. The ECEPP2 + polarization relative energies of the local aa minimum are in agreement with the reference calculations, lying between the MM2+ID and ab initio. Intramolecular H bonds contribute to the stabilization of the g–g+ conformers. The local g–g– and aa minima are stabilized by one H bond forming a five-membered ring N–H…N (g–g–) or N–H…O (aa); the global g–g+ and local ag+ minima show two shared H bonds forming a five-membered ring N–H…N and closing a seven-membered ring N H…O (g–g+), or forming two shared five-membered rings N–H…N (ag+); the local g–a minimum shows no H bond.
Table 3. Molecular mechanics (ECEPP2) results for For–Gly–NH2 conformations. Number of H bonds and total energy differences in kJ•mol-1
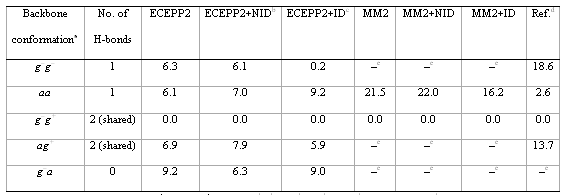
a g, gauche, a, anti, g–g– = g+g+, g–g+ = g+, ag+ = ag–, g–a = g+a.
b NID: polarization by non interacting induced dipoles.
c ID: polarization by interacting induced dipoles.
d Reference: ab initio SCF 3 21G (optimized geometry) taken from Reference 3.
e A dash (–) indicates no local minimum for this conformation.
There are 20 naturally occurring amino acids. A total of 18 of them have the same type of backbone folding, i.e. nine discrete conformations (table 1 and figure 3). The two other amino acids are exceptions. One exception is Pro, which is built into proteins like any other amino acid, but its N atom is locked in a five-membered ring. For Pro, f can only be in the vicinity of –60º and, therefore, only three backbone conformations are possible, viz. g–g–, g–a, and g–g+. The other unique amino acid is Gly, which is achiral. In the case of Gly, double degeneracy occurs in its conformational PES (g–g– = g+g+, g–g+ = g+g–, ag+ = ag–, g–a = g+a). Pro is fundamentally different from all the other 18 chiral amino acids in more than one respect: (1) the R group forms a five-membered ring with the backbone; (2) there is no peptidic N–H group in the residue to be involved in H bonding; (3) since there are two C atoms connected to the N atom, there is a greater chance of cis/trans isomerization in the peptide bond.
Notice that all nine conformations do occur in proteins (cf. table 4) [11]. For symmetric conformational pairs, e.g. g–g– (which is capable of producing a right-handed helix) and g+g+ (which is capable of generating a left-handed helix) of a given L amino acid, e.g. Ala, g–g– is more stable than g+g+. In proteins, therefore, the frequency of occurrence of the Ala residue in the g–g– conformation (2593 right-handed helix in 4894 conformations) is greater than that of g+g+ (54 left-handed helix in 4894 conformations); therefore, the ratio of frequencies of occurrences g–g–/g+g+ is much greater than unity (2593/54 = 48.019 >> 1). The only exception is achiral Gly, where g–g– is the specular image of g+g+ with the same energy. In proteins, therefore, the frequencies of occurrences of Gly in g–g– (850 right-handed helix in 4798 conformations) and g+g+ (631 left-handed helix in 4798 conformations) have practically identical relative abundance (i.e. g–g– H g+g+, g–g–/g+g+ = 850/631 = 1.347 H 1). The ratio is closer to unity in the total (g–g– + g–g+ + ag+ + g–a)/(g+g+ + g+g– + ag– + g+a) = 1.189 H 1. In general, the relative frequency of occurrence of these energetically favoured conformations of the 20 residues in proteins decreases as: g–a/g+a > g–g+/g+g– > g–g–/g+g+ >> ag+/ag– > aa/aa = 1. There is good agreement between ECEPP2 and ECEPP2 + polarization results. The results for all the amino acids relative to Gly are also calculated. For the 20 amino acids, there are g–g–/g+g+, etc. preferences, which diminish as: Pro >> Ile > Val > Leu > Thr > Met > Ala > Glu > Phe > Trp > Tyr > Gln > Lys > Ser > Cys > Arg > Asp > His > Asn > Gly. In particular, Pro is largely the amino acid with the gratest value of total (g–g– + g–g+ + ag+ + g–a)/(g+g+ + g+g– + ag– + g+a) relative to Gly (934.561), while the 19 other amino acids show this ratio in the range 1–42. Again, Pro is the amino acid with the greatest g–g–/g+g+, etc. ratios, because the Pro ring serves to intrinsically restrict its f dihedral angle ca. –60º. This is consistent with the fact that Pro strongly favours f dihedral angles ca. –60º [Pro conformations are fairly tightly clustered in the range f= (–63 ±15)º] [22]. Therefore, Pro greatly influences protein conformation.
Table 4. Relative Frequency of Occurrence of the Backbone Conformationsa of Amino-Acid (AA) Residues in Proteins

a g, gauche, a, anti.
For the different conformations, the g–g–/g+g+, etc. comparative frequencies of occurrences relative to Gly (cf. figure 4) show that g–a/g+a is the conformational parameter with the greatest variability.
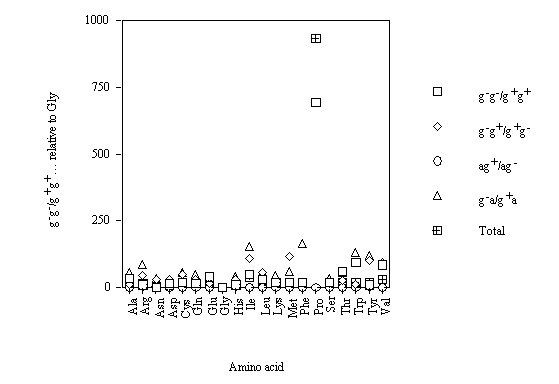
Figure 4. Comparative frequency of occurrence of conformations of amino acids relative to Gly (g, gauche, a, anti).
For the different conformations (table 4), the trend lines of the g–g–/g+g+, etc. comparative frequencies of occurrences relative to Gly are shown in figure 5. Two data for Pro have been eliminated to obtain better detail. Again, g–a/g+a shows the greatest variability. The slope of the trend lines decrease as: g–g–/g+g+ ˜ total >> g–a/g+a > g–g+/g+g– >> aa = 0 ˜ ag+/ag–

Figure 5. Trend line of comparative frequency of occurrence of conformations relative to Gly (g, gauche, a, anti).
Cluster analysis (CA) [23] was applied to the amino-acid residues in proteins. CA involved grouping the amino acids into clusters using hierarchical cluster analysis (HCA) [24]. There are many reasons why one might want to cluster a database of molecular structures [25–28]. A program has been written using the IMSL [29] subroutine CLINK to carry out HCA, based upon either a distance or a similarity matrix. Both single and complete-linkage HCAs allow building the dendrogram (binary tree) for the amino acids, corresponding to frequencies of occurrence of the backbone conformations and their ratios {g–g–, g+g+, aa, g–g+, g+g–, ag+, ag–, g–a, g+a, g–g–/g+g+, g–g+/g+g– , ag+/ag– , g–a/g+a} [30]. Both HCAs perform a binary taxonomy of the amino acids that separates first both units in class 1 (Gly and Pro, cf. figure 6 top), then class 2 (nine units, viz. Ala, Arg, Asn, Asp, Gln, Glu, His, Leu, and Lys, middle) and, finally, class 3 (nine units, viz. Cys, Ile, Met, Phe, Ser, Thr, Trp, Tyr, and Val, bottom). In particular, Pro (class 1) is the first separated amino acid.
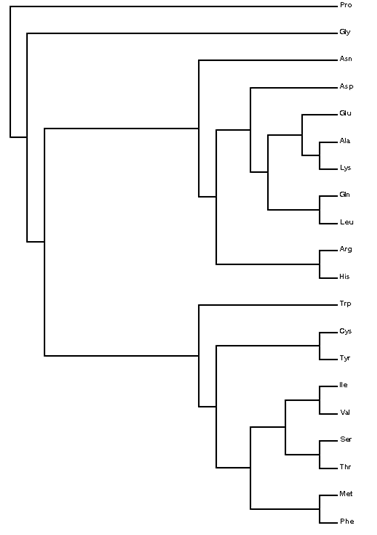
Figure 6. Dendrogram for the amino-acid residues in proteins according to frequency of occurrence and relative to Gly.
From both HCAs, the radial tree for the amino acids relating to {g–g–, g+g+, aa, g–g+, g+g–, ag+, ag–, g–a, g+a , g–g–/g+g+, g–g+/g+g–, ag+/ag–, g–a/g+a} separates first both units in class 1 (Gly and Pro, cf. figure 7 middle), then class 2 (nine units, viz. Ala, Arg, Asn, Asp, Gln, Glu, His, Leu, and Lys, bottom) and, finally, class 3 (nine units, viz. Cys, Ile, Met, Phe, Ser, Thr, Trp, Tyr, and Val, top). Again, Pro (class 1) is separated first. The classes correspond to the dendrogram (figure 6).

Figure 7. Radial tree for the amino-acid residues in proteins according to frequency of occurrence and relative to Gly.
Using the known structure of 29 proteins as determined via X ray crystallography, Chou and Fasman calculated the probabilities of a-helix [31], b-sheet [32], b-turn (sharp turn connecting b-strands) [33] and random coil (cf. table 5). The conformational parameters Pa, Pb, Pt and Pc were defined as the frequency with which a particular residue is found in a structure, relative to the average frequency for all amino acids being found in that structure. By definition, the means <Pa> = <Pb> = <Pt> = <Pc> = 1. In this study, a new conformational parameter Pglobal = – Pα – Pβ + Pt + Pc is proposed. By definition, the mean <Pglobal> = 0. Notice that <Pa relative to Gly > 1, etc.; furthermore, by definition, <Pglobal relative to Gly> = 0.
Table 5. Conformational Parameters of the Backbone Conformations of Various Amino-Acid Residues in Proteins

aPa: conformational parameter for the a helix.
bPb: conformational parameter for the b sheet.
cPt: conformational parameter for the b turn.
dPc: conformational parameter for random coil.
ePglobal = – Pa – Pb + Pt + Pc.
In particular, it can be seen from the conformational parameters that Pro is a strong a-helix breaker, strong b-sheet breaker, strong b-turn former and strong random-coil former. This is consistent with the fact that Pro plays a particular role in peptide and protein structural biology as a b-turn-promoting unit. Pro, of course, is an imino, not amino, acid. The ring structure prevents H bonding on the amide N atom, as well as makes its occurrence rare in b-sheet and a-helix. Instead, Pro along with Gly is more commonly found in b-turns [34–37], as well as rigid extended structural proteins, e.g. collagen and cuticle. Pro never participates directly in catalysis due to the chemical inertness of its methylene groups (–CH2–), though it may line a substrate pocket or provide rigidity to an active site. Peptide bonds other than those with Pro have a double bond character, and two consecutive Ca are generally trans with respect to this plane of the adjacent amide bond. Pro still emulates this double bond angle via steric hindrance, with the w dihedral angle seldom varying by more than 15º from peptide-planar. While the cis amide conformation is not sterically forbidden for non Pro amino acids in short peptides, the trans/cis ratio of the adjacent amide bond is nonetheless ca. 1000/1. For Pro, the cis imidic conformation (relative to the preceding residue) is less unfavourable, and the ratio of the adjacent imidic bond approaches 4/1. Although both conformers are in equilibrium [38,39], the activation energy is so high (ca. 80 kJ•mol-1 in model compounds [40]) that unassisted attainment of equilibrium can take minutes at physiological temperatures, much longer or never in large proteins [41].
The strong structural character of Pro (table 5) is in agreement with its strong relative frequency of occurrence of the conformations (table 4). Therefore, a new conformational parameter is proposed to maximize this difference: Pglobal = – Pa – Pb + Pt + Pc. The physical meaning of Pglobal is that this descriptor is high for an amino acid that is a strong a helix breaker, strong b-sheet breaker, strong b-turn former and strong random-coil former. For the different amino acids, Pglobal decreases as: Pro > Gly > Asn > Ser > Asp > Cys > Arg > Tyr > Lys > His > Thr > Glu > Gln > Trp > Ala > Phe > Leu > Met > Ile > Val. As expected, Pro is the amino acid with the greatest value of Pglobal. The results for all the amino acids relative to achiral Gly are also calculated. The comparative conformational parameters relative to Gly (cf. figure 8) shows that Pglobal is the conformational parameter with the greatest variability. The strong preference of Pro is in agreement with its character of strong a-helix breaker, strong b-sheet breaker, strong b-turn former and strong random-coil former. A new conformational parameter Pglobal maximizes Pro distinguished character.
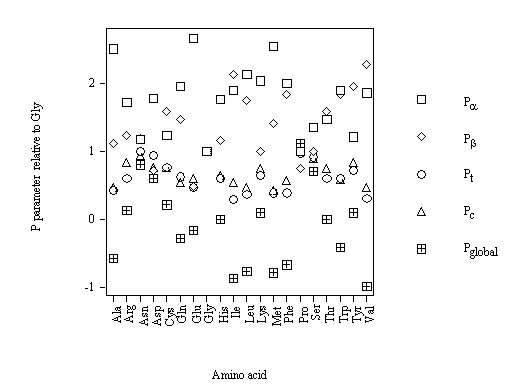
Figure 8. Comparative conformational parameters of the backbone conformations of amino acids relative to Gly.
The trend lines of comparative conformational parameters for the amino acids relative to Gly (Entries 1–20 in table 5) are illustrated in figure 9. The slopes of the trend lines decrease as: Pb >> 0 > Pc > Pt > Pa > Pglobal however, their absolute slopes diminish as: Pb > Pglobal > Pa > Pt > Pc.

Figure 9. Comparative conformational parameters of the backbone conformations of amino acids relative to Gly.
Figure 10 displays the variations of the conformational parameter Pglobal vs. the relative frequency of occurrence of the (g–g– + g–g+ + ag+ + g–a)/(g+g+ + g+g– + ag– + g+a) amino-acid residues and Pglobal relative to Gly vs. the relative frequency of occurrence of the (g–g– + g–g+ + ag+ + g–a)/(g+g+ + g+g– + ag– + g+a) amino acids relative to Gly. In both representations, the datum for Pro has been eliminated to obtain better deatil and fit. In particular, Pglobal drops quicker than Pglobal relative to Gly .
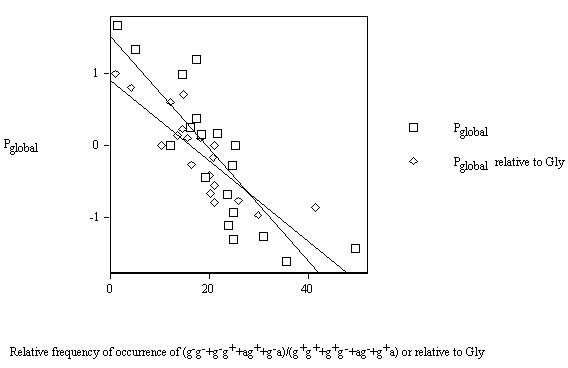
Figure 10. Variation of the conformational parameter Pglobal vs. the frequency of occurrence of the amino-acid residues
The regressions turn out to be, respectively:
Pglobal = 1.507 - 0.0776(g–g– + g–g+ + ag+ + g–a)/(g+g+ + g+g– + ag– + g+a) (9)
r = 0.839
Pglobal rel. Gly = 0.908 - 0.0556(g–g– + g–g+ + ag+ + g–a)/(g+g+ + g+g– + ag– + g+a)rel. Gly (10)
r = 0.839
As expected, the correlation coefficient is equal after both ordinates and abscissas are divided by their corresponding values for Gly.
From both HCAs, the radial tree for the amino acids relating to { Pa, Pb, Pt ,Pc, Pglobal } separates the five units in class 1 (Asn, Asp, Gly, Pro and Ser, cf. figure 11 top), class 2 (six units, viz. Ala, Arg, Glu, His, Lys, and Met, bottom) and, finally, class 3 (nine units, viz. Cys, Gln, Ile, Leu, Phe, Thr, Trp, Tyr, and Val, left), in moderate agreement with the dendrogram and radial tree obtained form the frequencies of occurrence of the backbone conformations and their ratios (figures 6–7). In particular, the best agreement is observed for class 1, which includes Pro.
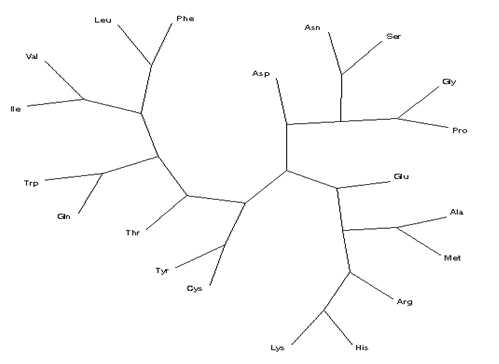
Figure 11. Radial tree for the amino-acid residues in proteins according to conformational parameter Pglobal .
The 4D-y–f map clearly indicates the practicality of the assignment of the backbone conformation of a peptide. Scheme 3 shows the explicit form of the linearized notation of backbone conformation for cytochrome b5 (PDB code 2B5C) [11]. The notation can be directly converted to a numerical format in a semi quantitative way, by using the idealized PES topology (table 1 and figure 3); e.g. Ala-ag+ corresponds to f ≈ 180º and y ≈ 60º.

The conformational assignment for the backbone conformation of the first eleven residues of a protein in PDB (cf. table 6) shows all the w angles indicating that all the residues are in the trans conformation. The trans conformation is due to the trapping of this conformation via hydrophobic, helix and sheet formation. The average w angle is 165º, 15º off from planarity (180º). In particular, the w angle is ca. 130º for Pro9, which is the residue with the greatest deviation from planarity.
Table 6. Conformational Assignment for the First Eleven Residues of a Brookhaven Protein Data Bank Protein
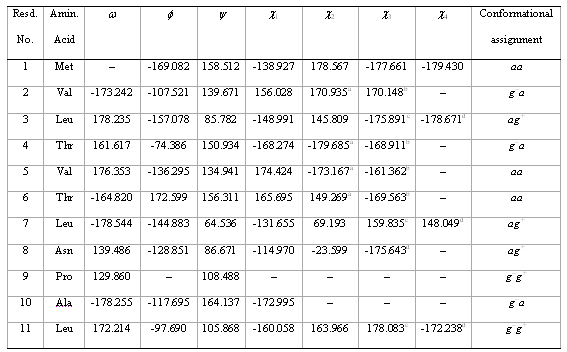
ac21. bc22. cc31.dc32.
Conclusions
From the precedent results and discussion, the following conclusions can be drawn.
1. An objective method based on quantitative geometric data has revealed to be useful to analyzing the description and classification of protein secondary and tertiary structures. The objective is to repeat a previous analysis of 258 proteins determined using ECEPP2, with the improved ECEPP2 + polarization, and there is good agreement between the two.
2. All nine conformations do occur in proteins. The relative frequency of occurrence of those conformations energetically favoured for L enantiomers in the idealized y -f map of the backbone conformations of the 20 amino acids in proteins decreases as: g–a > g–g+ > g–g– >> ag+ > aa. For the diverse amino acids, the same preference diminishes as: Pro >> Ile > Val > Leu > Thr > Met > Ala > Glu > Phe > Trp > Tyr > Gln > Lys > Ser > Cys > Arg > Asp > His > Asn > Gly. Achiral Gly relative frequencies of occurrence are close to one. Pro is the amino acid with the greatest g–g–/g+g+ preferences and greatly influences protein conformation. Pro and pseudo prolines (YPro) are applied in peptide-based drug and pro-drug design, molecular recognition studies, as well as protein folding and self aggregation processes [42,43].
Acknowledgment
The authors acknowledge financial support from the Spanish MEC DGI (Project No. CTQ2004 07768 C02 01/BQU) and Generalitat Valenciana (DGEUI INF01 051, INFRA03 047 and OCYT GRUPOS03 173).
References
[1] Csizmadia, I.G., General and Theoretical Aspects of the Thiol Group, in: Patai, S. (Ed.), The Chemistry of the Thiol Group, Wiley, New York, 1974, 1. [ Links ]
[2] Csizmadia, I.G., Multidimensional Theoretical Stereochemistry and Conformational Potential Energy Surface Topology, in: Bertrán, J.; Reidel, D. (Eds.), New Theoretical Concepts for Understanding Organic Reactions, Dordrecht, 1989, 1 [ Links ]
[3] Perczel, A.; Ángyán, J.G.; Kajtár, M.; Viviani, W.; Rivail, J.L.; Marcoccia, J.F.; Csizmadia, I.G., J. Am. Chem. Soc. 1991, 113, 6256. [ Links ]
[4] Mitchell, J.B.O.; Smith, J., Proteins 2003, 50, 563. [ Links ]
[5] Mezey, P.G.; Potential Energy Hypersurfaces, Elsevier, Amsterdam, 1987, 227. [ Links ]
[6] Perczel, A.; Kajtár, M.; Marcoccia, J.F.; Csizmadia, I.G., J. Mol. Struct. (Theochem) 1991, 232, 291. [ Links ]
[7] Bernstein, F.C.; Koetzle, T.F.; Williams, G.J.B.; Mayer, E.F.Jr.; Brice, M.D.; Rodgers, J.R.; Kennard, O.; Shimanouchi, T.; Tasumi, M., J. Mol. Biol. 1977, 112, 535. [ Links ]
[8] Abola, E.E.; Bernstein, F.C.; Bryant, S.H.; Koetzle, T.F., J. Weng, Protein Data Bank, in: Allen, F.H.; Bergerhoff, G.; Sievers, R. (Eds.), Crystallographic Database: Information Content, Software System, Scientific Applications, Data Commission of the International Union of Crystallography, Bonn–Cambridge–Chester, 1987, 107. [ Links ]
[9] Némethy, G.; Pottle, M.S.; Scheraga, H. A., J. Phys. Chem. 1983, 87, 1883. [ Links ]
[10] Sippl, M.J.; Némethy, G.; Scheraga, H.A., J. Phys. Chem. 1984, 88, 6231. [ Links ]
[11] Perczel, A.; Viviani, W.; Csizmadia, I.G., Peptide Conformational Potential Energy Surfaces and Their Relevance to Protein Folding, in: Bertrán, J. (Ed.), Molecular Aspects of Biotechnology: Computational Models and Theories, Kluwer, Dordrecht, 1992, 39. [ Links ]
[12] Torrens, F.; Voisin, C.; Rivail, J.L., Electric Polarization in a Force Field for the Study of Dipeptide Models, in: Glowinski, R. (Ed.), Computing Methods in Applied Sciences and Engineering, Nova Science, New York, 1991, 249. [ Links ]
[13] Torrens, F.; Sánchez-Marín, J.; Rivail, J.L., An. Fís. (Madrid) 1994, 90, 197. [ Links ]
[14] Torrens, F., Mol. Simul. 2000, 24, 391. [ Links ]
[15] Applequist, J., J. Phys. Chem. 1993, 97, 6016. [ Links ]
[16] Walters, F.H.; Parker Jr., L.J.; Morgan, S.L.; Deming, S.N., Sequential Simplex Optimization, CRC, Boca Raton, 1991. [ Links ]
[17] Torrens, F.; Ruiz-López, M.; Cativiela, C.; García, J.I.; Mayoral, J.A., Tetrahedron 1992, 48, 5209. [ Links ]
[18] Torrens, F., Polyhedron 2003, 22, 1091. [ Links ]
[19] Torrens, F., Int. J. Quantum Chem. 2004, 99, 963. [ Links ]
[20] Torrens, F., J. Inclusion Phenom. Mol. Recognit. Chem. 2004, 49, 37. [ Links ]
[21] Torrens, F., Molecules 2004, 9, 632. [ Links ]
[22] MacArthur, M.W.; Thornton, J.M., J. Mol. Biol. 1991, 218, 397. [ Links ]
[23] Tryon, R.C., J. Chronic Dis. 1939, 20, 511. [ Links ]
[24] Jarvis, R.A.; Patrick, E.A., IEEE Trans. Comput. 1973, C22, 1025. [ Links ]
[25] McGregor, M.J.; Pallai, P.V., J. Chem. Inf. Comput. Sci. 1997, 37, 443. [ Links ]
[26] Doman, T.N.; Cibulskis, J.M.; Cibulskis, M.J.; McCray, P.D.; Spangler, D.P., J. Chem. Inf. Comput. Sci. 1996, 36, 1195. [ Links ]
[27] Turner, D.B.; Tyrrell, S.M.; Willett, P., J. Chem. Inf. Comput. Sci. 1997, 37, 18. [ Links ]
[28] Reynolds, C.H.; Druker, R.; Pfahler, L.B., J. Chem. Inf. Comput. Sci. 1998, 38, 305. [ Links ]
[29] Integrated Mathematical Statistical Library (IMSL), IMSL, Houston, 1989. [ Links ]
[30] Page, R.D.M., Program TreeView, Universiy of Glasgow, 2000. [ Links ]
[31] Chou, P.Y.; Fasman, G.D., Biochemistry 1974, 13, 211. [ Links ]
[32] Chou, P.Y.; Fasman, G.D., Trends Biochem. Sci. 1977, 2, 128. [ Links ]
[33] Chou, P.Y.; Fasman, G. D., Annu. Rev. Biochem. 1978, 47, 251. [ Links ]
[34] Rose, G.D.; Gierasch, L.M.; Smith, J.A., Adv. Protein Chem. 1985, 37, 1. [ Links ]
[35] Müller, G.; Gurrath, M.; Kurz, M.; Kessler, H., Proteins: Struct., Funct., Genet. 1993, 15, 235. [ Links ]
[36] Richardson, J.S., Adv. Protein Chem. 1981, 34, 116. [ Links ]
[37] Smith, J.A.; Pease, L.G., CRC Crit. Rev. Biochem. 1980, 8, 315. [ Links ]
[38] Higgins, K.A.; Craik, D.J.; Hall, J.G.; Andrews, P.R., Drug Design Deliv. 1988, 3, 159. [ Links ]
[39] Weißhoff, H.; Wieprecht, T.; Henklein, P.; Frömmel, C.; Antz, C.; Mügge, C., FEBS Lett. 1996, 387, 201. [ Links ]
[40] Stein, R.L., Adv. Quantum Chem. 1993, 11, 1. [ Links ]
[41] Scherer, G.; Kramer, M.L. Schutkowski, M.; Reimer, U.; Fischer, G., J. Am. Chem. Soc. 1998, 120, 5568. [ Links ]
[42] Dumy, P.; Keller, M.; Ryan, D.E.; Rohwedder, B.; Wöhr, T.; Mutter, M., J. Am. Chem. Soc. 1997, 119, 918. [ Links ]
[43] Keller, M.; Sager, C.; Dumy, P.; Schutkowski, M.; Fischer, G.S.; Mutter, M., J. Am. Chem. Soc. 1998, 120, 2714. [ Links ]














