Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Anales de la Asociación Química Argentina
Print version ISSN 0365-0375
An. Asoc. Quím. Argent. vol.94 no.1-3 Buenos Aires Jan./July 2006
REGULAR PAPERS
QSPR modeling of metal halides lattice enthalpies
1Castro, E. A.; 2Toropova, A. P.; 2Toropov, A. A.; 2D. Mukhamedjanova, V.
1 INIFTA, Department of Chemistry, Faculty of Exact Sciences, La Plata National University, Suc. 4, C.C. 16, La Plata (B1906ZAA), Argentina,
Fax: 54-221-4254642, E-Mail: castro@quimica.unlp.edu.ar
2 Uzbekistan Republic, Academy of Sciences Geology & Geophysics Institute, 700125, Abdullaev Street 41, Tashkent, Uzbekistan
Received September 14th, 2005. In final form March 31st, 2006
Dedicated to Prof. Imre G. Csizmadia on the occasion of his 75th birthday
Abstract
By means of optimisation correlation of local invariant weights in graph of atomic orbitals, one-variable quantitative structure-property relationships have been obtained. Statistical characteristics of the best of such a model are the following: n = 13, r = 0.9999, s = 1.21 kJ/mol, F = 55060 (training set); n = 7, r = 0.9990, s = 7.68 kJ/mol, F = 2485 (test set)
Resumen
Se ha obtenido una relación estructura-propiedad cuantitativa unidimensional utilizando la optimización de la correlación local invariante de pesos en gráficos de orbitales atómicos. Las características estadísticas de dicho modelo son las siguientes : n = 13, r = 0,9999, s = 1,21 kJ/mol, F = 55060 (conjunto de preparación); n = 7, r = 0,9990, s = 7,68 kJ/mol, F = 2485 (conjunto de prueba)
Introduction
With the exception of the inert gases, all the elements in the periodic table form halides, often in several oxidation states, and halides generally are quite important and common compounds. There are almost as many ways of classifying halides as there are types of halides , and there are many. There are not only binary halides which can range from simple molecules, ionic or molecular lattices to complicated polymers but also oxyhalides, hydroxy halides, and other complex halides of various structural types.
Metal halides are substances of predominantly ionic character, although partial covalence is important in some of them. On the whole there is a uniform gradation from halides which are for all practical purposes purely ionic to those of intermediate character to those essentially covalent. As a rough guide we can consider those halides in which the lattice consists of discrete ions rather than definite molecular units to be basically ionic, although there may still be considerable covalence in the metal-halogen interaction. The size and polarizability of the halide ion is also important in determining the character of the halide. Thus we have the rather classic case of the aluminium halides, where AlF3 is basically ionic, whereas AlCl3, AlBr3, and AlI3 exist as covalent dimers.
Metal fluorides have a higher heat of formation than the remaining alkaline metal halides and this feature is due to the reduced heat of formation of the F2 molecule and the high lattice energy of the compounds themselves. Heat of formation of fluorides decreases when the cation volumes increase, but in the remaining halides this behaviour is just the opposite. This is due to the fact that the magnitude 1/(ranion + rcation) decreases rapidly in the fluoride series due to the smaller anion size. This change has more influence than the decrease of the ionisation potentials and sublimation energies of the corresponding metals.
Heat of formation of chlorides, bromides and iodides increase descending along I, II, IIIA, IVA and VA groups. In the remaining groups of the periodic table in general the inverse behaviour is observed, although there are some interesting enough irregularities, specially in the first two periods. The heat of formation of hypothetical halides can be calculated by means of standard treatments. Numerical models of physical and chemical properties of metal halides in general and their enthalpies in particular have many interesting applications in so diverse fields such as inorganic chemistry, physical chemistry and geochemistry [1].
Study of structure-property and structure-activity relationship continues to attract considerable attention in chemical literature. Various statistical methods have been found useful in such studies, including the Principal Component Analysis [2], the Pattern Recognition [3], the Partial Square method [4], the Artificial Neural Networks [5].The oldest data reduction method, the Multiple Regression Analysis (MRA) [6], is currently widely used. Most molecular descriptors used in MRA are characterized by fixed numerical values, which are independent of the property/activity under consideration [7]. To better describe the property/activity studies, Randic proposed the employment of some flexible descriptors [8-11] to improve regression results, with the idea that a variable parameter undergoes change during the regression analysis.
Hydrogen-suppressed and hydrogen-filled molecular graphs, which are a particular sort of valuable resource to define variable descriptors, are used as a particular representation of molecular structure in quantitative structure-property relationships (QSPR) of organic compounds, but they are not good tools to encode the main features of molecular structure of inorganic substances such as different crystalline arrangements. However, these substances are object of research works in mineralogy, geochemistry, and geology itself. Under such circumstances, it is preferable to use an alternative set of variable descriptors, recently described as graph of atomic orbitals (GAO) [1, 12-15].
The present study aims to estimate the capabilities of using the GAO approach in QSPR modelling of enthalpies of metal halides and to compare the results with available experimental data.
Method
Two types of molecular graphs are under consideration in this study. The first type calculated with classical molecular graphs (MG) of two vertices (metal and halogen) and one edge. Descriptors for such graphs are calculated as

where Ak denotes a metal or a halogen, N is the number of vertices and CW stands for Correlation Weights. The dk is the vertex degree in MG. In the case of the metal halides under consideration, dk= 1.
The second type of molecular graph is the GAO. GAO can be obtained from 'classical' graphs by means of a change of atoms by groups of atomic orbitals and the subsequent reconstruction of the adjacency matrix. The procedure was described in detail in Ref. [14], so that we deem it is not necessary to repeat them here. Descriptors for such graphs are obtained by means of the following formula

where AOk is an atomic orbital (i. e., 1s1,…, 2p3,…, 3d10 , …), dk is the vertex degree of the k-th vertex in the GAO, and N is total number of vertices (atomic orbitals) in the GAO.
Results and discussion
Atomic orbital groups on each atom under consideration are listed in table 1.
Table 1. Atoms and atomic orbital groups for alkaline and halogen atoms.

Numerical values of the CWs of Eq.(1) or Eq. (2) can be obtained by the method of Monte Carlo optimization [15], which produces the largest as possible correlation coefficient between the descriptors and enthalpies. After the CWs are determined one can calculate D(MG) or D(GAO) for metal halides of the training set, and by means of the Least Squares method one calculate C0 and C1 for the linear model

where G stands for MG or GAO.
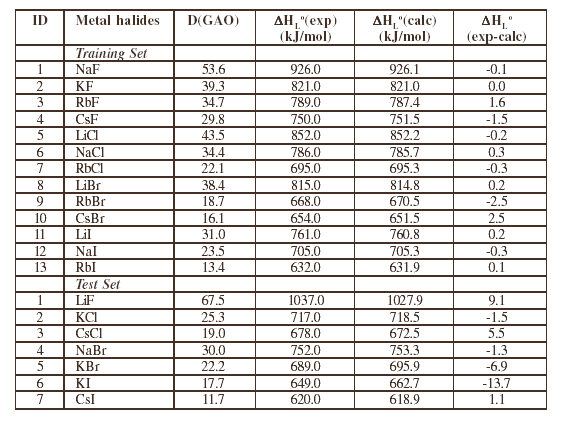
One can estimate predictive potential of the eq. (3) with substances of the test set. Results of three probes for such optimization procedure with MG and GAO are presented in table 2. Similar final results are obtained for each probe, so that we present data for just one of them. It can be seen from table 2 that GAO based models of enthalpies are better than MG based models. The GAO based model of enthalpy calculation obtained in the first probe of the optimization procedure is the following

It can be seen that in spite of the large number of optimised parameters (29), the most important attribute of the model is the lack of any information on metal halides belonging to the test set in the process of obtaining CWs (table 3) as well as the model to get eq. (4). Calculation of the enthalpy with eq.(4) is displayed in table 4. Experimental data have been taken from Ref. [12]. The percent deviations are rather small, so that the predictions are very accurate (see sixth column in table 4).
Table 2. Statistical characteristics of models of lattice enthalpies of metal halides obtained inthree probes of optimization of the correlation weightsin the
MG and results ofthree such probes on correlation weights in the GAO. Here r, s, F, and n arecorrelation coefficient, standard error,Fischer
F-ratio, and number ofcompounds in the set, respectively.

* r = regression coefficient, s = standard deviation, F = Fisher coefficient
Table 3. Correlation weights of local invariants in MG and GAO on three probes of the
Monte Carlo optimization method.

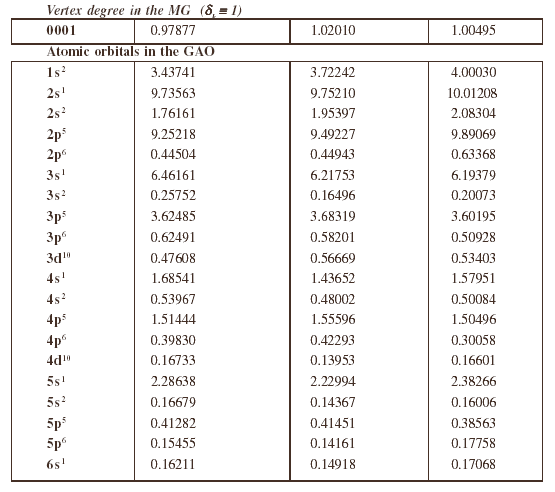

Table 4. Calculation of the Enthalpy with Eq. (4).
Conclusions
The enthalpies of metal halides are defined by the structure features of metal and halide atoms (i.e., by the presence of different types of atomic orbitals), since the statistical characteristics of the models based on information of structure atoms are better than those of models based only on information of the presence of metal and halogen atoms. We have outlined a novel way of deriving powerful structure-property models to calculate enthalpies of metal halides lattices. Even though the approach has been demonstrated here for one physical-chemical property of metal halides, it is general and can be applied to the analysis of other properties for different sort of molecules, as shown in several previous articles (see, for example, references [16-20]).
The advantage of the outlined approach is that it yields regressions accompanied with considerably smaller standard error than those given by similar studies using standard molecular descriptors (i.e. rigid molecular descriptors). The "flexibility" of the molecular descriptor, such as Graph of Atomic Orbitals employed in this study, makes it possible to describe very accurately metal halides lattice enthalpies. At present we are extending this treatment to other molecular sets in order to model different physical-chemical properties. Results will be presented elsewhere in the forthcoming future.
Acknowledgements
The authors are indebted to a reviewer for suggestions.
References
[1] Jenkins, H. D. B.; Glasser, L., Inorg. Chem. 2002, 41, 4378. [ Links ]
[2] Hotelling, H., J. Educ. Psychol. 1993, 24, 417. [ Links ]
[3] Wold, S.; Sjöstrom, M., in Chemometrics: Theory and Applications, ACS Symp. Ser. No. 52, Kowalski, B. R., Ed., American Chemical Society, Washington, D.C., 1977, p.243. [ Links ]
[4] Wold, S.; Sjöstrom, M.; Eriksson, L., Partial least squares projections to latentstructures (PLS) in chemistry, in Encyclopedia of Computational Chemistry, von Schleyer, R.; Allinger, N. L.; Clark, T.; Gasteiger, J.; Kollman, P. A.; Schaefer III, H. F.; Schreiner, P. R., Eds., Wiley, Chichester, England, 1998, 2006-2021. [ Links ]
[5] Zupan, J., Neural networks in chemistry, in Encyclopedia of Computational Chemistry, von Schleyer, R.; Allinger, N. L.; Clark, T.; Gasteiger, J.; Kollman, P. A.; Schaefer III, H. F.; Schreiner, P. R., Eds., Wiley, Chichester, England, 1998, 1813-1827. [ Links ]
[6] Malinowski, E. R.; Wiley, New York, 1991. [ Links ]
[7] Randic, M., New J. Chem. 2000, 24, 165-171. [ Links ]
[8] Randic, M., Chemom. Intel. Labl. Syst. 1991, 10, 213-223. [ Links ]
[9] Randic, M., J. Chem. Inf. Compout. Sci. 1991, 31, 970-980. [ Links ]
[10] Randic, M.; Pompe, M., J. Chem. Inf. Comput. Sci. 2001, 41, 631-638. [ Links ]
[11] Randic, M.; Basak, S. C., J. Chem. Inf. Comput. Sci. 2001, 41, 614-618. [ Links ]
[12] Pogliani, L., Croat. Chem. Acta, 2004, 77, 193-201 [ Links ]
[13] Castro, E. A.; Toropova, A. P.; Toropov, A. A.; Mukhamedjanova, D. V., J. Argent. Chem. Soc. (this Journal) 2003, 91, 85-90. [ Links ]
[14] Mercader, A.; Castro, E. A.; Toropov, A. A., Chem. Phys. Lett. 2000, 330, 612-623. [ Links ]
[15] Toropova, A. P.; Toropov, A. A., Russ. J. Struct. Chem. 2001, 42, 1230-1232. [ Links ]
[16] Pérez González, M.; Toropov, A. A.; Duchowicz, P. R.; Castro, E. A., Molecules 2004, 9, 1019-1033. [ Links ]
[17] Castro, E. A.; Torrens, F.; Toropov, A. A.; Nesterov, I. V.; Nabiev, O. M., , Molec. Simul. 2004, 30, 691-696. [ Links ]
[18] Castro, E. A.; Toropov, A. A.; Nesterova, A. I.; Nazarov, A. U., , J. Theor. Comput. Chem. 2004, 3, 31-41. [ Links ]
[19] Duchowicz, P. R.; Castro, E. A.; Toropov, A. A.; Nesterov, I. V.; Nabiev, O. M., Molec. Diversity 2004, 8, 325-330. [ Links ]
[20] Nesterov, I. V.; Toropov, A. A.; Duchowicz, P. R.; Castro, E. A., The Scientific World Journal 2004, 4, 956-964. [ Links ]














