Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Anales de la Asociación Química Argentina
Print version ISSN 0365-0375
An. Asoc. Quím. Argent. vol.94 no.1-3 Buenos Aires Jan./July 2006
REGULAR PAPERS
Complexation of Zn(II) by catechol in hydroxylic solvents
1Sancho, M.I.; 1Blanco, S.E.; 1Ferretti, F.H.; 2Jubert, A.H. ; 3Castro, E.A.
1 Department of Physical Chemistry, Faculty of Chemistry, Biochemistry and Pharmacy, San Luis National University, San Luis, Argentina
2 CEQUINOR, Department of Chemistry, Faculty of Exact Sciences, La Plata National University, La Plata, Argentina
3 INIFTA, Department of Chemistry, Faculty of Exact Sciences, La Plata National University, La Plata, Argentina
FAX:54-221-4254642.E-Mail: castro@quimica.unlp.edu.ar
Received April 25th, 2006. In final form May 18th, 2006
Dedicated to Prof. Imre G. Csizmadia on the occasion of his 75th birthday
Abstract
The stability of the complex formed by one molecule of 1,2-dihydroxybenzene and one molecule of zinc acetate in solutions with different permittivity and temperature was investigated by means of spectroscopic and chromatographic methods. The Becke hybrid three-parameter nonlocal exchange functional combined with the Lee-Yang-Parr dynamic correlation functional method (B3LYP/6-31G(d)) and the isodensity polarized continuum model (IPCM) were used in the calculations. It was assumed that the formation of the complex takes place by a reaction between ions of opposite charges. It was also proposed an equation to explain the changes of the constant of the complexation equilibrium with the permittivity of the reaction medium. The calculations allowed us to prove that the increase of the hydrogen-bond donor ability of the solvents favours a higher thermodynamic stability of the reactants with respect to the complex and, as a result, a decrease of the corresponding equilibrium constants. The non-planar structure proposed for the complex is consistent with the experimentally observed hyperchromic shift. The plane, in the complex molecule, containing the aromatic ring is tilted by approximately 18º with respect to that of the zinc and oxygen atoms. It was concluded that the formation of the complex is an endothermic process.
Resumen
Se investigó la estabilidad del complejo formado por una molécula de 1,2-dihidroxibenceno y una molécula de acetato de cinc, en soluciones con diferentes permitividad y temperatura, por medio de métodos espectroscópicos y cromatográficos. En los cálculos teóricos se usó el método B3LYP/6-31G(d) y el modelo IPCM. Se propuso que la formación del complejo ocurre por una reacción entre iones de carga opuesta. También se propuso una ecuación que explica los cambios de la constante de equilibrio de complejación con la permitividad del medio de reacción. Los cálculos realizados permitieron demostrar que el aumento de la capacidad donora de la unión hidrógeno del solvente favorece una mayor estabilidad termodinámica de los reactivos con respecto al complejo y por consiguiente una disminución de las correspondientes constantes de equilibrio. La estructura no planar propuesta para el complejo es coherente con el cambio hipercrómico observado experimentalmente. En la molécula del complejo, el plano que contiene el anillo aromático está inclinado aproximadamente 18º, con respecto al plano del cinc y de los átomos de oxígeno. Se concluyó que la formación del complejo es un proceso endotérmico.
Introduction
Flavonoids are an extensive group of poliphenolic compounds abundant in nature [1] and also obtainable by synthetic methods [2]. Due to their numerous physicochemical and biological properties [3], they are object of continuous investigations in several disciplines related to Biology and Chemistry. Commonly, the molecular structure of flavonoids of high biological activity like quercetin or naringenin [4] includes a group derived from resorcinol and/or catechol [5,6]. This quality is also shown by important flavonoids used in analytical chemistry like morin, which has been used as complexating reagent of Thorium (IV) [7]. As part of a program aimed at finding relationships among flavonoids, the complexation of Zn(II) by catechol in ethanol (EtOH), methanol (MeOH) and water was experimentally and theoretically studied. Besides, the complex structure and the influence of the temperature and permittivity on their stabilities was investigated.
Calculations
The structure of the complex of stoichiometric composition 1:1 and the practical numbering system adopted for carrying out the calculations are shown in fig. 1. The calculations were performed following known procedures [8]. The initial molecular geometries were modelled by the AM1 (Austin Model 1) method. The initial geometries were then optimized with the Gaussian 98 [9] program package. The final optimization of the molecular structures was performed with the B3LYP/6-31G(d) method. To analyse the solvent effects on the optimized structures in gas-phase the IPCM model [10] was used. In all the calculations default convergence criteria were used.

Fig. 1. Structure of the complex catecholate-zinc computed at B3LYP/6-31G(d) and the practical numbering system adopted in the calculations.
Experimental
Reagents. Catechol from Biomedicals, Zinc acetate dihydrate (purity >99.5% w/w) from Merck and HPLC grade methanol (MeOH) from Merck were used without further purification.
Instrumentation and Procedures.
The experiments performed comprised:
(a) The determination of the stoichiometry of the complex formed by zinc acetate and catechol in MeOH. The molar ratio method [11,12] was used for the spectrophotometric determination of the complex composition. The UV-visible spectra were recorded on a Shimadzu UV 160 A double beam spectrophotometer with 1 cm thermostatically controlled cells, between 240-320 nm at 25°C.
(b) The measurements of the complexation global rate by means of HPLC. The HPLC instrument consisted of a Gilson 322 series pump and a Gilson 152 UV-Vis detector, equipped with a Phenomenex column temperature controller. The system was controlled by the UniPoint system software v2.10 (Gilson). The analysis was carried out with a reverse-phase Luna (C18 (2), 250mm x 4.6 mm, 5 m) column from Phenomenex. Chromatographic studies were performed under isocratic elution with a mobile phase of 100% MeOH, a constant column temperature of 40ºC and a flow rate of 1.0 mL/min. The injection volume was 20 mL and the detector was set at 278 nm, which represents the maximum adsorption wavelength of catechol.
In a typical kinetic experiment, reacting mixtures containing 1.76 x 10-4 M of catechol and 6.96 x 10-4 M of Zinc were prepared in a mobile phase. The molar ratio 4:1 Zinc to catechol was chosen to assure the complexation reaction. These solutions were placed in volumetric flasks hermetically closed and thermostated (6ºC-30ºC). At increasing time intervals an aliquot of the reacting mixture was injected. Identification of remaining catechol was carried out by comparing retention times of unknown peaks with standards and quantification was carried out using calibration curves. Seven concentrations of catechol (3 x 10-4 M, 2.3 x 10-4 M, 2 x 10-4 M, 1.5 x 10-4 M, 1.2 x 10-4 M, 9.1 x 10-5 M, 6 x 10-5 M) were injected separately into the HPLC column to prepare the calibration curve. A square correlation coefficient (r2) was found for catechol standards (>0.99). The measurements of samples were performed until equilibrium was reached (3 – 4h).
Results and discussion
fig. 2 shows the UV spectra of catechol, both free (L) and complexed (C) with Zn(II) in MeOH. Likewise, fig. 3 shows the first derivative spectra of L and C. From fig. 2 it can be observed that at 278.1 nm, maximum absorption wavelength of L, both species absorb radiation. The main absorption band of L, in the presence of Zn(II), undergoes a hyperchromic shift.

Fig. 2. Zero-order UV spectra of 1,2-dihydroxy-benzene free and complexed with zinc acetate in methanol, at 25.0ºC.
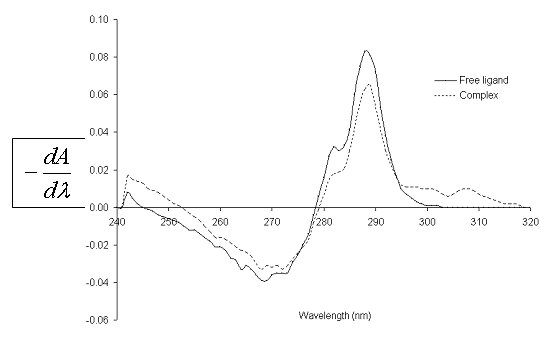
Fig. 3. First derivative UV spectra of 1,2-dihydroxy-benzene free and complexed with Zn(II) in methanol, at 25.0ºC.
Stoichiometry and formation of the complex
The existence of the complex Zn(II)L was detected by applying the molar ratio method [12]. fig. 4 shows the results of this method in MeOH at 25°C. From fig. 4 it can be observed that only the 1:1 ligand to metal complex is formed. Under our experimental conditions complexes with different ligand-metal stoichiometries were not detected.

Fig. 4. Determination of the stoichiometry of the complex formed between zinc acetate and 1,2-dihydroxy-benzene in methanol.
On the other hand, the 1:1 stoichiometric composition of the complex was confirmed by kinetic experiments. We proposed that the formation of the complex 1:1 occurs by the following reaction,
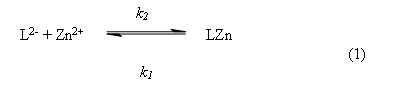
In the reaction above, L2-- is the catecholate dianion, LZn is the 1:1 ligand-metal complex and k2, k1 are the global reaction rate constants for the forward (second order) and reverse (first order) reaction rate, respectively. This reaction is characterized by the equilibrium constant KC, which is defined by the following equation,

In this equation, the brackets stand for molar concentrations. As an example, fig. 5 shows the graphical representation of the experimental data according to eq. (3),

Fig. 5. Formation of the complex between catechol and zinc acetate in methanol at 25.0°C. Graphic representation of Eq. (3). Error bars = 1%.
[L] = [ZnL]e exp [{-(kl*+ kl)} t] + [L]e (3)
where, t = time; [L] = the molar concentration of catechol for any time t; [L]e, [ZnL]e = the molar concentrations in equilibrium (t = oo") and k1* = the rate constant of pseudo first order for the forward reaction rate.
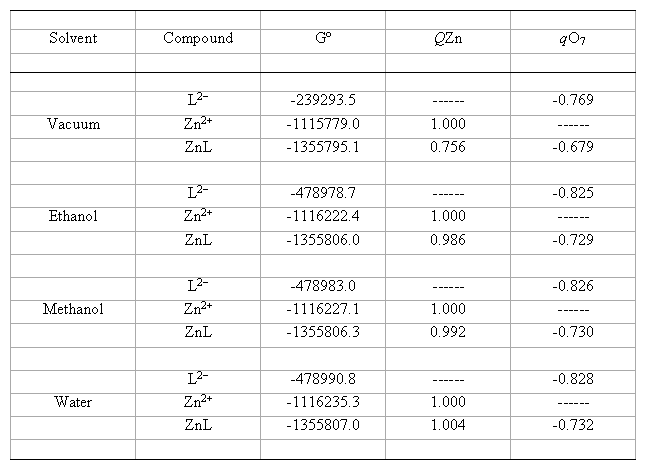
table 1 summarises the optimized values of molecular properties of all the species involved in the reaction described by eq. (1).
Table 1. Calculated molecular parameters and properties using the IPCM method at B3LYP/6-31G(d) level for catecholate
dianion (L2-), zinc ion (Zn2+) and ligand-metal complex 1:1 (LZn), in vacuum and hydroxylic solvents at 298 K
(Gº = Total Gibbs free energy, kcal mol-1; q = Mulliken's atomic charge of the indicated atom, au).
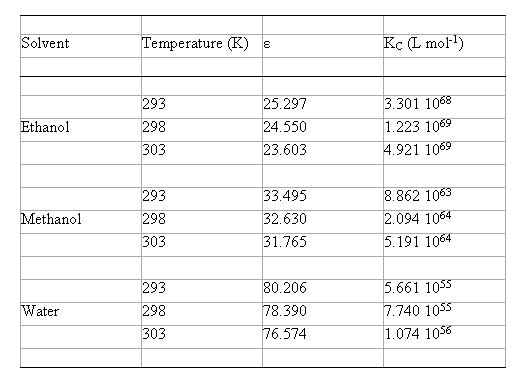
The values of KC calculated in EtOH, MeOH and water at different temperatures are summarised in table 2. It is obvious that these data are important for their comparative values and not for their absolute magnitudes.
Table 2. Calculated complexation equilibrium constants using the B3LYP/6-31G(d) method with the model IPCM, in hydroxylic solvents
( KC = equilibrium constant of Eq. (2); e = experimental permittivity values [ 13,14] ).
Solvent Effects
It is known that the influence of the relative permittivity (m) of the medium on the rate constant of a reaction between two ions may be described [15] by the equation,
lnk2 = lnk2o - (Ne2/2RT) {(ZA2/rA) + (ZB2/rB) - (Z‡2/r‡)} (1-1/e) (4)
In the equation above, k2o and k2 are the rate constants for media with unit and m relative permittivity; N is the Avogadro's number; e is the unit of electric charge; R is the universal gas constant; T is the absolute temperature; ZA, ZB, Z‡ are the charges of the two ions and the corresponding activated complex, respectively; rA, rB, r‡ are the radii of the two ions and activated complex, respectively.
Using the eqs. (1) and (4), the following relationship between KC and e was obtained,
ln KC = ln KCo - (Ne2/2RT) {(ZA2/rA) + (ZB2/rB) - (Z‡2/r‡)} (1-1/e) (5)
In this equation, KCo is the equilibrium constant for vacuum (e = 1). The KC values calculated at 298 K were plotted against 1/e as shown in fig. 6.

Fig. 6. Plot of ln KC against 1/e for the complexation reaction studied at 298K. KC is the equilibrium constant in L mol-1. Square correlation coefficient > 0.9995.
A linear relationship was obtained, as follows:
ln KC = 1129.5 (1/e) + 36.932 (r = greater than 0.9995) (6)
This equation indicates that when m increases the corresponding KC decreases. This signifies that the solvents with the lowest polarity favour the studied complexation reaction. Analysing Eqs. (5) and (6), it is inferred that {(ZA2/rA) + (ZB2/rB) - (Z‡2/r‡)} is a positive magnitude. If we assume that the involved radii are the same [15], that is rA = rB = r‡, it is deduced that (ZA2 + ZB2) > Z‡2 which is reasonable.
Influence of the temperature
The van't Hoff equation, which states the equilibrium constant of reactions increase with temperature if the process is endothermic but decreases if it is exothermic, may be expressed as,
ln KC = DHº/RT + DSº/R (7)
In the equation above, DH° and DS° are the standard heat and standard entropy of the reaction, respectively. The calculated complexation equilibrium constants in hydroxylic solvents between 20-30ºC were plotted according to this equation, as shown in fig. 7. The following expressions were obtained:

Fig. 7. Influence of the temperature (T, in K) on the equilibrium constant (KC, L mol-1) of the complexation reaction
between zinc acetate and catechol in ethanol, methanol and water
In EtOH:
ln KC = -24117 (1/T) + 240.01 (r = 0.9996) (8)
DH° = 47.9 kcal mol-1 (9)
DS° = 476.9 cal mol-1 K-1 (10)
In MeOH:
ln KC = -15779 (1/T) + 201.05 (r = 0.9996) (11)
DH° = 31.4 kcal mol-1 (12)
DS° = 399.5 cal mol-1 K-1 (13)
In Water:
ln KC = -5716.2 (1/T) + 147.87 (r = 0.9997) (14)
DH° = 11.4 kcal mol-1 (15)
DS° = 293.8 cal mol-1 K-1 (16)
From Eq. (7), it is evident that KC increases when DH° decreases and DS° increases. Moreover, from fig. 7 it can be observed that under similar conditions the KC constants decrease progressively as follows,
KC (EtOH) > KC (MeOH) > KC (Water) (17)
Taking this into account and considering the values above obtained for DH° and DS°, it is inferred that the weight of the DS° term on the KC values is higher than that of DH°. These results suggest that in EtOH the reactants are solvated more effectively than in water and MeOH with respect to the complex, or that in water and MeOH the complex is solvated more effectively than the reactants.
On the other hand, it must also be noted that the solvents capability for protonation, which depends on their acidity, is another property that affects the stability of the complex. The pKa values in ethanol, methanol and water at 298 K decrease as follows [16],
pKa (EtOH)=15.58 > pKa (MeOH)=14.26 > pKa (Water)=13.99 (18)
From eqs. (17) and (18) it is inferred that when the acidity of a reaction medium increases the stability of the complex decreases.
Molecular properties of reactants and metal complex
From tables 1 and 2 it can be observed that some of the calculated magnitudes significantly change with the solvent, whereas others show only slight variations. The free energies of all the compounds increase in absolute value in the order vacuum < ethanol < methanol < water. This is indicating the thermodynamic stability of the species increases with the solvent polarity. Moreover, the Mulliken's atomic charges in vacuum also suffer changes with respect to the pertinent charges in solution. For example, the charge qZn = 0.756 of the complex increases its value up to qZn = 1.004. Likewise, qO7= -0.679 of the complex increases (in absolute value) its value up to qO7 = -0.732, while qO7 = -0.769 of the catecholate dianion increases its value up to qO7= -0.828. These results suggest that the Mulliken's atomic charges of the reactants and complex increase with the solvent polarity.
It is evident that in solution the reactants and products are involved in specific solvent-solute interactions such as intermolecular hydrogen bonds (IHBs). The solvation parameters a and b [17,18] are very useful for describing these IHBs. The parameters a and b measure exclusively the hydrogen-bond donor (HBD) and hydrogen-bond-acceptor (HBA) properties of the solvents, respectively. Good relationships were obtained between the free energies of the involved species in the complexation reaction described by eq. (1), and the solvation parameters of the used solvents. figs. 8 and 9 show the increase in thermodynamic stability of the catecholate dianion and complex catecholate-zinc respectively, with the a-parameter of hydroxylic solvents. From fig. 8 and 9, it is observed that the obtained linear equations have good square correlation coefficients (r >0.99). It is worth noting that the straight line slope of the catecholate dianion is higher than the straight line slope of the complex. This fact indicates that the increase of the HBD capability of the solvents favour a higher thermodynamic stability of the reactants with respect to the complex and, therefore, a decrease in the corresponding equilibrium constants.

Fig. 8. Variations of the free energy of catecholate dianion with the a-parameter of ethanol, methanol and water.
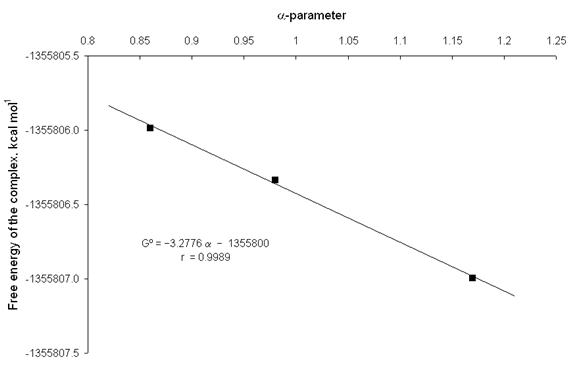
Fig. 9. Plot of the free energy of the complex catecholate-zinc against the a-parameter of hydroxylic solvents.
Recently, solvent effects on the conformational equilibrium between two conformations of catechol were studied by Rudyk et al. [8]. It was determined that in primary alcohols both conformations possess a planar structure. fig. 1 shows the non-planar structure of the complex catecholate-Zn(II) computed at B3LYP/6-31G(d). table 3 summarises the calculated properties of the complex in MeOH at 298 K.
Table 3. Calculated structural magnitudes at B3LYP/6-31G(d) for the complex catecholate-zinc in methanol at 25ºC. (Fig. 1, D = dihedral angle between the indicated atoms (º); r = bond length between the indicated atoms (Å); A = H-Bond angle (º); d = interaction distance between the indicated atoms (Å); q =total atomic charge of Mulliken (au)).

Comments from Table 3: (a) the null value of the dihedral angle D-O7C1C2O8 indicates that oxygen atoms bonded to Zn13 are in the same plane; (b) the D-C1C2O8Zn13 angle approximately measures the angle formed by the plane containing the phenyl ring and the plane containing the zinc and oxygen atoms. That is, the phenyl ring is tilted by 18.2º with respect to the oxygen and metal atoms plane.
Conclusions
The influence of the temperature and solvents on the stability of the complex formed by the catecholate dianion and the zinc ion was studied. It was assumed that the formation of the complex takes place by a reaction between ions of opposite charges. An equation was proposed to explain the changes of the complexation equilibrium constant with the medium permittivity. The calculated free energies for reactants and products with the specific solvation parameter a of the solvents were related. Several linear relationships were obtained, which support the increase of the equilibrium constant when the relative permittivity of the medium decreases. The calculations performed at B3LYP/6-31G(d) level using the IPCM method allowed us to prove that the formation of the metal complex implies an endothermic process in which the solvent-solute interactions play a fundamental role. Moreover, it was determined that the complex has a non-planar structure.
Acknowledgements
This work was supported by grants from San Luis National University, Argentine.
References
[1] Harborne, J.B., The Flavonoids. Advances in Research since 1986, Chapman & Hall/CRC, New York, 1999, pp. 57-440. [ Links ]
[2] Barros, A.I.; Silva, A.M. S.; Alkorta, I.; Elguero, J., Tetrahedron 2004, 60, 6513. [ Links ]
[3] Rice-Evans, A. and Packer, L., Flavonoids in Health and Disease, Marcel Dekker Inc., New York, 1998. [ Links ]
[4] Branham, W.S.; Dial, S. L.; Moland, C.L.; Hass, B.S.; Blair, R.M.; Fang, H.; Shi, L.; Tong, W.; Perkins, R.G.; Sheehan, D.M.; J. Nutr. 2002, 132, 658. [ Links ]
[5] Yang, B.; Kotani, A.; Aral, K.; Kusu, F., Anal. Sci. 2001, 17, 599. [ Links ]
[6] Bors, W.; Heller, W.; Michel, C.; Saran, M.; Structural Principles of Flavonoid Antioxidants, in: Csomos, G.; Feher, J., (Eds), Free Radicals and the Liver, Springer, Berlin, 1992, pp. 77-95. [ Links ]
[7] Ferretti, F.H.; Olsina, R.; Marone, C.B.; An. Asoc. Quím. Argent.(This Journal), 1982, 70, 501. [ Links ]
[8] Rudyk, R.A.; Molina, M.A.A.; Gómez, M. I.; S Blanco, E.; Ferretti. F.H., Internet Electron. J. Mol. Des. 2004, 3, 11, http://www.biochempress.com . [ Links ]
[9] Gaussian 98, Revision A.7, Frisch, M. J.; Trucks, G. W.; Schlegel, H. B.; Scuseria, G. E.; Robb, M. A.; Cheeseman, J. R.; Zakrzewski, V. G.; Montgomery, Jr., J. A.; Stratmann, R. E.; Burant, J. C.; Dapprich, S.; Millam, J. M.; Daniels, A. D.; Kudin, K. N.; Strain, M. C.; Farkas, O.; Tomasi, J.; Barone, V.; Cossi, M.; Cammi, R.; Mennucci, B.; Pomelli, C.; Adamo, C.; Clifford, S.; Ochterski, J.; Petersson, G. A.; Ayala, P. Y.; Cui, Q.; Morokuma, K.; Malick, D. K.; Rabuck, A. D.; Raghavachari, K.; Foresman, J. B.; Cioslowski, J.; Ortiz, V; Baboul, A. G.; Stefanov, V; Liu, G.; Liashenko, A.; Piskorz, P.; Komaromi, I.; Gomperts, R.; Martin, R. L.; Fox, D. J.; Keith, T.; Al-Laham, M. A.; Peng, C. Y.; Nanayakkara, A.; Gonzalez, C.; Challacombe, M.; Gill, P. M. W.; Johnson, B.; Chen, W.; Wong, M. W.; Andres, J. L.; Gonzalez, V; Head-Gordon, M.; Replogle, E. S.; Pople, J. A. Gaussian, Inc., Pittsburgh PA, 1998. [ Links ]
[10] Foresman, J.B.; Keith, T.A.; Wiberg, K.B.; Snoonian, J.; Frisch, M.J., J. Phys. Chem. 1996, 100, 16098. [ Links ]
[11] Yoe, J.H.; Jones, A.L., Ind. Eng. Chem. Anal. Ed. 1944, 16, 111. [ Links ]
[12] Momoki, K.; Sekino, J.; Sato, H.; Yamaguchi, N., Anal. Chem. 1969, 41, 1286. [ Links ]
[13] Lide, D.R., Handbook of Chemistry and Physics, 78th Ed, CRC Press, New York, 1997-1998, 6-173-6-175. [ Links ]
[14] Gaussian 98, User's Reference, Second edition, Gaussian, Inc., Pittsburgh PA, 1998, p. 172. [ Links ]
[15] Ruff, F.; Csizmadia, I.G., Organic Reactions. Equilibria, Kinetics and Mechanism, Elsevier, London, 1994, pp. 280-282. [ Links ]
[16] ChemSilicoTM, CSpKaTM Predictor, ChemSilico LLC, Tewksbury, MA 01876, USA, 2003. [ Links ]
[17] Marcus, Y., Chem. Soc. Rev. 1993, 22, 409. [ Links ]
[18] Isaacs, N., Physical Organic Chemistry, 2nd ed., Longman, London, 1996, pp. 216-223. [ Links ]














