Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Anales de la Asociación Química Argentina
versión impresa ISSN 0365-0375
An. Asoc. Quím. Argent. v.94 n.1-3 Buenos Aires ene./jul. 2006
REGULAR PAPERS
A model approach for food safety: The assessment of interactions by computing
1,2Kozmutza, C.; 1,3Varga* I.; 3,4Budaházy, I.
1 Department of Theoretical Physics, Budapest University of Technology and Economics, Budafoki ut 8, H-1111 Budapest, Hungary
2 HuKaSoft Ltd., Radna u. 7, H-1026 Budapest, Hungary
3 Kapuy Ede Research Foundation, Budafoki ut 8, H-1111 Budapest, Hungary.
4 Information Center and Library, Budapest University of Technology and Economics, Budafoki ut 4-6, H-1111 Budapest, Hungary.
FAX: +36 1 463 1110, E-Mail: varga@neumann.phy.bme.hu
Received December 5th, 2005. In final form March 17th, 2006
Dedicated to Prof. Imre G. Csizmadia on the occasion of his 75th birthday
Abstract
Recently, there has been growing international interest regarding food safety. Unlike many physical elements, the impact of most chemical and biological hazards is complex and has not been fully characterized. Establishing a database of parameters associated with such molecular interactions would not only be beneficial for the scientific community, but may allow consumers to wisely choose certain food products. By examining the interaction between a simple phenol and the divalent magnesium ion, we propose a new approach to assess the interactions between biologically relevant compounds using widely accepted theoretical methods such as ab initio computations, while taking into consideration recent developments in the field. Certain theoretical cases were examined, while others were collected from scientific literature on phenols/phenolics. Experimental and theoretical methods should complement each other to provide a more complete picture of molecular interactions. A common database of interactions between common chemicals detectable in foodstuffs and human systems will enable consumers to make more informed decisions regarding their purchases.
Resumen
Recientemente ha habido un creciente interés por la seguridad en los alimentos. A diferencia de muchos de los factores físicos, el impacto de la mayoría de los peligros químicos o biológicos son complejos y no han sido completamente caracterizados. El establecer una base de datos de parámetros asociados con tales interacciones moleculares no sería solamente beneficioso para la comunidad científica sino que le permitiría a los consumidores elegir mejor ciertos productos alimenticios. Examinando la interacción entre un simple fenol y el ion magnesio bivalente, proponemos una nueva aproximación como medida para la interacción entre compuestos biológicamente relevantes usando métodos teóricos altamente aceptados tales como cálculos ab initio, considerando recientes desarrollos en el campo. Algunos cálculos teóricos fueron examinados, mientras que otros fueron obtenidos a partir de la bibliografía sobre fenoles/fenolicos. Métodos experimentales y teóricos se complementarían entre si para proveer una mas completo cuadro de las interacciones moleculares. Una base de datos común de interacciones entre químicos comúnmente detectable en materia alimenticia y sistemas humanos les permitiría a los consumidores tomar decisiones más informadas respecto a sus compras.
Introduction
Phenols are a well-known group of compounds that include flavonols, flavones and isoflavones [1]. Due to their antioxidant activities, phenolics have attracted broad interest in recent years. As such, their structures have been examined experimentally as well as theoretically. The beneficial effect of the consumption of phenolics has been pointed out [2]. There are certain phenolic compounds that are commonly used as food additives (butylated hydroxytoluene). However, some phenolics are fungicides (orthophenyl phenol), as well as toxic by-products of detergent degradation (4-nonylphenol) [3].
Chemical and biological contaminants including chemical residues and additives may lead to health hazards in ingested food products. Unfortunately, there is limited empirical documentation of the interactions between exposure to such pollutants and human beings, creating an undesirable level of uncertainty when assessing the safety of food products. This paper will attempt to outline sound scientific procedures that should be implemented when characterizing these intermolecular interactions.
Independent experts recently stated that it is important to improve theoretical methods that could provide a better knowledge on how chemicals act on life processes [4]. A large number of scientists are convinced that computing methods based on molecular physics are applicable to this purpose. There is also a need to increase the research and development of experimental (e.g. analytical, spectroscopic, and crystallographic) procedures. It has also been suggested that the inclusion of some statistical procedures would allow for estimates to be made concerning biological interactions. Key parameters associated with uncertainties are not always given in literature, although these are increasingly expected to be carefully analyzed [5]. Some guidelines concerning food consumption and regulations in the EU are especially unclear (such as GEOs and GMOs). Consumers should be given access to data derived from independent sources in order to make informed decisions.
Both experimental and theoretical investigations have been carried out for mono-, di- and triphenols and the results obtained are often compared with the outcomes derived from the studies performed on more complex phenolics [6]. The possibility for the comparisons arises from certain topological similarities between phenols and phenolics. The mono-phenol molecule was thus selected as the first target in our study. Although this molecule has been extensively studied ([7] and references therein), we first intend to perform a systematic series of investigations of various simple phenols; analysis of phenolic compounds will be targeted in our forthcoming studies. In addition to the number and the position of OH groups, the impact of metal ions is also an important step in antioxidant activity. For this reason, the interaction between phenol and Mg2+ will be examined. In addition, the study of this interaction would allow considering the effect of the change of the geometric parameters of the phenol molecule.
In the present work, we have attempted to characterize the interaction between phenol and the Mg2+ ion using the ab initio/Separated Molecular Orbitals method. This has allowed us to develop a model system for further investigation of the interactions between various biologically relevant compounds such as phenol derivatives. The proposed computational method will be able to complement traditional discovery techniques and remove some of the uncertainty surrounding qualitative experiments.
Methods
Molecular properties can be determined by various experimental methods to a certain extent. When determining the uncertainty associated with experimental studies, some key parameters are traditionally used. A protocol for the analytical measurement to determine the amount of a phenolic compound in a given sample requires establishing parameters such as accuracy and precision. When using quantum chemical approaches, the level of uncertainty is linked to the type of the approximations applied. This also holds for ab initio methods. The geometric conformation of the molecular structures under investigation and a well-balanced basis set a priori are needed to obtain results by ab initio computations. It follows, then, that the geometry and the selected basis set could key parameters to uncertainty.
The success of theoretical methods depends on the geometry used for the system, and a key parameter could certainly be associated with geometric conformation. To assess the impact of geometry on the uncertainty, however, there has been a historical debate about which of experimentally or theoretically determined geometry data are applicable for ab initio calculations [8]. This arises from the fact that experimental methods are continually developing, and the size of the molecular structures under study is increasing and the structures themselves are becoming more and more complex. The long-standing goal of quantum chemistry is that theoretical treatments would support experimental measurements [9]. Structural chemistry may produce a skeleton conformation, which would then be successively filled by a theoretical scientist with the coordinates of atoms using ab initio calculations. However, the conformation of large molecular systems often cannot be uniquely determined, and model geometric values would thus be assigned with much difficulty. In general, this does not hold for weakly interacting molecular structures. "Independent" monomers, usually those with well-defined structures, are present in these systems.
Basis set dependence of quantum chemical means such as ab initio methods has been observed since the establishment of the procedure [10]. Although the variational method ensures that the total energy of the system under study could not increase as the basis set is extended, no universal technique has been developed to improve the quality of the basis set. Various basis sets have been established and are even currently under development [11]. The impact of the basis set on a theoretically calculated molecular property could therefore be a key parameter linked to uncertainty.
The method of Separated Molecular Orbitals (SMO) has already been used successfully to study various weakly interacting systems [12, 13]. Not only have molecule-molecule been investigated, but also molecule-ion structures. Total energy partitioning can be done using both the Hartree-Fock (also known as a self-consistent field), and the second, third and fourth order level of correlation using the many-body perturbation theory (MBPT). Recently, special attention has been paid to develop and apply the SMO method to describe the energetic components arising in interacting systems of four to six components. Encouraging results were obtained while analyzing various water clusters. Systematic basis set dependence studies accompanied the analyses in each case. The advantage of the SMO method lies in its simplicity. When considering self-consistent field (SCF) calculations, reliable information is provided for the interaction ability of contributing systems. The electronic structure of the supersystems is the readout, and no additional calculations, including corrections for basis set superposition error, are needed.
Results
We chose to use the HF SCF level of theory to study the phenol-Mg2+ interaction since the ab initio/SMO method generates the suitable energetic quantity of the monomeric behavior in weakly interacting systems. In this study, the effect of the Mg2+ ion approaching from different directions toward the phenolic OH group was examined. Each partitioned energy quantity, including the interaction energy as a contribution to the total energy at the HF level, is influenced by the quality of the basis set. As such, the impact of the basis sets on the partitioned interaction energy (PIE) was investigated. On one hand, the PIE value is a quantity that arises primarily from electrostatic interaction energy. Yet, the partitioned total energies of the monomers reflect the suitability of the applied basis set (see previous results obtained by the SMO method). This is expected from the partitioning scheme.
Calculations performed for the phenol-Mg2+ system were done using two well-known basis sets, 6-31G* and 6-311G*. The initial optimized geometry of phenol obtained by 6-31G* basis set was used when bringing the molecule to higher levels of theory and at different conformations (coordinates listed in table I). Four different conformations were considered (figure 1). The corresponding values are grouped in table II.
Table I: Geometry data of phenol (in Ångstroms)


Figure1. The interaction of the Mg2+ ion and the phenol molecule is investigated at four conformations.
Table II: Calculated partitioned interaction energies (in Hartrees). The distances (d) between the parent systems numerical values are given in atomic units.
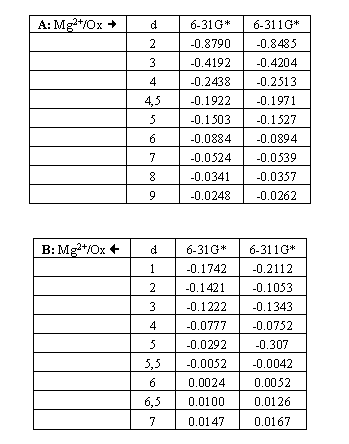

The Mg2+ ion approaches the oxygen atom of the OH group from its open side (Series A in table I). Series B records the values of PIE when the ion is approaching from the opposite side. Similarly, Series C and D represent the calculated PIE values when the hydrogen atom of the hydroxyl group is perturbed by a Mg2+ ion. The effect of the geometry parameters on PIE was considered by using both experimentally and theoretically determined configurations for the phenol molecule. The A1, B1, C1 and D1 series belong to the former conformation, while the A2, B2, C2 and D2 series represent the values obtained by using the latter geometric arrangement for phenol.
The results can be summarized as follows. PIE values shed light on the different attractive ability of the hydroxyl group, which also depends on the orientation of the approaching Mg2+ ion. In addition, analysis of the results affirms that the proposed method of assessing molecular interactions is sufficiently sensitive for the detection of different interaction capabilities. However, the geometric orientation of the atoms in phenol determined by both experimental measurement and theoretical optimization does not have a significant effect on PIE values.
We do not intend to generalize the conclusions prior to extensive calculations for studying interaction abilities in other molecular and/or ionic structures.
Discussion and Conclusion
Due to constraints in computing capabilities, only a skeleton of the model approach has been examined at great length here. This sample case examining the interaction between phenol and a single metal ion, however, allows us to demonstrate the manner in which the "geometry" parameter with its accompanying uncertainty could be considered. The results suggest that variation in the geometry of the monomer (phenol) does not only have a significant effect on PIE values, but that this influence is consistent along the series at each inter-atomic distance as well. The deviations do not exceed 1%. This is certainly due to the dominant electrostatic interaction that arises in the phenol-Mg2+ system and to the energy partitioning scheme applied at the HF level of theory in combination with the SMO method.
In regards to basis set dependence, the results suggest that there are systematic differences between different basis sets based on the calculated PIE values. The influence of the basis set variation on the partitioned energy terms obtained by the SMO method at the HF level has already been published for a large number of (weakly) interacting molecular structures [11-14]. Our results confirmed that the impact of the basis set is systematic in each case. This may be a result of the careful construction of the basis sets (all are well-balanced); this trend does not deteriorate when energy partitioning in the SMO method is applied. In this work, two basis sets were used; the deviations obtained for the PIE values were approximately 5% at each intermolecular distance.
Our model approach could therefore be implemented using the following steps. First, the coordinates of the monomers are to be fixed. These values may be obtained using experimentally or theoretically determined values (depending on time constraints). Uncertainty is not a large factor at this stage. Model structures might also be used, this possibility and its risk assessment will be discussed in a future work. Second, well-known basis sets must be chosen. We have shown that established basis sets provide reliable results with uncertainty limited in the range of 5%. Third, data collection must be systematic. While varying interatomic or intermolecular distances between the monomers involved in the interaction, PIE values should be computed using the ab initio/SMO method. Regular variations are expected when the distance between the approaching monomers is changing. Fourth, PIE values must be analyzed for variation so that conclusions could be drawn about possible affinities and interactions of the monomers. As affinity certainly depends on the actual conformations of the two molecules, all possible ("realistic") configurations should be tested for the ability to interact. The analyses are expected to enhance the understanding of interaction processes and may also allow for the prediction of favorable interactions.
Implementing some key parameters related to uncertainty in calculations would contribute to the harmonizing experimental and theoretical methods. Expressing uncertainty in a quantitative and coherent fashion would enhance the profile of the ab initio method for those who are not familiar with quantum chemistry. In addition, experimental and theoretical methods would be able to complement each other more fully. Interaction parameters for various molecular structures obtained through various methods will contribute to a much-needed database that will provide preliminary and explicit information on the interaction abilities of certain molecular structures. This protocol would enable the characterization of interactions between known chemicals and human systems, which could be deposited into a database accessible by both scientists and the consumer concerned with food safety.
Acknowledgements
C.K. is indebted to the Ministry of Education in Hungary for support related to the EU/FP6 projects. Assistance provided by Orsolya Kapuy during the preparation of this work is also acknowledged.
References
[1] Rusznyák, I.; Szent-györgyi, A., P. Vitamin: Flavonol as vitamins, Nature 1936 27, 138. [ Links ] Parmar, N.S.; Ghosh, M. N., Current trends in flavonoid research, Ind. J. Pharmac., 1990 12 (4), 213. [ Links ]
[2] Simon, C.; Barathieu, K.; Laguerre, M.; Schmitter, J.M.; Fouquet, E.; Pianet, I.; E.J., Biochemistry, 2003 42 (35): 1038. [ Links ] Brian, D. C.; Whichelow M.J.; A. T. , Public Health Nutrition, 2000, 3 (1), 19; [ Links ] Hour, T. C.; Liang, Y. Ch.; Chu, I. S.; Lin, J. K., Food and Chemical Toxicology 1999, 37, 569; [ Links ] Guerrero-Romero, F.; Rodriguez-Moran, M., Arch. Med. Res., 2005, 36 (3): 250. [ Links ]
[3] James Maguire, R., Water Quality Research Journal of Canada, 1999, 34 (1): 37; [ Links ] Restrictions on the marketing and use of nonylphenol, nonylphenol ethoxylate and cement, http://www.europarl.org.uk/news/infocus/nonylphenol2003.htm [ Links ]
[4] Risk analysis and food: The experts' view, Food and Agriculture Organization of the United Nations, http://www.fao.org/docrep/V9723T/v9723t08.htm; [ Links ] Vialette, M.; Pinon, A.; Leporq, B.; Dervin, C.; Membré, J. M., Meta-Analysis of Food Safety Information Based on a Combination of a Relational Database and a Predictive Modeling Tool, Risk Analysis, 2005, 25 (1), 75; [ Links ] FAO/UNEP/WHO GEMS: Food Contamination Monitoring Program, Summary of 1986-1988 Monitoring Data, WHO, Geneva, Switzerland 1999. [ Links ]
[5] Janssen, P.H.M.; Petersen, A.C.; van der Sluijs, J.P.; Risbey, J.S.; Ravetz, J.R., RIVM/MNP Guidance for Uncertainty Assessment and Communication, RIVM, Bilthoven 2003. [ Links ]
[6] Chung, K.T.; Wong,T.Y.; Wei, C.I.; Huang, Y.W.; Lin, Y., Tannis human health: a review, Crit. Rev. Food. Sci. Nutr. 1998, 38, 421; [ Links ] Crozier, A.; Burns, J.; Aziz, A.A.; Stewart, A.J.;Rabiasz, H.S.; Jenkins, G.I.; Edwards, C.A.; Lean, M.E.J., Biol. Res. 2000, 33: 79; [ Links ] Bravo, L., Nutr. Rev. 1998, 56, 317. [ Links ]
[7] Estacio, S.G.; Cabral do Couto, P.; Guedes, R.C.; Costa Cabral, B.J.; Nartinho J.A.; Simoes, Theor. Chem. Acc. 2004, 112, 282. [ Links ]
[8] van Lenthe, J.H.; van Duijneveldt, J.G.C.M.; van de Rijdt; van Duijneveldt, F.B.; Adv. Chem. Phys., 1987, 69 521-566. [ Links ]
[9] Hammami, F.; Nasr, S.; Belissent-Funel, M.C., J. Chem. Phys. 2005, 122, 064505. [ Links ]
[10] van Duijneveldt, F.; van Duijneveldt J.G.C.M.; van de Rijdt; van Lenthe, J.H. State of the Art in Counterpoise Theory, Chem Rev, 1994, 94, 1873. [ Links ]
[11] Ozaki, T.; Kirio, H., J. Chem. Phys., 2004, 121, 10879. [ Links ]
[12] Kozmutza, C., Tfirst, E., Transworld Research Network (ed.), Trivandrum, India, Vol.3, 169-209 (2002); [ Links ] Kozmutza, C., Tfirst, E., Adv. Quant. Chem., 1998, 31, 231. [ Links ]
[13] Kozmutza, C.; Varga, I.; Udvardi, L., J. Mol. Struct. (Theochem), 2003, 666-667, 95. [ Links ]
[14] Kapuy, E.; Kozmutza, C., Chem. Phys. Lett. 1994, 226, 484; [ Links ] Kozmutza, C.; Tfirst, E. and Kapuy E., Mol. Phys. 1996, 87, 569. [ Links ]














