Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Anales de la Asociación Química Argentina
versión impresa ISSN 0365-0375
An. Asoc. Quím. Argent. v.94 n.4-6 Buenos Aires ago./dic. 2006
REGULAR PAPERS
On the symmetry of bis benzene cromium(0) with D6d point group
Hamadanian, M.1; Reza Ashrafi, A.2
1Department of Chemistry, Faculty of Science, University of Kashan, Kashan, Iran
Fax: +98 361 552 930, E-mail: hamadani@kashanu.ac.ir
2Department of Mathematics, Faculty of Science, University of Kashan, Kashan, Iran
Received February 2nd, 2006. In final form November 14th, 2006
Abstract
An Euclidean graph associated with a molecule is defined by a weighted graph with adjacency matrix M = [dij], where for i≠ j, dij is the Euclidean distance between the nuclei i and j. In this matrix dii can be taken as zero if all the nuclei are equivalent. Otherwise, one may introduce different weights for distinct nuclei.In this paper, the automorphism group of the Bis Benzene Chromium(0) with D6d point group symmetry is computed. We also find an euclidean graph with an odd number of automorphisms. This solved a problem posed by the author in an earlier paper.
Resumen
Un gráfico euclidiano asociado a una molécula es definido por un gráfico con matriz adyacente M = [dij] donde i≠ j, dij es la distancia euclidiana entre los nucleos i y j. En esta matriz dii puede ser tomada como cero si todos los núcleos son equivalentes. De otra manera, se pueden introducir diferentes pesos para distintos núcleos. En este trabajo se calcula el grupo de automorfismo del Bis Benceno Cromo(0) con simetría D6d. Se encontró también un gráfico euclidiano con un número impar de automorfismos. Este resultado resuelve un problema planteado por el autor en un artículo publicado previamente.
Introduction
An Euclidean graph G = (V,E,w) is a combinatorial object consisting of a set V = V(G) of vertices which is a subset of R3, a set E = E(G) containing all possible unordered pairs {x,y} of distinct vertices of G called edges, and a function w: E(G) —> R in which w(e) is the Euclidean distance between the vertices x and y. An automorphism or symmetry of an euclidean graph G is a permutation g of the vertex set of G with the property that for every edge e, w(g(e)) = w(e). The set of all automorphisms of a weighted graph G, with the operation of composition of permutations, is a permutation group on V(G) denoted Aut(G).
In the literature [1,2], it was shown by Randic that a graph can be depicted in different ways so that its point group symmetry or three dimensional perception may differ, but the underlying connectivity symmetry is still the same as characterized by the automorphism group of the graph. However, the molecular symmetry depends on the coordinates of the various nuclei which relate directly to their three dimensional geometry. Although the symmetry as perceived in graph theory by the automorphism group of the graph and the molecular group are quite different, it was shown by Balasubramanian [3-9] that the two symmetries are connected.
The present authors earlier computed the full non rigid group of trimethylamine, cis and trans- platinum (II) and some other molecules, [10-13]. In this paper we consider only Euclidean graphs. The motivation for this study is outlined in Refs [3-9] and the reader is encouraged to consult these papers for background material as well as for basic
computational techniques. Our notation is standard and taken mainly from Refs. [14-20].
Methods
In this section we first describe some notation, which will be kept throughout the paper. Suppose X is a set. The set of all permutations on X, denoted by SX, is a group which is called the symmetric group on X. In the case that X = {1, 2,…, n}, we denote SX by Sn or Sym(n).
Our computations of the symmetry properties of molecules were carried out with the use of GAP [21] GAP stands for Groups, Algorithms and Programming. The name was chosen to reflect the aim of the system, which is a group theoretical software for solving computational problems in computational group theory. This software was constructed by the GAP’s team in Aachen. GAP contains a large library of functions, which are important for the calculations of this paper.
Suppose Pss is the permutation matrix corresponding to a permutation s. Such matrices are 0,1 matrices with a unique 1 in every row and column. Consider the equation (Ps)tAPs = A, where A is the adjacency matrix of the Euclidean graph G. It is a well known fact that for a graph G with adjacency matrix A, the set of all solutions of this equation constitutes the automorphism group of G. Suppose Aut(G) = {s1, s2,…, sm}. The matrix SG = [sij], where sij = si(j) is called a solution matrix for G. Since the rows of this matrix are elements of the automorphism group of G, to compute the automorphism group of G it is enough to calculate a solution matrix for G. The author in [16] proved a result that is useful for computing the symmetry of molecules. Using this result, Lemma 1 and its Corollary, we can write a MATLAB program [22] for computing a solution matrix for the automorphism group of Euclidean graphs.
A MATLAB Program for Computing the Symmetries of Molecules


Our program needs the Cartesian coordinates of the atoms to determine the Euclidean distances in the molecule under consideration. If we calculate these distances by HyperChem [23], Gaussian 03 [24] or another software, then for computing the symmetry of a molecule under consideration, it is enough to delete the first eight lines of the program and load the distance matrix of the molecule.
Results and Discussion
The aim of this section is to apply our program for computing the automorphism group of Euclidean graph of Bis Benzene Chromium(0). The Cartesian coordinates of the atoms of this molecule is computed by HyperChem. It is useful to mention that in our program the accuracy is very important. In fact, our calculations for computing the symmetry of some fullerenes show that, if we change the accuracy, then the automorphism group would be changed.
We now calculate the symmetry of Bis Benzene Chromium(0). Let Aut(G) be the automorphism group of Euclidean graph G of the mentioned molecule with D6d symmetry point group. Consider this molecule, Figure 1, to illustrate Euclidean graph, Figure 2, and its automorphism group. It is useful to mention here that we do not have to work with exact Euclidean distances since a mapping of weights into a set of integers suffices as long as different weights are identified with different integers. To illustrate this, let us use an euclidean edge weighting for Bis Benzene Chromium(0) obtained from Table 1 and our program. Suppose F is the 13 × 13 integer matrix obtained from Euclidean distances. From Table 1, the matrix F is as follows:

Figure 1: The Structure of Bis Benzene Chromium(0) With D6d Point Group

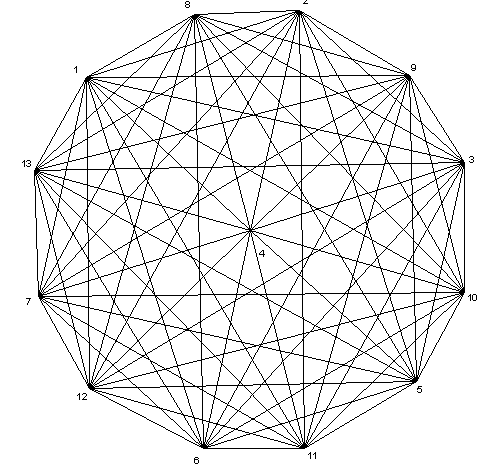
Figure 2: The Euclidean graph of Bis Benzene Chromium(0).
Not all 13! permutations of the vertices of the molecule belong to the automorphism group of its weighted graph since the weights of all the edges are not the same. For example, the permutation g = (1,2,3,4,5,6,7) does not belong to the automorphism group since the resulting graph does not preserve connectivity. Let X denote the set of all solutions of matrix equation PtFP = F. Then Aut(G) = {∞ ε S13 | P∞ ε X } is the automorphism group of Euclidean graph of Bis Benzene Chromium(0). We now apply our MATLAB program to find a solution matrix for this group. After running our program, we can see that G is a non-abelian group of order 8. Using the solution matrix and a simple GAP program, we can find the structure of the automorphism group G of the Euclidean graph of Bis Benzen Chromium(0). We mention that this program is very fast and its running time is less than 0.1 s.
G = { (1)(2)(3)(4)(5)(6)(7)(8)(9)(10),(2,3)(4,7)(5,9)(6,8)(11,12),
(1,4,10,7)(2,5,11,8)(3,6,12,9),(1,4)(2,6)(3,5)(7,10)(8,12)(9,11),
(1,7,10,4)(2,8,11,5)(3,9,12,6),(1,7)(2,9)(3,8)(4,10)(5,12)(6,11),
(1,10)(2,11)(3,12)(4,7)(5,8)(6,9),(1,10)(2,12)(3,11)(5,6)(8,9) }.
Table 1: Distance Matrix (angstroms) of Cr(C6H6)2

Conclusions
This method is usually very useful for calculating symmetries of the molecule, when the number of vertices is at most 100. In the case that the graph under consideration has a large number of vertices, it is better to find a subgroup of the full symmetric group containing automorphism group of our weighted graph. Then apply this subgroup and our GAP program to compute the automorphism group of the graph.
Acknowledgement
We are greatly indebted to the referees for their helpful remarks. The research of the second author was in part supported by a grant from CEAMA of the Isfahan University of Technology.
References
[1] Randic, M., Chem. Phys. Letters 1976, 42, 283-287. [ Links ]
[2] Randic, M., J. Chem. Phys. 1974, 60, 3920-3928. [ Links ]
[3] Balasubramanian, K., Chem. Phys. Letters 1995, 232, 415-423. [ Links ]
[4] Balasubramanian, K., J. Chem. Phys. 1980, 72, 665-677. [ Links ]
[5] Balasubramanian, K., Intern. J. Quantum Chem. 1982, 21, 411-418. [ Links ]
[6] Balasubramanian, K., Chem. Rev. 1985, 85, 599-618. [ Links ]
[7] Balasubramanian, K., J. Phys. Chem. 2004, 108, 5527-5536. [ Links ]
[8] Balasubramanian, K., Chem. Phys. Letters 2004, 391, 64-68. [ Links ]
[9] Balasubramanian, K., Chem. Phys. Letters 2004, 391, 69-74. [ Links ]
[10] Hao, J.F.; Xu, L., Computers and Chemistry 2002, 26, 119-123. [ Links ]
[11] Ivanov, J., J. Chem. Inf. Comput. Sci. 2004, 44, 596-600. [ Links ]
[12] Ivanov, J.; Schürmann, G., J. Chem. Inf. Comput. Sci. 1999, 39, 728-737. [ Links ]
[13] Longuet-Higgins, H.C., Mol. Phys. 1963, 6, 445-460. [ Links ]
[14] Ashrafi, A.R., MATCH Commun. Math. Comput. Chem. 2005, 53, 161-174. [ Links ]
[15] Moghani, G.A.; Ashrafi, A.R.; Hamadanian, M., J. Zhejiang Univ. SCI. 2005, 6B(3), 222-226. [ Links ]
[16] Ashrafi, A.R., Chem. Phys. Letters 2005, 406, 75-80. [ Links ]
[17] Ezra, G.S., Symmetry Properties of Molecules, Lecture Notes in Chemistry 28, Springer, Berlin-Heidelberg, 1982. [ Links ]
[18] Herndon, W.C., Chemical Applications Of Graph Theory And Topology, ed. R.B. King; Physical and Theoretical Chemistry; Elsevier, Amsterdam, 1983, 28, 231-242. [ Links ]
[19] Trinajstic, N., Chemical Graph Theory, CRC Press, Boca Raton, FL., 1992. [ Links ]
[20] Schönert, M.; Besche, H.U., Breuer, Th.; Celler, F.; Eick, B.; Felsch, V.; Hulpke, A.; Mnich, J.; Nickel, W.; Pfeiffer, G.; Polis, U.; Theißen, H.; Niemeyer, A., GAP, Groups, Algorithms and Programming, Lehrstuhl D für Mathematik, RWTH, Aachen, 1995. [ Links ]
[21] Ashrafi, A.R.; Hamadanian, M., Croatica Chem Acta 2003, 76, 299–303. [ Links ]
[22] Higham, D.J.; Higham, N.J., MATLAB Guide, Society for Industrial and Applied Mathematics (SIAM), Philadelphia, PA, 2000. [ Links ]
[23] HyperChem package Release 7.5 for Windows, Hypercube Inc., 1115 NW 4th Street, Gainesville, Florida 32601, U. S. A. 2002. [ Links ]
[24] Frisch, M; Truck, G. W. GAUSSIAN 03, Revision 03, Gaussian, Inc., Pittsburgh PA, USA, 2003. [ Links ]














