AYUDA DIDÁCTICA

Ambigüedades en términos científicos: El uso del “error” y el “sesgo” en estadística

 

Facundo J. Oddi^1,*; Francisco J. Aristimuño²; Carolina Coulin¹ & Lucas A. Garibaldi¹

¹ Instituto de Investigaciones en Recursos Naturales, Agroecología y Desarrollo Rural (IRNAD), Sede Andina, Universidad Nacional de Río Negro (UNRN) y Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET). San Carlos de Bariloche, Río Negro, Argentina.

² Centro de Estudios en Ciencia, Tecnología, Cultura y Desarrollo (CITECDE), Sede Andina, Universidad Nacional de Río Negro (UNRN) y Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET). San Carlos de Bariloche, Río Negro, Argentina.

* foddi@unrn.edu.ar

---

RESUMEN

El uso correcto de la estadística es clave para los profesionales que responden preguntas a partir de datos; entre ellos están los ecólogos. Sin embargo, a estos profesionales, la estadística les suele resultar confusa; en parte, esto se debe a dificultades relacionadas con la terminología. Muchas de estas dificultades derivan de los múltiples significados que tiene un término, tanto dentro como fuera del ámbito estadístico. Para los profesionales de habla hispana, la traducción de términos desde el inglés también aporta a esta confusión. En este trabajo exponemos (e intentamos clarificar) algunos de estos problemas a partir de dos de los términos que conforman la base de un curso de estadística introductorio: error y sesgo. Estos términos son discutidos en los diferentes contextos que se atraviesan en la resolución de problemas utilizando la estadística: muestreo, medición, inferencia y predicción. El error es inherente a la estadística y, según el contexto, se lo usa para cuantificar distintos tipos de variabilidad o para indicar la posibilidad de equivocarse al tomar una decisión. El sesgo, en cambio, refleja la tendencia hacia ciertos valores o elementos y, de no evitarse, conlleva a conclusiones erróneas. Proponemos que los problemas asociados con la ambigüedad léxica se aborden desde la enseñanza universitaria, y sobre esa base brindamos algunas recomendaciones. En este sentido, si bien el presente artículo provee una guía para que los profesionales hagan un uso adecuado de algunos términos estadísticos, también brinda un aporte para el ejercicio docente.

Palabras clave: Terminología estadística; Ambigüedad léxica; Aprendizaje estadístico; Muestreo; Medición; Estimación; Inferencia; Predicción.

ABSTRACT

Ambiguities in scientific terms: The use of “error” and “bias” in statistics.

The proper use of statistics is key for professionals who answer questions from data, including ecologists. However, statistics is generally confusing for these professionals, in part due to difficulties related to its terminology. Many of these difficulties derive from the multiple meanings that a term has, both inside and outside the statistical scope. For Spanish-speaking professionals, the translation of English terms also contributes to this confusion. In this paper we show (and intend to clarify) some of these problems from two key terms of an introductory statistics course: error and bias. These terms are discussed in the different contexts that involve problem resolution using statistics: sampling, measurement, estimation, inference and prediction. Error is inherent to statistics and is used to quantify different types of variability or to indicate the possibility of making mistakes on decision making, depending on the context. On the other hand, bias reflects the tendency towards certain values and/or elements, and leads to erroneous conclusions if not avoided. We propose that the problems associated with lexical ambiguity should to be addressed from university teaching and based on this, we offer some recommendations. Thus, the present article not only offers a guide for professionals to make an adequate use of some statistical terms but also provides a contribution for teaching.

Keywords: Statistic terminology; Lexical ambiguity; Statistic learning; Sampling; Measurement; Estimation; Inference; Prediction.

Recibido: 17 de noviembre de 2017
Aceptado: 28 de junio de 2018

Editora asociada: Roxana Aragón

---

INTRODUCCIÓN

En las últimas décadas, muchos expertos en educación señalaron las dificultades de la enseñanza y el aprendizaje en estadística (Garfield and Ahlgren 1988; Hogg 1991; Garfield 1995; Batanero et al. 2004; Garfield and Ben-Zvi 2007). En particular, la comunidad estadística enfatiza los problemas asociados con la ambigüedad léxica de su terminología (Richardson et al. 2013). Uno de estos problemas emerge cuando se aplica un mismo término a múltiples conceptos. Por ejemplo, error estándar y error estándar de estimación son conceptos con una terminología común, pero reflejan aspectos muy diferentes de un modelo estadístico. Otra dificultad surge de que muchos de estos conceptos son denominados por términos que también se usan en el lenguaje cotidiano (Menditto et al. 2007), por lo cual se deben re-aprender (Barwell 2005). Por ejemplo, cuando en los cursos de estadística se enseña el concepto de significancia, los estudiantes, además de incorporar el concepto estadístico, deben desvincularlo del uso ordinario que le dan a esta palabra, lo que les presenta una dificultad extra en el aprendizaje (Lavy and Mashiach- Eizenberg 2009; Richardson et al. 2013). Por otro lado, mientras que durante su formación los científicos y profesionales de distintas disciplinas, entre ellas la ecología, adquieren un manejo fluido de la jerga técnica propia de su área de conocimiento, la terminología estadística no conforma el núcleo de su contexto profesional. Como consecuencia, estos profesionales se enfrentan al problema de aplicar métodos de una disciplina que posee una terminología confusa en sus conceptos claves (Kaplan et al. 2009; Lavy and Mashiach- Eizenberg 2009) y que no compone la base de su formación académica (Richardson et al. 2013). El problema es todavía más marcado para los profesionales de habla hispana debido a que el inglés es el idioma dominante de la ciencia y la tecnología (van Weijen 2012). Por lo tanto, además de la confusión que presenta la jerga estadística en sí misma, se agrega la deformación asociada a su traducción. Todo ello afecta de forma negativa el avance del conocimiento y la resolución de problemas concretos, ya que tanto para formular preguntas en un lenguaje estadístico como para interpretar y comunicar los resultados obtenidos es necesario que la terminología sea definida con claridad y se la use de manera inequívoca (Hand 1994).

Una vez que se toma consciencia de las ambigüedades de un lenguaje técnico, la comprensión de sus conceptos mejora notablemente (Kaplan et al. 2010). El objetivo de este trabajo es mostrar que la terminología estadística española puede presentar un léxico ambiguo para sus usuarios. Para ello, identificamos y discutimos algunos términos claves que, aplicados en los distintos contextos por los que atraviesa la resolución de problemas utilizando la estadística, representan conceptos diferentes. También abordamos aspectos referentes a su ambigüedad léxica con el uso cotidiano por fuera de la estadística y mostramos algunos ejemplos donde la traducción desde la bibliografía inglesa potencia los problemas asociados a la terminología. Discutimos sólo dos términos (error y sesgo) de un universo considerablemente más amplio de términos estadísticos que pueden presentar confusión (Kaplan et al. 2009, 2010; Richardson et al. 2013). Si bien la selección fue subjetiva, éstos conforman buena parte de los principios básicos que el estudiante debería incorporar en un primer curso de estadística y son claves para responder preguntas con datos. Creemos que la enseñanza estadística es el ámbito desde el cual comenzar a solucionar la problemática abordada. En este sentido, si bien el presente artículo provee una guía para que los usuarios de la estadística hagan un uso adecuado de esta herramienta, también brinda un aporte para los docentes.

AMBIGÜEDAD LÉXICA EN TÉRMINOS ESTADÍSTICOS CLAVE

En esta sección exponemos los términos estadísticos seleccionados, acompañando cada concepto discutido con su denominación en el idioma inglés. Estos conceptos se circunscriben a los siguientes procesos: muestreo, medición, inferencia y predicción (Tabla 1). Nuestra intención es presentar y relacionar los conceptos de manera didáctica, sin dar definiciones formales ni presentaciones teóricas que sugerimos consultar en los textos introductorios de estadística en español (e.g., Sokal and Rohlf 2002; Anderson et al. 2008a). Para ello emplearemos el ejemplo de un cuadro de un establecimiento agropecuario donde hace algunos meses se sembró maíz. Nuestro objetivo es estudiar la altura que alcanzaron las plantas del cuadro para hacer inferencias sobre su media poblacional. La población de interés está conformada por todas las plantas de maíz del cuadro y cada planta representa la unidad experimental. Recolectamos una muestra de 30 plantas a las que, en el campo, les registramos la altura con una vara cuya unidad mínima es el centímetro (resolución del instrumento).

Tabla 1. Ambigüedad léxica en los términos error y sesgo según el contexto que se atraviesa en la resolución de problemas utilizando la estadística: muestreo, medición, inferencia (estimación y prueba de hipótesis) y predicción.
Table 1. Lexical ambiguity in the terms error and bias according to the context involving problems resolution using statistics: sampling, measurement, inference (estimation and hypothesis test) and prediction.

Será útil que antes de comenzar presentemos dos conceptos que son el eje de gran parte de los términos discutidos: parámetro poblacional y estimador muestral. El parámetro poblacional es una constante que caracteriza o representa a la población en algún aspecto y su valor es función de los datos de la población. Como ejemplo podemos citar la media poblacional (μ) o la varianza poblacional (σ²). En general, nos interesa conocer el parámetro poblacional, pero, dado que ello no es posible a menos que relevemos el total de la población, lo estimamos mediante los datos de una muestra. El cálculo que aplicamos en la muestra para estimar el parámetro poblacional es el estimador muestral; la media muestral (x) y la varianza muestral (s²), en el caso los parámetros mencionados como ejemplo. El estimador muestral es función de los datos de la muestra y, por lo tanto, varía con la misma.

Error

Es uno de los términos más utilizados en estadística y forma parte de múltiples conceptos (Tabla 1): puede asociarse a diferentes tipos de variabilidad (Walther and Moore 2005; Bolker 2008) y también al proceso de toma de decisiones (Garibaldi et al. 2017). Aplicado en el contexto de medición de unidades experimentales, refleja las disparidades entre la realidad y lo registrado por el observador (error de medición); estas disparidades pueden ser aleatorias (error aleatorio) o sistemáticas (error sistemático). Los valores obtenidos mediante el proceso de medición conforman la información proporcionada por la muestra, y aquí es necesario diferenciar la variabilidad entre unidades experimentales (desvío estándar) de la variabilidad entre muestras (error estándar). La variabilidad entre muestras es útil en el marco inferencial de la estimación para cuantificar las diferencias entre los estadísticos muestrales y los parámetros poblacionales (error de muestreo). Cuando la inferencia se utiliza para tomar decisiones, el término error se aplica a las dos equivocaciones que pueden cometerse al poner a prueba hipótesis sobre los parámetros poblacionales (error de tipo I y II). A su vez, se lo utiliza en el contexto de la predicción para reflejar las diferencias entre los valores observados y los que predice el modelo estadístico (error estándar de estimación).

Error de medición: error aleatorio y error sistemático

Una vez seleccionadas las unidades experimentales procedemos a registrar la(s) variable(s) de interés. En nuestro ejemplo, medimos la altura de las 30 plantas que conforman la muestra. Para cada planta que medimos existe una diferencia entre su altura real y la que registramos con el instrumento de medición, y ello es lo que se conoce como error de medición (en inglés, measurement error) (Rabinovich 2006). Esta diferencia se debe a la imposibilidad de observar perfectamente el mundo y depende, entre otras cosas, del instrumento, de la destreza del observador y de las condiciones de medición. Por ejemplo, si la verdadera altura de una de las plantas de la muestra fuera 1.4739 m, debido a la resolución de la vara, la mejor medición que podríamos obtener es 1.47 m (el valor de cuatro cifras decimales luego del centímetro sólo se usa con fines didácticos, ya que es poco probable que el valor real de una variable continua como la altura pudiera ser exacto; si así fuera, incluso, tampoco sería posible conocerlo a pesar de contar con un instrumento de una resolución mayor a 4 decimales de centímetro [e.g., si pudiéramos medir con una resolución de 1x10- 5 cm, sería imposible saber si la altura de esta planta es 1.47390 o 1.473901...]). La diferencia entre el valor real y el registrado podría ser incluso mayor como resultado de la impericia del observador o de las condiciones de contexto (e.g., viento que mueve las plantas). En este caso, podríamos haber registrado una altura de 1.49 m, con lo cual el error de esta medición sería de 0.0161m (Figura 1a). Esta diferencia se puede considerar azarosa, es decir, su valor (magnitud y dirección) se presenta de manera aleatoria dentro del error de medición y generalmente se lo denomina error aleatorio (en inglés, random error) (Rabinovich 2006). Sin embargo, los errores de medición no siempre son aleatorios. Por ejemplo, en caso que la vara de medición tuviera una falla de fabricación de modo que a su base le faltasen los dos primeros centímetros (y que ello no fuera percibido), en el caso antes mencionado registraríamos una altura de 1.51m (Figura 1a). En efecto, todas las alturas medidas con esta vara repetirían un error de 2 cm por encima del valor real. En este caso, se dice que el instrumento provoca un error sistemático (en inglés, systematic error) en la medición (Rabinovich 2006).

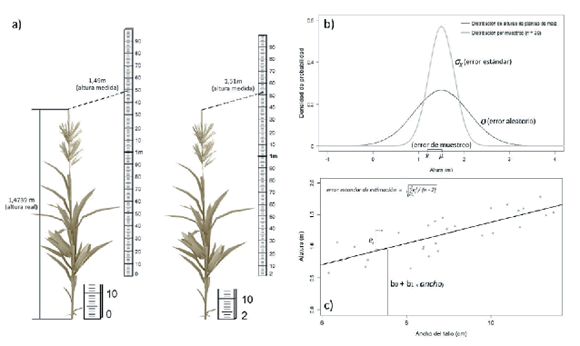
Figura 1. Error en los diferentes contextos estadísticos. a) Error debido a la observación imperfecta: la altura de una planta de maíz cuyo valor real es de 1.4739m es registrada como 1.49m (izquierda) debido a las limitaciones de escala en el instrumento de medición y a la impericia del observador. Error debido a la falta de calibración del instrumento: la altura de esta planta medida con una vara a la que le faltan dos centímetros en su base (derecha) registra un valor de 1.51m (con lo que se incurre en sesgo de medición, ver Figura 2 y Tabla 1). b) Error debido a relevar parte de la población: sobre el eje de abscisas se puede observar que el promedio de las alturas de las 30 plantas que conforman la muestra (, estimación puntual) difiere de la altura media de todas las plantas del cuadro (μ, parámetro poblacional). Error debido a la variabilidadentre unidades experimentales: la variabilidad entre las alturas de las plantas de maíz del cuadro puede ser representada por una distribución de probabilidades normal con media μ y desvío estándar σ. Error debido a la variabilidad entre muestras: suponiendo que se extraen un gran número de muestras de 30 plantas, la variabilidad entre sus medias puede ser representada por una distribución normal con media igual a la media poblacional y desvío estándar () igual a σ/ . c) Error debido a las fuentes de variabilidad que no están incluidas entre los predictores del modelo: la variabilidad en torno a las predicciones de un modelo que tiene el ancho del tallo como predictor de la altura es cuantificada mediante las diferencias entre los valores observados y los predichos por el modelo, las cuales se denominan errores (ε). Cada observación (i) tiene un error asociado (ε_i). El modelo se plantea en la población (β₀+β₁ ancho) y se estima con los datos de la muestra (b₀+b₁ ancho). A la diferencia entre un valor observado (alturai) y la predicción que le corresponde según el modelo estimado (b₀+b₁ anchoi) se le denomina residual (e_i); cada residual en la muestra es una estimación de un error en la población. El error estándar de estimación poblacional se estima con los residuales de acuerdo con

Figure 1. Error in the different statistical contexts. a) Error due to imperfect observation: the height of a corn plant is recorded at 1.49m, while its actual value is 1.4739m (left) due to the limitations of the scale of the measuring instrument and the lack of skill of the observer. Error due to the lack of calibration of the instrument: the height of the plant is measured with a rod that is missing two centimeters in its base (on the right) registers a value of 1.51m (incurring measurement bias, see Figure 2 and Table 1). b) Error due to collectpart of the population: the difference between the average of the heights of the 30 plants that make up the sample (, point estimate) and the average height of all the plants in the plot (μ, population parameter) is quantified on the x-axis. Error due to the variability among experimental units: the variability among the heights of corn plants in the plot can be represented by a normal probability distribution with mean μ and standard deviation σ. Error due to variability among samples: assuming that a large number of samples with 30 plants are taken, the variability among their means can be represented by a normal distribution with mean equal to the population mean and standard deviation () equal to σ/. c) Error due to variability sources which are not included among the predictors of the model: the variability around the predictions of a model which has stem width as a height predictor are quantified by the differences between the observed values and those predicted by the model, which are called errors (ε). Each observation (i) has an associated error (ε_i). The model is formulated for the population (β₀+β₁ width) but is estimated with sample values (b₀+b₁ width). The difference between an observed value (widthi) and the predicted value by the model (b₀+b₁ widthi) is named residual (e_i); each sample residual estimates an error in the population. The population standard error of the estimate is estimated with the sample residuals by

Desvío estándar y variabilidad aleatoria

Dado que las plantas no son todas iguales, es interesante tener una medida de cuán diferentes son entre ellas. Una de las medidas utilizadas para ello es el desvío estándar (en inglés, standard deviation) (Anderson et al. 2008a), a veces llamado desviación típica (Sokal and Rohlf 2002), de la población (σ):

donde x_i indica la altura de la planta i, y N la cantidad de plantas en el cuadro (el tamaño de la población). En estadística, la variabilidad entre unidades experimentales (las plantas en este caso) suele denominarse variabilidad aleatoria (en inglés, random variability) y σ es una medida de esa variabilidad. La variabilidad aleatoria se debe a diversas fuentes, que en nuestro ejemplo podrían ser las condiciones de micrositio donde la planta crece, su genética, la capacidad de la raíz para explorar el suelo y también el error aleatorio de medición. En efecto, la variabilidad entre las mediciones de las alturas se compone de la variabilidad real entre unidades experimentales y de la variabilidad provocada por el error de medición aleatorio. Dado que en la mayoría de los casos no hay una forma operativa de separar ambos componentes, se los estima de manera conjunta a través del desvío estándar muestral (s):

donde n representa el tamaño de la muestra. Volveremos sobre este estimador al discutir el sesgo.

Error de muestreo y error estándar

Luego de medir todas las plantas de la muestra, el promedio de alturas obtenido, es decir la media muestral (x), es nuestra estimación puntual de la altura media de todas las plantas del cuadro, o sea, de la altura media poblacional (μ). A la diferencia entre la estimación muestral y el parámetro poblacional se la denomina error de muestreo (en inglés, sampling error) (Figura 1b). Dado que el parámetro poblacional es desconocido, el error de muestreo también lo es y, por lo tanto, no se lo determina de forma directa, sino que se lo cuantifica a partir del error estándar (en inglés, standard error) (Anderson et al. 2008a), también conocido como error típico (Sokal and Rohlf 2002).

Las 30 plantas seleccionadas serían sólo una realización de una cantidad muy grande de posibles muestras de 30 plantas dentro del cuadro que estamos estudiando. Si recolectáramos nuevas muestras, cada una de estas tendría una media muestral que, dada la variabilidad implícita entre las unidades experimentales, diferiría del resto. Por lo tanto, existe variabilidad entre muestras, es decir, la estimación de la altura media poblacional varía de muestra en muestra. De igual manera que con las unidades experimentales, podríamos obtener el desvío estándar de las medias de las muestras de 30 plantas. Este desvío estándar ‘especial’ es el error estándar de la media. Según el Teorema Central del Límite, no es necesario recolectar varias muestras para estimarlo (este teorema demuestra que la distribución de la media muestral de una variable aleatoria con media y desvío estándar finito se aproxima a una distribución normal a medida que aumenta el tamaño de la muestra [n]. El n mínimo que se requiere para la media muestral se distribuya normalmente depende de la forma de la distribución de la variable aleatoria estudiada, y disminuye a medida que ésta se aproxima más a una normal. Además, el teorema demuestra que la media de esta distribución por muestreo es idéntica a la media de la variable aleatoria y que su desvío [error estándar] es igual al desvío estándar de la variable dividido por √n; la demostración de este teorema supone observaciones independientes e idénticamente distribuidas). Se demuestra, entonces, que conociendo la variabilidad entre unidades experimentales (σ) y el tamaño muestral (n) se puede determinar la variabilidad entre muestras (Figura 1b), es decir el error estándar de la media ():

Debido a que σ también es un parámetro desconocido, se utiliza su estimación (s) para obtener una estimación del error estándar de la media:

Si bien hemos discutido sobre el error estándar aplicado al estimador media muestral, cualquier parámetro poblacional de interés es estimado a partir de los datos de una muestra mediante un estadístico que tiene un error estándar asociado. En efecto, el error estándar es un concepto clave en el contexto de estimación y representa lo opuesto a la precisión.

Error de tipo 1 y error de tipo 2

Dado que las estimaciones muestrales varían de muestra en muestra, es posible considerarlas variables aleatorias y suponer una distribución de probabilidades, es decir, la distribución del estadístico. Esta distribución recibe el nombre de distribución por muestreo. En nuestro ejemplo, indicaría la distribución de probabilidades de las medias de todas las muestras de 30 plantas de maíz que podrían ser extraídas del cuadro. A partir de diversas aproximaciones es posible conocer la forma de esta distribución por muestreo. Por ejemplo, el Teorema Central del Límite también demuestra que a medida que el tamaño de la muestra aumenta, las medias muestrales tienden a una distribución normal con media igual a la media poblacional y, con un tamaño muestral suficientemente grande, desviación estándar igual al error estándar () (Figura 1b). Bajo este contexto, una estrategia de inferencia estadística muy utilizada es determinar qué tan probable es el estadístico muestral obtenido, o uno más extremo, dado un valor supuesto del parámetro poblacional. En términos técnicos, la suposición acerca del valor del parámetro se denomina hipótesis nula y la probabilidad de observar el estadístico muestral, o uno más extremo, dada la hipótesis nula, se denomina valor P. La lógica es que si el valor P es pequeño, entonces la hipótesis nula no es respaldada por los datos, esto es, no tiene soporte empírico. Supongamos que en nuestra muestra de 30 plantas registráramos una altura media de 1.38 m y un desvío estándar de 0.54 m. Con esta información podríamos corroborar hasta qué punto estos resultados apoyan una hipótesis relevante acerca del problema que abordamos. Por ejemplo, supongamos que la experiencia nos indicase que en la zona donde se ubica el establecimiento agropecuario las plantas de maíz deben alcanzar una altura promedio de al menos 1.5 m para que el rendimiento del cultivo cubra los costos de producción. Este es un contexto de toma de decisiones en el cual sería relevante conocer si nuestro cuadro presenta problemas de rendimiento. De acuerdo a la aproximación antes detallada, deberíamos plantear la hipótesis nula (H₀):

H₀: μ≥15 que representa la situación en la que el cuadro que se está estudiando no presenta problemas de rendimiento. Luego calculamos el valor P para la media muestral obtenida:

valor P = P(≤ 1.38μ = 1.5; = 0.10) = 0.11

Esta expresión indica que en caso que la altura media de las plantas del cuadro fuera 1.5 m o mayor (y el desvío estándar entre plantas fuera de 0.54 m, lo cual resultaría en un error estándar de 0.10 m), la probabilidad de obtener una media muestral menor o igual a 1.38 m es 0.11. El valor P obtenido surge de calcular el área bajo la curva entre -oo y 1.38 en una distribución normal con media 1.5 y desviación estándar 0.10. Ahora bien, ¿la hipótesis nula es respaldada por los datos o deberíamos rechazarla? Esta pregunta implica decidir si el resultado de la muestra (1.38 m) es un evento esperable en una población de plantas con una altura promedio de al menos 1.5 m o debería considerarse tan poco probable que contradice la hipótesis. Aquí, el marco de inferencia frecuentista sugiere establecer a priori un umbral de probabilidad y rechazar la hipótesis nula en caso de que el valor P sea menor al mismo. A este umbral se lo denomina nivel de significancia o probabilidad de cometer un error de tipo 1 (en inglés, type I error), error que se define como la equivocación al rechazar una hipótesis nula que es verdadera. En nuestro ejemplo, cometer un error de tipo I equivaldría a concluir que las plantas de maíz del cuadro no miden en promedio 1.5 m, o más, cuando en efecto esa es su altura. Lo usual es utilizar un nivel de significancia de 0.05, con lo cual, dado el valor P de 0.11, no existe evidencia suficiente para afirmar que la altura media de las plantas es menor a 1.5 m y, por lo tanto, concluiríamos que no tenemos pruebas suficientes para decir que el cultivo presenta problemas de rendimiento.

Sin embargo, podría suceder que la altura promedio del cuadro fuera en verdad menor a 1.5 m (e.g., 1.3 m) y que el contraste de hipótesis estadísticas no tuviese la capacidad de detectarlo (capacidad que se denomina potencia estadística). En este caso, habríamos tomado una decisión equivocada al no rechazar la hipótesis nula. Cuando ello sucede se dice que se comete un error de tipo 2 (en inglés, type II error), que se define como la equivocación de no rechazar una hipótesis nula que es falsa.

Error estándar de estimación y cuadrado medio del error

Supongamos ahora que la altura de las plantas (y) del cuadro se relaciona de manera lineal con el ancho del tallo (x) según el siguiente modelo estadístico:

y_i = β₀ + β₁ x_i + ε_i

ε_i ~ N(0, σ)_{independientes}

donde i indica la planta. Este modelo expresa que una parte de la altura de las plantas es explicada por una relación lineal con el ancho de su tallo (β₀+β₁x_i) y que el resto (ε_i) (Figura 1c) depende de otros factores (todas las fuentes de variabilidad aleatoria, excepto el ancho del tallo) y es representado por una distribución normal con media cero y desvío estándar σ. En efecto, σ es el desvío estándar de infinitas distribuciones normales, cada una con media igual a β₀+β₁x_i. Es decir, representa variabilidad aleatoria que, en la jerga del modelado estadístico, se denomina error estándar de estimación (en inglés, standard error of the estimate) (Tabla 1). Por lo tanto, a diferencia del error estándar, que cuantifica la variabilidad de un estadístico (variabilidad entre muestras), el error estándar de estimación refleja la variabilidad entre unidades experimentales que no es explicada por la componente matemática (la relación lineal) del modelo estadístico. Veámoslo de esta forma:

y_i = β₀ + ε_i

ε_i ~ N(0, σ)

representa un modelo en el cual la altura de las plantas no depende de otras variables (es decir, es un caso particular del modelo anterior, en el que β₁=0). En este caso, β₀ constituye la media poblacional de las alturas de las plantas (β₀=μ), con lo cual:

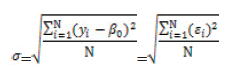
Es interesante mencionar que εi suele denominarse término de error de un modelo estadístico y que cuando éstos son evaluados mediante un ANOVA (análisis de la varianza), el cuadrado del error estándar de estimación (σ²) es denominado cuadrado medio del error (en inglés, mean square error ). El error estándar de estimación es clave en el contexto de predicción, ya que se lo usa como una medida de concordancia entre las predicciones del modelo estadístico y los datos observados, o sea, como medida de bondad de ajuste. Para cada observación (i) existe un error (ε_i) que en la muestra se denomina residual (e_i); el error estándar de estimación se estima con los residuales del modelo (Figura 1.c). De igual manera que con el error estándar, aquí también existe ambigüedad léxica (tanto el error estándar como el error estándar de estimación son, a su vez, desvíos estándar).

Sesgo

A diferencia del error, que es inevitable, siempre que se realiza una medición, estimación o predicción, el sesgo es evitable si se procede adecuadamente (en efecto, debe evitarse en cualquiera de los contextos de la resolución de un problema). Son cuatro los conceptos estadísticos asociados a sesgo que discutiremos: sesgo de muestreo, sesgo de medición, sesgo de estimación y sesgo de predicción (Tabla 1). Para una explicación más detallada, el lector puede recurrir a artículos como el de Walther y Moore (2005) o a textos como los de Sackett (1979) o Choi y Pak (2005), en los que se abordan otros tipos de sesgos que pueden ocurrir durante el proceso de investigación.

Sesgo de muestreo

El sesgo de muestreo (en inglés, sampling bias) hace referencia a la tendencia a seleccionar determinadas unidades experimentales por sobre otras cuando tomamos una muestra. Por ejemplo, la muestra sería sesgada si, para ahorrar tiempo, por ejemplo, al entrar al cuadro hubiésemos seleccionado las primeras 30 plantas de maíz que encontramos (Figura 2a). Podría suceder que en este sector del cuadro, el suelo fuera de mejor calidad, lo que resultaría en un crecimiento vegetal mayor. En este caso, registraríamos las plantas con las mayores alturas del cuadro y, en consecuencia, la muestra seleccionada no sería representativa de la población de interés (sobreestimaríamos el parámetro poblacional). Para no incurrir en sesgo de muestreo, todas las unidades experimentales deben tener la misma probabilidad de ser seleccionadas, para lo que se requiere aleatorizar el proceso de selección (Figura 2a). El sesgo de muestreo está muy relacionado con un concepto más amplio y fundamental en la teoría estadística: el de independencia.

Figura 2. Sesgo en los diferentes contextos estadísticos. a) Sesgo debido a la selección no aleatoria de las unidades experimentales: si las plantas de maíz que conforman la muestra (círculos negros) fueran seleccionadas en un solo sector del cuadro (izquierda), la muestra sería sesgada. Para que esto no ocurra, las plantas deberían ser seleccionadas aleatoriamente (derecha). b) Sesgo debido a la falta de calibración del instrumento: si las alturas de las plantas fueran medidas con una vara que está dañada en su base y no cuenta con sus dos primeros centímetros, todas las mediciones repetirán un error promedio de 2 cm por encima del valor real (arriba). En una vara bien calibrada, las desviaciones con respecto a la altura real serán, en promedio, nulas (abajo). c) Sesgo debido a utilizar un estimador sesgado: histogramas de dos estimadores del desvío estándar poblacional utilizando muestras de tamaño 30 extraídas de poblaciones normales estandarizadas (μ=0 yσ=1). Los histogramas fueron generados a partir de 100000 simulaciones en las que en cada una se estimó el desvío estándar utilizando como cociente el tamaño muestral (n) (arriba) y el tamaño muestral menos uno (n–1) (abajo). Mientras que en el histograma superior se observa que el promedio del estimador (línea punteada) es menor a 1, es decir E(s)̣≠σ, el promedio en el histograma inferior resulta ser igual a 1 (E(s)=σ). Por lo tanto, usar el tamaño muestral como divisor implica que el desvío estándar sea estimado con sesgo. d) Sesgo debido a especificar incorrectamente el tipo de relación entre la variable de interés y el predictor: si la relación entre la altura y el ancho del tallo fuera no lineal, un modelo lineal causaría rangos de subestimación y de sobreestimación.
Figure 2. Bias in the different statistical contexts. a) Bias due to the non-random selection of the experimental units: if the corn plants for the sample (black circles) were chosen from a single sector of plot (on the left), the sample would be biased. To avoid this, the plants should be selected at random (on the right). b) Bias due to the lack of calibration of the instrument: if the height of the plants were measured with a rod which is damaged in its base and misses the first two centimeters, all the measurements will repeat an average error of 2 cm over the real value (on the top). In a well-calibrated rod, the deviations with respect to the actual height will be, on average, zero (on the bottom). c) Bias due to the use of a biased estimator: histograms of two estimators of the population standard deviation as a result of 30-size samples drawn from standardized normal populations (μ=0 and σ=1). Histograms were generated from 100000 simulations in which the standard deviations were obtained using the sample size (n) (on the top) and the sample size minus one (n–1) (on the bottom) as a divisor. While in the upper histogram the average of the estimations (dotted line) is less than 1, that is E(s)≠σ, in the lower histogram the average turns out to be equal to 1 (E(s)=σ). Therefore, by using the sample size as a divisor implies the standard deviation to be estimated with bias. d) Bias due to applying a linear model to predict height of plants as a function of width stem. Since the relationship has a non-linear form, the model would have ranges with underestimation and ranges with overestimation.

Sesgo de medición

En caso de que el instrumento de medición presente un error sistemático (ver el apartado referente a error), se incurriría en sesgo de medición (en inglés, measurement bias). En nuestro ejemplo, si midiésemos las alturas con una vara a la que le faltan dos centímetros en su base, todas las plantas registrarían una altura de 2 cm por encima de su altura real y, por lo tanto, la estimación de la altura media poblacional también estaría sesgada en 2 cm (Figura 2b). El sesgo de medición se evita con el uso de instrumentos bien calibrados.

Sesgo de estimación

Los parámetros poblacionales son estimados mediante estadísticos (ambos conceptos fueron definidos al comienzo de la sección), los cuales son caracterizados por diferentes propiedades. Sesgo de estimación (en inglés, estimating bias) hace referencia justamente a una de ellas: el estimador se considera sesgado cuando su esperanza (E) difiere del valor del parámetro que estima (la esperanza, o valor esperado, es el valor medio de una variable aleatoria. Esto es, aquel valor que surge de promediar el producto entre cada resultado de la variable por su respectiva probabilidad para el caso de variables discretas, o la integración del producto entre la variable y su función de densidad de probabilidad a lo largo de todo su dominio en el caso de variables continuas. Matemáticamente, para variables discretas es E(x) = Σ〖xi*p(xi) 〗y para variables continuas es E(x) = ∫〖x*f(x)〗). Por ejemplo, si deseáramos conocer la variabilidad de las alturas de las plantas del cuadro, podríamos utilizar el desvío estándar muestral (s) para estimar el desvío estándar poblacional (σ). Sin embargo, si utilizáramos el desvío estándar definido como sigue:

esto es, con el tamaño muestral (n) como cociente, estaríamos recurriendo a un estimador sesgado ya que la esperanza de este estadístico difiere del parámetro poblacional (E(s)̣≠σ) (Figura 2c). En particular, subestimaríamos la variabilidad entre plantas. Se demuestra que un estimador insesgado del desvío estándar es:

Sesgo de predicción

El sesgo de predicción (en inglés, prediction bias) sucede cuando utilizamos un modelo estadístico que en ciertos rangos tiende a sub- o sobre- estimar los valores de la variable. Un ejemplo sería aplicar un modelo lineal entre la altura y el ancho del tallo (ver error) a una relación que fuera no-lineal (Figura 2d). En consecuencia, habría un rango de valores en el cual las predicciones del modelo serían menores a las alturas observadas (subestimación) y otro rango en el que estas predicciones serían mayores (sobreestimación). Para evitar este tipo de sesgo es necesario usar modelos adecuados , incluir los predictores necesarios, plantear correctamente la forma de la relación entre los predictores y la variable de interés, y utilizar una distribución de probabilidades adecuada para la variabilidad aleatoria.

USO COTIDIANO DE TÉRMINOS ESTADÍSTICOS

Respecto a la ambigüedad léxica con el uso cotidiano, es necesario remarcar que la connotación negativa que tiene la palabra error en el lenguaje corriente no es un aspecto menor (la Real Academia Española [RAE] lo define como: 1. Concepto equivocado o juicio falso; 2. Acción desacertada o equivocada; 3. Cosa hecha erradamente). En este sentido, su uso corriente se condice con las definiciones de error tipo I y II, y de igual manera con el error de medición, que representa una incongruencia con la realidad. Sin embargo, no se comete ninguna equivocación o error con el error de muestreo (Lawson 2010). Este error es una consecuencia inevitable de trabajar con muestras, y lo que podría juzgarse es si su magnitud es tolerable (o no) a los fines del problema. La misma consideración cabe para el error estándar de estimación, que refleja la variación no explicada por un modelo estadístico, y no es una equivocación del modelo sino una característica intrínseca de la representación de las poblaciones de interés mediante esta herramienta.

En el caso del sesgo, se lo define como la oblicuidad o torcimiento de algo hacia un lado, y en lo cotidiano se lo utiliza para indicar tendencia o inclinación en un sentido como, por ejemplo, al afirmar que ‘la opinión del periodista tiene un sesgo ideológico’ (de acuerdo con la RAE). En estadística, el sesgo hace referencia a diferentes conceptos de acuerdo al contexto en el que se lo aplique (ver sesgo). No obstante, siempre se lo emplea manteniendo el sentido que comúnmente se le da al término en su uso corriente.

Por lo tanto, mientras que en lo cotidiano al hablar de error nos referimos a un proceder incorrecto, para la estadística, en muchos de sus contextos, representa una característica intrínseca de los problemas que aborda. Recordemos que la estadística moderna ha surgido como respuesta a la variabilidad de las poblaciones y a la incertidumbre que conlleva la imposibilidad de relevarlas en su conjunto (Porter 1986; Stigler 1986). En cambio, el sesgo sí representa un inconveniente y debe evitarse en todas las fases de la resolución de un problema, ya que, en caso contrario, arribaremos a una respuesta equivocada. Para evitar la confusión léxica en torno a los términos estadísticos que se utilizan cotidianamente, es necesario que estos aspectos sean expuestos y discutidos durante el aprendizaje.

LA TRADUCCIÓN DE TÉRMINOS

La traducción del lenguaje técnico presenta dos problemas. El primero, asociado a la posible deformación al traducir la definición de un término. El restante, a la palabra con la que se lo traduce. Por ejemplo, la traducción más adecuada para el vocablo español error cuando indicamos una equivocación es “mistake”. En inglés, la equivocación (mistake) está incluida dentro del significado de la palabra error, aunque éste representa un concepto más amplio. Sin embargo, tanto mistake como error son traducidas al español como error, y ello impacta en la ambigüedad léxica discutida en la sección anterior.

En referencia al sesgo, se enfrentan problemas muy similares. En estadística, “skew” es un término que en la lengua anglosajona se aplica para indicar la forma de una distribución. “Skewed distribution” significa ‘distribución corrida hacia un lado (asimétrica)’ y, en general, se hace referencia al grado de ese corrimiento en términos de “skeweness of distribution” (asimetría de la distribución).

Sin embargo, a veces se lo traduce como sesgo de la distribución (por ejemplo, ver página 37 en Anderson et al. 2008b). Esto plantea evidentes problemas didácticos dado que el sesgo (“bias”) se relaciona con las propiedades de los estimadores o con problemas asociados con el diseño de muestreo, medición o predicción (ver en la sección anterior), pero en ningún caso con la forma asimétrica de la distribución.

CONSIDERACIONES FINALES

Es paradójico que, en general, quienes aplican la estadística encuentran mayores dificultades en la comprensión de los conceptos básicos de la disciplina que en el uso de modelos estadísticos de gran complejidad. Mientras la inclusión creciente de programas informáticos en la práctica de estudiantes y profesionales permitió simplificar el manejo de los modelos estadísticos, incluso aquellos extremadamente complejos, la apropiación de los conceptos fundamentales sigue presentando la misma dificultad que hace más de un siglo. Por ejemplo, durante el desarrollo de sus investigaciones, muchos ecólogos responden sus preguntas a partir de modelos lineales generalizados de efectos mixtos. Sin embargo, no siempre muestran una comprensión de los principios básicos que fundamentan su análisis, llevando a interpretar y comunicar resultados en forma incorrecta.

Parte de esta paradoja podría deberse a que el analista requiere aplicar (y comprender) conceptos básicos que presentan cierta confusión en su terminología. Dicha confusión podría menguar si durante los cursos de grado se remarcan especialmente los principios y conceptos que conforman las bases de la estadística como herramienta aplicada; entre ellos, error y sesgo (precisión e independencia también forman parte de este grupo). Es clave que, además de respetar la formalidad matemática, los docentes profundicen en la interpretación de los conceptos. Por ejemplo, al comunicar los resultados de un ejercicio resuelto en el aula el docente podría hablar de variabilidad entre unidades experimentales cuando informa el desvío estándar y de variabilidad entre muestras, en el caso del error estándar. La comprensión se vería favorecida si se exponen ejemplos integradores mediante los cuales explicar y contrastar los conceptos que pueden presentar confusión debido a su terminología (e.g., error de medición, error aleatorio, error de muestreo, error estándar, error estándar de estimación, errores de tipo I y II). Estos ejemplos deberían abarcar todos los contextos estadísticos por los cuales atraviesa la resolución de un problema (i.e., muestreo, medición, inferencia, predicción). También sería una buena práctica acompañar este proceso con tablas y gráficos como los expuestos en este trabajo. Además, se debería considerar que los términos también pueden contener ambigüedad léxica con el uso cotidiano. Si ello ocurre, se deberían remarcar las diferencias entre el concepto técnico del término y el uso corriente. Un aspecto no menor es que la bibliografía especializada se encuentra en su mayoría en inglés, lo que agrega una dificultad extra a los profesionales de habla hispana. En relación con ello, tanto la opción de ayuda como las salidas (resultados en pantalla) de muchos programas informáticos de análisis estadístico son presentadas en inglés. Por lo tanto, sería útil que, durante los cursos, la terminología estadística sea acompañada por su denominación en esta lengua.

En este trabajo expusimos casos en los que la terminología estadística puede presentarse ambigua o confusa para estudiantes y profesionales. Proponemos hacer conscientes de esta confusión a quienes toman cursos de estadística y también a quienes los dictan, a fin de favorecer tanto la resolución de problemas aplicados como el avance del conocimiento científico.

AGRADECIMIENTOS

A Alondra Crego, Aluminé Calfuquir y Florencia García Riva, quienes brindaron comentarios y reflexiones desde su visión como estudiantes y ayudantes en docencia enriqueciendo el desarrollo de este trabajo. Agradecemos también el financiamiento de la Universidad Nacional de Río Negro en investigación (UNRN, PI 40-B-567), la Agencia Nacional de Promoción Científica y Tecnológica (FONCyT, PICT 2016-0305) y la Fundación Bunge y Born (beca posdoctoral).

REFERENCIAS

1. Anderson, D. R., D. J. Sweeney, and T. A. Williams. 2008a. Estadística para administración y economía. 10ma edición. Thomson South-Western, Ohio.         [ Links ]

2. Anderson, D. R., D. J. Sweeney, and T. A. Williams. 2008b. Statistics for Business and Economics, Tenth Edition. Thomson South-Western, Ohio.         [ Links ]

3. Barwell, R. 2005. Ambiguity in the mathematics classroom. Language and Education 19(2):118-126.         [ Links ]

4. Batanero, C., J. D. Godino, and R. Roa. 2004. Training Teachers to Teach Probability. Journal of Statistic Education 12(1). URL: ww2.amstat.org/publications/jse/v12n1/batanero.html.         [ Links ]

5. Bolker, B. 2008. Ecological models and data. Princeton University Press, Princeton.         [ Links ]

6. Choi, B. C. K., and A. W. P. Pak. 2005. Bias, overview. Encyclopedia of Biostatistics. 1.         [ Links ]

7. Garfield, J. 1995. How Students Learn Statistics. International Statistical Review 63(1):25-34.         [ Links ]

8. Garfield, J., and A. Ahlgren. 1998. Difficulties in Learning Basic Concepts in Probability and Statistics: Implications for Research. Journal for Research in Mathematics Education 19(1):44-63.         [ Links ]

9. Garfield, J., and D. Ben-Zvi. 2007. How Students Learn Statistics Revisited: A Current Review of Research on Teaching and Learning Statistics. International Statistical Review 75(3):372-396.         [ Links ]

10. Garibaldi, L. A., F. Aristimuño, F. Oddi, and F. Tiribelli. 2017. Inferencia multimodelo en ciencias sociales y ambientales. Ecología Austral 27:348-363.         [ Links ]

11. Hand, D. J. 1994. Deconstructing Statistical Questions. Journal of the Royal Statistical Society. Series A (Statistics in Society) 157(3):317-356.         [ Links ]

12. Hogg, R. V. 1991. Statistical Education: Improvements Are Badly Needed. The American Statistician 45(4):342-343.         [ Links ]

13. Kaplan, J. J., D. G. Fisher, and N. T. Rogness. 2009. Lexical Ambiguity in Statistics: What do students know about the words association, average, confidence, random and spread? Journal of Statistics Education 17(3). URL: www.amstat.org/publications/jse/v17n3/kaplan.html.         [ Links ]

14. Kaplan, J. J., D. G. Fisher, and N. T. Rogness. 2010. Lexical Ambiguity in Statistics: How students use and define the words: association, average, confidence, random and spread. Journal of Statistics Education 18(1). URL: www.amstat.org/publications/jse/v18n2/kaplan.html.         [ Links ]

15. Lavy, I., and M. Mashiach-Eizenberg. 2009. The Interplay between Spoken Language and Informal Definitions of Statistical Concepts. Journal of Statistics Education 17(1). URL: www.amstat.org/publications/jse/v17n1/lavy.html.         [ Links ]

16. Lawson, J. 2010. Design and Analysis of Experiments with SAS. Champman and Hall, CRC Press, Boca Raton.         [ Links ]

17. Menditto, A., M. P Patriarca, and B. Magnusson. 2007. Understanding the meaning of accuracy, trueness and precision. Accreditation and Quality Assurance 12(1):45-47.         [ Links ]

18. Porter, T. M. 1986. The Rise of Statistical Thinking. Princeton University Press, New Jersey.         [ Links ]

19. Rabinovich, S. G. 2006. Measurement errors and uncertainties: theory and practice. Springer, New York.         [ Links ]

20. Richardson, A. M., P. K. Dunn, and R. Hutchins. 2013. Identification and definition of lexically ambiguous words in statistics by tutors and students, International Journal of Mathematical Education in Science and Technology 44(7): 1007-1019.         [ Links ]

21. Sackett, D. L. 1979. Bias in analytic research. Journal of Chronic Diseases 32:51-63.         [ Links ]

22. Sokal, R. R., and F. J. Rohlf. 2002. Introducción a la Bioestadística. Reverté S.A., Barcelona.         [ Links ]

23. Stigler, S. M. 1986. The History of Statistics. The Measurement of Uncertainty before 1900. Harvard University Press, Cambridge.         [ Links ]

24. Van Weijen, D. 2012. The Language of (Future) Scientific Communication. Research Trends 31. URL: www.researchtrends.com/issue-31-november-2012/the-language-of-future-scientific-communication.         [ Links ]

25. Walther, B. A., and J. L. Moore. 2005. The concepts of bias, precision and accuracy, and their use in testing the performance of species richness estimators, with a literature review of estimator performance. Ecography 28:815-829.         [ Links ]