Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Interdisciplinaria
versión On-line ISSN 1668-7027
Interdisciplinaria v.23 n.2 Buenos Aires ago./dic. 2006
Intervalos de confianza para las estimaciones de proporciones y las diferencias entre ellas
Robert G. Newcombe * y Cesar Merino Soto **
* PhD en Estadística Médica. Profesor de Estadística Médica del Departamento de Epidemiología, Estadística y Salud Pública de la Escuela de Medicina de Gales de la Universidad de Cardiff. E-Mail: Newcombe@cf.ac.uk
** Licenciado en Psicología. Responsable del Servicio de Psicología de la Defensoría Municipal de Chorrillos, Lima. E-Mail: sikayax@yahoo.com.ar
Resumen
En la actualidad se acepta por indicaciones de diferentes revistas científicas de ciencias sociales y salud, que los intervalos de confianza aportan información más descriptiva y son interpretativamente mejores que las pruebas de hipótesis, como una expresión de la incertidumbre que resulta del estudio de una muestra de limitado tamaño. En la investigación comparativo-descriptiva de las ciencias sociales, los métodos de análisis para variables categóricas parecen ser menos frecuentes, e incluso menos conocidos, que las variables independientes de intervalo. Hasta ahora, no hubo buenos métodos para calcular los intervalos de confianza para proporciones y diferencias entre proporciones. En este artículo se presentan métodos basados en trabajos de Newcombe (1998a, 1998b, 1998c) que superan los procedimientos tradicionales para estos cálculos y su cómputo es acompañado por una hoja de cálculo en MS Excel, en español, inglés y galés. Los métodos aquí presentados se basan en el método score, proveniente del trabajo de Wilson (1927). También se presentan ejemplos de los intervalos de confianza para proporciones simples y la diferencia entre ellas en muestras independientes y dependientes. Finalmente, se discute su uso juicioso en el contexto del diseño de la investigación.
Palabras clave: Intervalos de confianza; Proporciones; Diferencias; Método estadístico.
Abstract
Confidence intervals for estimations of proportions and their differences. It's nowadays accepted by many journals in diverse areas of health and social sciences, that confidence intervals give more descriptive information and they are better than hypothesis tests to express uncertainty resulting from limited sample size. The tool confidence intervals is a very useful descriptive frame to the researcher and to the consumer of statistical results, and their value as statistical summary is very important in descriptive and comparative studies. During decades, hypothesis tests have been the main support of statistical inference in comparative studies, whereas in comparative-descriptive research in social sciences, the method of analysis for categorical variables has been unusual. In fact, good methods to calculate confidence intervals for proportions and their differences, have not been generally available to researchers. Moreover, these methods have not been popular because they remain in statistical articles and away from non specialized users in mathematical knowledge. In this article methods based in works of Newcombe (1998a, 1998b, 1998c) and Wilson (1927) are reported. They overcome traditional methods for the proportion confidence intervals calculation.
Although this calculation is moderately simple, we took advantage of the computational technology to facilitate the process of calculus and to diminish errors. An Excel spreadsheet is now available, in Spanish, English and Welsh versions. Also equivalent versions were developed in the language of macros for SPSS and Minitab, which are all available in the internet address mentioned within the text of the article. These devices enable researchers to calculate the intervals using proven good methods; these methods come from the score method, which is derived from Wilson's work (1927). The typical situation for calculating intervals of confidence for proportions comes from a single sample of participants, and/or from a comparison between dependent and independent samples.The score method takes advantage of the calculation of a simple proportion, to extend it to the comparison between dependent and independent proportions.
The rationality of this extension is intuitive and is applied easily by means of the computer programs mentioned previously. Examples of confidence intervals calculus for a simple proportion and differences of proportions are presented and a discussion about their careful use in the context of research design is developed. Particularly, confidence intervals appear to be
one of the most useful forms to express the uncertainty in research findings, since the necessity to design studies using a limited sample from the population, makes that the appropriate interpretation of the intervals becomes a point of learning and agreement that the authors put in relevance.
Finally, the reader must have in mind that the estimation of the intervals does not give information in absolute terms, because it likewise offers a probability of containing the population value of interest (proportion). On the other hand, trying to reach the exact results is only one part of the problem. There are other important aspects as the choice of the statistical analysis and the study design, and within this last one, the sampling process, that continues being a prevalent source of weakness in research literature. If the specific sample is biased towards the population that we are trying to study (for example, certain population segment can be more motivated to fill in questionnaires or to participate in studies, in which case we are in front of a self-selected sample) or towards our expectations, every calculus that will be done will be biased. We hope that the readers of this article are aware and benefit of the usefulness of this old wine in new bottle method.
Key words: Confidence intervals; Proportions; Differences; Statistical method.
Introducción
De acuerdo con las normas mínimas y generales de publicación científica, los autores para someter sus manuscritos a revisión deben encarar una variedad de métodos a fin de resumir y presentar sus resultados. Estos incluyen resúmenes estadísticos, tales como media, desviación estándar y las proporciones, como así también las pruebas de hipótesis, que intentan dar criterios de decisión para saber si las diferencias o relaciones entre grupos son estadísticamente significativas. El uso de resúmenes estadísticos es fundamental en estudios descriptivos y comparativos. Durante muchas décadas, la prueba de hipótesis fue el soporte principal de la inferencia en los estudios comparativos. Frecuentemente surgen resultados no significativos cuando el tamaño de la muestra en estudio es muy pequeña como para detectar una diferencia importante.
En particular, los intervalos de confianza generalmente aparecen como la forma más útil de expresar la incertidumbre vinculada con los hallazgos de investigación, la misma que resulta del hecho que por necesidad, se estudia solo una muestra de limitado tamaño. Muchas publicaciones relacionadas con la salud, como la Revista Médica Británica, tienen tal política desde hace una década; pero esto se aplica no solamente al área de la investigación en salud, ya que por ejemplo Language Learning (2002) aclara en sus instrucciones que cuando se reporten hallazgos de investigación utilizando métodos estadísticos y cuantitativos, los autores deben informar acerca de las medidas de la magnitud del efecto y sus intervalos de confianza, al menos para los contrastes estadísticos más importantes que se informan.
Por otro lado, en las conceptualizaciones psicométricas la evaluación del error de medición ocupa un lugar prominente en la teoría clásica de los tests (Nunnally & Bernstein, 1995). La construcción de intervalos de confianza para los puntajes obtenidos es una práctica usual y a veces referida como un elemento esencial para la interpretación de los resultados de un sujeto (Gregory, 2000); la práctica de informar intervalos de confianza para los resultados advierte al usuario que no debe tomar como un indicador exacto la estimación cuantitativa del atributo medido. Las pruebas psicológicas que pretenden ser utilizadas para incrementar la información acerca de cómo tomar decisiones sobre un grupo de sujetos, frecuentemente en sus manuales presentan información para calcular intervalos de confianza basados en el error estándar de medición, por ejemplo, la muy conocida prueba de integración visomotora (Beery, 2000), la prueba Meeting Street para el desarrollo perceptual-motor (Woodburn, Boschini, Fernández & Rodríguez, 1993), la Escala de Dimensiones Conductuales (Bullock & Wilson, 1989) o las escalas de inteligencia de Weschler (Sattler, 1988). Incluso, recientemente se propuso reportar los intervalos de confianza para las estimaciones del coeficiente alpha, pues ello da al usuario una mejor información que la estimación puntual (Onwuegbuzie & Daniel, 2000, 2001).
Algunas cuestiones metodológicas tienen relevancia para aplicar técnicas de análisis. Por ejemplo, el tamaño del estudio se refiere, usualmente, al número de sujetos de un estudio o grupo. Pero también puede referirse a algún otro tipo de unidad de análisis más grande, como la familia o los episodios de crisis en una persona, aun cuando en el último caso se requiere gran precaución para considerar los diferentes episodios en el mismo sujeto, como eventos independientes. Otro aspecto es que muchos de los trabajos científicos de Psicología utilizan medidas continuas o al menos pseudocontinuas, tales como instrumentos llamados escalas. Al respecto, hay un considerable debate acerca de lo apropiado de considerar las puntuaciones en las pruebas psicológicas como escalas de intervalos, pero hay un fuerte sustento para considerarlas más bien como datos básicamente ordinales (Caruso & Cliff, 1997).
Los intervalos de confianza para las medias y las diferencias entre medias se calculan directamente con programas estadísticos comerciales, tales como el Statistica (StatSoft, 1995) o el Minitab (Minitab, 2000). Desafortunadamente, la mayoría de los métodos para calcular las proporciones y sus diferencias tienen serias deficiencias (Newcombe, 1998a, 1998b, 1998c).
El objetivo del presente trabajo es mostrar cómo calcular intervalos de confianza para proporciones y diferencias entre proporciones, aplicando métodos óptimos y explicar con ejemplos cómo se pueden interpretar. También se proporciona una hoja de cálculo MS Excel en español, inglés y galés, que ejecuta todos estos cálculos y que puede ser descargada gratuitamente de la siguiente dirección de internet:
http://www.uwcm.ac.uk/epidemiology_statistics/research/statistics/newcombe.htm
Muchas variables existentes en todas las áreas de investigación con sujetos humanos son binarias, es decir que tienen dos posibles valores, como por ejemplo, el género (varón o mujer), estatus del cliente (afectado o no afectado), respuesta al tratamiento (positivo o negativo), etc. Cuando se registra una variable binaria para cada individuo o unidad de la muestra, usualmente se reporta la proporción de casos que contiene cada grupo en particular y frecuentemente es expresada en términos de porcentaje. Por ejemplo, de 32 familias que tienen hijos jóvenes con esquizofrenia, 25 son calificadas con altos niveles de la expresividad emocional en el registro de línea base (Santos et al., 2001), aquí la proporción es .781 ó 78.1%. Las restantes siete familias tienen una baja expresividad emocional de 100 - 78.1 = 21.9%.
Aunque el intervalo de confianza de esta simple proporción se puede calcular fácilmente con una calculadora electrónica, sería más útil disponer de una computadora con el software apropiado. Generalmente se observa que las opciones por defecto de los programas de análisis estadísticos más difundidos tienen limitaciones para ayudar al usuario en esta área, así que la elaboración de una hoja de cálculo para calcular los intervalos de confianza para las proporciones y sus diferencias resultaría un elemento útil y accesible para los usuarios. También se desarrollaron versiones equivalentes en el lenguaje de macros para SPSS y Minitab, que incluso se encuentran disponibles en la dirección de internet mencionada.
Intervalo de confianza para una simple proporción
Se supone que de n individuos o unidades, r son positivos, es decir, que tienen una característica de interés. Entonces la proporción de respuestas positivas es p = r/n. Debido a ciertas necesidades analíticas y descriptivas, se quiere calcular un intervalo de confianza (IC) para tal proporción en la población de la cual se ha extraído la muestra. Un IC para p se calcula comúnmente como:
![]()
donde EE es el error estándar y queda definido como:
![]()
y z toma el valor usual de 1.96 para el 95% IC. Por ejemplo, con n = 32 y r = 25, p = .781, y el intervalo de confianza construido con la ecuación (1) va desde .638 a .924, es decir, desde 63.8% hasta 92.4%.
Si bien este es un cálculo muy sencillo, desafortunadamente tiene serias fallas. Tomando el ejemplo anterior, imaginemos que algunos datos se han registrado con una frecuencia igual a cero. Si se sustituye con p = 0 en la ecuación (1), se obtendrá un error estándar igual a cero y el intervalo resultante degenerará, de tal modo que el límite superior y el inferior serán cero. Similarmente, cuando p = 1 el límite superior y el inferior serán 1. Es más, cuando r es pequeño (1, 2 ó algunas veces 3), algo igualmente absurdo puede ocurrir: que se obtenga un límite inferior debajo de cero; igualmente, consideremos además que cuando n – r es pequeño, el límite inferior puede exceder a 1. Pero eso no es todo, pues aunque el intervalo de confianza esté delimitado al 95% para incluir la verdadera proporción poblacional, un estudio de simulación muestra que su verdadera probabilidad de cobertura está debajo del 90% para un moderado valor de n. Además, el intervalo tiende a estar ubicado bastante lejos de .5, que es el punto medio de la escala. La consecuencia directa es que el cálculo de un límite superior para, por decir, la incidencia de algún efecto adverso tenderá a estar falsamente declarado (Newcombe, 1998a). Por lo tanto, cuando la proporción p es muy pequeña y el tamaño de la muestra es bastante moderado, o cuando las proporciones obtenidas son 0 ó 1, las condiciones para obtener el IC por medio del enfoque tradicional (ecuación 1) llevarán a resultados cuestionables. En resumen, el método de Wald (ecuación 1) es aplicable si se cumple el criterio np > 5 y n (1-p) > 5. Pero la previa evaluación desarrollada en Newcombe (1998a) sugiere que la aplicación del método de Wald no es apropiada, considerando que el desempeño de este método es pobre aun cuando se cumple la condición descripta. Dados los resultados previos de Newcombe, se recomienda el método de Wilson, que es apropiado aun sin considerar el tamaño de la muestra ni las frecuencias o proporciones observadas.
Se formuló una variedad de métodos para afrontar estos problemas. Entre ellos, se recomienda el método de Wilson (1927), conocido como método score, porque tiene muy buenas propiedades para el análisis y es razonablemente aprovechado cuando se dispone de una calculadora. Primeramente, se han de calcular tres cantidades:
![]()

![]()
Luego, el intervalo de confianza está dado por:
![]()
De esta manera, con n = 32, r = 25 y z = 1.96, se pueden calcular los componentes de las ecuaciones 2 a 5:
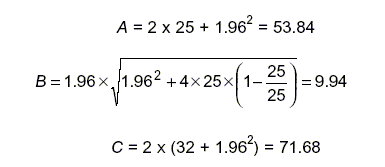
El intervalo de confianza al 95% para la proporción de familias, entre las que tienen un adolescente esquizofrénico quienes son calificadas con alto nivel de expresividad emocional, tiene un rango desde:
(53.84 – 9.94) / 71.68 = 0.612 hasta (53.84 + 9.94) / 71.68 = 0.890,
es decir, desde 61.2% hasta 89%. Obsérvese que la proporción obtenida, 78.1%, no es el punto medio del intervalo. Y, en efecto, el punto medio del intervalo solo puede ser igual a la proporción de interés (p), si este último es igual a .5.
El lector puede preparar una hoja de cálculo MS Excel para efectuar todas estas operaciones. Esta hoja ya está preparada en el archivo denominado ICPROPORCION.XLS. Para el ejemplo previo, la proporción observada es 25 de 32, es decir, .781. Colocando apropiadamente los valores en las ecuaciones, el límite de confianza al 95% es de .6125 y .8898. Si un intervalo requiere otros límites de confianza, por ejemplo .90 ó .999, simplemente se reemplaza el valor 95 por 90 ó 99.9.
La interpretación es muy similar a la del intervalo de confianza que se obtiene para la media. Asumiendo que estos resultados dan una guía confiable de las familias que tienen como miembro a un esquizofrénico en una amplia población, la mejor estimación es que en un 78.1% de familias como estas, el grado de expresividad emocional podría ser alto. Se admite que esta proporción poblacional podría ser tan baja como 61.2% o tan alta como 89%. El ancho de este intervalo es una expresión del grado de precisión que demarca los probables límites en que la verdadera proporción puede ubicarse.
Cuando r, y por lo tanto p es cero, el intervalo se simplifica desde cero hasta z2/(n + z2). Cuando r = n, de tal modo que p = 1, el intervalo abarca desde n/(n + z2) hasta 1. De esta manera, de las ocho familias en crisis, en las que el nivel de hostilidad del padre fue inicialmente bajo, ninguna cambió su estatus hacia altos niveles de hostilidad en el seguimiento. Un intervalo de confianza del 95% para esta proporción va desde 0 hasta 1.962/(8 + 1.962) = 0.324, es decir, desde 0 hasta 32.4%.
Intervalos de confianza para dos proporciones: Muestras independientes
En un estudio sobre el contacto corporal madre-niño, Sadurní y Rostan (2002) observaron un incremento del contacto en 27 (84.4%) de 32, en los períodos de regresión y 9 (14.3%) de 63 para períodos de no regresión. Esta diferencia resultó estadísticamente significativa (p < .001) según la prueba de ji cuadrado. La diferencia aquí es D = 0.844 – 0.143 = 0.701 ó 70.1%. Después de este resultado, sin embargo, se podría calcular un intervalo de confianza para una diferencia entre dos proporciones. Aquí, se puede pensar que hay una alta taza del 70% de incremento del contacto corporal durante los períodos de regresión comparados con aquellos que no tuvieron estos períodos, pero nos gustaría expresar el grado de precisión de este resultado, que proviene de una muestra limitada. El método que se aplica en este caso es sencillo, está estrechamente relacionado con el método tradicional para una simple proporción y comparte con él también varios inconvenientes. El cálculo tradicional del IC para la diferencia está dado por:
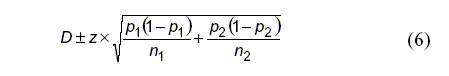
Pero un método mejor es calcular l1 y u1, los límites inferior y superior que definen el IC 95% para la primera muestra, y l2 y u2, que provienen del límite inferior y superior de la segunda muestra; este es el método score utilizado previamente. Entonces, el IC 95% para la diferencia calculada está dado por (Newcombe, 1998b):
![]()
En el ejemplo, p1 = 0.844, p2 = 0.143, D = 0.701, l1 = 0.682, u1 = 0.931, l2 = 0.077 y u2 = 0.250. Finalmente, el IC 95% para la diferencia es:

En otras palabras, desde 0.507 hasta 0.810. De esta forma, aunque la mejor estimación para la diferencia entre las proporciones es 70%, el IC 95% va desde 51% hasta 81%, demostrando la imprecisión que proviene del uso de una muestra de tamaño limitado. Este intervalo no incluye el valor cero, lo que se corresponde con la diferencia que fue juzgada como estadísticamente significativa en el artículo original después de aplicar la prueba ji cuadrado.
Intervalos de confianza para dos proporciones: Muestras dependientes
En el estudio de familias con un miembro esquizofrénico se evaluó la expresividad emocional en un punto de línea base y luego en un período de 9 meses. Así que la prevalencia en el primer momento fue de 25/32 y para el segundo momento, 20/32. Estas dos proporciones se basan en exactamente la mismas 32 unidades en este caso, familias. En esta situación el análisis puede tomar en cuenta la naturaleza apareada individualmente de los datos. Los autores de acuerdo a ello aplicaron la prueba McNemar, que es la versión para muestras dependientes de la prueba ji cuadrado. Sin embargo, también podría ser importante obtener los intervalos de confianza para las diferencias entre estas proporciones. El método (Newcombe, 1998c) se basa en el explicado anteriormente, pero es más complejo, por lo que es altamente recomendado el uso de una hoja de cálculo, como MS Excel.
Para ello, se necesita ubicar los datos tal como lo hicieron Santos y colaboradores (2001). Ahí, en 18 casos la expresividad emocional permaneció alta, en 2 casos se incrementó a un nivel alto, en 7 se decrementó de alto a bajo, y en 5 casos permanecieron bajos. Sustituyendo esta información en la sección final de la hoja ICPROPORCION.XLS, la diferencia estimada es simplemente (20-25)/32 = -0.1563 ó -15.6%, el signo negativo significa un decremento. Un intervalo al 95% de confianza se obtiene desde -0.3311 hasta +0.0317. Entonces, aunque se observa un moderado decremento, esto podría corresponder a un sustancial decremento tal como un 33%, o inversamente a un leve incremento de 3%, en la amplia población de familias similares. Este intervalo de confianza abarca el cero, en acuerdo con el resultado no significativo de la prueba de McNemar.
Discusión
En este artículo se ha descripto la utilidad del cálculo de intervalos de confianza con métodos sólidos y sencillos de aplicar. Tales cálculos pueden ser efectuados con la hoja de cálculo elaborada por los autores. Pero tener los resultados exactos es solamente una parte del problema. Hay otros aspectos tan importantes como la elección del análisis estadístico y del diseño de estudio y dentro de este último, el proceso de muestreo, que continúa siendo la fuente de sesgo altamente prevalente en la literatura de investigación.
Una pregunta importante a considerar es la siguiente: ¿Cuál es la unidad de análisis en los datos? Todos los tipos de análisis estadísticos involucran una elección implícita de la unidad de los datos. Un estudio que implique un número de sujetos que ha sido seleccionado independientemente y que proporciona cada uno un dato en un único punto de tiempo, se analiza apropiadamente usando al sujeto como unidad de análisis. Pero la unidad de estudio puede ser grande, como en el ejemplo de expresividad emocional citado anteriormente, en que la unidad de análisis fue la familia. Sin embargo, en el análisis del ejemplo de los períodos de regresión, esto puede parecer un defecto. El estudio utilizó solamente 18 infantes, pero se analizó como si los 95 períodos o episodios fueran independientes uno de otro. Errores de este tipo no son raros en los informes de investigación. El correcto análisis ahí podría ser complejo, considerando que el mismo infante puede contribuir a uno o más episodios de ambos tipos. Podría ser preferible un tipo de análisis intra-sujeto.
Por otro lado, se enfatiza que la construcción de un intervalo de confianza expresa solamente una forma de incertidumbre, que resulta de la naturaleza finita de la muestra bajo estudio. Aplicando tal estimación a una muestra representativa, en la que se incluyera un proceso aleatorio en la selección de las unidades definidas por el investigador, la discusión sobre la generalización de los resultados sería más o menos sencilla. Pero si por alguna razón la muestra no es representativa de la población relevante, tanto la estimación puntual (por ejemplo, la proporción específica de aquellos que han sido maltratados, por decir, 30%) como los intervalos de confianza a calcular (por decir, de 25% a 38%) serán afectados por esta situación. Si la muestra específica está sesgada hacia la población que se pretende estudiar (por ejemplo, cierto segmento puede estar más motivado para llenar cuestionarios o para participar en estudios y es una muestra autoseleccionada), todo lo que se calcule estará sesgado. Ninguna de las herramientas estadísticas tales como las estimaciones puntuales, los intervalos de confianza o las pruebas de hipótesis, puede corregir tal sesgo. Y más aún, no se debería postular que tales herramientas superan el sesgo. En otras palabras, el diseño de todo el proceso de investigación debe controlar las fuentes de posibles sesgos.
Finalmente, se debe recordar que la estimación de los intervalos no da una información en términos absolutos, pues también solo ofrece una probabilidad de contener la cantidad en estudio (Howell, 1997; May, Masson& Hunter, 1990). De esta manera, los intervalos son los límites que tienen una alta probabilidad de que ocurra un determinado valor poblacional y esta probabilidad es de una extensión del 95% u otro límite crítico.
Referencias bibliográficas
1 Beery, K.E. (2000). Prueba Beery-Buktenica del Desarrollo de la Integración Visomotriz [The Beery-Buktenica Developmental Test of Visual- Motor Integration], (4a ed.). México, DF: El Manual Moderno. [ Links ]
2 Bullock, L.M. & Wilson, M.J. (1989). Behavior Dimensions Rating Scale: Examiner's manual. TX: DLM Teaching Resources. [ Links ]
3 Caruso, J.C. & Cliff, N. (1997). Empirical size, coverage, and power of confidence intervals for Spearman's Rho. Educational and Psychological Measurement, 57(4), 637-654. [ Links ]
4 Gregory, R.J. (2000). Psychological testing: History, principles, and applications, (3a ed.). Boston: Allyn & Bacon. [ Links ]
5 Howell, D.C. (1997). Statistical methods for Psychology, (4a ed.). Belmont, CA: Duxbury. [ Links ]
6 Language Learning (2002). Instructions to authors, 52(1), 201-202. [ Links ]
7 May, R.B., Masson, M.J. & Hunter, M.A. (1990). Application of statistics in behavioral research. NY: Harper & Row. [ Links ]
8 Minitab, Inc. (2000). MINITAB [Computer program manual]. State College, PA: Minitab, Inc. [ Links ]
9 Newcombe, R.G. (1998a). Two-sided confidence intervals for the single proportion: Comparison of seven methods. Statistics in Medicine, 17, 857- 872. [ Links ]
10 Newcombe, R.G. (1998b). Interval estimation for the difference between independent proportions: Comparison of eleven methods. Statistics in Medicine, 17, 873-890. [ Links ]
11 Newcombe, R.G. (1998c). Improved confidence intervals for the difference between binomial proportions based on paired data. Statistics in Medicine, 17, 2635-2650. [ Links ]
12 Nunnally, J.C. & Bernstein, I.J. (1995). Teoría psicométrica [Psychometric theory], (3a ed.). México, DF: McGraw-Hill. [ Links ]
13 Onwuegbuzie, A. & Daniel, L.G. (2001, Abril). Indices of score reliability and their applications. Trabajo presentado en el Annual Meeting of the American Educational Research Association, Seattle, Washington. [ Links ]
14 Onwuegbuzie, A.A. & Daniel, L.G. (2004). Reliability generalization: The importance of considering sample specificity, confidence intervals, and subgroup differences. Research in Schools, 11(1), 60-74. [ Links ]
15 Sadurní, M. & Rostan, C. (2002). Regression periods in infancy: A case study from Catalonia. Spanish Journal of Psychology, 5, 36-44. [ Links ]
16 Santos, A., Espina, A., Pumar, B., González, P., Ayerbe, A. & García, A. (2001). Longitudinal study of the stability of expressed emotion in families of schizophrenic patients: A 9-month follow-up. Spanish Journal of Psychology, 4, 65-71. [ Links ]
17 Sattler, J.M. (1988). Evaluación de la inteligencia infantil y habilidades especiales [Assessment of children intelligence and special abilities], (2a ed.). México, DF: El Manual Moderno. [ Links ]
18 StatSoft, Inc. (1995). STATISTICA for Windows [Computer program manual]. Tulsa, OK: StatSoft, Inc. [ Links ]
19 Wilson, E.B. (1927). Probable inference, the law of succession, and statistical inference. Journal of the American Statistical Association, 22, 209- 212. [ Links ]
20 Woodburn, S.S., Boschini, C., Fernández, H. & Rodríguez, F. (1993). Nuestros niños (de 5 1/2 años a 8 1/2 años): Su desarrollo perceptual-motor y su perfil [Our children (5 ½ years old to 8 ½ years old: Profile and development perceptual-motor]. Heredia, Costa Rica: EUNA. [ Links ]
University of Wales, College of Medicine - Heath Park, Cardiff CF14 4XN, - United Kingdom
Servicio de Psicología - Defensoría Municipal del Niño y del Adolescente - Av. José Olaya 166 (Casa de la Cultura) - Chorrillos - Lima 9 - Perú
Fecha de recepción: 22 de abril de 2004
Fecha de aceptación: 31 de mayo de 2006














