Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Interdisciplinaria
versión On-line ISSN 1668-7027
Interdisciplinaria v.24 n.1 Buenos Aires ene./jul. 2007
Medida del funcionamiento diferencial del ítem en el marco de la teoría de respuesta al ítem*
María Ester Aguerri**, María Silvia Galibert***, Gabriela Susana Lozzia****, Facundo Juan Pablo Abal***** y Horacio Félix Attorresi******
* Este trabajo fue financiado con subsidios de la Universidad de Buenos Aires (UBACyT P020), del Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET PIP Nº 2426) y de la Agencia Nacional de Promoción Científica y Tecnológica (ANPCyT PICT 2004 Nº 20909).
** Magister Scientiae en Biometría y Licenciada en Ciencias Matemáticas. Profesora Regular Adjunta de Estadística y Co-Directora e Investigadora Formada en Proyectos de Investigación de: la Universidad de Buenos Aires (UBACyT), Agencia Nacional de Promoción Científica y Tecnológica (ANPCyT) y Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET). Agrelo 3555, (1224) Ciudad Autónoma de Buenos Aires.
*** Magister Scientiae en Biometría y Profesora de Enseñanza Especial en Ciencias Matemáticas. Profesora Regular Adjunta de Estadística y Co-Directora de proyectos de investigación de UBACyT, ANPCyT y CONICET.
**** Licenciada y Profesora en Psicología. Jefe de Trabajos Prácticos de Estadística, Becaria de Posgrado del Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET) e investigadora en proyectos de investigación de UBACyT y ANPCyT.
***** Licenciado en Psicología. Ayudante de Trabajos Prácticos de Estadística, Becario de Doctorado de la Universidad de Buenos Aires (UBA) e investigador en proyectos de investigación de UBACyT y ANPCyT.
****** Licenciado en Ciencias Matemáticas. Profesor Regular Titular de Estadística y Director de proyectos de investigación de UBACyT, ANPCyT y CONICET.
Resumen
En el estudio del funcionamiento diferencial del ítem (DIF - differential item functioning) la medición de su tamaño proporciona información relevante. Entre las medidas del DIF más utilizadas se encuentra el logaritmo de la razón común de las posibilidades de Mantel-Haenszel (Mantel-Haenszel Log Odds Ratio, MH-LOR). En el trabajo que se informa se analiza la similitud de los resultados al aplicar MH-LOR y una medida obtenida en el marco de la teoría de respuesta al ítem (TRI), a la que se denomina LOR-TRI, sobre datos reales y sobre datos simulados sin DIF. Los datos reales corresponden a una prueba de 20 ítem de razonamiento verbal, respondida por egresados del ciclo medio de enseñanza y por alumnos universitarios. Cada ítem presenta un par de palabras - base entre las cuales existe algún tipo de relación y cuatro opciones de pares de palabras entre las que se debe elegir aquel cuya relación sea la más cercana a la del par base. Para los datos simulados se consideraron las respuestas a un test de 20 ítem generadas según el modelo logístico de tres parámetros. Los grupos fueron elegidos de una población normal estándar con tamaño muestral 1,000 y se efectuaron 100 repeticiones. Tanto para los datos reales como para los simulados el modelo logístico adecuado es el de tres parámetros, sin embargo se observó que el ajuste del modelo de Rasch condujo a resultados de LOR-TRI, similares a MH-LOR. Para los respectivos errores estándar se observó la misma particularidad en cuanto a la similitud, siendo ésta aún más destacada.
Palabras clave: Funcionamiento diferencial del ítem; MH-LOR; Teoría de respuesta al ítem; Modelo logístico de tres parámetros; Modelo de Rasch.
Abstract
Measuring differential item functioning in the item response theory. In the study of differential item functioning (DIF), measuring its size is of great relevance. An easily interpreted measure is the Mantel-Haenszel Log Odds Ratio (MH-LOR): its sign shows the group which the item favors and its value is zero when the item does not show DIF. This research also considers a measure of DIF named LOR-IRT because it is linked to the log odds ratio and is formulated on the basis of the item parameters within the item response theory (IRT) framework. In order to study the similarity between the LOR-IRT measure according to the number of parameters of the adjusted model and MH-LOR, the DIF was analyzed through real data as well as non-DIF simulated data. The real data consists of a 20-item verbal reasoning test taken by 349 senior high school students and 865 sophomore students from the School of Psychology in the University of Buenos Aires. The simulated data includes answers to a 20-item test based on the three-parameter logistic model for two samples of 1,000 participants from a normal standard population. The parameters of the 20 items under study stem from the combination of four discrimination levels (0.4, 0.8, 1.2 and 1.6) and five difficulty levels (-2, -1, 0, 1 and 2). In order to replicate the conditions of the DIF analysis on the basis of real data, the value of the guessing parameter was set at 0.25 for all the items. Therefore, the chosen design was a 4 X 5 type with 100 repetitions. After analyzing the DIF of the verbal reasoning items on the basis of real data, we concluded that the LOR-IRT obtained upon the adjustment of the one-parameter logistic model (the Rasch model) led to results similar to those of MH-LOR. This statement holds true in the light of the following three facts: there is a 94.44% coincidence in the decisions about the presence of DIF, and both the lower sum of the squared differences and the higher correlation are obtained when compared with the results of the adjustment of the two or three-parameter model. The similarity between the corresponding standard errors is outstanding, the sum of the squared differences is almost zero, and the correlation is remarkably higher than that of the two or three-parameter logistic model. Considering that the verbal reasoning test presents four alternatives of which only one is correct, the items can be modeled according to the three-parameter logistic model, with a non-null guessing parameter. However, the LOR-IRT results are similar to those of MH-LOR in terms of magnitude and standard error when the one-parameter logistic model is adjusted. These results remained the same in the simulation study. In fact, the adjustment of the one-parameter logistic model led to LOR-IRT values which are, on average, similar to those of MH-LOR, and that both the lower sum of the squared differences and the higher correlation are obtained. As for the real data, the similarity between the corresponding standard errors is also outstanding. The sum of the squared differences is almost zero and the regression line is similar to the identity line when the Rasch model is adjusted. The purpose of future research will be to not only study similarities between LOR-IRT and MH-LOR on other designs in terms of test length, group sample size and impact presence, but also to assess their performance in the correct identification of items that show DIF.
Key words: Differential item functioning; MH-LOR; Item response theory; Three parameter logistic mode; The Rasch model.
En la evaluación psicológica y educativa se considera que un ítem exhibe funcionamiento diferencial (Differential Item Functioning, DIF) cuando sujetos de igual nivel en el rasgo medido, pero pertenecientes a diferentes grupos, no tienen la misma posibilidad de responderlo correctamente. Los métodos de detección del DIF, tanto las medidas como las pruebas de hipótesis, se pueden clasificar en dos grupos; están los que se encuadran en el marco de la teoría de respuesta al ítem (TRI) pues tilizan los parámetros de los ítem y los llamados métodos de tablas de contingencia. Estos últimos deben su nombre a la forma en que se pueden presentar los datos cuando se considera el grupo al que pertenece el sujeto, de referencia o focal según la literatura específica y la respuesta al ítem, correcta o incorrecta.
Fidalgo y Ferreres (2002) han señalado que las medidas del DIF proporcionan el tamaño del efecto y, por tanto, aportan información que se ha de tener en cuenta como guía de aceptación de la significación estadística.
Camilli y Shepard (1994) mencionaron las siguientes medidas del DIF en el marco de la TRI: las del área de Raju, los índices de la diferencia de probabilidad y la diferencia de los parámetros de dificultad. Entre los métodos de tablas de contingencia nombraron al estimador de la razón común de las posibilidades de Mantel-Haenszel
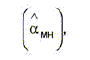
su logaritmo natural (Mantel-Haenszel Log Odds Ratio, MH-LOR) y el Delta-DIF de Mantel-Haenszel (MH D-DIF). Esta última medida fue presentada por Holland y Thayer (1985) y se define como:

o sea -2.35MH-LOR. El Educational Testing Service (ETS) utiliza una clasificación de los ítem según su DIF sobre la base de la magnitud y significancia del estadístico MH D-DIF, posiblemente sea ésta una de las razones por la que es una de las medidas de mayor aplicación. Fidalgo (1996) haciendo referencia al procedimiento Mantel-Haenszel, dentro del cual se encuentra MH D-DIF, afirmó que su comportamiento es óptimo cuando los ítem se ajustan al modelo logístico de un parámetro o modelo de Rasch, pero sigue dando buenos resultados aun cuando eso no ocurra. Entre otros trabajos pueden mencionarse el de Ferreres, González-Romá y Gómez (2002) quienes aplicaron el estadístico MH D-DIF para estudiar el DIF sobre datos reales y el de Aguerri, Galibert, Zanelli y Attorresi (2005) que analizaron sus ventajas y limitaciones sobre datos simulados.
Se han realizado estudios en los que se analiza la vinculación entre medidas del DIF obtenidas en el marco de la TRI con otras provenientes de los métodos de tablas de contingencia. Holland y Thayer (1988) mostraron que la razón común de las posibilidades (), para la cual Mantel y Haenszel (1959) propusieron el estimador

se puede obtener en función de la diferencia de los parámetros de dificultad del ítem mediante la siguiente expresión:
![]()
donde bF y bR corresponden respectivamente al parámetro de dificultad del ítem en el grupo focal y en el grupo de referencia habiéndose ajustado el modelo de Rasch. Donoghue, Holland y Thayer (1993) afirmaron que MH D-DIF estima a una cantidad que se expresa en función de los parámetros del ítem como -4a (bF-bR), donde a es el parámetro de discriminación en ambos grupos. Estos autores analizaron el efecto de la violación de los supuestos requeridos; trabajaron con conjuntos de datos simulados según el modelo logístico de tres parámetros de manera que el parámetro de discriminación era constante dentro de cada conjunto de datos analizado. Por otra parte, Camilli y Shepard (1994) mostraron que la cantidad 1.7a (bF-bR) coincide con MH-LOR cuando se ajusta el modelo de dos parámetros con el mismo parámetro de discriminación en ambos grupos. En el presente estudio se denomina LOR-TRI a la cantidad 1.7a (bF-bR) por vincularse con el logaritmo de la razón común de las posibilidades y estar formulada en función de los parámetros del ítem en el marco de los modelos de la TRI. Los objetivos de este estudio fueron:
1.- Comparar la similitud entre LOR-TRI y MH-LOR, según se ajuste el modelo de uno, dos o tres parámetros, en un estudio del DIF sobre datos reales.
2.- Analizar sobre datos simulados sin DIF la regularidad de los resultados obtenidos sobre los datos reales. Dentro del test se incluyen ítem con diferentes niveles del parámetro de discriminación.
Medidas del DIF
MH-LOR
La medida MH-LOR se obtiene mediante la expresión:
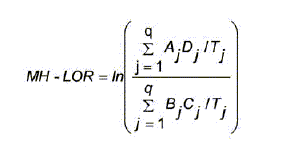
donde para cada nivel j de la puntuación total:
Aj es la cantidad de sujetos del grupo de referencia que respondió correctamente el ítem bajo estudio,
Bj la cantidad de sujetos del mismo grupo que respondió incorrectamente el ítem,
Cj y Dj son las respectivas cantidades en el grupo focal,
Tj la cantidad de sujetos de ambos grupos con puntuación total j y q la cantidad de ítem del test menos uno.
El programa EZDIF de Waller (1998) proporciona para cada ítem el valor del estadístico MH D-DIF y su error estándar.
Dado que MHLOR = MH D-DIF / (-2.35), puede obtenerse esta medida y su error estándar dividiendo por -2.35 y 2.35 respectivamente a MH D -DIF y a su error estándar. El programa EZDIF también proporciona la clasificación en tipo A, B ó C por su DIF según el criterio utilizado en el ETS. Tal clasificación, presentada por Zieky (1993), es:
- categoría A, o con DIF muy pequeño, cuando el estadístico MH D-DIF no es significativamente diferente de cero o en valor absoluto menor que 1,
- categoría C, con DIF grande, cuando MH D-DIF es significativamente mayor que 1 y en valor absoluto mayor o igual a 1.5,
- al resto de los ítem se les asigna categoría B, o con DIF moderado.
En cuanto a la clasificación del ítem por la sola magnitud de MH-LOR, y siendo MH-LOR = MH D-DIF / (-2.35), resulta que si el valor absoluto MH-LOR no supera a 0.425532, que es el recíproco de 2.35, se afirma que el ítem presenta DIF muy pequeño; si el valor absoluto de MH-LOR es mayor o igual a 0.638298, obtenido de hacer 1.5 dividido por 2.35, se afirma que el ítem tiene DIF grande y en el resto de los casos se considera que el ítem presenta DIF moderado.
LOR-TRI
La medida del DIF que en este trabajo se denomina LOR-TRI se obtiene mediante la siguiente expresión: LOR-TRI = 1.7 a (bF-bR).
El programa BILOG-MGTM (Zimowski, Muraki, Mislevy & Bock, 1996) proporciona para cada ítem una estimación del parámetro de discriminación, de la diferencia de los parámetros de dificultad y de su error estándar. Puesto que permite ajustar el modelo logístico de uno, dos y tres parámetros, se obtuvieron las cantidades que denominamos respectivamente LOR-TRI1, LOR-TRI2 y LOR-TRI3 y sus correspondientes errores estándar. Este programa efectúa la estimación de los parámetros bajo la restricción de que el parámetro c, de aciertos por azar, es el mismo para los dos grupos así como también es igual la potencia discriminatoria del ítem en los dos grupos, es decir: cR = cF y aR = aF. En el caso de ajustar el modelo de dos parámetros el parámetro de aciertos por azar es nulo y en el de un parámetro se agrega la condición de que todos los ítem tienen igual potencia discriminatoria.
Tanto MH-LOR como LOR-TRI son cantidades cuyos valores positivo, negativo o nulo conducen a considerar que se está respectivamente en presencia de un ítem con DIF que favorece al grupo de referencia, al grupo focal o sin DIF.
Estudio del DIF con datos reales
Método
Participantes
Se consideraron las respuestas de 865 alumnos de segundo año de la Carrera de Psicología de la Universidad de Buenos Aires y 349 egresados del ciclo medio de enseñanza de la Ciudad de Buenos Aires (Argentina). Estos datos fueron tomados de una investigación previa (cf. Galibert, 2000).
Materiales
Se estudió el DIF de los 20 ítem de una prueba de razonamiento verbal que mide la habilidad para identificar y discriminar relaciones (Attorresi, Pano, Fernández Liporace & Cayssials, 1994). Cada ítem presenta un par de palabras - base entre las cuales existe algún tipo de relación y cuatro opciones de pares de palabras entre los que se debe elegir aquél cuya relación sea la más cercana a la del par - base.
Procedimiento
Para comparar MH-LOR y LOR-TRI al ajustar el modelo de uno, dos y tres parámetros, se calculó la suma de los cuadrados de las diferencias en cada uno de los casos y se efectuaron análisis de correlación. En orden a predecir a MH-LOR se realizaron análisis de regresión tomando como variable predictora a LOR-TRI1, LOR-TRI2 o LOR-TRI3. Con análogos análisis se estudió la similitud de los respectivos errores estándar. Se registró la clasificación del ítem por su DIF según el criterio del ETS. En base a la magnitud de las medidas obtenidas también se consideró la clasificación del DIF del ítem en: muy pequeño, moderado y grande. Los puntos de corte para MH-LOR, LOR-TRI1, LOR-TRI2 y LOR-TRI3 fueron los mismos, esto es 0.425532 y 0.638298.
Resultados
Al grupo de mayor tamaño muestral, el de los alumnos de Psicología, se lo consideró grupo de referencia y a los del ciclo medio como grupo focal. Ambos grupos pueden considerarse pertenecientes a una misma población en cuanto a la capacidad de reconocer y discriminar relaciones puesto que la diferencia de sus medias no resultó significativa, t (1212) = 1.32, p = .1886.
El análisis del DIF se realizó sobre 18 ítem porque los ítem 14 y 19, que presentaron correlación biserial negativa, fueron excluidos del estudio para favorecer el supuesto de unidimensionalidad de los modelos de la TRI por ajustar.
En la Tabla 1 se presenta la clasificación por su DIF para cada ítem, según el criterio del ETS y los valores de MH-LOR y de LOR-TRI según se ajuste el modelo logístico de uno, dos o tres parámetros. En la Tabla 2 se presentan para cada ítem los valores de los respectivos errores estándar.
Tabla 1
Clasificación del íÍtem según su DIF y magnitud de la medidas MH-LOR y LOR-TRI para los ítem de la prueba de razonamiento lógico

Tabla 2
Error estándar de MH-LOR y de LOR-TRI para los ítem de la prueba de razonamiento lógico

Según el criterio del ETS, los ítem 4, 13 y 18 fueron clasificados en categoría B y los restantes 15 ítem en categoría A. A partir de la magnitud de MH-LOR se llegó a idéntica clasificación, fueron señalados con DIF muy pequeño 15 de los ítem y con DIF moderado los ítem 4, 13 y 18. Los dos primeros a favor del grupo de los alumnos de la Facultad de Psicología y el último a favor de los egresados del ciclo medio. Según la magnitud de LOR-TRI1 16 ítem fueron señalados con DIF muy pequeño, sólo el ítem 4 y el ítem 18 presentaron valores como para ser categorizados con DIF moderado en el mismo sentido que lo hizo MH-LOR. Por la magnitud de LOR-TRI2, 17 ítem fueron señalados con DIF muy pequeño, sólo el ítem 18 fue señalado con DIF moderado en el mismo sentido que lo hizo MH-LOR. Al considerar la magnitud LOR-TRI3 los ítem 4 y 12 fueron señalados con DIF moderado a favor, respectivamente, de los alumnos de la Facultad de Psicología y de los egresados del ciclo medio; el ítem 18 resultó con DIF grande también a favor de los egresados del ciclo medio y los restantes 15 ítem presentaron DIF muy pequeño. Luego el porcentaje de coincidencias en la detección del DIF, sea moderado o grande, entre MH-LOR y LOR-TRI es: 94.44% para el ajuste del modelo de un parámetro y 88.89% para el de dos y el de tres parámetros.
Para estudiar la similitud de las medidas se calculó la suma de los cuadrados de las diferencias entre MH-LOR y LOR-TRI para cada uno de los modelos. Los resultados obtenidos fueron 0.0181, 0.1282 y 0.1417 para el ajuste del modelo logístico de uno, dos y tres parámetros respectivamente. Tales sumas de cuadrados de las diferencias entre los respectivos errores estándar fueron 0.0006, 0.5710 y 1.0507. Se calculó el coeficiente de correlación entre MH-LOR y LOR-TRI para cada uno de los modelos ajustados. Los resultados obtenidos fueron respectivamente .9965, .9901 y .9917 para el modelo logístico de uno, dos y tres parámetros y .9815, .7632 y .7518 entre los correspondientes errores estándar. Al efectuar los análisis de regresión en orden a predecir a MH-LOR tomando como variable predictora a LOR-TRI, se obtuvieron los siguientes valores para la ordenada al origen y la pendiente de la recta de regresión según se ajuste el modelo de uno, dos o tres parámetros: (0.01; 1.06), (0.08; 1.06) y (0.07; 0.93). Al realizar los análisis de regresión para predecir el error estándar de MH-LOR tomando como variable predictora el error estándar de LOR-TRI tales valores fueron (0.001; 1.03), (0.13; 0.07) y (0.12; 0.08).
Estudio del DIF con datos simulados
Método
En orden a estudiar la regularidad de los resultados obtenidos sobre los datos reales se consideró la simulación sobre el diseño de mayor parsimonia. Por esto, para los datos simulados, ambos grupos son de tamaño 1,000 y pertenecen a una población normal estándar. No se consideró la presencia de desbalance (distinto tamaño muestral) ni de impacto (grupos que difieren en la habilidad medida) por ser factores potencialmente influyentes en la detección errónea del DIF (Aguerri et al., 2005).
Los datos fueron simulados con el programa PARDSIM® (Yoes, 1997). Se utilizó el modelo logístico de tres parámetros con los mismos parámetros generadores en ambos grupos, esto es sin DIF. Los parámetros de los 20 ítem bajo estudio resultan de combinar cuatro niveles de discriminación (0.4, 0.8, 1.2 y 1.6) con cinco niveles de dificultad (-2, -1, 0, 1 y 2). Con el propósito de replicar las condiciones del análisis del DIF sobre los datos reales se fijó en 0.25 el valor del parámetro de aciertos por azar para todos los ítem. Por tanto el diseño elegido fue del tipo 4 X 5 para el que se efectuaron 100 repeticiones. Con los datos simulados se realizaron estudios semejantes a los implementados sobre los datos reales, tanto en cuanto a la magnitud de las medidas MH-LOR y LOR-TRI como de los respectivos errores estándar. Los resultados registrados corresponden al promedio sobre las 100 repeticiones.
Resultados
Para estudiar la similitud entre las medidas MH-LOR y LOR-TRI se calculó la suma de los cuadrados de las diferencias para cada uno de los modelos; se obtuvo 0.0356, 0.0627 y 0.5327, en promedio en las 100 repeticiones, para el modelo de uno, dos y tres parámetros respectivamente. Tales sumas de cuadrados para los correspondientes errores estándar fueron, en promedio, 0.0006, 0.2247 y 1.727.
Se realizó el análisis de correlación de MH-LOR vs. LOR-TRI en las 100 repeticiones, el promedio de los coeficientes de correlación fue .95 para el modelo de un parámetro, .92 para el de dos parámetros y .66 para el de tres parámetros, y para los correspondientes errores estándar tales valores resultaron respectivamente .99, .87 y .44.
En cuanto al análisis de regresión en orden a predecir MH-LOR tomando como variable predictora a LOR-TRI, al ajustar el modelo de un parámetro se obtuvo, en promedio, 0.0009 para la ordenada al origen y 1.0746 para la pendiente. Tales valores fueron -0.0017 y 0.9131 al ajustar el modelo de dos parámetros y 0.0033 y 0.4786 al ajustar el modelo de tres parámetros. Al realizar el análisis de regresión entre los respectivos errores estándar tales valores fueron: (-0.0094; 1.0931), (0.0535; 0.3628) y (0.0166; 0.4418).
Discusión general
Cuando se analizó el DIF de los ítem de razonamiento verbal sobre datos reales se observó que la medida LOR-TRI obtenida al ajustar el modelo logístico de un parámetro condujo a resultados similares a los de MH-LOR. Tal afirmación se basa en que coinciden en el 94.44% de las decisiones acerca de la presencia de DIF, le corresponde la menor suma de los cuadrados de las diferencias y la mayor correlación con respecto a las obtenidas al ajustar el modelo de dos o tres parámetros. El resultado más destacable es en cuanto a la similitud de los respectivos errores estándar, pues la suma de los cuadrados de las diferencias es casi cero y la correlación es marcadamente más alta al ajustar el modelo logístico de un parámetro que cuando se considera el modelo logístico de dos o tres parámetros. Los ítem de la prueba de razonamiento verbal por presentar cuatro alternativas de las cuales sólo una es la correcta, son susceptibles de ser modelizados con el modelo logístico de tres parámetros. Este modelo considera un parámetro de aciertos por azar no nulo. Sin embargo los resultados de LOR-TRI en magnitud y error estándar se asemejan más a los de MH-LOR cuando se ajusta el modelo logístico de un parámetro. Estos resultados se sostuvieron en el estudio de simulación. Efectivamente, aunque los datos fueron simulados según el modelo logístico de tres parámetros, puede afirmarse que las medidas MH-LOR y LOR-TRI presentan una marcada similitud cuando se ajusta el modelo de Rasch tanto en cuanto a su magnitud como a la de su error estándar. Para el ajuste del mencionado modelo se observó que la recta de regresión para predecir la magnitud de MH-LOR tomando como variable predictora a LOR-TRI se asemeja más a la identidad. Esta similitud resultó aún más destacada para los respectivos errores estándar.
Las medidas del DIF brindan información apreciable pues dan cuenta de la magnitud del mismo y proporcionan el tamaño del efecto para asignarle significación práctica a la significación estadística del DIF. Holland y Thayer (1988), Donoghue, Holland y Thayer (1993) y Camilli y Shepard (1994) propusieron sobre diseños diferentes, la vinculación entre medidas del DIF relacionadas con el cociente común de las posibilidades y los parámetros del modelo de la TRI ajustado. El presente trabajo continuó en esa línea y la extendió. Esto se afirma por cuanto sobre datos reales se mostró la similitud entre MH-LOR y LOR-TRI para el ajuste del modelo de Rasch, aunque el modelo adecuado para los datos era el de tres parámetros; esta particularidad se mantuvo sobre datos simulados con el modelo logístico de tres parámetros en los que se consideró la presencia de ítem con diferentes niveles para el parámetro de discriminación.
Queda para futuras investigaciones continuar el estudio de la similitud entre LOR-TRI y MH-LOR sobre otros diseños, tanto en cuanto a la longitud del test, tamaño muestral de los grupos y presencia de impacto, así como evaluar el desempeño de ambas en la identificación correcta de los ítem que presenten DIF. Si se sostuvieran los resultados obtenidos en este trabajo se derivaría como regla práctica que, aunque las características de un test ameriten el ajuste del modelo logístico de tres parámetros, ha de calibrarse el modelo logístico de un parámetro para obtener una medida del DIF expresada en función de los parámetros del ítem con resultados semejantes a los de MH-LOR, tanto en magnitud como en error estándar.
Referencias bibliográficas
1 Aguerri, M.E., Galibert, M.S., Zanelli, M.L. & Attorresi, H.F. (2005). Detección errónea del funcionamiento diferencial del ítem. Una comparación de métodos [Erroneous detection of the differential item functioning. A comparison of methods]. Psicothema, 17, 335-340. [ Links ]
2 Attorresi, H.F., Pano, C.O., Fern ández Liporace, M.M. & Cayssials, A. (1994). Evaluación de la habilidad para identificar y discriminar relaciones [Assessment of the identifying and discrimination relationship aptitude]. Anuario de Investigaciones de la Facultad de Psicología, UBA, 3, 27-34. [ Links ]
3 Camilli, G. & Shepard, L. (1994). Methods for identifying biased test items. Thousand Oaks: Sage. [ Links ]
4 Donoghue, J.R., Holland, W.P. & Thayer, D.T. (1993). A Monte Carlo study of factors that affect the Mantel-Haenszel and standardization measures of differential item functioning. En P.W. Holland & H. Wainer (Eds.), Differential item functioning (pp. 137-166). Hillsdale, NJ: Erlbaum. [ Links ]
5 Ferreres, D., González-Romá, V. & Gómez, J. (2002). Funcionamiento diferencial de los ítems en una situación de contacto de lenguas [Differential item functioning and linguistic characteristics of examinees]. Psicothema, 14, 483-490. [ Links ]
6 Fidalgo, A. (1996). Funcionamiento diferencial de los ítems [Differential items functioning]. En J. Muñiz (Ed.), Psicometría (pp. 370-455). Madrid: Universitas. [ Links ]
7 Fidalgo, A. & Ferreres, D. (2002). Supuestos y consideraciones en los estudios empíricos sobre el funcionamiento diferencial de los ítems [Assumptions and considerations for detecting differential item functioning]. Psicothema, 14, 491-496. [ Links ]
8 Galibert, M.S. (2000). Modelización psicométrica de un test de razonamiento verbal en los marcos de la Teoría Clásica de Tests y de la Teoría de Respuesta al Ítem [Psychometric modeling of a verbal reasoning test within the framework of the Item Response Theory and the Classical Tests Theory]. Tesis de Maestría no publicada. Universidad de Buenos Aires. Buenos Aires, Argentina. [ Links ]
9 Holland, P.W. & Thayer, D.T. (1985). An alternate definition of the ETS delta scale of item difficulty. (Research Report No. 85-64). Princeton, NJ: Educational Testing Service. [ Links ]
10 Holland, P. W. & Thayer, D.T. (1988). Differential item functioning and the Mantel-Haenszel procedure. En H. Wainer & H.I. Braun (Eds.), Test validity (pp. 129-145). Hillsdale, NJ: Lawrence Erlbaum. [ Links ]
11 Mantel, N. & Haenszel, W. (1959). Statistical aspects of the analysis of data from retrospective studies of disease. Journal of the National Cancer Institute, 22, 719-748. [ Links ]
12 Waller, N.G. (1998). EZDIF: Detection of uniform and nonuniform differential item functioning with Mantel-Haenszel and logistic regression procedures. Applied Psychological Measurement, 22, 391. [ Links ]
13 Yoes, M. (1997). PARDSIM parameter and response data simulation [Software]. St. Paul, MN: Assessment System Corporation. [ Links ]
14 Zieky, M. (1993). Practical questions in the use of DIF statistics in item development. En P.W. Holland & H. Wainer (Eds.), Differential item functioning (pp. 337-347). Hillsdale, NJ: Erlbaum. [ Links ]
15 Zimowski, M., Muraki, E., Mislevy, R. & Bock, R. (1996). BILOG-MGTM: Multiple-group IRT analysis and test maintenance for binary items [Computer program]. Chicago, IL: Scientific Software International. [ Links ]
Instituto de Investigaciones, Facultad de Psicología, Universidad de Buenos Aires (UBA). Ciudad Autónoma de Buenos Aires - República Argentina.
Fecha de recepción: 2 de enero de 2007
Fecha de aceptación: 22 de mayo de 2007














