Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Interdisciplinaria
versión On-line ISSN 1668-7027
Interdisciplinaria v.26 n.1 Buenos Aires ene./jul. 2009
ARTÍCULOS
Aplicación del modelo LLTM de Fischer al análisis de las fuentes de dificultad de ítemes de razonamiento deductivo*
Horacio Félix Attorresi**, Jimena Picón Janeiro***, Facundo Abal****, María Ester Aguerri***** y María Silvia Galibert******
* La investigación que se informa fue realizada con subsidios de la Universidad de Buenos Aires (UBACyT P043) y de la Agencia Nacional de Promoción Científica y Tecnológica (ANPCyT PICT 20909).
** Licenciado en Ciencias Matemáticas. Profesor Titular de la Cátedra II de Estadística de la Facultad de Psicología de la Universidad de Buenos Aires (UBA). Director de los proyectos ANPCyT PICT 20909 y UBACyT P043. Rivera Indarte 132, 1er Piso, Dpto. A, (C1406DXD) Ciudad Autónoma de Buenos Aires - República Argentina. E-Mail: hattorre@psi.uba.ar
*** Licenciada en Psicología. Becaria del Proyecto ANPCyT PICT 20909 de la Agencia Nacional de Promoción Científica y Tecnológica y Ayudante de Primera de la Cátedra II de Estadística de la Facultad de Psicología de la Universidad de Buenos Aires (UBA).
**** Licenciado en Psicología. Becario del Proyecto UBACyT P043 de la Universidad de Buenos Aires (UBA) y Ayudante de Primera de la Cátedra II de Estadística de la Facultad de Psicología de la Universidad de Buenos Aires (UBA).
***** Magister Scientiae en Biometría. Profesora Adjunta Regular de las Cátedras de Estadística de la Facultad de Psicología de la Universidad de Buenos Aires (UBA). Codirectora del Proyecto UBACyT P043 e Investigadora del Proyecto PICT 20909, de la Agencia Nacional de Promoción Científica y Tecnológica.
****** Magister Scientiae en Biometría. Profesora Adjunta Regular de las Cátedras de Estadística de la Facultad de Psicología de la Universidad de Buenos Aires (UBA). Codirectora del Proyecto UBACyT P043 e Investigadora del Proyecto PICT 20909 de la Agencia Nacional de Promoción Científica y Tecnológica (ANPCyT).
Resumen
El Modelo Logístico Lineal de Rasgo Latente (LLTM) de Fischer permite descomponer la dificultad de un ítem como suma de los efectos debidos a las fuentes de dificultad predichas por las teorías cognitivas, decidir si éstos son significativos y estimarlos. En el estudio que se informa se diseñaron y elaboraron 24 ítemes de razonamiento deductivo teniendo en cuenta las fuentes de dificultad predichas por las teorías cognitivas y por la experiencia educacional. Se administraron a 251 estudiantes de la Carrera de Psicología de la Universidad de Buenos Aires (UBA). Se describe el procedimiento para seleccionar un subconjunto de los mismos al cual ajuste el modelo LLTM. El objetivo de este trabajo fue verificar la pertinencia de las fuentes de dificultad consideradas y orientar la construcción de nuevos ítemes. Se logró un buen ajuste del modelo de Rasch (p = .89) y del modelo LLTM (p = .11) sobre 12 de ellos. Los valores z de Wald resultaron no significativos para los 12 ítemes mencionados. La correlación de los parámetros de dificultad estimados en ambos modelos fue: r = .99. Se consideraron cinco componentes que resultaron significativos. Éstos fueron, en orden decreciente de dificultad, la presencia de: (a) falacias de afirmación del consecuente y de negación del antecedente, (b) negación afectando a la disyunción o conjunción, (c) contenido abstracto o simbólico, (d) cuantificadores y (e) condicionales. Se verificaron los supuestos de invariancia para los parámetros de los ítemes y de los sujetos. Los resultados de esta etapa exploratoria alientan a seguir construyendo ítemes tomando en cuenta las fuentes de dificultad halladas.
Palabras clave: Modelo LLTM de Fischer; Modelo de Rasch; Fuentes de dificultad; Razonamiento deductivo; Teorías cognitivas; Práctica educacional.
Abstract
Application of the Fischer LLTM model to the analysis of the sources of difficulty of deductive reasoning items.The processes involved in deductive reasoning have been studied by Cognitive Psychology since the seventies. Many hypotheses have been put forward to explain the difficulties in solving simple reasoning problems when considering their logical connectives, content and context of the tasks in which they are presented. These hypotheses have led to the development of different theories of reasoning like those based on the formal inference rules approach (Braine, 1978; Braine & O'Brien, 1991; Braine & Rumain, 1983; Rips, 1994), the Pragmatic Schemas Theory (Cheng & Holyoak, 1985) and the theory of semantic mental models (Johnson-Laird, 1983, Johnson-Laird & Byrne, 1991). The componential models of the Item Response Theory have allowed Psychometry to explain said these processes (Embretson, 1994). Thus, for instance, the Linear Logistic Latent Trait Model (LLTM) (Fischer, 1973, 1997), an extension of the Rasch model, expresses item difficulty as the sum of the effects due to the sources of difficulty predicted by the mentioned cognitive theories, which enables us to decide whether these effects are significant and estimate them. In other words, the Rasch item parameters β1 are linearly decomposed in the form
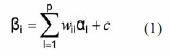
where p is the number of components considered, αl -the basic parameters of the model, expresses the difficulty of each component l, wil is the weight of αl with respect to the difficulty of the item i and c is an arbitrary normalization constant.
Formula (1) implies that the application of the LLTM model makes sense only when the Rasch model fits the data. On the other hand, if the proposed components were sufficiently exhaustive to explain the differences between the items, formula (1) would allow us, once the basic parameters αl have been estimated, to recover estimates ![]() similar to those obtained directly by the application of the Rasch model, which would imply a high correlation between the parameters estimated under both models. The identification of the difficulty components and the estimate of their effects may be useful to generate items with preset difficulty parameters.
similar to those obtained directly by the application of the Rasch model, which would imply a high correlation between the parameters estimated under both models. The identification of the difficulty components and the estimate of their effects may be useful to generate items with preset difficulty parameters.
This paper describes the process to find a subset of deductive reasoning items to which the LLTM model fits well. A set of 24 deductive reasoning items were designed and created considering the sources of difficulty predicted by cognitive theories and educational practice. The objective is to verify the suitability of such sources and to guide the construction of new items. Each item may consist of one, two or three premises and one conclusion. The individual must decide whether the conclusion is true or false. Nine items are made of concrete content, neutral to avoid any bias due beliefs or opinions, and the remaining ones have abstract or symbolic content. They were administered to a sample of 251 students of Psychology (Universidad de Buenos Aires - Argentina), composed of 24% males and 76% females, whose average age is 22.68 (DS = 6.35). Good fit for the Rasch model (p = .89) and for the LLTM model (p = .11) were obtained for 12 of them. The Wald z-values were not significant for the 12 items mentioned before. The linear correlation between the parameters estimated under both models was r = .99. Five components that turned out to be significant were considered. These components are listed in a decreasing level of difficulty: (a) affirmation of the consequent and negation of antecedent fallacies, (b) negation when affecting disjunction / conjunction, (c) abstract or symbolic content, (d) quantifiers and (e) conditionals. The two assumptions that refer to both, the item and subject parameter invariance, were checked. The results of this exploratory step encourage us to go on constructing new items taking into account the sources of difficulty that were found.
Key words: Fischer LLTM model; Rasch Model; Sources of difficulty; Deductive reasoning; Cognitive theories; Educational practice.
Los procesos involucrados en el razonamiento deductivo han sido objeto de estudio de la Psicología Cognitiva desde la década de 1970 (Fillenbaum, 1974; Roberge, 1976, 1978, 1979; Wason, 1977). Desde entonces muchas han sido las hipótesis generadas para explicar las dificultades que presenta la resolución de simples problemas de razonamiento con respecto a los conectivos lógicos involucrados, como también con el contenido y el contexto de la tarea en que se plantean. Éstas han dado lugar a la formulación de diferentes teorías sobre el razonamiento. Santamaría (1995) señala como las tres actualmente más importantes a las teorías de las Reglas Formales de Inferencia (Braine, 1978; Braine & O'Brien, 1991; Braine & Rumain, 1983; Rips, 1994), de los Esquemas y Reglas Sensibles al Contexto (Cheng & Holyoak, 1985) y de los Modelos Mentales Semánticos (Johnson-Laird, 1983; Johnson- Laird & Byrne, 1991).
Los Modelos Componenciales de la Teoría de Respuesta al Ítem le han posibilitado a la Psicometría dar cuenta de ciertos procesos estudiados por la Psicología Cognitiva (Embretson, 1994). Así, por ejemplo, el Modelo Logístico Lineal de Rasgo Latente (LLTM) de Fischer (1973, 1997) permite descomponer la dificultad de un ítem como suma de los efectos debidos a las fuentes de dificultad predichas por las teorías cognitivas, decidir si éstos son significativos y estimarlos. Más precisamente, el modelo LLTM expresa la descomposición de los parámetros de dificultad β1 modelo de Rasch como
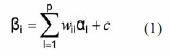
donde p expresa el número de componentes considerados, αl la dificultad del componente l, wil la frecuencia con la que ese componente está presente en el ítem i y c es una constante de escalamiento. Los αl se denominan parámetros básicos.
De la formulación del modelo LLTM mediante la ecuación (1) se sigue que su aplicación tiene sentido sólo si el modelo de Rasch se ajusta suficientemente bien a los datos. Por otra parte, si los componentes considerados explican de manera suficientemente exhaustiva las diferencias entre los ítemes, una vez estimados los parámetros se deberían recuperar a través de la ecuación (1) estimaciones ![]() similares a las obtenidas directamente del modelo de Rasch, lo que implicaría una alta correlación entre los parámetros estimados bajo ambos modelos.
similares a las obtenidas directamente del modelo de Rasch, lo que implicaría una alta correlación entre los parámetros estimados bajo ambos modelos.
La delimitación de los componentes de dificultad y la estimación de sus efectos pueden servir para la generación de ítemes con parámetros de dificultad preestablecidos. Revuelta y Ponsoda (1998) aplicaron el modelo LLTM en las primeras etapas de un trabajo para transformar un test de lápiz y papel en un test adaptativo basado en la generación automática de ítemes. Asimismo Real, Olea, Ponsoda, Revuelta y Abad (1999) lo ajustaron para el análisis de la dificultad de un test de matemática. Prieto y Delgado (2003) aplicaron el Modelo de Rasch al análisis de un test de matemática, aunque sin descomponer la dificultad de los ítemes y consideraron estos índices como un indicador global de la complejidad cognitiva que ellos requieren para su correcta resolución.
En este artículo se describe la etapa inicial de una elaboración de ítemes de razonamiento deductivo creados en vista a ser modelizados con el LLTM y que fueron administrados en una prueba piloto. El objetivo fue explorar el posible ajuste de este modelo a algún subconjunto de ellos que permita una interpretación de los componentes, teniendo en cuenta las fuentes de dificultad señaladas por las teorías cognitivas y por las investigaciones en el ámbito de la educación matemática. De ser así, en una segunda etapa se podrá avanzar en la construcción de una mayor cantidad de ítemes asociados a dichos componentes cuyos efectos se estimarían nuevamente con el modelo LLTM, estimaciones que quedarían disponibles para la generación de ítemes con índices de dificultad preestablecidos según los componentes de dificultad involucrados.
Método
Participantes
Los ítemes se administraron a 251 estudiantes de segundo año de la carrera de Psicología de la Universidad de Buenos Aires (UBA), con una edad promedio de 22.68 (DE = 6.35). La muestra estuvo integrada por un 76% de mujeres y 24% de varones.
Instrumento
El instrumento estuvo conformado por 24 ítemes que integran una prueba piloto de razonamiento deductivo. Cada ítem consiste en una, dos o tres premisas y una conclusión. El formato de respuesta es de verificación, es decir, el sujeto debe decidir si una conclusión se sigue válidamente o no de las premisas. Nueve de ellos son de contenido concreto neutro, para evitar el sesgo de creencias u opinión y 11 de contenido abstracto o simbólico. También se hallan en igual proporción los ítemes válidos y los inválidos. Algunos ítemes involucran operaciones simples como el Modus Ponens o Modus Tollens, mientras que otros combinan distintas operaciones. La totalidad de los ítemes se presenta en el Anexo, habiéndose separado premisas y conclusión por un punto aunque en su administración éstas se hallaban dispuestas unas debajo de otras.
Componentes
Es abundante la investigación cognitiva que hace referencia a las dificultades en el razonamiento deductivo debidas a conectivos lógicos como el condicional, la disyunción y la negación, especialmente cuando ésta se combina con dichos conectivos y con cuantificadores. En cuanto al condicional, los sujetos tienden a interpretarlo en ciertas situaciones como un bicondicional, lo que da lugar a las falacias llamadas de Negación del Antecedente (NA) y de Afirmación del Consecuente (AC) (Dasí & Al ga rabel, 2003; Marcus & Rips, 1979; Rips & Marcus, 1977). Problemas donde la negación opera en relación a la conjunción / disyunción requieren para su correcta resolución la aplicación de las leyes de De Morgan o de los silogismos conjuntivo / disyuntivo. Rips (1983, 1994) afirma que son más difíciles de resolver los problemas que necesitan las reglas de introducción de la negación o del silogismo conjuntivo que los que requieren la conjunción o del Modus Ponens. Principalmente en el ámbito de la educación matemática se han estudiado también las dificultades inherentes a la negación en presencia de disyunción, conjunción y cuantificadores. Lin y Cheng (1997) afirman que sentencias negadas con este tipo de operaciones resultan más difíciles para estudiantes secundarios y universitarios (citado en Lin & Yu, 1997). Lin, Lee y Yu (2003) hallaron que el 40% de estudiantes negaba el "todos" como "ninguno".
Por otra parte también ha sido muy estudiado el efecto del contenido, con resultados dispares. Hay quienes encontraron un efecto facilitador del contenido temático en las tareas de selección (Bracewell & Hidi, 1974; Johnson- Laird, Legrenzi, P. & Legrenzi, M., 1972; Van Duyne, 1974; Wason & Shapiro, 1971) y quienes no encontraron diferencias significativas asociadas a material estimular concreto o abstracto en relación al condicional (Manktelow& Evans, 1979).
Teniendo en cuenta estas fuentes de dificultad, las operaciones involucradas en los ítemes que componen la prueba y el número relativamente bajo de los mismos, en el presente trabajo se han considerado cinco componentes denominados: (a) Contenido, (b) Negación ![]() , (c) Condicional, (d) Falacias NA / AC y (e) Cuantificadores.
, (c) Condicional, (d) Falacias NA / AC y (e) Cuantificadores.
a.- Contenido: Cada ítem puede estar formulado con contenido simbólico, abstracto o concreto neutro. Los porcentajes de respuestas correctas para los ítemes de esta prueba (ver Tabla 1), tanto como para los de otras administraciones piloto de la misma investigación, mostraron que los ítemes de contenido abstracto o simbólico tendían a estar más próximos entre sí en cuanto a la dificultad y ser más difíciles que los de contenido concreto. Por esa razón se decidió dicotomizar el componente Contenido asignando los valores '0' si es concreto y '1' si es simbólico o abstracto.
Tabla 1
Porcentaje de respuestas correctas (p%) para cada ítem y matriz de diseño

b.- Negación ![]() : Este componente se refiere a la negación en relación a la conjunción o a la disyunción. Se halla presente en aquellos argumentos que involucran a las Leyes de De Morgan o a las reglas del silogismo hipotético conjuntivo o disyuntivo. Toma el valor '1' si cualquiera de estas leyes o reglas está presente y '0' en el caso contrario.
: Este componente se refiere a la negación en relación a la conjunción o a la disyunción. Se halla presente en aquellos argumentos que involucran a las Leyes de De Morgan o a las reglas del silogismo hipotético conjuntivo o disyuntivo. Toma el valor '1' si cualquiera de estas leyes o reglas está presente y '0' en el caso contrario.
c.- Condicional: Hace referencia a los ítemes cuyas premisas tienen la estructura de Modus Ponens o Modus Tollens aunque la conclusión puede ser válida o inválida. En el caso de invalidez no se consideran en este componente las NA o AC las cuales, por constituir un tipo de dificultad particular -fuertemente evidenciado en las pruebas piloto-, se han delimitado como un componente aparte. El valor '1' indica la presencia de este tipo de argumento en el ítem y el valor '0' su ausencia.
d.- Falacias NA / AC: Si un ítem contiene una falacia NA o AC el componente es codificado con '1' y de lo contrario con '0'.
e.- Cuantificadores: Algunos ítemes asociados a este componente sólo evalúan la comprensión de expresiones como "Todos", "Ninguno" o "Alguno" y otros evalúan lo que se entiende por la negación de las mismas. Se ha codificado con '1' la presencia de cuantificadores, negados o no, y con '0' la ausencia de toda dificultad asociada a cuantificadores. Por ejemplo, el "todo" que figura en el ítem 8 no es relevante para este componente y fue codificado con '0'.
No se ha considerado la negación como componente individual por estar ya involucrada en los otros componentes.
Ajuste del modelo LLTM
Se llevaron a cabo sucesivas corridas del Programa LPCM-Win (Fischer & Ponocny-Seliger, 1997), al principio con la totalidad de los ítemes. En cada una de ellas se observaba si el modelo ajustaba según el test de razón de verosimilitud condicional χ2 de Andersen (1973). Si no ajustaba, como ocurrió en las primeras etapas, se examinaba la gráfica de las correlaciones entre los parámetros de dificultad obtenidos con el modelo LLTM y con el modelo de Rasch para detectar los ítemes que más contribuían al desajuste. Estos ítemes fueron eliminados sucesivamente hasta encontrar un subconjunto donde el modelo ajustara, es decir, donde las estimaciones de los parámetros de dificultad no difirieran significativamente entre los dos modelos. La información que da la salida del programa LPCM-Win también se utilizó para:
a.- Verificar tanto el ajuste del modelo de Rasch al subconjunto hallado mediante el test χ2 de Andersen, como el ajuste de cada ítem a través del estadístico z de Wald (1943). Estos métodos requieren particionar la muestra, lo cual se hizo con respecto a la media de los puntajes.
b.- Examinar la correlación entre las estimaciones de los parámetros de dificultad obtenidas con las submuestras definidas a partir de la media de los puntajes; tanto mayor será la correlación cuanto mejor se satisfaga el supuesto de invariancia de la Teoría de Respuesta al Ítem.
c.- Verificar la unidimensionalidad de dos subconjuntos de ítemes mediante el test de Martin-Löf. Como entre los ítemes había la misma proporción con contenido concreto que abstracto / simbólico se tomó este factor como criterio de clasificación.
Resultados
Se obtuvo un subconjunto de 12 ítemes para el cual el modelo LLTM ajustó con un valor χ2 de Andersen de 9.91 (gl = 6; p = .11). La correlación entre los parámetros de dificultad de los ítemes estimados bajo el modelo de Rasch y bajo el LLTM es r = .99. El modelo de Rasch ajustó bien a dicho subconjunto (p = .89) y todos los ítemes tuvieron valores z de Wald no significativos al 5%. La correlación de las estimaciones de los parámetros de dificultad obtenidas a partir de las submuestras de sujetos con puntajes su periores e inferiores a la media es r = .98. Según los resultados del test de Martin-Löf, no se rechaza la hipótesis nula de que los ítemes de contenido concreto y los de contenido abstracto / simbólico miden el mismo rasgo latente (χ2 = 37.23; gl = 35; p = .37). En la Tabla 2 se detalla, para cada uno de los 12 ítemes, la estimación de los parámetros con el LLTM, con el modelo de Rasch, el error estándar de esta estimación y el valor z.
Tabla 2
Rasch, errores estándar, valores z y significación al 5%

Las estimaciones de los parámetros básicos resultaron significativas al 5% para el componente condicional y al 1% para los cuatro componentes restantes. Éstas se exhiben en la Tabla 3 junto con sus correspondientes errores estándar, puntuaciones z y significación. Las fuentes de dificultad ordenadas partiendo desde la que más dificultad introduce en un ítem son: la presencia de NA o de AC, la negación de la conjunción o disyunción, el contenido abstracto / simbólico, la presencia de cuantificadores y, finalmente, la presencia de condicionales con estructura de premisas Modus Ponens / Modus Tollens. La matriz del diseño se presenta en la Tabla 2 donde puede apreciarse a qué fuentes de dificultad está asociado cada ítem.
Tabla 3
Estimación de parámetros en el modelo LLTM

Discusión
Los resultados en esta etapa exploratoria alientan a seguir construyendo ítemes tomando en cuenta las fuentes de dificultad halladas y a considerar su administración a una muestra más grande para su mejor calibración. Es particularmente alentador haber podido obtener un subconjunto de ítemes para el cual el estadístico χ2 es no significativo, algo difícil de lograr según admite Fischer (1997). La creación de un número mayor de ítemes permitiría desglosar algunas de las fuentes de dificultad consideradas discriminando, por ejemplo, las NA de las AC o el Modus Ponens del Modus Tollens. También sería de interés introducir algunos silogismos cuyas fuentes de dificultad, como la figura o el modo han sido profusamente estudiadas, a fin de lograr una mayor exahustividad en la consideración de los componentes asociados a las dificultades en el razonamiento deductivo.
Una de las razones por las cuales es posible que sólo haya ajustado la mitad de los ítemes de la prueba es que ésta no estaba concebida como tal, como una unidad, sino como un conjunto de ítemes para poner a prueba y efectuar ciertas comparaciones; así es que, por ejemplo, algunos ítemes como el 4, 9 y 19 se encontraban replicados en versiones con distinto tipo de contenido, lo que implica dependencia lógica entre ellos que puede afectar la independencia local. De los tres mencionados, han quedado ajustados el 4 y el 19. También tienen la misma estructura argumental los pares de ítemes (2,18), (7,20), (12,15), la misma estructura de premisas el par (3,23) y son similares los del par (6,13). De cada uno de estos pares sólo uno de los ítemes ha sido retenido en el proceso de ajuste. Pero sin duda la principal razón de la reducción del número de ítemes es haber utilizado un procedimiento tan restrictivo como es la búsqueda del ajuste estadístico. Sin embargo, se ha asumido este costo en vistas a ir construyendo ítemes cuyas estimaciones de los componentes de dificultad sean confiables y queden disponibles para la generación de otros nuevos.
Tomando en cuenta estas consideraciones se concluye que conviene avanzar con la elaboración de una mayor cantidad y variedad de ítemes asociados a los componentes ya identificados, como también intentar ampliar el espectro de componentes a los referidos al razonamiento silogístico. En todos los casos se tratará de evitar la dependencia local, es decir, que haya dos ítemes que involucren exactamente las mismas operaciones.
Ítemes de razonamiento deductivo
1.- No se cumple que ningún elemento difiere de A. Por tanto: Algún elemento no es A. (Válido)
2.- Si se rompe el parabrisas suena la alarma. No se rompe el parabrisas. Por tanto: No suena la alarma. (Inválido)
3.- Si todos los archivos están comprimidos caben juntos en un CD. Los archivos no caben todos juntos en un CD. Por tanto: Hay algún archivo que está descomprimido. (Válido)
4.- Si R no es S entonces A es D. No se cumple que A sea C y D. A es C. Por tanto: R es S. (Válido)
5.- Si se hace buena publicidad y la gente está despreocupada por lo económico habrá alta demanda del servicio. No hubo alta demanda del servicio. Por tanto: No se hizo buena publicidad o la gente no estaba preocupada por lo económico. (Inválido)
6.- Todos los CD de la primera repisa son de música del siglo XVIII. Por tanto: Ningún CD de rock está en la primera repisa. (Válido)
7.- Si hay un punto también hay una raya. Hay una raya. Por tanto: Hay un punto. (In válido)
8.- Echaron a todo empleado que fuera deshonesto o incompetente. Norma no fue echada. Por tanto: Norma es honesta y competente. (Válido)
9.- Lucía dice que su novio es culto y adinerado pero ella miente aunque sí es culto. Si Lucía no se opone a los deseos de su madre se casará con un hombre adinerado. Lucía se casará con su novio. Por tanto: Lucía se opondrá a los deseos de su madre. (Válido)
10.- Todos los que son B ó C también son A. D no es A. Por tanto: D no es B ó D no es C. (Válido)
11.- En estos códigos siempre un número va seguido de una letra. El segundo carácter de este código es una letra. Por tanto: El primero tiene que ser un número. (Inválido)
12.- Si no se baja la palanca no se abre la compuerta. No se baja la palanca. Por tanto: No se abre la compuerta. (Válido)
13.- Todas sus amistades íntimas están fuera del ámbito laboral. Por tanto: No tiene ningún amigo íntimo dentro del ámbito laboral. (Válido)
14.- Si hay un círculo y no hay una letra, entonces hay una estrella. No hay una estrella. Por tanto: No hay un círculo o hay una letra. (Válido)
15.- Si K no es L, entonces M no es P. K no es L. Por tanto: M no es P. (Válido)
16.- No es verdad que ningún integrante del coro desafina. Por tanto: Algunos afinan. (Inválido)
17.- Si no todos los alumnos desaprobaron no se modificará ninguna nota. Algunos alumnos aprobaron. Por tanto: Algunas notas se modificarán. (Inválido)
18.- Si W es '1' entonces X es '2'. W no es '1'. Por tanto: X no es '2'. (Inválido)
19.- No se cumple que el redondo sea liso y rojo. El redondo es liso. Si el rectangular no es verde, entonces el redondo es rojo. Por tanto: El rectangular es verde. (Válido)
20.- Si Ana consume chocolate aumenta de peso. Ana ha aumentado de peso. Por tanto: Ana ha comido chocolate. (Inválido)
21.- Si algunos A son B, entonces ningún C es D. Algunos A son B. Por tanto: Algunos C son D. (Inválido)
22.- Todas estas cuchillas están afiladas. Por tanto: Entre estas cuchillas hay alguna desafilada. (Inválido)
23.- Si todos los A son B, entonces C es D. C no es D. Por tanto: Ningún A es B. (Inválido)
24.- Todos los A son distintos de B. Por tanto: Algún B puede ser A. (Inválido)
Referencias bibliográficas
1. Andersen, E. (1973). A goodness of fit test for the Rasch model. Psychometrika, 38, 123-140. [ Links ]
2. Bracewell, R. & Hidi, S. (1974). The solution of an inferential problem as a function of the stimulus materials. Quaterly Journal of Experimental Psychology, 26, 480-488. [ Links ]
3. Braine, M. (1978). On the relation between the natural logic of reasoning and standard logic. Psychological Review, 85, 1-21. [ Links ]
4. Braine, M. & O'Brien, D. (1991). A theory of if: A lexical entry, reasoning program, and pragmatic principles. Psychological Review, 98, 182-203. [ Links ]
5. Braine, M. & Rumain, B. (1983). Development of comprehension of 'or'. Journal of Experimental Child Psychology, 31, 46-70. [ Links ]
6. Cheng, P. & Holyoak, K. (1985). Pragmatic reasoning schemas. Cognitive Psychology, 17, 391-416. [ Links ]
7. Dasí, C. & Algarabel, S. (2003). Influencia del entrenamiento sobre el razonamiento deductivo: Importancia del contenido y transferencia entre dominios [Influence of training on deductive reasoning: Importance of content and transfer between domains]. Psicothema, 15, 440-445. [ Links ]
8. Embretson, S. (1994). Applications of cognitive design systems to test development. En C.R. Reynolds (Ed.), Cognitive assessment. A multidisciplinary perspective (pp. 107-135). New York: Plenum. [ Links ]
9. Fillenbaum, S. (1974). Or: Some uses. Journal of Experimental Psychology, 103, 913-921. [ Links ]
10. Fischer, G.H. (1973). The linear logistic test model as an instrument in educational research. Acta Psychologica, 37, 359-374. [ Links ]
11. Fischer, G.H. (1997). Unidimensional Linear Logistic Rasch Model. En W.J. Van Der Linden & R.K. Hambleton (Eds.), Handbook of modern item response theory (pp. 225-243). New York: Springer-Verlag. [ Links ]
12. Fischer, G.H. & Ponocny-Seliger, E. (1997). LPCM-WIN Program. Groningen: IEE, ProGamma. [ Links ]
13. Johnson-Laird, P. (1983). Mental models. Towards a cognitive science on language, inference, and consciousness. Cambridge: Cambridge University Press. [ Links ]
14. Johnson-Laird, P. & Byrne, M. (1991). Deduction. Hillsdale, NJ: LEA. [ Links ]
15. Johnson-Laird, P., Legrenzi, P. & Legrenzi, M. (1972). Reasoning and sense of reality. British Journal of Psychology, 63, 395-400. [ Links ]
16. Lin, F. & Cheng, Y. (1997). An explorative teaching on the argument principle of proof by contradiction. Chinese Journal of Science Education, 5(4), 557-591. [ Links ]
17. Lin, F. & Yu, J. (1997, July). False Proposition - As a means for making conjectures in mathematics classrooms. Asian Mathematical Conference, Singapore. Recuperado el 19 de abril de 2007 de http://www.math.nus.edu.sg/AMC/papers/Lin-Fou-Lai.pdf. [ Links ]
18. Lin, F., Lee, Y. & Yu, J. (2003). Students' understanding of proof by contradiction. La Lettre de la Preuve, 4, 443-450. International Newsletter on the Teaching and Learning of Mathematical Proof. Recuperado el 19 de abril de 2007, de http://www.lettredelapreuve.it/PME/PME27/RR_wu_yu.pdf [ Links ]
19. Manktelow, K. & Evans, J. (1979). Facilitation of reasoning by realism: Effect or non effect? British Journal of Psychology, 71, 227-31. [ Links ]
20. Marcus, S. & Rips, L. (1979). Conditional reasoning. Journal of Verbal Learning and Verbal Behavior, 18, 199-223. [ Links ]
21. Prieto, G. & Delgado, A. (2003). Análisis de un test mediante el modelo de Rasch [Rasch-modelling a test]. Psicothema, 15(1), 94-100. [ Links ]
22. Real, E., Olea, J., Ponsoda, V., Revuelta, J. & Abad, F. (1999). Análisis de la dificultad de un test de matemática mediante un modelo componencial [Analysis of the difficulty of a mathematics test using a componential model]. Psicológica, 20, 121-134. [ Links ]
23. Revuelta, J. & Ponsoda, V. (1998). Un test adaptativo informatizado de análisis lógico basado en la generación automática de ítemes [A logical analysis computerized adaptive test based on automatic item generation]. Psicothema, 10(3), 709-716. [ Links ]
24. Rips, L. (1983). Cognitive processes in propositional reasoning. Psychological Review, 90, 38-71. [ Links ]
25. Rips, L. (1994). The psychology of proof: Deductive reasoning in human thinking. Cambridge, MA: M.I.T. Press, Bradford Books. [ Links ]
26. Rips, L. & Marcus, S. (1977). Suppositions and the analysis of conditional sentences. En M.A. Just & P.A. Carpenter (Eds.), Cognitive processes in comprehension (pp. 185-220). Hillsdale, NJ: Lawrence Erlbaum. [ Links ]
27. Roberge, J. (1976). Effects of negation on adults' disjunctive reasoning abilities. Journal of General Psychology, 91, 23-28. [ Links ]
28. Roberge, J. (1978). Linguistic and psychometric factors in propositional reasoning. Quaterly Journal of Experimental Psychology, 30, 705-716. [ Links ]
29. Roberge, J. (1979). Facilitating insight into a reasoning task. British Journal of Psychology, 70, 227-231. [ Links ]
30. Santamaría, C. (1995). Introducción al razonamiento humano [Introduction to human reasoning]. Madrid: Alianza Editorial. [ Links ]
31. Van Duyne, P. (1974). Realism and linguistic complexity in reasoning. British Journal of Psychology, 65, 59-67. [ Links ]
32. Wald, A. (1943). Test of statistical hypotheses concerning several parameters when the number of observations is large. Transactions of the American Mathematical Society, 54, 426-482. [ Links ]
33. Wason, P. (1977). Self-contradictions. En P.N. Jonhson-Laird & P.C. Wason (Comps.), Thinking: Readings in cognitive science (pp. 114-128). Cambridge: Cambridge University Press. [ Links ]
34. Wason, P. & Shapiro, D. (1971). Natural and contrived experience in a reasoning problem. Quaterly Journal of Experimental Psychology, 23, 63- 71. [ Links ]
Instituto de Investigaciones, Facultad de Psicología, Universidad de Buenos Aires (UBA). Ciudad Autónoma de Buenos Aires, República Argentina
Fecha de recepción: 29 de abril de 2008
Fecha de aceptación: 27 de enero 2009














