Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Interdisciplinaria
versión On-line ISSN 1668-7027
Interdisciplinaria vol.27 no.1 Ciudad Autónoma de Buenos Aires jul. 2010
Validación de una nueva Escala de Expectativas de Resultados y Metas de Rendimiento para Matemática
Validity evidence for the new scales for mathematics outcome expectancies and performance goals
Marcos Cupani*
*Licenciado en Psicología. Profesor Asistente de la Cátedra Técnicas Psicométricas de la Facultad de Psicología, Universidad Nacional de Córdoba (UNC).
E-Mail: marcoscup@gmail.com
Los Onas 1212, 3er Piso Dpto. D, Barrio Crisol Sur (5014), Córdoba. República Argentina.
El autor agradece al Dr. Ricardo M. Pautassi, Profesor Adjunto de la Cátedra Escuela, Corrientes y Sistema de la Psicología Contemporánea de la Facultad de Psicologíade la Universidad Nacional de Córdoba (UNC), su colaboración en la redacción del abstract y a la Lic. María José Cupani, la revisión y sugerencias recibidas para la elaboración del manuscrito.
Resumen
Con el objetivo de poder evaluar los postulados de un modelo de rendimiento académico en Matemática basado en la Teoría Social Cognitiva del Desarrollo de Carrera (SCCT - Lent, Brown & Hackett, 1994), se adaptaron las subescalas de Expectativas de resultados en Matemática y Metas en Matemática de la Escala de Autoeficacia para Enseñanza Media (Fouad, Smith & Enochs, 1997). En esta adaptación (Cupani & Gnavi, 2007)se observó que la Subescala Metas en Matemática presentó una estructura factorial simple y una adecuada confiabilidad, aunque no evidenció poder predictivo del rendimiento académico. Por otro lado, la Subescala Expectativas de Resultados presentó valores bajos de consistencia interna y se observó que el contenido de algunos de sus ítemes parece no ser aceptable para nuestro medio cultural. Por lo tanto, para mejorar ambas escalas se realizaron nuevos estudios. En una primera fase, se efectuaron dos grupos de enfoque con el propósito de generar nuevos ítemes sobre las Expectativas de resultados y Metas de rendimiento de los estudiantes de nuestro medio cultural. De este estudio se obtuvo una nueva versión de las escalas Expectativas de Resultados y Metas de Rendimiento compuestas por 13 y 11 ítemes, respectivamente. En una segunda fase se administraron estos nuevos ítemes a una muestra de 420 adolescentes con un rango de edad de 13 a 16 años (M = 13.84, DT = .76). Se realizaron estudios de análisis factorial (exploratorio y confirmatorio) y de confiabilidad mediante y de validez test-criterio. Los resultados demostraron que ambas escalas poseen adecuadas propiedades psicométricas.
Palabras clave: Expectativas de resultados; Metas de rendimiento; Rendimiento académico.
Abstract
Lent and Brown (2006) suggest guidelines for creating and adapting assessment tools based on the Social Cognitive Career Theory (SCCT -Lent, Brown, & Hackett, 1994). In the last years, this theory has been the subject of substantial research, both basic and theoretical. The authors indicate that any assessment of SCCT should: (a) contextualize measures to make sure they are grounded in a particular, domain-specific context, (b) be reasonably comprehensive in sampling the domain, designing multifaceted measures when the criterion is correspondingly complex, and (c) ensure compatibility between predictors and criteria along key dimensions, including content, context, temporal orientation, and level of specificity. Additionally, it is important to use reliable and valid tests. Without sound measures, it is difficult, if not impossible, to establish whether theory-discrepant findings are attributable to problems with the theory, flaws in operationalizing it, or both. In Argentina, Cupani and Gnavi (2007) assessed a model of academic performance in Mathematic, based on the SCCT. Cupani and Gnavi adapted the subscales for Mathematic Outcome Expectancies and Performance Goals of the Middle School Self-Efficacy Scale (Fouad, Smith, & Enochs, 1997). Results indicated that the goals subscale has a simple factor structure with adequate internal consistence, although it did not predict academic performance in Mathematic. Moreover, the Subscale for Mathematics Outcome Expectancies showed low internal consistence and some of its items did not transfer well to our cultural setting. Therefore, two follow-up studies were carried out to improve the psychometric properties of both scales. The first study employed two focus groups (n per group ≥ 8) and aimed at generating ideas on the student's expectations of results and goals on academic achievement in our cultural setting. The information gathered was used to write 7 new items for the goals subscale and 12 items for the outcome expectancies. These items were then tested for clarity and understanding in a sample of adolescents. Language corrections were also carried out, yielding two new goals and outcome expectancies scales (11 and 13 items, respectively). On the second study, these scales were administered to a sample of 420 adolescents (M = 13.84; SD = .76). The internal structure of the scales was examined through exploratory and confirmatory factor analysis and their internal consistency was analyzed by Cronbach's alpha. The predictive validity for Academic Achievement in Mathematic was also analyzed. The scale of logical-mathematical self- efficacy from the (revised) Self-efficacy Inventory of Multiple Intelligences (Pérez & Cupani, 2008) was also administered. Exploratory and confirmatory factor analysis revealed that a single-factor structure for the scale of performance goals (GFI: .92; CFI: .95, RMSEA: .08) and for the Scale for Mathematic Outcome Expectancies (GFI: .95; CFI: .96, RMSEA: .06) is the most appropriate model for the data gathered. Both scales had optimal Cronbach's alpha values (.86 and. 85, for performance goals and outcome expectancies, respectively). The study on predictive validity also showed that logic-mathematic self- efficacy beliefs and achievement goals in Mathematic explain 32% of variance of math school performance. The results show that Academic Achievement in Mathematic is partially explained by the model. In summary, both scales allow a contextualized measurement of outcome expectancies and performance goals on Mathematic in teenagers from our cultural area. These scales have satisfactory psychometric properties, presenting a clear internal structure, and adequate internal consistence. Future application of path analysis will allow a more precise identification of the interrelations between outcome expectancies and performance goals on Mathematic and their direct and indirect effects upon academic achievement in it.
Key words: Outcome expectancies; Performance goals; Academic achievement.
Introducción
La Teoría Social Cognitiva del Desarrollo de Carrera (Social Cognitive Career Theory -SCCT-) propuesta por Lent, Brown y Hackett (1994) representa un notable esfuerzo de integración de diferentes modelos y constructos, y tiene como finalidad comprender los mecanismos que regulan el desarrollo de los intereses vocacionales, la elección de carrera y el rendimiento académico. Los autores proponen una serie de relaciones teóricas así como ciertas vías causales, respetando el modelo de causalidad triádica (Bandura, 1987) y enfatizando tres componentes del enfoque social-cognitivo: Creencias de autoeficacia, Expectativas de resultado y Metas.
En los últimos años, la SCCT ha recibido mucha atención de los investigadores, incluyendo algunos intentos recientes de verificar varias de sus proposiciones en minorías raciales, estudiantes universitarios y pre-universitarios (Fouad & Smith, 1996; Lapan, Shaughnessy & Boggs, 1996; López, Lent, Brown & Gore, 1997). El enfoque de la SCCT también parece tener consecuencias prácticas en el proceso de transición escuela-trabajo (Lent, Hackett & Brown, 2004) y la satisfacción laboral (Lent & Brown, 2005). También se ha observado un incremento de la investigación básica y teórica sobre los principales conceptos y procesos de la SCCT (v.g., Flores & O'Brien, 2002; Swanson & Gore, 2000), incluyendo esfuerzos para evaluar modelos alternativos y examinar la interacción entre las variables personales y contextuales (v.g., Rottinghaus, Lindley, Green & Borgen, 2002; Schaub & Tokar, 2005).
No obstante, Lent y Brown (2006) advierten que para evaluar las principales hipótesis de la SCCT es necesario contar con instrumentos confiables y válidos que midan los constructos propuestos por esta teoría. En caso contrario, se torna muy dificultoso diferenciar si los resultados obtenidos de una investigación realmente discrepan de los postulados teóricos, o se debe a una falla de la operacionalización de las variables, y porqué no, a ambas posibilidades. Es por ello, que los autores proponen una guía para la construcción o adaptación de instrumentos basados en la teoría social cognitiva.
Dentro de las principales consideraciones tratadas por estos autores se puede destacar:
a.- que los instrumentos deben ser correctamente contextualizados, es decir, procurar que el dominio de interés esté adecuadamente especificado al contexto de aplicación,
b.- que el muestreo del dominio sea razonablemente comprensivo, procurando que los ítemes del constructo abarquen desde lo más general a los niveles más específicos,
c.- asegurarse que el predictor y el criterio sean compatibles con respecto al contenido, el contexto, la orientación temporal y el nivel de especificidad (Ajzen, 1988) y
d.- seleccionar una variable dependiente que sea claramente articulada a la SCCT (Lent & Brown, 2006).
Además los autores sugieren consideraciones para una correcta instrucción del inventario, posibles formatos de escala según el constructo a medir (v.g., escala Likert de 5 ó 7 opciones de respuestas si la población meta del estudio está conformada por adolescentes), algunas recomendaciones de carácter psicométrico tales como redactar ítemes claros, explícitos y relativamente cortos, con un lenguaje adecuado a la población meta (Bandura, 2002), obtener valores de confiabilidad adecuados (v.g., > .70, preferentemente > .80) y obtener evidencias de validez, convergencia, test-criterio y especialmente, de estructura factorial (v.g., análisis factorial confirmatorio).
En Argentina, con el objetivo de evaluarlos postulados de un modelo de rendimiento académico en Matemática basado en la SCCT, se adaptaron las subescalas de Expectativas de Resultados y Metas en Matemática de la Escala de Autoeficacia para Enseñanza Media (Middle School Self-Efficacy Scale de Fouad, Smith & Enochs, 1997). La versión original de esta escala fue desarrollada para evaluar las creencias de autoeficacia (12 ítemes), las expectativas de resultados (5 ítemes), las intenciones y metas (5 ítemes) de estudiantes de educación media para la toma de decisión en un proceso de elección de carrera. También permite medir las Creencias de Autoeficacia en Matemática (5 ítemes) y ciencia (7 ítemes), las Expectativas de Resultados en Matemática (4 ítemes) y en ciencia (2 ítemes), las Intenciones y Metas en Matemática (2 ítemes) y en ciencia (4 ítemes).
En esta primera adaptación, y debido al reducido número de ítemes de las subescalas de Expectativas de Resultados y Metas en Matemática se agregaron reactivos pertenecientes a las subescalas de Expectativas y Metas en ciencia, con la modificación de la palabra ciencia por Matemática.
Posteriormente, se realizaron estudios psicométricos de: (a) análisis factorial exploratorio, (b) confiabilidad mediante el alpha de Cronbach y (c) evidencias de validez de criterio con respecto al rendimiento académico en Matemática (Cupani & Gnavi, 2007). Los resultados de estos primeros estudios demostraron que la Escala de Metas en Matemática presenta propiedades psicométricas aceptables, evidenciando una estructura factorial simple y una adecuada confiabilidad, teniendo en cuenta que la componen sólo 4 ítemes. Sin embargo, esta escala no evidenció poder predictivo del Rendimiento Académico en Matemática, tal como lo propone el modelo de rendimiento académico de la SCCT. Esta falta de contribución predictiva puede estar relacionada con la falta de variabilidad de las respuestas al test, ya que
"los puntajes de un test extenso poseen varianzas mayores y las puntuaciones obtenidas en pruebas breves tienen varianzas más reducidas y, por consiguiente,coeficientes de correlación inferiores con las medidas del criterio" (Tornimbeni, Pérez & Olaz, 2008, pp. 116-117).
Una de las soluciones posibles para incrementar la variabilidad de las puntuaciones es aumentar la cantidad de reactivos que componen la escala.
Por otro lado, la Escala de Expectativas de Resultados en Matemática presentó valores bajos de consistencia interna, según los estándares recomendables (α ≥ .70) y se observó que el contenido de algunos de sus ítemes parece no ser aceptable para nuestro ambiente cultural. Por ejemplo, el ítem "Si obtengo buenas notas en Matemática mis compañeros me respetarán" fue eliminado de esta primera escala ya que resulta inadecuado para nuestro contexto educacional, donde los alumnos más estudiosos y de mejor rendimiento no parecen ser valorados particularmente por sus pares (Cupani & Gnavi, 2007).
Para poder contar con instrumentos adecuadamente contextualizados y abarcar con mayor especificidad las Expectativas de Resultados y Metas de Rendimiento en Matemática, se realizaron nuevos estudios de adaptación. Ellos fueron realizados en dos fases. En la primera se generaron nuevos ítemes pertinentes a las Expectativas de Resultados y Metas de Rendimiento de los estudiantes de Córdoba (República Argentina). Luego, en una segunda fase, se realizaron los estudios psicométricos de validez y confiabilidad.
Fase 1
Método
En la primera fase se aplicó la técnica Grupo de Enfoque que consiste en focalizarse en un tema específico con el fin de profundizar en su análisis. Esta práctica, cuyo origen parte de la entrevista no-directiva de las Ciencias Sociales, se basa en la idea de que las personas que comparten un problema común estarán más dispuestas a hablar entre otras con el mismo problema (Krueger,1988). De este modo, se consideró que esta técnica permitiría generar ideas nuevas para redactar ítemes pertinentes a las Expectativas de Resultados y Metas de Rendimiento en Matemática de los adolescentes de la muestra en estudio.
Participantes y procedimiento
Para poder contar con los grupos de enfoque se pidió autorización a los directivos de dos instituciones escolares (una privada y otra estatal) de la ciudad de Córdoba (República Argentina) y se seleccionaron al azar, alumnos de ambos sexos, pertenecientes a octavo y noveno año del ciclo de Enseñanza General Básica (EGB). A estos estudiantes se les pidió su colaboración, enfatizando la naturaleza voluntaria de su participación. Sin embargo, sólo integraron los grupos de enfoque quienes presentaron el consentimiento informado, firmado por sus respectivos padres.
La muestra total para este estudio quedó compuesta por 21 adolescentes de 13 a 15 años que conformaron dos grupos de discusión: Uno de ellos estuvo integrado por 8 alumnos de una institución privada (3 de sexo femenino y 5 de masculino) y el otro, estaba compuesto por 13 estudiantes pertenecientes a una escuela estatal (7 de sexo femenino y 6 de masculino).
La tarea se llevó a cabo en las instituciones y en horario regular de clases. En cada grupo hubo dos moderadores, uno debía generar el intercambio de opiniones y otro, registrar notas de observación durante y después de la sesión. Para poder generar una dinámica favorable en los grupos, no se permitió la presencia de personas con una clara relación de autoridad (maestros o preceptores). El registro de la tarea se llevó a cabo a través de grabaciones de audio, cuyo contenido se transcribió posteriormente.
Instrumento
Con el fin de que ambos grupos de enfoque siguieran un mismo eje temático, se crearon preguntas que estaban organizadas de menor a mayor especificidad. El objetivo de estas preguntas era que funcionaran como disparador del debate entre los adolescentes.
Las primeras preguntas abarcaban aspectos generales sobre el ámbito académico (por ejemplo: "¿Cuáles son las materias que más les gustan?"), mientras que las de carácter más específico hacían referencia a las creencias sobre la asignatura ("¿Qué opiniones tienen sobre la asignatura Matemática?"), sobre sus metas ("¿Qué tipo de objetivos se proponen para obtener promedio en la asignatura Matemática?") y expectativas sobre la utilización de la materia ("¿Creen que es útil aprender Matemática para su futuro?").
Resultados
Tras la transcripción del contenido de las grabaciones se procedió al análisis de la información recogida. Para ello se partió de dos categorías predeterminadas, los objetivos o metas que se proponen los estudiantes en Matemática para alcanzar un buen rendimiento académico y las expectativas que tienen ellos sobre la utilidad de la materia.
En un primer nivel se realizó un resumen descriptivo del contenido, de las expresiones textuales y de extractos de diálogos que se consideraron clave. Luego, en un segundo nivel de análisis se redactaron los ítemes a partir del modelo teórico sobre el que se interpretó la información obtenida. En este caso, la información se interpretó desde la Teoría Social Cognitiva (Bandura, 1987) y se tuvieron en cuenta las pautas propuestas por Lent y Brown (2006) para la adaptación de escalas. De esta manera se redactaron 7 nuevos ítemes para la Escala de Metas de Rendimiento y 12 ítemes para la Escala de Expectativas de Resultados. En esta última escala se incorporaron ítemes redactados de forma negativa.
Para la redacción de los ítemes se tuvieron en cuenta algunas pautas convencionales tales como: (1) que fueran congruentes con el objetivo de medición, (2) evitar ítemes demasiado extensos, (3) evitar oraciones complejas con sentido ambiguo, (4) evitar frases con dobles negaciones, (5) evitar el uso de expresiones extremas (nunca, siempre, todos) y (6) utilizar un lenguaje apropiado al nivel de maduración y educativo de la población meta de la medición (Oesterlind, 1990).
Por otro lado, la mayoría de los autores recomienda que los ítemes preliminares sean revisados por expertos para evaluar la claridad semántica y corrección gramatical, la adecuación al nivel de comprensión de la población meta y congruencia con el constructo o dominio medido. Los ítemes fueron revisados por un especialista en construcción y adaptación de inventarios basados en la Teoría Social Cognitiva, quien sugirió algunos cambios en la redacción.
Luego, se realizó una prueba piloto con una muestra pequeña de 10 adolescentes para corroborar empíricamente que los ítemes fueran claros y comprensibles para la población meta del test. Posteriormente, se revisaron los ítemes señalados por los adolescentes como dificultosos y se realizaron las modificaciones idiomáticas pertinentes. En particular, los ítemes redactados en forma negativa de la Escala Expectativas de Resultados en Matemática fueron descartados después de este análisis ya que fueron los únicos reactivos que generaron algún tipo de dificultad en su comprensión. De esta manera quedó conformada una nueva versión de las escalas: Expectativas de Resultados en Matemática quedó compuesta por 13 ítemes (5 originales y 8 nuevos) y Metas de Rendimiento en Matemática, por 11 ítemes (4 originales y 7 nuevos).
Fase 2
Método
Participantes
La muestra estuvo compuesta por 420 adolescentes, 181 de sexo femenino (43.1%) y 239 de sexo masculino (56.9%), que cursaban octavo y noveno año de EGB, con edades entre 13 y 16 años (M = 13.84, DT = .76) y eran alumnos de colegios estatales (33%) y privados (67%).
Instrumentos
La nueva versión de la Escala para medirlas Expectativas de Resultados está compuesta por 13 ítemes y la Escala de Metas de Rendimiento, por 11 ítemes. Para responderlas, los adolescentes debían emplear una escala tipo Likert con cinco opciones de repuestas desde Muy en Desacuerdo (1) hasta Muy de Acuerdo (5).
Para el estudio de validez predictiva se utilizó la Escala de Autoeficacia Lógico-Matemática del Inventario de Autoeficacia para Inteligencias Múltiples Revisado (IAMI- R de Pérez & Cupani, 2008). El IAMI-R mide la confianza que los adolescentes poseen para realizar actividades escolares relacionadas con las inteligencias múltiples y está compuesto por 64 ítemes (por ej., realizar mentalmente cálculos numéricos). El individuo debe responderlos empleando una escala Likert de 10 alternativas, desde (1) Nada seguro de poder realizar esta actividad a (10) Totalmente seguro de poder realizar exitosamente esa actividad. Sus valores de consistencia interna son satisfactorios (α = .89).
Procedimiento
La administración de los ítemes fue colectiva y en el horario regular de clases, solicitando la colaboración de los alumnos y enfatizando la naturaleza voluntaria de su participación. Para la realización del estudio de validez predictiva se administró adicionalmente el IAMI-R (Pérez & Cupani, 2008) a una submuestra de la original (n = 340), y luego se obtuvieron los promedios finales en Matemática.
Resultados
Análisis descriptivos de los ítemes
Previo al análisis factorial se inspeccionaron los casos atípicos univariados mediante el cálculo de puntuaciones estándar para cada ítem (z > 3.29; p < .001) y no se descartó caso alguno. Para comprobar los supuestos de normalidad de la muestra se realizaron análisis de asimetría y curtosis en cada ítem y se observó que 23 ítemes presentaron valores entre +1,00 y -1,00, lo cual es considerado por la literatura como excelente, y el Item 8 de la Escala Metas de Rendimiento en Matemática presentó índices de asimetría y curtosis inferiores a 1.60, lo cual es considerado adecuado (George & Mallery, 2003).
Análisis factorial exploratorio y confirmatorio
Se realizó un análisis factorial exploratorio con los ítemes de cada escala utilizando máxima verosimilitud como método de estimación. La muestra fue dividida en dos partes de manera aleatoria. La primera mitad (n = 219) fue seleccionada para realizar el análisis factorial exploratorio y la segunda (n = 201), se reservó para conducir el análisis factorial confirmatorio. Para efectuar estos análisis se utilizaron los programas SPSS 15, el Factor Versión 7 (Lorenzo-Seva & Ferrando, 2006) y el AMOS 6,0 (Arbuckle, 2005).
Escala de Metas de Rendimiento en Matemática
Para esta escala, la medida de adecuación muestral de Kaiser-Mayer-Olkin (.885) y la prueba de esfericidad de Barttlet con valores de 846,947 (p ≤ .000) indican que es factible realizar el análisis factorial. La regla KG de autovalores superiores a 1 determinó la existencia de dos factores que explican un 53.22% de la variancia de respuesta al test, en cambio el gráfico Scree Test para la magnitud de los autovalores (Cattell, 1966) sugirió la extracción de un solo factor. De la misma manera, el análisis paralelo de Horn (1965) sugirió retener un solo factor. Por lo tanto, se obtuvo una estructura compuesta por un solo factor con pesos factoriales comprendidos entre .48 a .74 que conforman una estructura simple (ver Tabla 1).
Tabla 1. Peso factorial, coeficientes estandarizados y coeficiente alpha de Cronbach para la Escala Metas de Rendimiento en Matemática

Notas
α = .86
ª Item eliminado
Con la otra mitad de la muestra (n = 201) se realizó un análisis factorial confirmatorio utilizando el método de estimación máxima verosimilitud y para evaluar el ajuste del modelo se emplearon múltiples indicadores (Hu & Bentler, 1995). Específicamente, se utilizó el estadístico chi cuadrado, la razón de chi-cuadrado sobre los grados de libertad (CMIN / DF), el cambio en chi cuadrado de los modelos alternativos, el índice de ajuste comparativo (CFI), el índice de bondad del ajuste global (GFI) y el error cuadrado de aproximación a las raíces medias (RMSEA). El estadístico chi cuadrado indica el ajuste absoluto del modelo, pero es muy sensible al tamaño de la muestra. Por consiguiente, usualmente se interpreta también la razón de chi cuadrado sobre los grados de libertad, con valores inferiores a 3 indicando un buen ajuste. El cambio significativo en chi cuadrado indica que un modelo ajusta mejor que el restante (Jöreskog & Sörbom, 1993). Los índices CFI y GFI varían entre 0 y 1, indicando con 0, ausencia de ajuste y con 1 el ajuste óptimo. Valores de .95 o superiores son considerados excelentes y valores superiores a .90 sugieren un ajuste aceptable del modelo a los datos. El índice RMSEA es considerado óptimo cuando sus valores son de .05 o inferiores y aceptables en el rango .08 -.05 (Hu & Bentler, 1995).
Los resultados del análisis factorial confirmatorio indican que el modelo de medición de un factor ajusta aceptablemente (GFI: .90; CFI: .93, RMSEA: .09) pero no de manera óptima. Un examen de los índices de modificación permite observar que un cambio en los parámetros estimados entre el error 1 y 2 produce una ganancia considerable en el modelo. Por lo tanto, se procedió a analizar la matriz residual estandarizada de covariancia, donde si el modelo es correcto, esta matriz de covariancia debería presentar una distribución normal y valores absolutos menores que 2 (Jöreskog & Sörbom, 1993). El valor absoluto entre los ítemes 1 y 2 en el modelo es de 2,249. Quitando el Item 2, los índices de ajuste mejoran y el modelo de 10 ítemes relacionados con un factor es bueno. La Tabla 2 presenta un resumen de los índices de ajuste de los modelos.
Tabla 2. Indices de ajuste de los modelos de metas de rendimiento y expectativas de resultados en matemática
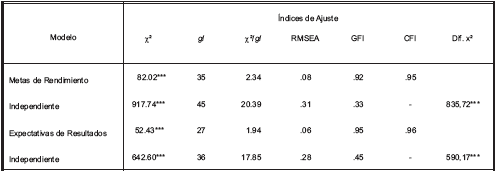
*** p < .000
Escala de Expectativas de Resultados en Matemática
La medida de adecuación muestral de Kaiser-Mayer-Olkin (.824) y la prueba de esfericidad de Barttlet con valores de 820,066 (p ≤ .000) indicaron que era posible la aplicación del análisis factorial. La regla KG de autovalores superiores a 1 determinó la existencia de cuatro factores que explican un 62.40% de la variancia de respuesta al test. El Scree Test para la magnitud de los autovalores (Cattell, 1966), en cambio, sugirió la extracción de un solo factor, mientras que el análisis paralelo de Horn (1965) sugirió retener dos factores. Por consiguiente, se procedió a analizar dos soluciones factoriales de uno y dos factores, a los fines de identificar la estructura más simple y teóricamente relevante.
La solución factorial de dos factores fue rotada mediante rotación oblicua Promax (Tabachnick & Fidell, 2001; Thompson, 2002). En esta estructura se observó que el Factor 2 estaba compuesto por 3 ítemes con pesos factoriales superiores a .30 y se consideró que esta solución factorial no es viable para nuestros datos ya que se recomienda que cada factor debe poseer al menos 4 ítemes con correlaciones iguales o superiores a.40 (Glutting, 2002). Debido a esto, se analizaron nuevamente los datos solicitando la extracción de un solo factor y se eliminaron los ítemes con pesos factoriales inadecuados, menores a .40. De este modo se retuvieron 9 ítemes con pesos factoriales entre .45 y .81, que con formaron una estructura factorial clara, explicando el 34.38% de la variancia de respuestas al test (ver Tabla 3).
Tabla 3. Peso factorial, coeficientes estandarizados y coeficiente alpha de Cronbach para la Escala Expectativas de Resultados en Matemática

Posteriormente, se realizó un análisis factorial confirmatorio para verificar el ajuste a los datos del modelo teórico de un solo factor de Expectativas de Resultados. Los resultados indicaron que el modelo de medición de un factor ajusta óptimamente (GFI: .95; CFI: .96, RMSEA: .06). Como se puede observar en la Tabla 3, los pesos de regresión estandarizados (p ≤ .05) oscilaron entre .45 y .78.
Análisis de consistencia interna
El estudio de la consistencia interna se realizó con el coeficiente alpha de Cronbach, resultando .86 y .85 los valores para Metas de Rendimiento en Matemática y Expectativas de Resultados en Matemática, respectivamente.
Evidencia de validez predictiva
Para el estudio de validez predictiva se administró adicionalmente la Escala de Autoeficacia Lógico-Matemática del Inventario de Autoeficacia para Inteligencias Múltiples Revisado (Pérez & Cupani, 2008) a una submuestra de la original (n = 340) y se obtuvieron los promedios finales en Matemática.
Luego se obtuvieron las medias, desviaciones típicas, índices de asimetría y curtosis de las variables incluidas en este análisis. Los índices de curtosis y asimetría de todas las variables están comprendidos entre -.42 y .94 y -.98 y -.17, respectivamente. Estos resultados son considerados óptimos para los análisis paramétricos propuestos (George & Mallery, 2003).
Posteriormente se efectuó un análisis correlacional bivariado (r de Pearson) con el objetivo de verificar la fuerza de las relaciones entre las variables incluidas en el modelo.
Se observó una correlación moderada entre Autoeficacia Lógico-Matemática y Metas de Rendimiento en Matemática con el Rendimiento Académico (.51 y .41, respectivamente). Las variables Autoeficacia Lógico-Matemática, Expectativas de Resultados y Metas de Rendimiento presentaron correlaciones moderadas entre sí (de .22 a .35).
En una segunda fase se realizó un análisis de regresión jerárquica por dos razones: este análisis puede determinar la contribución relativa de cada variable predictiva y permite evaluar la mediación de las variables, observando cómo el coeficiente estandarizado de una variable predictora (o conjunto de ellas) en un paso del análisis es reducido en el siguiente paso cuando ingresa otra variable predictora (o un conjunto de ellas). La mediación entre las variables se puede observar cuando: (a) hay una relación significativa entre el predictor, la variable mediadora y la variable a predecir y (b) cuando hay una reducción en la relación entre el predictor y la variable a predecir en presencia del mediador. Se puede observar una mediación total cuando la influencia inicial del predictor (o conjunto de ellas) es reducida a cero, o una mediación parcial, cuando la influencia del predictor es sólo substancialmente reducida (Baron & Kenny, 1986).
Previamente se realizó un chequeo de los supuestos multivariados para garantizar la validez del procedimiento (Tabachnik & Fidell, 2001). Mediante el estadístico d de Durbin-Watson (1951) se chequeó el supuesto de independencia entre los residuos. El valor obtenido fue 1.49, lo cual es considerado por la literatura como aceptable (George & Mallery, 2003). Se cumplimentaron los supuestos de homocedasticidad, linealidad y normalidad,con la inspección de los diagramas de dispersión de los Pronósticos Tipificados, de los Residuos Tipificados, del histograma de los residuos tipificados, del gráfico de probabilidad normal y del diagrama de regresión parcial. Finalmente, se realizó un chequeo de la colinealidad mediante los estadísticos nivel de tolerancia y su inverso (FIV). Se obtuvieron valores de tolerancia entre .79 y .86, y su inverso (FIV) entre 1,15 y 1,25, los que son considerados aceptables (George & Mallery, 2003).
Una vez chequeados los supuestos multivariados, se incorporaron las variables independientes al modelo explicativo siguiendo el orden establecido por la Teoría Social-Cognitiva del Desarrollo de Carrera (Lent, Brown & Hackett, 1994): en primer lugar, Autoeficacia Lógico-Matemática y Expectativas de Resultados, y finalmente las Metas de Rendimiento. La variable dependiente fue Rendimiento Académico.
Como se puede observar en la Tabla 4, en el primer paso del análisis, las Creencias de Autoeficacia Lógico-Matemática y las Expectativas de Resultados explican un 26% de la variancia [F (2, 337) = 59,76, p < .000]. En este paso, los estudiantes que presentaron altas creencias en Autoeficacia Lógico-Matemática (β = .49, t = 10.25, p < .00) obtuvieron mayor Rendimiento Académico. Expectativas de Resultados presentó un coeficiente de regresión estandarizado estadísticamente no significativo.
Tabla 4. Análisis de regresión jerárquica para variables que predicen el rendimiento académico en matemática

Nota
R² = Correlación múltiple al cuadrado
ΔR² = Incremento del cambio del coeficiente de correlación múltiple al cuadrado
β = Coeficiente de regresión estandarizado
* p = < .05
** p = < .01
*** p = < .001
En el segundo paso, al ingresar las Metas de Rendimiento, el incremento fue de un 6% de la variancia explicada [F (1, 336) = 28,84, p < .000)]. Se puede interpretar que los estudiantes que se proponen Metas de Rendimiento (β = .27, t = 5,37, p < .00) obtienen mejor Rendimiento Académico. También se puede tomar en consideración que el coeficiente de regresión estandarizado de las Creencias de Autoeficacia Lógico-Matemática disminuye levemente (de .49 a .42). Esto indica que las Creencias de Autoeficacia pueden estar mediadas parcialmente por las Metas de Rendimiento en Matemática.
Discusión y conclusiones
Algunos autores proponen que existen tres niveles de adaptación de las pruebas psicológicas (Van de Vijver & Leung, 1997). El primero corresponde a la aplicación, esto es, la simple y llana traducción de un test de un idioma a otro, asumiendo la equivalencia de constructo. La segunda opción es la adaptación en la cual se agrega la transformación, adición o substracción de algunos ítemes de la escala original.
Finalmente, la opción del ensamble, donde el instrumento original ha sido modificado tan profundamente que prácticamente se ha transformado en un nuevo instrumento (Fernández, 2006). En este último nivel de adaptación se podrían ubicar los estudios realizados en este trabajo, ya que si se consideran las diferentes modificaciones que se fueron realizando desde la primera adaptación de las subescalas de Expectativas de Resultados en Matemática (4 ítemes) y Metas en Matemática (2 ítemes) de la Escala de Autoeficacia para Enseñanza Media (Fouad, Smith & Enochs, 1997), hasta la versión obtenida en este estudio (10 ítemes para la Escala de Metas de Rendimiento y 9 para la Escala de Expectativas de Resultados), estaríamos en presencia de dos nuevas escalas para medir estos constructos.
Tal como lo mencionan Lent y Brown (2006), es esperable que instrumentos basados en la teoría social cognitiva presenten este nivel de adaptación y/o que escalas muy reconocidas y utilizadas en la literatura no presenten adecuadas propiedades psicométricas cuando se aplican en otras culturas. Esto se debe en gran medida al enfoque dinámico que propone la teoría social cognitiva, que a diferencia de los modelos taxonómicos que asumen que el comportamiento de las personas se mantiene relativamente estable en el tiempo y en diferentes contextos (por ejemplo, la Tipología Hexagonal de Holland, 1997), la perspectiva cognitiva social considera el funcionamiento humano en términos del modelo de reciprocidad triádica en el cual la conducta, los factores personales, cognitivos y de otro tipo y los acontecimientos ambientales actúan como determinantes interactivos (Lent, 2005). Por lo tanto, para poder medir los principales constructos de esta teoría (v.g, autoeficacia), es necesario que los instrumentos estén adecuadamente contextualizados al medio cultural y que en lo posible los ítemes del constructo abarquen desde los niveles más generales a los más específicos (Lent & Brown, 2006).
Siguiendo las pautas propuestas por Lent y Brown (2006), en el trabajo que se informa se realizaron nuevos estudios, organizados en dos fases, para poder obtener una media más contextualizada de las expectativas de resultados y metas de rendimiento en Matemática de los adolescentes argentinos.
En la primera fase se trabajó con dos grupos de enfoque que permitieron recabar información sobre las expectativas y metas de los estudiantes de nuestro contexto educacional. Luego, se redactaron los ítemes a partir de la definición de los dos constructos de interés, expectativas de resultados, que son las creencias personales acerca de los posibles resultados de nuestras respuestas (si hago esto, ¿qué pasaría?), y las metas, definidas como la determinación de las personas de involucrarse en determinada actividad o de conseguir un determinado resultado en el futuro (Bandura, 1987).
Para la redacción de los ítemes de Expectativas de Resultados se tuvieron en cuenta diferentes clases de expectativas tales como la anticipación de resultados físicos (v.g.,"Si aprendo Matemática, en el futuro podré conseguir un trabajo bien pago"), sociales (v.g., "Si aprendo Matemática, mis compañeros me considerarán más inteligente") y autoevaluativos (v.g., "Si aprendo Matemática, en el futuro podré estudiar mi carrera favorita").
De la misma manera, para los ítemes de Metas de Rendimiento, se tuvo en cuenta la diferencia entre metas distantes y submetas próximas, donde las primeras influyen en la elección de los cursos de acción pero están demasiado alejadas en el tiempo como para funcionar como incentivos efectivos para la acción presente (v.g., "Este año me he propuesto obtener buenas notas en Matemática"), mientras que las submetas próximas movilizan en forma efectiva el esfuerzo en las actividades que el sujeto realiza en el presente y conducen a aspirar a las metas últimas, creando las condiciones más favorables para la automatización (v.g., "Este año voy a atender y tomar notas en las clases de Matemática").
Como resultado de este estudio se redactaron 7 nuevos ítemes para la Escala de Metas de Rendimiento y 12 ítemes para la Escala de Expectativas de Resultados. En esta última se incorporaron ítemes redactados de forma negativa (v.g., "Aunque aprenda bien la Matemática, no me garantiza conseguir un buen trabajo en el futuro"), aunque luego fueron eliminados. Estos nuevos ítemes fueron administrados a una muestra piloto de adolescentes para corroborar empíricamente que los mismos fueran claros y comprensibles y se realizaron las modificaciones idiomáticas pertinentes, dando origen a una nueva versión de las escalas para medir Expectativas de Resultados y Metas de Rendimiento en Matemática compuesta por 13 y 11 ítemes, respectivamente.
En la segunda fase, los nuevos ítemes de ambas escalas fueron administrados a una muestra de adolescentes y posteriormente se realizaron los análisis psicométricos pertinentes. El análisis factorial exploratorio de mostró que una solución factorial de un solo componente es la más adecuada para ambas escalas. La Escala de Metas de Rendimiento quedó conformada por 11 ítemes y la Escala de Expectativa de Resultados quedó conformada por 9 ítemes. Para llegar a estos resultados se realizaron varios pasos: se factor analizaron los ítemes preliminares, se utilizó como criterio el Gráfico Scree y el análisis paralelo de Horn y finalmente se eliminaron aquellos ítemes con pesos factoriales inadecuados, menores a .40.
Esta estructura factorial fue ratificada con un análisis factorial confirmatorio que permitió verificar un ajuste aceptable de los datos del modelo teórico de un solo factor de Metas de Rendimiento y Expectativas de Resultados. En el caso particular de la Escala de Metas de Rendimiento se observó que con la elimnicación del Item 2, el modelo compuesto por 10 ítemes presentó un mejor ajuste.
Además, ambas escalas demostraron una consistencia interna adecuada, ya que presentaron valores de alpha superiores a los estándares recomendados como aceptables: mayores a .70; adecuados: mayores a .80). Concretamente, se puede destacar que la consistencia interna de la Escala de Expectativas de Resultados mejoró considerablemente desde la primera adaptación (α = .67, Cupani & Gnavi, 2007) a esta nueva versión de la misma (α = .85). Los resultados del estudio de validez predictiva, mediante el análisis de regresión jerárquica, dieron soporte a los postulados propuestos por el Modelo de Rendimiento Académico de la SCCT. En este trabajo se observa que las Creencias de Autoeficacia realizaron una contribución directa al Rendimiento Académico y una contribución indirecta, mediada por las Metas de Rendimiento en Matemática. Siguiendo a Baron y Kenny (1986) esta mediación de Metas de Rendimiento puede advertirse en este trabajo ya que se observó: (a) una relación significativa entre Autoeficacia y Metas de Rendimiento (r = .35; p ≤ .00) y entre Metas de Rendimiento y el Rendimiento Académico (β = .27; p ≤ .00) y (b) una reducción del coeficiente estandarizado de Autoeficacia hacia el Rendimiento Académico desde el primer paso del análisis de regresión jerárquica al segundo paso (de β =.49 a β =.42) cuando ingresó al modelo la variable Metas de Rendimiento. Cabe destacar que esta es una mediación parcial, ya que la influencia del predictor Creencias de Autoeficacia es sólo reducida ligeramente.
Las Metas de Rendimiento en Matemática realizaron una contribución predictiva al Rendimiento Académico, tal como lo propone la SCCT. Estos resultados difieren de los observados en otras investigaciones (Brown, et al., 2008; Cupani & Gnavi, 2007), en las cuales no se observó una relación significativa entre Metas de Rendimiento y Rendimiento Académico. Esta falta de poder predictivo de las Metas de Rendimiento puede deberse a problemas de operacionalización de esta variable (Brown et al., 2008). En efecto, al poder contar en este trabajo con una medida compuesta por ítemes que capturan el constructo de interés en diferentes niveles de especificidad, y además, con un número mayor de ítemes, los postulados teóricos propuestos por la SCCT pudieron ser corroborados.
Por otro lado, las Expectativas de Resultados no realizaron una contribución predictiva directa al Rendimiento Académico. Sin embargo, considerando las hipótesis propuestas por el modelo de rendimiento académico de la SCCT, esta falta de contribución predictiva apoya a los postulados de este modelo teórico. Lent y colaboradores (1994) proponen que aquellos estudiantes con fuertes expectativas de resultados (y creencias de autoeficacia), se propondrán metas más exigentes que aquellos con expectativas de resultados negativos (o bajas creencias de autoeficacia). Es decir, consideran que las expectativas de resultados contribuyen indirectamente a predecir el rendimiento académico. Es pertinente aclarar que la corroboración de esta hipótesis escapa a los objetivos de este trabajo. No obstante, la moderada correlación observada entre las Creencias de Autoeficacia Lógico-Matemática, Expectativas de Resultados y las Metas de Rendimiento en Matemática, puede dar indicios de que esta hipótesis pueda ser sostenida.
En conclusión, en este momento estamos en condiciones de poder evaluar las hipótesis de un modelo de rendimiento académico en Matemática propuesto por la Teoría Social-Cognitiva del Desarrollo de Carrera (Lent et al., 1994), ya que ambas escalas (ver Anexo) permiten medir contextualizada y específicamente las Expectativas de Resultados y las Metas de Rendimiento en Matemática de los adolescentes de nuestra región, y además poseen adecuadas propiedades psicométricas. Específicamente, se pretende realizar un análisis de sendero ya que esta técnica permitiría corroborar las relaciones directas e indirectas entre las variables y evaluar si el modelo teórico propuesto se ajusta a los datos empíricos.
Anexo
Escala de Expectativas de resultados y Metas de Rendimiento en matemática
Parte 1
Expresá por favor tu grado de acuerdo o desacuerdo con respecto a las siguientes afirmaciones relacionadas con la Matemática. Examiná detenidamente cada una de ellas y respondé utilizando una escala de 1 a 5, donde si colocás 1 estarás indicando Totalmente en desacuerdo y si colocás 5 estarás indicando Totalmente de Acuerdo. Podés emplear cualquier número de la escala.

Parte 2
Expresá por favor tu grado de acuerdo o desacuerdo con respecto a las siguientes afirmaciones relacionadas con la Matemática. Examiná detenidamente cada una de ellas y respondé utilizando una escala de 1 a 5, donde si colocás 1 estarás indicando Totalmente en desacuerdo y si colocás 5 estarás indicando Totalmente de acuerdo. Podés emplear cualquier número de la escala.

Referencias bibliográficas
1. Ajzen, I. (1988). Attitudes, personality, and behavior. Stony Stratford, UK: Open University Press. [ Links ]
2. Arbuckle, J. L. (2005). Amos 6.0 user's guide. Chicago, IL: SPSS Inc. [ Links ]
3. Bandura, A. (1987). Pensamiento y acción. Fundamentos sociales [Thought and action: Social foundations]. Barcelona: Martínez Roca. [ Links ]
4. Bandura, A. (2002). Guía para la construcción de escalas de autoeficacia [Guide for constructing self-efficacy scales]. Evaluar, 2, 1-37. [ Links ]
5. Baron, R. M. & Kenny, D. A. (1986). The moderator-mediator reliable distinction in social psychological research: Conceptual, strategic, and statistical considerations. Journal of Personal and Social Psychology, 51, 1173-1182. [ Links ]
6. Brown, S. D., Tramayne, S., Hoxha, D., Telander, K., Fan, X. & Lent, R. W. (2008). Social cognitive predictors of college students' academic performance and persistence: A meta-analytic path analysis. Journal of Vocational Behavior, 72, 298-308. [ Links ]
7. Cattell, R. (1966). The scree test for the number of factors. Multivariate Behavior Research, 1, 245-276. [ Links ]
8. Cupani, M. & Gnavi, G. A. (2007). Un modelo social-cognitivo del rendimiento en Matemática: Estudios de tres escalas [A social-cognitive model of Mathematics performance: Studies of three scales]. Perspectivas en Psicología, 4(1), 19-27. [ Links ]
9. Durbin, J. & Watson, G. S. (1951). Testing for serial correlation in least squares regressions II. Biometrika, 38, 159-178. [ Links ]
10. Fernández, A. (2006). Adaptación de tests a diversas culturas [Tests adaptation to different cultures]. Trabajo presentado en el Primer Encuentro Nacional de Evaluación Psicológica y Educativa: Avances teóricos y técnicos en la medición psicológica. Facultad de Psicología. Universidad Nacional de Córdoba, Córdoba. [ Links ]
11. Flores, L. & O'Brien, K. M. (2002). The career development of Mexican American adolescent women: A Test of Social Cognitive Career Theory. Journal of Counseling Psychology, 49(1), 14-27 [ Links ]
12. Fouad, N. A. & Smith, P. L. (1996). A test of a social cognitive model for middle school students: Math and science. Journal of Counseling Psychology, 43, 338-346. [ Links ]
13. Fouad, N. A., Smith, P. L. & Enochs, L. (1997). Reliability and validity evidence for the Middle School Self-Efficay Scale. Measurement and Evaluation in Counseling and Development, 30, 4 -16. [ Links ]
14. George, D. & Mallery, M. (2003). Using SPSS for Windows step by step: A simple guide and reference. Boston, MA: Allyn & Bacon. [ Links ]
15. Glutting, J. (2002). Some psychometric properties of a system to measure ADHD among college students. Measurement and Evaluation in Counseling and Development, 34, 194-209. [ Links ]
16. Holland, J. (1997). Making vocational choices: A theory of vocational personalities and work environments (3rd ed.). Odessa, Fl: Psychological Assessment Resources. [ Links ]
17. Horn, J. (1965). A rationales and test for the number of factor in factor analysis. Psychometrika, 30, 179-185. [ Links ]
18. Hu, L. & Bentler, P. (1995). Evaluating model fit. En R. Hoyle (Ed.), Structural equation modelling: Concepts, issues and applications (pp. 76-99). Thousand Oaks, CA: Sage. [ Links ]
19. Jöreskog, K. & Sörbom, D. (1993). LISREL VIII. Chicago, IL: Scientific Software. [ Links ]
20. Krueger, R. A. (1988). El grupo de discusión [The focus group]. Madrid: Pirámide. [ Links ]
21. Lapan, R. T., Shaughnessy, P. & Boggs, K. (1996). Efficacy expectations and vocational interests as mediators between sex and choice of math/science college majors: A longitudinal study. Journal of Vocational Behavior, 49, 277-291. [ Links ]
22. Lent, R. W. (2005). A social cognitive view of career development and counseling. En S. D. Brown & R. W. Lent (Eds.), Career development and counseling: Putting theory and research to work (pp. 101-127). New York: Wiley. [ Links ]
23. Lent, R. W. & Brown, S. D. (2005). Integrating person and situation perspectives on work satisfaction: A social-cognitive view. Journal of Vocational Behavior, 69(2), 236-247. [ Links ]
24. Lent, R. W. & Brown, S. D. (2006). On conceptualizing and assessing social cognitive constructs in career research: A measurement guide. Journal of Career Assessment, 14(1), 12-35. [ Links ]
25. Lent, R., Brown, S. & Hackett, G. (1994). Toward a unifying Social Cognitive Theory of career and academic interest, choice and performance. Journal of Vocational Behavior, 45, 79-122. [ Links ]
26. Lent, R. W., Hackett, G. & Brown, S. D. (2004). Una perspectiva social cognitiva de la transición entre la escuela y el trabajo [A social cognitive perspective of transition between school and job]. Evaluar, 4, 1515-1867. [ Links ]
27. López, F. G., Lent, R. W., Brown, S. D. & Gore, P. A. (1997). Role of social-cognitive expectations in high school students' mathematics-related interest and performance. Journal of Counseling Psychology, 44, 44-52. [ Links ]
28. Lorenzo-Seva, U. & Ferrando, P. J. (2006). FACTOR: A computer program to fit the exploratory factor analysis model. Behavioral Research Methods, Instruments and Computers, 38(1), 88-91. [ Links ]
29. Oesterlind, S. (1990). Establishing criteria for meritorius test items. Educational Research Quality, 3, 26-30. [ Links ]
30. Pérez, E. & Cupani, M. (2008). Inventario de Autoeficacia para Inteligencias Múltiples Revisado (IAMI-R). Revista Latinoamericana de Psicología, 40(1), 47- 58. [ Links ]
31. Rottinghaus, P. J., Lindley, L. D., Green, M. A. & Borgen, F. H. (2002). Educational aspirations: The contribution of personality, self-efficacy, and interests. Journal of Vocational Behavior, 61, 1-19. [ Links ]
32. Schaub, M. & Tokar, D. M. (2005). The role of personality and learning experiences in social cognitive career theory. Journal of Vocational Behavior, 66, 304-325. [ Links ]
33. Swanson, J. L. & Gore, P. A. (2000). Advances in vocational psychology theory and research. En S. D. Brown & R. W. Lent (Eds.), Handbook of counseling Psychology (3rd ed., pp.233-269). New York: Wiley. [ Links ]
34. Tabachnik, B. & Fidell, L. (2001). Using multivariate statistics (4th ed.). Boston: Allyn and Bacon. [ Links ]
35. Thompson, B. (2002). Exploratory and confirmatory factor analysis. Washington: APA. [ Links ]
36. Tornimbeni, S., Pérez, E. & Olaz, F. (2008). Introducción a la Psicometría [Introduction to Psychometric]. Buenos Aires: Paidós. [ Links ]
37. Van de Vijver, F. J. F. & Leung, K. (1997). Methods and data analysis for cross-cultural research. Newbury Park, CA: Sage. [ Links ]
Facultad de Psicología
Universidad Nacional de Córdoba (UNC)
Córdoba - República Argentina
Fecha de recepción: 20 de octubre de 2008
Fecha de aceptación: 18 de junio de 2009














