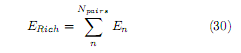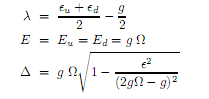FÍSICA NUCLEAR

Comparación entre las soluciones del Lipikin-Nogami y Richardson con energía compleja en el modelo del Lipkin

Comparison between the Lipkin-Nogami and Richardson solutions with complex single particle energy in the Lipkin’s model

 

Rodolfo M. Id Betan*

Instituto de Física Rosario (CONICET), Ocampo y Esmeralda, S2000EZP Rosario.
Departamento de Física. FCEIA (UNR), Av. Pellegrini 250, S2000BTP Rosario.
Instituto de Estudios Nucleares y Radiaciones Ionizantes (UNR), Riobamba y Berutti, S2000EKA Rosario.
* e-mail: idbetan@ifir-conicet.gov.ar

 

---

Resumen

La interacción de pairing es de gran interés debido a que es una de las componentes principales de la interacción residual en sistemas de muchos cuerpos. Las aproximaciones de Bardeen-Cooper-Schieffer (BCS) y Lipkin-Nogami (LN) dan soluciones aproximadas al Hamiltoniano de pairing. Por otro lado, el pairing constante, admite solución exacta, llamada solución de Richardson. Los núcleos alejados de la línea de estabilidad tienen importantes correlaciones con los estados de dispersión y por ende, los estados del continuo deben ser tenidos en cuenta en forma explícita en la descripción de tales sistemas. Una forma de incluir el continuo es a través de los estados de Gamow, este es, soluciones de la ecuación de Schroedinger con energía compleja. En este trabajo comparamos las soluciones aproximadas de BCS y LN con la solución exacta en el modelo simétrico de Lipkin con energía compleja. Encontramos que la solución de LN resulta muy parecida a la exacta y que la extensión de la solución de la BCS al plano de energía complejo produce soluciones puramente imaginarias para el gap cuando G<Gc.-

Palabras claves: Lipkin-Nogami; Richardson; Energía compleja; Apareamiento.

Abstract

The pairing interaction is one of the most important contribution of the residual interaction and then, it is of major importance for the study of many-body systems. One can get solutions of the pairing Hamiltonian throught the Bardeen-Cooper-Schieffer (BCS) or the Lipkin-Nogami (LN) approximations but, the pairing Hamiltonian admit exact solution worked out by Richardson. Nuclei far away from the stability line have important correlations with the continuum part of the energy spectrum, due that the Fermi level is very close to the contiuum thershold. The correlations with the continuum can be included in the many-body description through the complex energy states, called Gamow states. In this work we compare the approximates and exact solutions of the pairing Hamiltonian in real and complex-energy representations. In the application of this formulation to the symmetric Lipkin model, we found that the LN solution is in a good agreement with the exact one; besides, the extension of the BCS solution to the complex energy plane gives solution even for strength below the critical one, which is purely imaginary.

Keywords: Lipkin-Nogami; Richardson; Complex energy; Pairing.

Recibido: 07/02/17;
aceptado: 02/10/17

---

 

I. INTRODUCTION

Many-body configurations in the continuum is an important issue to understand the properties of loosely bound systems, as for example, nuclei close to the drip line^[1]. The complex energy poles of the scattering matrix correspond to complex energy eigenvalue of a single particle Hamiltonian with purely outgoind boundary condition. They are called Gamow states and they represent decay states in the continuum^[2]. They have information of the structure of the real energy continuum spectrum: the real part of the complex pole gives the resonant energy while the reciprocal of its imaginary part is proportional to half-live of the unstable state^[3].
The constant pairing interaction, although simple, is an important component of the particle-particle interaction^[4,5]. The pairing Hamiltonian can be solved using the Bardeen-Cooper-Schrieffer (BCS) approximation^[6]; but, for small number of particles, this approximation is not a satisfactory solution. An improve solution was given by Nogami^[7,8] using the technique developed by Lipkinir Ref.^[9], now known as Lipkin-Nogami (LN) approximation. The solutions in the LN approximation including the continnum single particle density was work out recently in Ref.^[10]. But, the constant pairing has exact solution worked out by Richardson^[11,12]. The eigenfunctions of the BCS and LN solutions do not conserve the number of particles of the system, while the Richardson solution does.
A test system, which is non trivial but it is simple enough to be exactly solvable was given by Lipkin, Meshkov and Glick^[13], now know as Lipkin model or symmetric model. It is used to test the validity of new formalisms and techniques as well as to illustrate more complicated models in many-bodysystems^[14–17].
In this work we calculated the many-body energy in the BCS, LN and Richardson frameworks with complex energy in the Lipkin model. The Lipkin formalism is described in section II. In section III the BCS, LN and Richardson solutions are given. The application to the Lipkin model is presented in section IV. Finally, in the last section V we draw some conclusions.

II. LIPKIN FORMALISM

Let us assume that |Φ˃ is an approximate solution of the unknown exact ground state of a many-body system which is described by a Hamiltonian H. The wave function (w.f.) |Φ˃ describes nicely some properties of the system but, at the same time, it violates some other property S. For example, the BCS w.f. ^[6] describes nicely the pairing property of the many-body system but it is not an eigenfunction of the particle number operator N. We may expand |Φ˃ in a basis |φS˃ of eigenfunctions of S, i.e., with ˂Φ|Φ˃ =1 =1 and cS real numbers.) In our example were N is even, N_max is the maximum particle number allowed by the representation and N|φN˃ = N|φN˃.
An approximation of the ground state energy would be ˂Φ|H|Φ˃, but since |Φ˃ does not conserve the property S, we hope that ˂Φ_s|H|Φ_s˃ will be a better approximation for some specific value of S of the observ- able S. The trick consist to use the approximate w. f. |Φ˃ (called model w. f.), which we assume it is easier to handle, to obtain ˂Φ_s|H|Φ_s˃, together with a model Hamiltonian H (to be build) for which our model w. f. is an eigenvector^[9].
We defined our model Hamiltonian as

with f(S)|Φ_S˃ = f(S)|Φ_S˃, then

If f(S) in is chosen in such a way that ) |Φ_S˃ are all degenerate eigenfunctions of H, i. e. H|Φ_S˃ = E|Φ_S˃ then

By combining Eqs. (2) and (3) weget,

notice that E is not the eigenvalue of our system but,

then, the above discussion assume that E = ˂Φ|H|Φ˃ is easier to calculate than ˂Φ_s|H|Φ_s˃, i. e., it is easier to solve the eigen value problem for the model Hamiltonian H|Φ˃ than the original one H|Φ_s˃.

Probably,theonlyexactlyknown f (S) is the momentum operator, in all the other cases this function has to be approximated by a Taylor’s series, with the hope that a few terms will be enough to reproduce the truly ground state energy. So, let us assume that

In the case that one truncates the series, the condition that ˂Φ_s|H|Φ_s˃ be degenerated for all S is not fulfill. In such a case one must complement the problem with some other subsidiary condition.
If S represents the particle number operator N, the simplest approximation of f(N) is when we keep the first term of the series, f(N)= λN, then H = H − λN, i. e. the BCS approximation. Then ˂Φ_BCS|H|Φ_BCS˃ = E_BCS and the subsidiary condition is that the mean value of the particle number operator is fixed, hence˂Φ_N|H|Φ_N˃ = E_BCS + λN. The condition ˂Φ_BCS| N|Φ_BCS˃ = N determines the value of the parameter λ.
The equation

can be rearranged to be written,

where each term can be interpreted as a correction term. This way of writing the mean value ˂Φ_S| H|Φ_S˃ is a bit tricky. For example, int he BCS example

and due the subsidiary condition ˂Φ_BCS|N|Φ_BCS˃ = N the correction would be zero. The point we must remember is that we built the model Hamiltonian because is was easy to manipulate with our model wave function, i. e. we don’t solve the eigenvalue problem ˂Φ|H|Φ˃,insteadwesolvetheeigenvalueproblem ˂Φ|H|Φ˃.In this way we never face terms of the form f_i(Sⁱ −˂Φ|Sⁱ|Φ˃)which could be zero. In our BCS example it means that we don’t solve ˂Φ_BCS|H|Φ_BCS˃ but ˂Φ_BCS|H H − λ|Φ_BCS˃.
The next step is to find a systematic way to obtain the parameters f_i for i ≥ 1 which does not involve the states |Φ_S˃ but instead involves the model w. f. |Φ˃. The model w. f. and the model Hamiltonian satisfies the relation

for any function g(S). We can choose a set of functions gi(S)= Si with i =1, 2,... in order to evaluate the coefficients fi. Then, a self-consistency conditions (independent of |Φ_S˃) is obtained by rearranged Eq. (10) with g(S)replaced by Si,

The application of this condition toour BCS example would give,

and then

By inserting |Φ_BCS˃ ˂Φ_BCS| between H N and using
the condition H₂₀ =0^[18,19] weget

which gives the standard condition used in BCS, ˂Φ_BCS|N|Φ_BCS˃ = N.

III. MODEL SOLUTIONS

The constant pairing Hamiltonian reads,

where

with a†jm ≡ (−)j−ma†j,−m, and g the strengt hof the interaction. The particle number operatoris is N =

A. Non conserving particle number solutions

In this section we will applied the Lipkin method^[9] of section II to obtain approximate solutions of the pairing Hamiltonian (15).

1. BCS solution

The Taylor’s expansion Eq. (6) in the particle number operator N up to first order defines the usual BCS model Hamiltonian

while the model w. f. is defined as^[20]

with the coeffcients u_j and v_j satisfying =1. The ground state energy in this approximation is

The gap parameter ∆ and the Fermi level λ are obtained by solving the following system of equations

2. Lipkin-Nogami solution

The model Hamiltonian we obtain by taking the Taylor’s expansion Eq. (6) in the particle number operator N up to the second order defines the Lipkin-Nogami (LN) model Hamiltonian^[7]

with H as Eq. (15). The model w. f. |ΨLN˃ is like Eq. (18) but with different coefficients u_j and v_j .They are determined in terms of the parameters ∆, λ^₁ and λ₂ by solving the following system of three equations

The ground state energy is

B. Conserving particle number solution

The conserving particle number solution for a system of even N fermions is given in terms N_pairs = N/2 parameter E_n called pair energies. These parameters are obtained by solving a system of N_pairs equations, called Richardson’s equations^[11,12]

The many-body ground state energy E_Rich is defined taken thelowest N_pairs pair-energy E_n

IV. APPLICATION: LIPKIN MODEL

The Lipkin model, also called symmetric model, consist of two equally degenerate levels with energies Eu and Ed at half filling. The notation of the previous section reduces to Hence, the degeneracy for each level is 2Ω and N = 2Ω. Let us introduce the parameter E > 0

which defines the energy separation between the two levels. The following values are used for the applications:

N =10
Ed = −0.5 MeV
Eu =(0.5 − iγ) MeV

By using the relations of the previous section we found the following algebraic solutions for the BCS and LN approximations:
a. BCS solution:

with

The ground state energy E_BCS Eq. (19), relative to the non-interacting system is

where

b. LN solution: The Lipkin-Nogami solution can also be obtained analytically,

with

Since 4λ₂−g> 0 we are interested in the positive α solution of the following cubice quation (see also Eq. (15) in Ref.^[8])

Figure 1 shows the three possible solutions of Eq. (36) for each value of the strength g in the range [0, 0.5] MeV. As the strength goes to zero, the parameter α goes to zero and to ±E (with E = 1 MeV).

FIG. 1: Solutions of the cubic equation (36) g ∈ [0, 0.5] MeV. Missing points in the figure is because no convergence was found.

The ground state energy ELN Eq. (28) relative to the non-interacting Fermi energy 2ΩEd gives,

where

Equations (32) and (35) show that in order to find solution for the BCS and LN approximations, respectively, the strength g has to begreater than g_c. Figure 2 shows the value of g_c as a function of g for α > 0. It is found that in order to have non trivial solution in the BCS approximation g has to be bigger that a threshold value, while the LN approximation has no trivial solution for any value of the strength.

FIG. 2: g_c of Eqs. (32) and (35) (for α > 0) versus g for the BCS and LN approximations, respectively.

Figure 3 extends the comparison done in Fig. 1 of Ref.^[8] between the BCS and LN gap parameter ∆ as a function of the strength g for α > 0 and γ = 0 to stronger strength. They compare well for strong correlation but they depart eachother for small value of the strength. The figure also shows the nonphysical behavior of the pairing gap in the BCS approximation, i. e.∆ = 0 for g . ≤ 0.1 MeV.

FIG. 3: Pairing gap versus g.

In Fig. 4 we show the gap parameter as complex magnitude in the BCS approximation for γ = 0,0.05, and 0.25 MeV. For complex energy the gap parameter is also complex but for γ = 0 the gap is purely real up to a minimum value and then it becomes purely imaginary, i.e., the trivial solution appears here as a complex solution with ∆ purely imaginary; hence, in the complex plane the constant gap has no trivial solution for any value of g.

FIG. 4: Real and imaginary part of the pairing parameter calculated in the BCS approximation for different value ofγ for g < 0.32 MeV .

The ground state energy relative to the free system of the non-conserving particles solutions are compared with the exact Richard sonsolution in Fig. 5 for γ = 0. We observe a very good agreement between the approximate LN and the exact (Richardson) solutions for all values of the pairing strength.

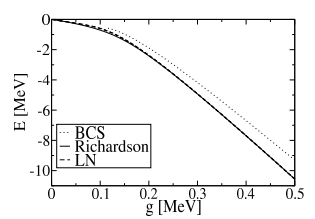
FIG. 5: Binding energyr elative to the non-interacting Fermi sea versus g for γ =0.

The ground state energy is calculated in the BCS and LN approximations for γ = 0.25 MeV and shown in Fig. 6. The energy of the BCS approximation diverges for values of the strength for which its gap is purely imaginary. While the imaginary part of the energy are similar in both approximations, the real one differs for the same value of the strength. Figure 6 also compare the real and imaginary parts of the energy with the exact Richardson solution. A good agreement with the LN approximation for all value of g can be observed.

FIG. 6: Real (upper graph) and imaginary (lower graph) parts of the ground state energy for γ = 0.25 MeV as a function of the pairing strength g for the BCS, Lipkin-Nogami and Exact solutions.

V. DISCUSSION AND CONCLUSIONS

The Lipkin model with complex energy had been solved in the BCS and LN approximations and compared with the exact Richardson solution.
The extension of the pairing solution to the complex energy plane, shows that there is solution for any value of the strength, even in the BCS approximation, but this solution is completely nonphysical since the energy diverges.
It was found the LN approximation agreed very well with the exact Richardson solution for real and complex energy for any value of the strength.
A limitation of the exact Richardson solution is that it can be applied only to constant pairing interaction. But the good agreement with the LN solution seems to indicate that, for more general interactions, the LN method would be a well founded alternative, even in a complex energy representation.

VI. ACKNOWLEDGMENTS

This work has been founded by the National Council of Research (Consejo Nacional de Investigaciones Científicas y Técnicas - CONICET) by the grant PIP-625.

Referencias

1. J. Okolowicz, M. Ploszajczak, and I. Rotter, Dynamics of quantum systems embedded in a continuum. Phys. Rep. 374, 271 (2003).         [ Links ]

2. N. Michel, W. Nazarewics, M. Plozajczak, and T. Vertse, J. Phys. G 36,13101 (2009).         [ Links ]

3. Theory of Resonances (Kluwer Academic Publishers, Dordrecht,1988).         [ Links ]

4. A. M. Lane, Nuclear Theory. Pairing Force Correlations and Collective Motion (New York, Benjamin, 1964).         [ Links ]

5. D. J. Dean and M. Hjorth-Jensen, Rev. Mod. Phys. 75, 607 (2003).         [ Links ]

6. J. Bardeen, L. N. Cooper, and J. R. Schrieffer, Phys. Rev. 108, 1175 (1963).         [ Links ]

7. Y. Nogami, Improved Superconductivity Approximation for the Pairing Interaction in Nuclei. Phys. Rev. 134, B313 (1964).         [ Links ]

8. Y. Nogami, On the superconductivity theory of the nuclear pairing interaction. Physics Letters 15, 335 (1965).         [ Links ]

9. H. J. Lipkin, Collective motion in many-particle systems. Annals of Physics 9, 272 (1960).         [ Links ]

10. R. M. Id Betan and C. E. Repetto, Pairing in the BCS and LN approximations using continuum single particle level density. Nucl. Phys. A 960, 131 (2017).         [ Links ]

11. R. W. Richardson, A restricted class of exact eigenstates of the pairing-force Hamiltonian. Phys. Lett. 3, 277 (1963).         [ Links ]

12. R. W. Richardson and N. Sherman, Exact eigenstates of the pairing-force Hamiltonian. Nucl. Phys. 52, 221 (1964).         [ Links ]

13. H. J. Lipkin, N. Meshkov, and A. J. Glick, Validity of many-body approximation methods for a solvable model: (I). Exact solutions and perturbation theory. Nucl. Phys. 62, 188 (1965).         [ Links ]

14. Hogaasen-Feldman, A study of some approximations of the pairing force. Nuclear Physics 28, 258 (1961).         [ Links ]

15. N. Meshkov, A. J. Glick, and H. J. Lipkin, Validity of many-body approximation methods for a solvable model: (II). Linearization procedures. Nucl. Phys. 62, 199 (1965).         [ Links ]

16. H. C. Pradhan, Y. Nogami, and J. Law, Study of approximations in the nuclear pairing-force problem. Nuclear Physics A 201, 357 (1973).         [ Links ]

17. P. Ring and P. Schuck, The Nuclear Many-Body Problem (Springer, 2004).         [ Links ]

18. A. L. Fetter and J. D. Walecka, Quantum theory of many-particle systems (McGraw-Hill Book Company. New York, 1971).         [ Links ]

19. J. F. Goodfellow and Y. Nogami, On the superconductivity approximation for the nuclear pairing interaction. Canadian Journal of Physics 44, 1321 (1966).         [ Links ]

20. J. Suhonen, From Nucleons to Nucleus, Concepts of Microscopic Nuclear Theory (Springer, 2007).         [ Links ]