ENSEÑANZA DE LA FÍSICA

Implementacion de una herramienta computacional para el estudio de problemas de fuerzas centrales

Implementation of a software tool for the study of central-force problems

 

F. Arriaga ^a, J. P. Staneck ^a, F. Lanzini ^a,b, O. Fornaro ^{a, b, c}

^a Facultad de Ciencias Exactas, Universidad Nacional del Centro de la Provincia de Buenos Aires, e Instituto de Física de Materiales Tandil (IFIMAT), Pinto 399 (7000), Tandil, Argentina.
^b Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET).
^c CIFICEN (UNCPBA-CICPBA-CONICET), Pinto 399, 7000 Tandil, Argentina.
e-mail: flanzini@exa.unicen.edu.ar

Recibido: 18/04/18;
aceptado: 20/06/18

---

Se presenta una implementación computacional desarrollada como herramienta de enseñanza para ser utilizada en el aula en el estudio del movimiento en un campo de fuerzas centrales. Esta implementación permite la visualización del potencial efectivo y de la trayectoria de una partícula de masa reducida alrededor del centro de fuerzas. El uso de esta herramienta permite complementar la resolución de problemas con solución analítica, y estudiar problemas no solubles analíticamente.

Palabras clave: Problema de fuerzas centrales; Enseñanza; Algoritmo de Verlet.

A computational implementation for the numerical solution of the central-force problem was developed for teaching purposes. The implementation allows the visualization of the effective potential and the path of a reduced mass particle around the center of force. The use of this tool allows to complement the resolution of problems with analytic solution, and to study problems not analytically solvable.

Keywords: Central-force problem; Teaching; Verlet algorithm.

---

 

I. INTRODUCCIÓN

Uno de los principales temas dictados en los cursos intermedios de Mecánica Clásica involucra el estudio del problema de cuerpos sometidos a fuerzas centrales. Este tema se extiende generalmente sobre una unidad completa de la materia. Los libros de texto tradicionales^[1-3] ponen mayor énfasis en aquellos problemas que son integrables de manera analítica. El número de problemas cuya solución puede expresarse en términos de funciones conocidas es reducido y, en general, las soluciones analíticas obtenidas suelen ser de cierta complejidad matemática (funciones circulares o integrales elípticas en coordenadas polares). Algunos textos proponen soluciones a problemas complejos a partir de la aproximación en serie de las soluciones ^[3,4].
En el problema de dos cuerpos interactuando por medio de fuerzas centrales, la fuerza entre los cuerpos está dirigida a lo largo de la línea que los une, esto es, (la fuerza que ejerce la partícula 1 sobre la 2) es paralela (o antiparalela), al vector de posición relativa . La magnitud de la fuerza depende por lo tanto de la distancia entre las partículas y no de la orientación en el espacio, es decir que la fuerza es función del módulo del vector . Por lo tanto,.
Cuando el movimiento traslacional del sistema en conjunto no es de interés, el problema se puede reducir al de una única partícula de masa reducida moviéndose alrededor de un centro de fuerzas fijo bajo la influencia de un potencial central
Dado que , el problema posee simetría esférica, condición bajo la cual el momento angular del sistema se conserva, y el problema se reduce a un movimiento en dos dimensiones, convenientemente descripto en coordenadas polares . La otra integral de movimiento es la energía total :

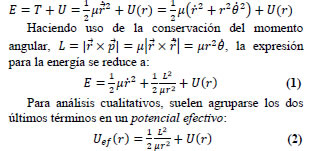
El primer término, que puede ser interpretado como una energía potencial centrífuga ^[1], está asociado con la energía cinética de rotación alrededor del centro de masas. A partir de (1) se obtiene una expresión para la velocidad radial,

Se pueden obtener soluciones de esta integral en términos de funciones conocidas sólo para determinadas formas del potencial. En los casos más simples, en que el potencial tiene la forma la solución puede ser escrita en términos de funciones circulares para , mientras que para algunos otros valores enteros y racionales de , la solución puede expresarse en términos de funciones elípticas ^[5,6]. R. Broucke ^[7] enumera seis potenciales más generales, expresables como sumas de potencias (semi)enteras de r, cuyas soluciones están dadas también en términos de funciones elípticas. De todas maneras, incluso en los casos cuya solución analítica es más sencilla, las expresiones matemáticas resultantes no permiten visualizar de manera inmediata la trayectoria de la partícula.En estos casos, es posible atacar el problema mediante la integración numérica de las ecuaciones de movimiento. Uno de los enfoques más utilizadoses el propuesto originalmente por Verlet [8], o alguna de las modificaciones posteriores tales como el algoritmo Verlet en velocidad o el método leapfrog ^[9].
En este trabajo describimos la implementación de una herramienta computacional, desarrollada con fines didácticos, que permite la visualización de la trayectoria para potenciales centrales expresables como sumas de potencias de la forma. Las ecuaciones de movimiento se resuelven en forma numérica aplicando el algoritmo de Verlet en velocidad. Por medio de la aplicación es posible graficar la órbita de la partícula y el potencial efectivo en el que esta se mueve, permitiendo modificar de manera flexible las condiciones iniciales (posición y velocidad) o las constantes de movimiento (energía y momento angular). Mediante esta aplicación es posible ejemplificar y estudiar cuantitativamente gran parte de las situaciones problemáticas planteadas en los libros de texto de nivel intermedio de Mecánica Clásica.

II. MÉTODOS

Algoritmo
El método utilizado para la integración de las ecuaciones de movimiento es el denominado algoritmo de Verlet en velocidad [8,9]. Para una partícula de masa sometida a una fuerza neta , la aceleración de la partícula está dada por

Conocidas la posición inicial (de la cual podemos deducir la aceleración inicial ) y la velocidad inicial , la evolución temporal del sistema se obtiene por aplicación sucesiva de las ecuaciones (5-7).

Detalles de la implementación
El programa fue implementado en lenguajeC++ (framework Qt). En la Figura 1 se muestra la interfaz con el usuario. El código está diseñado de forma de permitir la utilización de potenciales de la forma. Para indicar la forma del potencial el usuario debe introducir los coeficientes y los exponentes . La fuerza sobre la partícula está dada entonces por

Figura 1. Interfaz con elusuario de la aplicación desarrollada. A la izquierda se observa la sección de entrada de datos, y a la derecha las salidas gráficas: Ueff(r) (arriba) y trayectoria resultante (abajo).

Para iniciar la integración de las ecuaciones de movimiento se introducen las coordenadas cartesianas de la posición y velocidad iniciales. Las constantes de movimiento, y L se obtienen como:

Otra posibilidad para la inicialización del problema consiste en proporcionar las constantes de movimiento y , y la posición inicial, calculándose automáticamente las componentes de la velocidad inicial a partir de estos datos. Esto es particularmente útil cuando se desea obtener una trayectoria con características determinadas mediante el análisis cualitativo del potencial efectivo.
Otros parámetros de control son el tiempo final de cálculo y el paso temporal . El paso temporal debe ser lo suficientemente pequeño para evitar acumular errores por la suposición de que la aceleración es constante durante cada paso de cálculo. Para esto se utilizó un paso variable , siendo un parámetro introducido por el usuario, y , la aceleración en el instante . La utilización de un paso temporal variable es una práctica usual en este tipo de cálculos y ha sido discutido detalladamente en [10].

III. RESULTADOS

Se ilustra la utilización del método para tres situaciones problemáticas típicas.

Movimiento en un potencial kepleriano
Para el potencial de Kepler , la ecuación de la órbita (4) puede resolverse de manera exacta ^[1-3]. La trayectoria queda dada por

Estas ecuaciones representan una familia de cónicas con un foco en el centro de fuerzas, cuyo carácter (hipérbola, parábola, elipse, círculo) está determinado por el valor de la excentricidad ,cuyo valor depende de la posición y velocidad iniciales o de E y L, según se lo mire. En la Fig. 2 se muestran las trayectorias obtenidas numéricamente para diferentes situaciones iniciales.

Figura 2. Potencial efectivo (arriba) y diferentes trayectorias (abajo) correspondientes a las energías totales indicadas, para un potencial de Kepler.

Resulta sencillo en este ejemplo, solicitar al alumno que compruebe que el resultado obtenido concuerda con la solución analítica hallada en los textos. En el ejemplo, la elección de las condiciones iniciales conduce a una órbita circular para , donde la del potencial efectivo, elíptica para y parabólica para .

Movimiento en un potencial
Este potencial es un caso particular de las series de potencias que son integrables en términos de funciones elípticas ^[7]. Las posibles trayectorias en este potencial son analizadas extensa y cualitativamente en ^[4]. A partir de la expresión analítica de se puede ver que y que . Además, se encuentra que es una función monótonamente creciente cuando , y que, cuando poseerá un máximo (en ) y un mínimo (en )intermedios (Fig. 3); este último caso es el más interesante ya que conduce a una diversidad de trayectorias dependiendo del valor de la energía total.

Fig. 3. Potencial efectivo para

En la Figura 4 se muestran como ejemplo, trayectorias obtenidas mediante integración numérica para algunas de las energías indicadas en la Fig. 3.

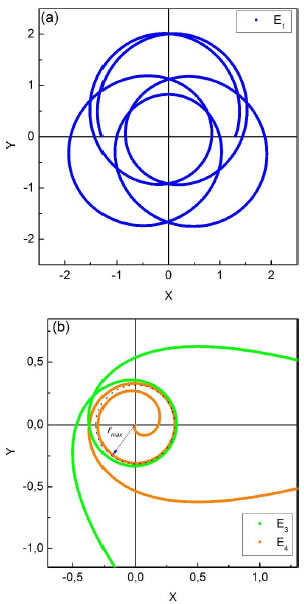
Fig. 4. Trayectorias en el potencial para diferentes valores de la energía total indicados en la Fig. 3.

Para una energía tal que ,el movimiento es posible en dos zonas. En la más cercana al centro de fuerza () la partículasiempre termina cayendo al centro rápidamente. En la segunda zona, la distancia radial al centro de fuerzas está acotada superior e inferiormente, y la trayectoria es como la ilustrada en la Figura 4(a). Se puede observar que el segundo término del potencial provoca un desplazamiento en la posición angular para los sucesivos valores de o , por lo que la órbita va completando una corona entre estos dos valores. Si en algún momento se repitiera la combinación de posición y velocidad la trayectoria será cerrada después de un número finitode revoluciones,aunque éste no sea el caso general.
Una partícula que se acerca desde el infinito con energía tiene una distancia mínima de aproximación al centro de fuerzas dada por la condición .Dado que , la partícula se alejará del centro de fuerzas disminuyendo su velocidad, por lo que la trayectoria es abierta(es decir la partícula no retorna)
Para una partícula que viene del infinito pierde velocidad radial a medida que se acerca al máximo del potencial efectivo( es proporcional a la diferencia , ec(3)), por lo que gira a una distancia alrededor del centro de fuerzas.Luego la velocidad radial cambia de signo y la partícula se aleja nuevamente (Fig. 4b).En este caso, el ángulo de salida de la partícula al alejarse dependerá del número de revoluciones que recorra en cercanías a, y por lo tanto depende fuertemente de la diferencia entre su energía y la del máximo del potencial efectivo. En este contexto, este potencial funciona como un dispersor no-lineal.
Para la velocidad radial disminuye en las proximidades de mientras que la velocidad angular permanece prácticamente constante, ya que . Por consiguiente la partícula tiende a girar a una distancia antes de incidir sobre el centro de fuerzas (Fig. 4b)

Perturbaciones al potencial kepleriano: precesión de la órbita
Como se presentó en el ejemplo anterior, cuando se añade al potencial kepleriano una pequeña perturbación , las trayectorias acotadas pueden dejarde ser cerradas, observándose que el perihelio se desplaza un ángulo por cada revolución (Figura 5).

Fig. 5. Órbita en un potencial kepleriano ligeramente perturbado con un término de la forma

Landau y Lifschitz ^[3] obtienen expresiones analíticas del ángulo de precesión para dos formas del potencial perturbativo, es decir cuando el potencial puede ser escrito como . Para ello, escriben la ecuación integral de la órbita, Ec. (4), como una derivada sobre el momento angular, y desarrollan la expresión integral correspondiente en potencias de , reteniendo el primer término del desarrollo. Para el caso en que la perturbación corresponde a un término inverso cuadrático, , obtienen a primer orden

En la Figura 6 se muestra la variación del ángulo de precesión en función de la magnitud (o ) del potencial perturbativo para ambos ejemplos. Las condiciones iniciales del cálculo están detalladas en el gráfico. Se puede ver que las expresiones analíticas aproximadas(8) y(9) concuerdan con los resultados numéricos para perturbaciones suficientemente pequeñas; pero para perturbaciones mayores, los términos de orden superiordel desarrollo en serie adquieren mayor relevancia.

Fig. 6. Ángulos de precesión obtenidos numéricamente y comparación con las expresiones analíticas (8) y (9)para dos formas del potencial perturbado.

IV. CONCLUSIONES

Se presenta una implementación numérica para resolver el problema de dos cuerpos que interactúan mediante un potencial central expresable como suma de potencias de . El código utiliza el método de integración de Verlet en velocidad para resolver las ecuaciones de movimiento de Newton, con un paso de tiempo variable. La interfaz gráfica se ha diseñado de forma de enfatizar el concepto de potencial efectivo: este es el enfoque utilizado en los libros de texto clásico para realizar análisis cualitativos (trayectorias acotadas/infinitas, puntos de retorno, velocidad radial en función de la posición). Consistentemente con este punto de vista, las condiciones iniciales pueden ser establecidas introduciendo la posición y velocidad de la partícula de masa reducida o, alternativamente, los valores de las constantes de movimiento y .
Se desarrollan tres ejemplos que corresponden a situaciones problemáticas típicas de los libros de texto clásicos: movimiento en un campo kepleriano, precesión de la órbita debido a pequeñas perturbaciones, y movimiento en un campo de la forma .
Esta implementación puede ser de utilidad en los cursos intermedios de Mecánica Clásica, sirviendo como complemento a la resolución analítica de problemas.

AGRADECIMIENTOS

Agradecemos al Ing. Martín Menchón (INTIA, UNCPBA) por su colaboración en el desarrollo de la interfaz gráfica. Este trabajo fue financiado por ANPYCT, CONICET, SECAT-UNCPBA and CICPBA. La aplicación desarrollada puede ser solicitada a los autores.

IV. REFERENCIAS

1. S. T. Thornton, J. B. Marion. Classical Dynamics of Particles and Systems, 5ta. ed.. Thomson Brooks/Cole, EE UU, 2004.         [ Links ]

2. H. Goldstein. Mecánica Clásica. Ed. Aguilar, Madrid, España, 1979.         [ Links ]

3. L. D. Landau, E. M. Lifshitz. Mecánica. Volumen 1 del Curso de Física Teórica. 2º edición corregida. Ed. Reverté, España, 1978.         [ Links ]

4. G. L. Kotkin, V. G. Serbo. Problemas de Mecánica Clásica, Editorial Mir, Moscú, 1980.         [ Links ]

5. E. T. Whittaker. A treatise on the Analytical Dynamics of Particles and Rigid Bodies. Cambridge University Press, Reino Unido, 1917.         [ Links ]

6. E. T. Whittaker, G. N. Watson. A course of Modern Analysis. Cambridge University Press, Reino Unido, 1952.         [ Links ]

7. R. Brouke. “Notes on the central force rn”. Astrophysics and Space Science 72 (1980), 33-53. DOI: 10.1007/BF00642162.

8. L. Verlet. “Computer ‘experiments’ on classical fluids. I. Thermodynamical properties of Lennard-Jones molecules”. Phys. Rev. 159 (1967), 98-103. https://doi.org/10.1103/PhysRev.159.98

9. W. H. Swope, H. C. Andersen, P. H. Berens, K. R. Wilson. “A computer simulation method for the calculation of equilibrium constants for the formation of physical clusters of molecules: Application to small water clusters”. J. Chem. Phys. 76 (1) (1982), 637. DOI: 10.1063/1.442716

10. W. Huang, B. Leimkuhler. “The adaptative Verlet method”. SIAM J. Sci. Comput. 18 (1) (1997), 239-256. DOI: 10.1137/S1064827595284658