FLUIDOS

Espermatozoides microconfinados: interacción con paredes

Microconfined spermatic cells: wall interaction

 

M.A. Bettera Marcat^*1,2, A.J. Banchio^1,2, and V.I. Marconi^1,2

¹ Instituto de Física Enrique Gaviola -IFEG (UNC-CONICET)
² Facultad de Matemática, Astronomía, Física y Computación (FaMAF), Universidad Nacional de Córdoba Av. Medina Allende s/n, Ciudad Universitaria (X5000HUA) - Córdoba - Argentina
mbettera@famaf.unc.edu.ar

Recibido: 18/06/18;
aceptado 10/09/18

---

Con el fin de reproducir numéricamente la dinámica de poblaciones de espermatozoides humanos confinados en microdispositivos, en este trabajo avanzamos en el modelado de la dinámica de espermatozoides microconfinados. Modelamos la dinámica de espermatozoides con una dinámica de Langevin bidimensional, y proponemos una interacción con las paredes más realista, que genera un torque a los micronadadores y alinea las trayectorias en forma paralela a la paredes. Se analizó el efecto de esta interacción en la distribución de células generadas con simulaciones y se redujo una sobreestimación de la acumulación presente en simulaciones sin el modelo de torque. Las distribuciones obtenidas cercanas a las paredes contenedoras presentan un muy buen acuerdo con resultados experimentales de la literatura.

Palabras Clave: Microfluídica; Confinamiento; Espermatozoides.

In order to reproduce numerically confined human sperm dynamics into micro-devices, in this work we improve previous models of such systems. We model the spermatic cells motility using a 2D Langevin dynamics and we propose a wall interaction generating a torque to the microswimmers that aligns its trajectories parallel to the walls, in closer connection with experimental observations. The effect of this interaction in the simulated cell distribution close to the walls was analized and it reduces an overestimation of the wall acummulation obtained with previous and simpler models. A nice agreement between the obtained distributions of cell close to the walls and previous experiments is obtained.

Keywords: Microfluidics; Confinement; Spermatozoa.

---

 

I. INTRODUCCIóN

Desde los trabajos innovadores de seguimientos (tracking) de micronadadores en tres dimensiones en los años '70¹, se ha abierto un campo de interés interdisciplinario, el estudio del comportamiento dinámico de sistemas biológicos, microorganismos autopropulsados, como bacterias, espermatozoides, y una gran variedad de microorganismos flagelados. Los avances en la última década en técnicas de microscopía han permitido un conocimiento más preciso del comportamiento de las células a escalas micro y sub micrónica². La física de estos sistemas es un tópico de interés actual en la comunidad que aporta al conocimiento sobre su comportamiento a nivel tanto microscópico como poblacional. Desarrollos teóricos, algunos resueltos numéricamente, han propuesto modelos para la hidrodinámica de estos sistemas^3-8, que son fundamentales para entender las interacciones de micronadadores con las superficies contenedoras y con otros micronadadores. De forma original se pudieron observar los campos hidrodinámicos de algunos micronadadores⁹, lo que ha servido como validación de las predicciones teóricas de forma cualitativa. La teoría hidrodinámica desarrollada y los modelos explican en gran parte el efecto observado de nado preferencial a lo largo de las paredes contenedoras de los micronadadores del tipo pushers, como por ejemplo espermatozoides de toro¹⁰ y bacterias E. coli¹¹. Este nado paralelo a paredes, induce una distribución de células entre superficies contenedoras con preferencia a la cercanía de paredes, que se ha obtenido experimentalmente, al igual que numéricamente^10-12.
El efecto observado de mayor densidad de micronadadores cercana a paredes ha llevado a proponer diversas aplicaciones: diferentes trabajos reportan que es posible rectificar poblaciones bacterianas, o espermáticas, con obstáculos gracias a su forma asimétrica^13-15, separar poblaciones por edad de las bacterias¹⁶, o por diferentes estrategias de nado^17,18, clasificar parte de una población de células según características dinámicas¹⁹, o lograr homogeneizar distribuciones de microorganismos autopropulsados²⁰. El avance en la micro- y nano-fabricación con materiales biocompatibles le ha dado novedosas herramientas a la comunidad científica de las ciencias de la vida, para diseñar nuevas aplicaciones y ampliar el conocimiento de sistemas biológicos en la escala micrométrica^21,22. Debido a que los micronadadores del tipo pusher²³, los que se autopropulsan con flagelos que baten detrás de su cuerpo, tienen una preferencia a nadar paralelamente a las paredes luego de llegar a ellas, es posible direccionar su movimiento gracias a dispositivos de confinamiento con la geometría adecuada. Esto ha motivado el diseño de múltiples microdispositivos que aprovechan este efecto para el control de su dinámica^13-18,20,22. En este trabajo buscamos un modelo fenomenológico simple que capture con el mayor detalle posible el comportamiento de espermatozoides humanos en un ambiente de microconfinamiento. En las condiciones que queremos modelar su dinámica, su movimiento se encuentra restringido a dos dimensiones en un contenedor con dos superficies separadas una distancia de ˜25µm, i.e. del orden del tamaño de los espermatozoides teniendo en cuenta la amplitud de su batido flagelar. En particular, nos ocupamos de extender el modelo propuesto en trabajos previos¹³ para capturar el fenómeno de alineación con las paredes observado experimentalmente.
La morfología de los espermatozoides humanos es la siguiente, consta de una cabeza elipsoidal de 5µm de largo y 3µm de ancho, y un flagelo de ˜55µm de largo²⁴. La velocidad de los espermatozoides en condiciones normales es mayor que en condiciones de microconfinamiento, bajo este régimen se ha reportado una velocidad media de ˜30µm∕ s^13,20. La autopropulsión del mismo se logra a través del movimiento del flagelo, que como consecuencia involucra un cabeceo de frecuencia ˜ 10Hz. En muchas especies, la envolvente del movimiento del flagelo en el seno del medio (lejos de paredes) tiene forma cónica, mientras que en el entorno de paredes sucede en un plano, o la componente fuera del plano es mucho menor que las otras^25,26. El modelado realista de espermatozoides es un paso importante para entender su dinámica poblacional y aportar en el diseño aplicaciones clínicas en medicina reproductiva. En este trabajo, partiendo del modelo previo de Ns espermatozoides cofinados en 2D y sin flujo¹³, con el objeto de reproducir el efecto de alineación con las paredes incluimos un torque en la interacción de las células con las paredes. En particular esta interacción induce un torque, que es lineal con el ángulo de orientación del micronadador con la pared, β(t). Al incluir dicho torque los espermatozoides se alinean con las paredes logrando un comportamiento más cercano a las observaciones. Como consecuencia de este fenómeno, la distribución de células dentro del microdispositivo también se modifica.

II. MODELO

Simulamos el movimiento de Ns microorganismos autopropulsados confinados en régimen de bajo número de Reynolds²⁷. Para que el modelo fenomenológico reproduzca la dinámica de espermatozoides humanos microconfinados utilizamos parámetros de movilidad realistas obtenidos de nuestras mediciones experimentales previas¹³. Debido al confinamiento restringimos su dinámica de Langevin a dos dimensiones, basado en modelos anteriores¹³. Cada nadador es representado con un disco de radio rs y esta restringido a una caja de dimensión Lx Ly, con condiciones periódicas de contorno en el eje y. ri son las coordenadas del nadador i, vi = ri su velocidad, con módulo vi constante y distribución normal en los nadadores, y φi es la orientación de su velocidad, ángulo con el eje x positivo (Fig. 1(a)). Cada nadador tiene 3 grados de libertad: dos coordenadas espaciales y la orientación de la velocidad. Debido a su dinámica sobreamortiguada, la suma de fuerzas y de torques sobre cada nadador es nula. Para obtener las ecuaciones de movimiento se iguala menos la fuerza de arrastre que ejerce el fluido sobre el nadador, al resto de fuerzas. Por otro lado se iguala menos el torque viscoso, al resto de torques. Las ecuaciones de movimiento resultantes para el nadador i son las siguientes:

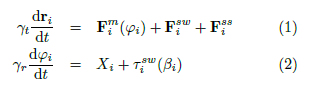
donde ϓt es el coeficiente de arrastre traslacional y ϓr es el coeficiente de fricción rotacional. Fmi (t; 'i) = t[vm i ^ek i ('i)+Ah!cos(!t+ i)^e?i ('i)] es la fuerza del motor. Esta representación de la autopropulsión tiene en cuenta el cabeceo presente en la dinámica de los espermatozoides, representado con un término sinusoidal. Los versores ^ek i ('i) = cos('i)^x + sin('i)^y y ^e?i ('i) = sin('i)^x + cos('i)^y son, respectivamente, paralelo y perpendicular a la velocidad vi. La fuerza de interacción con las paredes tiene la forma Fsw i = tFswPNw k=1 fi;k e impide que las células penetren en las paredes; siendo fik = (1 rik=rs)0:1^nk si rik < rs y nula si rik > rs. La distancia desde el nadador i a la pared k es rik, Nw es el número de paredes y ^nk el vector unitario normal de la pared k. Consideramos que la fuente de estocacidad del sistema es el ruido intrínseco del motor del nadador, el cual genera que las trayectorias se desvíen. Esto es tenido en cuenta con la variable aleatoria gaussiana X caracterizada por hXi(t)i = 0 y hXi(t)Xj(t+ t)i = 22 rDr i;j= t, donde Dr es el coeficiente de difusión rotacional y t es la discretización del tiempo en las simulaciones. La fuerza de interacción entre nadadores está dada por Fss i = tFssPNs j6=i gij , y previene que los nadadores se superpongan. gij = (1 rij=(2rs))^rij si rij < 2rs y nula si rij > 2rs, siendo rij = ri.
En la ecuación (2) incorporamos una nueva interacción con las paredes, un torque dependiente del ángulo del micronadador con la pared, β, en acuerdo con los trabajos teóricos²⁸, y con lo observado en experimentos recientos en micronadadores del tipo pusher. 2. En la Fig. 1(a) mostramos esquemáticamente el ángulo entre la dirección de movimiento de un espermatozoide con una pared, βi, y φi, que es el ángulo que define la dirección de movimiento en las coordenadas de la simulación. A partir de la representación de micronadadores con soluciones multipolares de las ecuaciones de Stokes en régimen de campo lejano, se predice un torque debido a la presencia de una superficie, dependiente del ángulo de incidencia para los nadadores tipo pusher, como los espermatozoides, que decae rápidamente con la distancia a la superficie, más rápido que la atracción hidrodinámica.²⁸ Nuestro modelo es el más simple que captura la dependencia con el ángulo con la pared, (t), u orientación cercana a la pared. Sólo queda libre un parámetro adimensional, la intensidad del torque, que puede utilizarse para ajustar con datos experimentales. El torque actúa sólo en el entorno de las paredes con un umbral h de distancia del nadador a la pared dsw. Se eligió h = 4rs (ver Fig. 1) teniendo en cuenta observaciones experimentales en otras especies que sugieren que los efectos hidrodinámicos son importantes a distancias del orden del tamaño del micronadador^2,29. Otra forma de lograr la alineación con las paredes en modelos simples es representar las células con esferas ligadas, un modelo de dos cuerpos³⁰.

Figura 1: (a) Esquema de un espermatozoide que se aproxima con un dado ángulo de incidencia a una pared (t = 0). Se remarca el ángulo, (t) 2 [= _=2], entre la pared y la velocidad del nadador. (b) Evolución temporal esquematizada en cercanías de la pared. El torque en el modelado es proporcional a (t).

Nuestro modelo propuesto de torque lineal con es el siguiente,

Resolvemos numéricamente las ecuaciones (1-3) con todo lo explicado en esta sección como en Guidobaldi et al. ¹³, y utilizando los mismos parámetros dinámicos. Para estudiar el comportamiento cerca de las paredes, no utilizamos la interacción entre nadadores y el paso de integración temporal fue t = 0:001s. Para estudiar las distribuciones de células se utilizó el modelo completo con t = 0:02s.

III. RESULTADOS

En la Fig. 2 se grafican los ángulos con la pared en función del tiempo, (t), con =0.5 s^-1 (intensidad de torque) para tres ángulos iniciales de incidencia, 0 = =6, =4 y =2 (incidencia normal a la pared). En el inset de esta gráfica se muestran las evoluciones temporales de para los valores de =0.5, 0.2 y 0.1 s^-1. Las curvas son promedios sobre 2000 espermatozoides, con la misma condición inicial de ángulo de incidencia. Para diferentes ángulos de incidencia y un mismo los tiempos de reorientación paralela a la pared son del orden de 7 segundos, mientras que el inset nos muestra que para un mismo ángulo de incidencia, el tiempo de reorientación es menor a mayor valor de como indica la flecha. Cualitativamente se obtiene el comportamiento esperado, con mayor intensidad de torque la alineación con la pared es más rápida y por construcción del modelo de torque lineal con , todos los nadadores con un mismo se alinean en el mismo tiempo. El comportamiento de (t) coincide notablemente con la solución analítica del problema sin ruido (curvas de lineas punteadas), (t) = 0 exp (t). Se observa que donde hay mayor alejamiento de este comportamiento es para los casos con menores, 0.2 y 0.1 s^-1, debido que cuanto menor tiene mayor importancia la difusión rotacional. En todos los casos se observa que luego de alcanzar la orientación paralela a la pared, = 0, los nadadores pueden escaparse (< 0 implica orientaciones de la velocidad apuntado hacia fuera de la pared, situación en que consideramos que los nadadores escaparon del entorno de la pared).

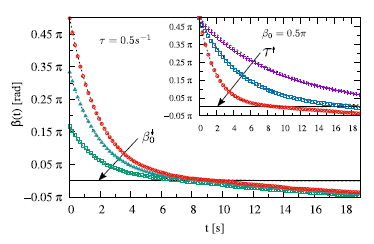
Figura 2: Evolución temporal del ángulo con paredes (t) para los ángulos iniciales de incidencia 0 = =2 (círculos rojos), =4 (triángulos celestes) y =6 (cuadrados verdes) con =0.5s^-1. En inset se muestra (t) para el caso de incidencia normal, 0 = =2, variando en los valores 0.1s^-1 (cruces violetas), 0.2^-1 (cuadrados azules) y 0.5^-1 (círculos rojos). En ambos gráficos se resalta = 0 (paralelo a la pared), < 0 implica que la velocidad apunta hacia fuera de la pared mientras que con > 0 hacia la pared.

La distribución de células normalizada entre dos paredes contenedoras se muestra en la Fig. 3 para valores de entre 0 y 1 s^-1. Para valores de mayores en todos los casos se observa una disminución de células en el entorno de las paredes junto con un aumento de células en las regiones lejanas a las paredes. Esto se produce porque el torque lleva las trayectorias paralelas a las paredes aumentando la probabilidad de escape de los micronadadores por difusión rotacional, comparado con los que llegan a las paredes y el único mecanismo para cambiar su orientación y escapar de las paredes es la difusión rotacional.

Figura 3: Distribución de células simuladas para varios valores de T . En escala logarítmica se resalta el aumento de la densidad de micronadadores en la región lejana a las paredes (paredes en x=L = 0 y x=L = 1) a mayor T.

En la Fig. 4 se muestra la distribución de espermatozoides humanos normalizada (de forma tal que L 0 P(x)dx = 1) generada con las simulaciones para diferentes valores de comparada con resultados experimentales obtenidos por Rothschild para espermatozoides de toro¹⁰ y por Berke et al para E. coli¹¹. Se puede observar que el torque genera una distribución de células con menor acumulación de células en las paredes aproximándose mejor a las distribuciones experimentales. La distribución generada con el modelo sin torque, acumula nadadores en las paredes en exceso. Esto se puede observar con detalle en la Fig. 5, donde se muestra la acumulación en la pared simulada, en función de valores de entre 0 y 0.5 s^-1, comparada con datos experimentales. Para cuantificar la acumulación en la pared consideramos el bin más cercano, que va de x=L = 0 a x=L = 0:09. Este es el máximo valor de P(x), y lo llamamos Pmax. Se puede observar que el modelo sin torque acumula en exceso en la pared, y valores altos de, como 0.5 s^-1, acumulan en menor medida que en las distribuciones experimentales. Son los valores entre 0.05 y 0.1 s^-1 los que más se acercan a distribuciones experimentales, que usan la misma discretización espacial.

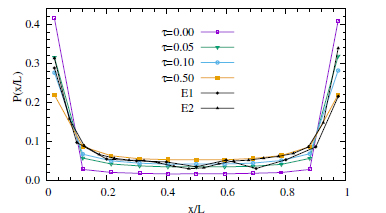
Figura 4: Distribución de células simuladas comparada con datos experimentales de micronadadores pushers, obtenidos de la literatura, E1 de Rothschild¹⁰ (espermatozoides de toro) y E2 de Berke et al.¹¹ (E. coli).

Figura 5: P_max, valor máximo de la distribución de células simuladas en función del parémetro libre del modelo T . Las últimas dos barras son los máximos de las distribuciones tomadas de la literatura (E1)¹⁰ y (E2)¹¹.

La Fig. 6 muestra el cociente entre el valor máximo de la distribución de probabilidad (cercano a la pared) y su valor mínimo (región central, lejos de las paredes). Dentro del rango de estudiados, se puede observar que la razón P_max=P_min disminuye rápidamente para valores de pequeños, para luego entrar en una región donde decae suavemente. Este comportamiento se puede atribuir, principalmente, a la relación entre, Dr = 0:01 rad=s2 y la velocidad media de los nadadores (v = 30 m=s). Para = 0s^-1 este cociente está completamente determinado por el coeficiente de difusión rotacional (y la velocidad), y a medida que aumenta (sin variar la velocidad), por efecto de la reorientación, a los espermatozoides les resulta más fácil alejarse del entorno de las paredes.

Figura 6: Relación entre la distribución de células en las paredes (máxima) y lejos de ellas (mínima).

IV. CONCLUSIONES

Se introdujo una nueva interacción de forma muy simple al modelo fenomenológico con el que estudiamos el comportamiento de sistemas reales de espermatozoides humanos microconfinados. Utilizando parámetros de entrada realistas, exploramos el rango de valores del único parámetro libre del modelo para obtener distribuciones espaciales de células.
Encontramos que es posible modificar la distribución espacial de espermatozoides, en particular variar la acumulación en paredes en función de la interacción orientacional con ellas. Al comparar con distribuciones experimentales de la literatura encontramos un muy buen acuerdo y una mejora en las distribuciones simuladas con el nuevo modelo. Es necesario ajustar este parámetro orientacional en paredes con trayectorias reales de espermatozoides y tener en cuenta heterogeneidades en la población, ya que el torque depende tanto de la velocidad como de la forma de los espermatozoides. Estamos trabajando en caracterizar experimentalmente este comportamiento para incorporar la dinámica orientacional entorno a paredes en nuestras simulaciones, por lo que este modelo puede ser una contribución relevante para mejorar las predicciones del comportamiento de poblaciones de espermatozoides bajo microconfinamiento y sus posibles aplicaciones en medicina reproductiva.

AGRADECIMIENTOS

Financiamiento de CONICET, SeCyT-UNC y PICT2015-0735. Agradecemos especialmente a nuestros colaboradores experimentales H.A. Guidobaldi, M.A. Cubilla y M.N. Gallea por fructíferas discusiones y a los recursos de cluster del GTMC-FAMAFUNC.

V. REFERENCIAS

1. H. C. Berg and Douglas A. Brown. Chemotaxis in Escherichia coli analysed by Three-dimensional Tracking. Nature, 239:500, 1972.         [ Links ]

2. S. Bianchi, F. Saglimbeni, and R. Di Leonardo. Holographic Imaging Reveals the Mechanism of Wall Entrapment in Swimming Bacteria. Phys. Rev. X, 7:011010, 2017.         [ Links ]

3. M. C. Marchetti, J. F. Joanny, S. Ramaswamy, T. B. Liverpool, J. Prost, M. Rao, and R. A. Simha. Hydrodynamics of soft active matter. Rev. Mod. Phys., 85:1143, 2013.         [ Links ]

4. J. Hu, A. Wysocki, R. G. Winkler, and G. Gompper. Physical Sensing of Surface Properties by Microswimmers - Directing Bacterial Motion via Wall Slip. Sci. Rep., 5:9586, 2015.         [ Links ]

5. E. Lauga. Bacterial Hydrodynamics. Annu. Rev. Fluid Mech., 48(1):105, 2016.         [ Links ]

6. R. G. Winkler. Low Reynolds number hydrodynamics and mesoscale simulations. Eur. Phys. J. Spec. Top., 225(11):2079, 2016.         [ Links ]

7. J. Elgeti and G. Gompper. Microswimmers near surfaces. Eur. Phys. J. Spec. Top., 225(11):2333, 2016.         [ Links ]

8. L. Alvarez, B. M. Friedrich, G. Gompper, and U. B. Kaupp. The computational sperm cell. Trends Cell Biol., 24(3):198, 2018.         [ Links ]

9. K. Drescher, J. Dunkel, L. H. Cisneros, S. Ganguly, and R. E. Goldstein. Fluid dynamics and noise in bacterial cell-cell and cell-surface scattering. Proc. Natl. Acad. Sci., 108(27):10940, 2011.         [ Links ]

10. L. Rothschild. Non-random Distribution of Bull Spermatozoa in a Drop of Sperm Suspension. Nature, 198:1221, 1963.         [ Links ]

11. A. P. Berke, L. Turner, H. C. Berg, and Eric Lauga. Hydrodynamic Attraction of Swimming Microorganisms by Surfaces. Phys. Rev. Lett., 101:038102, 2008.         [ Links ]

12. G. Li and J. X. Tang. Accumulation of Microswimmers near a Surface Mediated by Collision and Rotational Brownian Motion. Phys. Rev. Lett., 103:078101, 2009.         [ Links ]

13. A. Guidobaldi, Y. Jeyaram, I. Berdakin, V. V. Moshchalkov, C. A. Condat, V. I. Marconi, L. Giojalas, and A. V. Silhanek. Geometrical guidance and trapping transition of human sperm cells. Phys. Rev. E, 89:032720, 2014.         [ Links ]

14. P. Galajda, J. Keymer, P. Chaikin, and R. Austin. A Wall of Funnels Concentrates Swimming Bacteria. J. Bacteriol., 189(23):8704, 2007.         [ Links ]

15. C.J. O. Reichhardt and C. Reichhardt. Ratchet Effects in Active Matter Systems. Annu. Rev. Condens. Matter Phys., 8(1):51, 2017.         [ Links ]

16. E. S. Hulme, W. R. DiLuzio, S. S. Shevkoplyas, L. Turner, M. Mayer, H. C. Berg, and G. M. Whitesides. Using ratchets and sorters to fractionate motile cells of Escherichia coli by length. Lab Chip, 8:1888, 2008.         [ Links ]

17. I. Berdakin, Y. Jeyaram, V. V. Moshchalkov, L. Venken, S. Dierckx, S. J. Vanderleyden, A. V. Silhanek, C. A. Condat, and V. I. Marconi. Influence of swimming strategy on microorganism separation by asymmetric obstacles. Phys. Rev. E, 87:052702, 2013.         [ Links ]

18. I. Berdakin, A. V. Silhanek, H. N. Moyano Cortéz, V. I. Marconi, and C. A. Condat. Quantifying the sorting efficiency of self-propelled run-and-tumble swimmers by geometrical ratchets. Cent. Eur. J. Phys., 11(12):1653, 2013.         [ Links ]

19. E. Henry, Holm S. H., Zhang Z., Beech J. P., Tegenfeldt J. O., Fedosov D. A., and Gompper G. Sorting cells by their dynamical properties. Sci. Rep., 6:34375, 2016.         [ Links ]

20. H. A. Guidobaldi, Y. Jeyaram, C. A. Condat, M. Oviedo, I. Berdakin, V. V. Moshchalkov, L. C. Giojalas, A. V. Silhanek, and V. I. Marconi. Disrupting the wall accumulation of human sperm cells by artificial corrugation. Biomicrouidics, 9(2):024122, 2015.         [ Links ]

21. F. J. H. Hol and C. Dekker. Zooming in to see the bigger picture: Microuidic and nanofabrication tools to study bacteria. Science, 346(6208), 2014.         [ Links ]

22. R. Nosrati, P. J. Graham, B. Zhang, J. Riordon, A. Lagunov, T. G. Hannam, C. Escobedo, K. Jarvi, and D. Sinton. Microuidics for sperm analysis and selection. Nature Reviews Urology, 14:707, 2017.         [ Links ]

23. E. Lauga, W. R. DiLuzio, G. M. Whitesides, and H. A. Stone. Swimming in Circles: Motion of Bacteria near Solid Boundaries. Biophys. J., 90(2):400, 2006.         [ Links ]

24. E.A. Gaffney, H. Gadelha, D.J. Smith, J.R. Blake, and J.C. Kirkman-Brown. Mammalian Sperm Motility: Observation and Theory. Annu. Rev. Fluid Mech., 43(1):501, 2011.         [ Links ]

25. D. M. Woolley. Motility of spermatozoa at surfaces. Reproduction, 126(2):259, 2003.         [ Links ]

26. B. M. Friedrich, I. H. Riedel-Kruse, J. Howard, and F. Jülicher. High-precision tracking of sperm swimming fine structure provides strong test of resistive force theory. J. Exp. Biol., 213(8):1226, 2010.         [ Links ]

27. E. M. Purcell. Life at low Reynolds number. Am. J. Phys., 45(1):3, 1977.         [ Links ]

28. S. E. Spagnolie and E. Lauga. Hydrodynamics of selfpropulsion near a boundary: predictions and accuracy of far-field approximations. J. Fluid Mech., 700:105-147, 2012.         [ Links ]

29. P. D. Frymier, R. M. Ford, H. C. Berg, and P. T. Cummings. Three-dimensional tracking of motile bacteria near a solid planar surface. Proc. Natl. Acad. Sci., 92(13):6195, 1995.         [ Links ]

30. J. Dunstan, G. Miño, E. Clement, and R. Soto. A twosphere model for bacteria swimming near solid surfaces. Phys. Fluids, 24(1):011901, 2012.         [ Links ]