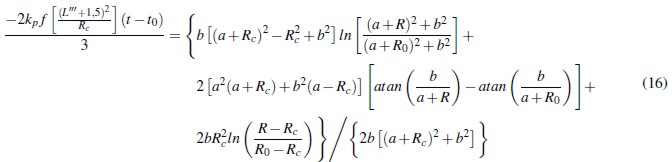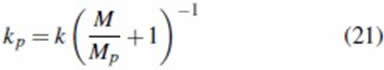https:/doi.org/10.31527/analesafa.2019.30.4.79

FÍSICA DE LA ATMÓSFERA, LA TIERRA Y EL AGUA. FÍSICA DEL MEDIO AMBIENTE

Evolución cinética de un cristal esférico 3D con partículas móviles usando Monte Carlo - Parte II

 

Kinetic evolution of a 3D spherical crystal with mobile particles using Monte Carlo - Part II

 

C.L. Di Prinzio^*1,2
P.I. Achával¹
D. Stoler¹
G. Aguirre Varela^1,2

¹ FAMAF (Facultad de Matemática, Astronomía, Física y Computación), Universidad Nacional de Córdoba, Medina Allende y Haya de la Torre, (5000) Ciudad Universitaria, Córdoba, Argentina.
² IFEG-CONICET (Instituto de Física “Enrique Gaviola”, Universidad Nacional de Córdoba, Medina Allende y Haya de la Torre, (5000) Ciudad Universitaria, Córdoba, Argentina.
Autor para correspondencia: C.L. Di Prinzio, email: carlosdiprinzio@gmail.com; pachaval@famaf.unc.edu.ar

Recibido: 15/11/2019
Aceptado: 27/11/2019

 

---

Resumen:
En este trabajo se estudió la evolución del tamaño de un cristal esférico tridimensional (3D) ante la presencia de partículas móviles usando un algoritmo de Monte Carlo. Se consideraron en este estudio distintas concentraciones de partículas f  y distintas movilidades M_p de las mismas. Se encontró que el grano llega a un radio crítico Rc que depende únicamente de f mediante la relación R_c ∞ f ^1/3.  También se encontró la ecuación dinámica de evolución del grano y su solución analítica. Dicha solución ajustó satisfactoriamente los resultados de las simulaciones. La fracción de partículas en el borde de grano fue también encontrada analíticamente y la misma concuerda con los datos computacionales.

Palabras clave: frenado Zener, cristal esférico, borde de grano, Monte Carlo.

Abstract:
In this work, the migration of the three-dimensional (3D) spherical crystal in the presence of mobile particles using a Monte Carlo algorithm was studied. Different concentrations of particles (f) and different particles mobilities (M_p) were used. It was found that the grain size reaches a critical radius (Rc) which depends exclusively on f. This dependence can be written as: R_c ∞ f ^1/3. The  dynamic equation of grain size evolution and its analytical solution were also found. The analytical solution successfully fits the simulation results. The particles fraction in the grain boundary was also found analytically and it fits with the computational data.

Keywords: Zener drag, spherical crystal, grain boundary, Monte Carlo.

---

 

I. Introducción 

El modelado por computadora del crecimiento de los granos en materiales  policristalinos (1,2,3,4) está ganando importancia en los últimos años. La evolución de los mismos es una de las características importantes para describir la microestructura que controla las propiedades mecánicas y funcionales de los materiales. Se trata de representar el aumento en el tamaño de grano promedio de un material policristalino durante un recocido posterior a la recristalización primaria.

Cuando se somete a materiales policristalinos de grano fino a tratamientos térmicos, se favorece el crecimiento de sus granos y la tendencia a transformar su textura a grano grande, con menos bordes de grano (BGs). Sin embargo, la presencia de partículas o impurezas ralentiza y hasta puede detener el crecimiento de los granos (5). Una comprensión cabal de la cinética de la evolución micro-estructural es esencial para diseñar nuevos materiales con propiedades especiales.

En un policristal libre de partículas, el tamaño medio R de los cristales aumenta de acuerdo a la relación:

donde ɣ es la energía media de los BGs, t el tiempo, v la velocidad media de los BGs y M la movilidad de los mismos.

La solución de la ecuación (1) es la muy conocida ley de crecimiento de grano normal:

donde R₀ es el radio medio inicial de los granos en el policristal a t₀ y k=Mɣ.

El movimiento de los BGs en un policristal con partículas móviles está descripto por:

donde R_c es el radio medio máximo que alcanzan los granos bajo la influencia de las partículas, y M_p es la movilidad de la partículas en la dirección del movimiento del BG. La solución de esta ecuación, que ya ha sido reportada por numerosos autores (6,7), es:

donde

Para explorar mejor la interacción de las partículas móviles con el BG, Choudhury y Jayaganthan (8)  estudiaron el movimiento de BG en bicristales "esféricos" en presencia de partículas móviles e inmóviles, en dos y en tres dimensiones (2D y 3D, respetivamente). Estos autores encontraron que los BGs se frenan más debido a la presencia de partículas móviles que a la presencia de partículas inmóviles.

En el presente trabajo se estudió, mediante un algoritmo computacional basado en el método de Monte Carlo, el movimiento de un BG esférico en presencia de partículas móviles. Se consideraron diferentes movilidades y concentraciones de partículas. También se propuso un nuevo planteamiento teórico del movimiento del BG en presencia de partículas móviles y se lo contrastó con los resultados computacionales.

II. Marco teórico

Si se tiene un BG esférico de radio inicial R₀, la evolución de su radio medio se puede describir mediante la siguiente relación:

donde P_c representa la fuerza de frenado debida a las partículas. La solución a esta ecuación para  es la ley de crecimiento de grano normal, y si se reemplaza Mɣ por k, se tiene:

Por otro lado, la ecuación (6) se puede reescribir de la forma:

Se puede ver que, si la fuerza de frenado P_c es constante e igual a ɣ/R_c, la solución es similar a la de la ecuación (4).

Alley y col.(6), encontraron que la fuerza P_c se puede expresar como:

donde f_bg es la fracción de partículas en el BG, L''' el tamaño de las partículas y α un parámetro adimensional que puede depender de la fracción f de partículas y de otros parámetros físicos. Esta fuerza de frenado va cambiando a medida que el tamaño del cristal esférico va disminuyendo y la misma toma su valor máximo cuando R alcanza el valor R_c, donde el movimiento cesa. Achával y col.(9) reportaron que el BG se frena cuando

Por lo tanto, se puede rescribir P_c como:

donde  

Se puede notar que, en este caso, la fuerza de frenado P_c  varía con el encogimiento del BG y la solución de la ecuación (8) no va a ser igual a la de la ecuación (4), usada ampliamente.

Para obtener una expresión de f_bg, se debe calcular, primero, el número de partículas n_bg en el BG esférico de radio R. Para ello se utiliza la siguiente ecuación:

donde n⁰_bg es el número de partículas en el BG al iniciar la simulación, L' es la distancia característica desde el BG donde se incluye todas las partículas que inicialmente están en el BG o en contacto con él, y L también es una distancia característica pero para los tiempos sucesivos. Las distancias L y L' pueden ser distintas ya que el BG puede ir deformándose durante su movimiento, es decir, no siempre es esférico.

Por otro lado, se puede deducir que  donde f_bg es la fracción de partículas en el BG. Además, el valor de n⁰_bges:

Entonces, remplazando en la ecuación (11) por (12) y considerando, en primera aproximación, L=L' se puede calcular la fracción de partículas en el BG como:

Sustituyendo esta ecuación en (10) y usando (8) se obtiene:

La ecuación (13) puede factorizarse como:

donde R₁ = - a - ib y R₂ = - a + ib son raíces complejas y conjugadas, y R_c es una raíz real positiva de la ecuación dR/dt = 0, de tal manera que:

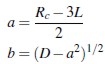
con   

Tomando k_p = kβ, donde β es el de la ecuación (5), la ecuación (15) puede integrarse por partes obteniéndose:

III. Algoritmo de cálculo

La simulación del decrecimiento del bicristal esférico 3D con MC usa los mismos procedimientos que se emplean en muestras en 2D (10,11) y 3D (5,9,12).

Inicialmente, se crea un cristal esférico dentro de una matriz de N sitios (N_x x N_y x N_z = N) donde el sitio i tiene una orientación única S_i > 0. En este modelo, el bicristal inicial tiene todos los sitios dentro del cristal esférico con S_i = 1, los sitios fuera del cristal esférico con S_i = 2 y las partículas con S = 0. 

El algoritmo sigue los siguientes pasos para sitios que pertenecen a uno de los cristales:

a) La energía total del policristal, W, está dada por:

con S_i y S_j orientaciones de los sitios de la red i y j respectivamente, J la energía de interacción entre sitios, V el número de vecinos al sitio i, y δ la función delta de Kronecker. En forma aleatoria se elige un sitio de la red perteneciente a un grano denominado i con una orientación Si. Mediante la ecuación (17) se calcula la energía alrededor del sitio i:

donde el supra índice in significa etapa inicial.

b) Luego, se remplaza la orientación del sitio i (S_i) por la orientación (S_j) del sitio j obtenido aleatoriamente de sus vecinos que pertenecen a un grano.

c) Se calcula nuevamente la energía del sitio i, W _i ^{f i}, donde el supra índice fi significa final.

d) Luego se calcula la diferencia de energías:

e) Si la ecuación (19) resulta negativa o nula el cambio se produce permanentemente, y si es positiva se calcula una probabilidad P dada por:

donde K es la constante de Boltzmann y T es la temperatura del policristal. Para permitir que el sistema produzca cambios por activación térmica, se elige un número aleatorio, Z, entre 0 y 1, y se compara con P. Si P es más grande que Z entonces se hace el cambio deS_i porS_j, en caso contrario no.

Las reglas que rigen el movimiento de las partículas móviles son las siguientes:

a) Las partículas móviles fueron representadas por cubos de lados de 3 píxeles (nombre utilizado para referenciar una unidad de distancia en la muestra), con la orientación S = 0, y se mantuvo su concentración fija a lo largo de la simulación (9,10,11,12). Las posiciones iniciales de las mismas se establecieron distribuyéndolas aleatoriamente en la muestra.

b) Es necesario saber si la partícula está dentro de un grano (G), en un BG o sobre el límite de la muestra. Sólo se mueven aquellas partículas que se encuentren en el BG.

c) La partícula en el BG es movida siempre que la misma siga perteneciendo al BG, se encuentre ubicada en el centro del BG y que no toque a otra partícula (12).

d) Se elige un sitio w al azar de la muestra y se verifica que el mismo tenga S = 0  o, lo que es lo mismo, que el sitio pertenezca a una partícula o a parte de ella.

e) Para mover una partícula se debe primero asegurar que el sitio elegido al azar, w, pertenezca al centro geométrico de la partícula.

No todas las partículas sobre el BG fueron movidas en un MCS (nombre utilizado para referenciar una unidad de tiempo). Al ser elegida una partícula en el BG se calcula un número aleatorio Ni entre 0 y 1. Si ese número es menor a una dada fracción N_p dada por la fórmula (11) con  δW = Q entonces la partícula elegida se mueve, en caso contrario no. Por lo tanto, N_prepresenta la fracción máxima de partículas en el BG que se pueden mover. El valor de Q es un parámetro físico relacionado con energía de activación de la movilidad de las partículas utilizadas.

f) Las partículas pueden acercarse entre sí hasta una distancia de 1 píxel y no pueden colapsar.

Se debe aclarar que si la partícula está en el BG y el sitio vecino elegido aleatoriamente produce un movimiento de la partícula hacia el límite de la muestra, se prohíbe ese estado y se elige un nuevo sitio vecino de manera aleatoria.

IV. Metodología

En este trabajo se utilizó un programa de crecimiento de grano en 3D, en muestras de (100 x 100 x 100) píxel³, con y sin partículas móviles y con energía de BG uniforme. El valor de J = 0,5 y está expresado en unidades de KT. De igual manera está expresado el valor de Q.

Se tomó V = 26 vecinos y el radio del cristal esférico fue de 40 píxeles (ver figura 1).

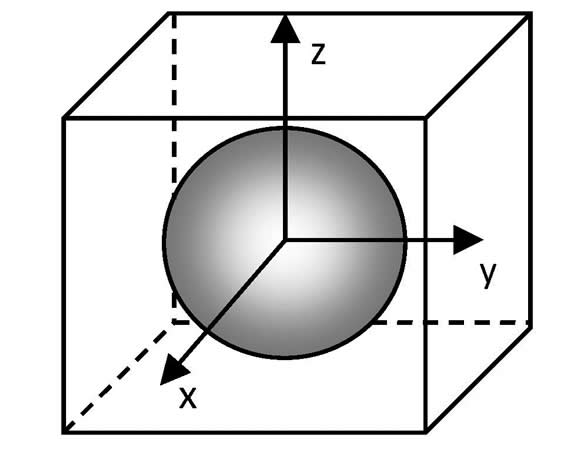
Figura 1: Bicristal esférico inmerso en una matriz de 100 x 100 x 100 píxel3 y un sistema de coordenadas.

Se simularon cristales esféricos sin partículas y con 0,1%, 0,2%, 0,3%, 0,4% y 0,5% de concentración volumétrica de partículas. Se hicieron tantos pasos de Monte Carlo (MCS) como fueron necesarios hasta lograr que el radio del cristal esférico se mantuviera constante o se hiciera cero.

En la figura 2 se presenta un corte de una muestra cristalina 3D usada en la simulación a los 0 MCS y a los 1000 MCS. Tiene partículas cúbicas de lados de 3 píxels y una concentración volumétrica de 0,5%. Las partículas son representadas por puntos negros y el BG por la línea negra.

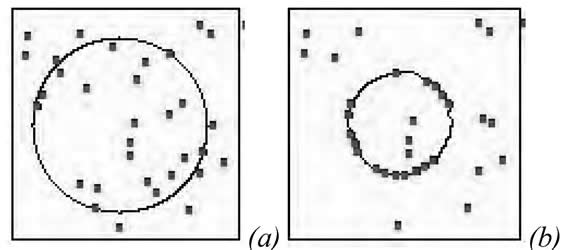
Figura 2: Evolución de un cristal esférico 3D para dos MCS diferentes: a) t = 0 MCS y b) t = 1000 MCS. El valor de Q = 1,6 KT (N_p = 0,2).

Para cada concentración de partículas f se eligieron valores de Q de tal manera que N_p fuera igual a 0,05; 0,1; 0,4; 0,8 y 1,0 respectivamente. Para cada uno de esos valores de N_p se simuló el movimiento del BG hasta un cierto valor de R_c. En cada paso se fue registrando el radio medio R del cristal esférico, y las cantidades de partículas n_bg el BG. El valor de L''' fue 3 al igual que en el trabajo de Achával y col.(9).

V. Resultado de las simulaciones y discusión

En la figura 3 se presenta el valor de R en función de t, para una muestra con f = 0,3% de partículas móviles y diferentes valores de N_p. Se puede observar que el valor de R disminuye con el tiempo hasta un valor constante R_c y ese valor de R_c es independiente del valor de N_p.

Figura 3: R vs t para diferentes muestras con N_p igual a 0,05; 0,1; 04; 0,8 y 1 con una fracción f de partículas de 0,3%.

En la figura 4 puede verse el mismo tipo de gráfico, pero para un valor de N_p = 0,05 y diferentes valores de f. En dicho grafico se nota que los valores de R disminuyen con t pero su variación es más notable si la concentración f es baja. También se puede observar que R_c depende únicamente de f.

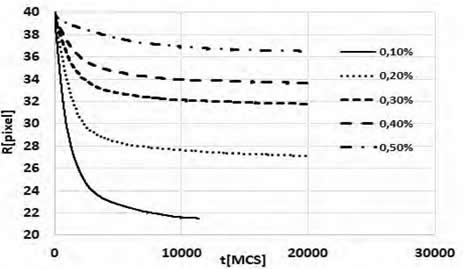
Figura 4: R vs t para diferentes fracciones f de partículas y con el valor de N_p = 0,05.

En la figura 5 se presenta el valor de la fracción de partículas en el BG (f_bg) en función de R para f = 0,2% y para diferentes valores de N_p. Puede verse que, en general, el valor de f_bg va aumentando a medida que el valor de R disminuye y el mismo no depende del valor de N_p. Los valores encontrados de f_bg fueron ajustados muy bien mediante la ecuación (13) obtenida analíticamente. En todos los casos se le asignó L el valor de 0,5 pixels ya que ese valor permite el mejor ajuste de los datos computacionales.

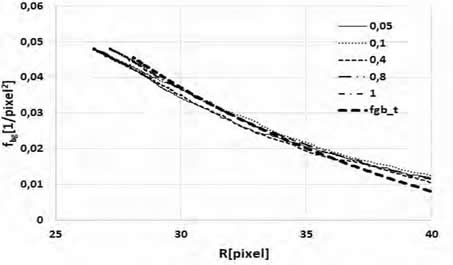
Figura 5: f_bg vs R para diferentes muestras con N_p igual a 0,05; 0,1; 0,4; 0,8 y 1 con una fracción f de partículas de 0,2%.

En la tabla 1 se presentan los valores de f, N_p, k_p, R_c y R_L para las simulaciones computadas en este trabajo. Se puede notar que el valor de R_c coincide con el valor de R obtenido de la ecuación  denominado R_L.

Tabla 1: Valores de  f, N_p, k_p, R_c y R_L para las simulaciones computadas en este trabajo.

Di Prinzio y col.(5) encontraron que en muestras policristalinas con partículas inmóviles el valor de R_c se relacionaba con f a través de la ecuación de Zener. En la figura 6 se presenta los valores de R_c para los valores de f  estudiados. Se puede advertir que la relación entre ellos es:

donde n ≈ 0.33 = 1/3  y m ≈ 20.

Sin embargo, es difícil comparar estos resultados computacionales con otros resultados de trabajos publicados. Como mencionan Yamanaka y Okamoto(13) en su trabajo, hasta el momento hay muy pocos trabajos computacionales publicados en muestras tridimensionales con partículas móviles.

Figura 6:  vs ln(f )para las diferentes muestras estudiadas (ver tabla 1).

Un futuro trabajo podría investigar la relación anterior en función del tamaño de las partículas.

En la figura 7 se presenta R en función de t para f = 0,1% y N_p = 0,05. Los valores computacionales fueron ajustados por medio de la función obtenida en este trabajo (ecuación (16), modelo_n) y por medio de la función obtenida de resolver la ecuación (8) con Pc constante(6) (modelo_v). Se puede observar que el presente modelo ajusta mucho mejor que el modelo presentado por Alley y col.(6) ampliamente utilizado en la bibliografía(7). En el modelo actual la fuerza de frenado no es constante, sino que va incrementándose a medida que el grano va reduciendo su tamaño e incorporando más partículas.

Figura 7: R vs t  para diferentes fracciones f de partículas y con un valor de Np = 0,05.

Finalmente, se puede notar que el valor de k_p difiere del valor de k = 0,5 correspondiente a una muestra sin partículas. En general k_p es menor y eso está relacionado con la movilidad de las partículas, M_p. Recordando que k_p = kβ y reemplazando con la ecuación (5) se tiene que:

de donde se obtiene:

Las partículas utilizadas son móviles, luego se puede deducir que su movilidad, M_p, depende directamente de N_p. Sin embargo, también puede deducirse que dicha movilidad es inversamente proporcional la fracción de partículas f. Las partículas tienen más movilidad cuando más baja es la concentración f  ya que las mismas pueden moverse mejor al tener más espacio libre. Al aumentar la concentración f, las partículas, a pesar de poder moverse, no lo hacen por tener partículas vecinas en sus proximidades y no poder colapsar. Por lo tanto, se tiene que:

Entonces, la ecuación (22) queda:

donde

y ε es una constante.

En la figura 8 se graficó 1/k_p en función de f  para N_p fijo y se pudo observar que la relación es lineal, como indica la ecuación (24), pero con distintas pendientes w.

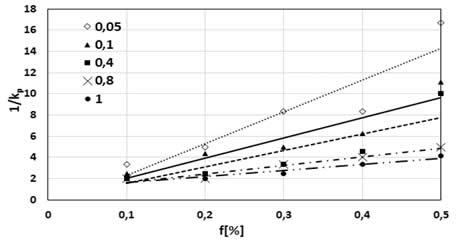
Figura 8: 1/k_p en función de f  para diferentes muestras con N_p  igual a 0,05; 0,1; 04; 0,8 y 1.

Si se grafican esas pendientes en función de 1/N_p (figura 9) se puede advertir que también guardan una relación lineal. Esto demuestra que las partículas móviles pueden no sólo contribuir con una fuerza de frenado P_c que varía con el tiempo sino además modificar la movilidad del BG (kp). En este caso, k_p se ve reducida cuando la movilidad de las partículas M_p disminuye y cuando la fracción de partículas f  aumenta.

Figura 9: w en función de 1/Np  con los datos extraídos de la figura 8.

VII. Conclusiones

En este trabajo se estudió, mediante un algoritmo computacional basado el método de Monte Carlo, el movimiento de un BG esférico en presencia de partículas móviles. Las partículas han presentado diferentes movilidades y diferentes concentraciones. Se puede concluir:

1) Cuanto mayor es f  más lento es el movimiento del BG y se detiene a valores de R cercanos a R_c.

2) El valor de R_c depende de f  y no de N_p.

3) Se puede afirmar que los R_c son prácticamente iguales a los RL calculados mediante la resolución de la ecuación . Los valores de R_c siguen una ley potencial con la concentración de partículas f.

4) Los valores de f_bg  computados son bien representados por la ecuación analítica (13).

5) Los valores del radio medio R son mejor ajustados por el nuevo modelo dado por la ecuación (16) que por la solución de la ecuación (8) manteniendo P_c constante, dada por otros autores y utilizada ampliamente.

6) Los valores de la movilidad de las partículas, M_p, son proporcionales al N_p utilizado en las simulaciones e inversamente proporcionales a  f.

7) El valor de k_p está ampliamente afectado por la movilidad de las partículas, M_p, como se planteó analíticamente. 

Agradecimientos

Este trabajo fue posible gracias a la colaboración de José Barcelona (de FAMAF, Córdoba) y del apoyo económico de SeCyT (Secretaría de Ciencia y técnica de la UNC).

Referencias

1. Y. J. Kim, S. K. Hwang, M. H. Kim, S. I. Kwun, and S. W. Chae. Three-dimensional Monte-Carlo simulation of grain growth using triangular lattice. Materials Science and Engineering A, 408(1-2):110-120, 2005.         [ Links ]

2. E. A. Holm and C. B. Corbett. The computer simulation of microstructural evolution. JOM, 53(9):20-23, 2001.         [ Links ]

3. Q. Yu and S. K. Esche. A Monte Carlo algorithm for single phase normal grain growth with improved accuracy and efficiency. Computational Materials Science, 27(3):259-270, 2003.         [ Links ]

4. D. Raabe. Scaling Monte Carlo kinetics of the Potts model using rate theory. Acta Materialia, 48(7):1617-1628, 2000.         [ Links ]

5. C. L. Di Prinzio, E. Druetta, and O. B. Nasello. More about Zener drag studies with Monte Carlo simulations. Modelling and Simulation in Materials Science and Engineering, 21(2):025007, 2013.         [ Links ]

6. R. B. Alley, J. H. Perepezko, and C. R. Bentley. Grain growth in polar ice: I. Theory. Journal of Glaciology, 32(112):415-424, 1986.         [ Links ]

7. E. A. Grey and G. T. Higgins. A velocity independent drag during grain boundary migration. Scripta Metallurgica, 6(3):253-258, 1972.         [ Links ]

8. S. Choudhury and R. Jayaganthan. Monte Carlo simulation of grain growth in 2D and 3D bicrystals with mobile and immobile impurities. Materials Chemistry and Physics, 109(2-3):325-333, 2008.         [ Links ]

9. P. I. Achával, C. A. Rodríguez Luca, and C. L. Di Prinzio. Kinetic evolution of a 3D spherical crystal with mobile particles using Monte Carlo. Anales AFA, 30:25-30, 2019.         [ Links ]

10. M. P. Anderson, D. J. Srolovitz, G. S. Grest, and P. S. Sahni. Computer simulation of grain growth: I. Kinetics. Acta Metallurgica, 32(5):783-791, 1984.         [ Links ]

11. D. J. Srolovitz, M. P. Anderson, P. S. Sahni, and G. S. Grest. Computer simulation of grain growth: II. Grain size distribution, topology and local dynamics. Acta Metallurgica, 32(5):793-802, 1984.         [ Links ]

12. P. I. Achával and C. L. Di Prinzio. Three-dimensional grain growth with mobile particles using Monte Carlo method. Matéria (Rio de Janeiro), 23(2), 2018.         [ Links ]

13. A. Yamanaka and M. Okamoto. Grain growth in a system containing finely dispersed mobile second-phase particles: a GPU-accelerated multi-phase-field study. In Proceedings of the 6th International Conference on Recrystallization and Grain Growth, pages 29-34, Pennsylvania, USA, 2016. Springer.         [ Links ]