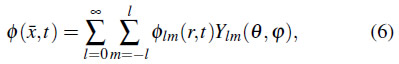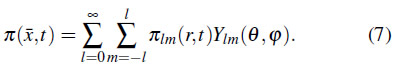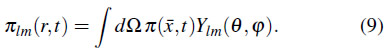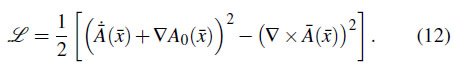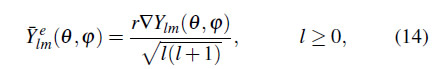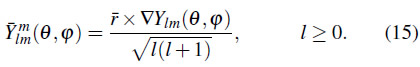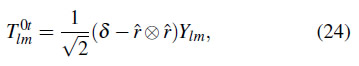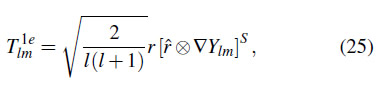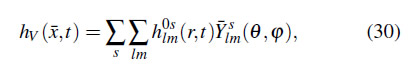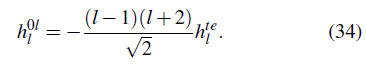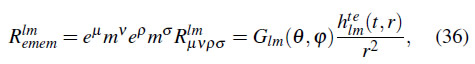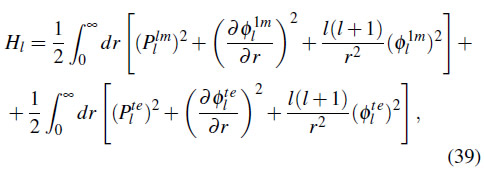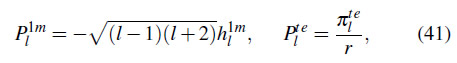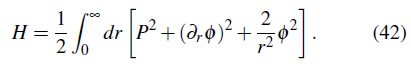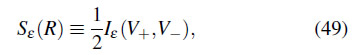https://doi.org/10.31527/analesafa.2020.31.2.71
MENCIÓN ESPECIAL DEL PREMIO LUIS MÁSPERI 2019: PARTÍCULAS Y CAMPOS

Entropía de entrelazamiento para un campo de espín 2 en una esfera

 

Entanglement entropy for spin 2 field on a shpere

 

V. Benedetti*¹
H. Casini¹

¹ Centro Atómico Bariloche - CONICET. Av. E. Bustillo km 9,500 (R8402AGP), Bariloche, Rio Negro, Argentina.
Autor para correspondencia: V. Benedetti, email: valentin.benedetti@gmail.com

Recibido: 28/02/2020
Aceptado: 04/05/2020

 

---

Resumen:
En este trabajo se presentan el cálculo de la entropía de entrelazamiento de gravitones linealizados (como partículas de helicidad 2) en una esfera definida sobre un espacio de Minkowski. Previamente, se analizan los cálculos para los campos escalares y vectoriales mediante una descomposición en armónicos esféricos. Luego se generaliza este método al caso tensorial. Se obtiene el término universal logarítmico y se analiza su relación con la anomalía conforme.

Palabras clave: entropía de entrelazamiento, espín, esfera.

Abstract:
In this paper we compute the entanglement entropy for linearized gravitons (as helicity 2 particles) on a sphere defined over a Minkowski background. Previously, we analyse the cases of the solar and vector fields by decomposition in spherical harmonics. Then we generalise this method for the tensor field. We obtain the universal logarithmic coefficient and we analyse its relation to the conformal anomaly.

Keywords: entanglement entropy, spin, sphere.

---

 

I. INTRODUCCIÓN

En una teoría cuántica de campos (QFT), a una región del espacio  siempre se le puede asignar una entropía, ya sea ésta una entropía térmica o producida por fluctuaciones del vacío. Para el segundo caso, dicha entropía puede obtenerse a partir de la entropía de von Neumann¹ correspondiente a la matriz densidad reducida  de la región  (ver Fig. 1) de la forma

Dicha entropía actuará como medida de las correlaciones del sistema. Además, si el estado global es puro, esta magnitud se conoce como entropía de entrelazamiento (EE) y podrá ser considerada una medición del entrelazamiento entre la región y su complemento.

Sin embargo, ciertas sutilezas deben tenerse en cuenta para definir la región . Las teorías cuánticas de campos continuas poseen un álgebra de von Neumman tipo-III.² Por esta razón las regiones no pueden definirse a partir de una factorización del espacio de Hilbert como se hace en sistemas localmente finitos. Más físicamente, este problema puede entenderse debido a la existencia de grados de libertad adyacentes arbitrariamente cerca dentro del UV.³

No obstante, las regiones pueden ser definidas a partir de un álgebra de observables con soporte en la región  que conmutan con operadores cuyo soporte está en regiones espacialmente separadas.

La situación es aún más compleja en teorías de gauge, dado que la construcción de un álgebra de operadores físicos requiere previamente una fijación del gauge. En este marco, distintas elecciones de gauge pueden corresponderse con diferentes regiones espaciales.⁴

En particular, necesitamos que el campo con el gauge fijado pueda escribirse en función de invariantes de gauge dentro de la región de estudio .

FIG. 1: Una región arbitraria y su complemento  definidos sobre una una superficie de Cauchi  de dimensión (d-1).

Por otro lado, en una teoría de campos conforme (CFT) en (3+1) dimensiones es de particular interés el estudio de regiones esféricas. Debido a la ausencia de escalas, por análisis dimensional la entropía de entrelazamiento (EE) asociada a dicha región debe tener la forma⁵

                 

donde  es el radio de la esfera en cuestión y  un regulador UV. El término  de es proporcional al área de la región y es la mayor contribución a la EE. Sin embargo dicho término depende del esquema de regularización utilizado. El termino logarítmico  depende únicamente del continuo de la teoría; en particular, esta relacionado con la anomalía conforme^6,7 y el teorema  de irreversibilidad del grupo de renormalización.⁸

En la Sec. II recordaremos propiedades útiles de los gravitones linealizados como un campo tensorial de espín 2. Luego, en la sección III, presentaremos brevemente la modalidad de trabajo para el cálculo de la EE de un campo escalar. Además, presentamos un método para calcular los coeficientes logarítmicos de los campos de espín 1 y 2. Por último, se discuten los resultados obtenidos. Este trabajo es principalmente una discusión de resultados presentados anteriormente.⁹

II. GRAVITONES LINEALIZADOS

La teoría libre no masiva de helicidad 2 puede ser pensada como un campo tensorial . Dicho campo puede ser pensado como una perturbación sobre la métrica de Minkowski  a partir de

                      

El campo  obedece las ecuaciones de Einstein a orden linealizado que pueden ser obtenidas como las ecuaciones de Euler-Lagrange del lagrangiano¹⁰

             

La teoría tiene invariancia de gauge ante la ley de transformación  para vectores  arbitrarios. Esto se corresponde con la invariancia ante difeomorfismos de la teoría de Einstein a nivel linealizado.

En una teoría de gravedad no lineal la curvatura no es invariante de gauge. Sin embargo, a nivel linealizado podemos utilizar al tensor de curvatura linealizado como un operador invariable de gauge ante difeomorfismos lineales. Dicho tensor se escribe, en función de las perturbaciones , de la forma

                  

En consecuencia, la EE del campo de espín 2 linealizado estará bien definida salvo los problemas usuales asociados a términos divergentes.

ENTROPÍA DE ENTRELAZAMIENTO A PARTIR DE MOMENTOS ANGULARES

Campo escalar (espín 0)

La EE de un campo escalar libre en una esfera puede ser fácilmente calculada mediante el uso de coordenadas esféricas y una descomposición del campo  y su momento conjugado  en una base de armónicos esféricos de la forma¹¹

               

               

Donde  y  son los respectivos coeficientes de Fourier dados por

             

Bajo este contexto, podemos reescribir el hamiltoniano del campo escalar e integrar en las variables angulares. De la ortonormalidad de los armónicos esféricos recuperamos el hamiltoniano radial

            

A partir de aquí, la EE puede ser calculada computacionalmente¹² usando el método de Peschel¹³ para estados gaussianos. Como resultado se tiene el valor a estándar de

                     

Campo de Maxwell (espín 1)

Un procedimiento similar puede ser aplicado para estudiar la EE del campo de Maxwell dado por el lagrangiano

                

Para estudiar una región esférica, necesitamos introducir una expansión en armónicos esféricos vectoriales.^14,15 Estos son una generalización de los armónicos esféricos escalares que actúan como una base con simetría esférica para vectores espaciales de tres componentes y vienen dados por

                 

               

      

En este caso, podemos introducir la expansión en armónicos esféricos sobre los campos invariantes de gauge  y ¹⁵ o bien sobre el campo ⁹ de la forma

                    

                   

Ahora, es necesario fijar el gauge para transformar los operadores en variables físicas. Es posible fijar la parte eléctrica a cero para cada  y . Haciendo esto vemos que

            

donde  es el versor en la dirección de  y  es la derivada en dicha dirección. Esta expresión muestra que podemos recuperar  en la esfera a partir del conocimiento de las componentes "eléctricas" del invariante de gauge  en la misma región. Si bien dicha relación es no local, permite mapear las componentes del campo a variables físicas del mismo radio. Como es de esperase⁴ se obtiene la fijación adecuada anulando algunas componentes paralelas a la superficie de la región espacial definida, pero no todas.

Tendremos  contribuciones idénticas a la EE por cada momento angular . Por esto, trabajaremos el caso real  suprimiendo el subíndice  de las ecuaciones.

Luego, remplazando en el lagrangiano, integrando sobre variables angulares. Además, trabajando bajo el esquema canónico tomamos la transformada de Legendre y trabajamos con  como multiplicador de Lagrange. De esta forma para cada  tenemos el hamiltoniano análogo a dos campos escalares en una esfera

           

donde tanto  y  como  y  son pares de variables canónicas conjugadas definidas como

con  y  las momentos canónicos conjugados de  y  respectivamente.

Para el caso  solo esta definido el armónico esférico radial. Realizando el mismo procedimiento recuperamos un hamiltoniano sin dinámica propia que no genera aportes a la EE.

En resumen la EE del campo de Maxwell será equivalente a la de dos campos escalares libres sin aportes del modo de momento angular cero.

El modo  se corresponde con un campo () dimensional no masivo en la semi-recta  con condiciones de contorno de Dirichlet en el origen. Su entropía es universal y logarítmica y viene dada por¹⁶

Entonces, el coeficiente logarítmico universal del campo del Maxwell vale . Es decir que la EE puede escribirse como

                  

Campo de gravedad lineal (espín 2)

Para estudiar el caso del campo tensorial de espín 2 introducimos los armónicos esféricos tensoriales¹⁴ dados por

Es importante que destacar que los armónicos esféricos de spin 0 están definidos para , los de spin 1 para  y los de spin 2 para . Además, los subíndices  hacen referencia a la parte simétrica y  a la parte trasversal al versor radial  y sin traza.

Considerando que el tensor  es simétrico, separamos al campo en las partes escalares  dada por la componente , la parte vectorial  dada por las componentes  y la parte tensorial  construida a partir de las componentes espaciales . Luego, introducimos la expansión en armónicos esféricos de la forma

Se puede ver que fijando la libertad de gauge asociada a difeomorfismos lineales se pueden fijar a cero ciertas componentes de manera que la parte vectorial y tensorial puedan escribirse como

Donde  es un grado de libertad asociado a la "dirección" dada por una la combinación lineal de los tensores  y .

Trabajamos nuevamente en el esquema canónico donde vemos que los campos , ,  no tienen dinámica propia. Luego, podemos derivar los vínculos asociados a estos multiplicadores de Lagrange. Con uno de ellos podemos escribir al campo  en función de  de la forma

Quedando solo los campos  y  como grados de libertad resultantes. A cada uno de estos, bajo esta fijación de gauge, podemos escribirlo como una contracción del tensor de Riemann. Para el caso de  tomamos la contracción en la dirección "eléctrica - radial - eléctrica - magnética" y tenemos

donde  es una función únicamente de las variables angulares que depende del valor de  y . Para el caso de  realizamos la contracción en la dirección "eléctrica - magnética - eléctrica - magnética"

donde nuevamente  es una función únicamente de las variables angulares que depende del valor de  y .

Nuevamente observaremos el caso . Las funciones  y  pueden escribirse en función de los polinomios asociados de Legendre  de la forma

Además, el hamiltoniano para  puede escribirse como el de dos campos escalares

donde tanto  y  como  y  son pares de variables canónicas conjugadas definidas como

con  y  las momentos canónicos conjugados de  y  respectivamente.

Para el caso  solo está definido el armónico esférico radial y los armónicos tensoriales de espín 0. Para  no se encuentran definidos los armónicos tensoriales de espín 2. Realizando el mismo procedimiento para  recuperamos un hamiltoniano nulo o sin dinámica propia que no genera aportes a la EE.

En resumen la EE del campo de gravitatorio lineal será equivalente a la de dos campos escalares libres sin aportes del modo de momento angular  y los modos de .

Tenemos que la entropía del campo escalar tiene un término logarítmico de . Además, el modo  tiene una contribución logarítmica de    dado que se corresponde con un escalar no masivo definido sobre una semi-recta en () dimensiones.

Entonces, para obtener el término logarítmico del campo lineal de espín 2 solo necesitamos conocer las características de la contribución asociada a los modos de . Estos, también, se corresponden a campos en () dimensiones definidos sobre la semi-recta . Sin embargo, el hamiltoniano ahora tiene la forma

El modelo de  es invariante de escala. Sin embargo, a diferencia del modo , contiene un término de potencial . La EE proviene el entrelazamiento asociado a fluctuaciones de alta energía alrededor del borde . Por este motivo, podemos despreciar el término de potencial y recuperaremos la misma contribución que en el caso . Debido a la ausencia de escalas dimensionales tenemos

Entonces, el coeficiente logarítmico universal del campo del gravitón linealizado viene dado por . Es decir que la EE puede escribirse como

Estos resultados fueron revisados numéricamente con cinco cifras de precisión.

Conjetura para spin superior

En vista de los resultados para los campos vectoriales y tensoriales, es esperable que exista una generalización para partículas de helicidad entera arbitraria  en una esfera. En particular, podría esperarse que la EE sea equivalente a la de dos campos escalares con los modos asociados a momentos angulares  sustraídos. Cada uno de estos modos tiene un hamiltoniano con un potencial

Consideramos que este potencial puede ser despreciado en el límite continuo por argumentos similares a la sección anterior. Entonces, cada modo tiene asociada una EE de la forma

                            

Realizando la sustracción correspondiente esperamos que el término universal logarítmico de la EE del campo de helicidad  esté dado por

Este mismo resultado también puede ser obtenido a partir de argumentos termodinámicos en un espacio De Sitter.^17,18

IV. DISCUSIÓN

La información mutua (MI) en teorías de campos es una cantidad definida sin ambigüedades o divergencias para regiones disjuntas. Dadas dos regiones  y  la MI se escribe como

La MI nos da una prescripción geométrica para definir una EE regularizada.¹⁹ En particular, los coeficientes universales obtenidos para los campos de espín 0, 1 y 2 en las ecuaciones (11), (22) y (44) respectivamente coinciden con los de la MI. Esto significa que no son afectados por términos de centro en el álgebra⁴ o por contribuciones asociadas a grados de libertad en la superficie de la región²⁰ ("edge modes"). Podemos escribir la EE regularizada (ver Fig. 2) como

donde  es un regulador geométrico que define a  como el complemento de la esfera de radio   y a  como la región esférica de radio .

FIG. 2: Regiones  y  definidas a partir del regulador geométrico.

Por otro lado existe la noción de que los coeficientes universales de la EE están relacionados con la anomalía conforme.⁶ En particular, para regiones esféricas en un espacio de Minkowski esperamos una contribución de la forma^6,7

con  la anomalía proporcional a la densidad de Euler en la traza del tensor energía-momento en espacios curvos.

Para el caso del campo escalar puede verse que el coeficiente logarítmico calculado mediante la anomalía coincide exactamente con el valor asociado a la MI.

En cambio, para campo de Maxwell observamos una disparidad entre ambos valores (ver Tabla 1). Esta disparidad puede ser considerada la contribución de los "edge modes" sobre la superficie de la esfera.²⁰ Más adecuadamente, el valor que coincide con la MI está asociado con la teoría libre, mientras que el valor obtenido a partir de la anomalía requiere el acople con cargas eléctricas y magnéticas "pesadas" cerca del UV.²¹

TABLA 1: Coeficientes universales para los campos de espín 0, 1 y 2 en una esfera obtenidos a partir de la información mutua y la anomalía conforme.

Para el gravitón lineal es diferente. Esto se debe a que la teoría enunciada en la Sec. II posee simetría conforme solo "on-shell",²² es decir cuando se obedecen las ecuaciones de movimiento dadas por .

Esto impide a priori relacionar el término logarítmico con la anomalía, debido a que la demostración de la ecuación (50) requiere utilizar un mapeo de Weyl de la esfera en Minkowski al "static patch" en De Sitter.⁷ Dicho mapeo conforme no puede realizase "on shell" debido a que el tensor de Ricci debe anularse.

Además, el campo gravitatorio lineal no posee un tensor energía-momento invariante de gauge debido al teorema de Weinberg-Witten.²³ Esto hace que la definición de la anomalía sea menos clara y precisa. Sin embargo, existen cálculos para la contribución logarítmica de la entropía sobre agujeros negros. En particular para métricas como Schwarzschild el término logarítmico es proporcional a una resta de las cargas  y  que se encuentra bien definida a partir de la acción efectiva.²⁴ En resumen, la relación de la anomalía conforme con los gravitones requiere ser estudiada con más detalle.

Por último, debería ser posible estudiar esta cantidad desde un punto de vista holográfico. La expresión holográfica para la entropía está dada por la fórmula de Ryu-Takayanagi²⁵ y sus correcciones cuánticas de primer orden por la entropía de los campos en el "bulk".²⁶ En este contexto, debido a argumentos en el espacio de fases de relatividad general, existe la noción que la corrección debido a gravitones solo está definida para superficies extremales.²⁷ La esfera no es una superficie extremal y por eso no es claro esperar que los resultados obtenidos en este trabajo para gravitones lineales puedan recuperarse como un límite bien definido de gravedad cuántica.

AGRADECIMIENTOS

Se agradece por discusiones a Pablo Bueno, Joan Camps y Marina Huerta. Este trabajo fue parcialmente financiado por CONICET, CNEA y la Universidad Nacional de Cuyo, Argentina. El trabajo de H. C. es parcialmente financiado por una subvención It From Qubit de la Simons foundation. Se agradece a la Asociación Fiísica Argentina por la posibilidad de presentar este artículo en el marco de una Mención Especial del Premio Luis Másperi 2019.

REFERENCIAS

1. M. Nielsen e I. Chuang. Quantum computation and quantum information (Cambridge University Press, Cambridge, 2000).         [ Links ]

2. E. Witten. APS Medal for Exceptional Achievement in Research: Invited article on entanglement properties of quantum field theory. Rev. Mod. Phys. 90, 45003 (2018).         [ Links ]

3. W. Donnelly y S. B. Giddings. How is quantum information localized in gravity? Phys. Rev. D 96, 086013 (2017).         [ Links ]

4. H. Casini, M. Huerta y R. J. A. Remarks on entanglement entropy for gauge fields. Phys. Rev. D 89, 085012 (2014).         [ Links ]

5. M. Rangamani y T. Takashanagi. Holographic Entanglement Entropy (Lecture Notes in Physics) ISBN: 978-3-319-52573-0 (Springer International Publishing, 2017).         [ Links ]

6. S. N. Solodukhin. Entanglement entropy, conformal invariance and extrinsic geometry. Phys. Lett. B 665, 305-309 (2008).         [ Links ]

7. H. Casini, M. Huerta y R. C. Myers. Towards a derivation of holographic entanglement entropy. J. High Energ. Phys. 2011, 36 (2011).         [ Links ]

8. H. Casini, E. Teste y G. Torroba. Markov Property of the Conformal Field Theory Vacuum and the a Theorem. Phys. Rev. Lett. 118, 261602 (2017).         [ Links ]

9. V. Benedetti y H. Casini. Entanglement entropy of linearized gravitons in a sphere. Phys. Rev. D 101, 045004 (2020).         [ Links ]

10. T. Ortín. Gravity and strings (Cambridge Monographs on Mathematical Physics) ISBN: 9780511616563 (Cambridge University Press, Cambridge, 2004).         [ Links ]

11. M. Srednicki. Entropy and Area. Phys. Rev. Lett. 71, 666 (1993).         [ Links ]

12. R. Lohmayer, H. Neuberger, A. Schwimmer y S. Theisen. Numerical determination of entanglement entropy for a sphere. Phys. Lett. B 685, 222-227 (2010).         [ Links ]

13. I. Peschel. Calculation of reduced density matrices from correlation functions. J. Phys. A: Math. Gen. 36, L205 (2003).         [ Links ]

14. K. S. Thorne. Multipole expansions of gravitational radiation. Rev. Mod. Phys. 52, 299 (1980).         [ Links ]

15. H. Casini y M. Huerta. Entanglement entropy of a Maxwell field on the sphere. Phys. Rev. D 93, 105031 (2016).         [ Links ]

16. P. Calabrese y J. L. Cardy. Entanglement entropy and quantum field theory. J. Stat. Mech. 2004, P06002 (2004).         [ Links ]

17. J. S. Dowker. Entanglement entropy for even spheres ar-Xiv:1009.3854 [hep-th]. 2010.         [ Links ]

18. J. S. Dowker. Note on the entanglement entropy of higher spins in four dimensions arXiv:1908.04870 [hep-th]. 2019.         [ Links ]

19. H. Casini, M. Huerta, R. Myers y A. Yale. Mutual information and the F-theorem. J. High Energ. Phys. 2015, 1-69 (2015).         [ Links ]

20. W. Donnelly y A. C.Wall. Entanglement entropy of electromagnetic edge modes. Phys. Rev. Lett. 114, 111603 (2015).         [ Links ]

21. H. Casini, M. Huerta, J. M. Magan y D. Pontello. Logarithmic coefficient of the entanglement entropy of a Maxwell field. Phys. Rev. D 101, 065020 (2020).         [ Links ]

22. D. Dorigonia y S. Rychkov. Scale Invariance + Unitarity => Conformal Invariance? arXiv:0910.1087 [hep-th]. 2009.         [ Links ]

23. S. Weinberg y E. Witten. Limits on massless particles. Phys. Lett. B 96, 59-62 (1980).         [ Links ]

24. S. N. Solodukhin. Entanglement entropy of black holes. Living Rev. Rel. 14, 8 (2011).         [ Links ]

25. S. Ryu y T. Takayanagi. Holographic Derivation of Entanglement Entropy from the anti-de Sitter Space/Conformal Field Theory Correspondence. Phys. Rev. Lett. 96, 181602 (2006).         [ Links ]

26. T. Faulkner, A. Lewcowycz y J. Maldacena. Quantum corrections to holographic entanglement entropy. J. High Energ. Phys. 2013, 74 (2013).         [ Links ]

27. J. Camps. Superselection Sectors of Gravitational Subregions. J. High Energ. Phys. 2019, 182 (2019).         [ Links ]