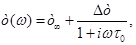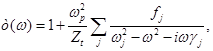I. INTRODUCCIÓN
La teoría del poder de frenado fue propuesta originalmente por Niels Bohr,1 sostenida por una visión clásica basada en trayectorias periódicas y cerradas descriptas por la acción cuantizada propuesta separadamente Wilson2 y Sommerfeld.3 Ésta descripción implicó la condición adiabática de Bohr, según la cual un electrón moviéndose en una de dichas trayectorias logra orbitar varios ciclos sin transferencia energética desde el ión cargado; e introdujo a su vez la necesidad de calcular una frecuencia promedio  con el objetivo de comparar los tiempos característicos de interacción con los períodos orbitales. El primer acercamiento de Bohr a este problema no fue capaz de lograr una definición acabada para este promedio, por lo que él mismo propuso un cálculo más preciso introduciendo el tratamiento de las colisiones lejanas y cercanas. Para ello, se utiliza el parámetro de impacto
con el objetivo de comparar los tiempos característicos de interacción con los períodos orbitales. El primer acercamiento de Bohr a este problema no fue capaz de lograr una definición acabada para este promedio, por lo que él mismo propuso un cálculo más preciso introduciendo el tratamiento de las colisiones lejanas y cercanas. Para ello, se utiliza el parámetro de impacto  , siendo el régimen de colisión distante aquel para el cual
, siendo el régimen de colisión distante aquel para el cual  , donde
, donde  es la posición del electrón vista desde el núcleo, considerado como armónicamente ligado en la condición adiabática, lo cual indujo a Bohr a proponer la primera definición de
es la posición del electrón vista desde el núcleo, considerado como armónicamente ligado en la condición adiabática, lo cual indujo a Bohr a proponer la primera definición de  como un promedio geométrico:
como un promedio geométrico:
expresión en la cual  representa las frecuencias características de oscilación,
representa las frecuencias características de oscilación,  la fracción de electrones atómicos oscilando a frecuencia
la fracción de electrones atómicos oscilando a frecuencia  , también denominadas intensidades de los osciladores, y la normalización satisface la regla de suma de Thomas-Reiche-Kuhn4
, también denominadas intensidades de los osciladores, y la normalización satisface la regla de suma de Thomas-Reiche-Kuhn4
 , siendo
, siendo  el número atómico (
el número atómico ( ) del material.
) del material.
Una definición de  cuya base fuera la mecánica cuántica debió esperar hasta 1930, siendo Hans Bethe5,6 quien extendió el cálculo del poder de frenado utilizando la ecuación de Schrödinger. Este modelo también es válido dentro de cierto rango, delimitado por el conocido como parámetro de Sommerfeld
cuya base fuera la mecánica cuántica debió esperar hasta 1930, siendo Hans Bethe5,6 quien extendió el cálculo del poder de frenado utilizando la ecuación de Schrödinger. Este modelo también es válido dentro de cierto rango, delimitado por el conocido como parámetro de Sommerfeld ,7 donde
,7 donde  es la carga eléctrica del proyectil y
es la carga eléctrica del proyectil y  su velocidad. Además, se logró una expresión similar a la fórmula (1) para el cálculo de la energía media de excitación
su velocidad. Además, se logró una expresión similar a la fórmula (1) para el cálculo de la energía media de excitación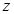 , básicamente reemplazando
, básicamente reemplazando  , donde
, donde  representa los niveles de energía del átomo. La intensidad de los osciladores está dada por
representa los niveles de energía del átomo. La intensidad de los osciladores está dada por  , donde
, donde  corresponde a las intensidades de los osciladores generalizadas.6
corresponde a las intensidades de los osciladores generalizadas.6
Ambas aproximaciones son válidas en un régimen de baja densidad (acercándose incluso al caso de un gas ideal), situaciones en las que las interacciones pueden aproximarse como uno a uno entre el ión y los electrones atómicos. En casos realistas debe considerarse que el campo eléctrico del proyectil es capaz de afectar otros átomos, por lo tanto dando lugar a efectos de polarización no despreciables.8,9 Para la descripción del poder de frenado en estas condiciones, se utiliza la electrodinámica clásica.10,11 En este aspecto, cabe remarcar que se obtiene nuevamente un promedio sobre las posibles frecuencias capaces de recibir los electrones atómicos, pero pesado en términos de la función de respuesta dieléctrica óptica , que contiene información sobre las características dinámicas del material en relación a su respuesta a una perturbación externa:
, que contiene información sobre las características dinámicas del material en relación a su respuesta a una perturbación externa:
donde  es la parte imaginaria de
es la parte imaginaria de  . La función de respuesta dieléctrica depende, típicamente, del momento transferido
. La función de respuesta dieléctrica depende, típicamente, del momento transferido 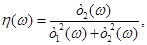 , además de la frecuencia
, además de la frecuencia  . De hecho, la función
. De hecho, la función  se conoce como superficie de Bethe del material, y el caso asintótico
se conoce como superficie de Bethe del material, y el caso asintótico  se conoce como límite óptico.12,13 En el presente trabajo se modelará la función óptica de pérdida de energía u
se conoce como límite óptico.12,13 En el presente trabajo se modelará la función óptica de pérdida de energía u  (por sus siglas en inglés optical energy loss function), dada por
(por sus siglas en inglés optical energy loss function), dada por  . Una expresión general para la función de respuesta dieléctrica es
. Una expresión general para la función de respuesta dieléctrica es  ,11 y la
,11 y la  puede a partir de aquí escribirse como:
puede a partir de aquí escribirse como:
donde puede verificarse directamente que  . Esta propiedad será muy útil para el modelo que se desarrollará en este trabajo.
. Esta propiedad será muy útil para el modelo que se desarrollará en este trabajo.
Existen en la literatura, excelentes trabajos que buscan aproximar el valor de  para distintos materiales. Particularmente interesantes e importantes son los trabajos sobre la molécula de agua líquida de D. Emfietzoglou y M. Dingfelder14,15 que ilustran en detalle cómo aplicar un procedimiento estándar para un caso particular. Más allá del excelente trabajo modelando la superficie de Bethe para los niveles moleculares discretos y continuos (ionizaciones), con un tratamiento particular del estado fundamental, e incluso alejándose del límite óptico (
para distintos materiales. Particularmente interesantes e importantes son los trabajos sobre la molécula de agua líquida de D. Emfietzoglou y M. Dingfelder14,15 que ilustran en detalle cómo aplicar un procedimiento estándar para un caso particular. Más allá del excelente trabajo modelando la superficie de Bethe para los niveles moleculares discretos y continuos (ionizaciones), con un tratamiento particular del estado fundamental, e incluso alejándose del límite óptico (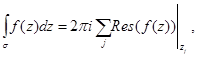 ),16,17 sigue sin presentarse un entendimiento profundo de las razones teóricas que permiten utilizar funciones tipo Drude como herramienta para integrar los diferentes mecanismos de pérdida energética del ión. En el presente trabajo se establece una primera aproximación a este análisis, mostrando que la
),16,17 sigue sin presentarse un entendimiento profundo de las razones teóricas que permiten utilizar funciones tipo Drude como herramienta para integrar los diferentes mecanismos de pérdida energética del ión. En el presente trabajo se establece una primera aproximación a este análisis, mostrando que la  (3) puede ser integrada como según la Ec. (2) por medios analíticos, sin recurrir al cálculo numérico. Estas justificaciones pretenden dar relevancia a los resultados de métodos numéricos aplicados a distintos materiales, particularmente a aquellos incluidos en los trabajos de Emfietzoglou y Dingfelder.
(3) puede ser integrada como según la Ec. (2) por medios analíticos, sin recurrir al cálculo numérico. Estas justificaciones pretenden dar relevancia a los resultados de métodos numéricos aplicados a distintos materiales, particularmente a aquellos incluidos en los trabajos de Emfietzoglou y Dingfelder.
II. MÉTODOS Y TEORÍA
Método analítico propuesto para la integración
El método analítico que se propone consiste principalmente en la utilización del análisis complejo, como sigue:
Las integrales de la fórmula (2) pueden extenderse al plano complejo utilizando alguna curva adecuada  de la forma:
de la forma:
Debe chequearse que las integrales extendidas convergen a la integral impropia original sobre el eje real de frecuencias. Para ello se utiliza la siguiente propiedad:18 si existe un número real  tal que
tal que  , entonces:
, entonces:
donde  es la longitud de la curva.
es la longitud de la curva.
Finalmente, una vez verificada la convergencia, puede aplicarse el teorema de los residuos a las integrales extendidas, utilizando los polos correspondientes según la  :18
:18
Modelos de respuesta dieléctrica
Un ejercicio didáctico consiste en estudiar el modelo de Debye.19 El mismo se caracteriza por una función de respuesta dieléctrica que supone al material conformado por dipolos no interactuantes en presencia de un campo externo alternante (en este caso el del ión). Normalizando a la permitividad dieléctrica del vacío, el modelo resulta:
donde  ,
,  es la permitividad estática (en el límite de baja frecuencia),
es la permitividad estática (en el límite de baja frecuencia),  es la permitividad de alta frecuencia y
es la permitividad de alta frecuencia y  el tiempo de relajación característico del material.
el tiempo de relajación característico del material.
Por otro lado, se utilizará el modelo de Drude.20 Este modelo basado en la mecánica clásica, considera los electrones ligados con una fuerza armónica amortiguada, sobre los cuales actúa además un campo eléctrico. Si se normaliza a la permitividad de vacío, este modelo asume la siguiente forma:
donde  es la frecuencia de plasmón,
es la frecuencia de plasmón,  la intensidad de los osciladores,
la intensidad de los osciladores,  las frecuencias características de oscilación y
las frecuencias características de oscilación y  las constantes de amortiguamiento. La energía de plasmón del agua líquida es
las constantes de amortiguamiento. La energía de plasmón del agua líquida es 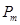 eV. Este modelo propone describir los electrones como osciladores armónicos ligados al núcleo, y es por tanto adecuado para realizar un tratamiento de datos fenomenológicos de excitación. Sin embargo, estos parámetros que provienen de la mecánica cuántica pueden ser directamente determinados por medios teóricos. Típicamente, el modelo de Drude es utilizado para calcular el aporte de los niveles de ionización en vez de las excitaciones discretas, porque para éstos últimos se utiliza la función de Drude derivada,14,15 que es más pronunciada en su máximo alrededor de
eV. Este modelo propone describir los electrones como osciladores armónicos ligados al núcleo, y es por tanto adecuado para realizar un tratamiento de datos fenomenológicos de excitación. Sin embargo, estos parámetros que provienen de la mecánica cuántica pueden ser directamente determinados por medios teóricos. Típicamente, el modelo de Drude es utilizado para calcular el aporte de los niveles de ionización en vez de las excitaciones discretas, porque para éstos últimos se utiliza la función de Drude derivada,14,15 que es más pronunciada en su máximo alrededor de  , y por lo tanto “más discreta”, presentando además un decaimiento asintótico del orden
, y por lo tanto “más discreta”, presentando además un decaimiento asintótico del orden  para altas frecuencias. Sin embargo, como el comportamiento a altas frecuencias de las funciones de Drude estándar es suficiente para que las integrales sean convergentes, y dado que el modelo de Drude está diseñado a partir de considerar electrones ligados armónicamente, el presente trabajo implementará dicho modelo junto con parámetros ajustados a partir de estimaciones experimentales de las secciones eficaces de interacción inelásticas IXS (a partir de las siglas en inglés inelastic cross section).15 Nuevamente, cabe señalar, que estos parámetros pueden ser obtenidos de forma teórica, pero con el objetivo de probar el modelo propuesto, utilizar parámetros ajustados es suficiente.
para altas frecuencias. Sin embargo, como el comportamiento a altas frecuencias de las funciones de Drude estándar es suficiente para que las integrales sean convergentes, y dado que el modelo de Drude está diseñado a partir de considerar electrones ligados armónicamente, el presente trabajo implementará dicho modelo junto con parámetros ajustados a partir de estimaciones experimentales de las secciones eficaces de interacción inelásticas IXS (a partir de las siglas en inglés inelastic cross section).15 Nuevamente, cabe señalar, que estos parámetros pueden ser obtenidos de forma teórica, pero con el objetivo de probar el modelo propuesto, utilizar parámetros ajustados es suficiente.
 -ésimo estado excitado de Drude
-ésimo estado excitado de Drude
Para generalizar el procedimiento basado en el modelo de Drude al tratar en simultáneo  niveles de excitación, la
niveles de excitación, la  toma la siguiente forma:
toma la siguiente forma:
donde  es un polinomio de grado
es un polinomio de grado  . Además,
. Además,  es un polinomio mónico y consecuentemente:
es un polinomio mónico y consecuentemente:
donde  y
y  son los coeficientes del polinomio del numerador y del denominador respectivamente. Una extensión al plano complejo junto a la desigualdad triangular en el caso
son los coeficientes del polinomio del numerador y del denominador respectivamente. Una extensión al plano complejo junto a la desigualdad triangular en el caso  permiten acotar:
permiten acotar:
Con todas las propiedades enumeradas puede comprobarse que las integrales de la expresión (2) convergen para el modelo de Drude. Particularmente, el denominador de la Ec. (2) puede extenderse utilizando un lazo que es el semicírculo superior de radio  con el segmento de línea sobre el eje real entre
con el segmento de línea sobre el eje real entre  y
y  (ver Fig. 2b) como sigue:
(ver Fig. 2b) como sigue:
Utilizando las fórmulas (4), (9) y (10), junto con  ,
,  , y
, y  , el segundo término satisface:
, el segundo término satisface:
lo cual se acerca a cero si  tiende a infinito, demostrando la convergencia de la integral de línea hacia la integral impropia.
tiende a infinito, demostrando la convergencia de la integral de línea hacia la integral impropia.
Observando el numerador de la expresión (2), se observa que si la integral se lleva a cabo en frecuencias reales, no hay posibilidad de extender los límites independientemente de la paridad de la  . Esto sucede porque el logaritmo natural, incluso extendido al plano complejo, no tiene paridad ni expansión en serie de Laurent.18 La integral de la fórmula (2) contiene un factor
. Esto sucede porque el logaritmo natural, incluso extendido al plano complejo, no tiene paridad ni expansión en serie de Laurent.18 La integral de la fórmula (2) contiene un factor  de forma que
de forma que  , con lo cual la integral puede realizarse utilizando un contorno que eluda la rama no definida
, con lo cual la integral puede realizarse utilizando un contorno que eluda la rama no definida  , como el que se observa en la Fig. 1. Es apropiado mencionar que para llevar a cabo este cálculo, es necesario utilizar
, como el que se observa en la Fig. 1. Es apropiado mencionar que para llevar a cabo este cálculo, es necesario utilizar 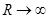 (en vez de sólo
(en vez de sólo  ) para obtener la correcta extensión al plano complejo:
) para obtener la correcta extensión al plano complejo:
Para probar la validez de esta expresión, conviene separar la integral sobre el contorno  de la Fig. 1 en los siguientes términos:
de la Fig. 1 en los siguientes términos:
para luego evaluarlos separadamente.
Tramo  : en el círculo
: en el círculo  ,
,  en donde
en donde  . De esta forma, utilizando las Ecs. (4), (9) y (10) se obtiene:
. De esta forma, utilizando las Ecs. (4), (9) y (10) se obtiene:
y en el límite  converge a cero.
converge a cero.
Tramo  : aquí
: aquí  y como
y como  , se pueden usar las Ecs. (4), (10) y (11):
, se pueden usar las Ecs. (4), (10) y (11):
que claramente tiende a cero si  .
.
Tramo  : en este segmento de línea,
: en este segmento de línea, 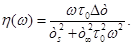 , con
, con  variando entre
variando entre  y
y  . Entonces, si
. Entonces, si 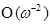 tiende a cero,
tiende a cero,  se aproxima a
se aproxima a  desde el semiplano superior. Más aún, el símbolo de límite
desde el semiplano superior. Más aún, el símbolo de límite 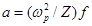 puede insertarse bajo el símbolo de integral debido al teorema de convergencia dominada de Lebesgue,21 obteniendo:
puede insertarse bajo el símbolo de integral debido al teorema de convergencia dominada de Lebesgue,21 obteniendo:
Tramo  : en este caso
: en este caso  , con
, con  entre
entre  y
y  . Entonces, si
. Entonces, si  se aproxima a cero,
se aproxima a cero,  tiende a
tiende a  desde el semiplano inferior. Aplicando los mismos argumentos que en el segmento
desde el semiplano inferior. Aplicando los mismos argumentos que en el segmento  anterior, se obtiene:
anterior, se obtiene:
Finalmente, la adición de los cuatro términos en sus correspondientes límites, las integrales en 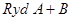 y
y  son nulas, y los términos (13) y (14) suman al término con
son nulas, y los términos (13) y (14) suman al término con  , obteniéndose la expresión (12).
, obteniéndose la expresión (12).
III. RESULTADOS
Modelo de Debye
La  para el modelo de relajación de Debye puede calcularse a partir de la fórmula (6) utilizando la Ec. (3):
para el modelo de relajación de Debye puede calcularse a partir de la fórmula (6) utilizando la Ec. (3):
La tendencia de los integrandos, teniendo en cuenta el comportamiento de la  para altas frecuencias (
para altas frecuencias ( ), implica que existirá una divergencia tanto para numerador como para denominador de la expresión (2) y consecuentemente, dichas integrales no pueden calcularse. Esto debe chequearse, para lo cual se puede extender las integrales al plano complejo utilizando una curva compuesta por un semicírculo de radio
), implica que existirá una divergencia tanto para numerador como para denominador de la expresión (2) y consecuentemente, dichas integrales no pueden calcularse. Esto debe chequearse, para lo cual se puede extender las integrales al plano complejo utilizando una curva compuesta por un semicírculo de radio 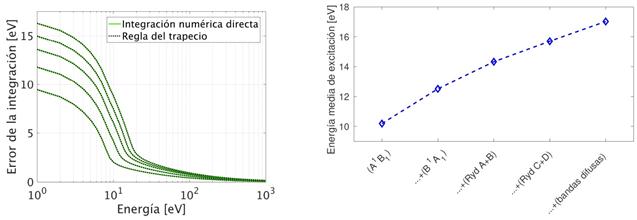 en el plano superior y el segmento de línea recta sobre el eje real entre
en el plano superior y el segmento de línea recta sobre el eje real entre  y
y 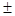 (ver Fig 2b), siendo que
(ver Fig 2b), siendo que  . La divergencia surge sobre el semicírculo, dado que allí
. La divergencia surge sobre el semicírculo, dado que allí 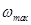 con
con  , y utilizando la relación (4) se satisface:
, y utilizando la relación (4) se satisface:
Evaluando el límite  se observa la no convergencia. Más aún, el integrando debería decaer al menos como
se observa la no convergencia. Más aún, el integrando debería decaer al menos como 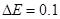 para altas frecuencias, para que la
para altas frecuencias, para que la  presente un comportamiento asintótico
presente un comportamiento asintótico 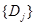 como condición débil para que el modelo propuesto funcione y las integrales puedan converger.
como condición débil para que el modelo propuesto funcione y las integrales puedan converger.
La primera aproximación consiste en evaluar la  a partir de la fórmula (7), y luego utilizar la Ec. (3), obteniéndose:
a partir de la fórmula (7), y luego utilizar la Ec. (3), obteniéndose:
donde 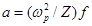 ,
,  y
y  . Esto preserva la forma de la fórmula (8). Utilizando los parámetros IXS para el primer estado excitado de la molécula de agua líquida,15 el nivel
. Esto preserva la forma de la fórmula (8). Utilizando los parámetros IXS para el primer estado excitado de la molécula de agua líquida,15 el nivel  , las raíces del denominador para esta
, las raíces del denominador para esta  (que son polos en el plano complejo) están dados por:
(que son polos en el plano complejo) están dados por:
donde el índice  toma en cuenta las diferentes combinaciones de signos. Utilizando los mismos parámetros IXS para el nivel
toma en cuenta las diferentes combinaciones de signos. Utilizando los mismos parámetros IXS para el nivel  dichos polos son calculados como
dichos polos son calculados como  eV y reportados en la Fig. 2b. Los cuatro dígitos elegidos como significativos se deben a la comparación realizada con el procedimiento de integración numérica. Dos polos se encuentran en el interior del semicírculo en el plano superior, y por lo tanto la integración del denominador de la Ec. (2) puede realizarse con el teorema de los residuos (fórmula (10)) tomando en cuenta sólo los polos del plano superior (ver Fig. 2b).
eV y reportados en la Fig. 2b. Los cuatro dígitos elegidos como significativos se deben a la comparación realizada con el procedimiento de integración numérica. Dos polos se encuentran en el interior del semicírculo en el plano superior, y por lo tanto la integración del denominador de la Ec. (2) puede realizarse con el teorema de los residuos (fórmula (10)) tomando en cuenta sólo los polos del plano superior (ver Fig. 2b).
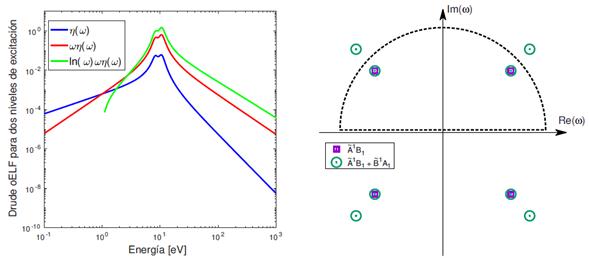
FIG. 2: (a) oELF para el modelo de Drude utilizando dos niveles en simultáneo para el agua líquida: ˜A1B1 y ˜B1A1. (b) Polos de la oELF en el plano complejo para uno (cuadrados) y dos niveles en simultáneo (círculos). Semicírculo en el plano superior, para extender las integrales de la fórmula (2).
Por otro lado, el lazo con forma de cerradura de la Fig. 1 utilizada para el denominador en la Ec. (2) encierra los cuatro polos, lo cual implica la evaluación de dos términos más. Utilizando las fórmulas (5) y (12), la contribución del nivel de excitación  al valor de
al valor de  puede calcularse analíticamente, obteniéndose:
puede calcularse analíticamente, obteniéndose:

Como se esperaba, estimar  considerando sólo el primer nivel de excitación resulta en un valor lejano al típicamente aceptado en la literatura.14,15,22-26 Descripciones teóricas más precisas en términos de las
considerando sólo el primer nivel de excitación resulta en un valor lejano al típicamente aceptado en la literatura.14,15,22-26 Descripciones teóricas más precisas en términos de las  requieren no sólo de la evaluación de varios estados excitados, sino también ionizaciones y un tratamiento exhaustivo del estado fundamental. Dichas evaluaciones podrían llevarse a cabo utilizando el mismo esquema analítico aquí presentado.
requieren no sólo de la evaluación de varios estados excitados, sino también ionizaciones y un tratamiento exhaustivo del estado fundamental. Dichas evaluaciones podrían llevarse a cabo utilizando el mismo esquema analítico aquí presentado.
Modelo de Drude para los niveles 
La forma funcional de las  al considerar dos niveles en simultáneo, particularmente pensando en las expresiones asociadas a los coeficientes de los polinomios, no es tan simple como para un solo nivel. La Fig. 2a reporta la función de Drude para dos niveles en simultáneo, utilizando los datos IXS para los niveles discretos
al considerar dos niveles en simultáneo, particularmente pensando en las expresiones asociadas a los coeficientes de los polinomios, no es tan simple como para un solo nivel. La Fig. 2a reporta la función de Drude para dos niveles en simultáneo, utilizando los datos IXS para los niveles discretos  y
y  . Si se requiere de más niveles con parámetros IXS relevantes (
. Si se requiere de más niveles con parámetros IXS relevantes (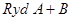 ,
,  y las bandas difusas), pueden agregarse cuidadosamente, pero debe remarcarse que considerar dos niveles de excitación producen una
y las bandas difusas), pueden agregarse cuidadosamente, pero debe remarcarse que considerar dos niveles de excitación producen una  de por sí complicada (fórmula (15)), por lo cual el uso de programas de manipulación algebraica se torna indispensable. Para dos niveles, la
de por sí complicada (fórmula (15)), por lo cual el uso de programas de manipulación algebraica se torna indispensable. Para dos niveles, la  queda:
queda:
donde:
Este resultado preserva nuevamente la forma de la Ec. (8), pero en este caso el denominador presenta ocho polos, mostrados en la Fig. 2b. Es interesante notar que los primeros cuatro corresponden al primer estado de excitación (5), y los otros cuatro evaluando los parámetros IXS son  eV, con
eV, con  . Aplicando el mismo formalismo que para un solo nivel, la contribución simultánea de los dos primeros niveles a la energía media de excitación es:
. Aplicando el mismo formalismo que para un solo nivel, la contribución simultánea de los dos primeros niveles a la energía media de excitación es:
Como se esperaba, existe un incremento en su valor numérico, pero no es substancial. Todos los niveles discretos y continuos deberían ser tenidos en cuenta para obtener  con la magnitud esperada. Incluso se necesita una alta precisión para modelar la capa K. De todas maneras, el cálculo para dos niveles es útil y didáctico para señalar las pautas del método propuesto para obtener
con la magnitud esperada. Incluso se necesita una alta precisión para modelar la capa K. De todas maneras, el cálculo para dos niveles es útil y didáctico para señalar las pautas del método propuesto para obtener  de forma analítica. A esto se suman las determinaciones numéricas de
de forma analítica. A esto se suman las determinaciones numéricas de  presentadas en la siguiente sección, donde se obtienen resultados similares para dos modelos de integración numérica diferentes, y en comparación con los valores teóricos mostrados en esta sección.
presentadas en la siguiente sección, donde se obtienen resultados similares para dos modelos de integración numérica diferentes, y en comparación con los valores teóricos mostrados en esta sección.
Contribución de todos los niveles de excitación
La aplicación directa del modelo propuesto adicionando uno a uno todos los niveles de los cuales se poseen parámetros IXS, permite las estimaciones analíticas del potencial medio de excitación mostradas en la primer columna de la Tabla 1. Para dicha evaluación, se utilizó la Ec. (5) repetidamente mientras se adhieren niveles de excitación, y se calculan los correspondientes polos de la  . En el gráfico de la derecha en la Fig. 3 puede apreciarse la evolución del valor de
. En el gráfico de la derecha en la Fig. 3 puede apreciarse la evolución del valor de  a medida que se agregan niveles.
a medida que se agregan niveles.

FIG. 3: Izquierda: correspondiente valor de la desviación respecto del valor analítico de para los cálculos numéricos, mostrando convergencia para la adición de cada nivel de excitación. Derecha: evolución del valor de
para los cálculos numéricos, mostrando convergencia para la adición de cada nivel de excitación. Derecha: evolución del valor de a medida que se agregan las contribuciones de los distintos niveles.
a medida que se agregan las contribuciones de los distintos niveles.

FIG. 4: Integración numérica para estimar el valor de , mostrando convergencia para todos los niveles de excitación utilizados, por el método directo y la regla del trapecio.
, mostrando convergencia para todos los niveles de excitación utilizados, por el método directo y la regla del trapecio.

TABLA 1: Evolución de la energía media de excitación a medida que se agregan niveles de excitación a la  , estimadas teóricamente y confirmadas por integración numérica con límite de 1 MeV y dos métodos diferentes (el
, estimadas teóricamente y confirmadas por integración numérica con límite de 1 MeV y dos métodos diferentes (el 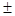 indica desviación respecto del valor teórico, y no incerteza).
indica desviación respecto del valor teórico, y no incerteza).
Para poder corroborar estos cálculos analíticos, se realizaron integrales numéricas de la  , eligiendo un límite de integración
, eligiendo un límite de integración 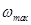 en la Ec. (2). Como se observa en la Fig. 4, estas integrales numéricas convergen exactamente al valor teórico calculado a través del teorema de los residuos. Para ello se utilizaron dos métodos de integración, una llamada integración directa, que consiste en la suma simple de la función evaluada en cada paso del intervalo de integración; y la típica regla del trapecio.27 Estos métodos presentan velocidades de convergencia diferentes, pero cuanto mayor el límite de integración
en la Ec. (2). Como se observa en la Fig. 4, estas integrales numéricas convergen exactamente al valor teórico calculado a través del teorema de los residuos. Para ello se utilizaron dos métodos de integración, una llamada integración directa, que consiste en la suma simple de la función evaluada en cada paso del intervalo de integración; y la típica regla del trapecio.27 Estos métodos presentan velocidades de convergencia diferentes, pero cuanto mayor el límite de integración  , más rápido convergen las desviaciones, como se reporta en el gráfico de la izquierda de la Fig. 4. Estas desviaciones se calculan utilizando el valor teórico exacto (conocido):
, más rápido convergen las desviaciones, como se reporta en el gráfico de la izquierda de la Fig. 4. Estas desviaciones se calculan utilizando el valor teórico exacto (conocido):  . El límite de la integración (
. El límite de la integración (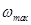 ) fue elegido
) fue elegido  MeV, lo cual está lejos de los rangos típicos de energía óptica, y el paso para la integración fue elegido como
MeV, lo cual está lejos de los rangos típicos de energía óptica, y el paso para la integración fue elegido como 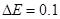 eV. Los valores de
eV. Los valores de  estimados numéricamente para los cinco niveles utilizados en este trabajo muestran convergencia al valor analítico para ambos métodos de integración, como se reporta en la Tabla 1 y en la Fig. 4.
estimados numéricamente para los cinco niveles utilizados en este trabajo muestran convergencia al valor analítico para ambos métodos de integración, como se reporta en la Tabla 1 y en la Fig. 4.
El comportamiento de la desviación del valor de  respecto del valor exacto para todos los niveles fue calculado a medida que se avanza en la integración, y la tendencia del valor de
respecto del valor exacto para todos los niveles fue calculado a medida que se avanza en la integración, y la tendencia del valor de  de formar una meseta a medida que se agregan niveles, como se muestra gráficamente, evidencia que la contribución de las bandas difusas, tratadas separadamente, debería volverse despreciable. Ambos resultados se encuentran reportados en la Fig. 4.
de formar una meseta a medida que se agregan niveles, como se muestra gráficamente, evidencia que la contribución de las bandas difusas, tratadas separadamente, debería volverse despreciable. Ambos resultados se encuentran reportados en la Fig. 4.
IV. CONCLUSIONES
Se presentó en este trabajo, un marco referencial original para el cálculo de la contribución de los niveles de excitación a la energía media de excitación  de los materiales. Éste requiere únicamente de parámetros que bien pueden calcularse teóricamente utilizando la mecánica cuántica u obtenerse por medio del ajuste de datos de sección eficaz inelástica experimentales. El cálculo fue satisfactoriamente llevado a cabo para los primeros cuatro niveles de excitación y las bandas difusas de la molécula de agua líquida, y contrastados con estimaciones numéricas que confirman los resultados. Este procedimiento podría repetirse utilizando las funciones de Drude con datos asociados a los niveles de ionización, preservando los datos de excitación para la llamada función de Drude derivada que es más pronunciada (“más discreta”). Esta función presenta un comportamiento asintótico de
de los materiales. Éste requiere únicamente de parámetros que bien pueden calcularse teóricamente utilizando la mecánica cuántica u obtenerse por medio del ajuste de datos de sección eficaz inelástica experimentales. El cálculo fue satisfactoriamente llevado a cabo para los primeros cuatro niveles de excitación y las bandas difusas de la molécula de agua líquida, y contrastados con estimaciones numéricas que confirman los resultados. Este procedimiento podría repetirse utilizando las funciones de Drude con datos asociados a los niveles de ionización, preservando los datos de excitación para la llamada función de Drude derivada que es más pronunciada (“más discreta”). Esta función presenta un comportamiento asintótico de 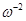 para altas frecuencias, y por esta razón la
para altas frecuencias, y por esta razón la  asociada decaerá como
asociada decaerá como  , lo cual es típicamente utilizado en la literatura. Es consecuentemente posible realizar todas las integrales involucradas. Tareas futuras incluyen encontrar algún patrón en los polos de la
, lo cual es típicamente utilizado en la literatura. Es consecuentemente posible realizar todas las integrales involucradas. Tareas futuras incluyen encontrar algún patrón en los polos de la  en términos de los coeficientes de los polinomios
en términos de los coeficientes de los polinomios  y
y 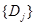 (y consecuentemente los parámetros del modelo) que permita llegar a conclusiones más profundas sobre este procedimiento. Sin embargo, debe remarcarse que contar con un procedimiento analítico para calcular la energía media de excitación utilizando información específica sobre cada nivel, sustentaría fuertemente el trabajo numérico realizado por Dingfelder, Emfietzoglou y colaboradores al resolver el problema de Bethe.
(y consecuentemente los parámetros del modelo) que permita llegar a conclusiones más profundas sobre este procedimiento. Sin embargo, debe remarcarse que contar con un procedimiento analítico para calcular la energía media de excitación utilizando información específica sobre cada nivel, sustentaría fuertemente el trabajo numérico realizado por Dingfelder, Emfietzoglou y colaboradores al resolver el problema de Bethe.