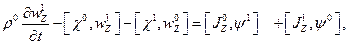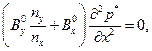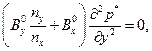I. INTRODUCCIÓN
La interacción entre cuerpos conductores y plasmas magnetizados en movimiento relativo tiene lugar en una variedad de escenarios en los plasmas espaciales, situaciones en las que se generan alas de Alfvén, como en sistemas constituídos por satélites artificiales moviéndose en la ionosfera1,2, las lunas jovianas3 y asteroides como Ida y Gaspra4.
La influencia de los términos de Hall y de gradiente de presión electrónica en la ley de Ohm, tanto en la propagación de ondas de Alfvén como en la formación de las alas ha sido estudiado por Sallago y Platzeck en 20045, en adelante SP04, donde mostraron que en HMHD pueden propagarse ondas de de Alfvén de gran amplitud si la densidad de corriente satisface una ”condición de polarización” y pueden construirse alas para plasmas de fondo uniformes. En este caso, una cantidad llamada presión generalizada P∗ se mantiene constante dentro del ala y, para que se satisfagan las condiciones de contorno en el borde del ala, aparece una densidad de corriente en su superficie.
Por otra parte, el estudio de la estabilidad de ondas de Alfvén de gran amplitud ha sido abordado tanto desde el punto de vista teórico como experimental, tanto para plasmas MHD como para plasmas dispersivos6,7, permaneciendo bajo estudio durante mucho tiempo. Sallago y Platzeck8, en adelante SP07, mostraron la estabilidad de las alas de Alfvén en MHD para plasmas uniformes, frente a perturbaciones incompresibles que tengan la misma simetría que el ala, como una extensión del método desarrollado por Palumbo (1998)9 para estructuras estáticas.
Debe tenerse presente que el ala es una región cilíndrica, la forma de la sección transversal depende de la forma de la fuente. El borde de la sección transversal del ala nunca es la proyección de una línea de campo de inducción magnética y no es posible tener una proyección cerrada de una línea de campo magnético en la sección trasversal del ala. Estas son las mismas condiciones que se consideran en SP078.
En la Sec. II se presenta una breve descripción del método extendido para el estudio de la estabilidad de las alas de Alfvén en MHD contenido en SP078. El mismo es extendido para alas de Alfvén en HMHD en la Sec. III. De la misma manera que sucedía en el caso de alas en MHD, el espacio puede dividirse en dos regiones relativas al ala, en la Sec. IV se analizan las soluciones en las regiones exterior e interior al ala en HMHD. La solución en la región exterior es trivial y, utilizando las mismas herramientas que en el caso MHD, se utiliza el método de las características para resolver las ecuaciones en la región interior. Finalmente, se muestra la estabilidad lineal de las alas de Alfvén en HMHD en presencia de perturbaciones incompresibles simétricas.
II. MÉTODO
Para estudiar este problema de la estabilidad de las alas de Alfvén en HMHD, primero se describe brevemente el método aplicado para el estudio de la estabilidad de las mismas en MHD.
En un sistema de coordenadas cartesiano (𝑥,𝑦,𝑧), cuando las cantidades son independientes de una variable (𝑧), se pueden definir funciones corriente para todas las magnitudes de divergencia nula: el flujo de masa 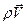 , el campo de inducción magnética
, el campo de inducción magnética  , la vorticidad
, la vorticidad  y la densidad de corriente
y la densidad de corriente 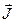 . De este modo los campos pueden escribirse:
. De este modo los campos pueden escribirse:
donde  ,
,  ,
, 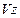 y
y 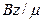 son funciones corriente.
son funciones corriente.
Partiendo de las ecuaciones de la MHD, usando las funciones corriente, se obtiene un sistema de ecuaciones entre jacobianos de las distintas magnitudes físicas10-12. El método comienza considerando un estado de equilibrio inicial para la estructura bajo estudio y una perturbación incompresible de pequeña amplitud con la misma simetría que la estructura. Se elige una perturbación incompresible porque ésta tiene disponible toda su energía para inestabilizar a la estructura13. Se linealiza el sistema de ecuaciones y las cantidades físicas se identifican con los super-índices ”0” y ”1” relativo al estado de equilibrio y a la pequeña perturbación respectivamente. Solamente se toman en consideración casos en que la densidad del plasma es uniforme, por lo tanto, de la ecuación de continuidad se tiene que la perturbación en densidad es nula. Para el problema del estudio de la estabilidad de las alas de Alfvén en MHD el sistema de ecuaciones resulta:
Como el espacio puede dividirse en dos regiones relativas al ala, se analizan las soluciones en las regiones exterior e interior al ala. Tomando como dirección invariante al eje del ala, identificando a los valores en el interior del ala con super-índice “0” se tendrá14:
Notar que los campos de fondo son uniformes y las alas de Alfvén están formadas por ondas de Alfvén de corte que son perturbaciones incompresibles (ver Ec. (9)).
En el caso MHD se definen dos funciones auxiliares  y
y  ,
,
de modo que el sistema de ecuaciones (5-8), luego de un poco de álgebra resultan:
En la región exterior al ala se tiene  ,
,  ,
,  , y
, y  , todas cantidades uniformes y las funciones corriente correspondientes a la región exterior son
, todas cantidades uniformes y las funciones corriente correspondientes a la región exterior son 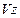 y
y 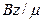 . En la región interior las magnitudes están dadas por las Ecs. (9)-(12). El sistema de ecuaciones debe satisfacerse en todas partes. Supongamos que la dependencia temporal de la perturbación incompresible es del tipo
. En la región interior las magnitudes están dadas por las Ecs. (9)-(12). El sistema de ecuaciones debe satisfacerse en todas partes. Supongamos que la dependencia temporal de la perturbación incompresible es del tipo  .
.
En la región exterior, debido a los valores de los campos no perturbados, las Ecs. (15) y (16) toman la forma de una ecuación diferencial de primer orden con solución del tipo:
donde 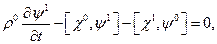 es una constante. Como para distancias lejanas al ala la perturbación debe estar acotada, las únicas pertubaciones con frecuencias imaginarias (
es una constante. Como para distancias lejanas al ala la perturbación debe estar acotada, las únicas pertubaciones con frecuencias imaginarias (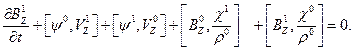 =
=  ) son las de amplitud nula. Por lo tanto
) son las de amplitud nula. Por lo tanto  y
y 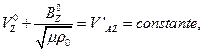 son nulas y en consecuencia lo es
son nulas y en consecuencia lo es 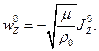 . Teniendo en cuenta que
. Teniendo en cuenta que  ,
, 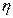 y
y  son continuos en el borde del ala
son continuos en el borde del ala 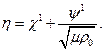 , ya que los elementos del plasma pasan a través de dicho borde, puede mostrarse usando la primer identidad de Green que
, ya que los elementos del plasma pasan a través de dicho borde, puede mostrarse usando la primer identidad de Green que  ,
,  ,
,  y
y 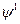 son nulas en la región exterior.
son nulas en la región exterior.
En la región interior se utilizó el método de las características para mostrar que las perturbaciones también son nulas. En este caso se tomó una perturbación lineal de frecuencia imaginaria de la forma 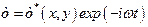 .
.
Teniendo en cuenta que  es continua en el borde del ala, puede escribirse una ecuación diferencial para
es continua en el borde del ala, puede escribirse una ecuación diferencial para 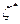 en la región interior que puede resolverse por el método de las características:
en la región interior que puede resolverse por el método de las características:
donde la ecuación de las líneas características es
por lo que las líneas características son la proyección de las líneas del campo de inducción magnética sobre la sección transversal del ala. Integrando la Ec. (18) pueden obtenerse los valores de 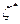 sobre cada curva característica en función de sus valores en el borde del ala y en consecuencia, resulta que
sobre cada curva característica en función de sus valores en el borde del ala y en consecuencia, resulta que  es nulo también en la región interior. Para mostrar que lo mismo sucede con
es nulo también en la región interior. Para mostrar que lo mismo sucede con 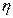 se recurrió a un método utilizado por Sommerfeld (1949)15 para la resolución de ecuaciones diferenciales de segundo orden. Este muestra que a partir de los valores de la variable dependiente y su derivada normal en una curva dada
se recurrió a un método utilizado por Sommerfeld (1949)15 para la resolución de ecuaciones diferenciales de segundo orden. Este muestra que a partir de los valores de la variable dependiente y su derivada normal en una curva dada 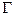 ( que no sea una curva característica) es posible obtener todas sus derivadas parciales sobre la misma y, por lo tanto, construir la solución en la región circundante a la curva expandiendo la variable dependiente en serie de Taylor. Como las curvas características son proyecciones de las líneas de campo de inducción magnética sobre la sección transversal del ala y como no es posible tener proyecciones cerradas de líneas de campo de inducción magnética en la región interior, uno puede adentrarse en el ala siguiendo el mismo procedimiento. De esta manera se mostró en SP07 que la única solución posible para una perturbación lineal que tiene frecuencia imaginaria es la de amplitud nula y en consecuencia el ala de Alfvén en MHD resulta estable frente a perturbaciones incompresibles simétricas.
( que no sea una curva característica) es posible obtener todas sus derivadas parciales sobre la misma y, por lo tanto, construir la solución en la región circundante a la curva expandiendo la variable dependiente en serie de Taylor. Como las curvas características son proyecciones de las líneas de campo de inducción magnética sobre la sección transversal del ala y como no es posible tener proyecciones cerradas de líneas de campo de inducción magnética en la región interior, uno puede adentrarse en el ala siguiendo el mismo procedimiento. De esta manera se mostró en SP07 que la única solución posible para una perturbación lineal que tiene frecuencia imaginaria es la de amplitud nula y en consecuencia el ala de Alfvén en MHD resulta estable frente a perturbaciones incompresibles simétricas.
III. CASO HMHD
Para algunos plasmas totalmente ionizados es más representativa la ley de Ohm generalizada (ver Ref.13):
donde  es el término de Hall y
es el término de Hall y 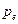 la presión electrónica. El término de Hall es de importancia cuando la densidad es baja y el campo de inducción magnética es intenso y expresa la condición de que los electrones pueden moverse en espiral libremente antes de colisionar. Al considerar los términos de Hall y de gradiente de presión electrónica de la ley de Ohm solamente se modifica la ecuación de inducción del conjunto de ecuaciones que gobierna al plasma.
la presión electrónica. El término de Hall es de importancia cuando la densidad es baja y el campo de inducción magnética es intenso y expresa la condición de que los electrones pueden moverse en espiral libremente antes de colisionar. Al considerar los términos de Hall y de gradiente de presión electrónica de la ley de Ohm solamente se modifica la ecuación de inducción del conjunto de ecuaciones que gobierna al plasma.
Supongamos que en estas condiciones se mueve en el plasma un cuerpo conductor que, entre otras perturbaciones, genera ondas de Alfvén en HMHD que construyen alas de Alfvén en forma similar al caso MHD. En el caso con término de Hall también puede tomarse como coordenada ignorable a la dirección de la velocidad de grupo que en este caso es
donde el valor de  resulta de resolver la siguiente ecuación
resulta de resolver la siguiente ecuación
donde  es la masa del protón y
es la masa del protón y  es una cantidad inversamente proporcional al tamaño de la fuente ( a menor tamaño de la fuente mayor es la importancia relativa del término de Hall). El valor de
es una cantidad inversamente proporcional al tamaño de la fuente ( a menor tamaño de la fuente mayor es la importancia relativa del término de Hall). El valor de 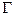 también es el factor de proporcionalidad entre la densidad de corriente debida a las perturbaciones de Alfvén y su rotor.
también es el factor de proporcionalidad entre la densidad de corriente debida a las perturbaciones de Alfvén y su rotor.
Siguiendo los pasos anteriores, se puede reescribir el sistema de ecuaciones de la HMHD utilizando funciones corriente para que los campos presenten divergencia nula (ver SP04). De esta manera se obtuvo los siguientes valores para el interior del ala de Alfvén con término de Hall:
La siguiente expresión es cierta solamente para las ondas de Alfvén, pero si la cantidad se escribe dentro del jacobiano, se puede hacer un abuso de notación y decir que
Con la intención de evaluar la estabilidad de las alas de Alfvén en HMHD se la testea mediante una perturbación incompresible con la misma simetría y polarización que las ondas de Alfvén que componen a la estructura. Como las ondas de Alfvén en HMHD son perturbaciones incompresibles, y la perturbación es incompresible, de la ecuación de continuidad se tiene nuevamente que no hay perturbación en densidad. El sistema de ecuaciones de la HMHD escrito con las funciones corriente toma el siguiente aspecto
A continuación se definen las funciones auxiliares  ,
, 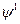 y
y 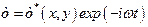 , tal que
, tal que
Luego de reemplazar (22)-(27) y (32)-(34) en las Ecs. (28)-(31) se tiene
Luego de un poco de álgebra, considerando la misma polarización para la perturbación, pueden escribirse las siguientes ecuaciones diferenciales:
IV. ANALISIS DE LA ESTABILIDAD DEL ALA
Se divide el espacio en las regiones interior y exterior al ala: en la región exterior las magnitudes de interés 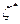 ,
,  ,
,  y
y 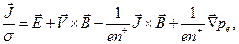 son uniformes y en consecuencia las funciones corriente son
son uniformes y en consecuencia las funciones corriente son  =
= 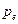 y
y  =
=  ; mientras que en la región interior los valores de las magnitudes corresponden a los dados por (22)-(27). Nuevamente, el sistema de ecuaciones debe satisfacerse en todas partes y la dependencia temporal para la perturbación incompresible se toma del tipo
; mientras que en la región interior los valores de las magnitudes corresponden a los dados por (22)-(27). Nuevamente, el sistema de ecuaciones debe satisfacerse en todas partes y la dependencia temporal para la perturbación incompresible se toma del tipo 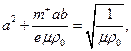 .
.
Región exterior
En la región exterior las ecuaciones toman el siguiente aspecto:
La Ec. (42) es una ecuación diferencial parcial de primer orden, para la misma se propone la solución
Como 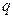 debe tomar un valor acotado para
debe tomar un valor acotado para 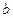 , la frecuencia debe tomar valores reales. En el caso en que la frecuencia tome valores imaginarios,
, la frecuencia debe tomar valores reales. En el caso en que la frecuencia tome valores imaginarios,  por ejemplo, entonces
por ejemplo, entonces  debe ser nulo en la región exterior. Teniendo en consideración este resultado puede verse fácilmente de (43) y (44) que lo mismo sucede con
debe ser nulo en la región exterior. Teniendo en consideración este resultado puede verse fácilmente de (43) y (44) que lo mismo sucede con  ,
,  y con
y con 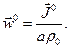 (ver (34)). Como
(ver (34)). Como 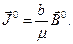 es nulo, de (35) resulta que
es nulo, de (35) resulta que 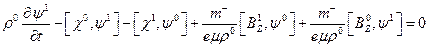 es nulo y por lo tanto lo es
es nulo y por lo tanto lo es 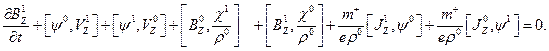 . Para encontrar el valor de
. Para encontrar el valor de  en la región exterior debe tenerse en cuenta que
en la región exterior debe tenerse en cuenta que 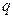 ,
,  y por lo tanto
y por lo tanto  , son continuos en el borde del ala ya que los elementos del plasma pasan a través de la misma. En consecuencia, en el borde del ala del lado interior se tiene de la Ec. (38) que
, son continuos en el borde del ala ya que los elementos del plasma pasan a través de la misma. En consecuencia, en el borde del ala del lado interior se tiene de la Ec. (38) que 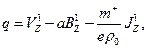 . Si
. Si 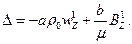 es distinto de cero en el borde del ala del lado interior, significa que la densidad de corriente sobre ella es no nula. Si esto sucede, significa que los gradientes de
es distinto de cero en el borde del ala del lado interior, significa que la densidad de corriente sobre ella es no nula. Si esto sucede, significa que los gradientes de  y de
y de  son paralelos. Como el borde del ala es una superficie de
son paralelos. Como el borde del ala es una superficie de 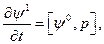 constante, entonces
constante, entonces  es constante sobre el borde del ala. Luego, usando la continuidad de
es constante sobre el borde del ala. Luego, usando la continuidad de  y la primer identidad de Green se tiene que
y la primer identidad de Green se tiene que 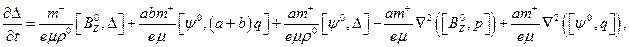 es constante en el borde del ala del lado exterior, esta constante puede valer cero. Por lo tanto
es constante en el borde del ala del lado exterior, esta constante puede valer cero. Por lo tanto  es nulo en el región exterior y en consecuencia lo son
es nulo en el región exterior y en consecuencia lo son 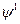 y
y  (32) y (37)).
(32) y (37)).
En la región exterior, donde el plasma es uniforme, ninguna perturbación puede causar la inestabilidad del plasma.
Región interior
En esta subsección se muestra que, en la región interior, las amplitudes de las perturbaciones de las distintas magnitudes son nulas cuando se consideran perturbaciones lineales de la forma 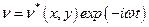 con frecuencias imaginarias, ya que las mismas son nulas en el exterior del ala, de la misma manera que sucedía en el caso MHD (SP07) y en consecuencia, las alas de Alfvén en HMHD resultarán estables frente a perturbaciones incompresibles que tengan la misma simetría y polarización.
con frecuencias imaginarias, ya que las mismas son nulas en el exterior del ala, de la misma manera que sucedía en el caso MHD (SP07) y en consecuencia, las alas de Alfvén en HMHD resultarán estables frente a perturbaciones incompresibles que tengan la misma simetría y polarización.
Primero se analiza el caso de 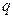 para frecuencias imaginarias, recordando que debe ser continuo en el borde del ala. La ecuación diferencial para
para frecuencias imaginarias, recordando que debe ser continuo en el borde del ala. La ecuación diferencial para  teniendo en cuenta (21) y (27) resulta (ver Ec. (39)):
teniendo en cuenta (21) y (27) resulta (ver Ec. (39)):
Nótese que (46) es del tipo de la Ec. (17), siendo la única diferencia el valor de la constante. Por lo tanto, la curva característica es la proyección de las líneas de campo sobre la sección transversal del ala. La ecuación de las características puede integrarse para encontrar el valor de 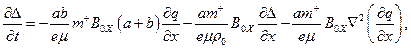 sobre cada una de ellas en función del valor en el borde del ala. Como en el borde del ala es nulo, resulta que
sobre cada una de ellas en función del valor en el borde del ala. Como en el borde del ala es nulo, resulta que 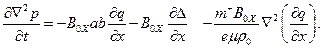 es nulo en el interior del ala.
es nulo en el interior del ala.
Una vez reemplazado el resultado en las Ecs. (40) y (41), éstas pueden desacoplarse fácilmente obteniendo
Al reemplazar la forma de la perturbación en la ecuación para  , Ec. (47) toma forma similar a la Ec. (46) por lo que, con los mismos argumentos, resulta que
, Ec. (47) toma forma similar a la Ec. (46) por lo que, con los mismos argumentos, resulta que  y por lo tanto
y por lo tanto  es nula en el interior del ala.
es nula en el interior del ala.
Para mostrar que  es nula en la región interior para perturbaciones lineales con frecuencia imaginaria, se utiliza el método basado en el de las características, utilizado por Sommerfeld15 para la resolución de segundo orden que fue mencionado en la Sec. II. Se muestra que, a partir de los valores de la variable dependiente y de su derivada normal a una curva dada
es nula en la región interior para perturbaciones lineales con frecuencia imaginaria, se utiliza el método basado en el de las características, utilizado por Sommerfeld15 para la resolución de segundo orden que fue mencionado en la Sec. II. Se muestra que, a partir de los valores de la variable dependiente y de su derivada normal a una curva dada  (que no sea una característica), es posible obtener todos las derivadas parciales sobre ésta, y por lo tanto, construir la solución en el región vecina, expandiendo la variable dependiente en una serie de Taylor.
(que no sea una característica), es posible obtener todos las derivadas parciales sobre ésta, y por lo tanto, construir la solución en el región vecina, expandiendo la variable dependiente en una serie de Taylor.
Como en la región exterior  y
y 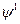 y todas sus derivadas primeras son cero (para frecuencias imaginarias) y son continuas en
y todas sus derivadas primeras son cero (para frecuencias imaginarias) y son continuas en 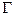 , también son todas nulas en el lado interior de
, también son todas nulas en el lado interior de 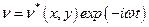 . En consecuencia, las derivadas tangenciales a
. En consecuencia, las derivadas tangenciales a 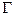 de las derivadas primeras de
de las derivadas primeras de 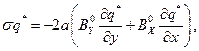 y
y 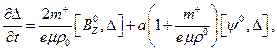 son también nulas en el lado interior de
son también nulas en el lado interior de  . Este resultado brinda relaciones entre las derivadas segundas de
. Este resultado brinda relaciones entre las derivadas segundas de  y
y  y, además pueden obtenerse en forma independiente otras relaciones por derivar la Ec. (30). Este proceso es similar al mostrado por en SP07 en el análisis de la estabilidad de las alas en MHD, por lo que finalmente se obtiene que del lado interior de
y, además pueden obtenerse en forma independiente otras relaciones por derivar la Ec. (30). Este proceso es similar al mostrado por en SP07 en el análisis de la estabilidad de las alas en MHD, por lo que finalmente se obtiene que del lado interior de 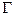 :
:
donde  ,
,  son las componentes del vector unitario normal a la curva
son las componentes del vector unitario normal a la curva  . Como
. Como 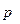 no es la proyección de una línea de campo de inducción magnética,
no es la proyección de una línea de campo de inducción magnética,  es distinto de cero, por lo que todas las derivadas segundas de
es distinto de cero, por lo que todas las derivadas segundas de 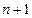 también son nulas en
también son nulas en  . Utilizando esta misma idea, calculando las derivadas tangenciales del
. Utilizando esta misma idea, calculando las derivadas tangenciales del 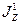 y usando la ecuación diferencial (48) de nuevo puede obtenerse sucesivamente que las derivadas de orden
y usando la ecuación diferencial (48) de nuevo puede obtenerse sucesivamente que las derivadas de orden 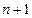 de
de  son nulas en
son nulas en 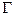 si lo son las de orden
si lo son las de orden  . Finalmente, expandiendo
. Finalmente, expandiendo  en serie de Taylor en las vecindades de
en serie de Taylor en las vecindades de 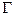 , resulta que
, resulta que  es nula. Como no es posible tener en la región interior al ala proyecciones de las líneas de campo de inducción magnética cerradas, se puede repetir el procedimiento e ir hacia zonas alejadas del borde interior del ala.
es nula. Como no es posible tener en la región interior al ala proyecciones de las líneas de campo de inducción magnética cerradas, se puede repetir el procedimiento e ir hacia zonas alejadas del borde interior del ala.
Como  y
y 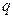 son cero de (35) resulta que
son cero de (35) resulta que  es cero y de (33) se tiene que
es cero y de (33) se tiene que  es cero (y en consecuencia
es cero (y en consecuencia 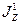 por la condición de polarización). Como
por la condición de polarización). Como  es cero, de (34) resulta que
es cero, de (34) resulta que  es cero. Como
es cero. Como  es cero, de la Ec. (37) resulta que
es cero, de la Ec. (37) resulta que 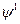 es cero y de (32) lo es
es cero y de (32) lo es  .
.
De esta manera, usando el método empleado en SP07, se ha mostrado que para perturbaciones simétricas incompresibles las alas de Alfvén son estructuras estables en plasmas donde se tiene en consideración el término de Hall de la ley de Ohm, cuando las perturbaciones tienen la misma polarización que las ondas de Alfvén que construyen las alas.
V. CONCLUSIONES
En este trabajo se muestra que, en los plasmas en los que se tiene en consideración el término de Hall de la ley de Ohm (HMHD), las alas de Alfvén en plasmas uniformes son estructuras estables en presencia de perturbaciones lineales incompresibles que tienen la misma simetría que el ala y polarización. En el estudio del problema se utilizó el método adaptado por Sallago y Platzeck en 2007 partiendo de otro desarrollado por Palumbo. Se obtiene un sistema de ecuaciones diferenciales; en la región exterior del ala, cuando la frecuencia es imaginaria, este sistema admite solo la solución de amplitud nula. Como la densidad de corriente no es nula en el límite del ala, también en la región interior la solución es nula, para esto se utilizó el mismo método basado en el método de las características que fue empleado para analizar la estabilidad de las alas de Alfvén en MHD.