La Teoría Cuántica de Campos (‘Quantum Field Theory’ o QFT) describe sistemas cuánticos con infinitos grados de libertad, y juega un rol central en modelos de altas energías y sistemas fuertemente correlacionados en materia condensada. En las últimas décadas la QFT ha visto un progreso revolucionario en aspectos no perturbativos al utilizar métodos provenientes de la Teoría de Información Cuántica. Entre ellos, medidas basadas en la entropía de entrelazamiento en conjunto con la unitariedad y causalidad han establecido la irreversibilidad del grupo de renormalización (RG) en 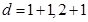 y
y 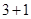 dimensiones espacio-temporales para QFTs relativistas.1-3 También, resultados de Teorías de Campos Conformes (CFT)4 así como de Teorías de Campos libres5 han brindado nuevas visiones acerca de la estructura general de QFT.
dimensiones espacio-temporales para QFTs relativistas.1-3 También, resultados de Teorías de Campos Conformes (CFT)4 así como de Teorías de Campos libres5 han brindado nuevas visiones acerca de la estructura general de QFT.
La mayoría de los resultados existentes en la literatura hasta el momento han estado relacionados con QFTs relativistas. La razón es que las restricciones que imponen la simetría de Lorentz y la estructura causal juegan un rol fundamental en los enfoques antes mencionados. En contraste, son mucho menos conocidos resultados en QFTs no relativistas y, en particular, en QFTs no relativistas a densidad finita como sería relevante para la descripción del límite al continuo de materia cuántica. En particular, ha sido sugerido que la entropía de entrelazamiento puede presentar un comportamiento no monótono en ciertos modelos no relativistas, y esto podría implicar que el grupo de renormalización no fuese irreversible más allá de las teorías Lorentz invariantes.6
Una lección clave de los análisis invariantes de Lorentz es que, desde el punto de vista de medidas de información cuántica, las QFTs libres proveen una arena no trivial para obtener resultados más generales que se aplican más ampliamente.5 Motivados por esto, en este artículo estudiamos fermiones de Dirac libres a densidad finita, empleando tanto métodos analíticos en teoría de información cuántica así como simulaciones numéricas. Nos restringimos al caso más simple posible de 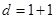 dimensiones espacio-temporales, donde los resultados son todavía no triviales. Planeamos extender nuestro trabajo a dimensiones más altas en un futuro. Cabe destacar que este presentación es una discusión de algunos resultados publicados con anterioridad en.7
dimensiones espacio-temporales, donde los resultados son todavía no triviales. Planeamos extender nuestro trabajo a dimensiones más altas en un futuro. Cabe destacar que este presentación es una discusión de algunos resultados publicados con anterioridad en.7
En esta sección estudiaremos algunos aspectos teóricos de fermiones de Dirac a densidad finita tanto en el continuo como en la red.
Teoría en el continuo
Los fermiones de Dirac libres tienen una simetría continua 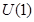 ,
, 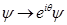 . Una densidad de carga finita
. Una densidad de carga finita 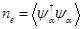 puede obtenerse al introducir un potencial químico
puede obtenerse al introducir un potencial químico 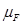 . Es por eso que la acción (con signatura
. Es por eso que la acción (con signatura 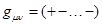 , en
, en 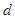 dimensiones espacio-temporales) resulta
dimensiones espacio-temporales) resulta
Tanto el término de masa como el de potencial químico son operadores relevantes por contaje de potencias, e inducen un flujo no trivial del grupo de renormalización (RG) desde una CFT UV de un fermión de Dirac no masivo.
Los autovalores de energía son
De aquí en adelante siempre trabajaremos con 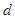 . Es por esto que
. Es por esto que  siempre será negativo y como de costumbre dará origen a las antipartículas; además, la banda
siempre será negativo y como de costumbre dará origen a las antipartículas; además, la banda 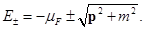 tiene una energía tal que se anula a momento de Fermi finito
tiene una energía tal que se anula a momento de Fermi finito 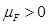 . Esto define una superficie de Fermi esférica.
. Esto define una superficie de Fermi esférica.
Reconocemos el correlador de densidad finita como la deformación del resultado relativista, definiendo el mismo como 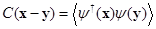 ,
,
con
Aquí utilizamos la notación.
Trabajamos con una red espacial infinita, 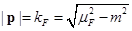 ,
, 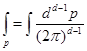
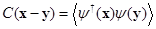 , poniendo el espaciado de red
, poniendo el espaciado de red 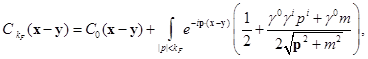 . Simetrizando las derivadas espaciales en () y discretizando las derivadas como
. Simetrizando las derivadas espaciales en () y discretizando las derivadas como 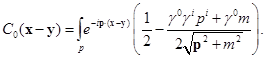 , el Hamiltoniano en la red es
, el Hamiltoniano en la red es
Los autovalores de energía vienen dados por
Cuando 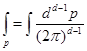 , el estado de vacío es el estado que contiene cero partículas
, el estado de vacío es el estado que contiene cero partículas 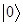 , aniquilado por
, aniquilado por 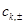 . Cuando
. Cuando 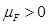 , el nuevo estado fundamental se obtiene al llenar los estados de energía negativa
, el nuevo estado fundamental se obtiene al llenar los estados de energía negativa 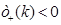 en la banda de partículas,
en la banda de partículas, 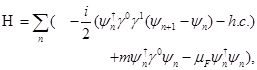 .
.
Luego, las partículas llenan la superficie de Fermi con momento de Fermi
El correlador en el discreto se define como 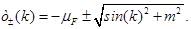 y se corresponde con el resultado del continuo (),
y se corresponde con el resultado del continuo (),
Primero, consideremos el límite no masivo 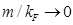 . Es útil elegir la base quiral
. Es útil elegir la base quiral 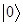 ,
, 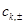 . En términos de los usualmente denominados left/right movers,
. En términos de los usualmente denominados left/right movers, 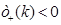 , obtenemos
, obtenemos
El potencial químico puede ser removido con una transformación unitaria local,
Esto da dos fermiones quirales moviéndose a la velocidad de la luz,
Ahora consideremos el límite opuesto, es decir, el límite no relativista 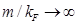 . A energías y momentos mucho más pequeños que la masa, la relación de dispersión (2) resulta
. A energías y momentos mucho más pequeños que la masa, la relación de dispersión (2) resulta
con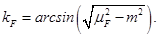 . Las antipartículas con energía
. Las antipartículas con energía 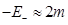 se desacoplan de la teoría de bajas energías. Luego, la teoría efectiva de bajas energías resulta
se desacoplan de la teoría de bajas energías. Luego, la teoría efectiva de bajas energías resulta
Este es el mismo resultado que se obtuvo en la teoría con dos fermiones quirales (11), excepto que ahora la velocidad de propagación es la velocidad de Fermi.
En esta sección consideramos la entropía de entrelazamiento (EE) o entropía geométrica asociada a la matriz densidad reducida de una región espacial 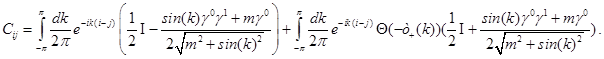 del estado puro de vacío. La misma se define a partir de la entropía de Von Neumann como5
del estado puro de vacío. La misma se define a partir de la entropía de Von Neumann como5
donde 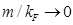 es el complemento de
es el complemento de 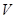 , y
, y 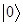 es el estado de vacío.
es el estado de vacío.
Nuestra motivación en cuanto al estudio de la EE en esta dirección provino de6, que argumentó acerca de la violación de la irreversibilidad del flujo del RG en modelos no relativistas. En más detalle, una superficie de Fermi en 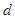 dimensiones espacio-temporales conlleva a la violación logarítmica de la ley de áreas para la EE,
dimensiones espacio-temporales conlleva a la violación logarítmica de la ley de áreas para la EE,
donde 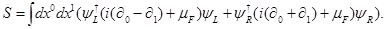 es una región esférica de radio
es una región esférica de radio 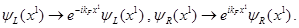 . Para
. Para 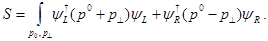 grande, esta contribución crece más rápido que el término dominante de la ley de áreas,
grande, esta contribución crece más rápido que el término dominante de la ley de áreas,
que aparece en modelos locales, como las QFTs con puntos fijos UV.
En contraposición a la EE que es UV divergente, la cantidad
es finita y es proporcional a la carga central intrínseca  en los puntos fijos UV e IR. También está bien definida por fuera de los puntos fijos, en cuyo caso decrece monotonamente para flujos unitarios del RG en teorías relativistas1,2. Computaremos la cantidad finita (17) en presencia de densidad de carga finita, y la usaremos para estudiar potenciales violaciones de la monotonicidad. Para ello, haremos simulaciones numéricas utilizando un método denominado de tiempo real5,8. En este, la entropía de entrelazamiento en la red puede computarse a partir de la matriz de correlación (ver (8))
en los puntos fijos UV e IR. También está bien definida por fuera de los puntos fijos, en cuyo caso decrece monotonamente para flujos unitarios del RG en teorías relativistas1,2. Computaremos la cantidad finita (17) en presencia de densidad de carga finita, y la usaremos para estudiar potenciales violaciones de la monotonicidad. Para ello, haremos simulaciones numéricas utilizando un método denominado de tiempo real5,8. En este, la entropía de entrelazamiento en la red puede computarse a partir de la matriz de correlación (ver (8))  restringida a
restringida a 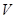 (
(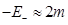 ),
),
Para fermiones de Dirac quirales, habíamos encontrado una transformación unitaria (10) que mapea la teoría con densidad de carga finita a un modelo relativista de carga cero. Ambas funciones de dos puntos  en el continuo tienen los mismos autovalores y, entonces, las respectivas matrices también tienen los mismos autovalores. Por lo tanto, las medidas de información cuántica que dependen sólo de los autovalores de la matriz densidad reducida, como la EE, coinciden en ambas teorías. Esto se encuentra plasmado en el cálculo numérico de la EE en la Fig.1.
en el continuo tienen los mismos autovalores y, entonces, las respectivas matrices también tienen los mismos autovalores. Por lo tanto, las medidas de información cuántica que dependen sólo de los autovalores de la matriz densidad reducida, como la EE, coinciden en ambas teorías. Esto se encuentra plasmado en el cálculo numérico de la EE en la Fig.1.
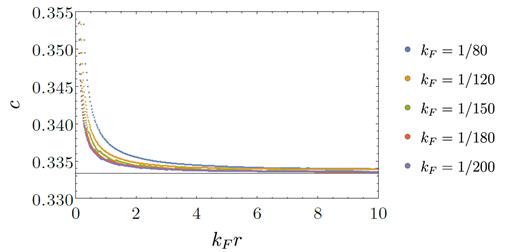
FIG. 1: Función 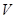 entrópica para un fermión quiral a densidad finita. Para
entrópica para un fermión quiral a densidad finita. Para  y
y 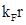 fijos, los gráficos tienden a
fijos, los gráficos tienden a 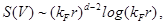 , como en un CFT de
, como en un CFT de 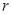 .
.
Analicemos ahora el caso de fermiones de Dirac masivos. Para desarrollar intuición analítica, es útil considerar primero los límites asintóticos UV e IR, en conjunto con los comportamientos ultra-relativistas y no relativistas. Desde el punto de vista de la EE y la función entrópica 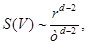 , el UV se corresponde con
, el UV se corresponde con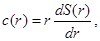 . El término de masa es una deformación relevante estándar, y por tanto su efecto es despreciable en el UV. La densidad de carga puede ser más sutil dado que el estado fundamental cambia a densidad finita. Asumiendo que también se comporta como una deformación relevante, el límite UV debería dar
. El término de masa es una deformación relevante estándar, y por tanto su efecto es despreciable en el UV. La densidad de carga puede ser más sutil dado que el estado fundamental cambia a densidad finita. Asumiendo que también se comporta como una deformación relevante, el límite UV debería dar 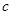 . Nuestros resultados numéricos mostrarán que de hecho este es el caso (ver Fig. 2).
. Nuestros resultados numéricos mostrarán que de hecho este es el caso (ver Fig. 2).
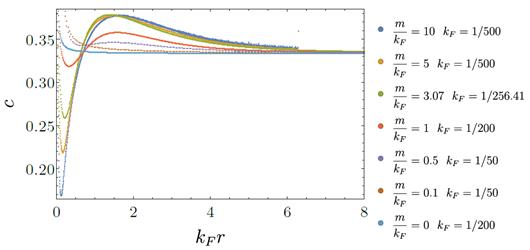
FIG. 2: Función 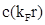 para distintos regímenes de
para distintos regímenes de 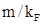 para fermiones de Dirac a densidad finita. La función
para fermiones de Dirac a densidad finita. La función  entrópica es una cantidad finita que exhibe un comportamiento no monótono del RG.
entrópica es una cantidad finita que exhibe un comportamiento no monótono del RG.
El comportamiento intermedio entre los puntos fijos depende de 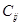 . En el régimen relativista
. En el régimen relativista , los efectos de la carga no trivial siempre dominan en el sentido del RG, y el comportamiento es similar al de los fermiones quirales.
, los efectos de la carga no trivial siempre dominan en el sentido del RG, y el comportamiento es similar al de los fermiones quirales.
En el régimen no relativista, 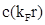 rápidamente decrece a escalas del orden de
rápidamente decrece a escalas del orden de 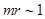 . Esto es consistente con el RG siendo dominado por la masa. Para valores más grandes de
. Esto es consistente con el RG siendo dominado por la masa. Para valores más grandes de 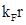 ,
, 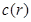 crece, alcanzando un máximo a
crece, alcanzando un máximo a 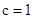 , para finalmente tender a
, para finalmente tender a 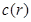 . El mínimo y el máximo en
. El mínimo y el máximo en 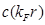 reflejan la competencia entre los operadores
reflejan la competencia entre los operadores 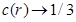 ; el primero trata de inducir un gap masivo y entrelazamiento nulo, mientras que el segundo (recordando que
; el primero trata de inducir un gap masivo y entrelazamiento nulo, mientras que el segundo (recordando que  ) trata de inducir entrelazamiento de largo alcance. La función
) trata de inducir entrelazamiento de largo alcance. La función 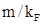 entrópica sensa la creación de entrelazamiento debido a la densidad finita.
entrópica sensa la creación de entrelazamiento debido a la densidad finita.
Las entropías de Renyi y las correspondientes funciones 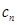 entrópicas se definen como5
entrópicas se definen como5
Además de brindar los autovalores de 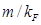 , las entropías de Renyi también son importantes debido a su rol en el replica trick.
, las entropías de Renyi también son importantes debido a su rol en el replica trick.
En la Ref.9 estudiaron el modelo 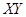 en una red 1d y encontraron un comportamiento sorprendente de las
en una red 1d y encontraron un comportamiento sorprendente de las 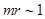 , reminiscente de las oscilaciones de Friedel en un metal. Su predicción analítica de
, reminiscente de las oscilaciones de Friedel en un metal. Su predicción analítica de 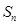 en el límite de gran distancia
en el límite de gran distancia 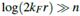 es
es
con
y 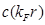 en su caso. Similarmente a (18), las entropías de Renyi pueden ser computadas en términos de la función de dos puntos
en su caso. Similarmente a (18), las entropías de Renyi pueden ser computadas en términos de la función de dos puntos 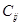 restringida a una región espacial
restringida a una región espacial 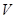 ,
,
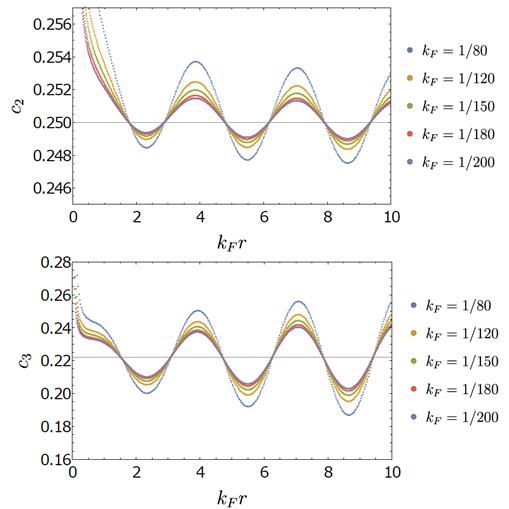
FIG. 3: Funciones 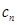 y
y 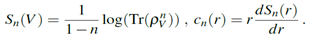 para un fermión quiral a densidad finita. El límite al continuo se corresponde con
para un fermión quiral a densidad finita. El límite al continuo se corresponde con 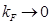 para
para 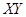 finito, en donde las amplitudes de las oscilaciones tienden a desvanecerse.
finito, en donde las amplitudes de las oscilaciones tienden a desvanecerse.
Comencemos nuestro análisis con fermiones de Dirac no masivos en la red (5). Esto nos proveerá un ejemplo de oscilaciones de Friedel en modelos en la red que desaparecen en el límite al continuo, como se aprecia en la Fig. 3.
A continuación, consideramos el caso masivo. La Fig. 4 muestra nuestros resultados numéricos para 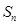 y
y 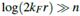 en diferentes regímenes de
en diferentes regímenes de 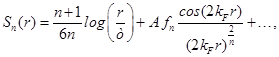 .
.
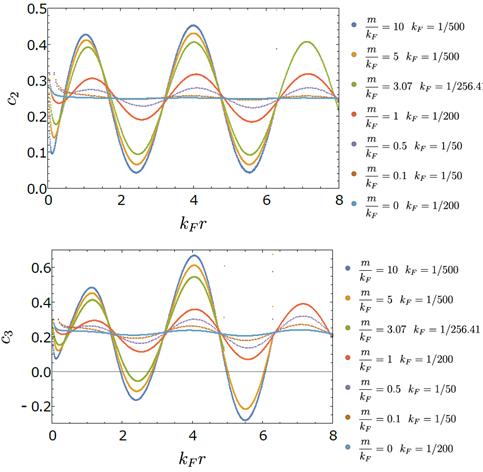
FIG. 4: Funciones 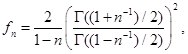 y
y 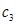 para todos lo regímenes de fermiones de Dirac a densidad finita. En todos ellos, excepto para
para todos lo regímenes de fermiones de Dirac a densidad finita. En todos ellos, excepto para 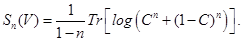 , hay oscilaciones de Friedel de período
, hay oscilaciones de Friedel de período  como función de
como función de 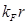 .
.
Para 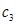 encontramos oscilaciones de Friedel en el límite al continuo, no sólo cuando
encontramos oscilaciones de Friedel en el límite al continuo, no sólo cuando 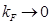 sino que para otros rangos de
sino que para otros rangos de 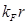 también. Las oscilaciones tienen un valor medio
también. Las oscilaciones tienen un valor medio  debido a la contribución proveniente de fermiones livianos de la teoría a bajas energías (13). Más aún, hemos verificado que la dependencia de distancia grande (20) también ajusta correctamente lejos del límite no relativista. Teóricamente, estos comportamientos pueden explicarse en términos de una expansión en producto de operadores sobre los bordes del intervalo.7
debido a la contribución proveniente de fermiones livianos de la teoría a bajas energías (13). Más aún, hemos verificado que la dependencia de distancia grande (20) también ajusta correctamente lejos del límite no relativista. Teóricamente, estos comportamientos pueden explicarse en términos de una expansión en producto de operadores sobre los bordes del intervalo.7
En esta sección analizaremos la información mutua, una medida de información que permite cuantificar la correlaciones entre dos regiones 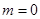 y
y 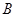 . La misma puede definirse en términos de la EE como
. La misma puede definirse en términos de la EE como
y también su versión de Renyi, dada por
Si se consideran como regiones 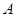 y
y 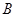 dos intervalos de longitudes
dos intervalos de longitudes 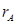 y
y 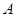 respectivamente, la contribución dominante para una CFT en el límite
respectivamente, la contribución dominante para una CFT en el límite 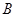 resulta10
resulta10
donde 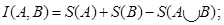 indica la mínima dimensión asociada a un operador de intercambio admisible por la teoría. En el presente caso, esto se corresponde con bilineales fermiónicos, con lo cual
indica la mínima dimensión asociada a un operador de intercambio admisible por la teoría. En el presente caso, esto se corresponde con bilineales fermiónicos, con lo cual 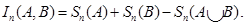 . Estas contribuciones tienen el mismo comportamiento de escaleo que los términos no oscilantes que no mezclan
. Estas contribuciones tienen el mismo comportamiento de escaleo que los términos no oscilantes que no mezclan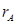 . Por tanto, siguiendo un argumento similar para la deducción de (25), la información mutua de Renyi en el límite de grandes distancias resulta
. Por tanto, siguiendo un argumento similar para la deducción de (25), la información mutua de Renyi en el límite de grandes distancias resulta
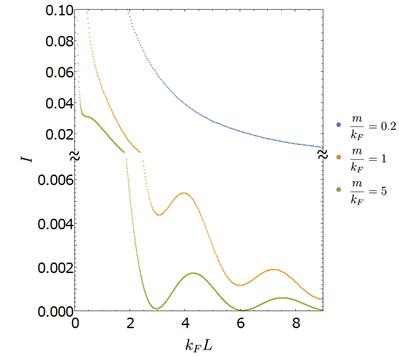
FIG.5:
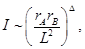 para un
para un 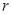 fijo para fermiones de Dirac masivos a densidad finita. Las longitudes
fijo para fermiones de Dirac masivos a densidad finita. Las longitudes 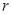 fueron
fueron 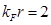 ,
, 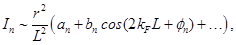 y
y 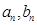 para
para 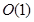 ,
,  y
y 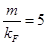 respectivamente. Están presentes oscilaciones de período
respectivamente. Están presentes oscilaciones de período 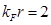 como función de
como función de 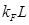 . Sus amplitudes se anulan conforme
. Sus amplitudes se anulan conforme 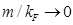 .
.
Los resultados numéricos de la información mutua se muestran en la Fig. 5. El decaimiento es más abrupto para curvas con mayor 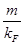 , dado que las correlaciones asociadas a operadores que no están localizados en los extremos de los intervalos replicados, tienden a desvanecerse significativamente para
, dado que las correlaciones asociadas a operadores que no están localizados en los extremos de los intervalos replicados, tienden a desvanecerse significativamente para 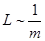 . Asimismo, para
. Asimismo, para 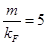 se observan oscilaciones en todos los regímenes.
se observan oscilaciones en todos los regímenes.
Los resultados numéricos de la información mutua de Renyi se muestran en la Fig. 6. Los paneles a), b) y c) muestran el comportamiento para diferentes masas y para diferentes parámetros de Renyi 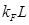 . Finalmente, en el panel d) verificamos que la predicción del límite de grandes distancias (26) está en excelente acuerdo con los resultados numéricos.
. Finalmente, en el panel d) verificamos que la predicción del límite de grandes distancias (26) está en excelente acuerdo con los resultados numéricos.
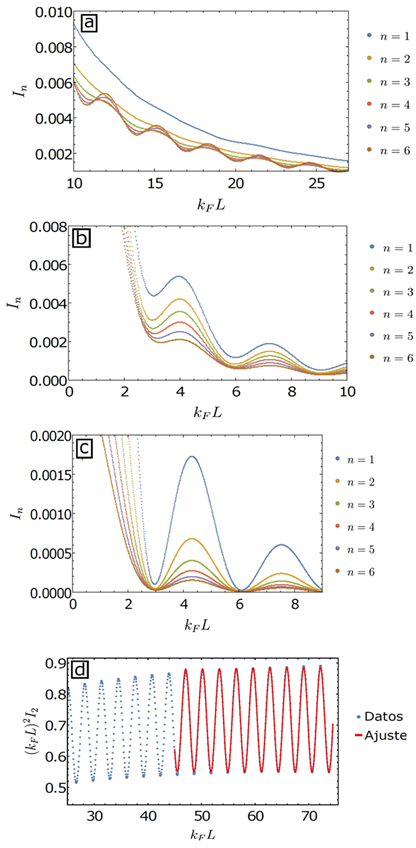
FIG. 6: Las subfiguras a), b) y c) muestran las simulaciones de 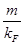 para un valor fijo r para un fermión de Dirac masivo. Los parámetros son
para un valor fijo r para un fermión de Dirac masivo. Los parámetros son 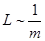
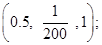
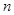 , respectivamente. Observamos oscilaciones de Friedel de período kFL, con amplitud dependiente de
, respectivamente. Observamos oscilaciones de Friedel de período kFL, con amplitud dependiente de  . En la subfigura d) chequeamos el acuerdo con (26). Ajustamos
. En la subfigura d) chequeamos el acuerdo con (26). Ajustamos 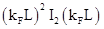 en el límite
en el límite 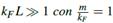 ,
, 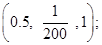 y
y 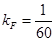 . La expresión usada fue
. La expresión usada fue 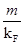 obteniéndose
obteniéndose 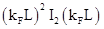 .
.
En esta sección nuestro análisis virará la atención hacia otra pregunta en información cuántica: ¿cómo distinguir a dos matrices densidad 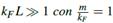 y
y 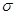 ? La principal medida para llevar a cabo esta tarea es la entropía relativa entre dos estados
? La principal medida para llevar a cabo esta tarea es la entropía relativa entre dos estados 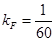 y
y 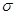 . La misma se define como
. La misma se define como
Existe una interesante generalización uniparamétrica de la entropía relativa11,12
para 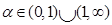 y que para
y que para 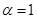 recupera a la entropía relativa. Estas están usualmente referidas como las entropías relativas de Renyi.
recupera a la entropía relativa. Estas están usualmente referidas como las entropías relativas de Renyi.
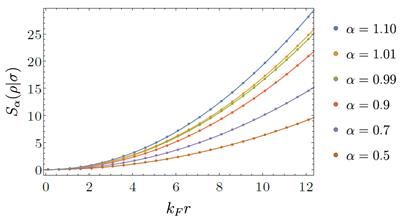
FIG. 7: Gráficos de 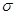 con
con 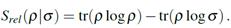 para
para 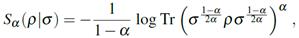 , comparando estados con
, comparando estados con 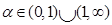 y
y 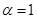 . La dependencia funcional
. La dependencia funcional  es observada y graficada con una línea continua para todos los
es observada y graficada con una línea continua para todos los 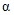 considerados. Cuando
considerados. Cuando 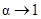 los gráficos crean una cota por debajo y por encima de la entropía relativa.
los gráficos crean una cota por debajo y por encima de la entropía relativa.
En la Fig. 7 se muestran los resultados numéricos (que se computaron utilizando fórmulas obtenidas en13) que comparan a los estados con 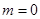 fijo, con
fijo, con 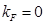 (
(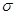 ) y con
) y con 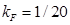 (
(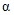 ). Lo notable en este caso es el comportamiento super-extensivo dado por
). Lo notable en este caso es el comportamiento super-extensivo dado por 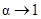 para todo
para todo 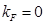 .
.
En este artículo hemos estudiado varias medidas de información cuántica en Teoría de Campos a densidad finita. Nos enfocamos en fermiones de Dirac libres a densidad finita en 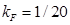 dimensiones espacio-temporales.
dimensiones espacio-temporales.
Hemos establecido que la función 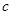 entrópica no es monótona, en rotundo contraste con el comportamiento de QFTs Lorentz-invariantes. En el análisis de entropías de Renyi se destacan las oscilaciones de Friedel, que modifican el resultado de la CFT en el orden subdominante. En un futuro, podría ser interesante testear la existencia de oscilaciones en teorías interactuantes, como por ejemplo, en non-Fermi liquids. Otro resultado importante a destacar es que encontramos que la información mutua detecta a la superficie de Fermi todavía en el orden dominante vía nuevos términos oscilatorios. Esta es una medida prometedora para testear sistemas correlacionados. Finalmente, estudiamos la entropía relativa (y su generalización uniparamétrica) como medida de distinguibilidad entre estados cuánticos. La entropía relativa exhibe un comportamiento super-extensivo para estados en distintos sectores de superselección de carga, y además es monótona y finita. Estas propiedades resultan útiles para un entendimiento no perturbativo de aspectos del flujo del RG a densidad finita. Para continuar en esta línea, sería muy importante poder determinar cómo extraer propiedades intrínsecas de los puntos fijos a partir de la entropía relativa. También sugerimos extender el presente trabajo a
entrópica no es monótona, en rotundo contraste con el comportamiento de QFTs Lorentz-invariantes. En el análisis de entropías de Renyi se destacan las oscilaciones de Friedel, que modifican el resultado de la CFT en el orden subdominante. En un futuro, podría ser interesante testear la existencia de oscilaciones en teorías interactuantes, como por ejemplo, en non-Fermi liquids. Otro resultado importante a destacar es que encontramos que la información mutua detecta a la superficie de Fermi todavía en el orden dominante vía nuevos términos oscilatorios. Esta es una medida prometedora para testear sistemas correlacionados. Finalmente, estudiamos la entropía relativa (y su generalización uniparamétrica) como medida de distinguibilidad entre estados cuánticos. La entropía relativa exhibe un comportamiento super-extensivo para estados en distintos sectores de superselección de carga, y además es monótona y finita. Estas propiedades resultan útiles para un entendimiento no perturbativo de aspectos del flujo del RG a densidad finita. Para continuar en esta línea, sería muy importante poder determinar cómo extraer propiedades intrínsecas de los puntos fijos a partir de la entropía relativa. También sugerimos extender el presente trabajo a 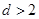 y explorar modelos holográficos.
y explorar modelos holográficos.
AGRADECIMIENTOS
Se agradece a Horacio Casini por distintas discusiones y comentarios a lo largo del trabajo. LD cuenta con el apoyo de CNEA y UNCuyo, Inst. GT cuenta con el apoyo de CONICET, ANPCyT, CNEA, y UNCuyo, Inst. Balseiro. RM cuenta con el apoyo de IST Austria. MS cuenta con el apoyo de CONICET y UNCuyo, Inst. Balseiro. También se agradece a la Asociación Argentina de Física por la posibilidad de presentar este artículo en el marco de una Mención Especial por el Premio Luis Másperi 2020.














