I. INTRODUCCIÓN
In the context of the Hydride Delayed Cracking phenomena (DHC), Zirconium based alloys are currently used in reactors due to their low neutron absorption and their good response to high temperature corrosion. Since hydrogen can be present in the alloys as a remnant impurity of the manufacturing process, and can also enter during the service life of the material, it is very important to evaluate the response of the alloys to hydrogen.
The microstructure, solubility and diffusion coefficient of H in the alloy are variables that allow us understand the DHC phenomena. For example, the Zr-2.5Nb alloy is bi-phasic with grains of phase  (hcp, with 0.6 % Nb) surrounded by plates of
(hcp, with 0.6 % Nb) surrounded by plates of  phase (bcc, with 20 % Nb).
phase (bcc, with 20 % Nb).
With thermal treatments, the original plates of  Zr lose their continuity and interrupts the fast paths for the hydrogen diffusion in the axial direction of the tube and, at the same time, their percentage of Nb is altered evolving to the stable phase
Zr lose their continuity and interrupts the fast paths for the hydrogen diffusion in the axial direction of the tube and, at the same time, their percentage of Nb is altered evolving to the stable phase  Nb (bcc, with 90 - 100%Nb).
Nb (bcc, with 90 - 100%Nb).
From this experimental evidence, the following questions arise:
Since
 Nb must have a hydrogen solubility lower than that of pure Nb, then: It is possible to calculate the solubility of H in pure Nb and of the Zr-Nb alloys, with different percentages of Nb?
Nb must have a hydrogen solubility lower than that of pure Nb, then: It is possible to calculate the solubility of H in pure Nb and of the Zr-Nb alloys, with different percentages of Nb?Is the loss of continuity of the original sheets effectively responsible for the observed decrease in the diffusion coefficient of H as time passes at a given temperature?
Is the diffusion and / or solubility of hydrogen in the alloy affected by the Nb content?
This is a work prior to that carried out in Ref.,1 in which the authors have successfully answered questions 2 and 3 posed by our experiments. Here we focused on the study of the hydrogen’s diffusivity on  Zr.
Zr.
Concerning atomic diffusion, several efficient methods have been developed in recent years for finding activated states or, mathematically, saddle points from which diffusion can be studied. Here we employ the Monomer one, developed previously in our laboratory2 and The Dimer method3 as implemented in Vasp.4 The Monomer, in coupled to Siesta’s code5 to be interfaced as a subroutine.6
The Monomer computes the least local curvature of the potential energy surface using only the forces furnished by Siesta. The force component along the corresponding eigenvector is then reversed (pointing ‘up hill’), thus defining a pseudo force that drives the system towards saddles. Both, local curvature and configuration displacement stages are performed within independent conjugate gradients loops. The method is akin to the Dimer one from the literature,3 but roughly employs half the number of force evaluations.
These methods are very efficient at obtaining the migration barriers from which we study the atomic diffusion in metals. In this way, Ishioka and Koiwa7 have studied the interstitial diffusion in hcp metals, involving octahedral and tetrahedral sites. They have proposed an on-lattice random walk model to derive the diffusivities of impurity atoms on a crystal lattice containing multiple sublattices, such as the octahedral and tetrahedral sites in hcp crystals.
Here we focused on the study of the hydrogen’s behavior in Zr-Nb. In this sense we study some relevant diffusion parameters, namely: (i) the hydrogen solubility, (ii) the hydrogen binding energies of the H-H and H-Nb complexes, (iii) the mixing solution energy of Nb-Zr and (iv) the hydrogen diffusion coefficients in hcp Zr. With this purpose, we perform ab-initio calculations with Siesta5 and Vasp,4 in order to obtain the hydrogen migration barriers in the bulk of  Zr using the model developed in Ref..7 Classical calculations were also performed in order to check some structure consistence.
Zr using the model developed in Ref..7 Classical calculations were also performed in order to check some structure consistence.
The present paper is structured as follows: Section II describes our calculation methodology with the DFT based codes as Siesta and Vasp, and from classical codes. Sections III show the way as the lattice parameter is calculated from the fit of a third-order Birch-Murnagahn equation of state, EOS,.8 Section IV, is devoted to summarize the energetic of Hydrogen in the Zr-Nb system. Section V describes the way as the H-diffusion coefficients were calculated in  Zr together with our numerical results. In brief, Section VI, describes the structure of the three stable zirconium-hydrides in
Zr together with our numerical results. In brief, Section VI, describes the structure of the three stable zirconium-hydrides in  Zr. The last section presents some conclusions.
Zr. The last section presents some conclusions.
II. CALCULATION METHODOLOGY
Ab initio calculations were performed as implemented in Siesta and Vasp. Siesta, is a freely available code,5 which is based on pseudopotentials and numerical, atomic-like, basis functions. The pseudopotential and basis for Zr are according to Ref..6 Pseudopotential for H was downloaded from Siesta’s home page, and the corresponding base was automatically generated using the code itself.
Present Siesta calculations were carried out within the generalized gradient approximation (GGA) for exchange and correlation, according to the PBE parameterization described in Ref..9 A spatial mesh cutoff of 460.0 Ry were used, with a smearing temperature of 0.15 eV, within a Fermi-Dirac scheme. Reciprocal space is partitioned in a 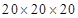 Monkhorst-Pack grid. All calculations were atomically relaxed, though the cell boundary remains fixed. For hydrogen, we used a so called TZDP basis with a split norm parameter of 0.5, which is the accurate one that most efficiently relaxes the bulk containing H.
Monkhorst-Pack grid. All calculations were atomically relaxed, though the cell boundary remains fixed. For hydrogen, we used a so called TZDP basis with a split norm parameter of 0.5, which is the accurate one that most efficiently relaxes the bulk containing H.
Vasp uses a projector augmented-wave formalism to describe the interactions between atoms.10 An energy cutoff of 460 eV and fine  -centered k-point meshes automatically generated with the Monkhorst-Pack scheme11 of
-centered k-point meshes automatically generated with the Monkhorst-Pack scheme11 of  -k points mesh ensured electronic convergence of the calculations. For the term of exchange and correlation we use the PBE-GGA approximation, with the Methfessel-Paxton broadening scheme with a
-k points mesh ensured electronic convergence of the calculations. For the term of exchange and correlation we use the PBE-GGA approximation, with the Methfessel-Paxton broadening scheme with a  eV width. Concerning optimum structures, relaxation was done until the residual forces were below 0.02 eV/Å.
eV width. Concerning optimum structures, relaxation was done until the residual forces were below 0.02 eV/Å.
In both, Siesta and Vasp, we have used two supercell sizes of 48 and 54 atoms, respectuvely for  Zr and
Zr and  Nb. The supercell of
Nb. The supercell of  Zr with 48 atoms is constructed by reproducing the conventional cell, of 4 atoms, along the lattice vectors of the hexagonal primitive cell a, b and c, in
Zr with 48 atoms is constructed by reproducing the conventional cell, of 4 atoms, along the lattice vectors of the hexagonal primitive cell a, b and c, in  .
.
In addition, we have performed calculations with the molecular statics technique (MS), implemented in an in-house code, provided with suitable EAM interatomic potentials for Zr.12 We use a simulation cell of  and
and  respectively containing 6000 Zr or Nb atoms, with periodic boundary conditions.
respectively containing 6000 Zr or Nb atoms, with periodic boundary conditions.
These methods are very efficient at obtaining the equilibrium positions of the atoms by relaxing the structure via the conjugate gradients technique. Impurity and defect relaxation, includes interstitial H atoms in 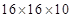 Zr,
Zr,  Nb, as well as, in the Zr-Nb alloy structure. The needed migration barriers of several jumps were calculated coupling both EAM and Siesta techniques to the Monomer method,2,6 while we used the DIMER as implemented in Vasp.3
Nb, as well as, in the Zr-Nb alloy structure. The needed migration barriers of several jumps were calculated coupling both EAM and Siesta techniques to the Monomer method,2,6 while we used the DIMER as implemented in Vasp.3
Finally, our calculations were carried out at constant volume, and therefore the enthalpic barrier  is equal to the internal energy barrier
is equal to the internal energy barrier  .
.
The empirical formula (EF)
The EF is an expression that represents the simplest proportion in which the atoms are present in the alloy. In the case of the Zr-2.5Nb alloy, we start from a hypothetical sample with 100 gr of Zr-2.5Nb. From the % of Nb we defined that in 100 gr of the sample there are 2.5 gr of Nb while the rest, (100-2.5) = 97.5 gr, are of Zr. The moles of Zr and Nb that are present in those 100 gr of Zr-2.5Nb, are obtained through the ratio between the grams of each species in the sample by their respective molecular weights,  and
and  , as,
, as,
In Eqs. (1) and (2) the ratio between species that contains the least number of moles gives the empirical formula  for the alloy. This assumes that Nb atoms are located at periodic positions and not randomly; Also, this does not consider the different compositions of the alpha and beta phases.
for the alloy. This assumes that Nb atoms are located at periodic positions and not randomly; Also, this does not consider the different compositions of the alpha and beta phases.
From this result, we were considered two sizes of supercells, one of 36 atoms of Zr and another one with 48 atoms of Zr.
III. STRUCTURE OPTIMIZATION
For  Nb and
Nb and  Zr, in order to better describe bulk zirconium properties, we determine a cut-off for the needed size of k-point mesh. On a
Zr, in order to better describe bulk zirconium properties, we determine a cut-off for the needed size of k-point mesh. On a 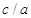 cell consisting of two Nb or Zr atoms, several calculations were done using k-point meshes with sizes of
cell consisting of two Nb or Zr atoms, several calculations were done using k-point meshes with sizes of  ,
,  ,
,  ,
,  ,
,  and
and  with the use of 95, 180, 352, 549, 800 and 1122 irreducible k-points, respectively.
with the use of 95, 180, 352, 549, 800 and 1122 irreducible k-points, respectively.
Using a general convergence cut-off of 5 meV/atom, it was shown that the choice of  k-point mesh would be sufficient to represent the both, Nb and Zr
k-point mesh would be sufficient to represent the both, Nb and Zr  supercells while keeping the computational effort at the minimum level. In subsequent calculations, choice of k- point mesh would be made based on the ratio between the size of the new supercell and that of the
supercells while keeping the computational effort at the minimum level. In subsequent calculations, choice of k- point mesh would be made based on the ratio between the size of the new supercell and that of the  supercell.
supercell.
With the chosen k-point mesh, equation of state calculations were done in determining the computational lattice parameters of bulk  Zr and
Zr and  Nb as follows: We perform an automated volume scan by means of a shell script loop.sh, with lattice parameters above and below the experimental value. Then, the procedure was to get the energy as a function of volume using by regression fitting DFT results to third-order Birch-Murnagahn equation of state, EOS.8
Nb as follows: We perform an automated volume scan by means of a shell script loop.sh, with lattice parameters above and below the experimental value. Then, the procedure was to get the energy as a function of volume using by regression fitting DFT results to third-order Birch-Murnagahn equation of state, EOS.8
In Eq. (3),  was found from the regression fitting in Fig. 1, which corresponds to the cell volume that result in the lowest possible total energy of the system. One last calculation to calculate the Zr lattice parameter was to optimize the ionic structure of a zirconium cell with a fixed volume equal to the value of
was found from the regression fitting in Fig. 1, which corresponds to the cell volume that result in the lowest possible total energy of the system. One last calculation to calculate the Zr lattice parameter was to optimize the ionic structure of a zirconium cell with a fixed volume equal to the value of  . In addition, by getting the energy as a function of volume using third-order Birch-Murnagahn EOS, information about bulk modulus was also found.
. In addition, by getting the energy as a function of volume using third-order Birch-Murnagahn EOS, information about bulk modulus was also found.
The optimization procedure is also used with hcp structures. The fitting of the best  and
and  or
or  for hcp crystals is more difficult than in the previous case of the cubic lattices. This is because for hcp alloys, one should define a global minimum of the total energy of a crystal as a function of both, the volume of the unit cell and the structural relation
for hcp crystals is more difficult than in the previous case of the cubic lattices. This is because for hcp alloys, one should define a global minimum of the total energy of a crystal as a function of both, the volume of the unit cell and the structural relation  .
.
We have obtained a lattice parameter of  Å and
Å and  Å for a supercell containing 16 and 54 Nb atoms, respectively.
Å for a supercell containing 16 and 54 Nb atoms, respectively.
Also, the above procedure, is performed in order to obtain the optimal lattice parameter of the structure including interstitial (H) and substitutional (Nb) defects. For  Zr and
Zr and  Zr containing impurities, a test value of structural relation
Zr containing impurities, a test value of structural relation  was fixed. The standard optimization procedure, like in the case of cubic lattices, was used to define the optimal volume of the unit cell corresponding to the minimum of the total energy as a function of the unit cell volume,
was fixed. The standard optimization procedure, like in the case of cubic lattices, was used to define the optimal volume of the unit cell corresponding to the minimum of the total energy as a function of the unit cell volume,  , where i=1,...,N, the number of test values for the structural relation
, where i=1,...,N, the number of test values for the structural relation  .
.
The obtained empiric data as the dependence  , were approximated by the functional dependence. The minimum of this dependence corresponds to the optimal value of the structural relation
, were approximated by the functional dependence. The minimum of this dependence corresponds to the optimal value of the structural relation  . Next, for the determined
. Next, for the determined 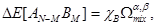 , the standard optimization procedure was made to determine a global minimum of the total energy and the optimal unit cell volume, respectively.
, the standard optimization procedure was made to determine a global minimum of the total energy and the optimal unit cell volume, respectively.
Using the standard definition for the volume of the HCP unit cell  the optimal lattice constant
the optimal lattice constant  was determined for each case. Table 1, summarizes present results of the optimized lattice parameters from Zr and Nb.
was determined for each case. Table 1, summarizes present results of the optimized lattice parameters from Zr and Nb.
Table 1 reports the calculated lattice parameters of  ,
,  Zr and
Zr and  Nb, namely: The lattice parameters,
Nb, namely: The lattice parameters,  and
and  , the Bulk modulus,
, the Bulk modulus,  , the Cohsive energy,
, the Cohsive energy,  , the vacancy formation energy,
, the vacancy formation energy,  , and the vacancy migration energy,
, and the vacancy migration energy,  , in comparison with experimental and theoretical values reported in the literature.
, in comparison with experimental and theoretical values reported in the literature.
Fig. 1, show our results of the optimized lattice parameter from the fit of Eq. (3) of a supercell containing 16 atoms of  Nb. In this case the Bulk modulus was obtained, as well as, the resulting pressure of the supercell after relaxation. The same procedure was followed from 2 up to 54 atoms of Nb and Zr atoms with bcc structure.
Nb. In this case the Bulk modulus was obtained, as well as, the resulting pressure of the supercell after relaxation. The same procedure was followed from 2 up to 54 atoms of Nb and Zr atoms with bcc structure.
The comparison in Table 1 shows that the predicted geometries of the GGA (PBE) slightly overerestimated the experimental lattice parameters. Although the regression fitting of the EOS in Eq. (3) overestimates  by about 1.0%, this discrepancy between the DFT results and the reported experimental data was acceptable for this study. Then, the current set up of zirconium supercells with the chosen k-points mesh is approximately accurate in representing the actual zirconium and niobium metal structure.
by about 1.0%, this discrepancy between the DFT results and the reported experimental data was acceptable for this study. Then, the current set up of zirconium supercells with the chosen k-points mesh is approximately accurate in representing the actual zirconium and niobium metal structure.
The dependence of the lattice parameter, 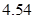 , for
, for  Zr-Nb alloys versus niobium concentration was previously evaluated in Ref..25 The authors have shown that with an increase in the niobium concentration the lattice constant decreases according to the linear law. This result is consistent with the well known approximate empirical rule, called in metallurgy Vegard’s law. Also, at 0% of Nb the lattice parameter of
Zr-Nb alloys versus niobium concentration was previously evaluated in Ref..25 The authors have shown that with an increase in the niobium concentration the lattice constant decreases according to the linear law. This result is consistent with the well known approximate empirical rule, called in metallurgy Vegard’s law. Also, at 0% of Nb the lattice parameter of  Zr is
Zr is 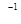 Å while for pure
Å while for pure 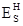 Nb is
Nb is  Å. Present calculations give
Å. Present calculations give  Å.
Å.
IV. THE ENERGETIC OF THE Zr-Nb SYSTEM
IV.1 Mixing solution energy
The mixing solution energy,  , of a substitutional B atom in a matrix of A atoms with
, of a substitutional B atom in a matrix of A atoms with  or
or  structure, is obtained as,19
structure, is obtained as,19
with  the energy of the supercell with (N-M) A atoms and M B-atoms,
the energy of the supercell with (N-M) A atoms and M B-atoms,  the reference energy of the matrix calculated with the same supercell and
the reference energy of the matrix calculated with the same supercell and  the energy per atom of B in its state of reference (bcc for
the energy per atom of B in its state of reference (bcc for  and hcp for
and hcp for  ). This excess energy is the solution energy weighted by the solute concentration
). This excess energy is the solution energy weighted by the solute concentration  as in Ref.,19
as in Ref.,19
High and positive values of Eq. (5), show a strong tendency to Zr and Nb atoms not to mix in the Zr-Nb alloy. Here, for the diluted limit, we have used a supercell of 108 and 144 atoms respectively for bcc Nb and hcp Zr.
As  and defining
and defining 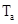 we obtain
we obtain  eV for a substitutional Zr diluited in
eV for a substitutional Zr diluited in  , and
, and  eV for a substitutional Nb atom in
eV for a substitutional Nb atom in  . The last results are in agreement with previous DFT ones of 0.61 eV26 and 0.68 eV.27
. The last results are in agreement with previous DFT ones of 0.61 eV26 and 0.68 eV.27
Our results show that Nb has a low solubility in  given the high value of 0.63 eV, while Zr has high solubility in
given the high value of 0.63 eV, while Zr has high solubility in  . For the supercells with 54 and 48 atoms of
. For the supercells with 54 and 48 atoms of  Nb and
Nb and 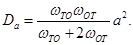 Zr,
Zr,  eV and
eV and  eV, respectively.
eV, respectively.
IV.2 Hydrogen solution energies
The hydrogen solution energy,  , at stable sites were calculated according to the following expression,28
, at stable sites were calculated according to the following expression,28
In Eq. (6)
 is the energy of the supercell containing N atoms plus an absorbed hydrogen at a determined interstitial site,
is the energy of the supercell containing N atoms plus an absorbed hydrogen at a determined interstitial site,  the energy of supercell without defects,
the energy of supercell without defects,  the energy of the hydrogen in the gaseous phase, and
the energy of the hydrogen in the gaseous phase, and  , the zero point energy (ZPE) that corresponds to quantum corrections. The value of the solution energy in a given site gives us information about the stability of such a site.
, the zero point energy (ZPE) that corresponds to quantum corrections. The value of the solution energy in a given site gives us information about the stability of such a site.
In Eq. (6), the third term corresponds to half of the total energy of the hydrogen molecule, is calculated using a cell of sides  Å
Å containing only the dimer,
containing only the dimer,  , in the center of the cell for a single k-point. While the last term, correspond to the zero point energy due to quantum corrections.
, in the center of the cell for a single k-point. While the last term, correspond to the zero point energy due to quantum corrections.
Fig. 2 shows the obtained equilibrium bond length of 0.750 Å for the hydrogen molecule, and a dimer energy of 6.765 eV, from which we calculate a binding energy of  eV for the hydrogen molecule, in agreement with experimental values of 0.741 Å, and 4.75 eV,29 respectively.
eV for the hydrogen molecule, in agreement with experimental values of 0.741 Å, and 4.75 eV,29 respectively.
The calculated  vibration frequency are 4401 cm
vibration frequency are 4401 cm , that agrees with the experimental value of 4395 cm
, that agrees with the experimental value of 4395 cm .30 Finally, present result of the ZPE 0.27 eV, reproduces the experimental value 0.274 eV.29
Table 2, summarizes our results of the H solution energy in the
.30 Finally, present result of the ZPE 0.27 eV, reproduces the experimental value 0.274 eV.29
Table 2, summarizes our results of the H solution energy in the  and
and  respectively for a supercell of 48 and 54 atoms.
respectively for a supercell of 48 and 54 atoms.
High and negative values of the solution energies mean stable sites, while positive values can infer that the site will be unoccupied or, the site is not favorable for hydrogen solubilization.
The results in Table 2 reveal that H is highly soluble on both the T and O sites of  Zr phase, with the following energy relationship
Zr phase, with the following energy relationship  . Concerning
. Concerning  Nb, H preferentially dissolves at the T site, whose solubility is much higher than at the O site. In regarding the energy of solution for the 2H in the
Nb, H preferentially dissolves at the T site, whose solubility is much higher than at the O site. In regarding the energy of solution for the 2H in the  Zr phase, we observe that the T site is the preferential site for 2H whose energy of solution is more than double that of the isolated H in the same phase, showing that there is a slight interaction between the 2H.
Zr phase, we observe that the T site is the preferential site for 2H whose energy of solution is more than double that of the isolated H in the same phase, showing that there is a slight interaction between the 2H.
IV.3 Binding energies
The hydrogen binding energy in a crystal containing N atoms of Zr plus  atoms of Nb on substitutional sites, was calculated with the following expression,
atoms of Nb on substitutional sites, was calculated with the following expression,
In Eq. (7)
 and
and  are respectively the energy of the supercell of Zr containing
are respectively the energy of the supercell of Zr containing  substitutional atom of Nb, plus
substitutional atom of Nb, plus  -atoms of interstitial H, and the energy o the supercell with (
-atoms of interstitial H, and the energy o the supercell with ( ) atoms of Zr plus a substitutional Nb.
) atoms of Zr plus a substitutional Nb.  is the energy of the crystal containing
is the energy of the crystal containing  -atoms of Zr with a single interstitial H at its minimum configuration, while
-atoms of Zr with a single interstitial H at its minimum configuration, while 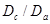 is the energy of the perfect Zr lattice. Negative/positive values of
is the energy of the perfect Zr lattice. Negative/positive values of 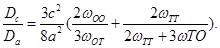 indicate repulsion/attraction between the H and the solute atom. Table 3 summarizes present results with Siesta and Vasp.
indicate repulsion/attraction between the H and the solute atom. Table 3 summarizes present results with Siesta and Vasp.

TABLE 3: Binding energies (in eV) with Siesta/Vasp calculations for a supercell with N=48 atoms of Zr, n=1 or 2 H atoms and k=1 atom of substitutional Nb. 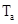 and
and  correspond to tetrahedral sites for H in the basal and axial axes, respectively.
correspond to tetrahedral sites for H in the basal and axial axes, respectively.
Our calculations predict T-sites as the preferential sites of hydrogen dissolved in  Zr, with
Zr, with 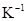 eV the energy difference between T- and O- hydrogen sites. In presence of Nb, this energy difference was maintained.
eV the energy difference between T- and O- hydrogen sites. In presence of Nb, this energy difference was maintained.
Results in Table 3, show that  were mostly positive, indicating that the interactions are attractive, that is, energetically favorable for the formation of the complexes, according to Domain et al..32
were mostly positive, indicating that the interactions are attractive, that is, energetically favorable for the formation of the complexes, according to Domain et al..32
The exception is the binding energy of -0.01 / -0.02 eV, weak and negative, showing that the two T- hydrogen do not interact with Nb in the axial plane. The other negative energy of -0.02 eV reveal a slight repulsion between the two O-hydrogen first neighbors of Nb, in the basal plane.
From values in Table 3, we assume that the presence of Nb in  Zr, with a positive binding energy with H, can be interpreted as a reduction in the hydrogen diffusivity by the hydrogen trapped locally by the Nb atom.
Zr, with a positive binding energy with H, can be interpreted as a reduction in the hydrogen diffusivity by the hydrogen trapped locally by the Nb atom.
V. HYDROGEN DIFFUSION COEFFICIENT
Hydrogen diffusion in hcp Zr involving T and O sites driven by interstitial mechanism were studied with a model proposed by Ishioka and Koiwa,33 using an on-lattice random walk model for hcp crystals. The diffusivity along  and
and 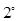 directions are expressed as,
directions are expressed as,
In Eqs. (8) and (9),  are the mean jump frequencies
are the mean jump frequencies  of the four possible hydrogen transitions, namely:
of the four possible hydrogen transitions, namely: 
 ,
,  and
and  .
.
In order to compute the mean jump frequencies  in Eqs. (8) and (9), we use the Vineyard formalism,34 that corresponds to the classical limit, where the vibrational prefactors,
in Eqs. (8) and (9), we use the Vineyard formalism,34 that corresponds to the classical limit, where the vibrational prefactors,  , do not depend on the temperature, that is
, do not depend on the temperature, that is
In (10),  are the vacancy migration energies at
are the vacancy migration energies at  K, while
K, while
with  and
and  the frequencies of the normal vibrational modes at the initial and saddle points, respectively, and
the frequencies of the normal vibrational modes at the initial and saddle points, respectively, and  the Deby’s frequency. Migration barriers were calculated with the Monomer2 coupled to Siesta,6 and the DIMER Method3 as implemented in Vasp. Present results of the migration barriers (in eV) are summarized in Table 4.
the Deby’s frequency. Migration barriers were calculated with the Monomer2 coupled to Siesta,6 and the DIMER Method3 as implemented in Vasp. Present results of the migration barriers (in eV) are summarized in Table 4.

TABLE 4: Hydrogen migration energies,  (in eV), in
(in eV), in  calculated with Siesta and Vasp for a supercell of N=48 atoms of Zr and one interstitial H.
calculated with Siesta and Vasp for a supercell of N=48 atoms of Zr and one interstitial H.
The anisotropy of hydrogen diffusion in  Zr has been widely studied from Monte Carlo Kinetic (KMC),7,35 using individual H jumps between first neighbors (1NN) T and O sites. These authors have found an expression of the diffusion coefficient
Zr has been widely studied from Monte Carlo Kinetic (KMC),7,35 using individual H jumps between first neighbors (1NN) T and O sites. These authors have found an expression of the diffusion coefficient  m
m s
s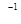 , which is higher than the experimental value of
, which is higher than the experimental value of  m
m s
s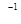 36 for
36 for  K.
K.
On the other hand, Sawatzky et al.35 have obtained the diffusion coefficient for hydrogen in annealed and extruded specimens as  m
m s
s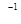 with
with  KJ/mol over the temperature range 473 to 973 K from KMC calculations. While, Zhang et al.,7 are who have obtained results closer to the experimental ones. Fig. 3 shows our results of
KJ/mol over the temperature range 473 to 973 K from KMC calculations. While, Zhang et al.,7 are who have obtained results closer to the experimental ones. Fig. 3 shows our results of  and
and  in
in  calculated from Eqs. (8) and (9) using both, Siesta and Vasp codes.
calculated from Eqs. (8) and (9) using both, Siesta and Vasp codes.
Experimental data from Ref.37 and previous numerical results from KMC calculations in Ref.,35 are also included. Experimental results of hydrogen diffusion in  Zr-2.5Nb,38 are shown in blue line.
Zr-2.5Nb,38 are shown in blue line.
The mean jump frequencies were calculated from Eqs. (10) and (11) with the migration barriers listed in Table 4, verify  .
.
Fig. 3(c) shows the behavior of the mean jump frequencies with the inverse of the temperature.

FIG. 3: Hydrogen diffusion coefficients vs 1/T (K−1). The hydrogen diffusion coefficients Dc and Da in black solid and dashed lines respectively, from present calculations with: (a) Siesta, and (b) Vasp. In open triangles and stars DH from experimental data 36 and KMC results 35. The experimental hydrogen diffusion coefficient in Zr-2.5Nb 38 (in blue solid line) is also shown. (c) Mean jump frequencies vs 1/T (K−1). 
Fig. 3(a)-(c), show our numerical results of  and the mean jump frequencies in
and the mean jump frequencies in  Zr in terms of 1/T (in K
Zr in terms of 1/T (in K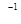 ), compared with experimental data in pure metal and the alloy Zr-2.5 Nb. Our results with Vasp reproduce very well the experimental data and the numerical results of KMC.
), compared with experimental data in pure metal and the alloy Zr-2.5 Nb. Our results with Vasp reproduce very well the experimental data and the numerical results of KMC.
The anisotropy of the H diffusion in hcp Zr along the  and
and  axes, is measurable from the
axes, is measurable from the 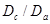 ratio,
ratio,
The dependence on the temperature of the ratio 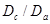 , defined in Eq. (12) is through the mean jump frequencies
, defined in Eq. (12) is through the mean jump frequencies  . Fig. 4 shows that the results of the ratio
. Fig. 4 shows that the results of the ratio 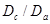 in Ref.7 (symbols in orange) agree better with present results with Vasp (in dashed line) than with Siesta (solid line). Possibly because Siesta overestimate the values of the migration barriers.
in Ref.7 (symbols in orange) agree better with present results with Vasp (in dashed line) than with Siesta (solid line). Possibly because Siesta overestimate the values of the migration barriers.

FIG. 4:
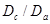 vs
vs (in
(in 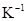 ). Symbols in black show our results with Vasp (open stars) and Siesta (full stars). In orange the results in Ref. 7
). Symbols in black show our results with Vasp (open stars) and Siesta (full stars). In orange the results in Ref. 7
VI. ZIRCONIUM HYDRIDES
The three most stables zirconium-hydrides in Zr based alloys are  ,
,  ,
,  . The
. The  hydride is the most frequent in Zr-2.5Nb which appears at slow speed of cooling low than
hydride is the most frequent in Zr-2.5Nb which appears at slow speed of cooling low than 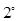 C/ min. The composition of the
C/ min. The composition of the  -hydride is
-hydride is  with
with  (56.7 to 66 % at Hydrogen, simulated as
(56.7 to 66 % at Hydrogen, simulated as  ). This hydride forms plates located at the grain boundaries or trans-granular interphases.
). This hydride forms plates located at the grain boundaries or trans-granular interphases.
This particular form is associated with the following relation of orientation:  and
and  , which generates a
, which generates a  plane that is practically parallel to the basal plane of Zr39 and precipitates mostly in the radial direction, as shown in Fig. 5.40
plane that is practically parallel to the basal plane of Zr39 and precipitates mostly in the radial direction, as shown in Fig. 5.40
We present our preliminary results in Table 5, of the three stable hydrides schematized in Fig. 6. Our results reproduce well the ones obtained by Glasoff.41 We have followed the same methodology to familiarize ourselves with this type of structures. The equilibrium lattice constants were determined by lattice relaxation, minimizing the total energy of the system by varying atomic positions with the calculation parameters defined in Section II.

FIG. 6: Crystal structure of the 3 stable hydrides in zirconium: orthorrombic  ; cubic
; cubic  and tetragonal
and tetragonal  .
.
In Table 5, the values of the lattice parameter of each cell vary little from one hydride to another. Our results agree very well with the calculations made by Glazoff41 and with the available experimental data. The hydride formation enthalpy,  , is calculated as Glasoff.41
, is calculated as Glasoff.41
VII. CONCLUSIONS
In summary, we have studied the hydrogen diffusion by ab initio methods in  Zr. Also, the energetic of hydrogen in the Zr-Nb system were also studied. We remark that,
Zr. Also, the energetic of hydrogen in the Zr-Nb system were also studied. We remark that,
our DFT results of the lattice parameters are in well agreement with the experimental values.
The calculated formation energies are within the range of values of previous references and experimental values.
The mixing energy in the dilute limit shows that Zr is energetically favorable to dissolve in the bcc phase of Nb, and on the contrary, Nb has a low solubility in hcp Zr.
The presence of Nb in hcp Zr moderately increases the solubility of H around the impurity, implying in a slight reduction in diffusivity of the H by trapping H locally, forming the H-Nb complex.
The hydrogen solution energy shows that tetrahedral sites are the most stable for H.
The H-diffusion coefficient in hcp Zr, calculated with Vasp reproduce very well the experimental values and previous results from KMC.


















