1- INTRODUCCIÓN

La corona solar está formada por un plasma magnetizado caracterizado por altas temperaturas del orden de 10 6 K. Allí tienen lugar variados fenómenos. Entre los más energéticos y extremadamente intermitentes encontramos las erupciones solares. Cuando una de ellas ocurre el plasma coronal se calienta, localmente, hasta alcanzar temperaturas del orden de 10 7 K en tiempos extremadamente cortos (entre 10 y 1000 segundos). En los últimos 30 años las erupciones solares han sido intensamente estudiadas y se han observado usando diversas técnicas y en un gran número de longitudes de onda¹ puesto que emiten radiación que se extiende ampliamente en el espectro electromagnético: desde las ondas de radio hasta ondas cortas y rayos gamma, mientras liberan energía en un rango de 10 27 a 10 33 erg.

El análisis estadístico de la energía liberada y la duración de las erupciones solares ha puesto en evidencia que la distribución de frecuencias de ambas cantidades (entre otras) sigue la forma de una ley de potencias que se extiende por varios órdenes de magnitud.^2,3

Durante los años ochenta, y a partir de sus trabajos sobre la reconexión magnética en plasmas, Eugene Parker sugirió que este era el mecanismo que permitía relacionar la liberación de energía cinética con el campo magnético coronal. Según la hipótesis de Parker los campos magnéticos coronales anclados en el plasma fotosférico (altamente turbulento) sufren fuertes deformaciones que se acumulan formando complejas hojas de corrientes. Cuando la intensidad de la corriente en dichas hojas aumenta más allá de un cierto umbral el fenómeno de reconexión magnética domina (localmente) la dinámica coronal y la energía magnética se libera en forma de energía cinética y energía térmica.^4,5

Para constatar la hipótesis de Parker es necesario resolver numéricamente las ecuaciones de la magnetohidrodinámica. Esta tarea resulta muy engorrosa puesto que la disparidad de escalas temporales y espaciales a resolver en un mismo código es inabarcable con las simulaciones que la comunidad dispone en este momento. Por ejemplo Dmitruk y Gómez⁶ han desarrollado simulaciones numéricas sobre un modelo de Parker bidimensional simplificado en el cual pudieron identificar eventos intermitentes asimilables con avalanchas que han sido analizados en detalle.⁷

El paradigma de la criticalidad auto-organizada (self-organized criticality, -SOC-⁸) es una alternativa menos costosa (desde el punto de vista computacional) y que puede usarse como una alternativa para tratar el problema de la existencia de las erupciones solares y su comportamiento estadístico. En 1991 Lu & Hamilton⁹ propusieron que la corona solar se encuentra en un estado de criticalidad auto-organizada y la dinámica del campo magnético coronal podría modelarse a través de un autómata celular, pudiendo, de esta forma, explicar su comportamiento auto-similar. El impacto de este trabajo en la comunidad fue inmediato y a lo largo de los siguientes 20 años se produjeron muchos trabajos cuyo objetivo fue modelar de forma sencilla y eficaz las erupciones solares (ver ^{Charbonneau, 2001} y numerosas referencias incluidas en dicho trabajo¹⁰) y obtener resultados que pudieran comparse con las observaciones realizadas por misiones como SOHO, STEREO, AIA, etc..³

El mayor éxito del modelo de Lu & Hamilton puede asociarse a la posibilidad de calcular exponentes críticos relacionados con la energía total liberada y a la duración de los eventos eruptivos en la corona mientras que el cálculo de las distribuciones estadísticas del tiempo entre eventos waiting time ha suscitado varios interrogantes discutidos extensamente.^11,12

En este trabajo retomaremos la discusión del problema de tiempo entre eventos para el caso del modelo de Lu & Hamilton proponiendo nuevas definiciones operativas del mismo que, por otra parte, resultan más afectivas a la hora de comparar los resultados sintéticos con las observaciones solares. En la Sección 2 se presenta el modelo de Lu & Hamiton; en la Sección 3 se describen las simulaciones realizadas en este trabajo. En la Sección 4 se presentan las definiciones de tiempo entre eventos utilizadas y los resultados obtenidos. También se discuten sus alcances y limitaciones. Finalmente, la Sección 5 está dedicada a las conclusiones.

2- MODELO DE LU & HAMILTON

El primer modelo de avalancha de erupciones solares fue planteado por ^{Lu & Hamilton en 1991} (de ahora en más LH91). Esencialmente, se trata de una red de nodos interconectados (en 2 o 3 dimensiones) en cada uno se define una cantidad . Es posible interpretar esta cantidad como una medida del campo magnético de modo que representa la energía magnética de red.

La Fig. 1 muestra una grilla cartesiana bidimensional donde cada nodo interactúa con sus primeros vecinos. Tiene tamaño lineal y, entonces, el número total de nodos es . Cada nodo interior tiene primeros vecinos. Como condición de contorno se asume en los bordes de la grilla.

FIG. 1: Grilla cartesiana bidimensional. Se define una cantidad B en cada nodo. El nodo negro será perturbado y los nodos grises son los correspondientes primeros vecinos. 

Se define el valor medio del campo en la grilla como:

(1)

y la energía de la grilla

(2)

donde las sumas sobre son para cada coordenada de la dimensión, desde hasta .

Por las características del plasma coronal, y desde un punto de vista energético, es suficiente considerar la dinámica del campo magnético, dado que la energía magnética domina la energía total del sistema.¹³

Forzado del sistema

La corona solar se encuentra en un estado estacionario (global). Para simular dicho estado a partir del autómata celular se requiere que la cantidad física definida en la grilla sea forzada externamente. Para lograr eso, se selecciona, aleatoriamente, un nodo perteneciente al interior de la red y se incrementa su valor conforme a la siguiente regla:

(3)

El incremento es también un número aleatorio en el intervalo:

(4)

con y seleccionados para que el valor medio de la distribución de perturbaciones sea , de modo que el valor medio del campo crece en la grilla con el aumento de las iteraciones. El objetivo de sumar representa numéricamente el lento reajuste del campo magnético en la frontera fotosférica.

Criterio de estabilidad

En cada iteración se estudia la estabilidad en cada uno de los nodos de la red. Para ello es necesario establecer un criterio específico de estabilidad. En este caso, un nodo es considerado inestable si el valor de una medida de la curvatura del campo excede cierto umbral prefijado :

(5)

donde la suma se realiza sobre los primeros vecinos en la grilla -dimensional. Esta ecuación tiene la forma de una diferencia finita centrada de segundo orden para el operador laplaciano -dimensional actuando sobre el campo . El valor numérico de no tiene influencia en el comportamiento general del modelo, solo deber ser distinto de cero. La presencia de un umbral de estabilidad es crucial, pues le permite al sistema acumular energía.

El umbral de estabilidad es análogo aquí al umbral de corriente que desencadena el proceso de reconexión en la corona solar.¹⁴

Redistribución de energía en la red

Una vez que se verifica que un nodo dado es inestable, es necesario poner en marcha un procedimiento para restablecer la estabilidad. El objetivo de esta regla de redistribución es representar la relajación del campo magnético debido al proceso de la reconexión magnética. Un proceso natural es disminuir del nodo inestable y distribuirlo entre los correspondientes nodos vecinos:

(6)

(7)

con 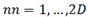, y para los nodos que se encuentren en el borde de la grilla truncar su valor de a 0 (lo que equivale a dejar que los granos de arena caigan fuera del sistema).

El reajuste es sólo una difusión local del campo que reduce el valor local de y hace que el campo sea estable en ese punto, pero cambia el valor de en puntos cercanos. Siguiendo la regla, uno o más vecinos pueden exceder el umbral de inestabilidad. En ese caso, la regla de redistribución se aplica a esos nodos, y así hasta restablecer la estabilidad en todos lados. La secuencia de eventos de redistribución representa la realización de una avalancha.

Mientras en el sistema se está produciendo una avalancha se interrumpe el mecanismo de perturbación que solo se retoma cuando todos los nodos de la red han alcanzado la estabilidad. De este modo, el modelo representa a un sistema en el que la escala de tiempo de perturbación es mucho más larga que la escala de tiempo de reajuste, es decir que el campo añadido durante una avalancha puede ser despreciado. No perturbar el campo durante avalanchas corresponde al límite en el que los cambios en el campo magnético coronal debido a las condiciones de frontera subfotosféricas pueden ser ignorados durante la el tiempo que dura una fulguración.

Esta regla de redistribución es localmente conservativa en la variable, entonces permanece constante. Sin embargo, la cantidad decrece considerando los nodos implicados en la redistribución:

(8)

donde la energía liberada se asigna al nodo inestable . Recordando que es la energía magnética, la energía total liberada por todos los nodos inestables en una dada iteración es similar a la energía liberada por unidad de tiempo por una fulguración:

(9)

Estrictamente, solo se cumple para avalanchas que no alcanzan los límites de la grilla, ya que la condición en los contornos también elimina la energía del sistema en una forma no contabilizada en la Ec. (9). La energía liberada por un único nodo que excede el umbral de estabilidad en una cantidad infinitesimal es: . Esto representa la menor cantidad de energía liberada por la grilla.

Esta regla de redistribución es análoga a la descripción de los nanoflares en la conjetura de Parker: la inestabilidad activa la reconexión magnética local y el reajuste implica una difusión local rápida del campo con la consecuente reducción de la energía del mismo. Tanto este modelo como el campo magnético de la región activa solar son ejemplos de sistemas disipativos ya que la energía del campo no se conserva en una inestabilidad.

3- CARACTERIZACIÓN Y ESTADÍSTICA DE AVALANCHAS

Realizamos simulaciones con una versión 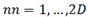del modelo de Lu & Hamilton para redes de tres tamaños: y con diferentes umbrales:

FIG. 2: El gráfico (A) muestra la serie temporal de la energía total para una red con las siguientes características: . La energía se ha normalizado con la unidad mínima de energía . En el estado de criticalidad auto-organizada la energía se estabiliza. El gráfico (B) ilustra la variabilidad observada durante la fase estacionaria de la simulación. 

Las series temporales de la energía total de la red y de la energía liberada por uno de estos sistemas ilustra, en la Fig. 2, el comportamiento típico de estos autómatas: la energía aumenta con la evolución temporal del sistema e ingresa energía en el sistema hasta que, cerca de la iteración esta se nivela de forma bastante brusca y se mantiene más o menos constante. Al mismo tiempo, en el caso de la energía liberada se observan inicialmente avalanchas pequeñas que dan cuenta de la liberación de energía que ocurren durante la fase de crecimiento de energía. Cuando el sistema alcanza su estado estacionario, las avalanchas incrementan notablemente su tamaño (ver Fig. 3).

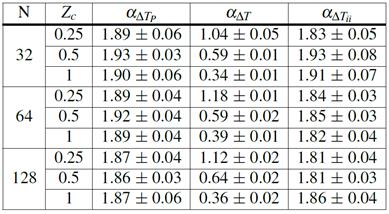
TABLA 1: Para cada una de las simulaciones realizadas se presentan los exponentes de las leyes de potencia estimados: la energía , el pico y la duración , y la relación entre las variables E vs P y P vs T ( y ), todos con sus respectivos errores. 

Es interesante mencionar que se trata de un estado estadísticamente estacionario de modo que en escalas temporales suficientemente largas el campo magnético (y la energía magnética asociada) no crecen ni decrecen. Vemos que, a pesar de que la perturbación introducida es constante, la disipación de energía se produce de manera altamente intermitente: avalanchas, autosimilares en espacio y tiempo.

FIG. 3: El gráfico (A) muestra la serie temporal de la energía liberada por las avalanchas para . Cuando el sistema alcanza el estado SOC se observa dramático aumento del tamaño de las avalanchas. El gráfico (B) muestra una pequeña porción de iteraciones donde se liberó energía, e ilustra la naturaleza discreta del proceso intermitente de liberación de energía. Se identifican en (B): el pico de liberación de energía , la energía total y la duración de la avalancha definidas en el texto. 

FIG. 4: Distribución de probabilidades para E, P y T calculada a partir de los datos con N^D =128² y Z_c =0.5 superpuesta al ajuste lineal (línea punteada). 

Para caracterizar las avalanchas producidas por el modelo de Lu & Hamilton estudiamos el comportamiento estadístico de ciertas cantidades típicas: la cantidad total de energía liberada en la vida de una avalancha ; el valor máximo de energía liberada 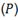en la avalancha y, la duración de un evento .

Para cada simulación se identificaron las avalanchas ocurridas durante la fase estacionaria, se midieron , y y se graficó su distribución de probabilidades (Probability distribution function -PDF). En la Fig. 4 se muestran los resultados obtenidos para una red de y umbral . Se observa un claro comportamiento del tipo ley de potencia que se extiende por más de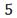 órdenes de magnitud para la energía y el pico de las avalanchas. Para cada uno podemos realizar un fiteo lineal y, el valor de la pendiente obtenido, es lo que llamamos los exponentes críticos del sistema. En el caso de la duración el comportamiento tipo ley de potencias se reduce un poco puesto que el tamaño de la red reduce la duración máxima de las avalanchas.

En la Tabla 1 se presenta un resumen de los valores obtenidos para cada uno de los exponentes críticos. Vemos que en todos los casos se trata de cantidades robustas ante el cambio de escala y que el umbral elegido no tiene incidencia final en el valor del exponente reportado. De esta manera corroboramos que la dinámica del sistema es un emergente de la interacción de los elementos que la componen.

4- EL TIEMPO ENTRE EVENTOS: DEFINICIONES Y ESTADÍSTICA

Hay otra cantidad fundamental para estudiar la capacidad predictiva de los modelos de avalanchas de erupciones solares: el tiempo transcurrido entre una avalancha y otra. Cuantificar esta cantidad puede ser muy sencillo en el caso de las simulaciones numéricas pero en el caso de las erupciones observadas no está claro cuándo la avalancha ha comenzado y cuándo ha finalizado.

Definiciones alternativas del tiempo entre avalanchas se han utilizado al estudiar otros sistemas críticos¹⁵ y algunas de ellas pueden ser mucho más propicias para describir las erupciones solares.

La forma tradicional de caracterizar el tiempo de espera entre avalanchas es considerar el espacio temporal (número de iteraciones) entre el fin de una avalancha y el principio de la siguiente: . Por otra parte, se define como el tiempo transcurrido entre el inicio de una avalancha y el inicio de su consecutiva y, finalmente se define como como la distancia temporal entre los picos de energía de una avalancha y la avalancha consecutiva.

Para cada una de las simulaciones presentadas en la Sección 3, se realizó un histograma de frecuencias para las tres variables . Para el caso de la definicón más habitual del tiempo de espera encontramos el resultado previamente reportado por¹¹ y.¹² El comportamiento estadístico de esta variable es exponencial: donde es la tasa media de avalanchas en toda la simulación (el número de avalanchas sobre el número de iteraciones sin avalanchas). Esto implica que el mecanismo para producir una avalancha tiene una distribución tipo Poisson, lo cual es esperado ya que la perturbación que se le agrega al sistema tiene una distribución uniforme.¹¹ En la Fig. 5 se observa la distribución de y su ajuste para una simulación de tamaño y.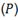

FIG. 5: Función distribución del tiempo entre avalanchas a partir de los datos superpuesta al ajuste lineal (línea punteada) de un sistema de y. 

La distribución estadística para las dos definiciones alternativas presentan una distribución tipo ley de potencias que se extiende por casi tres órdenes de magnitud, como puede observarse en la Fig. 6 para el caso de una de las simulaciones realizadas para y.

FIG. 6: Izquierda: PDF de 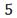. Derecha: PDF de . Ambos calculados a partir de los datos superpuesta al ajuste lineal (línea punteada) de un sistema de y. 

En la Tabla 2 se presentan, para cada simulación realizada, los exponentes de las leyes de potencias estimados para la definición de waiting time , junto con el exponente que caracteriza a la distribución exponencial, /). Puede observarse que, para 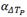y los valores obtenidos son robustos para los distintos umbrales y tampoco se observan cambios significativos para diferentes tamaños de grilla. Este último resultado puede comparse con el trabajo realizado por Boffeta y colaboradores¹⁶ en el cual, a partir de observaciones de fulguraciones en todo el disco solar, obtuvieron, para el tiempo entre el máximo de una fulguración y de su consecutiva, un comportamiento estadístico tipo ley de potencias con un valor del exponente un poco mayor que el obtenido en este trabajo . Los autores mencionan que el valor obtenido puede estar levemente afectado por escasez de fulguraciones de larga duración ya que el tiempo de observación limita la máxima duración de los registros disponibles.

TABLA 2: Exponentes para las tres definiciones de tiempo de espera para cada simulación realizada. 

5- CONCLUSIONES

Por más de 25 años el modelo de avalanchas de Lu & Hamilton ha sido utilizado como una gran herramienta para modelar la liberación de energía en la corona a partir de su efectividad para reproducir en un autómota muy sencillo las avalanchas de fulguraciones propuestas en el modelo de Parker.

En este trabajo se revisita dicho modelo bidimensional y se parte de nuevas definiciones del tiempo de espera entre avalanchas a.k.a. waiting time para discutir las posibilidades de pronosticar erupciones solares a partir de estos modelos sintéticos.

Por primera vez en modelos numéricos de este tipo se trabajó con dos definiciones alternativas al clásico tiempo entre avalanchas. Para el caso del tiempo entre el fin de una avalancha y el inicio de la siguiente el comportamiento estadístico observado fue el ya reportado por otros autores. Para el caso de las dos nuevas definiciones de tiempo de espera; el tiempo entre picos o el tiempo entre inicios de avalanchas se encontró que un comportamiento tipo ley de potencias que, en el caso del tiempo entre picos evoca los resultados obtenidos por otros autores para las fulguraciones observadas en todo el disco solar.

Estos nuevos resultados permiten asumir que utilizar el tiempo entre picos de dos avalanchas consecutivas podría ser una buena estrategia para aproximarse a la predicción de fulguraciones sintéticas como las que se obtienen a partir del modelo de Lu & Hamilton. Este camino podría ser especialmente ventajoso para estudiar la predictibilidad de eventos extremos producidos por este tipo de simulaciones (cuestión que diferimos para un próximo trabajo) y, en última instancia podría aportar nuevas ideas en el pronóstico de la influencia de las fulguraciones extremas en el clima espacial.