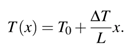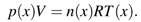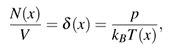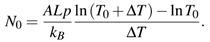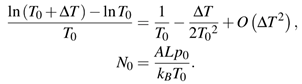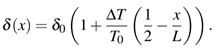1. INTRODUCCIÓN

La termodinámica es una disciplina sutil; basta un curso de cálculo para poder lidiar con la matemática involucrada pero hay algunos conceptos que son de difícil comprensión por parte de los estudiantes. Podríamos citar como ejemplo el caso de proceso cuasi-estático, y ni hablar del concepto de entropía que desvela aún a los expertos. Si la termodinámica usual tiene sus dificultades, con mucha mayor razón las tiene la termodinámica de no-equilibrio. No es intención de este artículo tratar sobre los problemas específicos que atañen a la enseñanza de la disciplina sino mostrar dos fenómenos térmicos de no-equilibrio que con un poco de astucia pueden ser tratados con la termodinámica que se enseña en nuestros cursos universitarios de grado ^[1-3]. El lector interesado en los problemas pedagógicos que entraña la enseñanza de esta disciplina encontrará en la Ref. ^[4] un excelente punto de partida.

El objetivo de este trabajo es reunir dos problemas de sistemas térmicos fuera de equilibrio que están al alcance de un estudiante de grado con un curso usual de termodinámica. Se va a presentar el caso de un gas ideal en un gradiente térmico, lo que genera un gradiente en la densidad del gas. A este problema, se le dedicará más atención. Después consideraremos el caso de la conducción del calor en una varilla metálica y veremos que es posible calcular la producción de entropía por unidad de tiempo. Estos dos problemas se resuelven aplicando el mismo truco: el sistema se fracciona en muchas secciones (o rodajas) que son lo suficientemente grandes como para poder aplicar la termodinámica y lo suficientemente pequeñas como para considerar que las magnitudes termodinámicas tienen un valor constante en cada sección.

El problema de la generación de entropía en la conducción del calor a través de una varilla ha sido publicado con anterioridad ^[5], no así el relacionado con la conducción de calor en un gas. Por esta razón, este problema será tratado en primer lugar y con detalle en este artículo. Respecto al otro, solo recordaremos los resultados obtenidos y remitiremos a la publicación original para el lector interesado en los cálculos detallados.

2. CONDUCCIÓN DEL CALOR EN UN GAS IDEAL

La situación experimental que se analiza se muestra en la Fig. 1. Se tiene un recipiente de longitud L y sección transversal A -ver Fig. 1a- que contiene N ₀ moléculas de un gas ideal a una temperatura inicial T ₀ y una presión inicial p ₀. Se considera que las paredes laterales del recipiente están aisladas por lo que no entra ni sale calor por ellas. Las otras dos paredes son diatérmicas, es decir, permiten el intercambio de calor. Seguidamente se pone en contacto uno de los extremos del recipiente con un reservorio térmico a temperatura T ₀ y el otro extremo con un reservorio a temperatura T ₀ + ∆T tal como se muestra en la Fig. 1b. Es claro que se va a establecer un flujo de calor desde el extremo más caliente al más frío. Supondremos que la diferencia de temperatura entre los dos extremos, ∆T es pequeña de forma tal que no aparezcan fenómenos de convección dentro del gas. Entonces, la transmisión del calor se produce sólo por conducción. Si es así se está en una situación análoga a la transmisión de calor a lo largo de una barra sólida, y es sabido que luego de un transitorio, la distribución de temperaturas en la barra es la mostrada en la Fig. 2a. Es decir, se puede escribir:

(1)

FIG. 1: Aquí se muestra el problema considerado en esta sección. (1a) Las dimensiones geométricas del recipiente y las condiciones termodinámicas iniciales del gas T₀, p₀, δ_o. (1b) El sistema se saca de equilibrio al colocar un extremo a una temperatura mayor que la inicial; se establece un flujo de calor de derecha a izquierda. (1c) Para poder resolver el problema, se considera al sistema partido en secciones (rodajas) de ancho tal que las magnitudes termodinámicas tengan un valor constante en su interior. Ahora la temperatura, presión y densidad son función de la posición. 

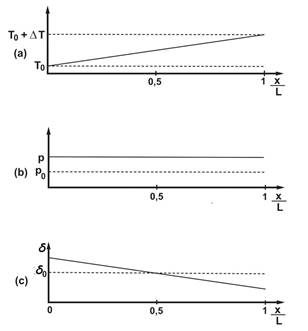
FIG. 2: Aquí se grafica en unidades arbitrarias, las magnitudes termodinámicas una vez que el sistema está en un estado estacionario. (a) La temperatura tiene un crecimiento lineal entre ambos extremos del recipiente. (b) La presión del gas aumenta a un nuevo valor p. (c) Aparece un gradiente en la densidad δ. 

Si algún estudiante que no está convencido de la Ec. (1) se lo puede enviar al sitio de internet citado en el próximo apartado ^[6] donde se resuelve la ecuación de la conducción del calor numéricamente y se muestra que para tiempos largos se obtiene la expresión anterior¹.

En la conducción del calor, el sistema está fuera de equilibrio por lo tanto en principio no se podría utilizar la termodinámica ya que ésta trata solo de sistemas que están en equilibrio. Sin embargo hay un truco sencillo que nos permite usar lo que sabemos y aplicarlo a esta situación. La forma de hacerlo es dividir el gas en celdas pequeñas, tal como se muestra en la Fig. 1c. Cada una de esas celdas es lo suficientemente grande como para contener una gran cantidad de moléculas, pero lo suficientemente pequeñas como para que las variables termodinámicas tengan valores constantes en su interior. Este es un procedimiento usual para analizar sistemas que no están demasiado alejados del equilibrio y nos permite utilizar toda la artillería de la termodinámica clásica. Podemos así definir una temperatura, presión y concentración que son función de la posición: T(x), p(x), n(x) y que localmente cumplen con la ecuación de los gases ideales:

(2)

Como es usual, en la Ec. (2) R es la constante universal de los gases, que puede escribirse como R = k _B N _A , siendo k _B la constante de Boltzmann y N _A el número de Avogadro, n(x) es la cantidad de moles contenidas en el volumen V de la celda elemental que está a una distancia x de la pared izquierda tal como se muestra en la Fig. 1c. Para uso posterior es conveniente tener en cuenta que n(x) R = n(x) k _B N _A = N(x) k _B siendo N(x) el número de moléculas presentes en la celda.

Es importante que el estudiante distinga entre un estado de equilibrio y uno estacionario. El sistema estudiado por nosotros está fuera de equilibrio pero lo analizamos cuando ha alcanzado el estado estacionario, esto es, cuando las variables relevantes ya no cambian con el tiempo. Entonces, una vez que ha transcurrido el transitorio, la presión en el tubo debe ser constante. Si no fuera así el gas fluiría hasta que se igualara en todo el recinto. Entonces, en la situación estacionaria, se tiene p(x) = p. Notar que esta presión no tiene por qué coincidir con la presión inicial p ₀ del gas y habrá que calcularla.

A partir de la Ec. (2) podemos calcular la concentración en función de la distancia y es conveniente rescribir nR como se explicó más arriba. Se tiene así:

(3)

δ(x) es la densidad del gas expresada en moléculas por unidad de volumen y que depende de la posición. La Ec. (3) va a ser usada para calcular la nueva presión p. El número total de moléculas no ha cambiado y por lo tanto, la integral de (3) en todo el volumen debe cumplir:

(4)

A partir de (4) se puede obtener la nueva presión del gas. Si se resuelve la integral utilizando la distribución de temperatura dada por (1), resulta:

(5)

La Ec. (5) sugiere fuertemente un desarrollo en series para el logaritmo y esto se puede hacer ya que hemos supuesto que ∆T es pequeño. Por otra parte, el número inicial de partículas N ₀ puede escribirse en términos de la temperatura y presión originales. Se tiene así:

(6)

Reemplazando las expresiones de (6) en (5) resulta:

(7)

La expresión (7) está graficada en la Fig. 2b. Resulta interesante evaluarla para algunos valores típicos. Supongamos que el gas inicialmente está a temperatura ambiente, T ₀ = 298 K, y la temperatura de un extremo se incrementa en 10 K. Entonces, el incremento porcentual de la presión será p / p ₀ = 1,017.

Una vez conocido el nuevo valor de la presión, se puede calcular la nueva densidad del gas. Reemplazando (1) y (7) en (3):

(8)

Dado que en todo el cálculo hemos supuesto que ∆T es pequeño, resulta razonable expandir la expresión anterior en potencias de ∆T y quedarse con el término de primer

orden. Se obtiene entonces:

(9)

Como es obvio δ ₀ es la densidad inicial dada por δ ₀= p ₀ T ₀ /k _B . En la Fig. 2c se grafica la ec. (9). Observar que para x = 0 la densidad es mayor que la inicial, mientras que para x = L resulta menor. Para los valores numéricos supuestos anteriormente resulta δ(0)/δ ₀ = 1,017 mientras que δ(L)/δ ₀ =0,983. En términos físicos esto significa que en el extremo caliente el aumento de presión de debe a un aumento en la temperatura mientras que en el extremo frío está asociado con un aumento en la densidad del gas.

Este ejercicio nos permite aprender dos cosas para sistemas fuera de equilibrio. En primer lugar, un gradiente en una magnitud termodinámica genera un gradiente en otra magnitud. En lo que mostramos más arriba, un gradiente de temperatura genera un gradiente de densidad. Pero hay otro ejemplo que los estudiantes conocen bien: las termocuplas que se utilizan cotidianamente en el laboratorio. En este caso una diferencia de temperatura genera una diferencia de potencial que puede ser medida con un voltímetro; es el denominado efecto Seebeck. Lamentablemente el análisis de este efecto no es tan sencillo como los casos tratados en este artículo.

El segundo aprendizaje que se deriva de nuestro ejercicio, es que se puede dividir un sistema en muchas partes que localmente están en equilibrio y aplicar las herramientas de la termodinámica usual a esas porciones del sistema. En nuestro caso, dividimos la columna de gas en secciones o rodajas y supusimos que en cada una de ellas podíamos aplicar lo que sabemos de termodinámica. Esta idea la vamos a aplicar a otro ejemplo en la próxima sección.

3. PRODUCCIÓN DE ENTROPÍA EN LA CONDUCCIÓN DEL CALOR A TRAVÉS DE UNA BARRA

Este problema ya fue publicado por el autor ^[5] y ha sido desarrollado numéricamente por el Prof. Ángel Franco García en un curso de física interactiva en internet [6] por lo que nos limitaremos a plantear el problema y mostrar el resultado central.

La situación física planteada es parecida a la considerada en la sección anterior: se tiene una varilla metálica aislada térmicamente y sus extremos se ponen en contacto con dos reservorios a temperatura T _h y T _c . Obviamente se establece un flujo de calor desde el reservorio caliente (T _h ) hacia el frio (T _c ) a través de la barra. El problema es calcular la tasa de producción de entropía dS/dt. Y hay que tener en cuenta que esa producción de entropía tiene dos orígenes: por un lado se genera en los reservorios y por otro se genera también en la varilla. Para calcular este último se recurre al mismo truco usado en la sección anterior: se fracciona la varilla en secciones; así se puede estimar la producción de entropía en cada una de ellas usando las herramientas termodinámicas usuales. Los detalles teóricos pueden verse en ^[5] y son muy interesantes los cálculos numéricos llevados a cabo en ^[6]. Ahí se resuelve explícitamente la ecuación de la conducción del calor y se muestra que para tiempos largos la distribución de temperaturas está dada por (1). Y lo que es más interesante, se calcula cómo varía con el tiempo la producción de entropía en los reservorios, en la varilla y en todo el sistema. El resultado puede verse en la Fig. 3. Es muy instructivo lo que muestra ese gráfico: la producción de entropía en la barra tiende a cero y en tiempos largos solo es relevante la producción de entropía que tiene lugar en los reservorios térmicos.

Con este ejercicio se muestra nuevamente la utilidad de fraccionar el sistema en secciones y estudiarlas con las herramientas convencionales. También se muestra que para sistemas fuera de equilibrio la entropía no alcanza un valor estacionario sino que aumenta con el paso del tiempo. Hay un teorema debido a Prigogine ^[7] que afirma que en un sistema fuera de equilibrio la tasa de producción de entropía es mínima. En un antiguo trabajo publicado en esta revista [8] se mostró como se puede usar ese resultado para obtener la distribución de corrientes y potenciales en circuitos eléctricos sencillos.

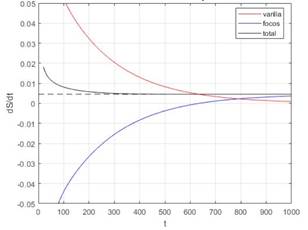
FIG. 3: Aquí se muestra cómo cambia con el tiempo la producción de entropía en el caso de la conducción del calor en una varilla. La producción de entropía tiene dos fuentes: la que se produce en los reservorios térmicos y la que se genera en la varilla. Esta última tiende a cero para tiempos largos. El desarrollo teórico de este problema se encuentra en ^[5] y los cálculos numéricos en ^[6]. 

4. COMENTARIOS FINALES

La tarea está concluida. Se ha mostrado cómo se puede estudiar un gas ideal sometido a un gradiente térmico usando los conocimientos proporcionados por un curso usual de termodinámica. Se ha encontrado que el gas aumenta su presión y se establece un gradiente de densidad en sentido opuesto al gradiente de temperatura: donde la temperatura es mayor, la densidad es menor. Para poder resolver el problema se dividió al sistema en secciones suficientemente pequeñas como para suponer que las magnitudes termodinámicas tienen valores constantes en su interior. Este mismo enfoque se utilizó en un trabajo anterior para estudiar la producción de entropía en un problema de conducción del calor unidimensional. Queda así demostrada la efectividad de este procedimiento ingenioso para atacar algunos problemas de sistemas térmicos fuera de equilibrio.