Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Ciencia del suelo
versión On-line ISSN 1850-2067
Cienc. suelo vol.27 no.1 Ciudad Autónoma de Buenos Aires ene./jun. 2009
TRABAJOS
Persistencia del efecto del subsolado sobre el movimiento del agua en el suelo en siembra directa. Uso de dos modelos teóricos
C German Soracco*1,2; Roberto R Filgueira1,2; Guillermo O Sarli1; Lidia L Fournier1; Pablo R Gelati1 & Jorge Hilbert3
1Facultad de Ciencias Agrarias y Forestales, UNLP, 60 y 119, La Plata. fisica@agro.unlp.edu.ar;
2CONICET;
3INTA
*Autor con el que se debe mantener la correspondencia (Correo electrónico: gsoracco@agro.unlp.edu.ar)
Recibido: 18-09-08
Aceptado: 08-05-09
RESUMEN
La superficie bajo siembra directa continua se incrementa en forma sostenida. La maquinaria utilizada en dichos sistemas posee gran peso y muchas veces se utiliza fuera de los rangos de humedad aconsejados. Todo lleva a un aumento generalizado del fenómeno de densificación de los suelos. Las variables hidráulicas serían las más afectadas por este fenómeno. Para mejorar esta situación se ha propuesto el uso de la descompactación mediante un subsolador. El efecto de descompactación favorecería la entrada de agua en el perfil del suelo. Existe una serie de modelos físico-matemáticos para estimar valores de variables hidráulicas a partir de experimentos de infiltración, con un infiltrómetro de disco. Los resultados obtenidos con estos modelos son a veces contradictorios. Los objetivos de este trabajo fueron evaluar el efecto de la tarea de descompactación sobre las variables hidráulicas en un suelo conducido en siembra directa con y sin tareas de descompactación y estudiar la sensibilidad de métodos físico-matemáticos para determinar el efecto sobre dichas variables. Las variables investigadas fueron Infiltración Básica (q∞), Conductividad Hidráulica Saturada (Ksat) y Sortividad (S0) a partir de ensayos con un infiltrómetro de disco. La descompactación produjo el aumento de la Ksat respecto del testigo. Luego del pasaje de la cosechadora no se verificaron cambios en dicha variable para el testigo, mientras que en el tratamiento con descompactación se registró una disminución significativa de Ksat. La S0 no mostró una tendencia clara en su dependencia con el momento del muestreo, el sistema de labranza o el modelo utilizado, lo que indica la necesidad de seguir investigando en este tema. Adicionalmente, se concluyó que la Infiltración Básica (q∞) obtenida con un infiltrómetro de disco no siempre es equivalente a Ksat.
Palabras clave. Flujo estacionario; Flujo transitorio; Infiltrometría.
Persistence of subsoiling effect on soil water movement in a no tillage system. Use of two theoretical models
ABSTRACT
Use of the no-till system in Argentina is under continuous expansion. The machinery used in this system, characterized by a high axle load, is often used beyond the recommendable soil-moisture range and has led to a generalized increment in the bulk density of the soils. Hydraulic properties are the most affected by this process, and loosening is recommended to improve water entry into the soil profile. Different physico-mathematical models for estimating hydraulic properties based on use of the tension disc infiltrometer method give rise to different and often contradictory results. The aim of this study was to determine the effect of soil loosening on hydraulic properties in plots under no-till management with and without loosening practices, and to evaluate the performance of two theoretical models to detect differences between treatments. The studied variables were Steady State Flux (q∞), Saturated Hydraulic Conductivity (Ksat) and Sorptivity (S0), working with a disc infiltrometer. Loosening led to an increase in Ksat with respect to the control. The level of Ksat did not change in control plots after harvesting traffic. In loosened plots, however, harvesting traffic led to a significant decrease in Ksat. Sorptivity values showed no clear dependency on measurement time, treatment or model, suggesting the need for further study. Moreover, it was concluded that q∞ obtained using the disc infiltrometer method could not always be taken as equivalent to Ksat.
Key words. Steady-state flux; Unsteady-state flux; Infiltrometry.
INTRODUCCIÓN
El agua es un elemento vital para el correcto crecimiento y desarrollo de los cultivos. Es importante conocer el contenido y la dinámica del agua en el suelo. Esta dinámica se ve afectada por una gran cantidad de factores, siendo de particular relevancia el sistema de labranza utilizado y las cargas a que es sometido el suelo debido al tránsito de máquinas. En los últimos años se ha visto incrementado el peso de la maquinaria agrícola, y su efecto se traduce en la compactación de los suelos, sobre todo ocasionada por el tránsito en condiciones de humedad no adecuadas para ello (Alakukku et al., 2003). Los procesos de compactación afectan el flujo de agua en los suelos. Esta alteración se produce por una reconfiguración del espacio poroso (Horton et al., 1994; Strudley et al., 2008). Sin embargo, Strudley et al. (2008) afirman que no existe una tendencia marcada del efecto de la compactación sobre el movimiento del agua en el suelo en siembra directa. Estos autores compararon numerosos trabajos de varios países y encontraron que incluso para suelos similares los comportamientos de las variables físicas no mostraban una clara tendencia. Horton et al. (1994) se expresaron de manera similar respecto a las variables hidráulicas, diciendo que la comprensión de los efectos del manejo sobre estas variables era una gran necesidad y que esto requiere esfuerzos conjuntos de desarrollo de teoría, mediciones a campo y la validación de modelos físico-matemáticos. Los procesos de compactación, y su efecto sobre el movimiento del agua en el suelo, dependen de un gran número de factores, incluido el sistema de labranza aplicado (Sommer & Zach, 1992; Horton et al., 1994; Álvarez et al., 2006). En particular, Álvarez et al. (2006) evaluaron el efecto de la descompactación en siembra directa sobre algunas propiedades físicas del suelo, a la siembra y a la cosecha del cultivo de maíz; en dos sitios de la provincia de Buenos Aires y uno de Santa Fe. La densidad aparente no mostró variaciones significativas a la siembra y a la cosecha. Respecto a la variable infiltración, la conclusión fue que el trabajo de descompactación con un subsolador antes de la siembra influye notablemente sobre el ingreso del agua al suelo, pero que esto no se mantuvo en el tiempo. La medida de infiltración reveló que al momento de la cosecha los valores de infiltración no mostraban diferencias significativas con el testigo de siembra directa sin subsolado.
Por otro lado, Cabria & Culot (2000) estudiaron los efectos de la labranza convencional sobre la sortividad y la conductividad hidráulica saturada en suelos de la provincia de Buenos Aires. Las mediciones de conductividad hidráulica saturada se hicieron por un método convencional (Klute & Dirksen, 1986), mientras que las sortividades fueron tomadas de un trabajo anterior de los autores (Cabria & Culot, 1999). La conclusión de los autores fue que la labranza convencional ejerce un efecto de largo plazo sobre la sortividad y la Ksat. Un resultado llamativo de este trabajo fue que en cuatro de las seis situaciones evaluadas los valores de Ksat fueron mayores que los de q∞.
Filgueira et al. (2006) estimaron sortividades y Ksat de un suelo sometido a labranza convencional, pastura y un sitio compactado por pisoteo de animales, utilizando un infiltrómetro de disco y modelos de flujo estacionario y transitorio. A pesar de que ambos modelos fueron capaces de detectar a través de las variables hidráulicas las diferencias en el manejo, de los análisis resultaron contradicciones importantes con el uso del modelo transitorio.
Estos son algunos argumentos que hablan de la importancia que posee el estudio de las propiedades hidráulicas de los suelos y su relación con los diferentes sistemas de labranza, y el procesamiento de los datos experimentales, para lograr un conocimiento pleno de la problemática y tender así hacia una producción sustentable.
La tarea de cosecha se caracteriza por una elevada intensidad de tráfico y luego de concluida, un gran porcentaje de la superficie del terreno queda afectada por el tránsito de la maquinaria (Kuipers & van de Zande, 1994). Las hipótesis de este estudio fueron que el efecto de descompactación del suelo favorece la entrada de agua en el perfil y dicho efecto persiste hasta la cosecha del cultivo implantado y que las diferencias en las propiedades hidráulicas del suelo pueden ser detectadas a través de distintos métodos físico-matemáticos de interpretación de datos de infiltración.
Los objetivos de este trabajo fueron determinar los efectos que provocan el tiempo y el tránsito de la cosechadora sobre las variables hidráulicas sortividad y conductividad hidráulica saturada en un suelo conducido en siembra directa, con y sin tareas de descompactación, y estudiar la sensibilidad que presentan dos métodos físico- matemáticos para determinar dichas variables.
MATERIALES Y MÉTODOS
El ensayo se realizó en el establecimiento agropecuario «La Fe» ubicado en las cercanías de la localidad de San Antonio de Areco (34º18'10"S y 59º56'58"O). El suelo fue descripto como Argiudol típico (Soil Taxonomy, 1999), perteneciente a la Serie Río Tala (INTA, 1973). Los lotes bajo ensayo presentaban una historia de cinco años bajo siembra directa con y sin descompactación. La tarea de descompactación se realizaba anualmente previa a la siembra. La densidad aparente en superficie en el testigo se mantuvo sin cambios a los largo de todo el ciclo (1,26±0,07 Mg m-3). En la parcela con descompactación se registraron valores de densidad aparente iniciales de 1,13±0,08 y al final del ciclo de 1,25±0,08 Mg m-3. El contenido de materia orgánica fue de 39±6 g kg-1 para el suelo sin descompactación y de 42±10 g kg-1 para el suelo con descompactación.
Las parcelas experimentales tenían 9 metros de ancho y 50 metros de longitud. Se planteó un diseño experimental completamente al azar, sin replicaciones, con dos tratamientos: siembra directa con labores de descompactación (SDCD) y siembra directa sin labores de descompactación (T). A su vez, se realizaron mediciones en tres épocas: en diciembre de 2006, y en mayo de 2007, antes y después de la cosecha. Los tratamientos se identificaron de la siguiente forma: 1= Siembra directa con descompactación en diciembre, 2= Siembra directa sin descompactación en diciembre, 3= Siembra directa con descompactación en precosecha, 4= Siembra directa sin descompactación en precosecha, 5= Siembra directa con descompactación en poscosecha y 6= Siembra directa sin descompactación en poscosecha.
El sistema utilizado para remover el suelo en las parcelas de SDCD fue un descompactador de montantes curvos (designación comercial «cultivie»), con dos planos de acción distanciados a 0,6 m, montantes dispuestos en forma convergente, con un distanciamiento entre puntos de vinculación al bastidor de 0,88 m en el plano delantero, determinando una separación de 0,55 m entre órganos activos. En el plano trasero, la distancia entre los puntos de vinculación al bastidor fue de 1,88 m, determinando una separación entre órganos activos de 1,6 m. El despeje del implemento fue de 0,85 m, encontrándose equipado con cuchillas de corte de residuos por delante de la línea de acción de los órganos activos. La profundidad de trabajo efectiva fue entre 0,25-0,30 m. La humedad del suelo en el momento en el que se pasó el descompactador de montantes curvos fue del 17% en promedio.
La cosechadora utilizada fue de la marca comercial AGCO, modelo Gleaner R 62, con rodado delantero 30,5-32 y trasero 16,9- 26, con una masa total de 14,2 Mg, carga sobre eje delantero 11,4 Mg, sobre eje trasero 2,8 Mg.
Marco teórico
Cuando se aplica agua sobre la superficie del suelo seco ésta penetrará el mismo siguiendo un gradiente de potencial. Para el caso de un suelo seco, los potenciales más importantes son el mátrico y el gravitacional. A medida que el agua entra en el suelo el potencial de la matriz va desapareciendo ya que ésta va llenándose de agua y no existe expresión del fenómeno capilar, dejando como protagonista al potencial gravitatorio. El fenómeno que incluye la expresión de los potenciales mátrico y gravitacional, y que determina la entrada del agua en el suelo, es llamado infiltración. En relación a este fenómeno se define una variable que expresa la cantidad de agua que penetra en el suelo por unidad de área; la Infiltración acumulada (I). Dicha variable es función del tiempo transcurrido y se expresa en unidades de longitud ya que resulta de dividir un volumen de agua por un área afectada en el proceso de infiltración. La curva I(t) es continua y siempre ascendente. En términos matemáticos I(t) puede expresarse como:
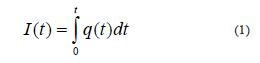
Donde q (L T-1) se define como la tasa de infiltración (o flujo de agua). Esta tasa de infiltración decrece rápidamente con el tiempo y se aproxima a un valor constante. Para t---0, q---∞,y, para--- t∞, q---constante. En teoría, si t--∞, q---conductividad hidráulica saturada, en el modelo unidimensional. En el proceso de infiltración se pueden reconocer dos estados; el transitorio y el estacionario. El primero se caracteriza por presentar una variación de la tasa de infiltración con el tiempo. Mientras que en el estado estacionario la tasa de infiltración se mantiene constante. Desde el punto de vista teórico esta tasa de infiltración constante se alcanza para tiempo infinito, en cuyo caso suele llamarse tasa de infiltración básica (q∞). En la práctica, este tiempo puede variar entre media hora y algunas horas dependiendo de las características del suelo (texturales, estructurales, etc.) y, fundamentalmente, del contenido de humedad inicial del mismo.
El fenómeno de infiltración ha sido descripto mediante diferentes modelos (Green & Ampt, 1911; Kostiakov, 1932; Swartzendruber, 1993; Horton, 1940; Holtan, 1961; Philip, 1957). De todos estos modelos el de Philip (1957) ha sido el más utilizado. Dicho modelo expresa la Infiltración Acumulada como una serie de potencias:
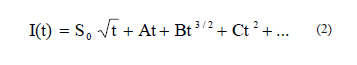
donde I (L) es la infiltración acumulada, S0 (LT-1/2) es la Sortividad capilar, y A(LT-1), B(LT-3/2), C (LT-2), etc., son coeficientes que se encuentran relacionados con la conductividad hidráulica.
Conductividad hidráulica
La definición de Conductividad Hidráulica se desprende de la ley de Darcy (Kutilek & Nielsen, 1994). Dicha ley relaciona el flujo de agua a través de un material conductor (el suelo) con el gradiente que genera dicho flujo. Si el flujo se produce en saturación la forma de la ley es:
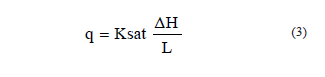
donde Ksat es la Conductividad Hidráulica Saturada y es el gradiente hidráulico. Dicho gradiente representa la «fuerza motriz» del flujo.
Como se desprende de lo anterior la conductividad hidráulica expresa la capacidad de un medio poroso para transmitir agua. Esta constituye un concepto más general que la permeabilidad, de la que se diferencia porque depende no sólo de las características del espacio poroso, sino también de la condición misma del agua.
Sortividad
Esta variable fue introducida y definida por Philip (1957) como la medida de la entrada de agua en el suelo sin el efecto de la gravedad, es decir por efecto capilar. En un estadío inicial del fenómeno de infiltración éste se encuentra mayormente dominado por esta variable, lo que representaría una forma truncada de la ecuación (2).
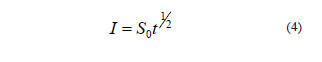
Recordando que q puede expresarse como:
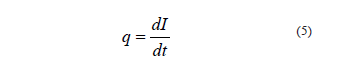
entonces, si se deriva respecto de t la ecuación (4), se llega a una expresión para el estado inicial del proceso de infiltración:
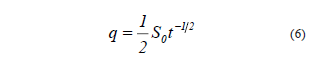
La sortividad es comúnmente estimada utilizando la ecuación (4), bajo el supuesto de que en los instantes iniciales del proceso de infiltración los efectos de la gravedad son pequeños y se pueden ignorar. De forma que si representamos I(t) vs. t para los primeros instantes del proceso obtendremos una recta; la pendiente de dicha recta es la Sortividad. Existen otras formas de estimar S0 como se verá en el presente trabajo.
Métodos físico-matemáticos para la obtención de variables hidráulicas utilizando el infiltrómetro de disco Método del estado estacionario (MEE)
Wooding (1968) propuso una ecuación para analizar e interpretar los valores de la tasa de infiltración básica (q∞) desde un disco, cuya expresión es:
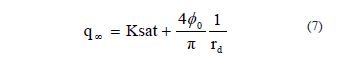
donde Ksat (L T-1) es la conductividad hidráulica saturada, r d(L) es el radio del disco y 0 φ (L2 T-1) es el potencial de flujo mátrico definido como:
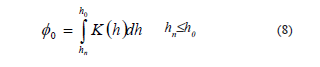
donde h representa el potencial hídrico, K(h) es la conductividad hidráulica. El subíndice 0 se refiere a la condición impuesta desde el disco y el subíndice n a la condición de humedad antecedente del suelo, antes que el proceso de infiltración ocurra.
La ecuación propuesta por Wooding (1968) para una fuente circular puede ser resuelta experimentalmente mediante el uso de múltiples radios para un mismo valor de h0 (Smetten & Clothier, 1989); o de múltiples cargas hidráulicas para un mismo radio del disco (Ankeny et al., 1991). Otra manera de solucionar la ecuación (7) es asumiendo como verdadera la siguiente suposición (White & Sully, 1987):
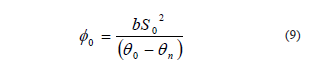
donde b es un parámetro de forma que está en el intervalo (1/2, π/4), tomándose habitualmente como 0,55; y θ0 y θn son contenidos de agua volumétricos (L3 L-3). Como ya se mencionó precedentemente, se puede estimar S0 utilizando la ecuación (4) mediante la obtención de la pendiente de la recta que surge de graficar los resultados experimentales I(t) vs. t1/2 para los primeros tiempos del proceso de infiltración. Una vez obtenido el valor de S0, midiendo además los contenidos de humedad volumétrica inicial y final, y recurriendo a las ecuaciones (7) y (9) es posible obtener el valor de Ksat de la siguiente ecuación:
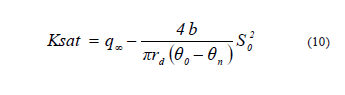
Método del estado transitorio (MET)
Otros investigadores orientaron su análisis al estudio del flujo transitorio desde un infiltrómetro de disco (Turner & Parlange, 1974; Warrick & Lomen, 1976; Warrick, 1992; Haverkamp et al., 1994; Smettem et al., 1994; Zhang, 1997; Vandervaere et al., 2000). Existen algunas ventajas de trabajar sobre el modelo de flujo transitorio como ser: i) El supuesto de homogeneidad del suelo se vuelve más realista con una reducción del volumen de suelo muestreado en experimentos de corta duración; ii) la variación vertical de las propiedades hidráulicas puede ser determinada con alta resolución llevando a cabo experimentos de corta duración; iii) experimentos cortos permiten la realización de un número mayor de repeticiones en el campo; iv) el régimen transitorio de infiltración contiene más información, la cual no es utilizada cuando se usa el régimen estacionario (Filgueira et al., 2006).
Los resultados de los estudios realizados tienen en común la siguiente expresión para la infiltración acumulada en el flujo transitorio (Warrick, 1992; Haverkamp et al., 1994; Zhang, 1997; Vandervaere et al., 2000):
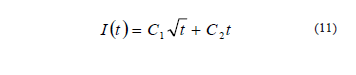
donde C1 y C2 son constantes, y t es el tiempo. Sobre la base de la ecuación (11) Haverkamp et al. (1994) establecieron una ecuación de infiltración con base física para infiltrómetros de disco válida para períodos iniciales e intermedios del proceso de infiltración:
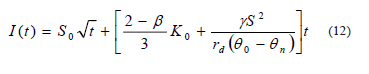
donde β es una constante comprendida entre 0 y 1 y γ es una constante teórica (Haverkamp et al., 1994). La ecuación (12) tiene la misma forma general que la ecuación (2) donde los términos en t3/2, t2 y siguientes se desprecian.
Debido a problemas matemáticos de ajuste de la función representada por la ecuación (11) a los datos experimentales, Smiles & Knight (1976) propusieron linealizar la misma. La idea consistió en dividir ambos miembros de la ecuación (11) por t , la que finalmente toma la forma:
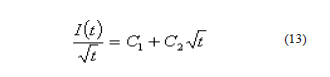
Si se grafica vs. se obtiene una recta que posee C1 como ordenada al origen y C2 como la pendiente. Así, con un simple ajuste lineal, pueden obtenerse los valores de estas constantes. Una vez hallados C1 y C2 la conductividad hidráulica se calcula utilizando la siguiente expresión:
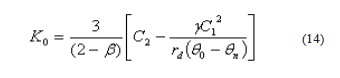
de la comparación de las ecuaciones (11) y (12) resulta evidente que:
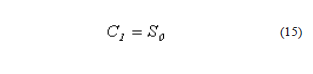
Ensayo de infiltración
Las determinaciones de infiltración se realizaron en el horizonte superficial mediante el uso de un infiltrómetro de disco a tensión (Perroux & White, 1988). El instrumento posee un disco de 120 mm de diámetro. Los sitios de mediciones fueron elegidos al azar, entre los surcos, evitando zonas con huella de maquinaria en diciembre y en precosecha, y entre los surcos y sobre la huella de la cosechadora en poscosecha. En los momentos de medición no era posible detectar con precisión la línea de pasaje del descompactador.
En el lugar designado para ubicar el instrumento se eliminó la vegetación y residuos presentes, buscando que la superficie del terreno estuviera nivelada y lisa. Para establecer un buen contacto entre la base del disco y el suelo, se colocó una delgada capa de arena entre ambos. La infiltración se estudió en tres períodos del ciclo para los dos tratamientos de labranza. Se realizaron 21 determinaciones en diciembre, 8 en precosecha y 8 en postcosecha. En todos los casos se necesitaron alrededor de dos horas para alcanzar el estado estacionario. Para más detalles sobre el uso del infiltrómetro ver Filgueira et al. (2006). A partir de la información obtenida, la determinación de Ksat y S0 se hizo de dos formas. La primera fue mediante el modelo estacionario (MEE), donde S0 se estimó utilizando los datos resultantes de los primeros instantes de infiltración, a partir de la pendiente de la recta que resultó de graficar I vs. t1/2 [ (ecuación (4)] . Una vez estimada S0 se utilizó la ecuación (10) para encontrar Ksat. La segunda forma de estimación fue procesando los datos de manera que se pudiera utilizar la ecuación (13). En una representación I/t1/2 versus t1/2, del ajuste por mínimos cuadrados se pudieron obtener C1 y C2. Se usó la ecuación (14) para determinar Ksat y la ecuación (15) para determinar S0.
Para el análisis estadístico se utilizó el programa Statgraphics plus 4.0. Se realizó un ANOVA y el test de LSD para la comparación entre la medias (P=0,05).
RESULTADOS Y DISCUSIÓN
Valores de infiltración básica
En la Figura 1 se puede observar el comportamiento de la infiltración acumulada en función del tiempo para el tratamiento con descompactación de suelo, en dos situaciones, antes y después del tránsito de la cosechadora.
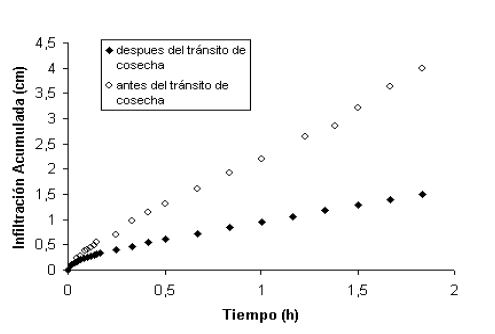
Figura 1. Efecto del paso de la cosechadora sobre la infiltración acumulada en sitios bajo siembra directa con descompactación de suelo (SDCD). Tratamientos 3 (o) y 5 (♦).
Figure 1. Effect of harvesting traffic on cumulative infiltration in a soil under no till management with loosening (SDCD). Treatments 3 (o) and 5 (♦).
Es evidente cómo el pasaje de la cosechadora redujo la infiltración acumulada en poscosecha en SDCD.
En la Figura 2 se pueden observar dos ejemplos del comportamiento de la infiltración acumulada en función del tiempo para el tratamiento testigo, en dos situaciones, antes y después del tránsito de la cosechadora. En este caso se visualiza que I(t) se comportó de manera similar en ambos casos.

Figura 2. Efecto del paso de la cosechadora sobre la infiltración acumulada en sitios bajo siembra directa sin laboreo de descompactación (T). Tratamientos 4(o) y 6(♦).
Figure 2. Effect of harvesting traffic on cumulative infiltration in a soil under no till management without loosening (T). Treatments 4(o) and 6(♦).
Con los datos experimentales se realizó un ANOVA multifactor tomando como variable respuesta la infiltración básica (q∞) y como factores el sistema de labranza y el momento de realización del muestreo. Se observó que estos factores presentaron una interacción para la variable respuesta estudiada.
Para eliminar el efecto de dichas interacciones se realizó un ANOVA de una vía tomando como tratamientos cada una de las combinaciones de los factores antes ensayados. En la Figura 3 se presentan los valores de q∞ para cada una de las situaciones ensayadas.
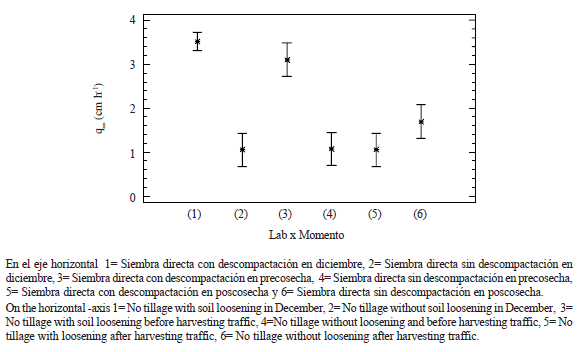
Figura 3. Valores medios de la tasa de infiltración básica (cm h-1) para cada para cada sistema de labranza y momento del muestreo.
Figure 3. Steady state flux values (cm h-1) for each treatment and time.
Del análisis estadístico se deduce que al menos uno de los tratamientos ensayados presenta una tasa de infiltración básica media diferente a los otros. Para determinar qué tratamiento difirió de los otros se realizó un test de LSD (P=0,05). En la Tabla 1 se muestran los resultados obtenidos.
Tabla 1. Comparación entre las medias de infiltración básica para los tratamientos, usando el test de LSD (P=0,05)
Table 1. Steady state flux mean values for different treatments, using the LSD test (P=0.05)
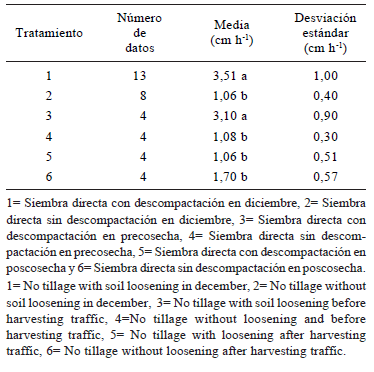
De la Tabla 1 se extrae que dos de los seis tratamientos presentan homogeneidad estadística para la variable estudiada (q∞), diferenciándose con un valor más alto del resto. Estos resultados coinciden con lo expuesto por Horne et al. (1992) quienes, para suelos franco-limosos, encontraron que la tasa de infiltración básica era menor en el suelo con 10 años de siembra directa continua que en labranza conservacionista. Resultados similares fueron reportados por Sasal et al. (2006) para un suelo de Pergamino de la misma textura y por Alegre et al. (1991) en una revisión de varios casos en Latinoamérica. En el caso de Sasal et al. (2006) los valores de infiltración básica medidos con un infiltrómetro oscilaron entre 2 y 3 cm h-1, lo cuál está de acuerdo con los valores obtenidos en el presente estudio. Gómez et al. (1999) encontraron que la tasa de infiltración era mayor en siembra directa que en labranza convencional en un ensayo de 15 años de duración. Existen, además, otros casos en los que se registra una tasa de infiltración básica mayor en siembra directa que en tratamientos con remoción de suelo (Azooz & Arshad, 2001; Strudley et al., 2008). Por su parte, el estudio de Ávarez et al. (2006) sobre la variable infiltración de tres suelos en siembra directa con y sin descompactación, detectó diferencias estadísticas entre ambos tratamientos al momento de la siembra. Algunos de los valores reportados son muy altos (e.g. San Gregorio 1.273 mm h-1). A su vez, la infiltración en el tratamiento que recibiera descompactación experimentó una disminución estadísticamente significativa al momento de la cosecha (Junín 115 mm h-1, San Gregorio 81 mm h-1, Chivilcoy 63 mm h-1), respecto del momento de siembra (Junín 163 mm h-1, San Gregorio 1.273 mm h-1, Chivilcoy 455 mm h-1). Este último efecto no fue detectado en nuestro estudio, donde la disminución se produjo en postcosecha, en el tratamiento descompactado. Al momento de la cosecha, en el trabajo de Álvarez et al. (2006), las diferencias estadísticas existentes entre los dos sistemas de labranza desaparecieron. Esta evolución de la tasa de infiltración no coincide con nuestras observaciones en el presente trabajo, donde desde diciembre hasta antes de la cosecha la infiltración se mantiene estadísticamente igual para cada uno de los tratamientos (aunque menor en el testigo). Recién luego de la cosecha se produce la disminución estadísticamente significativa de la infiltración básica para el tratamiento descompactado con el cultivie. Para el tratamiento sin descompactar no se registraron disminuciones (Tabla 1 y Fig. 3).
Todo esto indica que el efecto de la siembra directa continua sobre el movimiento del agua en el suelo se encuentra aún lejos de poder ser generalizado.
Aplicación de los modelos de análisis
En una profundización del estudio se estimaron la sortividad y la conductividad hidráulica saturada por los dos modelos propuestos. El número de mediciones de infiltración estudiadas fueron treinta y siete. Tanto con el MEE como con el MET se obtuvieron dos valores de Ksat negativos. Esto concuerda con lo reportado por otros investigadores (Logsdon & Jaynes, 1993; Cabria & Culot, 1999; Aoki & Sereno, 2004) y fueron eliminados del análisis estadístico por no tener sentido físico.
Se hizo un ANOVA multifactor tomando como variable independiente la Ksat y como factores el método de análisis (MEE y MET), el sistema de labranza (siembra directa con y sin descompactación) y el momento del ciclo en que la medición fue realizada (Diciembre, Precosecha y Poscosecha). Se observó una interacción entre el sistema de labranza y el momento de muestreo. Esto significa que el comportamiento de la Ksat fue distinto para cada sistema de labranza según el momento de muestreo.
A continuación, y para evitar dicha interacción, se realizó un ANOVA multifactor para Ksat tomando como factores el método de análisis utilizado (MEE y MET) y una nueva variable que surge de la combinación del sistema de labranza y el momento del muestreo (1= Siembra directa con descompactación en diciembre, 2= Siembra directa sin descompactación en diciembre, 3= Siembra directa con descompactación en precosecha, 4= Siembra directa sin descompactación en precosecha, 5= Siembra directa con descompactación en poscosecha y 6= Siembra directa sin descompactación en poscosecha). Las medias de Ksat y sus desviaciones estándar se presentan en la Figura 4.
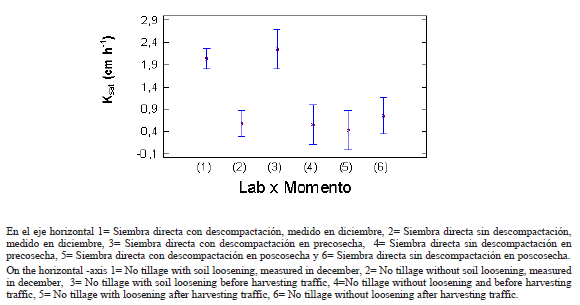
Figura 4. Comportamiento de los valores de Ksat (cm h-1) para cada sistema de labranza y momento del muestreo.
Figure 4. Ksat values (cm h-1) for each treatment and time.
De dicho análisis se desprende, como resultado notable, que no existe efecto del método de análisis sobre la variable estudiada, o sea que ambos métodos físico-matemáticos no difirieron significativamente en los valores que arrojaron para la Ksat. Es decir, ambos métodos registraron de igual forma el efecto de la labranza y del momento de muestreo. También surge de dicho análisis que la nueva variable creada (sistema de labranza x momento de muestreo) afectó el comportamiento de la Ksat.
Para evidenciar las diferencias entre los distintos tratamientos se realizó un test de medias cuyo resultado (LSD, P=0,05), se muestra en la Tabla 2.
Tabla 2. Valores medios de Ksat según el sistema de manejo, modelo físico y tratamiento. Letras diferentes indican diferencias estadísticas significativas (P=0,05).
Table 2. Mean values of Ksat according to tillage management, physical model and treatment. Different letters indicate significant differences (P=0.05).
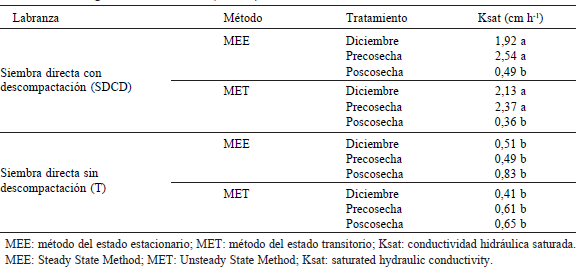
De la Tabla 2 puede extraerse que la Ksat en SDCD en diciembre y en precosecha difirieron estadísticamente de los valores obtenidos en postcosecha. Esto indicaría que el tráfico de la maquinaria de cosecha produjo una disminución significativa de Ksat y dicha disminución fue detectada por ambos modelos matemáticos de ajuste. El tratamiento sin descompactación, en cambio, no evidenció diferencias significativas a lo largo de todo el ciclo, ni por el tránsito de maquinaria o por el método de elaboración de los datos. Los valores de Ksat para SDCD fueron mayores que para T en diciembre y en precosecha En poscosecha no se encontraron diferencias significativas entre SDCD y T.
A modo de resumen del comportamiento de los métodos estudiados se presenta, en la Figura 5, los resultados obtenidos de Ksat con los modelos de flujo estacionario y transitorio.
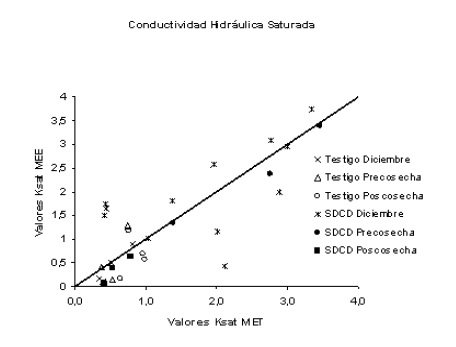
Figura 5. Valores de Ksat (cm h-1) obtenidos por los dos métodos de análisis estudiados. La recta tiene una pendiente 1.
Figure 5. Ksat values (cm h-1) obtained from the two analytical methods (MEE and MET) are presented. The straight line has slope 1.
En lo que hace al análisis de la sortividad se realizó un ANOVA tomando como factores el sistema de labranza, el momento de muestreo y el método de análisis físico- matemático utilizado. Dicho análisis mostró una interacción estadísticamente significativa para los factores que afectan la variable estudiada. A partir de ello, se generó una nueva variable definida como las combinaciones de los factores previamente mencionados (Labranza x momento de muestreo x método de análisis). Se realizó un ANOVA de una vía tomando como variable la sortividad y como factor que la modifica la nueva variable a 12 niveles (2 sistemas de labranza, 2 métodos de análisis y 3 momentos de muestreo). Posteriormente, sobre los otros se realizó un test de medias (LSD, P=0,05, Tabla 3).
Tabla 3. Valores medios de sortividad (cm h-1/2) según el sistema de manejo, modelo físico y tratamiento.
Table 3. Mean sorptivity values (cm h-1/2) according to tillage management, physical model and treatment.
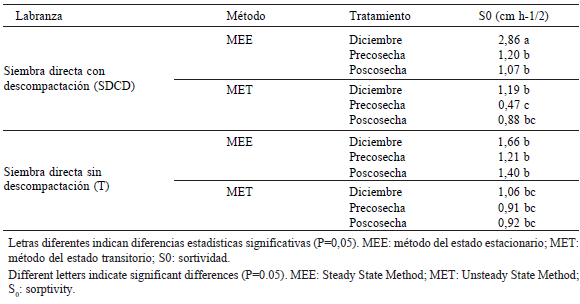
De acuerdo a lo reportado por Drees et al. (1994) la labranza afecta el diseño del espacio poroso produciendo una interrupción de los poros interconectados que caracterizan a los suelos no disturbados. Esto haría que la sortividad aumente. Dicho efecto fue observado por Cabria & Culot (2000) en Udoles del sudeste de la provincia de Buenos Aires. En nuestro estudio ninguno de los dos métodos de análisis mostró tendencias significativas en el comportamiento de esta variable. En la Figura 6 se pueden ver los comportamientos de los valores de S0, obtenidos por cada uno de los métodos fisicomatemáticos aplicados. Se puede apreciar claramente que el análisis con el modelo de flujo transitorio da como resultado valores de sortividad mayores que los obtenidos con el modelo de flujo estacionario.
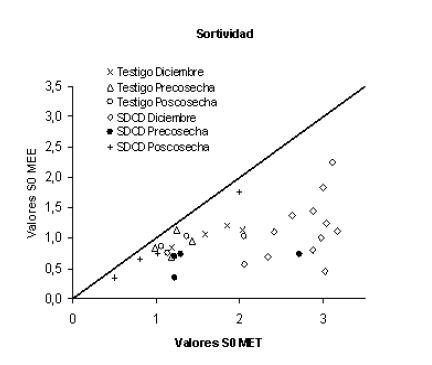
Figura 6. Comparación entre los valores de S0 (cm h-1/2) obtenidos por los dos métodos de análisis estudiados. La recta tiene pendiente 1.
Figure 6. Comparison between S0 values (cm h-1/2) obtained from each analytical method. The straight line has slope 1.
En estudios que utilizan el infiltrómetro de disco a tensión se encuentra difundida la utilización del q∞, generalmente bajo la denominación de infiltración básica, como indicador de la dinámica del agua en el suelo en estado saturado (Gil, 2002; Sasal et al., 2006). En alguna ocasión, incluso, se considera que dicho valor es equivalente a la conductividad hidráulica saturada (Gil, 2002). Dicha aproximación debe manejarse con cuidado y no puede generalizarse. La equiparación de q∞ con Ksat implica físicamente suponer S0=0, lo cual en un flujo no confinado no sería correcto, aún una vez alcanzado el estado estacionario. Filgueira et al. (2006), trabajando en otro suelo (franco arcilloso con marcados problemas de salinidad) reportaron que dicha simplificación conduce a errores mayores cuanto mayor es la compactación que ha sufrido el suelo ensayado.
En las Figuras 7a y b se puede ver el comportamiento de q∞ vs Ksat para cada uno de los métodos utilizados para el análisis, se puntualiza que en todos los casos Ksat fue menor que q∞, ya que Ksat es sólo un componente de la tasa de infiltración (ecuación 10 y 12).
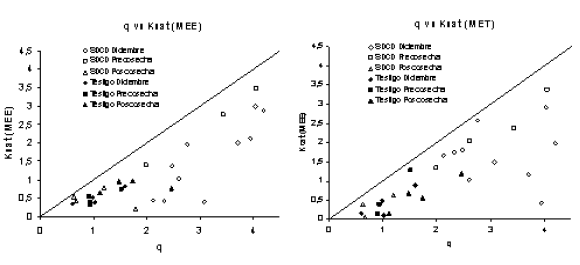
Figura 7 a y b: Comparación entre los valores de q∞ y Ksat para cada uno de los métodos de análisis utilizados. La línea recta tiene pendiente 1.
Figure 7 a y b: Comparison between q∞ and Ksat values for each analytical method. The straight line has a slope of 1.
CONCLUSIONES
Para el tratamiento del suelo bajo siembra directa sin descompactación la q∞ estimada con el infiltrómetro de disco no mostró cambios estadísticamente significativos durante el ciclo del cultivo de soja.
Para el tratamiento del suelo bajo siembra directa con descompactación la q∞ estimada con el infiltrómetro de disco fue mayor que en la situación sin descompactación y no mostró cambios estadísticamente significativos entre diciembre y precosecha pero sí evidenció una disminución significativa en postcosecha.
El comportamiento de la Ksat estimada por el ajuste de los datos con los dos modelos usados mostró la misma tendencia estadística que q∞.
Ambos métodos físico matemáticos fueron capaces de detectar diferencias en la Ksat.
El comportamiento de la S0 no mostró una tendencia clara, planteando la necesidad de seguir profundizando el estudio del tema, tanto teórico como experimental.
Los valores de Ksat y q∞ fueron siempre diferentes. En estudios donde se requiera precisión en los valores de las variables hidráulicas no es conveniente equipararlos.
AGRADECIMIENTOS
Al CONICET y a la UNLP por el apoyo económico recibido.
BIBLIOGRAFÍA
1. Alakukku, L; P Weisskopf; WCT Chamen; FGJ Tijunk; JP Van Der Linden; S Pires; C Sommer & G Spoor. 2003. Prevention strategies for field traffic-induced subsoil compaction: a review. Part 1. Machine soil interactions. Soil Till Res 73: 145-160. [ Links ]
2. Álvarez, CR; MA Taboada; C Bustingorri & FH Gutiérrez Boem. 2006. Descompactación de suelos en siembra directa: efectos sobre las propiedades físicas y el cultivo de maíz. Ciencia del Suelo 24: 1-10. [ Links ]
3. Alegre, JC; DK Cassel & E Amezquita. 1991. Tillage systems and soil properties in Latin America. Soil Till. Res. 37: 223-238. [ Links ]
4. Ankeny, MD; M Ahmed; TC Kaspar & R Horton. 1991. Simple field method for determining unsatured hydraulic conductivity. Soil Sci. Soc. Am. J. 55: 467-470. [ Links ]
5. Aoki, AM & R Sereno. 2004. Comparación de dos metodologías de cálculo de propiedades hidráulicas de un suelo, a partir de datos medidos con infiltrómetro de disco a tensión. En: Metodologías físicas para la investigación del suelo: penetrometría e infiltrometría, (eds.) Filgueira RR & Micucci FG. Editorial de la Universidad Nacional de La Plata. 180 pp. [ Links ]
6. Azooz, RH & MA Arshad. 2001. Soil water drying and recharge rates as affected by tillage under continuous barley and barleycanola cropping systems in northwestern Canada. Can. J. Soil Sci. 81: 45-52. [ Links ]
7. Cabria, FN & JPh Culot. 1999. Sortividad y Conductividad Hidráulica Saturada de Udoles del Sudeste Bonaerense, Argentina. Ciencia del Suelo 17: 8-19. [ Links ]
8. Cabria, FN & JPh Culot. 2000. Efectos de la labranza convencional sobre la sortividad y la conductividad hidráulica saturada en Udoles del sureste de la provincia de Buenos Aires. Ciencia del Suelo 18: 1-8. [ Links ]
9. Drees, LR; AD Karathanasis; LP Wilding & RL Blevins. 1994. Micromorphological characteristics of long-term and no-till and convetionally tilled soils. Soil Sci. Soc. Am. J. 58: 508-517. [ Links ]
10. Filgueira, RR; CG Soracco; GO Sarli & LL Fournier. 2006. Estimación de propiedades hidráulicas de suelos por mediciones a campo y el uso de modelos de flujo estacionario y transitorio. Ciencia del Suelo 24: 39-49. [ Links ]
11. Gil, R. 2002. Manual de uso del infiltrómetro y permeámetro de disco. [ Links ]
12. Gómez, JA; JV Giraldez; M Pastor & E Ferreres. 1999. Effects of tillage method on soil physical properties, infiltration and yield in an olive orchard. Soil Till Res. 52: 167-175. [ Links ]
13. Green, WH & GA Ampt. 1911. Studies on soil physics: I. Flow of air and water through soils. J. Agr. Sci. 4: 1-24. [ Links ]
14. Haverkamp, R; PJ Ross; KRJ Smettem & JY Parlange. 1994. Three dimensional analysis of infiltration from the disc infiltrometer. Part 2. Physically based infiltration equation. Water Resour. Res. 30: 2931-2935. [ Links ]
15. Holtan, HN. 1961. Concept of infiltration estimates in watershed hydrology. USDA Tech. Bull. 1435. [ Links ]
16. Horne, DJ; CW Ross & KA Hughes. 1992. Ten years of a maize oats rotation under three tillage systems on a silt loam in New Zealand. 1. A comparison of some soil properties. Soil Till. Res. 22: 131-143. [ Links ]
17. Horton, RE. 1940. An Approach towards a physical interpretation of infiltration capacity. Soil Sci. Soc. Am. Proc. 5: 399-417. [ Links ]
18. Horton RE; MD Ankeny & RR Allmaras. 1994. Effects of compaction on soil hydraulic properties. In: Soane BD & C van Ouwerkerk (eds.). Soil compaction in crop production. Elsevier, Amsterdam. Pp. 141-165. [ Links ]
19. INTA. 1973. Carta de suelos de la República Argentina: hoja 3360- 33. Baradero. Buenos Aires. [ Links ]
20. Klute, A & C Dirksen. 1986. Hydraulic conductivity and diffusivity: laboratory methods. In: Methods of soil analysis, Part. 1, Physical and Mineralogical Methods, Monograph Nº 9. ASA, SSSA, Madison, USA. 687-734. [ Links ]
21. Kostiakov, AN. 1932. On the dinamics of the coefficient of waterpercolation in soil and on the necessity of studying it from a dynamic point of view for porposes of amelioration. Trans. Sixth Comm. Intl. Soc. Soil Sci., Part A:17-21. [ Links ]
22. Kuipers, H & JC van de Zande. 1994. Quantification of traffic systems in crop production. In: Soane BD & C van Ouwerkerk (eds.). Soil compaction in crop production Ed. Elsevier, Amsterdam. Pp. 417-446. [ Links ]
23. Kutilek, M & D Nielsen. 1994. Soil Hydrology. Catena Verlag, Germany. [ Links ]
24. Logsdon, SD & DB Jaynes. 1993. Methodology for determining hydraulic conductivity with tension infiltrometers. Soil Sci. Soc. Am. J. 57: 1426-1431. [ Links ]
25. Perroux, KM & I White. 1988. Designs for disc permeameters. Soil Sci. Soc. Am. J. 52: 1205-1215. [ Links ]
26. Philip, JR. 1957. The Theory of infiltration: 4. Sorptivity and algebraic infiltration equations. Soil Sci. 84: 257-264. [ Links ]
27. Sasal, MC; AE Andriulo & MA Taboada. 2006. Soil porosity characteristics and water movement under zero tillage in silty soils in Argentinian Pampas. Soil Till. Res. 87: 9-18. [ Links ]
28. Smetten, KRJ & BE Clothier. 1989. Measuring unsaturated sorptivity and hydraulic conductivity using multiple disc permeameters. J. Soil Sci. 40: 563-568. [ Links ]
29. Smettem, KRJ; JY Parlange; PJ Ross &. R Haverkamp. 1994. Three-dimensional analysis of infiltration from the disc infiltrometer. Part 1. A capillary-based theory. Water Resour. Res. 30: 2925-2929. [ Links ]
30. Smiles, DE & JH Knight. 1976. A note on the use of the Philip infiltration equation. Aust. J. Soil Res. 14: 103-108. [ Links ]
31. Soil Taxonomy. 1999. US Departament of Agriculture. NRCS. US Government Printing Office, Washington DC 20402. [ Links ]
32. Sommer, C & M Zack. 1992. Managing traffic-induced soil compaction by using conservation tillage. Soil Till. Res. 24: 319-336. [ Links ]
33. Strudley, MW; TR Green & JC Ascough II. 2008. Tillage effect on soil hydraulic properties in space and time: state of the science. Soil Till. Res. 99: 4-48. [ Links ]
34. Swartzendruber, D. 1993. Revised attribution of the power form infiltration equation. Water Resour. Res. 29: 2455-2456. [ Links ]
35. Turner, NC & JY Parlange. 1974. Lateral movement at the periphery of a one-dimensional flow of water. Soil Sci. 118: 70-77. [ Links ]
36. Vandervaere, J-P; M Vauclin & DE Elrick, 2000. Transient Flow from Tension Infiltrometers: II. Four Methods to Determine Sorptivity and Conductivity. Soil Sci. Soc. Am. J. 64: 1272-1284. [ Links ]
37. Warrick, AW. 1992. Models for disc infiltrometers. Water Resour. Res. 28: 1319-1327. [ Links ]
38. Warrick, AW & DO Lomen. 1976. Time-dependent linearized infiltration. Part III. Strip and disc sources. Soil Sci. Soc. Am. J. 40: 639-643. [ Links ]
39. White, I & MJ Sully. 1987. Macroscopic and microscopic capillary length time scales from field infiltration. Water Resour. Res. 23: 1514-1522. [ Links ]
40. Wooding, RA. 1968. Steady infiltration from a shallow circular pond. Water Resour. Res. 4: 1259-1273. [ Links ]
41. Zhang, R. 1997. Determination of soil sorptivity and hydraulic conductivity from the disc infiltrometer. Soil Sci. Soc. Am. J. 61: 1024-1030. [ Links ]














