Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Meteorologica
versión On-line ISSN 1850-468X
Meteorologica vol.29 no.1-2 Ciudad Autónoma de Buenos Aires ene./dic. 2004
ARTÍCULOS ORIGINALES
Obtención de un índice de riesgo de erosión eólica y su aplicación en la provincia de Buenos Aires, Argentina
Susana Goldberg* y Gabriel Weiss
Departamento de Tecnología, Universidad Nacional de Luján Luján, Argentina
*Dirección electrónica: susagold@mail.unlu.edu.ar
Manuscrito recibido el 29 de abril de 2003, en su versión final el 22 de diciembre de 2004
RESUMEN
En este trabajo se propone un índice climático para estimar el riesgo de ocurrencia de erosión eólica basado en las leyes físicas que cuantifican el efecto de la agresión del medio (turbulencia atmosférica) sobre la resistencia del sistema (textura del suelo). Este indicador es obtenido en función de observaciones meteorológicas estándar a partir de un modelo que incluye la alteración del perfil vertical del viento ocasionada por la presencia de partículas de suelo en el aire y es expresado en términos de la probabilidad de que la potencia del viento supere las condiciones umbrales para el comienzo del proceso. Si bien el índice fue obtenido para suelo seco y desnudo, la metodología permite avanzar hacia un modelo de evaluación de riesgo más general, si se determinan previamente los valores de velocidad de fricción umbral que corresponden a distintas condiciones que afectan la resistencia del suelo tales como la humedad del suelo, el contenido de materia orgánica, cobertura y uso de la tierra. Este modelo ha sido utilizado para evaluar la distribución espacial del riesgo de erosión eólica en la Provincia de Buenos Aires, Argentina.
Palabras clave: Erosión Eólica; Índice de Riesgo; Perfiles de Viento; Buenos Aires.
Erosion risk index attainment and its application in the Buenos Aires province, Argentina
ABSTRACT
This paper proposes a climatic index to estimate the wind erosion risk based upon physical laws that quantify the effect of environment's aggression (atmospheric turbulence) on system resistance (soil texture). This index is obtained as a function of standard meteorological observations including the alteration of the wind profile produced by the presence of soil particles in the air and it is expressed in terms of the probability for the wind power to exceed the threshold conditions. Although this index was obtained for dry and bare soil, it may mean an advance towards a more general model for risk evaluation if other factors intervening in soil resistance, such as soil humidity, organic material content, land cover and use are included. This model has been used to evaluate the spatial distribution of the wind erosion risk in Buenos Aires Province, Argentina.
Keywords: Wind Erosion; Risk Index; Wind Profile; Buenos Aires.
1. INTRODUCCIÓN
La erosión eólica es uno de los procesos que contribuyen a la degradación del suelo, a la vez que es responsable, entre otros, de daños mecánicos en plantas y animales, acumulación de polvo en vías férreas, caminos y zonas urbanas (Massobrio y Gutierrez 1998).
La provincia de Buenos Aires, que posee una extensión de aproximadamente 300.000 km2 y que concentra un alto porcentaje de la actividad agrícola-ganadera del país, presenta entre un 25 y 30% de su superficie con suelos susceptibles a la erosión eólica, lo que implica graves riesgos tanto para la actividad productiva rural como para las economías y la salud de los núcleos urbanos cercanos (Massobrio y Gutierrez 1998).
La toma de decisiones acerca de las medidas de protección y control requiere de la cuantificación de los procesos a través de modelos elegidos en función de la escala de análisis y de la información disponible.
El mecanismo de la erosión eólica plantea un problema complejo ya que es un caso especial de un flujo de dos fases (gaseosa y sólida) y un proceso de transporte, interceptación y deposición (Anderson y Haff 1991; Berkofsky y McEwan 1994; Bintanja 2000; Zou y otros 2001).
Los métodos utilizados para su descripción pueden ser divididos en dos: los denominados empíricos y los basados en modelos matemáticos (Zou y otros 2001). Ambos han contribuido a grandes progresos en la comprensión de los mecanismos de erosión eólica. La complejidad de los procesos intervinientes, los objetivos buscados, el nivel de detalle, como así también los datos disponibles, determinan la importancia de la elección de la metodología a utilizar.
Los modelos empíricos desarrollados, como por ejemplo la llamada "ecuación de erosión eólica" (Food Agricultural Organization (FAO) 1980; Skidmore y Williams 1991) suelen ser utilizados con fines climáticos, responden a las condiciones locales y su validez es limitada cuando se pretende su extrapolación. En general evalúan el riesgo de erosión eólica en términos de pérdida de masa de suelo por unidad de área y de tiempo.
Los modelos teóricos, que tienen en cuenta la interacción de los distintos componentes que intervienen en el proceso (Anderson y Haff 1991, Zou y otros 2001), permiten una estimación más precisa del fenómeno, se amplía el espectro de daños evaluables y son de validez más generalizada, pero su aplicación requiere de bases de datos completas (McKenna-Neuman y Nikling 1994; Skidmore y otros 1997). Su utilización en situaciones con escasa información ambiental exige una serie de aproximaciones y simulaciones. Si lo que se desea obtener son estimaciones de erosión en tiempo real, dichas aproximaciones reducen la validez de los resultados, mientras que si lo que se busca es evaluar el riesgo climático, el nivel de detalle requerido no justifica la utilización de dichos modelos.
El proceso de erosión eólica depende de la relación entre las fuerzas ejercidas por el viento sobre las partículas de suelo en la superficie terrestre (erosividad del viento) y la resistencia que ejercen las mismas a ser levantadas y desplazadas con el flujo de aire (erodabilidad del suelo) (Chepil y Woodruff 1963). La erosividad es función de la turbulencia atmosférica y es evaluable a través del gradiente vertical de velocidad del viento. La erodabilidad es función de la textura superficial, del contenido de materia orgánica, del contenido de humedad, del uso del suelo y de su cobertura vegetal, entre otros factores (Skidmore y Williams 1991).
En general, para la estimación de la erosividad en condiciones de campo se cuenta sólo con la información de las estaciones meteorológicas estándar (velocidad del viento medido a 10 m de altura); esto requiere adoptar el perfil logarítmico (ecuación (1)), característico de la capa superficial atmosférica en condiciones de estabilidad neutral, como modelo para describir su variación vertical (McKenna-Neuman y Nickling 1994; Skidmore y otros 1997).
|
| (1) |
donde u* es la velocidad de fricción, k es la constante de von Karman y u(zi) es la velocidad del viento a la altura zi.
Sin embargo, en experiencias realizadas en condiciones de erosión eólica, se observó que dichos modelos no describen satisfactoriamente los perfiles verticales de velocidad medidos (Owen 1964; Anderson y Haff 1991). Este hecho se atribuye a que, una vez iniciado el proceso de erosión eólica se genera una capa de aire de altura H con partículas de suelo que se mueven en saltación y que actúan como sumidero de cantidad de movimiento (Berkofsky y McEwan 1994; McKenna-Neuman y Nickling 1994; Nemoto y Nishimura 2001). Despreciar este efecto puede conducir a importantes errores cuando se evalúa el transporte de suelo por este mecanismo (Goldberg y Massobrio 1991).
Sobre la base de lo expuesto los objetivos del presente trabajo son:
1. Proponer un índice de riesgo climático de ocurrencia de erosión eólica basado en los procesos físicos que intervienen, expresado en función de observaciones meteorológicas estándar que considere las alteraciones del perfil vertical de la velocidad del viento.
2. Aplicar el índice de riesgo para condiciones extremas (suelo seco y desnudo) a fin de obtener su distribución espacial en la Provincia de Buenos Aires.
2. FUNDAMENTOS TEÓRICOS
La erosión eólica ocurre cuando el nivel de turbulencia atmosférica excede la resistencia al desprendimiento y transporte de los materiales de superficie (Skidmore 1986).
Durante los eventos de erosión eólica, asociados con altas velocidades del viento, la turbulencia se origina por efecto de las fuerzas de fricción ejercidas por la superficie terrestre sobre el flujo de aire. Esto da lugar a un perfil de velocidades que generan un transporte de cantidad de movimiento (τ), definida como (Panofsky y Dutton 1984).
| (2) |
donde ρ es la densidad del aire y u* es la velocidad de fricción, que puede ser caracterizada por la variación vertical de la velocidad del viento.
A partir de experiencias en túnel de viento sobre distintos tipos de suelo, Chepil y Woodruff (1963), encontraron que la cantidad de suelo levantado y transportado por el viento (Q) es proporcional al cubo de la velocidad de fricción:
| (3) |
donde α es una constante que depende de la distribución de tamaños de partículas de suelo.
Estos resultados fueron adoptados por Skidmore (1986) para la obtención de un factor climático (CE), una de las variables utilizadas en la metodología FAO para la estimación de pérdida potencial de suelo.
| (4) |
donde R es la resistencia del suelo tal que R = τt+ γ, τ es la tensión superficial, el subíndice t indica condiciones umbrales para el comienzo del proceso de erosión y γ es una función del contenido medio de humedad del suelo.
Para expresar CE en función de las observaciones meteorológicas estándar, Skidmore (1986) supone la validez del perfil logarítmico dado por la ecuación (1) y propone un factor climático en términos de la probabilidad de que la potencia del viento supere las condiciones umbrales
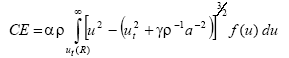 | (5) |
|---|
donde u es la velocidad del viento media a 10 m de altura; ut(R) es su valor umbral y depende de la resistencia del suelo; a es una constante que resulta de la aplicación del perfil logarítmico en la estimación de la velocidad de fricción en función de la velocidad a 10 m de altura; f(u) es la función de distribución de probabilidad de Weibull.
Sobre la base del esquema propuesto por Skidmore para el cálculo del factor climático (CE), en este trabajo se propone un índice (IR) que cuantifica el riesgo de erosión potencial tal que,
| (6) |
o de otra forma
| (7) |
donde se realizan las siguientes consideraciones:
a. R es sólo función de la velocidad de fricción umbral (u*t ).
b. Se excluye el término de humedad del suelo. La resistencia del suelo es afectada por el contenido de agua de los horizontes más superficiales, que dada su gran variabilidad espacial y temporal no es incluida en esta escala de trabajo.
c. Se incluye la alteración del perfil logarítmico generada por la presencia de partículas de suelo que se mueven en saltación y actúan como sumidero de cantidad de movimiento. Se propone para la descripción de la variación vertical de la velocidad del viento el modelo propuesto por Goldberg y Mazzeo (1996) que se describe a continuación:
1. Si la velocidad de fricción no supera los valores umbrales (u* < u*t ), el proceso de erosión no se ha iniciado por lo que u* es constante con la altura y por lo tanto se verifica la relación (1) (Panofsky y Dutton 1984).
2. Si la velocidad de fricción supera los valores mínimos para el inicio del proceso (u* > u*t ), se forma sobre la superficie terrestre una capa de aire de altura H con partículas de suelo que se mueven en saltación y donde se verifica que (Goldberg 1996):
Por encima de la capa (z > H) la variación vertical de la velocidad del viento es descripta adecuadamente por la ecuación (1), en cuyo caso se considera que u*= u*s (velocidad de fricción superior).
Dentro de la capa de saltación (z < H), la variación vertical de la velocidad resulta de integrar numéricamente la siguiente expresión:
| (8) |
donde KM(z) es el coeficiente de intercambio turbulento de cantidad de movimiento; Cd(z) y a(z) son respectivamente el coeficiente de arrastre y el área de arrastre de las partículas de suelo en el flujo de aire.
Para la variación vertical de KM se optó por la forma sugerida por Thom (1971) suponiendo para los obstáculos un comportamiento similar al de las canopias vegetales.
| (9) |
Las variaciones verticales del coeficiente de arrastre y del área de arrastre se describen a través de las expresiones encontradas por Goldberg (1996) para distintos tipos de suelo y rugosidad superficial.
| (10) |
| (11) |
Los coeficientes A, B, C y D dependen del tipo de suelo y se incluyen en la Tabla I. La altura de la capa H fue definida por Chepil (1945) como el nivel por debajo del cual se detectaron el 99% de las partículas de suelo moviéndose en saltación e identificada por McKenna-Neuman y Nickling (1994) en laboratorio como el nivel donde se detecta un marcado aumento del gradiente de velocidades.

Tabla I: Coeficientes A, B, C y D incluidos en las funciones a(z) y Cd(z)
De la integración de la ecuación (8) se obtienen valores discretos de velocidad del viento y su derivada a distintas alturas dentro de la capa de saltación.
Con el objeto de encontrar una expresión analítica que permita incluir estos resultados en el índice de riesgo, se ajustan las soluciones de la ecuación (8) a través de una función logarítmica cuya pendiente, por similitud con el modelo estándar, puede ser interpretada como función de una "velocidad de fricción interior", (u*i), representativa de la capa de saltación, de distinta magnitud que la superior, u*s. En este caso se verifica que:
| (12) |
De lo antes expuesto, se utilizan las ecuaciones (1) y (12) para expresar la ecuación (7) en función de la velocidad del viento a 10 metros de altura.
De esta forma:
| (13) |
| (14) |
con zo : longitud de rugosidad, tal que u(zo) = 0.
Combinando las ecuaciones (13) y (14) se obtiene:
| (15) |
donde
| (16) |
con β = u* i /u* s.
Reemplazando en la ecuación (7) el valor de velocidad de fricción umbral por su equivalente a la velocidad del viento umbral medida a 10 m obtenida de la ecuación (15) se obtiene:
| (17) |
donde u y ut son, respectivamente, la velocidad del viento media y la velocidad umbral medida a 10 metros de altura.
A fin de obtener el índice en términos de la potencia del viento cuando las fuerzas ejercidas por el mismo superan la velocidad umbral y que incluya la probabilidad de ocurrencia de estas condiciones, se propone una modificación a la expresión propuesta en la ecuación (17) tal que (Skidmore 1986):
 | (18) |
|---|
donde λ, definida por la ecuación (15), relaciona la velocidad de fricción con la velocidad del viento a 10 m de altura; f(u) es la distribución teórica de Weibull que ajusta adecuadamente la distribución de frecuencias de la velocidad del viento (Barros 1983; Brizuela y Aguirre 1989; Skidmore 1986), tal que:
| (19) |
donde c es el factor de escala y κ es el factor de forma.
3. APLICACION DEL MODELO
Para calcular el índice de riesgo utilizando la ecuación (18) se requiere conocer:
1. Los parámetros de la función de distribución de la velocidad del viento.
2. La velocidad del viento umbral a 10 m de altura a través de la ecuación (15), para lo que es necesario determinar previamente el valor de λ.
3.1 Función de distribución de la velocidad
El índice IR surge de la integración de la ecuación (16). Para obtener una solución analítica de la misma se supone κ=2 (Skidmore 1986) con lo cual la f(u) se reduce a la distribución de Rayleigh, en cuyo caso el parámetro de escala toma la forma:
| (20) |
3.2 Obtención del parámetro λ
Con el uso de la ecuación (8) se realizaron simulaciones de la variación vertical de la velocidad del viento entre la superficie y la altura H para distintos tipos de suelo, rangos de velocidad del viento y de velocidad de fricción fuera de la capa (u*s) (Weiss 1999). Los perfiles resultantes fueron ajustados mediante la ecuación (12). Para cada simulación se determinaron los valores de z0 y u*i .
Para la obtención de la altura H, se han considerado los valores medidos o estimados, en condiciones de campo, por Chepil (1945), por Fryrear y Saleh (1993) y por Goldberg (1996) quienes informaron valores de H entre 60 y 110 cm para distintos tipos de suelo. Por otro lado, de un análisis de sensibilidad realizado por Goldberg (1996) sobre las soluciones de la ecuación (8) se concluye que diferencias del 40% en la estimación de H podrían generar errores menores o iguales que el 20% en la velocidad del viento. Estos resultados, sumados al hecho de que la información es utilizada en cálculos dentro de una escala climatológica, avalaron el criterio de haber optado por el valor de 1 metro para caracterizar la altura de capa de saltación.
Se calculó el cociente entre las velocidades de fricción superior e inferior que define el parámetro β. Los valores de β obtenidos varían entre 1,19 y 1,22, mientras que los de zo, entre 0,03 m y 0,09 m.
Con las mismas consideraciones de escala realizadas anteriormente, se asume para β y zo valores medios de 1,2 y 0,05 respectivamente, con lo que resulta un valor del parámetro λ constante.
3.3 Obtención de la velocidad del viento umbral (ut ) a 10 m de altura
Chepil (1945) encontró que la velocidad umbral es función del tipo de suelo y rugosidad superficial e informó los valores correspondientes a una altura de 30 cm para suelos arcilloso pesado, arcilloso, franco arcillo limoso, franco arcilloso, franco, franco liviano y franco arenoso fino.
Para obtener la velocidad umbral en las localidades estudiadas, se identificó el tipo de suelo que se encuentra en mayor proporción dentro de cada dominio edáfico o subregión, determinándose la textura y su correspondiente velocidad umbral (Weiss 1999; Costa y Weiss 1999) y se le asoció a cada uno el valor de velocidad umbral informado por Chepil (1945), que luego fue corregido a 10 metros de altura con la ecuación (15).
Los valores obtenidos para distintos tipos de suelo se incluyen en la Tabla II y la distribución espacial en la zona de estudio se muestra en la Figura 1.
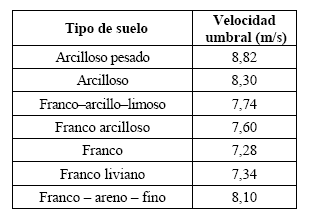
Tabla II: Velocidad del viento umbral a 10 m de altura (m/s) en función de la textura del suelo.

Figura 1: Distribución espacial de la velocidad del viento umbral a 10 m de altura (m/s).
Los datos de suelo utilizados para el cálculo de la velocidad umbral, pertenecen a la carta de suelo de la Provincia de Buenos Aires (1:500000, Secretaría de Agricultura, Ganadería y Pesca (SAGyP) e Instituto Nacional de Tecnología Agropecuaria (INTA), 1989), donde se ubicaron los dominios edáficos y subregiones (Goldberg y otros 2000).
3.4 Obtención del índice de riesgo
Con la consideración de κ=2 y λ constante, se integra la ecuación (18) que resulta:
| (21) |
donde γ = 1,33 proviene de la utilización de la función Gamma en el proceso de integración (Brizuela y Aguirre 1989; Skidmore 1986).
Con la metodología antes descripta se calcularon los valores del índice de riesgo (IR) para 35 localidades de la Provincia de Buenos Aires ubicadas en los mapas de las Figuras 2 y 3. Los valores de velocidad del viento utilizados fueron obtenidos de las estadísticas climatológicas del Servicio Meteorológico Nacional (1961-1970 y 1971-1980) y del informe sobre recursos eólicos de la Provincia de Buenos Aires (Brizuela y Aiello 1988); su distribución espacial se incluye en la Figura 2.

Figura 2: Distribución espacial de la velocidad del viento media a 10 m de altura (m/s).
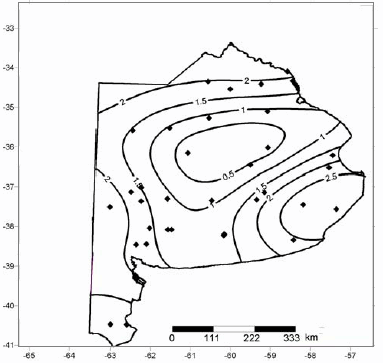
Figura 3: Distribución espacial del índice de riesgo climático de erosión eólica (IRM).
Dado que no se contaba con parámetros objetivos que cuantifiquen los efectos de la erosión en condiciones de campo, no fue posible una contrastación del modelo con datos reales. Como primera aproximación, se optó por una comparación con los valores de riesgo obtenidos simultáneamente para 17 localidades mediante la metodología propuesta por FAO (1980). Las categorías del riesgo según FAO se incluyen en la Tabla III y los resultados de la comparación se presentan en la Figura 4.

Tabla III: Categorías de erosión eólica de acuerdo a la metodología FAO.

Figura 4: Comparación de evaluaciones del riesgo a través de la metodología FAO y del índice de riesgo modificado (IRM)
4. DISCUSIÓN
El índice obtenido con la ecuación (22) permite contar con una expresión simple para la evaluación del riesgo climático de ocurrencia de erosión eólica. El mismo fue calculado para suelo seco y desnudo (condiciones de máxima susceptibilidad), pero el modelo permite incluir otros aspectos que hacen a la resistencia del suelo (contenido de materia orgánica, la cobertura vegetal o el uso del suelo, entre otros) considerados en los respectivos valores de velocidad umbral.
Se trata de una estimación de riesgo relativo. No puede por ahora ser traducido en valores socioeconómicos absolutos.
Las características del modelo planteado permiten la estimación del índice en escalas de trabajo mayores, 1:50.000 o incluso a nivel de predio; para ello se requiere avanzar en la evaluación de la velocidad de fricción umbral para los otros factores que hacen a la resistencia del suelo y por otro lado, tener en cuenta la variabilidad de parámetros tales como la longitud de rugosidad y la altura de la capa de saltación.
En esta escala de trabajo, el índice propuesto sigue aproximadamente la misma tendencia que los valores obtenidos por la metodología FAO. Su distribución geográfica para suelo seco y desnudo sigue, en general, el mismo patrón que la distribución de la velocidad media del viento con excepción del extremo noreste de la Provincia de Buenos Aires donde predomina el efecto de resistencia de los suelos que son principalmente argiudoles. Los elevados índices obtenidos para el sur de la Provincia se deben fundamentalmente a la elevada velocidad del viento característico de la zona, mientras que los valores hallados en el noroeste de la Provincia (suelos tipo Hapludol) se explican por un efecto combinado de la velocidad del viento y baja velocidad umbral características de la zona.
En la metodología presentada se han utilizado los valores de velocidad del viento umbral encontrados por Chepil (1945) que son sólo función de la textura superficial. Cuando el mismo es utilizado en zonas caracterizadas por suelos con alto contenido de materia orgánica, factor que aumenta la cohesión entre las partículas de suelo, la metodología propuesta puede dar lugar a una sobrestimación del riesgo. Tal podría ser el caso de la zona centro-sudeste de la Provincia de Buenos Aires donde se detecta un máximo que no representa las condiciones observables en la zona.
Se considera necesario avanzar en la determinación de la velocidad umbral en función del contenido de materia orgánica como así también de otros factores que hacen a la resistencia del suelo tales como el contenido de humedad de suelo en las capas superficiales, la cobertura vegetal y uso del suelo entre otros; en especial cuando se quiere aplicar esta metodología en escalas mayores.
5. CONCLUSIONES
Se propone una expresión simple para evaluar el riesgo climático de ocurrencia de erosión eólica basado en el hecho de que el flujo de partículas de suelo es proporcional al cubo de la velocidad de fricción, cuando la misma supera los valores umbrales para el comienzo del proceso.
Las principales ventajas del método son: i) Se basa en el proceso físico con el que se describe el proceso de erosión eólica, ii) Tiene en cuenta la probabilidad de ocurrencia de las condiciones umbral, iii) Su expresión en función de observaciones meteorológicas estándar (viento a 10 m de altura) tiene en cuenta la modificación del perfil de viento que se genera ante la presencia de partículas de suelo que se mueven en saltación. El índice fue obtenido para suelo seco y desnudo, pero la metodología permite generalizar el modelo determinando los valores de velocidad de fricción umbral asociada a distintas condiciones que afectan la resistencia del suelo.
Agradecimientos: Agradecemos al Dr. Marcelo Massobrio, al Dr. Nicolás Mazzeo por sus apreciadas sugerencias, al Lic. Raúl Righini e Ing. Agr. Marcos Angelini por sus aportes en la elaboración del material cartográfico, y especialmente a la Dra. de Garín por sus valiosos aportes y el apoyo brindado. Deseamos manifestar nuestro agradecimiento a los señores evaluadores por sus valiosas sugerencias y comentarios.
REFERENCIAS:
1. Anderson, R.S. y Haff, D., 1991. Wind modification and bed response during saltation of sand in air. Acta Mechanica (suppl.), 1, 21-51. [ Links ]
2. Barros, V., 1983. Evaluación del potencial eólico en la Patagonia. Meteorologica, 14, Nº 1 y 2, 473-484. [ Links ]
3. Berkofsky L. y McEwan, I., 1994. The prediction of dust erosion by wind: An interactive model. Boundary Layer Meteorology, 67, 385-406. [ Links ]
4. Bintanja, R., 2000. Snowdrift suspension and atmospheric turbulence. Part 1: Theoretical Background and model description. Boundary Layer Meteorology, 95, 343-368. [ Links ]
5. Brizuela, A. y Aiello, J., 1988. El recurso eólico en la Provincia de Buenos Aires. 1ra. Parte: Estadísticas del viento. Red Solarimétrica. Comisión Nacional de Investigaciones Espaciales. Argentina. 152 págs. [ Links ]
6. Brizuela, A. y Aguirre, C., 1989. El recurso eólico en la Provincia de Buenos Aires. 2da. Parte: Evaluación del recurso. Red Solarimétrica. Comisión Nacional de Investigaciones Espaciales. Argentina. 70 págs. [ Links ]
7. Chepil, W.S., 1945. Dynamic of wind erosion: II. Initiation of soil movement. Soil Science, 60, 5, 397-411. [ Links ]
8. Chepil W.S. y Woodruff, N., 1963. The physics of wind erosion and its control. Advances in Agronomy, 15, 211-302. [ Links ]
9. Costa, C. y Weiss, G., 1999. Evaluación de la erosión eólica en la región semiárida pampeana utilizando la metodología FAO. Sin publicar. [ Links ]
10. FAO, 1980. Metodología provisional para la evaluación de la degradación de los suelos. Roma. 44 págs. [ Links ]
11. Fryrear, D.W y Ali Saleh, 1993. Field wind erosion: vertical distribution. Soil Science, 155, 4, 294-300. [ Links ]
12. Goldberg, S. y Massobrio, M., 1991. Impacto de la aplicación de diferentes modelos de capa superficial atmosférica en la estimación de la erosión eólica. Actas del VI Congreso Argentino de Meteorología, 83-84, 23 al 27 de setiembre de 1991, Buenos Aires, Argentina. [ Links ]
13. Goldberg, S. y Mazzeo, N., 1996. Estudio del comportamiento del viento en las capas de la atmósfera cercanas al suelo en condiciones de erosión eólica. Actas VII Congreso Argentino de Meteorología, y VII Congreso Latinoamericano e Ibérico de Meteorología. 299-300, 2 al 6 de setiembre de 1996, Buenos Aires, Argentina. [ Links ]
14. Goldberg, S., 1996. Estudio del comportamiento del viento en las capas de la atmósfera cercanas al suelo en condiciones de erosión eólica. Trabajo de tesis Doctoral, UBA, Dto. de Ciencias de la Atmósfera y los Océanos. 136 págs. [ Links ]
15. Goldberg, S., Costa, M.C. y Weiss, G., 2000. Riesgo de erosión eólica en las provincias de Buenos Aires y La Pampa. Cálculo de la velocidad del viento umbral. Abstracts de la 11º Conferencia de la Organización Internacional de la Conservación de Suelo, 56, 22 al 27 de octubre de 2000, Buenos Aires, Argentina. [ Links ]
16. Massobrio, M. y Gutierrez, P., 1998. Environmental economic evaluation of wind erosion effects in an area of La Pampa Province, Argentina. Proceedings fifth biennal meeting International Soc. for Ecological Economic, 1, 180, 15 a 19 de noviembre de 1998, Santiago de Chile, Chile. [ Links ]
17. McKenna-Neuman C. y Nickling W.G., 1994. Momentum extraction with saltation: Implications for experimental evaluation of wind profile parameters. Boundary Layer Meteorology, 68, 35-50. [ Links ]
18. Nemoto, M. y Nishimura, K., 2001. Direct measurement of shear stress during snow saltation Boundary Layer Meteorology, 100, 149-170. [ Links ]
19. Owen, P.R., 1964. Saltation of uniform grains in air. J. Fluid Mech., 20, 2, 225-242. [ Links ]
20. Panofsky, H. y Dutton, J.A., 1984. Atmospheric turbulence, model and methods for engineering applications. Wiley, New York, U.S.A. 397 págs. [ Links ]
21. SAGyP e INTA, 1989. Mapas de suelos de la provincia de Buenos Aires, Proyecto PNUD ARG 85/019. 525 págs. [ Links ]
22. Servicio Meteorológico Nacional, Estadísticas Climatológicas 1961-1970. Fuerza Aérea Argentina, 188 págs. [ Links ]
23. Servicio Meteorológico Nacional, 1986. Estadísticas Climatológicas 1971-1980. Fuerza Aérea Argentina, 169 págs. [ Links ]
24. Skidmore, E.L., 1986. Wind erosion climatic erosivity. Climatic Change, 9, 195-208. [ Links ]
25. Skidmore, E.L y Williams J.R., 1991. Modified EPIC Wind Erosion Model. Modeling Plant and Soil System- Agronomy Monograph Nº 31, ASA-CSSA-SSSA. U.S.A. págs. 457-469. [ Links ]
26. Skidmore, E.L., Tartako, J. y Wagner, L.E., 1997. Climate database for wind erosion prediction model. Proceedings of the Workshop on Climate and Weather Research. Denver, U.S.A., 98-110. [ Links ]
27. Thom, A. S., 1971. Momentum absorption by vegetation. Quart. J. Roy. Met. Soc., 97, 414-428. [ Links ]
28. Weiss, G., 1999. Determinación de un índice de erosividad eólica potencial para condiciones de suelo seco y desnudo. Su aplicación a la región semiárida pampeana. Trabajo final de aplicación para acceder al título de Ingeniería Agronómica. Universidad Nacional de Luján, Buenos Aires, Argentina. 98 págs. [ Links ]
29. Zou X.Y., Wang, Z.L., Hao, Q.Z., Zhang, C.L., Liu, Y.Z. y Dong, G.R., 2001. The distribution of velocity and energy of saltating sand grains in a wind tunnel. Geomorphology, 36, 155-165. [ Links ]














