Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista electrónica de investigación en educación en ciencias
versión On-line ISSN 1850-6666
Rev. electrón. investig. educ. cienc. vol.2 no.1 Tandil ene./jul. 2007
ARTÍCULOS ORIGINALES
Los estudiantes ante formas de argumentar aristotélicas y no aristotélicas. Un estudio de casos
Cecilia Crespo Crespo
Instituto Superior del Profesorado "Dr. Joaquín V. González". Buenos Aires (Argentina)
Centro de Investigaciones en Ciencia Aplicada y Tecnología Avanzada. CICATA-IPN. (México)
Resumen
Este trabajo muestra la presencia en el aula de matemática de algunas formas de argumentación no correctas desde la lógica aristotélica. Se observó la aplicación por parte de estudiantes de argumentaciones no válidos y se obtuvieron en las experiencias que se reportan, declaraciones de los estudiantes sobre su posición frente a formas de argumentación clásicas, que denotan la no aceptación de las formas aristotélicas. El objetivo de la investigación de la que forma parte este reporte, es comprender el carácter sociocultural de las argumentaciones matemáticas, intentando mostrarlas como resultado de acciones de una comunidad en un escenario sociocultural. Nuestra cultura, con base aristotélica, ha construido formas de argumentación basadas en esta lógica. Sin embargo, en el aula se ponen de manifiesto situaciones que evidencian el carácter de construcción social de la argumentación matemática y que consideramos tiene que ser tenidas en cuenta en el discurso matemático escolar.
Palabras clave: Socioepistemología; Argumentación; Construcción sociocultural; Argumentación no aristotélica; Convicción
Abstract
This work shows that in mathematics classroom appear many argumentations that are not correct for aristotelic logic. We observe that some students have used not valid argumentations. We reporte some of their declarations that show a position in front of classic forms of argumentation and that denote the nonacceptance of the aristotelian forms. This report is part of a research which aim is to understand the sociocultural character of the mathematical argumentations, trying to show them as result of actions of a community into a sociocultural stage. Our culture, with aristotelic sustenance, has constructed forms of argumentation based on this logic. Nevertheless, in the classroom there are revealed some situations that demonstrate the character of social construction of mathematical argumentations and that we consider it has to be taken in account in the mathematical school discourse.
El enfoque socioepistemológico de las argumentaciones matemáticas
Este trabajo forma parte de una investigación que se está llevando a cabo, en la que se presenta y analiza a la argumentación matemática como una construcción sociocultural que emerge dentro de la comunidad matemática, y es desarrollada de acuerdo con las características del escenario sociocultural en el que se pone de manifiesto.
Las argumentaciones lógicas y las demostraciones han desempeñado un papel importante en el desarrollo de la matemática a lo largo de toda la historia de la humanidad. Esta influencia e interacción se manifiesta no sólo en la fundamentación de esta ciencia, sino también en su enseñanza, pudiendo afirmarse que es usual relacionar estrechamente el concepto de lógica con el de matemática, aunque el tipo de relación existente ha variado en las distintas culturas y tiempos.
Durante siglos, la matemática ha sido considerada como una ciencia, en la que la verdad de las afirmaciones se sustenta en el carácter deductivo de la lógica. El conocimiento matemático se sustenta básicamente en dos modos de comprensión y expresión: uno se realiza de forma directa, y corresponde a la intuición y el otro se lleva a cabo de forma reflexiva, es decir lógica. Sin embargo, a lo largo de la historia, las concepciones relacionadas con las demostraciones no se han mantenido estáticas, sino que han cambiado notablemente reflejando características de los escenarios socioculturales en los que se desenvolvieron.
La línea de investigación que desarrolla la matemática educativa en relación a la construcción social del conocimiento, considera necesario dotar a la investigación de una aproximación sistémica y situada, o sea que atiende a las circunstancias y escenarios socioculturales particulares, que permita incorporar las cuatro componentes fundamentales en la construcción del conocimiento: su naturaleza epistemológica, su dimensión sociocultural, los planos de lo cognitivo y los modos de transmisión vía la enseñanza. Esta aproximación se ha llamado formalmente el acercamiento socioepistemológico (Cantoral& Farfán, 2003). De esta manera, en una investigación, se deben analizar cuatro componentes: cognitiva, epistemológica, didáctica y social, pero no de manera aislada, sino integradas sistémicamente.
Puede decirse que la problemática de estudio de la matemática educativa es "el examen de los fenómenos que se suceden cuando el saber matemático, constituido socialmente fuera de la institución escolar, se introduce y se desarrolla en el sistema de enseñanza" (Farfán, 2003, p.5). Este proceso por el cual de incorporan los saberes matemáticos en el sistema educativo, plantea una serie de problemas de carácter tanto teórico como práctico que necesitan acercamientos teóricos y metodológicos adecuados. El enfoque socioepistemológico a través del análisis integral desde las cuatro componentes citadas anteriormente, permite comprender al conocimiento matemático como una construcción sociocultural que se realiza en un escenario sociocultural determinado. A través del reconocimiento de la naturaleza y construcción social del conocimiento matemático, se prioriza la actividad humana contrastando con otros enfoques teóricos que giran alrededor del objeto matemático. La actividad humana, se torna central en el enfoque socioepistemológico a través del análisis de las prácticas sociales asociadas a un conocimiento matemático.
Es básico en el enfoque socioepistemológico, el papel de los escenarios históricos, culturales e institucionales en las explicaciones del conocimiento desde la matemática educativa. El concepto de escenarios se afianzó a partir de la introducción del estudio de los contextos escolares e institucionales, comprendidos como fundamentales en la construcción y transmisión del conocimiento matemático (Martínez, 2005). En este marco, que parte de la consideración de que los saberes matemáticos son construcciones socioculturales, se comprende a los procesos de convención matemática como procesos sociales de construcción del conocimiento.
Desde la perspectiva socioepistemológica, la construcción del conocimiento es condicionada por circunstancias cognitivas (propias del funcionamiento mental), didácticas (propias de la conformación de los distintos sistemas didácticos), epistemológicas (propias de la naturaleza y significados del pensamiento matemático) y sociales (como proceso de síntesis de los objetos y herramientas de una sociedad). Estas circunstancias, de naturaleza diversa son las que originan que la matemática educativa enfoque desde las cuatro componentes correspondientes y de manera integral su estudio e investigación.
En la perspectiva socioepistemológica, se identifican algunas unidades de análisis a tener en cuenta en una investigación (Martínez, 2005). Entre ellas, se pueden citar las nociones de actividad humana, resignificación del conocimiento y práctica social. La noción de actividad humana, permite explicar el conocimiento en términos de herramientas usadas por el hombre para hacer matemática. La noción de resignificación se orienta a presentar el conocimiento con significados propios, contextos, historia e intención, contraponiéndolo a la idea platónica de preexistencia de los objetos y procesos matemáticos. La noción de práctica social, medular en la socioepistemología, se refiere a las acciones intencionales de los grupos humanos para transformar la realidad social y material.
Esta perspectiva, de esta manera se enfoca actualmente en ciertas nociones que en su carácter de práctica social logran una resignificación en el proceso de construcción del conocimiento. Por ejemplo, tal como lo presenta Gustavo Martínez, la noción de convención matemática, usualmente considerada como preestablecida e inmóvil, es entendida por la socioepistemología como un proceso de construcción del conocimiento, como una conveniencia para la matemática con el objeto de evitar contradicción o dar unidad. Esta visión permite cuestionar la idea de validez universal del conocimiento matemático, comprendiendo la condición social de las convenciones, que son de esta manera, entendidas como un proceso de búsqueda de consensos en el seno de la comunidad que trabaja para dar unidad y coherencia a un conjunto de conocimientos. La sociedad matemática, de esta manera, en escenarios adecuados, construye conocimiento a partir de las prácticas sociales en ese escenario.
Para el enfoque socioepistemológico, al igual que para semiótica cultural, la actividad humana es central en la construcción del conocimiento, pero el énfasis socioepistemológico no está puesto en el objeto, sino en la práctica social, con el fin de modelar situaciones para la intervención didáctica (Cantoral et al., 2006). Analicemos más profundamente la concepción de práctica social tal como la ve la socioepistemología. Identificaremos posteriormente cuál es su relación con las argumentaciones y demostraciones matemáticas.
La presente investigación se enfoca desde la perspectiva socioepistemológica. El objetivo de la investigación es comprender el carácter sociocultural de las argumentaciones matemáticas, intentando mostrarlas como resultado de las acciones de una comunidad en un escenario sociocultural. De esta manera, podemos afirmar que las argumentaciones lógicas que subyacen al conocimiento matemático no son inherentes a la forma de razonar del ser humano, sino que dependen del escenario sociocultural en el que se desempeñen (Crespo Crespo, 2005a, Crespo Crespo & Farfán, 2005).
Comprender a las argumentaciones matemáticas como una construcción sociocultural implica, por una parte asumir que es posible construir socialmente el conocimiento matemático e identificar cuál es el papel que desempeña la demostración, y más generalmente la argumentación matemática en esa sociedad. La visión de las argumentaciones como una construcción matemática, que subyace a los objetos matemáticos y sus propiedades y que permite avanzar y dar sentido a las diversas construcciones que realiza la comunidad matemática en cuanto sociedad, la institución en la que se construye, se valida y se difunde el saber, permitirá llevar a cabo nuestro objetivo. Faculta también admitir la posibilidad de que en escenarios socioepistemológicos distintos se utilicen formas de argumentación distintas que caractericen a distintos tipos de demostraciones matemáticas aceptadas por una sociedad.
La postura socioepistemológica considera que la matemática no es una ciencia que surge y se desarrolla aislada de la sociedad, sino inmersa en ella, que forma parte de ella, que en su desarrollo refleja claramente características de los escenarios en los que se desenvuelve, nutriéndose de ellos. De esta manera, recibe influencias fuertemente basadas en el pensamiento, las necesidades y características del escenario en que se desarrolla. Así, es que el contexto social, cultural e históricamente determinado actúa como parte indiscutible de este proceso de nacimiento, desarrollo y evolución de la ciencia. El escenario sociocultural adquiere en esta visión un papel medular, ya que es el que permite la construcción característica de la argumentación, en tanto objeto matemático de esa sociedad.
Argumentaciones en el aula de matemática
En los últimos años, es posible encontrar en publicaciones sobre la enseñanza y el aprendizaje de la matemática, muchos trabajos en los que se describen dificultades que se detectan en el aula de matemática ante las demostraciones y las formas de argumentación utilizadas (Balacheff, 1982; Godino & Recio, 2001; Ibañes, 2001, Duval, 1999, 2000; Valverde, 1990; de Villiers, 1993; Arsac, 1987; Hanna, 1997, 2000). Estas realizan abordajes desde distintos enfoques, pero todas coinciden en que no se logra en el aula el tipo de argumentación esperada por los docentes y los matemáticos. Para cada una de ellas, los términos argumentación, demostración, explicación, prueba, entre otros, adquieren significados que evidencian la epistemología subyacente. Sin embargo, según lo reportado en estas investigaciones, las demostraciones obtenidas en el aula de matemática en los distintos niveles educativos, distan mucho de las que los docentes considerarían como correctas a pesar de las estrategias que se pongan en juego para lograrlas; si bien en el aula actual los docentes no demuestran ni argumentan los conceptos matemáticos y algo similar ocurre en algunos libros de texto actuales, los docentes reconocen la importancia y necesidad de las demostraciones en el aula de matemática (Crespo Crespo, 2003, 2004, 2005b).
Por otra parte, es usual que se afirme tanto en ámbitos académicos como no académicos que para entender la matemática es esencial ser capaz de razonar, que el desarrollo y construcción de los conocimientos matemáticos se basan en las argumentaciones y demostraciones matemáticas (NTNM, 2000). También, desde ciertas concepciones cognitivas se afirma que la razón tiene que ver con un mecanismo en el lenguaje natural del ser humano (Núñez& Lakoff, 2000). De manera inmediata, cabe preguntarse, entonces, por qué resulta tan complejo el aprendizaje de la matemática y por qué es que justamente esa visión asociada a la construcción racional de la matemática no se logra en nuestras aulas...
Existen oportunidades en las que encontramos en el aula de matemática formas de argumentación que son incorrectas desde la lógica aristotélica y todas las que se construyeron sobre los principios lógicos de aquella. A pesar de que se las corrige en reiteradas oportunidades, se observa que reaparecen de manera insistente. Esto dio origen a que nos cuestionáramos intentando buscar su origen de manera más profunda acerca de la causa por la que algunos estudiantes presentan reiteradamente formas de argumentación no correctas.
Un ejemplo de argumentación en el aula de matemática
En una de sus publicaciones, Bruno D´Amore introduce a partir de las características de la lógica nyaya (D´Amore, 2005a, Hiriyanna, 1960), una experiencia en la que identifica en ejemplos extraídos de las clases de matemática de alumnos de entre 14 o 15 años, ciertos comportamientos argumentativos que se acercan a estructuras argumentativas nyayas.
La filosofía nyaya surge en la antigüedad en la India oponiéndose como forma de pensar al budismo y al jainismo. Se basa en los Vedas y los medios del conocimiento para los nyayas son: el testimonio, como lo digno de fe, transmitido en forma oral o escrita; la analogía que permite definir un objeto sobre la base de semejanzas con otros objetos; la percepción, vista como la relación entre los objetos captables por medio de los sentidos y la imagen que tenemos del objeto y, finalmente, la inferencia, teniendo en cuenta que el esquema del silogismo nyaya se basa en cinco enunciados (afirmación, razón, ejemplificación, generalización y conclusión). En estas argumentaciones no se realiza una deducción lógica al estilo aristotélico, sino que tiene cierto carácter abductivo por medio de la búsqueda de causas que se constituyen en condiciones que por medio de la ejemplificación conducen a la afirmación de la tesis. Este carácter abductivo se pone en evidencia cuando habiéndose afirmado una implicación y su consecuente se afirma como consecuencia su antecedente.
Un ejemplo en el que puede observarse la aplicación de esta forma de argumentación de origen nyaya y las etapas que la forman es la siguiente:
- En la colina hay fuego (Afirmación)
- Porque en ella hay humo (Razón)
- Donde hay humo hay fuego, por ejemplo en la cocina (Proposición general seguida de ejemplificación o aplicación)
- En la colina hay humo, que va siempre acompañado de fuego (Generalización o tesis)
- Por consiguiente en la colina hay fuego (Conclusión)
En las experimentaciones reportadas por D´Amore, estas formas de argumentaciones se presentaron de manera espontánea en estudiantes, sin que hubieran sido producidas por el investigador, ni por procesos previos de aprendizaje llevados a cabo en el aula. D´Amore afirma:
"Yo no creo, incluso después de esta investigación que estos estudiantes piensen en estricto acuerdo con la lógica nyaya. El recurrir a esta lógica en el análisis del razonamiento matemático de los estudiantes, evidencia sin embargo, el hecho que el análisis didáctico presupone, de una forma u otra, un marco de referencia y que existen diferentes lógicas posibles para dar explicación del comportamiento deductivo de los estudiantes"
(D´Amore, 2005a, p. 84)
Desde nuestra óptica, los resultados de la investigación anterior, estarían denotando algo más: que la forma de razonar aristotélica, que usualmente se presupone como la única presente en el aula de matemática, es una construcción sociocultural que a veces resulta a los alumnos con carácter artificial y que no es comprendida por ellos como evidente y que produzca convicción.
Para la cultura occidental, ha parecido y se ha asumido durante siglos que la construida sobre los principios aristotélicos es la forma de razonar del ser humano, pero esto se debe simplemente a que hemos nacido en una sociedad que tiene sumamente arraigada tal cultura, nos hallamos inmersos en ella y es muy complejo tomar distancia del escenario en el que interactuamos para poder analizar objetivamente sus características. Esta es la causa por la que no resulta fácil comprender las formas de razonamiento como construcciones socioculturales.
En la investigación que presenta D'Amore, pueden identificarse claramente las etapas del pensamiento lógico védico en el planteo e intentos de demostración de propiedades matemáticas por parte de los estudiantes.
Sobre la base de la publicación citada y tomándola como antecedente, se observó el razonamiento presentado por una maestra, participante de un curso de capacitación de geometría, en la que se evidenció un esquema argumentativo de características similares. Este caso, en el que aparecieron argumentaciones que recuerdan al esquema nyaya, permitió indagar acerca de las opiniones de la estudiante del curso de capacitación que la presentaba, sobre su opinión acerca de la corrección de la misma y la convicción que en ella genera.
Se le había presentado el siguiente enunciado:
Si un cuadrilátero tiene sus diagonales perpendiculares y se cortan mutuamente en su punto medio, entonces es un rombo.
La maestra tenía que realizar la demostración de la propiedad y exponerla a la docente del curso. Tras la lectura del enunciado, los pasos que siguió y reflexiones que realizó fueron los siguientes:
- AB=BC=CD=DA (dibuja un rombo y le da los nombres correspondientes a los vértices)
- Yo sé que BD⊥AC, se cortan en O, y AO=OC y BO=OD
- Pero si las diagonales son perpendiculares y se cortan en partes iguales, entonces los lados son iguales, o sea es un rombo (mientras habla va marcando en la figura que realizó).
- Las diagonales son perpendiculares y se cortan en partes iguales.
- Los cuatro lados son iguales, es un rombo.
La propiedad no está demostrada, pero la actuación de esta estudiante frente al problema planteado es similar a la que reporta D'Amore. En ella se identifican las etapas de la argumentación nyaya. Cada uno de los pasos propuestos pueden hacerse corresponder a las fases de las argumentaciones nyayas:
- Afirmación: P(A). La afirmación aún no probada es afirmada inicialmente
- Razón: F(A) Se afirma la causa que se atribuye para que P(A) ocurra
- Tesis: ∀(X) [F(X) ⇒P(X)] Se enuncia la proposición general y ejemplifica la tesis en un caso particular: F(B)⇒P(B), en este caso marcando en la figura de análisis realizada.
- Aplicación: F(A) Se afirma la hipótesis del caso general se vuelve al caso en examen: una fuerza ejerce una acción sobre la figura analizada.
- Afirmación: P(A). Se reafirma el consecuente que se quería probar.
Al llegar a este punto, la propiedad es asumida. Indudablemente, si se analiza la corrección del razonamiento, se dirá que no es correcto. Sin embargo, la maestra, participante del curso de capacitación que realizó este razonamiento, afirmó que lo había probado aunque no fuera de una manera formal. Era conciente de que no se le aceptaría matemáticamente su razonamiento, pero ella lo aceptaba como una prueba de la propiedad. Se acababa de poner en juego una estrategia de argumentación no aristotélica, pero que satisfacía a su autora.
Llamó la atención el hecho de que ella afirmaba que era conciente de que esta no era la forma de argumentación esperada por su docente, pero que le parecía más convincente.
Otro ejemplo de argumentaciones en el aula de matemática
En este estudio de casos, se analizó además una situación presentada en el aula. A continuación, se presenta esta experiencia en la que es posible identificar la presencia de formas de argumentar que no tienen carácter aristotélico y, posteriormente, opiniones de una estudiante acerca de formas de argumentar aristotélicas y que al igual que en el caso anterior, no una convicción con corrección de las mismas.
La siguiente experiencia que se presenta en este trabajo, ha sido realizada con una estudiante del Profesorado de Informática, durante la cursada de la asignatura Matemática 2, cuyos contenidos consisten en la presentación de los conceptos fundamentales de la lógica clásica (proposicional y de predicados), su mecanización mediante las álgebras de Boole y, finalmente de algunos rudimentos de las lógicas no clásicas (lógicas polivalentes y lógica difusa). Los estudiantes del curso, en el momento de la experimentación que reportamos habían adquirido los conocimientos de la lógica clásica, pero no han abordado ningún concepto de lógicas no clásicas aún. Por esta causa, no es posible considerar que la experiencia que se describe a continuación tenga influencias de estudios realizados por la alumna.
La siguiente actividad había sido planteada a los alumnos durante una evaluación escrita. Este tipo de ejercicio había sido resuelto previamente en clase en diversas oportunidades, discutiéndose su resolución y fundamentación, además en la práctica de la materia se encontraban ejemplos similares que habían sido consultados por los estudiantes y explicados, a veces de manera individual y otras frente a todo el grupo del curso.
Dado el siguiente razonamiento, se pide:
a. Formalizarlo en lógica de predicados de primer orden. Indicar los dominios de cada función proposicional.
b. Formalizarlo como proposiciones categóricas.
c. Determinar su validez.
d. Si es válido, demostrarlo por el método deductivo. Si no lo es, modifique una premisa para que lo sea. Algunos físicos son matemáticos. Ningún químico es matemático. Por lo tanto, algún físico no es químico.
La solución esperada para la actividad era la siguiente:
a. P(x) = x es físico
Q(x) = x es matemático
R(x) = x es químico
DomP = DomQ = DomR = {personas}
∃x (P(x) ∧ Q(x))
∀x(R(x) ⇒ ∼ Q(x))
∃x (P(x) ∧ ∼ R(x))
Se definían las funciones proposicionales correspondientes y sus correspondientes dominios y a continuación se realiza la formalización del razonamiento en lógica de predicados.
b. A = clase de los físicos
B = clase de los matemáticos
C = clase de los químicos
U = {personas}
Algún A es B.
Ningún C es B
Algún A no es C.
En este ítem, se declaran las clases en juego y el universal que las incluye, y a continuación se formalizan las proposiciones como proposiciones categóricas.
c.
Retomando la formalización como proposiciones categóricas, se representa cada una de las premisas en diagramas de Venn, con la convención de que una cruz marcada en un sector, significa la existencia de algún elemento en ese sector de los conjuntos, mientras que un sector rayado, significa que el mismo se encuentra vacío.
Los diagramas de Venn así obtenidos serían, por ejemplo los siguientes:
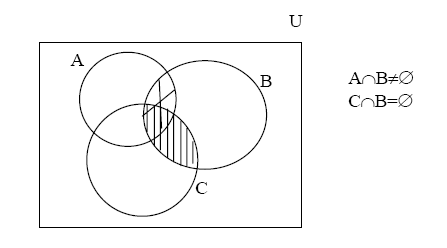
A partir de la representación de las premisas, y observando el sector que corresponde a la conclusión: A\C, se observa la existencia de algún elemento en el mismo, de donde se infiere que el razonamiento es válido., ya que lo afirmado por la conclusión ya se encontraba marcado en el diagrama de Venn a partir de la representación en el mismo de las premisas del razonamiento.
d.
A partir de la determinación de que se trata de un razonamiento válido, se procede a la aplicación del método deductivo:
- ∃x (P(x) ∧ Q(x)) Premisa
- ∀x(R(x) ⇒ ∼ Q(x)) Premisa
- P(s*) ∧ Q(s*) Regla de especialización existencial: 1
- R(s*) ⇒ ∼ Q(s*) Regla de especialización universal: 2
- P(s*) Regla de simplificación: 3
- Q(s*) Regla de simplificación: 3
- ∼ ∼ Q(s*) Regla de doble negación: 6
- ∼ R(s*) Modus Tollendo Tollens: 4,7
- P(s*) ∧ ∼ R(s*) Regla de conjunción: 5,8
- ∃x (P(x) ∧ ∼ R(x)) Regla de generalización existencial: 9
Una de las estudiantes, presentó la siguiente resolución: los puntos a y b fueron realizados según lo esperado. Sin embargo, al llegar al punto c, en vez de aplicar el método de los diagramas de Venn, planteó una variante de la prueba de invalidez que se utiliza en la lógica proposicional. En este método, a partir de la verdad de las premisas, se supone la falsedad de la conclusión y se intenta asignar valores de verdad a las proposiciones simples; si esta asignación se logra se concluye que el razonamiento es no válido, si se llega a una contradicción, se concluye que es válido. Este método no es aplicable a la lógica de predicados pues debido a la presencia de cuantificadores, puede tratarse de dominios infinitos, y además no puede en general especializarse todas las proposiciones en el mismo elemento con seguridad.
La estudiante eliminó los cuantificadores, supuso la verdad de las premisas, pero también de la conclusión, presentando lo siguiente:
(P(x) ∧ Q(x)) v(P(x) ∧ Q(x)) = V
(R(x) ⇒ ∼ Q(x)) v(R(x) ⇒ ∼ Q(x)) = V
(P(x)∧ ∼ R(x)) v(P(x)∧ ∼ R(x)) = V
"Si v(P(x) ∧ Q(x)) = V, entonces v(P(x)) = V, v(Q(x)) = V
Entonces v(∼ Q(x)) = F.
Pero para que v(R(x) ⇒ ∼ Q(x)) = V, tiene que darse entonces
v(R(x)) = F.
En ese caso, v(∼ R(x)) = V.
Haciendo la conjunción de P(x) y ∼R(x), se tiene que:
v(P(x) ∧ ∼ R(x)) = V.
Y por lo tanto el razonamiento es válido."
Esta manera de pensar desde la lógica aristotélica es incorrecta. No es posible inferir la validez del razonamiento de la secuencia utilizada por la alumna. Ella, a continuación realizó de manera correcta el ítem d de la actividad.
La respuesta dada por la estudiante pudo haber sido considerada incorrecta, pero la misma generó en su docente una serie de interrogantes que hicieron que la experimentación continuara más allá de la evaluación, en una entrevista en la clase siguiente durante la devolución del parcial.
Las preguntas que surgían de observar lo que la alumna había realizado para resolver la problemática planteada son:
¿Por qué no aplicó el método de los diagramas de Venn?
¿Qué la llevó a intentar una estrategia parecida a la prueba de invalidez, pero realizando también de manera incorrecta las suposiciones originales?
¿Por qué eliminó los cuantificadores?
¿Conocía realmente lo que estaba haciendo o era producto de una construcción incompleta del conocimiento?
Con la finalidad de buscar respuesta a algunas de estas preguntas, se tuvo, con ella una entrevista. Se trató de una entrevista no estructurada, en la que las preguntas que enumeramos anteriormente, se le realizaron a la estudiante, con la finalidad de clarificar cuáles eran los fundamentos sobre los que había presentado la resolución que hemos descrito. La entrevista duró media hora, en la que primero se analizaron las respuestas dadas por la alumna y posteriormente se buscó que ella fundamentara o explicara por qué había presentado las mismas. El extracto de la entrevista entre la alumna (A) y su profesora (P), se transcribe a continuación:
P- ¿Por qué eliminaste los cuantificadores?
A- Los cuantificadores los eliminé por las regla de especialización.
P- ¿En qué elemento especializaste?
A- En cualquiera, en x.
P- Pero hay un cuantificador existencial.
A- Sí, pero yo quería un elemento cualquiera para poder demostrar que es válido. Esas reglas las usé en la parte d.
En relación a las causas por las que no había utilizado el método de los diagramas de Venn, que había sido visto en clase:
P- ¿Por qué no utilizaste los diagramas de Venn?
A- No me gusta demostrar con dibujos. Los matemáticos siempre dicen que los dibujos no son seguros, que es mejor escribirlo en matemática.
P- ¿Escribirlo en matemática? ¿Qué es eso?
A- Como lo hacen ustedes, que lo dicen con palabras y lo escriben con símbolos.
P- De manera más formal, ¿quieres decir? ¿Usando formalismo?
A- Sí. En clase utilizamos el método de los diagramas de Venn para este tipo de problemas, pero a mí no me gusta. Me parece más seguro este. Además, funciona bien, porque es válido, pude hacer el punto d y de esa manera me di cuenta de que estoy pensando bien.
La docente tenía evidencia obtenida en clases anteriores de que la alumna conocía el método de prueba que se le había solicitado, ya que en la clase anterior a la actividad planteada, los alumnos habían resuelto problemas aplicando el mismo, y esta alumna los había realizado correctamente. Parecía extraño que hubiera confundido su aplicación si pocos días antes la aplicaba correctamente En este caso, lo que presentaba parecía inspirado en la prueba de invalidez, por lo que se le preguntó:
P- El método que utilizaste ¿es similar a la prueba de invalidez?
A- Sí, pero no es igual. Eso de suponer que no es válido para ver que es válido no me convence. Si quiero ver que es válido, veo si es válido. Si quiero ver si es inválido, veo si es inválido. ¿Por qué voy a mezclar?
P- Pero, ¿hay otra posibilidad aparte de que sea válido o inválido?
A- No, creo o al menos no definimos nada más. Pero yo pienso para adelante. Me propongo lo que quiero ver y avanzo. Si no llego me propongo lo otro y avanzo. Eso de suponer que no para ver que luego es sí, me parece rebuscado.
De esta entrevista se puede inferir que la alumna conoce las reglas de inferencia y los métodos de determinación de validez de razonamientos, sin embargo su uso no es el esperado.
La no utilización de diagramas de Venn para la determinación de la validez del razonamiento es fundamentada en la no aplicación de recursos gráficos, se observa en la estudiante una clara inclinación a la aplicación de recursos analíticos por sobre los gráficos.
Surgen de la explicación presentada la presencia de formas de argumentación inductivas, a través de formas de razonar abductivas, por ejemplo en la manera en que ella afirma que por haber podido afirmar el consecuente de la implicación, debe ser verdadero el antecedente de la misma, que para la estudiante vuelve a ser sostenida como una forma convincente de argumentación.
En el caso del rechazo hacia las argumentaciones gráficas, se observa cómo se ha construido la no aceptación de este tipo de argumentaciones a partir de experiencias previas en el aula, en las que la estudiante afirma que las argumentaciones gráficas no son aceptadas por los docentes de matemática. Claramente no ha asumido la importancia de las figuras de análisis y la diferencia de su utilización en relación al razonamiento sobre casos particulares. Sin embargo, los libros de texto enseñan la utilización de este tipo de métodos, que son enseñados en diversas asignaturas.
También se observa un rechazo a las argumentaciones indirectas, mediante el uso de la reducción al absurdo. Al igual que como ocurriera en experimentaciones que reportamos anteriormente (Crespo Crespo, 2005a, Crespo Crespo & Farfán, 2005, 2006), se evidencia en los estudiantes de carreras informáticas el rechazo de los métodos de argumentación indirectos, mostrando una clara inclinación a las argumentaciones directas.
Comentarios acerca de las respuestas obtenidas
Si se analizan las respuestas dadas por la alumna en la entrevista y la resolución presentada, podemos detectar ciertos rasgos de pensamiento no aristotélico:
√ No aceptación del método de los diagramas de Venn, por considerarlo un método gráfico, y por ende poco fiable.
√ Preferencia de los métodos analíticos por encima de la utilización de figuras de análisis, no diferenciando entre la argumentación a partir de un caso particular y el uso de una figura de análisis, lo que equivaldría a no diferenciar entre la comprobación de una propiedad en un caso particular y una argumentación deductiva realizada con auxilio de una figura de análisis.
√ No aceptación de la prueba de invalidez, basándose en la poca fiabilidad de los métodos de demostración indirectos (Crespo Crespo, 2005a, Crespo Crespo & Farfán, 2005, 2006).
√ No aceptación del principio del tercero excluido, deja abierta la posibilidad de existencia de otro tipo de razonamiento aparte de los válidos e inválidos. Esta posición daría lugar a pensar en la construcción espontánea de valores de verdad intermedios, entre el verdadero y el falso.
√ Creencia de la necesidad de formalismo en la clase de matemática. Como nos aclara (D´Amore, 2005b) refiriéndose a la interpretación de "contrato didáctico", en la escuela el alumno piensa que debe hacerlo de acuerdo a lo que supone espera el maestro y estimando que en matemática debe hacer "cálculos", por lo tanto lo que se les pedía no es matemática.
√ Presentación de una forma de razonamiento no aristotélica, con gran similitud del pensamiento nyaya, tal como se reporta en la investigación mencionada (D'Amore, 2005a). La estudiante partió de la tesis, de suponer que el razonamiento era válido. Para ello debía exponer la razón: si las premisas son verdaderas, la conclusión también. En ese punto, recurrió a ejemplificar la proposición general: la ejemplificó eliminando los cuantificadores y llegando a realizar la asignación de los valores de verdad de las proposiciones simples. Finalmente, realizó la generalización correspondiente.
√ Resulta notable y también interesante que de la entrevista se infiere que aquellas respuestas que podrían haber sido consideradas incorrectas en una corrección, no provenían del hecho de que la alumna no tuviera los conocimientos necesarios, sino de que la construcción que había realizado en cuanto a las formas de razonamiento válidas, difieren de las que fueron enseñadas en clase, desde una visión aristotélica.
Algunas consideraciones a tener en cuenta
En este trabajo se presentan dos ejemplos de formas de argumentar presentes en el aula de matemática. Ambas argumentaciones difieren de lo que se esperaría para ser consideradas válidas.
El primero de los casos presentado se trata de una estructura de argumentación que recuerda las que se utilizaban en la India en el período védico. Si bien no es posible pensar que esta forma de razonamiento sea conocida por quien la utilizó, nos pone frente a formas de argumentación que no tienen influencia aristotélica y que sin embargo producen convicción.
El otro ejemplo se presenta la que a través de las respuestas y explicaciones de una estudiante, que inicialmente da respuestas a una situación problemática escolar presentada dentro de un escenario académico, en la que si bien no resuelve aplicando argumentaciones lógicas aristotélicas, muestra en la entrevista posterior conocimiento de las mismas, aunque en algunos casos no las acepta y considera mejores las que realizó ella.
Las formas de argumentación en su carácter de construcciones socioculturales, constituyen la base de las prácticas sociales de demostración que caracterizan a la comunidad matemática. Nuestra forma de argumentar, nuestra matemática, evidentemente se han construido en una cultura de base fuertemente aristotélica, lo que hace que se asuma esta lógica como innata. Sin embargo, a pesar de que hemos analizado en este trabajo sólo dos ejemplos de posición frente a ciertas argumentaciones presentes en el aula de matemática, estos no son ejemplos aislados, ya que presenta opiniones que en muchos casos hemos detectado en nuestras clases y que consideramos deben ser analizadas cuidadosamente.
Las dificultades que se ponen de manifiesto en la realización de demostraciones matemáticas en el aula, se deben en muchas oportunidades a que no se detecta la existencia y características de estos tipos de argumentaciones, asumiendo como natural al razonamiento aristotélico. Las maneras de argumentar en matemática no se han mantenido estáticas, ya que se trata de construcciones socioculturales. Es la comprensión de ese carácter de construcción social para las argumentaciones y de las demostraciones como prácticas sociales, la que, consideramos, podrá ayudar a tener una mayor percepción de las formas de argumentación en el aula.
Para lograr que los alumnos comprendan la necesidad de argumentar matemáticamente e incluso de demostrar propiedades matemáticas, resulta indispensable que construyan la significatividad de la argumentación. Esta significatividad deberá ser comprendida a partir de que los docentes podamos asumir a las demostraciones matemáticas como prácticas sociales. Consideramos que de esta manera es posible que los alumnos comprendan la importancia de la argumentación para justificar y dar validez a las propiedades matemáticas. En esta significatividad se estará reconociendo el status de las argumentaciones como construcciones socioculturales.
Referencias bibliográficas
1. Arsac, G. (1987). El origen de la demostración: ensayo de epistemología didáctica. Recherches en Didactique des Mathématiques, 8(3), 267-312. [ Links ]
2. Balacheff, N. (1982). Preuve et démonstration en mathématiques au collège. Recherches en Didactique des Mathématiques, 3(3), 261-304. [ Links ]
3. Cantoral, R., Farfán, R. M. (2003). Matemática Educativa: Una visión de su evolución. En Revista Latinoamericana de Matemática Educativa. 6 (1), 27- 40. [ Links ]
4. Cantoral, R., Farfán, R. M.; Lezama, J. y Martínez Sierra, G. (2006). Sociología y representación: algunos ejemplos. Revista Latinoamericana de Matemática Educativa, Número especial, 83-102. [ Links ]
5. Crespo Crespo, C. (2003). Las demostraciones como contenido matemático. En VII Escuela de Invierno y VII Seminario de Investigación en Didáctica de las Matemáticas. Chilpancingo, Guerrero, México. [ Links ]
6. Crespo Crespo, C. (2004). Argumentar matemáticamente: su importancia en el aula. En II Congreso Virtual de Enseñanza de la Matemática, Guadalajara, México. [ Links ]
7. Crespo Crespo, C. (2005a). El papel de las argumentaciones matemáticas en el discurso escolar. La estrategia de deducción por reducción al absurdo. Tesis de Maestría sin publicar. CICATA del IPN, México. [ Links ]
8. Crespo Crespo, C. (2005b). La importancia de la argumentación matemática en el aula. Premisa (Revista de la Sociedad Argentina de Educación Matemática), 7(23), 23-29. [ Links ]
9. Crespo Crespo, C., Farfán, R. (2005). Una visión de las argumentaciones por reducción al absurdo como construcción sociocultural. Relime Vol. 8 (3), pp.287-317. [ Links ]
10. Crespo Crespo, C., Farfán, R. (2006). Las argumentaciones por reducción al absurdo como construcción sociocultural. En Martínez, G. (Ed.) Acta Latinoamericana de Matemática Educativa. Volumen 19. Clame, México (pp.766-781). [ Links ]
11. D´Amore, B. (2005a). La argumentación matemática de jóvenes alumnos y la lógica hindú (nyaya). En UNO. 38, 83-99. [ Links ]
12. D´Amore, B. (2005b). Bases filosóficas, pedagógicas, epistemológicas y conceptuales de la Didáctica de la Matemática. Barcelona: Editorial Reverté [ Links ].
13. de Villiers, M. (1993). El papel y la función de la demostración en matemáticas. Épsilon. 26, 15-30. [ Links ]
14. Duval, R. (1999). Argumentar, demostrar, explicar: ¿continuidad o ruptura cognitiva? México: Grupo Editorial Iberoamérica. [ Links ]
15. Duval, R. (2000). Écriture, raisonnement el découverte de la démostration en mathématiques. Recherches en Didactique des Mathématiques. 20(2), 135- 170. [ Links ]
16. Farfán, R. M. (2003). Matemática Educativa: un camino de filiaciones y rupturas. En Delgado Rubí, J. R. (Ed.) Acta Latinoamericana de Matemática Educativa. Volumen 16, Tomo 1. Santiago de Chile: Ediciones Lorena (pp. 5-10). [ Links ]
17. Godino, J. D. y Recio, Á. M. (2001). Significados institucionales de la demostración. Implicaciones para la educación matemática. Enseñanza de las ciencias, 19 (3), 405-414. [ Links ]
18. Hanna, G. (1997). The ongoing value of proof. En A. Gutiérrez y L. Puig (Ed.), Proceeding of PME 20. 1 (pp.21-34). Valencia. [ Links ]
19. Hanna, G. (2000). Proof, explanation and exploration: an overview. Educational Studies in Mathematics, 44, 5-23. [ Links ]
20. Hiriyanna, M. (1960). Introducción a la filosofía de la India. Buenos Aires: Editorial Sudamericana. [ Links ]
21. Ibañes, M. (2001). Aspectos cognitivos del aprendizaje de la demostración matemática en alumnos de primer curso de bachillerato. Tesis doctoral no publicada, Universidad de Valladolid, Valladolid. [ Links ]
22. Lakoff, G. y Núñez, R. (2000). Where Mathematics Comes From: How the Embodied Mind Brings Mathematics into Being. New York: Basic Books. [ Links ]
23. Martínez, G. (2005). Los procesos de convención matemática como generadores de conocimiento. Revista Latinoamericana de Investigación en Matemática Educativa, 8(2), 195-218. [ Links ]
24. NCTM (National Council of Teachers of Mathematics) (2000). Principios y Estándares para la Educación Matemática. Sevilla: Sociedad Andaluza de Educación Matemática Thales. [ Links ]
25. Valverde, L. (1990). Un método para contribuir a desarrollar la habilidad para fundamentar-demostrar una proposición matemática, tomando como base una asignatura de álgebra de primer año de los ISP. Tesis de Doctorado no publicada, Instituto Superior Pedagógico "Enrique José Varona", La Habana. [ Links ]














