Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista electrónica de investigación en educación en ciencias
versión On-line ISSN 1850-6666
Rev. electrón. investig. educ. cienc. vol.2 no.2 Tandil jul./dic. 2007
ARTÍCULOS ORIGINALES
Organizaciones Matemáticas en la Universidad en torno a las nociones de límite y continuidad de funciones: un estudio de caso
Parra Verónica 1,2, Otero Maria Rita1,3
vparra@exa.unicen.edu.ar; rotero@exa.unicen.edu.ar
1Núcleo de Investigación en Enseñanza de las Ciencias y Tecnología. UNCPBA. Tandil, Argentina.
2CICBA-Argentina
3CONICET-Argentina
Resumen
Esta investigación se propone describir las Organizaciones Matemáticas (OM) que conviven en una Institución universitaria en torno a las nociones de límite y continuidad de funciones. Se trata de un estudio de caso realizado en la disciplina denominada Análisis Matemático y sus Aplicaciones que corresponde a primer año de una carrera referida a la Economía y a la Administración. Esta investigación es de tipo descriptiva y utiliza como referente teórico la Teoría Antropológica de lo Didáctico (TAD) de Chevallard (1992, 1997,1999, 2000). Se ha concluido en la existencia de Organizaciones Matemáticas puntuales y rígidas y, del fenómeno del autismo temático también en la Universidad. Este hecho didáctico, lejos de mostrar una ruptura entre la enseñanza secundaria y universitaria, señalan una continuidad, al menos en esta institución.
Palabras clave: Universidad; Límite y Continuidad de funciones; Organización Matemática; Teoría Antropológica de lo Didáctico.
Abstract
This work describes the Mathematical Organizations (OM) around the concepts of limit and continuity of functions that coexist at the University. This work is a case study based on the Mathematical Analysis applied to Economy and Administration in the first university level in this area. It is a descriptive investigation using the Anthropological Theory of Didactic (TAD) (Chevallard; 1992, 1997.1999, 2000). The existence of punctual and rigid Mathematical Organizations and the existence of phenomenon of the thematic autism also in the University are concluded. This didactic fact, don't show a rupture between secondary education and university education, therefore indicates continuity, at least in this institution.
Key words: University; Limit and Continuity of functions; Mathematical Organizations; Anthropological Theory of Didactics.
1. INTRODUCCIÓN
El análisis matemático en Administración y Economía trata frecuentemente de cambios y por ello, el Cálculo es un medio de estudio muy valioso en esas áreas. El análisis marginal es quizás la aplicación más directa del Cálculo en las Ciencias Administrativas y Económicas. La relación de cambio marginal, o sea, la "variación en el margen", se expresa analíticamente como la primera derivada de la función considerada. El Cálculo Diferencial es también el método mediante el cuál se obtienen los valores máximos y mínimos de funciones. Por consiguiente, utilizando sus procedimientos, se pueden resolver problemas relativos a la maximización de utilidades o la minimización de costos, según ciertos supuestos. La programación matemática, que tiene como finalidad maximizar o minimizar funciones sujetas a restricciones, se emplea cada vez más en Administración y Economía.
El concepto de intensidad de variación, o tasa de cambio de una función, es la base del Cálculo Diferencial. Aunque la relación de cambio instantáneo, la derivada, se comprenda quizá más fácilmente en términos del movimiento físico, puede generalizarse a cualquier tipo de relación funcional. Por ejemplo, el costo total es función de la cantidad producida, y a menudo cambia con intensidad variable, a medida que varía la producción. El costo marginal es la relación instantánea de la variación del costo total con respecto al cambio en la cantidad producida, y es así, la derivada del costo total. El costo marginal es función de la cantidad producida, y puede evaluarse para cualquier cantidad que sea de interés.
En términos matemáticos, las tasas de variaciones se definen utilizando los conceptos de límite y continuidad. Pero, tales conceptos se utilizan con frecuencia en razonamientos y expresiones ajenos a la matemática. Por ejemplo, la producción máxima teórica de una máquina industrial o de una fábrica, es un "límite", es decir, el rendimiento ideal (o límite) que en la práctica nunca es alcanzable, pero al cual es posible aproximarse arbitrariamente. Esta misma idea se aplica al comportamiento de cualquier equipo mecánico o electrónico, para el cuál los ingenieros o electrónicos pueden calcular un funcionamiento ideal (o límite). Es aplicable también, por ejemplo, a las utilidades obtenibles en condiciones ideales, al rendimiento (kilómetros por litro) de la gasolina consumida en condiciones ideales, etc. En forma similar, hay límites inferiores de costo, desgaste, desperdicio, etc.
2. TEORÍA ANTROPOLÓGICA DE LO DIDÁCTICO
La TAD asume que el saber matemático se construye como respuesta a situaciones problemáticas y surge como el producto de un proceso de estudio. Esta teoría supone que toda actividad humana regularmente realizada puede describirse con un modelo único, que se resume con la palabra praxeología. El término praxis hace referencia al saber hacer, es decir, los tipos de problemas o tareas que se estudian y las técnicas que se construyen para solucionarlos. El término logos, se identifica con el saber e incluye las descripciones y explicaciones que nos permiten entender las técnicas, esto es, el discurso tecnológico y la teoría que da sentido a los problemas planteados. Tipos de tareas, técnica, tecnología y teoría son los elementos que componen una praxeología. (Bosch, Espinoza, Gascón; 2003).
Esta teoría distingue dos tipos de praxeologías u organización praxeológica: las Organizaciones Matemáticas (OM) y las organizaciones Didácticas (OD). Las primeras se refieren a la realidad matemática que se pretende estudiar y las segundas, a la forma en que eso ocurre. Ambas praxeologías, Matemáticas y Didácticas, tienen como componentes un bloque práctico-técnico, formado por tareas y técnicas, y un bloque tecnológicoteórico, formado por tecnologías y teorías.
Relacionado con los componentes de las OM, Chevallard (1999) distingue cuatro niveles de organizaciones matemáticas:
- Organizaciones matemáticas puntuales: son aquellas que se construyen alrededor de un único tipo de tareas teniendo una técnica común.
- Organizaciones matemáticas locales: están formadas por la articulación de las organizaciones matemáticas puntuales entorno a un discurso tecnológico común, es decir, teniendo una tecnología común a cada una de las técnicas.
- Organizaciones matemáticas regionales: están formadas por la articulación de organizaciones matemáticas locales alrededor de una teoría común, es decir, una teoría común a cada una de las tecnologías.
- Organizaciones matemáticas globales: son producto de la agregación de organizaciones regionales, sería una teoría de las teorías. (Bosch, Espinoza, Gascón, 2003)
Relacionado con la articulación e integración entre los componentes de las OM, Bosch, Fonseca y Gascón (2004) se refieren a la completitud de las organizaciones matemáticas. Aseguran que no tiene sentido referirse a OM completas ni incompletas, sino que la noción de completitud es relativa y que hay que referirse a grados decompletitud. A continuación, se enumeran los indicadores del grado de completitud de una OM, que proponen Bosch, Fonseca y Gascón (2004):
- Integración de los tipos de tareas: En una OM conviven diferentes tipos de tareas, relacionadas entre sí, por un discurso tecnológico o por una serie de técnicas. Así, una OM local será menos completa cuanto más aislados estén sus diferentes tipos de tareas, es decir, desarrolladas por técnicas que no estén relacionadas mediante ningún componente tecnológico.
- Diferentes técnicas y criterios para elegir entre ellas: Una OM local será mas completa en la medida en que puedan existir técnicas alternativas (que pueden ser variaciones de una misma técnica) para resolver algunos de sus tipos de tareas. Esto permitirá cuestionar las distintas técnicas alternativas y decidir cuál es la más fiable o económica.
- Independencia de los ostensivos que integran las técnicas: Para que una OM sea flexible, se requiere que ésta no se identifique con los objetos ostensivos (Bosch, Chevallard; 1999) que se utilizan para describirlas y para aplicarlas. Se espera que acepten representaciones ostensivas, dependiendo de la actividad matemática en la que están inmersas.
- Existencia de tareas y de técnicas inversas: Otro indicador de la flexibilidad de las técnicas, y por lo tanto, del grado de completitud, es el hecho de que existan en la OM local técnicas "reversibles", es decir, que permitan resolver un tipo de tareas y también la tarea inversa. Se entiende por tarea inversa a aquella que se define, por ejemplo, intercambiando los datos por las incógnitas y viceversa.
- Interpretación del resultado de aplicar las técnicas: Una OM local tendrá mayor grado de completitud en la medida en la que su discurso tecnológico adquiera mayor funcionalidad, es decir, explique, justifique técnicas y especialmente, interprete el funcionamiento de la técnica y de su resultado. Esto es, que en la OM estén los elementos tecnológicos necesarios para interpretar la técnica o las técnicas.
- Existencia de tareas matemáticas abiertas: Este punto se refiere a dos consideraciones de las tareas abiertas. Por un lado, se considera como tal a aquellas situaciones en las que los datos son valores conocidos, pero que se los trata como desconocidos (parámetros) y, las incógnitas no son objetos matemáticos concretos sino las relaciones que se establecen entre ellos. Por otro lado, se considera como abiertas a aquellas tareas en las que el alumno debe decidir, de acuerdo al contexto de la situación, que datos utilizar y cuáles son las incógnitas más pertinentes.
- Incidencia de los elementos tecnológicos sobre la práctica: Este indicador hace referencia a las relaciones que se establecen entre los componentes tecnológicos de una OM. Un indicador importante del grado completitud lo constituye la medida en que la tecnología permite producir técnicas nuevas capaces de ampliar los tipos de tareas de la OM.
2.1. El fenómeno del autismo temático
Para transmitir conocimientos sobre cierta cuestión (en este caso, Matemática) hay que recorrer un camino que empieza en la sociedad, continúa por la institución (escuela media o universidad), sigue por cierta área dentro de una disciplina en la que se estudia la cuestión, por cierto sector dentro del área y por cierto tema del sector (Chevallard, 2001). Este recorrido se puede esquematizar del siguiente modo:
Sociedad → Institución → Disciplina → Área → Sector→ Tema → Cuestión
Esta sucesión de niveles de organización es relativa no sólo a la cuestión o grupo de cuestiones consideradas, sino también al periodo histórico y a la institución escolar en la que nos situemos (Gascón, 2002) En cada una de estas etapas, se imponen restricciones y condiciones que acaban definiendo lo que es posible hacer para estudiar la cuestión considerada, es decir para crear y transmitir una praxeología que sea la respuesta esperada a la cuestión: una OM si se trata de una cuestión de matemática (Chevallard, 2001).
En general se observa un abandono, por parte del profesor, de los niveles superiores desde el de la sociedad y la institución hasta, incluso el nivel de los sectores, lo que provoca un retraimiento de su acción sobre el nivel de los temas. Este encierro en los temas constituye el fenómeno didáctico que Chevallard (1999) denomina el autismo temático del profesor.
Gascón (2003) propone hablar de autismo temático de la institución escolar en lugar de autismo temático del profesor. Asegura que, de hecho antes de que el profesor se encierre en los temas, puede observarse como el currículo oficial que proponen las sucesivas reformas, los documentos de las administraciones educativas y los libros de texto aprobados por éstas, consideran implícitamente que, más allá del nivel de la organización de los temas, todo es transparente e incuestionable.
Paralelamente al fenómeno del autismo temático ocurre un fenómeno relacionado con la pérdida de sentido de las cuestiones que se estudian en la escuela (ya sean cuestiones matemáticas, lingüísticas, históricas o biológicas). Éstas parecen surgir de temas aislados, cuya justificación está implícitamente en la disciplina en cuestión (en nuestro caso, la Matemática) (Gascón, 2003).
Así, la inmensa mayoría de las cuestiones matemáticas que se proponen para ser estudiadas en la escuela surgen en el nivel temático y, sólo están conectadas nominalmente a los niveles superiores de organización (sectores, áreas y disciplina) que son transparentes e incuestionables. Dado, además, que los temas matemáticos escolares no se estructuran propiamente como OM locales y, por tanto, no llegan nunca a integrarse de manera funcional en OM regionales ni globales, resulta que las cuestiones matemáticas escolares no sólo están muy débilmente conectadas a los citados niveles superiores de organización sino que, además, aparecen como cuestiones bastante independientes entre sí. (Bosch, Espinoza, Gascón; 2003)
3. PREGUNTAS DE LA INVESTIGACIÓN
3.1. ¿Qué características tiene la Organización Matemática de Referencia (OMR)?
3.2. ¿Qué características tiene la Organización Matemática Propuesta para Enseñar en los libros de texto (OMPET)?
3.3. ¿Qué características tiene la Organización Matemática Propuesta para Enseñar en el material teóricopráctico (OMPE)?
3.4. ¿Qué características tiene la Organización Matemática Efectivamente Enseñada (OMEE)?
3.5. ¿Existe el fenómeno del autismo temático en la Institución Universidad? ¿Cuáles son los indicadores de la existencia de este fenómeno?
4. METOLOGÍA DE LA INVESTIGACIÓN
Esta investigación se realizó en un curso de Matemática de primer año del nivel universitario de una carrera referida a la Economía y a la Administración. Se observó durante un cuatrimestre el proceso de estudio de dos grupos de alumnos de un curso de Matemática denominado Análisis Matemático y sus Aplicaciones. De hecho, se trata de un curso de Cálculo en funciones de una y dos variables. Cada grupo estaba constituido por aproximadamente 40 alumnos con su respectivo Profesor. Ambos docentes poseían una prolongada trayectoria en la Institución. Se considerarán para este trabajo sólo las cuatro clases relativas a límite y continuidad de funciones de uno de los profesores. Este profesor es el más seguido por los estudiantes y es quién ha elaborado el material teórico-práctico Los registros de clase permitirán describir la OM efectivamente enseñada por este profesor.
Se realizaron observaciones de carácter no participante recopilando los datos en video, audio y registros escritos, así como también las evaluaciones y los resultados obtenidos por los estudiantes y notas de campo. Además se analizan los materiales teóricos y prácticos comunes a los dos grupos de estudio, el programa analítico con los contenidos por unidad, la bibliografía recomendada a los alumnos y las evaluaciones escritas. Los encuentros de clases se realizaban en dos sesiones semanales de tres horas cada una.
A continuación, se describen las categorías de análisis generadas a partir del marco teórico:
1) OMR: La Organización Matemática de Referencia. Para analizar las OM que se proponen a estudiar y las que efectivamente se enseñan en una determinada institución, es necesario describir un "modelo" de organización matemática que actúe de referente. Este modelo se denomina OM de referencia y es donde vive el "saber sabio". La construcción de esta OM dependerá, no sólo de las nociones matemáticas, sino también de las consideraciones personales del investigador y, de las características propias de la institución en la que se desarrollan las OM.
2) OMPE: Organización Matemática Propuesta para Enseñar. Se distinguen dos tipos de OMPE, dependiendo del origen de los datos.
a. OMPET: Organización Matemática Propuesta para Enseñar en los libros de texto referidos al Análisis Matemático y sus aplicaciones en la Economía y la Administración. Para la construcción de esta OM, se han analizado diversos libros de texto, pero se ha reconstruido la OMPE sólo con dos de ellos. La elección de ambos libros se debe a la recomendación que de ellos hacen los profesores durante las clases.
b. OMPE: Organización Matemática Propuesta para Enseñar en el material teórico-práctico. Se ha construido esta OM a partir del material teóricopráctico y del programa analítico que los profesores editan para sus estudiantes.
3) OMEE: Organización Matemática Efectivamente Enseñada. Esta OM se ha construido considerando los registros de clase y las notas de campo.
A continuación, se describen las subcategorías de análisis, generadas a partir de los componentes del bloque prácticotécnico y tecnológico-teórico de las OM:
- Tareas: Se identifican en esta subcategoría las tareas que se proponen en las clases, en los materiales teóricos y en los libros de textos.
- Técnicas: Si incluyen aquí las técnicas de resolución que se proponen para resolver las tareas anteriores.
- Tecnologías: Se ubican en esta subcategoría a las justificaciones que respalden el funcionamiento de esas técnicas.
- Teorías: Se ubican aquí a los teoremas-demostraciones; proposiciones-demostraciones, definiciones, cualquier discurso que justifica alguna tecnología o embrión de la misma.
A continuación, se describen cada una de las tablas construidas para facilitar el análisis de los registros. La Tabla 1 permite identificar los elementos del bloque práctico-técnico y tecnológico-teórico de las Organizaciones Matemáticas Propuestas para enseñar (OMPE y OMPET) y de la Organización Matemática Efectivamente Enseñada (OMEE).
En la primera columna, se explicitan las nociones matemáticas referidas a límite y continuidad de funciones que intervienen en cada una de las OM. La columna dos informa acerca de los Géneros de tareas que se identifican en la OMPET, en la OMPE y en la OMEE, como por ejemplo: calcular (C), demostrar (Dm), definir (Df), determinar (Dt) y analizar (A). La tercera columna muestra las tareas que se identifican en cada OM en torno a las nociones matemáticas de la columna uno. La cuarta columna informa acerca de las técnicas matemáticas que se utilizan para resolver las tareas de la columna tres. Finalmente, la quinta columna proporciona las tecnologías y teorías que intervienen en cada OM considerada.
La Tabla 2 fue construida para tener una visión más general de la OMPET, la OMPE y las OMEE porque agrupa las tareas en Tipos y, los Tipos en Géneros.
La primera columna señala los géneros de tareas (Gi) relativos a las nociones de límite y continuidad de funciones. Cada uno de estos géneros tiene diferentes tipos de tareas, los cuáles se explicitan en la columna dos: Tipos de Tareas (j) asociado al género (i) (Tij). La columna tres muestra las tareas identificadas en cada tipo de tareas. Esto es: tareas (k) asociada al tipo de tarea (j) del género (i) (tijk). Luego, la columna siguiente contiene las técnicas matemáticas asociadas a cada una de las tareas propuestas: Técnica matemática (k) asociada a la tarea (k) ![]() . Finalmente, se enumeran los elementos tecnológicos teóricos de cada OM analizada: Elementos tecnológicos
. Finalmente, se enumeran los elementos tecnológicos teóricos de cada OM analizada: Elementos tecnológicos ![]() -teóricos
-teóricos ![]() asociado al tipo de tarea (j)
asociado al tipo de tarea (j) ![]() .
.
5. ANÁLISIS Y DESCRIPCIÓN DE LAS OM EN TORNO A LAS NOCIONES DE LÍMITE Y CONTINUIDAD DE FUNCIONES
5.1. Descripción de la OM de Referencia: OMR
Chevallard (2000) distingue cuatro niveles de OM, que van desde las OM puntuales hasta las OM globales. La idea de globalidad sugiere la identificación de al menos una teoría común a cada una de las OM regionales. Esto hace necesaria la identificación de las "fronteras" de las teorías matemáticas, para decidir así, qué OM regionales responden a esa teoría y cuáles, no lo hacen. De igual manera ocurre con las OM locales. En este caso se deberá delimitar la tecnología común a los diferentes tipos de tareas. Si bien, las OM locales que componen una OM regional están conectadas y articuladas entre sí, resulta apropiado realizar una separación entre ellas, a los efectos de facilitar la descripción de las OM regionales. En esta investigación, se construirá la OM de referencia, que es una OM regional, a partir de la articulación de tres OM locales, que se describen brevemente a continuación:
- OM1: Esta OM gira en torno a la definición usual1 del límite y la cuestión generatriz es si existe el límite de una determinada función. La tecnología de esta OM local es la definición del límite de funciones.
- OM2: Esta OM gira en torno al álgebra del límite y su cuestión generatriz es cómo calcular el límite, habiendo establecido que existe. La tecnología de esta segunda OM es el conjunto de las propiedades del límite de funciones.
- OM3: Esta OM gira en torno a modelización de situaciones económicas usando la noción el límite. Así, una vez que se prueba la existencia del límite y se lo calcula, surge la cuestión de cómo se modelizan situaciones de la Economía y a la Administración.
Tanto en la segunda como en la tercer OM local podrían incluirse las aplicaciones del límite de funciones. Dentro de esas aplicaciones y por lo tanto, dentro de esas OM estaría incluida la noción de Derivada y por consiguiente, todo el análisis en Economía respecto de las tasas de variación. Conviene aclarar que las OM en torno a la noción de Deriva no serán tratadas en esta investigación.
Estas tres OM y las articulaciones entre ellas, constituyen la OM de referencia en torno a las nociones de límite y continuidad de funciones, la cuál responde a la cuestión de la derivabilidad de ciertos tipos de funciones. Esta cuestión, de hecho es lo que da sentido a las OM referidas a límite y continuidad de funciones en esta Institución. La OM de referencia se fundamenta en la teoría de la construcción de los números reales y, de acuerdo a los niveles de OM descritos por Chevallard (1999), tiene el carácter de regional. En el proceso de construcción de los números reales, es esencial, entre otros, la noción de sucesión. Pero, su inclusión en ciertos cursos de Cálculo va a depender de la institución en la que se desarrollan las OM y, del sentido dado a las mismas. Así, las razones de ser de las OM referidas al límite de funciones no son las mismas en una Facultad de Económicas que en una Facultad de Ciencias Exactas. En esta investigación, se construirá la OM de referencia prescindiendo del tratamiento de sucesiones y, se estudiará el límite de funciones para luego poder definir la noción de derivada de una función, que en definitiva, es el concepto central en la modelización de situaciones de la Economía y la Administración.
5.2. Descripción de la OM propuesta para enseñar en los libros de texto: OMPET
La OMPET fue reconstruida a partir de algunos libros de texto que se refieren al Análisis Matemático con aplicaciones a la Economía y a la Administración. Se observó que la OMPET sigue la secuencia de tareas representada en el Esquema 1. Dado un tema de estudio, existen tres niveles de acción:
Nivel uno: se define cierta noción matemática;
Nivel dos: se enuncian propiedades y/o operaciones;
Nivel tres: se muestran varias tareas a modo de ejemplos.
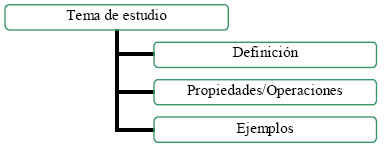
Esquema 1
Se identificará si esta misma secuencia es común en las restantes organizaciones matemáticas en torno a las nociones de límite y continuidad de funciones: la OMPE y la OMEE.
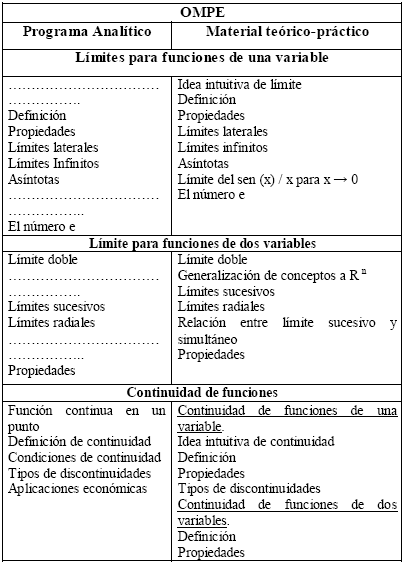
5.3. Descripción de la OM propuesta paraenseñar en el material teórico-práctico: OMPE
En la Tabla 3, se enumeran los contenidos de la OMPE relativos a "límite y continuidad de funciones" y su secuenciación.
Se aprecia que los contenidos y su secuenciación son los mismos tanto en el programa analítico como en el material teórico-práctico. Teniendo en cuenta la secuenciación de los temas de estudio propuestos en el material teóricopráctico (OMPE) se ha observado la siguiente secuencia de tareas:

Esquema 2
Se identifica en algunos casos, una secuencia de tareas que, además de considerar estos tres niveles (definición, propiedades/operaciones y ejemplos) contiene un cuarto nivel referido a "interpretación geométrica" ó "idea intuitiva". Esto ocurre respectivamente con el límite doble para funciones de dos variables y con la introducción a la noción de continuidad de funciones.
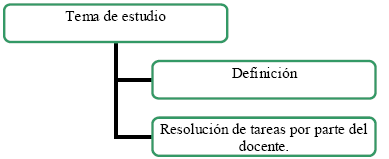
5.4. Descripción de la OM efectivamente enseñada: OMEE
La OMEE corresponde a la organización matemática efectivamente enseñada. Esta OM fue reconstruida a partir de los registros de clase de uno de los profesores observados. Durante la mayoría de los episodios de clase, se identifica la secuencia de tareas ilustrada en el Esquema 3.
El último nivel del Esquema 3 se refiere a las tareas resueltas por el docente pues durante las clases, el alumno no resuelve tareas. Se observa que la secuencia de tareas de la OMPET se sigue también en la OMPE y en la OMEE. Este hecho se debe a que, la OMPE reproduce parcialmente los elementos prácticos-técnicos y tecnológicos-teóricos de la OMPET y, la OMEE, los elementos de la OMPE.
5.5. Bloque práctico-técnico y bloque tecnológico-teórico de la OMPET, la OMPE y la OMEE
El bloque práctico-técnico de las tres OM está formado por un abundante número de duplas constituidas por tareastécnicas. La OMPET, la OMPE y la OMEE tienen los mismos géneros de tareas. Se detectan diferencias sólo en algunos de los tipos de tareas. A continuación se enumeran los géneros de tareas (Gi) con sus respectivos tipos de tareas (Ti j):
G1: Calcular límites para funciones de una variable independiente: f(x).
T11: Calcular ![]()
T12: Calcular límites laterales: Límite lateral por Derecha y límite lateral por izquierda: ![]() y
y ![]()
T13: Calcular límites en el infinito: ![]()
G2: Calcular límites para funciones de dos variables independientes: f(x; y).
T21: Calcular Límites radiales y Cuadráticos: ![]()
T22: Calcular límites iterados o sucesivos.
T23: Calcular límite doble: ![]()
T24: Decidir la existencia del límite doble.
G3: Demostrar límites por definición.
T31: Demostrar que ![]() (Límites finitos para funciones de una variable independiente)
(Límites finitos para funciones de una variable independiente)
T32: Demostrar que![]() y/ó
y/ó![]() (Límites infinitos y límites en el infinito para funciones de una variable independiente)
(Límites infinitos y límites en el infinito para funciones de una variable independiente)
T33: Demostrar que ![]() (Límite finito para funciones de dos variables independientes)
(Límite finito para funciones de dos variables independientes)
G4: Analizar la continuidad de funciones.
T41: Analizar la continuidad de funciones de una variable independiente f(x) en x = a.
T42: Analizar la continuidad de funciones de dos variables independientes f(x; y) en (x; y) = (a; b).
T43: Determinar puntos de discontinuidad de funciones f(x) y f(x, y) y clasificarlos en evitables y no evitables.
T44: Determinar puntos y/o subconjunto de continuidad de funciones f(x, y)
T45: Redefinir funciones.
T46: Analizar la continuidad de funciones de tres variables independientes en un subconjunto.
G5: Analizar aplicaciones económicas de la noción de continuidad.
Los géneros G1 y G2 se refieren únicamente al cálculo de límites de funciones. Aquí se utilizan técnicas de resolución que involucran la factorización, la racionalización y el uso de algunos límites especiales, entre otras. El género G3 contiene tareas relativas a "demostrar" límites usando la definición. Conviene aclarar que el término "demostrar" en este caso se refiere de hecho a "verificar" ó "probar" que efectivamente el límite de una función vale L.
El género G4 está formado por tareas en las que se analiza la continuidad de diversas funciones. Las tareas se refieren a encontrar puntos de discontinuidad, a decidir la continuidad de cierta función en un punto, a hallar subconjuntos de continuidad y a redefinir funciones. Los tipos de tareas "Determinar puntos de discontinuidad de funciones f(x) y f(x, y) y clasificarlos en evitables y no evitables" (T43) y "Determinar puntos y/o subconjunto de continuidad de funciones f(x, y)" (T44) parecerían contener las mismas tareas pero, conviene aclarar que no es así. La distinción entre estos dos tipos radica en que las técnicas matemáticas asociadas a los mismos, no son las mismas.
El género G5 contiene tareas referidas a la aplicación de la noción de continuidad en situaciones de la Economía y la Administración. Se aplica la noción de continuidad en situaciones que involucran funciones definidas a trozos y además, se interpretan resultados usando las nociones de curvas de nivel.
La OMPE y la OMEE pierden dos de los tipos de tareas propuestos en la OMPET: el T44 y el T46. Así, lo que se propone para enseñar y lo que efectivamente se enseña es, en gran medida, lo que se considera el saber textualizado (Chevallard, 1991).
El bloque tecnológico-teórico de la OMPET y el de OMPE, está formado por un abundante número de definiciones; algunos teoremas y pocas proposiciones con sus demostraciones. En la OMEE, el bloque tecnológicoteórico está constituido, en su mayoría, por definiciones formuladas algunas en lenguaje cotidiano y otras, en lenguaje matemático. El siguiente esquema muestra como se incluyen las OM analizadas aquí:
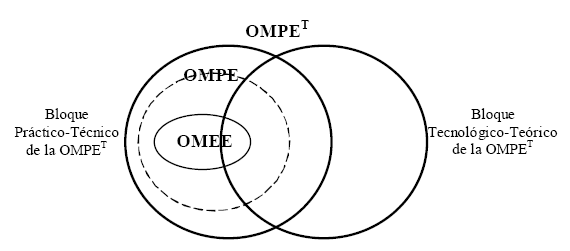
Esquema 4
La OMPE está parcialmente contenida en la OMPET pues el material teórico-práctico reproduce parte de lo que se propone a ser enseñado en los libros de texto. Se dice que la reproducción es parcial pues, existe una pérdida importante de elementos tecnológicos-teóricos y de las razones de ser de las OM referidas al límite de funciones. Es sabido que, del saber sabio (la OMR) al saber textualizado (la OMPET) existe una transposición didáctica, la cuál es necesaria para que el saber pueda ser enseñado. En este caso, no sólo existe tal transposición entre estas OM, sino también, existe una transposición entre el saber textualizado y el saber que vive en el material teórico-práctico (OMPE). Se advierte que, en esta última transposición, se pierden elementos tecnológicosteóricos, tales como la demostración de propiedades que son necesarias para explicar el por qué de determinadas técnicas matemáticas. La sigla TD que se observa en el Esquema 5 se refiere a la transposición didáctica que existe entre las distintas OM:

Esquema 5
En la OMPE se reproducen los elementos prácticostécnicos de la OMPET. Las mismas tareas y las técnicas asociadas a ellas, se advierten tanto en la OMPET como en la OMPE. Además, ambas OM no proponen ni desarrollan tareas referidas a la modelización de situaciones relacionadas con la Economía y la Administración. Paradójicamente, en un curso donde la Matemática adopta el estatus de herramienta y, donde se estudian diversos modelos económicos que son interpretaciones de sistemas propios de la Matemática, existen escasas modelizaciones en el área de la Economía. Esta ausencia se advierte tanto en la OMPET como en la OMPE. Sólo existen tareas relacionadas con la aplicación de la noción de límite en la continuidad de funciones. La mayoría de los libros de textos, remarcan la importancia de los distintos tipos de discontinuidades en las aplicaciones a funciones de costo, oferta y demanda de ciertos productos. Se menciona además, que el límite de funciones es esencial para definir posteriormente la derivada de una función y así, a través de esta noción, analizar las tasas de cambio de ciertas variables económicas.
En la OMEE existen escasos elementos tecnológicosteóricos y comparte con la OMPE la mayoría de las tareas. Tampoco en la OMEE se identifican tareas relacionadas con modelos económicos que utilicen la noción de límite de funciones. Tanto la OMPET como la OMPE y la OMEE se alejan ampliamente de la OM de referencia.
Esta OM, tal como se ha descrito, tiene el carácter de regional pues integra tres OM locales: una OM en torno a la cuestión de la existencia del límite, la cuál tiene como componente teórico, la unicidad del mismo en caso de existir. Una segunda OM local referida al cálculo del límite y finalmente; una OM local en torno a la modelización del límite. Cada una de estas OM, responde a una cuestión generatriz y, se articulan bajo una OM regional que responde a la cuestión de la derivabilidad de ciertas funciones. Esta cuestión es la que da sentido a las OM en torno al límite de funciones en el área de la Economía y la Administración, debido a la diversidad de modelos económicos que utilizan la noción de derivada.
Se observa que en la OMPE y en la OMEE, se enfatiza en la OM en torno al cálculo y, proponen algunas tareas en torno a la definición del límite, sin desarrollar ningún aspecto de la OM referida a la modelización. Por consiguiente, el estudio de las OM, se sesga al estudio de un único tipo de tareas. Por lo tanto, la OM propuesta para enseñar en el material teórico-práctico y la OM efectivamente enseñada, adquieren el carácter de puntual.
Enfatizar en un género de tareas sin relacionarlo con los demás niveles de determinación descritos por Chevallard, provocan un encierro en los temas con la consiguiente pérdida de sentido de las razones de ser de las OM que se estudian. Además, en estas OM desaparece por completo la cuestión generatriz de cómo modelizar a través del límite. Estos hechos son indicadores del fenómeno del autismotemático en la Institución Universidad.
Tanto la OMPET como la OMPE y la OMEE tienen un bloque tecnológico-teórico insuficiente para justificar e interpretar la cantidad de técnicas que se proponen en torno a las tareas. A pesar de que la OMPET enumera y demuestra una serie de propiedades, éstas no emergen del bloque práctico-técnico. No se identifica la justificación de técnicas relacionadas con ciertas tareas. Por ejemplo, las referidas a determinar la existencia o inexistencia del límite doble. Tampoco se menciona bajo qué condiciones puede calcularse un límite sucesivo. Esta insuficiencia es más notable aún en la OMPE y en la OMEE, donde no se identifican elementos tecnológicos y, muy pocos elementos teóricos. Por consiguiente, la OMPET, la OMPE y la OMEE no pueden integran los tipos de tareas pues no dispone de elementos tecnológicos-teóricos suficientes para ello.
No se identifican diferentes técnicas, lo cuál no permite elegir entre diversas técnicas que permitan resolver una misma tarea. Cada tarea está asociada a una única técnica, identificando así una dupla formada por tarea-técnica; nueva tarea-nueva técnica. No existe una interpretación de los resultados producto de la ausencia de un bloque tecnológico-teórico que lo permita. Para que ocurra la interpretación del resultado de aplicar las técnicas es condición necesaria que la OM tenga los elementos tecnológicos necesarios para ello.
La OM de referencia posee una tecnología común a los diferentes tipos de tareas que componen cada OM local y, a su vez, cada técnica tiene en principio, un embrión de tecnología. En la OMPE y en la OMEE no existen tecnologías explícitas y menos aún, embriones de ella. La mayoría de elementos teóricos identificados en la OMPET, la OMPE y en la OMEE son las definiciones de las nociones matemáticas. Estos hechos y, de acuerdo a los indicadores del gado de completitud de las OM propuestos por Bosch, Fosnseca y Gascón (2003), son indicadores de la existencia de OM rígidas, poco articuladas entre sí y con un bajo grado de completitud.
El carácter puntual, el bajo grado de completitud de las OM y el fenómeno del autismo temático lejos de mostrar una ruptura entre la enseñanza secundaria y la universitaria, señalan una continuidad, al menos en este aspecto de las OM y en esta institución. La universidad debería resolver este hecho didáctico, retomando las organizaciones locales del nivel anterior e integrándolas en otras regionales. Este es uno de los desafíos que la investigación didáctica tiene pendiente.
6. CONCLUSIONES
Las preguntas de la investigación se centraban en la caracterización de las OM en torno a las nociones de límite y continuidad de funciones. Esta caracterización se llevó a cabo a partir de la identificación de las tareas, técnicas, tecnologías y teorías de la OM de referencia (OMR), la OM propuesta para enseñar en los libros de texto (OMPET), la OM propuesta para enseñar en el material teórico-práctico (OMPE) y la OM efectivamente enseñada (OMEE). A su vez, la articulación entre esos componentes permite concluir sobre el grado de completitud y sobre el carácter de las OM, es decir, si se tratan de praxeologías puntuales, locales, regionales o globales. Las conclusiones obtenidas de este análisis son las siguientes:
- Tanto el programa analítico como el material teórico comparten los mismos contenidos y la misma secuenciación. El bloque práctico-técnico de la OMPET, la OMPE y la OMEE está formado por cinco géneros de tareas que se refieren a: calcular y demostrar límites para funciones de una y dos variables, determinar puntos de discontinuidad, clasificar discontinuidades en evitables y no evitables y, analizar aplicaciones económicas. Por lo tanto, las tres OM comparten los mismos géneros de tareas.
- Tanto la OMPET como la OMPE y la OMEE tienen un bloque tecnológico-teórico insuficiente para justificar e interpretar la cantidad de técnicas asociadas a los tipos de tareas. La mayoría de los elementos tecnológicos-teóricos de la OMPE y de la OMEE son definiciones y propiedades sin demostrar que no emergen del bloque prácticotécnico. Por lo tanto, los elementos tecnológicosteóricos que componen la OM de referencia, se pierden progresivamente en la OMPET, la OMPE y la OMEE y carecen de sentido.
- En la OMPET, la OMPE y la OMEE, existe un predominio del bloque práctico-técnico por sobre el tecnológico-teórico y, más aún, un predominio del género de tareas calcular. Esto reduce a las OM en torno al límite de funciones al nivel de OM puntual en la Institución Universidad. A pesar de estar formadas por diversos tipos de tareas, se enfatiza sólo en el género Calcular y sólo en un tipo de tareas: Calcular el límite de funciones de una variable en un valor finito. Este hecho se aleja ampliamente de las OM ideales de la Universidad, las cuáles deberían intentar plantearse como OM regionales tratando de articular las OM locales propias de la escuela media.
- Las OM no se articulan a través de un discurso tecnológico-teórico debido a la insuficiencia del mismo y, por lo tanto, se estudian OM rígidas, con escasas relaciones entre sí.
- La ausencia de articulación de los tipos de tareas, la escasa existencia de técnicas alternativas, el discurso tecnológico teórico poco funcional y la ausencia del cuestionamiento de las técnicas, provoca que las OM resulten poco completas. Por lo tanto, en esta institución se tendrían OM puntuales con un bajo grado de completitud.
- Las razones de ser de las OM en torno al límite de funciones en Economía y Administración se formulan en la OM de referencia y también en la OMPET. Pero, a pesar de ello, la OMPET no las desarrolla. En la OMPE y en la OMEE tales razones no se formulan y no se advierten pues no existen tareas referidas a la modelización del límite. Así, el sentido de las OM en torno a las nociones de límite y continuidad de funciones están totalmente ausentes en la OMPE y en la OMEE y, por lo tanto, carecen de sentido para los alumnos.
- Los indicadores del autismo temático en la Universidad son los siguientes:
- La ausencia del bloque tecnológico-teórico, lo cuál genera un saber matemático transparente e incuestionable;
- La pérdida de sentido de las razones de ser de las OM que se estudian debido a que las cuestiones surgen del nivel de los temas;
- Y, el estudio de OM puntuales y poco articuladas entre sí, lo que genera OM rígidas y con un bajo grado de completitud.
1 La definición usual de límite es la siguiente:![]() si para cada
si para cada ![]() existe un número
existe un número![]() , tal que
, tal que![]() para
para ![]()
REFERENCIAS
1. Bosch, M. ; Chevallard, Y. (1999). La sensibilité de l'activité mathématique aux ostensifs: objet d'étude et problématique. Recherche en Didactique desMathématiques, 19(1), 77-124 [ Links ]
2. Bosch, M.; Espinoza, L.; Gascón, J. (2003) El profesor como director de procesos de estudio. Análisis de organizaciones didácticas espontáneas. Recherches enDidactique des Mathématiques 23 (1), 79 -135. [ Links ]
3. Bosch, M.; Fonseca, C.; Gascón, J. (2004) Incompletitud de las Organizaciones Matemáticas Locales en las Instituciones Escolares. Recherches en Didactique desMathématiques, 24 (2), 205-250. [ Links ]
4. Chevallard, Y. (1991) La transposición didáctica. Del saber sabio al saber enseñado. Aique. ISBN 950-701-380-6. [ Links ]
5. Chevallard, Y. (1992) Concepts fondamentaux de la didactique : Perspectives apportées peu une approche anthropologique. Recherches en Didactique desMathématiques, 12 (1) 73-112. [ Links ]
6. Chevallard, Y. (1997) Familière el problématique, la figure du professeur. Recherches en Didactique des Mathématiques, 17 (3), 17-54. [ Links ]
7. Chevallard, Y. (1999) L´analyse des practiques enseignantes en théorie anthropologique du didactique. Recherches en Didactique des Mathématiques, 19 (2), 221- 266. [ Links ]
8. Chevallard, Y. (2000) La recherche en Didactique et la formation des professeurs: problematiques, concepts, problemes. Actas de la Xème École d'Été de Didactique desMathématiques, I, 98-112. [ Links ]
9. Chevallard, Y (2001) Aspectos problemáticos de la formación docente. XVI Jornadas del SeminarioInteruniversitario de Investigación en Didáctica de las Matemáticas, Huesca. Disponible en: http://www.ugr.es/local/jgodino/siidm.htm [ Links ]
10. Gascón, J. (2002) El problema de la Educación Matemática y la doble ruptura de la Didáctica de las Matemáticas. Gaceta de la Real Sociedad Matemática Española, 5 (3), 673-702. [ Links ]
11. Gascón, J. (2003) Efectos del autismo temático sobre el estudio de la Geometría en Secundaria I. Desaparición escolar de la razón de ser de la Geometría. Revista Suma, 44, 25-34-ISSN 1130-488X. [ Links ]