Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista electrónica de investigación en educación en ciencias
versión On-line ISSN 1850-6666
Rev. electrón. investig. educ. cienc. vol.3 no.2 Tandil ago./dic. 2008
ARTÍCULOS ORIGINALES
Resignificando la linealidad en una experiencia de educación a distancia en línea
Mónica García Zatti 1, Gisela Montiel Espinosa 2
gzatti@criba.edu.ar, gmontiel@ipn.mx
1Facultad Regional Bahía Blanca, Universidad Tecnológica Nacional, Argentina
2Centro de Investigación en Ciencia Aplicada y Tecnología Avanzada, Unidad Legaria del Instituto Politécnico Nacional, México
Resumen
Este documento reporta la investigación que desarrollamos en torno a la resignificación de la linealidad, como propiedad de la relación funcional de dos variables, en una experiencia de educación a distancia en línea. Nuestra investigación se ubica en la denominada aproximación socioepistemológica, por lo que contemplamos cuatro dimensiones en la construcción de conocimiento matemático: la social, la epistemológica, la cognitiva y la didáctica.
Nociones acuñadas en esta perspectiva tienen la característica de ser unidades de análisis para explorar el origen social del conocimiento. De entre ellas, dos fundamentales son: la resignificación y las prácticas sociales. Una vez que se reconocen a las prácticas sociales como generadoras de conocimiento y que se distingue la naturaleza propia de cada función, las situaciones que se diseñan fundamentadas en la socioepistemología permiten hacer evidentes herramientas y argumentos; que permiten, a su vez, construir nuevos significados y/o modificar los previos.
Las posibilidades que provee el escenario en línea, en cuanto a la incorporación de herramientas tecnológicas, permite reflexionar acerca de papel de las mismas en el aprendizaje en línea y en la construcción del conocimiento matemático.
Palabras clave: Función; Socioepistemología; Resignificación; Práctica social; Linealidad
Abstract
This document reports de investigation performed around the resignification of the linearity, like property of the functional relationship of two variables, in an experience of distance and on line education. Our investigation is placed within the so-called socioepistemological framework. For that reason, we envisaged four components of the construction of mathematical knowledge; namely, the epistemological, cognitive, didactic and social dimensions.
Notions coined in this perspective have the characteristic of being analysis units to explorer the social origin of knowledge. Two among them are fundamental: the resignification and the social practice. Once the social practice are recognized as a source of knowledge and the nature property of each function is properly distinguished, the situations designed based on socioepistemology show tools and arguments that allow, in turn, to build news meaning and / or modify previous.
The possibilities that the on line scene provide, as for incorporation of technological tools, permit to think about the role of itself in the on line learning and in the construction of mathematical knowledge.
Keywords: Function; Socioepistemology; Resignification; Social practice; Linearity
1. INTRODUCCIÓN
Las dificultades con la que nos encontramos a diario al desarrollar los contenidos de matemática en nuestras clases y al analizar los resultados poco satisfactorios que observamos en el primer año de universidad, nos llevan a reflexionar acerca de los fenómenos relacionados con la enseñanza de la matemática, sobre todo, los relacionados con la naturaleza, formas y condiciones de la construcción del conocimiento matemático.
Nuestro trabajo de investigación se ubica en una didáctica en escenarios socioculturales (Cantoral y Farfán, 2003)y en consecuencia contempla cuatro dimensiones en la construcción del conocimiento matemático, a saber, la social, la epistemológica, la cognitiva y la didáctica. El concepto alrededor del cual se desarrolla la actividad didáctica diseñada es el de función, particularmente la lineal. El interés por este concepto surge por ser uno de los temas de mayor importancia en la matemática a partir del nivel medio superior. Esto se ve reflejado por el lugar que ocupa en los programas oficiales en diferentes sistemas escolares, y por su papel en el campo de la enseñanza de las ciencias, en donde uno de los objetivos principales es la obtención de modelos matemáticos que permitan comprender mejor como determinadas magnitudes dependen de otras y expresar esta dependencia de una manera sencilla.
Al seno de nuestra disciplina se han desarrollado diversas investigaciones en torno a los fenómenos didácticos relacionados con la noción de función y se han realizado propuestas didácticas basadas en sus resultados (Lezama, 1999; Farfán y Ferrari, 2001; Montiel, 2005). Nuestro objetivo es partir de estos resultados y propuestas para diseñar secuencias didácticas que permitan que el alumno confronte sus concepciones y resignifique la noción de función, en un escenario en línea.
La modalidad en línea de la educación a distancia plantea un escenario diferente de cualquier otro que le preceda en educación a distancia, en consecuencia es esencialmente una práctica sin fundamentos de investigación (Hopper, 2001). En consecuencia, la práctica educativa en este ambiente ha permitido cambiar de forma integral la enseñanza, moviéndose de un modelo de escuela tradicional y centralizada, a uno flexible y descentralizado, incorporando los nuevos mecanismos de comunicación y facilitando el acceso al conocimiento. A partir de las peculiaridades de esta modalidad se reconoce la viabilidad de la educación permanente, dentro y fuera del aula; la divulgación del conocimiento a través de los medios tecnológicos existentes; y la participación de las universidades y otros centros de educación superior en el entrenamiento, capacitación y formación de recursos humanos acordes a los requerimientos científicos y sociales (Sánchez-Aguilar, 2003; García et al, 2005) Pero es necesario acompañar el enorme y continuo crecimiento de esta modalidad de instrucción por investigaciones que aporten resultados teóricos y prácticos que permitan caracterizar los fenómenos y las problemáticas que en ésta se presentan.
1.1 Antecedentes de investigación
En lo que se refiere a las investigaciones relacionadas con la didáctica de la función (Youschkevitch, 1976; Sierpinska, 1989 y 1992; Ruiz Higueras, 1998), aquellas que han aportado más elementos a nuestro trabajo pueden clasificarse en: históricas-epistemológicas, cognitivas y didácticas
El análisis histórico realizado por Youschkevitch, (1976) muestra que la matemática es un conjunto de conocimientos en evolución continua y en dicha evolución ha desempeñado un papel destacado su intervención en otras ciencias y la necesidad de resolver determinados problemas. En su trabajo el autor ofrece consideraciones sobre las tres etapas, que a su modo de ver, son las principales en el desarrollo de la noción de función hasta mediados del siglo XIX: el mundo antiguo, la edad media y el período moderno.
Sin embargo, y para efectos de un trabajo de investigación en matemática educativa, es necesaria la ampliación a un análisis epistemológico, con base a la revisión histórica de los conceptos. Así podemos observar las disparidades entre el saber científico y el enseñado, así como identificar los obstáculos epistemológicos1 inherentes a los conceptos. En esta dirección, y vinculado a las concepciones en los estudiantes, Sierpinska (1989 y 1992) realiza las primeras investigaciones sobre el concepto que nos interesa, el de función. En el primero de los dos trabajos mencionados, se identifican cinco obstáculos epistemológicos inherentes a este concepto:
-
Los objetos variables son aceptados en ciencias naturales o en aplicaciones, pero no en la matemática pura.
-
Las magnitudes son entidades cualitativamente diferentes de los números; la proporcionalidad es diferente de la igualdad.
-
Fuerte creencia en el poder de las operaciones formales con las expresiones algebraicas.
-
Lo más importante de la matemática es proveerse de un cálculo poderoso que permita a los científicos resolver sus problemas.
-
Los objetos geométricos son tomados implícitamente como un todo que contiene en él mismo sus longitudes, su área o su volumen.
Además de localizar estos obstáculos, Sierpinska (1989) caracteriza las concepciones de los estudiantes en:
-
Concepción primitiva. Cuando una función es un desplazamiento de puntos sobre el plano o sobre una línea.
-
Concepción de razón o proporción.Cuando en el desplazamiento de puntos sobre el plano, la nueva posición se puede describir en relación con la posición inicial por una razón de distancias desde un punto fijo
-
Visión sintética. Cuando una función se identifica como su representación en el plano. Las funciones son pensadas como objetos geométricos y se clasifican de acuerdo con la forma de esos objetos.
-
Tabla numérica. Cuando una función viene dada por su tabla de valores.
-
Expresiones algebraicas. Cuando una función se identifica por su ecuación.
-
Visión analítica de la curva. Cuando la función es un ente abstracto en unos ejes de coordenadas.
-
Relación funcional. Cuando existe un tipo especial de relaciones que llamamos funciones.
En las conclusiones a las que llega, la autora valora en forma muy positiva el contexto social en el que se ha desarrollado la experiencia e identifica como un obstáculo epistemológico el concebir a la matemática como un conocimiento algorítmico, ya que esto puede entorpecer el desarrollo de las concepciones sobre función.
En un estudio posterior, Sierpinska (1992) presenta cuatro categorías de los actos de entendimiento de un concepto matemático:
i. Identificación (de un objeto entre sus varios objetos)
ii. Discriminación (entre dos objetos, detectando diferencias y propiedades relevantes)
iii. Generalización (extender el orden de las aplicaciones, abrir posibilidades de interpretación y descubrimiento)
iv. Síntesis (la percepción de hechos aislados se pueden organizar en un todo consistente)
También identifica diecinueve categorías que se pueden determinar en la comprensión del concepto de función. Sobre estas categorías haremos referencia más adelante.
Sierpinska concluye su investigación añadiendo que también son importantes factores tales como la motivación, los contextos introductorios, los contextos de desarrollo, la comprensión de la noción de función, los prerrequisitos, las representaciones, las definiciones y la metodología.
Posteriormente, Ruiz Higueras (1998) incorpora a la componente epistemológica y a la cognitiva, la componente didáctica de un escenario particular. Entre sus resultados más significativos señala que las concepciones en el estudiante están determinadas por las concepciones históricas ligadas a la noción de función, por el estatus que se le da dentro de los programas oficiales y por cómo es presentado en los libros de texto y por el profesor en clase. A los diferentes obstáculos epistemológicos asociados a la evolución histórica de la noción de función los agrupa en:
-
Obstáculos a nivel de creencia y convicciones (Obstáculo de la concepción estática, Obstáculo de la disociación existente entre magnitudes y números)
-
Obstáculos a nivel de esquemas de pensamiento (Obstáculo de la razón o proporción, Obstáculo de la homogeneidad de las variables, Obstáculo de la concepción geométrica de las variables)
-
Obstáculos a nivel de conocimiento teórico (Obstáculo de la concepción algebraica, Obstáculo de la concepción mecánica de curva)
La componente didáctica de la investigación de Ruiz Higueras contempla a la noción de función como objeto a enseñar, como objeto de enseñanza y como objeto enseñado, lo que le permite analizar cómo "vive" el objeto función en el sistema de enseñanza español y aportar elementos y fenómenos didácticos relacionados con el proceso de transposición didáctica de este concepto.
En lo que se refiere a investigaciones en matemática educativa a distancia, hemos contemplado como antecedentes principales las desarrolladas por Montiel (2002) y Sánchez-Aguilar (2003), por ser las más cercanas a nuestro grupo de investigación. Sin embargo, somos concientes del creciente movimiento mundial en esta línea de investigación (Borba y Villareal, 2005; Albano, 2005a y 2005b).
El trabajo de Montiel (2002) abrió una línea de investigación en educación a distancia orientada a poner en funcionamiento elementos teóricos de la matemática educativa, en este caso en el escenario en línea. La investigación comienza caracterizando con precisión lo que se entiende por contrato didáctico, distinguiéndolo de los contratos escolares o pedagógicos, para estudiar con detalle la interacción entre alumnos y profesor con relación al saber. Este trabajo ha abierto espacios para la investigación en el campo de la matemática educativa como son el diseño de ingenierías didácticas propias del escenario, caracterización de las variables de control, la reproducibilidad en escenarios de educación a distancia, entre otros.
Esta investigación nace en la aproximación socioepistemológica, aproximación sistémica a la que haremos referencia en el marco teórico, lo que permite hacer una extensión de la teoría de las situaciones didácticas para explicar los fenómenos de enseñanza y aprendizaje que se llevan a cabo en una situación específica.
Por su parte, Sánchez-Aguilar (2003) trata de caracterizar la comunicación de ideas y objetos matemáticos durante un proceso de interacción y de adecuar las metodologías de análisis al campo de la educación a distancia y el tipo de información que es posible obtener de cada una de ellas.
El medio por el cual se hace posible la interacción entre estudiantes y profesores en cualquier escenario educativo es la comunicación. En el caso particular de la educación a distancia esta comunicación puede realizarse por diversos medios: e- mail, foros sincrónicos (Chat), foros asincrónicos, conversaciones de voz, medios impresos, videoconferencias, etc. Las comunicaciones escritas a distancia (e-mail, foros sincrónicos, foros asincrónicos) poseen características propias que las hacen diferir ampliamente de las comunicaciones verbales que tradicionalmente se utilizan en medios presenciales. Estas características únicas son las que hacen que el autor se planteé como problemática de investigación el estudio de las interacciones del tipo estudiante - estudiante y la comunicación de conceptos matemáticos durante esos procesos de interacción.
Para ello analiza dos interacciones entre estudiantes, la primera utilizando un foro sincrónico y la segunda, un foro asincrónico, con dos herramientas metodológicas diseñadas originalmente en el ámbito de la educación matemática presencial. Estas dos herramientas metodológicas son: Metodología del Análisis Focal y la Teoría Antropológica de lo Didáctico.
Luego del análisis de las interacciones según estas dos metodologías, Sánchez - Aguilar (2003) señala:
-
La naturaleza de las interacciones dependen del medio de comunicación escrita en el cual se desarrollan pero que a pesar de esto, independientemente del medio escrito en el que se desarrolle la actividad, el proceso de interacción no permite ver con claridad la etapa de acción de los estudiantes sobre la actividad matemática en cuestión.
-
Durante un proceso de interacción en un escenario virtual, los estudiantes involucrados se presentan a la escena de la interacción con formulaciones y preconcepciones sobre la actividad matemática a tratar. Una vez que inicia el proceso de interacción, los estudiantes entran en un proceso de validación o consenso en el cual se confrontan las diferentes formulaciones de los estudiantes, en las que se ponen en juego diferentes propuestas, técnicas y discursos tecnológicos. Sobreviven a este proceso aquellas que más se apeguen al discurso matemático escolar.
-
La tecnología puede cambiar la forma en que los estudiantes acceden, perciben y comunican los conceptos matemáticos e influir en sus procesos de validación presentes en los procesos de interacción.
-
Los procesos de interacción entre estudiantes privilegian los contextos analítico y algebraico como herramientas de argumentación, originando en algunos casos conclusiones matemáticamente erróneas por parte de los estudiantes.
En nuestra investigación debimos abordar diversas temáticas: función, función lineal, modelación, educación a distancia. Para cada uno de estos temas, es posible encontrar un número importante de investigaciones en el contexto de diferentes disciplinas y aproximaciones teóricas. Esto nos llevó a acotar nuestros antecedentes a aquellas investigaciones dentro de nuestra disciplina, Matemática Educativa, que aportan mayores elementos a nuestro trabajo y que están fuertemente vinculados con el Marco Teórico que desarrollamos a continuación.
2. MARCO TEÓRICO
La evolución de la didáctica de la matemática ha ido modificando la manera como se entienden los hechos didácticos. En (Cantoral y Farfán, 2003) se presenta una serie de momentos que muestran la evolución de esta problemática comenzando por lo que ellos llaman una didáctica sin alumnos, donde el objetivo era producir lo que la escuela debía de consumir, pero sin estudiar a profundidad la cultura escolar.
El segundo momento que plantean es aquel en donde los hechos didácticos son interpretados cognitivamente mediante la observación y la descripción sistemática de los logros de los estudiantes y de las diversas experiencias de aprendizaje. El objetivo es explicar cómo se aprende matemática. Es la llamada didáctica sin escuela.
Como tercer momento presentan una didáctica en la escuela, pero sin escenarios. En un medio determinado se analizan en forma sistémica los fenómenos didácticos teniendo en cuenta los distintos polos: el del saber, el de quien aprende y el de quien enseña.
Finalmente, se presenta una didáctica en escenarios socioculturales. Esta es una aproximación sistémica que recibe el nombre de aproximación socioepistemológica y que incorpora las cuatro componentes fundamentales en la construcción del conocimiento: su naturaleza epistemológica, su dimensión sociocultural, los planos de lo cognitivo y los modos de transmisión vía la enseñanza. Es en esta última, la didáctica en escenarios socioculturales, que ubicamos nuestra investigación.
La socioepistemología se plantea el examen del conocimiento social, histórica y culturalmente situado, problematizándolo a la luz de las circunstancias de su construcción y difusión. El principal problema de esta aproximación es cómo llevar a la práctica la postura sistémica para analizar las interacciones entre las cuatro dimensiones que la componen. La solución clásica a este problema es a través del establecimiento de unidades de análisis, cada una de las cuales retiene en forma simple las propiedades significativas de todo el sistema. Según el parecer de algunos investigadores que adhieren a esta aproximación, algunas de las nociones acuñadas en la perspectiva socioepistemológica tienen la característica de ser unidades de análisis para explorar el origen social del conocimiento. De entre ellas, dos fundamentales son: la resignificación y las prácticas sociales.
La noción de resignificación busca hacer una distinción de origen con respecto a la idea platónica que establece la preexistencia de los objetos y procesos matemáticos y que implica considerar la unicidad de los significados. La noción de resignificación emerge, entonces, como elemento para dar cuenta de que el conocimiento tiene significados propios, contextos, historia e intención; lo que señala la posibilidad de enriquecer el significado de los conocimientos en el marco de los grupos humanos.
Según las investigaciones más recientes, la noción de práctica social es la parte medular de la perspectiva socioepistemológica. Se entiende por práctica social a aquel conglomerado de supuestos socialmente compartidos, mayoritariamente implícitos, que norman la actividad. La tesis central es sostener que son las prácticas sociales las que generan conocimiento. Ejemplos de estas prácticas son la modelación (Arrieta, 2003) y la predicción (Cantoral y Farfán, 1998; Cantoral et al, 2000; Cantoral, Molina y Sánchez, 2005).
Investigaciones realizadas en el seno de la Matemática Educativa, a través de estudios de corte socioepistemológico y de lo que sucede en los sistemas didácticos, han dado evidencias de cómo el discurso matemático suele favorecer sólo algunos aspectos relacionados con los conceptos matemáticos, dejando de lado elementos presentes en la construcción social del mismo, tales como los argumentos y las herramientas relacionadas, cuando en realidad son estos los elementos que permiten entender los aspectos y formas de la actividad humana que transforman o resignifican al conocimiento (Cordero, 2003).
Se plantea entonces la hipótesis básica de que una epistemología basada en prácticas sociales favorece un estudio de la construcción social de la matemática a través de la reconstrucción de significados asociados al saber matemático. De esta manera se favorece el carácter funcional del mismo. Un ejemplo de esto es la socioepistemología formulada para lo periódico en (Buendía, 2005) que explica que la predicción como práctica social resulta ser un argumento para construir lo periódico, ya que al predecir se reconstruyen los significados asociados a la repetición de un movimiento.
El análisis epistemológico del concepto de función según esta aproximación, permite determinar que cada tipo de función tiene un origen en un contexto específico lo que implica que cada una posea su propia naturaleza, que la distingue de las demás, y problemáticas propias relativas a su apropiación.
Una vez que se reconocen a las prácticas sociales como generadoras de conocimiento y que se distingue la naturaleza propia de cada función, las situaciones que se diseñan fundamentadas en la socioepistemología permiten hacer evidentes herramientas y argumentos; que permiten, a su vez, reconstruir significados.
De esta manera, y a diferencia de otras aproximaciones teóricas, en la socioepistemología el foco de atención está puesto en las prácticas sociales y no exclusivamente en lo conceptos como objetos preconstruidos. Es decir, la socioepistemología busca y atiende las situaciones que están presentes cuando se estudia al hombre en actividad matemática y no sólo en su producción última. Investigaciones realizadas en el marco de esta aproximación (Lezama, 1999; Farfán y Ferrari, 2001; Montiel, 2005) dan cuenta de ello ya que las mismas se centran en el desarrollo del pensamiento matemático ligado a nociones como periodicidad, covariación, linealidad, funcionalidad, más que a conceptos u objetos matemáticos eruditos, incluso aquellos tradicionalmente escolares (propiedad periódica, función, derivada, etc.)
2.1 Un estudio sistémico de la resignificación de la función lineal
Buscar la resignificación de un concepto supone que los estudiantes han tenido ya un acercamiento escolar del mismo. En este trabajo, nuestro objetivo es romper con el discurso matemático escolar tradicional a través de secuencias orientadas por la construcción social de la linealidad.
El análisis didáctico del concepto matemático función nos lleva ubicarlo como concepto escolar. Las experiencias que esta investigación reporta fueron desarrolladas por veintisiete alumnos del curso Naturaleza del Pensamiento Matemático del Programa de Maestría en Ciencias en Matemática Educativa del Centro de Investigación en Ciencia Aplicada y Tecnología Avanzada del Instituto Politécnico Nacional (CICATA-IPN) de México, en la modalidad en línea. El programa se apoya en un modelo basado en redes de Internet, sistemas de telecomunicaciones, tecnologías de información y comunicación, así como modelos de enseñanza y aprendizaje a distancia (Montiel, 2002).
Los alumnos de este programa de postgrado poseen diferentes formaciones académicas pero todos son docentes de matemática del nivel medio, medio superior y/o superior. De distintas nacionalidades, desempeñan su labor docente en diferentes sistemas educativos.
La primera actividad del curso consistió en responder a un cuestionario de diecinueve preguntas que diseñamos con el objetivo de tener un primer acercamiento a la noción de función que los alumnos - docentes manejaban, así como también conocer la referencias bibliográficas que utilizaban para abordar el tema y el status que le otorgaban a cada una de las representaciones del concepto, tanto en el desarrollo de sus clases como al momento de evaluar a sus alumnos.
El análisis tanto las respuestas dadas en este cuestionario, como el vocabulario utilizado en las mismas y el tipo de argumentos que las justificaban, nos permitió vincular las definiciones de función dadas por los docentes con los obstáculos y concepciones ya identificados por Sierpinska (1989). Así, notamos que mayoritariamente se identifica a la función como un tipo especial de relación, entendiéndola más como una asignación entre objetos que como una dependencia entre cantidades variables o una forma de identificar los efectos de un cambio.
En la redacción de estas definiciones, se encontraron distintos niveles de formalismo, expresando, implícita o explícitamente, la condición de existencia y unicidad. En el mismo cuestionario se mostraban dieciséis gráficas y la consigna era señalar cuáles correspondían a una función y por qué. Notamos que cuando más formales eran en sus definiciones, no identificaban como funciones a aquellas funciones discretas o con asíntotas verticales (no se cumplía la condición de existencia) o cuyos dominios eran partidos (justificaban diciendo que no se veía que cumplieran la condición de unicidad).
Otro dato importante que arroja el análisis de los resultados de este cuestionario es que, si bien al contestar acerca los aspectos del tema (algebraico, geométrico / gráfico, numérico, verbal) a los que les otorgaban mayor importancia cuando desarrollaban el tema en clase, ubicaban en los primeros lugares al geométrico / gráfico, este aspecto era el que obtenía menor porcentaje en un ejemplo de evaluación en el que se les planteaba un mismo problema resuelto de cuatro maneras diferentes, destacando en cada caso alguno de los aspectos antes mencionados.
Al trabajar con profesores de diferentes países y sistemas educativos el análisis del concepto de función como concepto escolar lo realizamos a través del análisis de una de las principales fuentes de recursos didácticos del profesor: el libro de texto. Encontramos que algunos textos son mencionados por la mayoría de los profesores, a pesar de sus distintas formaciones y de pertenecer a distintos sistemas educativos. De entre ellos, seleccionamos dos y realizamos un análisis didáctico teniendo en cuenta aspectos como: estrategias de comunicación, cómo se introducía el tema, tipos ejemplos y ejercicios, tipo de dibujos o metáforas que se utilizaban para el tratamiento del concepto, etc. Encontramos que estos textos brindan una presentación clásica o tradicional del concepto: definición de función, fórmula, puntos en el plano, unión de puntos y gráfica.
Nuestra componente epistemológica se constituyó con base en el estudio de Sierpinska (1992), mencionado anteriormente. Replanteamos (dado el contexto institucional y las características de nuestro sistema didáctico) las diecinueve categorías para el entendimiento del concepto en cinco momentos para la resignificación de la función lineal.
-
Momento 1 relacionado con los cambios, que implica no solamente identificar los cambios observados en el mundo que nos rodea, sino que también incluye identificar qué es lo que cambia y cómo cambia.
-
Momento 2, al que llamamos variable, en el que ubicamos la discriminación entre dos modos de pensamiento matemático (en términos de cantidades conocidas y desconocidas y en términos de variables y constantes) y la discriminación entre variables dependiente e independiente.
-
Momento 3 donde encontramos la síntesis entre el concepto de ley y el concepto de función, la discriminación entre una función y las herramientas analíticas que se usan para describir su ley y la síntesis de la concepción general de la función como un objeto.
-
En el momento 4 ubicamos las diferentes formas de expresar una función, lo que incluye la discriminación entre los diferentes significados de la representación de funciones y las funciones mismas y la síntesis de las diferentes formas de expresar las funciones, representar las funciones y hablar sobre funciones.
-
Por último, en el momento 5 encontramos la relación funcional y relación causal que implica síntesis de los "roles" de la noción de función y de causa y la discriminación entre las nociones de relación causal y funcional.
Vemos en estos momentos que el estudio del cambio es crucial para significar la noción de función, lo cual guarda coherencia con lo reportado en (Youschkevitch, 1976) sobre el surgimiento del concepto como relación funcional. La noción de cambio denota la modificación de estado, de apariencia, de comportamiento o de condición de un cuerpo, de un sistema o de un objeto. Al tratar de entender cómo y cuánto cambia el cuerpo, sistema u objeto dado, es cuando surge la noción de variación, ya que esta se entiende como una cuantificación del cambio. En este sentido, decimos que una persona utiliza argumentos y estrategias de tipo variacional cuando hace uso de ideas, técnicas o explicaciones que de alguna manera reflejan y expresan el reconocimiento cuantitativo y cualitativo del cambio de un cuerpo, sistema u objeto que se esté estudiando (Cantoral, Molina y Sánchez, 2005)
El estudio del cambio para el caso de la función lineal nos lleva a estudiar una forma de cambio particular: la "proporcionalidad directa". La revisión de investigaciones referidas a este tema (Azcárate y Deulofeu, 1996; Fiol y Fortuna, 1990; Grupo Beta, 1997; Suhit, 1995), así como también la revisión de tres textos escolares (Álvarez, Álvarez, Arribas, Martínez y Ruiz, 1999; Guzmán, Colera y Salvador, 1987) nos permite identificar, que en general, la idea que subyace en las definiciones y ejemplos dados es que dos magnitudes son proporcionales cuando al aumentar o disminuir una, la otra aumenta o disminuye de la misma manera. Para el caso de la proporcionalidad directa, si aumenta (disminuye) una, aumenta (disminuye) la otra, y en el caso de la inversa, si aumenta (disminuye) una, disminuye (aumenta) la otra. Esa "misma manera" de aumentar o disminuir se relaciona con la noción de factor de proporción, coeficiente de proporcionalidad o reducción a la unidad.
En Suhit (1995) se señala que esta idea en ocasiones conduce al error de interpretar como proporcionales magnitudes entre las que existe cualquier relación de crecimiento (o decrecimiento) simultáneo.
En esta revisión encontramos que las definiciones formales, algebraicas o coloquiales, indican que dos magnitudes son directamente proporcionales cuando el cociente entre dos valores correspondientes es una constante. En el caso de la proporcionalidad inversa, indican que en ese caso el producto entre dos valores correspondientes es constante. Generalmente estas definiciones van acompañadas de ejemplos y ejercicios, que involucran el completar tablas y representar en un sistema de coordenadas los valores encontrados en dichas tablas para así identificar qué tipo de curva determinan.
Entendemos que la idea intuitiva que antes mencionamos puede conducir a errores si no va acompañada de un análisis de cómo es encontrado el factor de proporcionalidad. Nos referimos a los casos de proporcionalidad directa donde el factor de proporcionalidad es negativo, ya que en ese caso, cuando una magnitud aumenta, la otra disminuye y podría conducir al error de identificar como inversa a esa relación (ambas magnitudes aumentan pero en valor absoluto)
Como dijimos anteriormente, la perspectiva socioepistemológica sostiene que son las prácticas sociales las que generan conocimiento. Diferentes investigaciones dentro de esta perspectiva han reportado como una de estas prácticas a la predicción (Cantoral y Farfán, 1998), describiéndola como la práctica que permite determinar el estado futuro de un sistema, de un objeto o de un fenómeno con base en el estudio sistemático de las causas que lo generan y los efectos que produce. Esta práctica está íntimamente relacionada con la variación ya que para predecir es necesario cuantificar y analizar los cambios. Es decir, la variación es una herramienta de análisis necesaria para la predicción.
En nuestra disciplina, la Matemática Educativa, la concepción de modelo tiene diversos significados. Lo que distingue a la aproximación socioepistemológica de otras perspectivas es la intención: los modelos son usados como herramientas para argumentar (Arrieta, 2003). Pero incluso dentro de esta aproximación existe actualmente el debate entre considerar a la modelación como práctica social o como actividad.
En tanto asumimos la modelación como una actividad restringida a un propósito común, nuestro diseño buscó que el alumno-docente transitara por los cinco momentos antes mencionados, a través de la resolución de secuencias que implicaran la construcción de modelos que incluyeran: el uso de diferentes representaciones y la necesidad de identificar las variables que intervenían en el fenómeno que se estaba estudiando y como se relacionaban, estudiando en el mismo proceso de establecer las relaciones entre las variables, la forma que esa relación adoptaba. De aquí que la resignificación que buscamos sea la de linealidad.
El análisis de la dimensión cognitiva implica entender cuáles son las concepciones de los alumnos en referencia al contenido matemático que va a ser tratado.
Entendemos que existen cuatro modos de representación del concepto función: descripción verbal, tabla numérica, gráfica y fórmula. En su génesis histórica, cada uno de estos modos ha jugado un papel importante. Sin embargo, como se señala en (Cantoral y Farfán, 1998), el concepto de función devino protagónico hasta que se lo concibe como una fórmula, es decir, hasta que logró la integración de dos dominios de representación: el álgebra y la geometría.
Investigaciones desarrolladas en el seno de la Matemática Educativa entorno a la noción de función muestran en la enseñanza tradicional una sobrevaloración de los aspectos formales y algorítmicos que, en general, carecen de significado para el estudiante y se dejan de lado las argumentaciones visuales y los enfoques numéricos, entre otras causas, por no considerarlos matemáticamente válidos. En (Cantoral y Farfán, 1998) se afirma que tener un dominio del contexto visual tanto en la algoritmia, la intuición y la argumentación permite el tránsito entre las diversas representaciones y se plantea que la hipótesis central consiste en asumir que: previo al estudio del cálculo se precisa de la adquisición de un lenguaje gráfico que posibilite, esencialmente, la transferencia de campos conceptuales virtualmente ajenos a causa de las enseñanzas tradicionales, estableciendo un isomorfismo operativo entre el álgebra básica y el estudio de curvas, mejor aún, entre el lenguaje algebraico y el lenguaje gráfico.
3. METOLOGÍA
3.1. Diseño de las secuencias
La metodología utilizada para el diseño de las secuencias experimentales fue la Ingeniería Didáctica. El término de ingeniería didáctica surge, en el seno de la escuela francesa, en analogía al quehacer en ingeniería, ya que se apoya en resultados científicos, involucra la toma de decisiones y el control sobre las diversas componentes inherentes al proceso. Así la ingeniería didáctica se constituye como una metodología de investigación que se aplica a los productos de enseñanza basados o derivados de ella y como una metodología de producción para guiar las experimentaciones en clase. Su sustento teórico proviene de la teoría de la transposición didáctica y de la teoría de las situaciones didácticas.
En esencia esta metodología contempla cuatro fases (Artigue, 1995; Farfán, 1997):
-
Análisis preliminar
-
Concepción y análisis a priori de las situaciones didácticas de la ingeniería
-
Experimentación
-
Análisis a posteriori y Evaluación,
A las que Lezama y Farfán (2001) denominan fase de planeación, fase de diseño, fase experimental y fase de validación, respectivamente.
El análisis preliminar contempla sólo las componentes epistemológica, didáctica y cognitiva a la investigación. Incorporar la componente social y modificar la interacción sistémica de las cuatro componentes para explicar el fenómeno didáctico es lo que se ha planteado en el marco teórico.
Ahora bien, en la fase de diseño distinguimos las restricciones y variables de control que imponía trabajar con profesores e interactuar en un escenario en línea. Incluyendo las reportadas por Montiel (2002) y Sánchez-Aguilar (2003), consideramos:
-
La oportunidad de consultar bibliografía antes de intervenir en el espacio en línea que comparten con sus pares, así que podemos esperar respuestas formales o definiciones de libros,
-
La facilidad de interactuar con otros colegas o profesores (de cursos anteriores) por vías externas al curso, como el correo electrónico y la mensajería instantánea (Chat)
-
La modalidad en línea permite el uso de materiales digitales diversos disponibles en Internet, aunque no estén indicados en el curso. Estos materiales incluyen herramientas didácticas y tecnológicas, relacionadas o no con la enseñanza y el aprendizaje de las matemáticas, así como bibliografía especializada en matemática educativa.
-
El alumno-docente, por su formación y experiencia profesional, tiene familiaridad con las nociones matemáticas involucradas en la actividad matemática,
-
En el proceso de validación o consenso en el cual se confrontan las diferentes formulaciones de los alumnos-docentes, sobreviven a este proceso aquellas que más se apeguen al discurso matemático escolar.
-
La tecnología puede cambiar la forma en que los alumnos-docentes acceden, perciben y comunican los conceptos matemáticos e influir en sus procesos de validación presentes en los procesos de interacción.
-
Los procesos de interacción entre estudiantes privilegian los contextos analítico y algebraico como herramientas de argumentación, originando en algunos casos conclusiones matemáticamente erróneas por parte de los estudiantes.
-
La tecnología como mediador en el proceso formativo(la computadora y la interfaz), la tecnología como recurso de trabajo y lectura (software de aplicación2) y la tecnología como herramienta en la resolución de secuencias didácticas (software didáctico3), modifican el intercambio de información entre el objeto de aprendizaje y el sujeto cognoscente,
Tomando en consideración estos elementos diseñamos cinco secuencias didácticas, que permitieran a los alumnos-docente transitar por los cinco momentos que construimos a partir de las categorías de entendimiento del concepto de función que presenta Sierpinska (1992).
Como indicamos anteriormente, esta experiencia se llevó a cabo en el curso Naturaleza del Pensamiento Matemático, del Programa de Maestría en Ciencias en Matemática Educativa que ofrece completamente en línea el CICATA-IPN desde la Ciudad de México. En el trabajo a través de Internet se utilizó la plataforma de trabajo Blackboard y, debido a problemas técnicos de esta plataforma, el sistema de trabajo compartido BSCW. Ambos ambientes de trabajo en línea tienen la característica de ser asíncronos.
Si bien la comunicación entre los actores de la experiencia analizada estaba abierta a realizarse vía correo electrónico, vía telefónica o incluso presencial, para aquellos que tuvieran oportunidad, se consideró registrar, exclusivamente, la comunicación que se dio en los foros de discusión, ya que permite la lectura de varias intervenciones y puntos de vista, pero sobre todo porque este espacio es el más apropiado para indagar en el pensamiento e ideas de los profesores, dado el tipo de interacción y espontaneidad que permiten (Castañeda, Sánchez y Molina, 2006). En el desarrollo del curso hubo dos tipos de foros, uno que se iniciaba con una pregunta por parte del profesor, y otro que surgía a partir de los comentarios y preguntas a partir de las secuencias resueltas en forma individual o en grupo, y en los que el profesor intervenía con observaciones y nuevas preguntas.
Se diseñaron cinco secuencias para resolver en cuatro semanas y se utilizaron materiales digitales de diferentes tipos, que proporcionaran flexibilidad y dinamismo a la actividad didáctica.
Secuencia 1
La intencionalidad de esta primera secuencia fue poner de manifiesto tres aspectos fundamentales: el reconocimiento de la proporcionalidad directa en diferentes contextos, las estrategias de cálculo utilizadas y la identificación del factor de proporción y el análisis de su significado. Con esto, se pretendía que los estudiantes transitaran por los dos primeros momentos que identificamos en el análisis de las categorías de entendimiento del concepto de función que determinamos a partir de (Sierpinska, 1992): cambios y variables.
La secuencia se proporcionó en un archivo en Word, para que pudiera modificarse directamente y no se perdiera el orden de la resolución. Los ejercicios incluían preguntas para resolver en un contexto numérico-aritmético e incluían la organización de información en tablas.

Secuencia 2
La intención de la segunda secuencia fue construir las expresiones ![]() con el objetivo de poder utilizarlos como una herramienta de predicción. Se transitaría por los restantes momentos que identificamos.
con el objetivo de poder utilizarlos como una herramienta de predicción. Se transitaría por los restantes momentos que identificamos.
Utilizando diferentes estrategias, se esperaba que los estudiantes identificaran en las dos situaciones planteadas los parámetros a y b, que los utilizaran para responder preguntas relacionadas con los posibles valores de las variables, que explicaran cómo la variación de esos parámetros modifican las condiciones iniciales o de reproducción, y que explicaran las características del dominio y de la imagen que habían considerado según la representación elegida. En el foro correspondiente a la segunda secuencia, el debate giró alrededor de la noción de modelo en el sentido de cómo fue construido en la secuencia, qué elementos de la secuencia anterior fueron útiles, las diferentes formas de representación y el tránsito de una a otra, el dominio y la imagen del fenómeno y el dominio y la imagen de la expresión algebraica que lo modeliza, y el uso del modelo como una herramienta de predicción.
De nuevo, la secuencia se proporcionó en un archivo en Word, esta vez incluyendo el contexto numérico-aritmético y el contexto gráfico relacionado a una situación de variación.

Secuencia 3
En la tercera secuencia se utilizó el Programa SIRES (Sistema de resortes) desarrollado por el grupo que encabeza el Dr. Jaime Arrieta en el Instituto Tecnológico de Estudios Superiores de Acapulco, México, quienes en la línea de investigación "Las prácticas sociales en la emergencia del conocimiento matemático", intentan dar explicación de cómo en el ejercicio de las prácticas sociales los actores construyen sus conocimientos como herramientas para la intervención; construcción que no se concibe como un proceso aislado, sino como un proceso social de construcción conjunta. De esta manera, si bien la intencionalidad era la misma que en la secuencia anterior, se planteaba a los alumnos un contexto diferente a los utilizados en las anteriores secuencias. El ambiente de un "Laboratorio Virtual" pretendió que el alumno-docente experimentara una situación física relacionada con la linealidad de una función. Esta simulación logra que el participante viva la situación y la haga propia, manipule objetos y reciba información a cambio, para hacer observaciones, así como construir conjeturas y argumentos (a discutir en los foros).
Por un lado, el alumno-docente tuvo acceso al ambiente virtual del SIRES y por otro se le proporcionó un archivo en Word, para responder ahí directamente, que incluía pantallas del programa para guiar la actividad. Se contemplaron los contextos físico, numérico (aritmético y tabular) y gráfico.

Secuencia 4-5
Incorporando herramientas tecnológicas, con las secuencias 4 y 5, se buscaba favorecer la construcción de un universo gráfico en el terreno de las funciones algebraicas a partir de las operaciones básicas de suma y multiplicación, desde una aproximación visual que involucra simultáneamente herramientas analíticas y numéricas, y que implica una interpretación gráfica de las operaciones entre funciones. Los planteamientos de la secuencia se retomaron de (Cantoral y Montiel, 2001) y por lo tanto asumimos también que debido a la tradición algebraica-algorítmica que domina en la escuela, centrarse en el contexto gráfico pone en funcionamiento los recursos más familiares del alumno-docente, en este caso argumentos numéricos y algebraicos, lo que fomenta la articulación de varios registros de representación y en consecuencia, enriquece el significado de la noción de función.
La discusión en los foros correspondientes a estas secuencias giró alrededor del tipo de lenguaje, explicaciones y argumentos que se utilizaron en el desarrollo de las secuencias, las diferencias con el lenguaje, explicaciones y argumentos presentes en el Discurso Matemático Escolar tradicional, y cómo éste se vería afectado por la incorporación de esta propuesta.

La actividad final del curso consistió en un informe final grupal realizado a través la discusión, en un foro organizado por el mismo grupo, de las notas, la bibliografía complementaria y la experiencia con las secuencias 1 a la 5.
Como dijimos anteriormente, en la resolución de estas secuencias buscábamos que los alumnos transitaran por los cinco momentos identificados en nuestro análisis epistemológico. Buscando la articulación de dichos momentos en la producción de los alumnos - docentes, encontramos que en aquellas situaciones donde debía encontrarse la forma que adoptaba la relación entre las variables o magnitudes presentes, la linealidad aparecía como primera opción, justificando la elección de este modelo o bien por la representación gráfica de los datos dados o bien por la identificación de una regularidad en una tabla numérica. A continuación, se encontraba la fórmula o expresión algebraica correspondiente y a partir de ahí, ésta jugaba un papel importante en las respuestas que se daban, por considerarla más "precisa" o "exactas" en comparación con otro tipo de representaciones.
En aquellas situaciones que no correspondían a un modelo lineal, se encontraron respuestas de tres tipos: se manipulaba la información dada de manera tal de poder adaptar la situación a una situación de linealidad, se manifestaba la imposibilidad de resolución de problema, o se buscaba otro tipo de estrategias o de reglas de cálculo que permitieran dar respuesta las preguntas planteadas.
Este análisis nos permite afirmar que la linealidad versus la no linealidad no está presente en todas las resoluciones porque de por sí no es una discusión que esté presente en los argumentos de los alumnos. Por ejemplo, cuando en el primer de foro de discusión se les pedía que caracterizaran o clasificaran los problemas propuestos, las respuestas estuvieron referidas al grado de dificultad de dichos problemas y no a los elementos que les permitían identificar proporcionalidad directa como forma de relación entre las magnitudes y que les permitía diferenciarlas de otras que presentaban relaciones de crecimiento o decrecimiento simultáneo.
En donde si encontramos esta comparación es en las respuestas a aquellas secuencias en las que gráficamente debían argumentar que la suma de dos rectas es una recta pero que al multiplicar dos rectas la linealidad se perdía.
4. RESULTADOS
En la fase de validación confrontamos los resultados obtenidos en la fase experimental con los elementos teóricos de nuestro análisis a priori, en la fase de diseño. Esta confrontación la generamos a través de las siguientes direcciones:
-
La noción de cambio: ¿qué es lo que cambia y cómo cambia?
La práctica social de predicción (Cantoral y Farfán, 1998) está íntimamente relacionada con la variación, ya que para predecir es necesario cuantificar y analizar los cambios, es fundamental no sólo reconocer lo qué cambia, sino también cómo cambia.
En el análisis de la resolución de las actividades propuestas para reconocer la proporcionalidad en diferentes contextos, encontramos que si bien los estudiantes conocen el concepto "proporcionalidad directa", poseen estrategias de cálculo relacionadas con él y reconocen las características de su representación gráfica (el término "lineal" es reiteradamente utilizado como sinónimo de proporcional), lo sobre utilizan al reconocer como proporcionales magnitudes entre las que existe cualquier relación de crecimiento (o decrecimiento) simultáneo y lo sobrevaloran al decir que determinadas situaciones no tienen solución porque este concepto no es aplicable.
Esto nos permite concluir que la idea intuitiva de proporcionalidad directa ("a más, más: a menos, menos") puede conducir a errores si no va acompañada de una identificación del factor de proporción, de un análisis de cómo es encontrado dicho factor y de una interpretación del mismo en el contexto de la situación planteada.
En el Marco Teórico, en el análisis de la dimensión didáctica, mencionamos la utilización por parte de los alumnos - docentes del concepto de función como una relación, correspondencia, asociación o aplicación entre elementos de conjuntos y no como una forma de representar un cambio o transformación.
Al identificar en las situaciones planteadas la presencia de un cambio se observa el tránsito por el Momento 1 planteado en el análisis epistemológico, aunque no se justifique o explicite la forma que ese cambio tiene. Pero la concepción de función como una asignación entre variables, hace que las funciones sean definidas y utilizadas para asignar a determinados valores de la variable independiente, el correspondiente valor de la variable dependiente y no como una forma de representar los cambios identificados.
Es posible que el identificar e interpretar en contexto el factor de proporción, permita entender el concepto de función como una forma de representar el cambio sufre la variable independiente al transformarse en la variable dependiente, y viceversa.
-
La propiedad de linealidad en diferentes contextos. Representación y argumentos.
En relación con lo observado en el apartado anterior, encontramos que en la resolución de secuencias escolares que podríamos llamar tradicionales, el modelo lineal es adoptado prácticamente en todos los casos con ausencia de argumentos o explicaciones que justifiquen dicha adopción; así como también que se elije por su exactitud a la fórmula como la mejor forma de representar la relación entre las variables, a pesar de reconocer que en la situaciones planteadas la tabla fue la forma más fácil para obtener los datos y la gráfica para predicciones aproximadas.
En la resolución de este tipo de secuencias encontramos el tránsito por los cinco momentos identificados en el análisis epistemológico. Los elementos que nos permiten afirmar esto son: la identificación de las variables involucradas; la elección del modelo, en la que si bien el debate de lo lineal vs lo no lineal no está presente, implica identificar una forma de cambio; las distintas representaciones y el tránsito de una a otra; la elección de una de las formas de representación como la mejor manera de representar a las variables; y la utilización del modelo como herramienta de predicción.
Al confrontar las resoluciones y participaciones de los estudiantes en los foros correspondientes a estas secuencias, con las respuestas que dieron en el cuestionario inicial, encontramos que si bien al momento de desarrollar este contenido en clase el aspecto algebraico aparece en los últimos lugares en cuanto al lenguaje al que se le da más importancia o al lugar ocupa a lo largo de la exposición, esto difiere al momento de analizar posibles respuestas en una evaluación ya que este aspecto es el que mayor porcentaje se le asigna. Entonces, esta confrontación parecería indicar que en el caso de las secuencias escolares del tipo tradicional no todos los tipos de representación tienen para el alumno - docente el mismo status y que el paso previo por el lenguaje verbal, gráfico o numérico antes de llegar a la fórmula es para poder darle diferentes interpretaciones a la misma e ir avanzando gradualmente en cuanto a exactitud o precisión. Es decir, caracterizar en contextos gráficos y/o numéricos pero formular y validar en contextos analíticos.
En nuestro trabajo, las que llamamos secuencias escolares no tradicionales incluían trabajar con software para la simulación y la interactividad, y con el método de las operaciones, que implicaba la incorporación de herramientas tecnológicas como por ejemplo las herramientas de dibujo de Word.
Como ya lo mencionamos en la sección anterior, en la secuencia 3 los estudiantes trabajaron con el Programa SIRES. Si bien en la resolución de las secuencias 1 y 2 los alumnos-docentes habían utilizado software didáctico como son los graficadores, en el trabajo con el Programa SIRES es posible observar algunas características, podríamos decir propias de la interacción con este tipo de programas.
En principio, el contexto en el cual se realiza la experiencia. A diferencia de las secuencias anteriores, en la que los datos experimentales se daban como parte del enunciado, en el caso de SIRES, se presenta un "laboratorio virtual" en dónde se simula mediante el software una situación experimental a partir de la cual se obtienen los datos necesarios para dar respuesta a las preguntas planteadas en la secuencia. Entonces es posible observar que la interacción estudiante - interfase es diferente ya que permite una manipulación de los elementos que proporciona el programa, tanto para familiarizarse con el mismo como para obtener la información requerida en la secuencia.
En las secuencias anteriores los datos les eran proporcionados "sin ruido", esto es, los datos aportados en las tablas eran proporcionales. Cuando los datos eran obtenidos por el estudiante, el ruido aparecía ya que los datos no eran estrictamente proporcionales y esto originaba que se manipularan los instrumentos de medición o los elementos del montaje para que los datos sí se ajustaran a un modelo lineal.
En el análisis de las resoluciones, tanto en las individuales como en las grupales, encontramos coincidencias con las estrategias antes utilizadas: una vez obtenidos los datos, encontrar la expresión algebraica y utilizarla para dar respuesta a todas las preguntas de la secuencia. Aunque en esta secuencia también aparece como una posible estrategia de resolución la interpolación de datos.
El método de las operaciones aplicado en las secuencias 4 y 5 permite bosquejar gráficas a partir de un análisis visual que involucra simultáneamente herramientas analíticas y numéricas. La expresión "operar gráficamente" hace referencia a las operaciones entre funciones, pero desde una perspectiva gráfica. Cabe aclarar que este método no pretende ser un recetario o una lista de pasos a seguir para que el estudiante grafique correctamente. Uno de sus objetivos principales es propiciar la relación existente entre objetos matemáticos aparentemente disjuntos, esto es, vincular y transitar entre diversas representaciones de una función (Cantoral y Montiel, 2001)
Es en este tipo de secuencias no tradicionales, y por las posibilidades que provee el escenario en línea, es donde observamos un cambio en el tipo de argumentos, estrategias y formas de explicar los procedimientos.
Pregunta de la Secuencia 5. Con un ejemplo (dos rectas cualesquiera) muestra en los registros numérico, gráfico y algebraico, que la suma de dos rectas es también una recta.
Respuesta de un alumno-docente. Para mostrar, por medio de un ejemplo, que la suma de dos rectas da como resultado otra recta, manejaré la recta uno como
y la recta dos como
(ambas rectas serán llamadas rectas generadoras). Utilizaré los tres registros de manera simultánea (el numérico, el gráfico y el algebraico), a fin de visualizar mejor el resultado.
Vamos a graficar ambas rectas
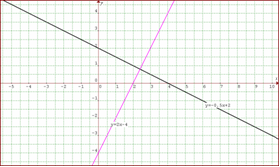
A partir de las rectas, podemos encontrar la gráfica de la ecuación de la recta que resulta de sumar ambas ecuaciones, la que llamaremos recta suma. La recta suma tiene como característica que cada punto sobre ella es resultado de la suma de las alturas con respecto al eje de las abscisas de las rectas generadoras, en esa misma coordenada x
Por ejemplo, cuando x=0 la altura de la recta uno con respecto al eje x es igual a -4, mientras que la altura de la recta dos es igual a 2, por lo que la suma de las dos alturas de las rectas generadores es igual a ![]() , por tanto un punto de la recta suma se encuentra en (0,-2). Gráficamente:
, por tanto un punto de la recta suma se encuentra en (0,-2). Gráficamente:

Ahora, cuando x=2 es claro que la altura de la recta uno con respecto al eje de las abscisas es 0, mientras que la altura de la recta dos con respecto al eje x es igual a 1, que hace que la suma de las dos alturas de las rectas generadoras es igual a 1, por lo que otro punto de la recta suma se encuentra en (2,1). Gráficamente:

Por último, cuando x=4 es claro que la altura de la recta uno con respecto al eje de las abscisas es 4, mientras que la altura de la recta dos con respecto al eje x es igual a 0, que hace que la suma de las dos alturas de las rectas generadoras es igual a 4, por lo que otro punto de la recta suma se encuentra en (4,4). Gráficamente:

Uniendo los tres puntos encontrados, (0,2), (2,1) y (4,4), se encuentra la recta suma
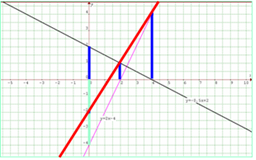
Para encontrar esta ecuación de la recta se utiliza la ecuación de la recta forma dos puntos. Si x1=0, y1=-2, x2=2, y2=1 entonces:

Por lo que la ecuación de recta suma es igual a ![]()

El escenario en línea y la modalidad asincrónica le da al alumnos - docentes la oportunidad de usar diferentes herramientas didácticas que le permiten ilustrar sus explicaciones escritas, usando diferentes registros de representación. Sin embargo, observemos que no solo se obtiene la gráfica de las funciones con un software, sino que hay manipulación de los objetos a través del trazo de ordenadas usando rectas verticales de colores. Esto lo relacionamos directamente con el diseño de la secuencia, donde usamos la idea de operaciones gráficas (Cantoral y Montiel, 2001) para manipular los objetos gráficos y relacionarlos con sus representaciones numéricas y algebraicas.
El cambio de argumentos, estrategias y formas de explicitar los procedimientos que se pone de manifiesto en la resolución de estas secuencias escolares no tradicionales nos lleva concluir que este cambio es el que permite hacer explícitas las características de la linealidad como propiedad de la relación funcional de dos variables. Características que observamos que no son del todo explícitas al adoptar el modelo lineal en la resolución de secuencias escolares tradicionales.
Por otro lado, entendemos que el priorizar el lenguaje gráfico fue lo que hizo posible poner de manifiesto este cambio a la hora de justificar respuestas, desarrollos o procedimientos.
-
Naturaleza de las variables. Sobre el dominio y la imagen de las funciones.
Las reflexiones referidas al tipo de variable y a las características del dominio y la imagen que eligieron en cada actividad las encontramos en las participaciones de los alumnos - docentes en los foros de discusión relacionados con cada secuencia.
Con respecto a la naturaleza de las variables, encontramos que en forma unánime los estudiantes consideran "por definición" que los modelos matemáticos son continuos, y que eventualmente debe analizarse su validez en los contextos particulares dados por cada situación, en donde es posible encontrar que una o ambas variables son discretas.
Por otra parte, encontramos en la mayoría de las resoluciones dominios diferentes para la representación gráfica y para la representación algebraica de la misma función. Esto está en relación con lo ya manifestado por los mismos alumnos acerca de la creencia de que la fórmula es la mejor forma de representar la relación entre las variables debido a su exactitud. Esto nos permite concluir que estos tipos de representación no tienen para el estudiante el mismo status, y que el lenguaje gráfico está subordinado al lenguaje algebraico, que posee reglas más exactas y precisas. Entendemos que esto está vinculado con la formación recibida en los estudios de grado y por los textos escolares citados como material de referencia.
-
Comportamiento o peculiaridades en un escenario en línea.
Como lo señalamos en los antecedentes de investigación, el trabajo de Montiel (2002) abrió una línea de investigación en educación a distancia orientada a poner en funcionamiento elementos teóricos de la matemática educativa, en este caso en el escenario en línea. La caracterización del contrato didáctico que allí realiza nos brindó elementos teóricos que nos permitieron explicar algunos de los fenómenos observados durante la puesta en escena de las secuencias diseñadas. En particular, la clasificación de los episodios de ruptura de la tradición escolar (cuando las respuestas de los alumnos-docentes evocaron a argumentos de cambio en los contextos gráfico, analítico y numérico), los procesos de adhesión al discurso (en las respuestas al cuestionario inicial y las participaciones en los foros) y las rupturas del contrato didáctico (en las intervenciones del profesor en el foro, ayudando a hacer explícitos los argumentos implícitos sobre los que subyacían las resoluciones de los estudiantes)
Entre las variables de control distinguidas en la fase de diseño, mencionamos que la tecnología puede cambiar la forma en que los alumnos-docentes acceden, perciben y comunican los conceptos matemáticos e influir en sus procesos de validación presentes en los procesos de interacción, y que la tecnología, como herramienta en la resolución de secuencias didácticas, modifica el intercambio de información entre el objeto de aprendizaje y el sujeto cognoscente. En este sentido, encontramos en todas las resoluciones analizadas la utilización de software educativo (en su mayoría graficadores) aún cuando no era parte de la consigna la incorporación de esta herramienta o se brindaba algún tipo de apoyo escrito para graficar "a mano", y que algunas de las participaciones en los foros fueron acompañadas de archivos adjuntos en Word o PowerPoint con la intención de argumentar gráficamente dicha participación. Entendemos que es el escenario particular en el que se llevó a cabo esta experiencia el que permitió el uso de este tipo de herramientas, pero recalcamos lo observado anteriormente cuando nos referimos a que no sólo se obtuvieron las gráficas de las funciones con un software, sino que hubo manipulación de los objetos, sobre todo en la resolución de secuencias escolares no tradicionales. Las nuevas tecnologías no cumplen un papel de suplementación sino de reorganización, constituyen junto a los estudiantes, docentes y otros medios de diversa naturaleza (lápiz, papel, libros, calculadoras, computadoras) un colectivo pensante, un sistema constituido por seres humanos y dispositivos tecnológicos que generan, en conjunto, conocimientos matemáticos (Villareal, 2004).
La incorporación de este tipo de tecnología permitió también la resolución de las secuencias 4 y 5 en las que, como ya mencionamos, se buscaba favorecer la construcción de un universo gráfico en el terreno de las funciones algebraicas. La discusión llevada a cabo en los foros posteriores giró en torno al tipo de lenguaje que se utiliza en este tipo de secuencias al tratar de expresar que es lo que se ve, cómo este tipo de lenguaje puede ser utilizado para interpretar y construir significados, y cómo el Discurso Matemático Escolar se vería modificado si prioriza el lenguaje gráfico. Aquí los alumnos coinciden que si el Discurso Matemático Escolar priorizara el lenguaje gráfico esto ayudaría a la comprensión de conceptos fundamentales, sobre todo del Cálculo, pero que sería necesaria la incorporación de TICS pero no desempeñando un papel meramente utilitario sino como herramientas para construir significados.
5. CONCLUSIONES
En el marco de la socioepistemología, y asumiendo la modelación como una actividad, la intencionalidad de las secuencias planteadas no fue la reconstrucción y resignificación del concepto de función lineal, sino de la linealidad como propiedad de la relación funcional de dos variables. Encontramos que esta resignificación se hace evidente en la resolución de las secuencias escolares no tradicionales, que con la incorporación de herramientas tecnológicas, junto con las características del escenario en línea, permitieron priorizar el lenguaje gráfico y realizar cambios en el tipo de argumentos, estrategias y formas de explicitar los procedimientos.
La confrontación de los resultados empíricos de toda la secuencia con los elementos teóricos que enmarcan esta investigación nos proveyó de valiosos elementos para un probable rediseño de las secuencias. El análisis realizado en esta fase de validación nos hace pensar en el replanteo de algunas de las situaciones para que la noción de función se utilizada como una forma de representar el cambio, para hacer más explícito el tránsito por los cinco momentos identificados en el análisis epistemológico con base en Sierpinska (1992), y con elementos que permitan justificar la elección, o no, el modelo lineal.
El mayor cambio en la actividad matemática escolar de nuestros alumnos - docentes es lograr que reflexionaran sobre su propio conocimiento y sobre su práctica docente, pues es uno de los propósitos de su formación como matemáticos educativos.
Por la modalidad educativa, entendemos que hay momentos del proceso educativo que no están al alcance de nuestro análisis, por ello nos centramos en los registros de interacción de nuestro sistema didáctico: el profesor, el alumno-docente y el contenido. Esto es, la comunicación abierta entre alumnos y la facilidad de consultar recursos didácticos de diferente naturaleza tienen, indudablemente, un efecto sobre el proceso de enseñanza-aprendizaje, pero desconocerlos y no poder controlarlos es una variable didáctica esencial de estos escenarios.
Movilizó esta investigación la preocupación planteada al inicio de nuestro trabajo sobre las dificultades observadas al desarrollar los contenidos de matemática en nuestras clases y al analizar los resultados poco satisfactorios que observamos en el primer año de universidad. Los elementos teóricos obtenidos en la fase de validación de esta investigación son importantes para pensar en un rediseño de estas secuencias esta vez orientadas a alumnos de nivel medio o medio superior. En este rediseño deberemos tener en cuenta la formación diferente de los actores a los que se orienta la propuesta, ya que no se trataría de profesionales cursando un estudio de postgrado, sino de alumnos en formación de grado, quienes posiblemente han trabajado este tema en niveles anteriores, por eso seguiríamos hablando de resignificación de la propiedad de linealidad. Es posible que esto permita trabajar de manera diferente otras nociones como, por ejemplo, razón de cambio y tasa de variación, aporte elementos que favorezcan la noción de función como una forma de identificar los efectos de un cambio y no solamente como una asignación entre objetos, y promueva el uso de la visualización matemática como una estrategia para la formación adecuada de los conceptos.
Entendemos que las restricciones y variables de control identificadas para esta investigación cambiarían: tantos los actores, como la familiaridad con el uso de la tecnología educativa, el escenario (aunque seguiría siendo en línea) y el contexto serían diferentes.
Si una fase importante de la modelación en la educación es la experimentación (Borba y Villareal, 2005), en un escenario en línea las simulaciones juegan un papel importante para que esta fase sea vivida por el alumno. Reafirmamos lo expresado anteriormente en referencia a la utilización de software como el Programa SIRES, que proporcionan ambientes de simulación e interactividad para la actividad controlada de un alumno que aprende en la modalidad en línea. A pesar que su aplicación crea nuevas formas de interacción sin control por parte del profesor, consideramos que la posibilidad de llevar la modelación a este tipo de escenarios, la ventaja de poder manipular tanto el fenómeno como su reproducción, la continua disponibilidad de los experimentos, y la posibilidad de interactuar a distancia, (Martínez, Arrieta y Canul, 2005) son elementos suficientes para afirmar que este tipo de interfaces son herramientas útiles para la construcción de conocimiento y que las actividades que diseñen en base a uso y aplicación se constituyen en el centro del aprendizaje en línea.
Una de las primeras preguntas que nos planteamos antes de iniciar este trabajo de investigación era si aún en escenarios virtuales, con características propias tan diferentes a los escenarios de origen, era posible la construcción de conocimiento matemático. El desarrollo de esta investigación y los resultados a los que arribamos nos han dado muestra de que sí es posible.
Así como en el marco de la Socioepistemología identificamos el origen, naturaleza y problemáticas propias de cada tipo de función, también diferenciamos dos escenarios educativos de naturaleza tan distinta como son los escenarios tradicionales y a distancia, en este caso, virtuales. El entender estas diferencias y características propias hizo que nuestra investigación no buscara comparar resultados de una modalidad con otra, sino por el contrario, utilizarlas como restricciones y variables de control en la fase de diseño de secuencias pensadas para implementar en este tipo de modalidad.
Consideramos que nuestra investigación aporta elementos a la línea de investigación que surge dentro de la matemática educativa con el trabajo (Montiel, 2002). El haber podido mostrar las posibilidades que los escenarios en línea permiten en cuanto a la incorporación de nuevas tecnologías y el priorizar el lenguaje gráfico con el consiguiente cambio en el tipo de argumentos, estrategias y formas de explicitar los procedimientos dan cuenta de ello.
1Obstáculos identificados en la génesis histórica de un concepto; concepto introducido por Brosseau en 1983 a la Didáctica de las Matemáticas (citado en Ruiz Higueras, 1998)
2Tal es el caso de los Programas como Microsoft Word, Acrobat Reader y los Simuladores como SIRES
3En nuestro caso particular los programas Casio ClassPad Manager y Graphmatica,
REFERENCIAS
1. Albano, G. (2005a). Mathematics and e-learning: students' beliefs and waits. Proceed ings of the Commission Internationale pour l'Étude et l'Amélioration de l'Enseignement des Mathématiques, 153 - 157. Versión digital disponible al 21 de mayo de 2007 en http://math.unipa.it/~grim/cieaem/cieaem57_albano.pdf [ Links ]
2. Albano, G. (2005b). Mathematics and e-learning: a conceptual framework. Paper of the Fourth Congress of the European Society for Research in Mathematics Education. Versión digital disponible al 21 de mayo de 2007 en http://cerme4.crm.es/Papers%20definitius/9/albano.pdf [ Links ]
3. Álvarez, C., Álvarez, F., Arribas, A., Martínez, S., Ruiz, A. (1999) Matemática 1. Humanidades. Barcelona: España. Editorial Vincens Vives. [ Links ]
4. Arrieta, J. (2003) Las prácticas de modelación como proceso de matematización en el aula. Tesis doctoral no publicada, Departamento de Matemática Educativa, Cinvestav, México. [ Links ]
5. Artigue, (1995) Ingeniería didáctica. En P. Gómez (ed) Ingeniería didáctica en educación matemática. Un esquema para la investigación, la innovación en la enseñanza y el aprendizaje de las matemáticas (pp 33-59). México: Grupo Editorial Iberoamérica. [ Links ]
6. Azcárate, C., Deulofeu, J. (1996). Funciones y gráficas. Madrid. España: Editorial Síntesis. [ Links ]
7. Borba, M. y Villareal, M. (2005). Humans-with-Media and Reorganization of the Mathematical Thinking. USA: Springer. [ Links ]
8. Buendía, G. (2005) Prácticas Sociales y Argumentos: El Caso de lo Periódico. En Acta Latinoamericana de Matemática Educativa (Vol 18, pp. 451-456). México. [ Links ]
9. Cantoral, R., Farfán, R. (1998) Pensamiento y lenguaje variacional en la introducción al análisis. Épsilon, 42, 353-369. [ Links ]
10. Cantoral, R., Farfán, R., Cordero, F., Alanís, J., Rodríguez, R., Garza, A. (2000). Desarrollo del pensamiento matemático. México: Editorial Trillas. [ Links ]
11. Cantoral, R., Farfán, R. (2003) Matemática Educativa: una visión de su evolución. Revista Latinoamericana de Matemática Educativa, Vol. 6, Num. 1, (pp. 27-40). Thompson. [ Links ]
12. Cantoral, R., Molina, J., Sánchez, M. (2005) Socioepistemología de la Predicción. En Acta Latinoamericana de Matemática Educativa (Vol 18, pp. 463-468). México. [ Links ]
13. Cantoral, R. y Montiel, G. (2001) Funciones: visualización y pensamiento matemático. México: Prentice Hall. [ Links ]
14. Castañeda, A., Sánchez, M. y Molina, G. (2006). Estudio del pensamiento del profesor en un curso de formación docente a distancia. En Memorias del 22 Simposio Internacional de Computación en la Educación. SOMECE 2006. México Versión digital disponible al 14 de mayo de 2007 en http://www.mateducicata.ipn.mx/publicaciones/(Castaneda,2006a).pdf [ Links ]
15. Cordero, F. (2003) Lo social en el conocimiento matemático: reconstrucción de argumentos y significados. En Acta Latinoamericana de Matemática Educativa (Vol 16, Tomo I, pp. 73-78). México [ Links ]
16. Farfán, R. (1997) Ingeniería didáctica: un estudio de la variación y el cambio. México: Grupo Editorial Iberoamérica. [ Links ]
17. Farfán, R., Ferrari, M. (2001) Una visión socioepistemológica. Estudio de la función logaritmo en Antologías, Programa editorial Red de CIMATES, Número 1, pp 249-291. México. [ Links ]
18. Fiol, L., Fortuna, J., (1990) Proporcionalidad directa. La forma y el número. Madrid. España: Editorial Síntesis. [ Links ]
19. García, M., Escobar, G., Suhit, G., Vidal, M., De Lucca, M., Frank, C. y Bambill, E. (2005) Educación a distancia: una experiencia para el ingreso en la FRBB. En Acta Latinoamericana de Matemática Educativa (Vol 18, pp. 655-657). México [ Links ]
20. Grupo Beta (1997) Proporcionalidad geométrica y semejanza. Madrid. España: Editorial Síntesis. [ Links ]
21. Guzmán, M., Colera, J., Salvador, A. (1987) Matemáticas. Bachillerato 1 y 2. Madrid, España: Editorial Anaya. [ Links ]
22. Hopper, K. (2001). Is the Internet a classroom? TechTrends 45(5), 35-43. [ Links ]
23. Lezama, J. (1999). Un estudio de reproducibilidad: El caso de la función exponencial. Tesis de maestría, no publicada. DME, Cinvestav-IPN. México. [ Links ]
24. Lezama, J., Farfán, R. (2001) Introducción al estudio de la reproducibilidad. Revista Latinoamericana de Matemática Educativa, Vol. 4, Num. 2, (pp. 161 - 193). Thompson [ Links ]
25. Montiel, G. (2002) Una caracterización del Contrato Didáctico en un Escenario Virtual. Tesis de Maestría no publicada. Departamento de Matemática Educativa, Cinvestav - IPN, México. [ Links ]
26. Montiel, G. (2005) Estudio socioepistemológico de la Función Trigonométrica. Tesis de Doctorado no publicada. Centro de Investigación en Ciencia Aplicada y Tecnología Avanzada - IPN, México. [ Links ]
27. Ruiz Higueras, L. (1998) La noción de función: Análisis epistemológico y didáctico. Tesis de doctorado publicada. Universidad de Jaén, Colección Juan Pérez de Moya, Jaén, España. [ Links ]
28. Sánchez-Aguilar, M. (2003) Un estudio sobre interacciones y comunicación en educación matemática a distancia Tesis de Maestría no publicada. Departamento de Matemática Educativa, Cinvestav - IPN, México. [ Links ]
29. Sierpinska, A. (1989). On 15-17 years old students´ conceptions of functions, iteration of functions and attractive points. Warsaw, Poland: Institute of Mathematics, Polish Academy of Sciences, Preprint, 454. [ Links ]
30. Sierpinska, A. (1992). Understanding the notion of function. En G. Harel y E. Dubinsky (Eds), The concept of function. Aspects of Epistemology and Pedagogy (pp 25-58) USA: Mathematical Association of America. [ Links ]
31. Suhit, G. (1995) Proporcionalidad: un Contenido Matemático con amplia significatividad real. En Capacitación docente 1995. Desarrollo de los temas de los contenidos básicos comunes. Módulo 6. (pp 41-64).Buenos Aires, Argentina: Dirección General de Cultura y Educación de la Provincia de Buenos Aires. [ Links ]
32. Villareal, M. (2004) Transformaciones que las tecnologías de la información y la comunicación traen para la educación matemática. Yupana. Revista de Educación Matemática de la Universidad Nacional del Litoral. Num. 1, (pp. 41 - 55). Universidad Nacional del Litoral [ Links ]
33. Youschkevitch (1976), The concept of function up to the middle of the 19th century, (R. Farfán, trad) en Traducciones 2 (1996) CINVESTAV - IPN, México. [ Links ]














