Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista electrónica de investigación en educación en ciencias
versión On-line ISSN 1850-6666
Rev. electrón. investig. educ. cienc. vol.4 no.1 Tandil ene./jul. 2009
ARTÍCULOS ORIGINALES
Una construcción del significado del número complejo
Gustavo Martínez Sierra1 y Rocío Antonio Antonio2
gmartinezsierra@gmail.com, antonny_81@yahoo.com.mx
1Programa de Matemática Educativa. Centro de Investigación en Ciencia Aplicada y Tecnología Avanzada - Unidad Legaria. Calzada Legaria #694 Col. Irrigación Del. Miguel Hidalgo,C.P.11500, México, D.F.
2Profesora de instituciones educativas del estado de Guerrero, México.
Resumen
En el presente artículo se ofrecen resultados de una investigación sobre construcción de conocimiento. En particular estamos interesados en el estudio de los procesos presentes en la articulación de los sistemas conceptuales matemáticos a los que hemos llamado procesos deconvención y articulación matemática (Martínez-Sierra, 2005). De manera específica este trabajo indaga sobre qué alternativas pueden ser factibles para la construcción escolar del significado de los números complejos, bajo la hipótesis de que su significado puede ser construido a través del proceso de convención matemática. El análisis de la producción de los estudiantes, al trabajar una secuencia de actividades diseñada por nosotros en base a la hipótesis anterior, da evidencia de que a pesar que los estudiantes insistían en que "las raíces cuadradas de números negativos no existen", nuestra secuencia los indujo a operar con ellos y de esta manera construir un significado en el plano operativo.
Palabras clave: Construcción de conocimiento; Proceso de convención matemática; Epistemología del número complejo; Raíces de polinomios.
Abstract
This article presents the results of an investigation into the construction of knowledge. We are particularly interested in studying the processes involved in the articulation of conceptual mathematics systems which we have called processes of convention and mathematical articulation (Martínez-Sierra, 2005). More specifically, this work looks further into which alternatives may be feasible for the construction of the meaning of complex numbers in schools, under the hypothesis that meaning can be built through the process of mathematical convention. The analysis of the students' production, while working on a sequence of activities designed by us based on the above hypothesis, provides evidence that in spite of the students' insistence that "square roots of negative numbers do not exist," our sequence induced them to operate with them and in this way build a meaning on the operative plane.
Key words: Construction of knowledge; Mathematical convention process; Complex number epistemology; Roots of polynomials.
1. INTRODUCCIÓN
En trabajos previos (Martinez-Sierra, 2005) hemos desarrollado algunas nociones teóricas que han sido útiles, por un lado, en la explicación de algunos fenómenos didácticos y, por el otro, en la interpretación de procesos de construcción de conocimiento. En particular, en el plano de la construcción de conocimiento, hemos dado evidencia de que ciertas piezas de conocimiento, a las que hemos llamado convenciones matemáticas, pueden ser entendidas como producto de un proceso de articulación matemática o de un proceso de integración de conocimientos. En este mismo sentido, en el plano de la explicación de fenómenos didácticos, hemos dado evidencia de que algunas de las rupturas conceptuales presentes en la escuela tienen su origen en la desarticulación de cierta parte del corpus de la matemática escolar (Martínez- Sierra, 2005).
De manera específica este trabajo indaga sobre qué alternativas pueden ser factibles para la construcción escolar del significado de los números complejos, bajo la hipótesis de que su significado puede ser construido a través del proceso de convención matemática. Al respecto, a partir de un análisis histórico-epistemológico de la búsqueda de solución general de ecuaciones de tercer grado de la forma ![]() , afirmamos que el significado del número complejo, en un plano algebraico,puede ser interpretado como elemento unificador entre elgrado de la ecuación y sus soluciones.
, afirmamos que el significado del número complejo, en un plano algebraico,puede ser interpretado como elemento unificador entre elgrado de la ecuación y sus soluciones.
Para contrastar empíricamente la hipótesis anterior se procedió metodológicamente de la siguiente manera: 1) se diseñó una secuencia de actividades, en donde se traspuso (en sentido de Chevallard) tal hipótesis constructiva a polinomios de la forma ![]() , 2) se realizó una puesta en escena de la secuencia con 10 estudiantes del nivel medio superior mexicano (15 a 18 años) y 3) se analizó la producción de los estudiantes.
, 2) se realizó una puesta en escena de la secuencia con 10 estudiantes del nivel medio superior mexicano (15 a 18 años) y 3) se analizó la producción de los estudiantes.
2. MARCO TEÓRICO
2.1. Aproximación socioepistemológica en Matemática Educativa
La socioepistemología es una aproximación sistémica que permite tratar los fenómenos de producción y de difusión del conocimiento desde una perspectiva múltiple, al incorporar el estudio de las interacciones entre la epistemología del saber, su dimensión sociocultural, los procesos cognitivos asociados y los mecanismos de institucionalización a través de la enseñanza1 (Cantoral y Farfán, 2004). Más precisamente, dentro de la teoría socioepistemológica en Matemática Educativa se considera que al menos cuatro grandes dimensiones interdependientes son las que condicionan/determinan la construcción y la difusión del conocimiento matemático: las dimensiones cognitivas, didácticas, epistemológicas y sociales. Esta última condiciona/determina, a su vez, las tres primeras. La dimensión didáctica atiende aquellas circunstancias propias del funcionamiento de los diferentes sistemas didácticos y de enseñanza. La dimensióncognitiva se ocupa de las circunstancias que son relativas al funcionamiento y la actividad mental de las personas. La dimensión epistemológica se aboca a aquellas circunstancias que son propias de la naturaleza y significados del saber matemático. La dimensión social atiende a las circunstancias conformadas por las normativas y valoraciones sociales del saber y la manera en como éstas influyen en las demás dimensiones. En este sentido, las prácticas del artesano, del ingeniero, del médico, del profesional, o más ampliamente de una época o una cultura, son consideradas como constituyentes indisociables del saber escolar.
2.2. El proceso de convención matemática
Un proceso de convención matemática puede ser entendido como un proceso de búsqueda de consensos al seno de la comunidad que trabaja en dar unidad y coherencia a un conjunto de conocimientos. La producción de consensos es posible debido a que en esta comunidad existe la prácticade integración sistémica de los conocimientos; es decir existe una normativa de la actividad para relacionardiversos conocimientos y articularlos en un todo coherentee interrelacionado. Por su naturaleza esta práctica se encuentra en el plano de la teorización matemática, entendiendo por esto a la elaboración de conceptos interrelacionados que intentan describir, explicar un objeto de estudio, el cuál es, en este caso el sistema de conocimientos aceptados. Este proceso de síntesis conlleva al surgimiento de propiedades emergentes no previstas por los conocimientos anteriores. Las convenciones matemáticas serían una parte de las propiedades emergentes (Martínez-Sierra, 2003, 2005).
En el sentido anterior entonces, una convención matemática puede ser entendida como un consenso al seno de la comunidad que trabaja por dar unidad y coherencia a un conjunto de conocimientos. Un ejemplo en relación a los exponentes, extraídos de la historia de las ideas matemáticas, servirán para precisar nuestro planteamiento del "principio de conveniencia" en la que descansa nuestra caracterización de convención matemática (Martínez- Sierra, 2005).
Primer ejemplo. Hacia finales del Siglo XVI se sabía que las curvas ![]() (n = 1, 2, 3, 4,…), llamadas de índice n, tenían una propiedad que era llamada su "razón característica". Este conocimiento era parte general de la problemática fundamental de la época referente al cálculo de áreas determinadas por distintas curvas, tanto mecánicas como algebraicas (Bos, 1975), y a los significados que lasáreas guardan en contextos de variación2. Tomando como ejemplo la curva
(n = 1, 2, 3, 4,…), llamadas de índice n, tenían una propiedad que era llamada su "razón característica". Este conocimiento era parte general de la problemática fundamental de la época referente al cálculo de áreas determinadas por distintas curvas, tanto mecánicas como algebraicas (Bos, 1975), y a los significados que lasáreas guardan en contextos de variación2. Tomando como ejemplo la curva ![]() se decía que tiene razón característica igual a 1/3; ya que si tomamos un punto C arbitrario de la curva (Figura 1) el área de AECBA guarda una proporción de 1:3 con respecto al área del rectángulo ABCD o lo que el mismo que la proporción entre el área de AECBA y el área AECDA es de 1:2. En general se sabía de que la razón característica de la curva de índice n es 1/(n +1) para todos los enteros positivos n3.
se decía que tiene razón característica igual a 1/3; ya que si tomamos un punto C arbitrario de la curva (Figura 1) el área de AECBA guarda una proporción de 1:3 con respecto al área del rectángulo ABCD o lo que el mismo que la proporción entre el área de AECBA y el área AECDA es de 1:2. En general se sabía de que la razón característica de la curva de índice n es 1/(n +1) para todos los enteros positivos n3.

Figura 1. Razón Característica de la curva ![]()
En sus investigaciones acerca de la cuadratura de las curvas John Wallis (Struik, 1986) utilizó lo anterior para hacer el siguiente razonamiento, que en el fondo es una manera de convenir que el índice de ![]() debe ser igual a 1/2 con el objetivo de unificar la noción de razón característica con la noción de índice (aquí presentamos una paráfrasis del razonamiento):
debe ser igual a 1/2 con el objetivo de unificar la noción de razón característica con la noción de índice (aquí presentamos una paráfrasis del razonamiento):
‘Como la curva ![]() tiene una razón característica de 1/3, la curva
tiene una razón característica de 1/3, la curva ![]() también debe poseer una razón característica y debe ser igual a 2/3 (baste observar que las áreas debajo de ambas curvas se complementan para formar el rectángulo). Además, como la curva de índice 2 posee razón característica es de suponer que una curva que posea razón característica también posea un índice, entonces ¿Qué índice debe tener la curva
también debe poseer una razón característica y debe ser igual a 2/3 (baste observar que las áreas debajo de ambas curvas se complementan para formar el rectángulo). Además, como la curva de índice 2 posee razón característica es de suponer que una curva que posea razón característica también posea un índice, entonces ¿Qué índice debe tener la curva ![]() ? Como 2/3=1/(1+1/2) el índice debe ser 1/2'
? Como 2/3=1/(1+1/2) el índice debe ser 1/2'
3. UNA EPISTEMOLOGÍA DE LOSNÚMEROS COMPLEJOS A TRAVÉS DELPROCESO DE CONVENCIÓNMATEMÁTICA
A lo largo de la historia se pueden identificar cuatro grandes etapas, caracterizadas por los cambios observados en las concepciones epistemológicas de los números complejos (Gómez y Pardo, 2005; Rosseel y Schneider, 2003, 2004): 1) Algebraica. Primeras apariciones de las raíces cuadradas de cantidades negativas, 2) Analítica. Aceptación y generalización del uso de las expresiones imaginarias gracias al desarrollo del análisis infinitesimal, 3) Geométrica. Introducción de un eje de imaginarios que tiene asociado ![]() como unidad perpendicular a 1, y 4) Formal. Formalización de los números complejos. Nuestro análisis histórico epistemológico se ubica en el contexto de la etapa algebraica.
como unidad perpendicular a 1, y 4) Formal. Formalización de los números complejos. Nuestro análisis histórico epistemológico se ubica en el contexto de la etapa algebraica.
En 1545 Cardano publicó (Stillwell, 1989) en su Ars Magna el método de solución de Tartaglia. Esta solución se conoce como el método de Cardano, la cual para el caso ![]() toma la forma:
toma la forma:

En términos modernos la fórmula implica a los números complejos cuando ![]() . Sin embargo, no era posible considerar esto como un caso sin solución, porque se sabía en ese entonces que una ecuación cúbica siempre tiene al menos una raíz real. Así, la fórmula de Cardano plantea el problema de convenir un valor numérico , encontrado por la inspección, digamos, con una expresión de la forma4:
. Sin embargo, no era posible considerar esto como un caso sin solución, porque se sabía en ese entonces que una ecuación cúbica siempre tiene al menos una raíz real. Así, la fórmula de Cardano plantea el problema de convenir un valor numérico , encontrado por la inspección, digamos, con una expresión de la forma4: ![]() (siendo N un número natural).
(siendo N un número natural).
Cardano no hizo frente a este problema (la simplificación de ![]() , llamado el caso irreducible) en su Ars Magna, consideró que estos números eran "tan sutiles como inútiles"; fue incapaz de hacer algo con el llamado "caso irreducible" de la ecuación cúbica, en el cual hay tres soluciones reales que aparecen como la suma o diferencia de lo que ahora llamamos números complejos.
, llamado el caso irreducible) en su Ars Magna, consideró que estos números eran "tan sutiles como inútiles"; fue incapaz de hacer algo con el llamado "caso irreducible" de la ecuación cúbica, en el cual hay tres soluciones reales que aparecen como la suma o diferencia de lo que ahora llamamos números complejos.
Esta dificultad fue resuelta en el siglo XVI por Rafael Bombelli, cuya Algebra apareció en 1572 (Struik, 1986, pp.121-124). De estamanera Bombelli calculó el álgebra formal de los números complejos (llegando a formular las cuatro operaciones con los números complejos en la forma actual) con el objetivo particular de reducir expresiones ![]() a la forma
a la forma ![]() , así su método le permitió mostrar la "realidad" de algunas expresiones que son resultado de la fórmula de Cardano. Por ejemplo, la solución, dada por la fórmula de Cardano y con la propiedad de la multiplicación con radicación de números negativos, de
, así su método le permitió mostrar la "realidad" de algunas expresiones que son resultado de la fórmula de Cardano. Por ejemplo, la solución, dada por la fórmula de Cardano y con la propiedad de la multiplicación con radicación de números negativos, de ![]() es:
es:
 (I)
(I)
Por otra parte, la inspección da la solución y = 4, Bombelli desarrolló la idea de que las dos partes de "y" en la fórmula de Cardano eran de la forma ![]() ,
, ![]() y él encontró por cubos estas expresiones formalmente, usando
y él encontró por cubos estas expresiones formalmente, usando ![]() :
:
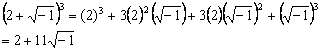
Esto ciertamente sería:
![]()
![]() (II)
(II)
![]()
![]() (III)
(III)
Sustituyendo (II) y (III) en (I) se obtiene:
![]()
por lo tanto ![]()
En conclusión, nuestra hipótesis de construcción de conocimiento se basa en la consideración de que la primera formulación (Bombelli-Cardano citados en Stillwell; 1989, Struik; 1986 y Dunham, 1999) en relación a los números de la forma A + B − N (Siendo N un número natural) fueron aceptados en un dominio algebraico; porque ellos aparecieron como útiles en la solución de ecuaciones de tercer grado ![]() (y no en las ecuaciones de segundo grado como se presentan en los libros de texto modernos). Nuestra interpretación es que se aceptó la existencia de la raíz cuadrada de números negativos, junto a su operatividad, para articular una fórmula algebraica:
(y no en las ecuaciones de segundo grado como se presentan en los libros de texto modernos). Nuestra interpretación es que se aceptó la existencia de la raíz cuadrada de números negativos, junto a su operatividad, para articular una fórmula algebraica:  , con el hecho de que una ecuación cúbica siempre tiene al menos una raíz real. Es decir, la existencia del número complejo puede admitirse como elemento unificador entre el grado de la ecuación y sus soluciones. A tal proceso lo caracterizamos con lo que hemos llamado convención matemática.
, con el hecho de que una ecuación cúbica siempre tiene al menos una raíz real. Es decir, la existencia del número complejo puede admitirse como elemento unificador entre el grado de la ecuación y sus soluciones. A tal proceso lo caracterizamos con lo que hemos llamado convención matemática.
4. DISEÑO, PUESTA EN ESCENA Y ANÁLISIS DE UNA SECUENCIA DE ACTIVIDADES
Para la construcción de la secuencia de actividades a la hipótesis constructiva anterior la hemos transpuesto5 a polinomios de la forma ![]() . En particular, el objetivo de la secuencia es propiciar la aceptación de losnúmeros complejos y la operatividad de la raíz cuadradade números negativos en estudiantes de nivel medio superior, dentro de un contexto de cálculo de raíces de polinomios, de manera específica con polinomios de la forma
. En particular, el objetivo de la secuencia es propiciar la aceptación de losnúmeros complejos y la operatividad de la raíz cuadradade números negativos en estudiantes de nivel medio superior, dentro de un contexto de cálculo de raíces de polinomios, de manera específica con polinomios de la forma ![]() . Consideramos que mediante este contexto es posible construir el significado de número complejo y su operatividad (en el proceso algorítmicoalgebraico del cálculo de las ‘n-raíces' de una ecuación) como convención matemática, es decir, como elemento unificador entre el grado de la ecuación y sus soluciones. Creemos que la aceptación puede apoyarse en la idea de que tales polinomios tienen ‘n-raíces diferentes'; idea que a su vez puede ser apoyada con la aceptación de la operatividad de las raíces cuadradas de números negativos.
. Consideramos que mediante este contexto es posible construir el significado de número complejo y su operatividad (en el proceso algorítmicoalgebraico del cálculo de las ‘n-raíces' de una ecuación) como convención matemática, es decir, como elemento unificador entre el grado de la ecuación y sus soluciones. Creemos que la aceptación puede apoyarse en la idea de que tales polinomios tienen ‘n-raíces diferentes'; idea que a su vez puede ser apoyada con la aceptación de la operatividad de las raíces cuadradas de números negativos.
El diseño de nuestra secuencia consta de trece actividades, las cuales están agrupadas en cuatro fases: I. Recordar el cálculo de raíces de una ecuación (únicamente con raíces reales), II. Identificar el conocimiento previo que tiene el estudiante sobre la raíz cuadrada de un número negativo, III. Aceptar y operar con raíces cuadradas de números negativos en el cálculo de raíces; polinomios de la forma ![]() y IV. Presentar ib como la denotación formal de una raíz cuadrada de un número negativo y su propiedad (Para mayores detalles de la secuencia se puede consultar el Anexo del presente escrito).
y IV. Presentar ib como la denotación formal de una raíz cuadrada de un número negativo y su propiedad (Para mayores detalles de la secuencia se puede consultar el Anexo del presente escrito).
4.1 La puesta en escena
La exploración de la secuencia fue realizada en el plantel de nivel medio superior en la ciudad de Chilpancingo, (Capital del estado mexicano de Guerrero), donde se trabajó con diez estudiantes (6 alumnas y 4 alumnos) de primer grado por tres horas y media. Con los estudiantes se formaron tres equipos de trabajo: dos de ellos contaron con tres estudiantes (equipo 1 y 3) y uno de cuatro integrantes (equipo 2). Aquí únicamente se reportan los resultados del equipo 1 y 2. El tiempo abarcado, estuvo determinado por el rendimiento de la participación de los estudiantes en la secuencia, la cual les permitió llegar hasta la actividad diez de la tercera fase.
En la producción de los estudiantes observamos que los objetivos propuestos para las dos primeras fases: Recordar el cálculo de raíces "reales" y el de identificar el conocimiento previo de la raíz cuadrada de un número negativo, sí se alcanzaron. Algunas de las actividades de estas fases son:
I) Recordar el cálculo de raíces "reales"
1.Utilice la fórmula general de segundo grado para encontrar las dos raíces de la ecuación ![]() verifica que efectivamente son raíces de esa ecuación.
verifica que efectivamente son raíces de esa ecuación.
4. Encuentre las tres raíces de la ecuación ![]() verifica que efectivamente son raíces de esa ecuación.
verifica que efectivamente son raíces de esa ecuación.
6. Verifique que los números x =1, x = −2 , x = 3 y x = −1 son raíces de la ecuación ![]()
II) Identificar el conocimiento previo de la raízcuadrada de un número negativo
8. Utilice la fórmula general de segundo grado para encontrar las dos raíces de la ecuación ![]() verifica que efectivamente son raíces de esa ecuación.
verifica que efectivamente son raíces de esa ecuación.
El objetivo de la tercera fase (actividades 9,..,12), el de aceptar y operar con las raíces cuadradas de números negativos no se alcanzó de manera general por dos motivos: la primera por motivos de tiempo, los equipos no llegaron abarcar todas las actividades que contempla esta fase, sólo hasta la actividad 9 y 10. Y segunda, en las actividades abarcadas no todos los integrantes de los equipos realizaron las operaciones solicitadas (la comprobación de las raíces encontradas). Las actividades de esta tercera fase son:
III) Aceptar y operar con las raíces cuadradas denúmeros negativos en el cálculo de raíces.
9. Utiliza la factorización de una diferencia de cubos y la fórmula general de segundo grado para encontrar las tres raíces de la ecuación![]() . Además verifica que efectivamente son raíces de esa ecuación.
. Además verifica que efectivamente son raíces de esa ecuación.
10. Utiliza la factorización de una diferencia de cuadrados y la fórmula general de segundo para encontrar las cuatro raíces de la ecuación ![]() . Además verifica que efectivamente son raíces de esa ecuación.
. Además verifica que efectivamente son raíces de esa ecuación.
4.2 La producción de los estudiantes
Fase I.Recordar el cálculo de raíces de una ecuación (únicamente raíces reales).
En la primera fase (Actividades 1,2,. y 6). Se desea que el estudiante recuerde el cálculo de raíces de una ecuación (que de acuerdo al grado mayor de la ecuación son las cantidades de raíces a encontrar). En la tabla siguiente mostramos la producción de algunos estudiantes.

Se cuestionó a los equipos para conocer con más detalle el porqué de su respuesta, acerca en qué fijarnos para conocer la cantidad de soluciones que tiene una ecuación (Respuestas del equipo 2. "en el término ya sea cuadráticoo cúbico", "de que grado es y el número del exponente"). En el siguiente dialogo presentamos un extracto de ello. La letra "P" se representa como la participación del profesor:
P: ¿Todas me hablan sobre el exponente? Pero ¿qué exponente debe ser?
D: De dos en adelante, dos, tres (la interrumpe G).
G: No, de uno en adelante
P: Entonces, ¿de dos en adelante? si yo tengo esto (escribe una ecuación cuarta y les pregunta 7 6 0 4 3 2 x − x − x + x + = ) ¿en cuál me debo de fijar?
D: ¿En el primero?
P: En ese exponente, pero ese exponente ¿cómo es a los demás?
E: Es mayor (tratan de agregarlo a sus respuestas)
P: Entonces si tenemos una ecuación cúbica ¿Cuántas soluciones vamos a encontrar?
E: Tres
P: ¿Una cuarta?
E: Cuatro
Fase II. Identificar el conocimiento previo que tiene elestudiante sobre la raíz cuadrada de un númeronegativo.
La segunda fase (Actividades 7 y 8) tiene como objetivo identificar el conocimiento previo (como denota a la raíz cuadrada de un número negativo y la familiaridad que tiene con ella) de los estudiantes, al calcular las raíces de la ecuación cuadrática ![]() a través de la petición explícita del uso de la fórmula general de segundo grado. El resultado general encontrado es que el conocimiento previo identificado en los dos equipos es que "las raícescuadradas de números negativos no existen". En la tabla siguiente mostramos la descripción e interpretación de la producción de los estudiantes.
a través de la petición explícita del uso de la fórmula general de segundo grado. El resultado general encontrado es que el conocimiento previo identificado en los dos equipos es que "las raícescuadradas de números negativos no existen". En la tabla siguiente mostramos la descripción e interpretación de la producción de los estudiantes.


Fase III. Aceptar y operar con raíces cuadradas denúmeros negativos en el cálculo de raíces, depolinomios de la forma ![]()
En esta tercera fase (Actividades. 9, 10, 11 y 12) se esperaba que el estudiante operara y aceptara a las raíces cuadradas de números negativos como soluciones de estas ecuaciones. Para motivar a esto se les pidió que verificaran si satisfacían a la ecuación las raíces encontradas. Aquí se utilizaron las herramientas del desarrollo de un binomio, factorización y la fórmula general de segundo grado. El objetivo de estas actividades es que al realizar las factorizaciones de los polinomios en las actividades 10, 11 y 12 los estudiantes podrían darse cuenta que ya se tienen algunas de sus raíces, las cuales encontraron en las actividades anteriores y esto los llevaría sólo a verificar si eran raíces de la ecuación propuesta. En las tablas siguientes mostramos la descripción e interpretación de la producción de los estudiantes en los dos equipos aquí reportados.


Equipo 1 - Actividad 10

Equipo 2 - Actividad 9
En este equipo no hubo argumentos concretos al término de estas actividades (9 y 10), en por qué son raíces los valores encontrados de las ecuaciones propuestas, lo único que nos dijeron fue lo que observaron al calcularlas: sondifíciles de hacer, siguen un procedimiento largo y quealgunas son más difíciles que otras de menor potencia

Equipo 2 - Actividad 10

5. CONCLUSIÓN
La investigación aquí presentada indaga sobre qué alternativas pueden ser factibles para la construcción escolar del significado de los números complejos, bajo la hipótesis de que su significado puede ser construido a través del proceso de convención matemática. Al respecto, a partir de un análisis histórico-epistemológico de la búsqueda de solución general de ecuaciones de tercer grado de la forma ![]() , se afirmó que elsignificado del número complejo, en un plano algebraico,puede ser interpretado como elemento unificador entre elgrado de la ecuación y sus soluciones.
, se afirmó que elsignificado del número complejo, en un plano algebraico,puede ser interpretado como elemento unificador entre elgrado de la ecuación y sus soluciones.
Para contrastar empíricamente la hipótesis anterior se procedió metodológicamente de la siguiente manera: 1) se diseñó una secuencia de actividades, en donde se traspuso (en sentido de Chevallard) tal hipótesis constructiva a polinomios de la forma ![]() , 2) se experimentó la secuencia con 10 estudiantes del nivel medio superior mexicano (15 a 18 años) y 3) se analizó la producción de los estudiantes.
, 2) se experimentó la secuencia con 10 estudiantes del nivel medio superior mexicano (15 a 18 años) y 3) se analizó la producción de los estudiantes.
En la producción de la puesta en escena se evidencia de que a pesar que los estudiantes insistían en que "las raícescuadradas de números negativos no existen", nuestra secuencia los indujo a operar con ellos, para encontrar y comprobar las raíces de algunos polinomios propuestos en las actividades 8, 9 y 10. y de esta manera propiciándolos a la aceptación de estos números. Para comprobar las raíces encontradas en los polinomios propuestos se les tuvo que apoyar en algunos equipos en los siguientes procedimientos operacionales que presentaban:
-
En el cálculo de potencias donde multiplicaban la base por el exponente, ejemplo:
 .
. -
En la potencia de un número fraccionario, donde sólo aplicaban el exponente al numerador:
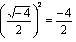
-
En el cálculo de potencias impares de raíces cuadradas de números negativos. Ejemplo en
 , ya que para ellos era más familiar la obtención de potencias cuadradas, eliminando directamente el radical con el exponente.
, ya que para ellos era más familiar la obtención de potencias cuadradas, eliminando directamente el radical con el exponente. -
, En el significado de la denotación ± en la fórmula general para describir las "dos" soluciones que representa: Ejemplo:
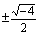 y
y 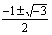
El argumento básico por parte de los estudiantes para aceptar la operatividad de los números complejos como raíces de los polinomios propuestos en las actividades 8, 9 y 10, es que "se pueden igualar", es decir, que al sustituir estos valores encontrados en la ecuación, su resultado es cero, ejemplo en el cálculo de las raíces de ![]() se obtiene en el equipo 1:
se obtiene en el equipo 1:![]() y para el equipo 2:
y para el equipo 2: ![]() . Mencionamos lo anterior considerando que no comprobaron todos los valores obtenidos en las ecuaciones solamente algunos de ellos como por ejemplo:
. Mencionamos lo anterior considerando que no comprobaron todos los valores obtenidos en las ecuaciones solamente algunos de ellos como por ejemplo:
-
En la actividad 9 (el cálculo de las raíces de
 ), donde sólo comprobaron en los dos equipos un valor
), donde sólo comprobaron en los dos equipos un valor 
-
En la actividad 10 (el cálculo de las raíces de
 ) sólo se comprobaron dos de las soluciones en cada equipo. Para el equipo 1, comprobaron
) sólo se comprobaron dos de las soluciones en cada equipo. Para el equipo 1, comprobaron 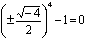 , utilizando el siguiente razonamiento: si
, utilizando el siguiente razonamiento: si  (donde eliminan directamente la raíz cuadrada con el "exponente cuatro" y elevan al denominador al cuadrado) se obtiene que,
(donde eliminan directamente la raíz cuadrada con el "exponente cuatro" y elevan al denominador al cuadrado) se obtiene que,  . Para el equipo 2 sólo trabajaron con los valores encontrados:
. Para el equipo 2 sólo trabajaron con los valores encontrados: 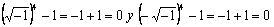 :
:
Es así, como consideramos que los resultados de nuestra secuencia de actividades da indicios de que es posible construir el significado del número complejo y su operatividad en tanto el proceso de convención matemática bajo el cálculo de raíces de la forma ![]() . Lo anterior considerando una metodología más adecuada con respecto al tiempo y un rediseño de actividades:
. Lo anterior considerando una metodología más adecuada con respecto al tiempo y un rediseño de actividades:
-
En la primera fase: el recordatorio en cálculo de raíces reales (aplicación de la fórmula general para segundo grado y factorizaciones) y
-
Para la segunda fase: Identificar el conocimiento previo de la raíz cuadrada de un número negativo (en particular se considera que sería más factible solicitar el cálculo de las raíces de la actividad 7.
 no darle directamente las raíces para comprobar )
no darle directamente las raíces para comprobar )
ANEXO: La secuencia de actividades
1. Utilice la fórmula general de segundo grado para encontrar las dos raíces de la ecuación ![]() y verifica que efectivamente son raíces de esa ecuación.
y verifica que efectivamente son raíces de esa ecuación.
2. Encuentre las raíces de la ecuación ![]() y verifica que efectivamente son raíces de esa ecuación.
y verifica que efectivamente son raíces de esa ecuación.
3. Construye una ecuación que tenga por raíces a los números 4 y 5.
4. Encuentra las tres raíces de la ecuación ![]() y verifica que efectivamente son raíces de esa ecuación.
y verifica que efectivamente son raíces de esa ecuación.
5. Construye una ecuación que tenga por raíces a los números 1, 2, y 3.
6. Verifica que los números x = 1, x = −2 , x = 3 y x = −1 son raíces de la ecuación ![]()
a) ¿En qué debemos fijarnos, para identificarcuántas raíces tiene una ecuación?
7. Verifica que la ecuación ![]() tiene dos raíces, x =1 y x = −1.
tiene dos raíces, x =1 y x = −1.
8. Utiliza la fórmula general de segundo grado para encontrar las dos raíces de la ecuación ![]() y verifica que efectivamente son raíces de esa ecuación.
y verifica que efectivamente son raíces de esa ecuación.
9. Utiliza la factorización de una diferencia de cubos y la fórmula general de segundo grado para encontrar las tres raíces de la ecuación ![]() . Además verifica que efectivamente son raíces de esa ecuación.
. Además verifica que efectivamente son raíces de esa ecuación.
10. Utiliza la factorización de una diferencia de cuadrados y la fórmula general de segundo para encontrar las cuatro raíces de la ecuación ![]() . Además verifica que efectivamente son raíces de esa ecuación.
. Además verifica que efectivamente son raíces de esa ecuación.
11. Utiliza la factorización de una diferencia de cuadrados y la fórmula general de segundo grado para encontrar las seis raíces de la ecuación ![]() . Además verifica que efectivamente son raíces de esa ecuación.
. Además verifica que efectivamente son raíces de esa ecuación.
12. Utiliza la factorización de una diferencia de cuadrados y la fórmula general de segundo grado para encontrar las ocho raíces de la ecuación ![]() . Además verifica que efectivamente son raíces de esa ecuación.
. Además verifica que efectivamente son raíces de esa ecuación.
a) ¿Que observaste al calcular las raíces?
b) ¿Cómo son las raíces que has encontrado?
Definición: Un número imaginario es un número cuyo cuadrado es negativo. Cada número imaginario puede ser escrito como ib donde b es un número real e i es la unidad imaginaria con la propiedad:![]() .
.
13. Escriba las raíces de la actividad 11 y 12 con la nueva notación i y realiza otra vez los cálculos solicitados.
1"La socioépistémologie procède d'une approche systémique qui permet d'aborder les phénomènes de production et diffusion de la connaissance dans une perspective multiple, qui intègre l'étude des interactions entre l'épistémologie du savoir, sa dimension socioculturelle, les procédés cognitifs asocies et les mécanismes de l'institutionnalisation via l'enseignement" (Cantoral y Farfán 2004, p. 139).
2Por ejemplo es bien conocida la forma en que Galileo estableció su ley de caída de los cuerpos a través de entender el área determinada por una gráfica velocidad-tiempo como la distancia recorrida por el cuerpo.
3En términos modernos la noción de razón característica se apoya en que (a > 0) 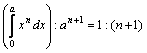
4Se considera que para llegar a esta generalización desde la fórmula de Cardano fue necesario plantearse la propiedad de la multiplicación con radicación, para el caso en que la propiedad no es valida dentro del conjunto de los números reales: ![]() y
y ![]()
5Utilizamos este término en el sentido de la Trasposición didáctica de Chevallard (1991).
6. REFERENCIAS
1. Antonio, R. (2008). Una construcción del significado del número complejo y su operatividad a través del proceso de convención matemática. Tesis de maestría. Universidad Autónoma de Guerrero-Maestría en Matemática Educativa de la Facultad de Matemáticas. [ Links ]
2. Bagni, G. (2001). La introducción de la historia de las matemáticas en la enseñanza de los números complejos. Una investigación experimental en la educación media superior'. Revista Latinoamericana de Matemática Educativa 4(1), 45-62. [ Links ]
3. Cantoral, R. & Farfán, R. M. (2004) La sensibilité à la contradiction: logarithmes de nombres négatifs et origine de la variable complexe. Recherches en Didactique des Mathématiques 24(2.3), 137 - 168. [ Links ]
4. Chevallard Y., (1991). La transposition didactique. Du savoir savant au savoir enseigné. France: La pensée sauvage. [ Links ]
5. Dunham, W. (1999). Euler. The master of us all. The Dolciani mathematical expositions, N.22, EEUU: The Mathematical Association of America. [ Links ]
6. Goméz, A. y Pardo, T. (2005). La enseñanza y el aprendizaje de los números complejos. Un estudio en el nivel universitario. Actas del Noveno Simposio de la Sociedad Española de Educación Matemática SEIEM, pp.251-260. [ Links ]
7. Martínez-Sierra, G. (2005). Los procesos de convención matemática como generadores de conocimiento. Revista Latinoamericana de Investigación en Matemática Educativa 8 (2), 195-218. [ Links ]
8. Martínez-Sierra, G. (2003). Caracterización de la convención matemática como mecanismo deconstrucción de conocimiento. El caso de su funcionamiento en los exponentes. Tesis doctoral CICATA. [ Links ]
9. Rosseel H. ; Schneider M. (2003). Ces nombres que l'on dit "imaginaires". Petit X 63, 53-72. [ Links ]
10. Rosseel H. y Schneider M. (2004). Des nombres qui modélisent des transformations. Petit X 66, 7-34. [ Links ]
11. Tillwell, J. (1989). Mathematics and its history. New York: Springer-Verlag. [ Links ]
12. Struik, D. J. (1986). A source book in mathematics 1200-1800. EEUU: Princeton University Press. [ Links ]














