Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista electrónica de investigación en educación en ciencias
versión On-line ISSN 1850-6666
Rev. electrón. investig. educ. cienc. vol.5 no.2 Tandil ago./dic. 2010
ARTÍCULOS ORIGINALES
Los registros de representaciones que emplean docentes de Educación Primaria: un estudio exploratorio
Varettoni, Marcos1; Elichiribehety, Inés2
varrebox@yahoo.com.ar , ielichi@exa.unicen.edu.ar
1 ETR de Capacitación de Matemática. Centro de Investigaciones Educativas (CIE) de la DGCyE, Provincia de Buenos Aires, Argentina.
2 NYECYT, Universidad Nacional del Centro de la Provincia de Bs. As. Paraje Arroyo Seco s/n, Tandil, Argentina.
Resumen
En este trabajo se adopta una perspectiva didáctica para analizar resultados acerca de las representaciones externas y marcos de resolución que utilizan docentes de la Educación Primaria cuando resuelven algunos problemas que podrían ser propuestos en sus clases. Se busca indagar los procedimientos que realizan, las anticipaciones que proponen y el sentido de los conceptos matemáticos que serán construidos. Los resultados muestran que la mayoría de los docentes utilizan los registros de representación simbólicos-aritméticos para resolver y que en muy pocos casos pueden conjugar más de un sistema de representación y utilizar más de un marco.
Les registres des représentations utilisés par les maîtres d'Education primaire: une étude exploratoire
Résumé
Dans ce travail on adopte une approche didactique pour analyser des résultats liés aux représentations externes et aux cadres de résolution qui utilisent les maîtres de l'école primaire quand ils résolvent problèmes, lesquelles pourraient être proposés dans leur clases. On veut relever les procédures et les anticipations qu'ils fassent et le sens donnés aux connaissances mathématiques qui seront construits. Les résultats montrent que la majorité des maîtres utilisent les registres de représentation symbolique-arithmétique pour résoudre les problèmes et seulement dans quelques cas ils peuvent joindre plus d'un système de représentation et utiliser plus d'un cadre.
Mots clés : Registres de représentation; Résolution de problèmes; Maîtres d'école; Education Primaire.
Representation Logs used by Primary School Teachers: an exploratory study.
Abstract
In this paper it is adopted a didactic perspective to analyze the results on the external representations and resolution frameworks used by Primary Education teachers when solving some problems that could be dealt with in their classes. The study tries to investigate the procedures performed, the anticipations proposed and the meaning of the mathematical concepts to be constructed. The results show that most teachers use symbolic-arithmetic representation logs to solve and that in very few cases they can combine more than one system of representation and use more than one framework.
Keywords: Representation logs; Problem solving; Teachers; Primary Education.
1. INTRODUCCIÓN
Este trabajo presenta un estudio desde una perspectiva didáctica acerca de las representaciones y marcos de resolución que utilizan docentes de la Educación Primaria (EP) cuando resuelven y analizan algunos problemas que podrían ser propuestos en sus clases. Con el objeto de indagar los procedimientos que realizan, las anticipaciones que proponen y el sentido de los conceptos matemáticos que serán construidos. En esta instancia, se presentan resultados parciales referidos a la resolución de un problema en una población de N=17 docentes, correspondientes a los cursos de Capacitación de la Dirección General de Cultura y Educación de la Provincia de Buenos Aires, realizados durante el año 2008 en la Región 18.
El problema surge a partir de las dificultades que manifiestan los docentes en las instancias de capacitación. Ellos señalan que en la gestión de sus clases tienen inconvenientes con los diferentes procedimientos y formulaciones que realizan sus alumnos; la manera de relacionar los conceptos matemáticos con las representaciones y la forma de identificar esta información. Estas cuestiones, entre otras, refieren a la compleja relación entre los conceptos matemáticos y sus formas de representación.
Para la elaboración del presente trabajo se asumen aportes de la Escuela Francesa en Didáctica de la Matemática, principalmente de la Teoría de las Situaciones Didácticas de Brousseau (1986, 2007), la Dialéctica Instrumento - Objeto y Juego de Marcos de Douady (1986) y La Teoría de los Registros de Representación Semiótica de Duval (1993, 1996, 2006); contribuciones de investigaciones sobre procedimientos de resolución y registros de representación (Castro, Castro, 1997; Hugues, 1987; Peltier, 2003; Vergnaud, 1990, 1991, 2007; entre otros) y aportes de estudios y trabajos realizados en nuestro país sobre la enseñanza de la matemática y la construcción del sentido de los conocimientos (Parra, 1994; Panizza, 2003; Sadovsky, 2005; entre otros).
Según Panizza (2003), la relación entre objetos de conocimiento y representaciones, articulados con el de adquisición del sentido, es fundamental para la enseñanza de la matemática. Además, son aspectos importantes para una didáctica que tenga en cuenta la especificidad del nivel en el que se desarrolla la enseñanza y el tiempo que lleva el logro de aprendizajes, porque no es inmediato.
Este trabajo se ocupa de lo que Martí y Pozo (2000), citado por Brizuela, denominan sistemas externos de representación. Estas representaciones externas son los sistemas de representación compartidos y desarrollados a través de los procesos humanos sociales, es decir, cada vez que se haga referencia al término representaciones o registros de representación se estará refiriendo a aquellas que son realizadas con lápiz y papel y que tienen una existencia física.
El Diseño Curricular de la Educación Primaria (Pcia. de Buenos Aires, 2008) alienta el surgimiento de diferentes formas de representar los conocimientos matemáticos como un modo de "hacer matemática en el aula". Este aspecto prescripto en el diseño curricular no convivirá en las aulas de un día para el otro, depende -entre otros condicionantes -de proyectos de enseñanza elaborados a largo plazo, de las decisiones didácticas que se tomen, de las concepciones que tienen los docentes sobre la enseñanza de la matemática, de su conocimiento sobre la relación entre conceptos matemáticos y representaciones y de la gestión de la clase.
Para que coexistan diversas estrategias de resolución de un concepto matemático, se requiere que la intervención del docente se inicie antes que la propuesta sea llevada al aula. Es la instancia de anticipación la que permitirá al docente estudiar las diversas estrategias de resolución que pueden surgir en los problemas, las diferentes representaciones que pueden utilizar los alumnos, los acuerdos a los que se pretende arribar, entre otros aspectos que de no ser previstos, seguramente estarán lejos de la construcción del sentido de los conocimientos por parte de los alumnos.
Desde la didáctica, se propicia el juego de marcos (Douady, 1984) en la búsqueda de soluciones para un problema, los diferentes marcos y sus sistemas de representación asociados, serían disparadores de la construcción de los conocimientos matemáticos. Es importante que el docente contemple este aspecto, también constitutivo del sentido de un conocimiento.
Se asume que el trabajo áulico con diferentes representaciones y con diferentes marcos de resolución es parte constitutiva de la producción, la enseñanza y el aprendizaje de la matemática con sentido, el mismo debe considerarse desde proyectos planificados a largo plazo, es decir, el trabajo y el reconocimiento de diferentes representaciones de conceptos matemáticos y la posibilidad de interactuar con diferentes marcos debe vivir en el aula desde los primeros años de la escolaridad.
El empleo sistemático de la noción de representación en Educación Matemática data de la década del 80. En estos trabajos, el concepto de representación es asociado a una señal externa que muestra y hace presente un concepto matemático, también como signo o marca con el que los sujetos piensan la matemática. Entre varias alternativas conceptuales similares pero no equivalentes: símbolos (Skemp, 1980), sistema matemático de signos (Kieran y Filloy, 1989), sistemas de notación (Kaput, 1992), sistema de registros semióticos (Duval, 1993), la comunidad de matemáticos dio prioridad al uso del término representaciones (Rico, 2009).
Las representaciones matemáticas desde entonces se entienden, en sentido amplio, como todas aquellas herramientas -signos o gráficos- que hacen presentes los conceptos y procedimientos matemáticos y con los cuales los sujetos particulares abordan e interactúan con el conocimiento matemático, es decir, registran y comunican su conocimiento sobre las matemáticas (Radford, 1998; Martí y Pozo, 2000; Rico, Castro, Romero, 2000). Se sabe que, para quién se está apropiando de las mismas y aún para quienes las dominan, dicha interacción no resulta un proceso sencillo.
2. MARCO TEÓRICO
En el campo de la investigación en didáctica de la matemática se han realizado numerosas investigaciones para precisar el término representación (Bosch, 1994, Bosch y Chevallard, 1994, Descaves (1999) Dubinsky, 1991, 1996; Duval, 1993, 1995; Contreras et al 2004; Godino, 1994, 1998; Hughes (1987); Hurbert y Carpenter, 1992, Kaput, 1987, 1991, 1992; Peltier (2003); Riviere, 1986, Tall, 1998, Vergnaud, 1991, 1994, 2007; entre otros, citado por Font).
Riviere (1986), Hurbert y Carpenter (1992) definen a las representaciones en función de su utilidad para la comunicación de los procedimientos realizados, estableciendo que para pensar y razonar sobre ideas matemáticas es necesario hacerse una representación interna de forma que la mente tenga posibilidad de operar con tales representaciones. Para comunicar estas ideas es preciso representarlas externamente para que sea posible dicha comunicación.
La Teoría de los Registros de Representación Semiótica de Duval (1993, 1995) constituye un marco teórico adecuado que permite analizar las representaciones que los alumnos -y los docentes- emplean para resolver un problema. Considera que los sistemas de representación que utiliza la matemática son las figuras, las gráficas, la escritura simbólica y el lenguaje natural. Su postura señala que es esencial para la actividad matemática que se puedan movilizar varios signos en el curso de una misma acción, o bien que se pueda elegir un signo en vez de otro.
Se pregunta bajo qué condiciones un numeral o un dibujo, por ejemplo, funcionan como representaciones de los objetos matemáticos correspondientes, estableciendo que una representación funciona verdaderamente como representación cuando da acceso al objeto representado.
"(...) es necesario que el objeto no sea confundido con sus representaciones y que se le reconozca en cada una de ellas. Es bajo esas dos condiciones que una representación funciona verdaderamente como representación, es decir que ella proporciona el acceso al objeto representado" (Duval, 1993).
En forma general divide a las representaciones en internas (privadas) y externas (visibles y observables públicamente), considerando que estas últimas son por naturaleza semióticas, ya que se producen mediante un sistema de signos y son accesibles a todos los sujetos capaces de interpretar este sistema de signos. Refiriéndose al aprendizaje de la matemática, establece que la diversificación de representaciones semióticas de un mismo objeto aumenta la comprensión de los sujetos y recíprocamente, las representaciones externas (enunciados, fórmulas, gráficas, etc.) son el medio por el cual las personas exteriorizan sus imágenes y representaciones mentales haciéndolas accesibles a otras personas. Así asigna a las representaciones externas un doble papel:
-
Actúan como un estímulo para los sentidos en los procesos de construcción de nuevas estructuras mentales.
-
Expresan la red de significados personales de los sujetos que los usan.
Se identifica una actividad ligada a la producción de representaciones, y otra ligada a la aprehensión conceptual de los objetos representados. Llama semiosis al primer tipo de actividad y noesis a la aprehensión conceptual del objeto. Además, postula que la actividad de producción de representaciones es la que permite la comprensión, es decir, la semiosis es la que determina las condiciones de posibilidad de la noesis.
Para que un sistema semiótico sea un sistema de representación, según Duval (1993), debe permitir la realización de las tres actividades cognitivas ligadas a la semiosis: la identificación de la presencia de una representación; el tratamiento y la conversión de una representación.
Sin embargo, conviene aclarar que la conversión de una representación es una actividad cognitiva diferente e independiente de la del tratamiento. Por ejemplo, al realizar un cálculo con números racionales, los alumnos pueden efectuar muy bien la suma de dos números con su escritura decimal o con su escritura fraccionaria, y de ninguna manera pensar en convertir una en la otra (o viceversa) o fracasar en esta conversión. Se constituyen procesos complejos, pasar de un registro de representación a otro (conversión) o representar un objeto de diferentes maneras en un mismo sistema de representación (tratamiento) no es evidente y mucho menos sencillo para los sujetos.
Los problemas a los que se enfrentan los sujetos para realizar el tratamiento y la conversión de representaciones es una dificultad a la que Duval llama fenómeno de no-congruencia, el cual se da entre las representaciones de un mismo objeto que provienen de sistemas semióticos diferentes y el pasaje entre ellas no es inmediato. En cambio, si se dan de manera espontánea, son congruentes.
Para explicar las producciones de los docentes se emplea también como marco teórico el juego de marcos, basado en las ideas de Doaudy (1986). Se analiza y complementa con la teoría de las representaciones semióticas de Duval con el propósito de abordar aspectos relacionados con la Didáctica de la Matemática.
El conocimiento matemático se presenta, según Douady (1991), como una doble dimensión. En primer lugar, saber matemática es tener la disponibilidad de ciertas nociones o teoremas matemáticos que sirvan como instrumento para resolver problemas. Se entiende por instrumento su funcionamiento científico en los diversos problemas que permite resolver. Además, un concepto toma sentido por su carácter instrumental. No obstante, ese carácter pone en juego las relaciones que mantiene con los otros conceptos implicados en el mismo problema. Es decir, desde una mirada instrumental, no se puede hablar de un concepto sino de una red de conceptos que gravita eventualmente alrededor de un concepto principal.
En segundo lugar, una vez que un concepto ha funcionado como instrumento en la resolución de problemas-es decir, cuando el alumno ha contextualizado el conocimiento-, es el momento de institucionalizar dicho conocimiento identificando definiciones, propiedades, teoremas, hasta su descontextualización, pasando el concepto matemático de su carácter de instrumento al de objeto de conocimiento. Luego, se aplicará el conocimiento a nuevos contextos, lo que demandará nuevas contextualizaciones. Los instrumentos pueden pertenecer a diferentes marcos de resolución: físico, geométrico, numérico, gráfico u otro; teniendo cada marco sus objetos, relaciones y formulaciones.
Sin embargo, se precisa distinguir entre marcos de resolución y registros de representación semiótica. Un registro de representación se determina con un sistema semiótico que ha de cumplir las tres funciones cognitivas de comunicación, tratamiento y conversión. Los marcos de resolución, en cambio, se determinan en relación con objetos de conocimientos matemáticos. Se puede cambiar de marco de resolución sin cambiar de registro y cambiar de registro sin hacerlo de marco, pues un marco de resolución puede movilizar varios registros (Duval, 1996, 357).
Se pone en evidencia que las representaciones externas pueden pertenecer a diferentes registros que no están directamente vinculados a la teoría. Por tanto, diferentes teorías comparten los mismos registros de representación, por ejemplo, la aritmética y el álgebra comparten los signos de las operaciones aritméticas. Mientras que, una misma teoría puede recurrir a diferentes registros, por ejemplo, el álgebra utiliza números y letras.
También Perrin-Glorian, (1993), señala (...) cuando se representan gráficamente ecuaciones mediante rectas, se podrán utilizar propiedades geométricas como el paralelismo, los puntos de intersección... que pueden traducirse en el marco algebraico. Por el contrario, cuando se pasa de las notaciones fraccionarias a las notaciones decimales, hay un cambio o conversión de registro dentro del marco numérico. Las conversiones de registro, por ejemplo, los cambios de notación de los números, son actividades que contribuyen al sentido al mismo tiempo que desarrollan las técnicas.
Este trabajo se propone responder las siguientes preguntas:
-
¿Qué representaciones externas utilizan los docentes en la resolución de los problemas propuestos?
-
¿Qué anticipaciones realizan los docentes acerca de los posibles procedimientos de resolución que podrían surgir en el aula?
3. METOLOGÍA
3.1 Metodología y diseño de la investigación
Se diseñaron cuatro propuestas de trabajo, cada una de las cuales incluye un problema extraído del Diseño Curricular de la Educación Primaria (DGC y E, 2008). Este trabajo se enmarca en un estudio cualitativo. El análisis de datos tuvo un carácter exploratorio, descriptivo e interpretativo. El contexto de realización corresponde a las instancias de Capacitación de la Dirección General de Cultura y Educación de la Provincia de Buenos Aires realizadas durante el año 2008.
Se realizó en varios distritos de la provincia que pertenecen a la región 18. Como instrumento para recoger los datos se utilizaron pruebas de lápiz y papel que han permitido formular y describir las categorías de análisis.
En esta presentación se analizarán los resultados del Problema 1, para N=17 docentes.
3.2 Análisis y descripción del Problema 1
El análisis y descripción del problema seleccionado se realizo en base a las siguientes premisas:
- Los conceptos matemáticos se elaboran a partir de la interacción con un conjunto de problemas que le dan sentido.
- El conocimiento de los alumnos puede avanzar a partir de que establezcan correspondencia entre las distintas formas de representación que una situación admite.
Problema 1:
![]()
El problema está propuesto como orientación para el contenido "resolver problemas de reparto en los cuales el resultado puede expresarse usando fracciones". Este tipo de problemas puede ser una situación propicia para trabajar a partir del concepto de división y del análisis del resto, la relación entre fracción y cociente, por lo tanto puede permitir la entrada de las fracciones en la escuela primaria. Dicha relación puede ser establecida a partir de diferentes procedimientos de resolución y del trabajo que realice el docente para hacer evolucionar los modos espontáneos de resolución.
3.2 Formulación y descripción de categorías de análisis
El estudio de las producciones realizadas se divide en tres ejes principales:
-
Resolución del problema por parte del docente.
-
Identificación de los conceptos que permiten resolver el problema.
-
Anticipación que realiza el docente de las posibles resoluciones que podrían surgir al proponerle el problema a sus alumnos.
Se construyeron dos tablas para facilitar el análisis de los registros. La primera tabla permite identificar los registros de representación utilizados por los docentes, la identificación de los conceptos matemáticos y los marcos de resolución.
Se formularon las siguientes categorías:
Registros de representación verbal-escrito (RVD): Alude a las resoluciones en lenguaje natural escrito.
Registros de representación pictográficas (RPD): esta categoría se refiere a la resolución mediante dibujos que intentan representar lo más fielmente posible los elementos involucrados en el problema.
Registros de representación icónicos (RID): se refiere a la resolución mediante representaciones que no dan cuenta de la cualidad de los elementos involucrados en el problema (bosquejos, líneas, marcas, puntos, cruces, etc.).
Registros de representación simbólicos (RSD): atiende a aquellas resoluciones en las que utilizan símbolos convencionales utilizados por la matemática.
Identifica conceptos matemáticos que permiten resolver el problema (ICMD): se refiere a la identificación del problema y las representaciones utilizadas en su resolución con los conceptos matemáticos que son su herramienta de resolución.
Marco/s de resolución (MRD/MRA): Analiza el/los marcos en que los docentes (MRD) resuelven el problema y anticipan posibles resoluciones de sus alumnos (MRA). Se consideran los siguientes: marco numérico (MRDN) - marco geométrico (MRDG) - marco algebraico (MRDA).
La segunda tabla registra las mismas categorías, excepto (ICMD). Se elaboro con el propósito de analizar las anticipaciones realizadas por los docentes acerca de posibles resoluciones de los alumnos del problema propuesto.
4. RESULTADOS
4.1 Análisis de las resoluciones de los docentes
Las resoluciones de los docentes que participaron en esta investigación referidas al Problema 1 se apoyan en sus conocimientos sobre la división y su sentido relacionado con las situaciones de reparto. En la mayoría de los trabajos predomina la categoría de los registros de representación simbólicos N=13 con respecto a los registros de representación pictográficas y a los registros de representación icónicos. Los protocolos siguientes ejemplifican los registros (RSD):
![]()
M.P1.1

M.P1.7
![]()
M.P1. 4
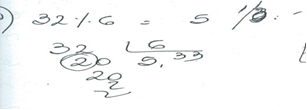
M-P1. 11
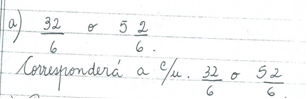
M.P1.12
Se observa en las resoluciones de los docentes el uso del algoritmo de la división, la escritura fraccionaria y la escritura decimal. Las categorías (RSD) y (RVD) se presentan como registros de representación en la mayoría de los protocolos. De acuerdo con Duval, se infiere que los docentes utilizaron el cálculo como una forma de tratamiento propio de las escrituras simbólicas. Si bien la conversión es una actividad cognitiva diferente e independiente de la del tratamiento, se deduce que 32/6; 5 2/6; 5 1/3; 5,33...; tienen una significación operatoria diferente pero representan al mismo número. Entonces, se puede inferir en el protocolo M.P1.11 una conversión de registros de la escritura decimal a la escritura fraccionaria de la representación del mismo número. La conversión requiere, según Duval (1993) que el sujeto haya percibido de la diferencia entre lo que Frege llamaba el sentido y la referencia de los símbolos o de los signos.
Con respecto a la categoría (RID), el protocolo M. P1.15 es un ejemplar de esta categoría:
![]()
M.P1.15
Este registro de representación constituye la única respuesta al problema planteado. Se infiere que los docentes no perciben el objetivo del problema y confunden el registro de representación con los conceptos matemáticos involucrados.
Con escasa presencia en la población estudiada se presenta la categoría (RPD). Los protocolos M.P1.5 y M.P1.3 representan la respuesta al Problema 1, muy próximas a las que pueden realizar sus alumnos en sus primeros intentos por resolver este tipo de problemas.

M.P1.5

M.P1.3
Se presenta en estos casos una ilustración que es una conversión de una representación en lenguaje natural en una representación pictográfica. En M.P1.5 el nuevo registro conserva sólo una parte del contenido de la representación inicial, reparte sólo 4 chocolates a cada amigo.
Con respecto a los resultados de la categoría Identifica conceptos matemáticos que permiten resolver el problema (ICMD) N=8de los docentes, no explicitan claramente cuál es o cuáles son los conceptos matemáticos que permiten resolver el problema (conocimiento que sería objeto de enseñanza a partir del problema planteado). Asimismo, se lo relaciona con la tarea involucrada en el problema (reparto) e inclusive se encuentran presentes conceptos que no tienen relación con la situación o directamente no intervienen en la resolución.
Mientras que, N=9 de los docentes para esta categoría, pudo identificar la relación entre el sentido del problema y los conceptos matemáticos que son herramienta de solución, identificación que es posible asociar con los contenidos establecidos en el diseño curricular del nivel y no con los procedimientos de resolución (ya que aparecen redactados en forma textual al Diseño Curricular).
Estos protocolos evidencian lo señalado anteriorme.
![]()
M.P1.1

M.P1.5
![]()
M.P1.7
4.2 Análisis de las anticipaciones
En relación a las anticipaciones respecto de las posibles resoluciones de los alumnos del Problema 1, en la mayoría de las producciones se considera que los alumnos realizarán representaciones icónicas que permitan realizar el reparto o recurrirán al algoritmo de la división. En este último caso se reconoce que la dificultad estará relacionada con el análisis del resto, anticipándose que en los primeros acercamientos de los alumnos a estos problemas el mismo quedará sin repartir.
Los protocolos M.P1.1 y M.P1.6 permiten establecer que los docentes anticipan que los alumnos recurrirán a representaciones icónicas (rectángulos que representan los chocolates) que les permitirán realizar el reparto o se apoyarán en el algoritmo de la división, recursos de resolución que se encuentran relacionados o en líneas generales coinciden con los procedimientos utilizados por ellos mismos al resolver este problema.

M.P1.1

M.P1.6
En M.P1.2 se intentan realizar aproximaciones desde la resolución mediante dibujos o desde el algoritmo de la división a la representación en forma fraccionaria del cociente obtenido. Pero el análisis considera conocimientos que seguramente no estarán disponibles en los alumnos en sus primeras resoluciones como lo es el trabajo con fracciones equivalentes.
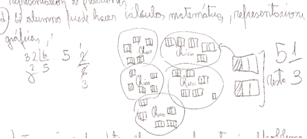
M.P1.2
En todos los casos no se realiza un tratamiento sobre alguna de esas representaciones que permita relacionarla con las demás o acercarlas a las del concepto que se pretende enseñar. Seguramente, la ausencia de los aspectos señalados reduce considerablemente el valor didáctico de la instancia de anticipación.
Con referencia a la categoría Registros de representación verbal - escrito (RVA), los docentes utilizan sólo este registro, para anticipar sobre posibles resoluciones de sus alumnos. Este recurso quizás puede ser una de las causas de las dificultades que se les presentan para analizar, reconocer y permitir evolucionar diferentes representaciones surgidas en el aula, pues la información que puede obtenerse de esas expresiones no permite tomar decisiones que admitan intervenir y gestionar la clase.
Se considera la necesidad de partir de representaciones gráficas - pictográficas o icónicas (predominantemente estas últimas)- para producir escrituras simbólicas relacionadas con los conceptos puestos en juego en la resolución, este aspecto se manifiesta tanto en los procedimientos de los docentes como en los que se prevén para los alumnos.
Se observa en los siguientes protocolos M.P1.3 y M.P1.4 la Categoría (RVA):

M.P1.3
![]()
M.P1.4
Los registros analizados permiten establecer que, en general, las resoluciones de los docentes sirvieron de apoyo para la anticipación de los procedimientos de los alumnos. Esto permite inferir que los docentes no consideran diferencias en relación a los conocimientos disponibles entre ellos y los alumnos.
CONCLUSIONES
El presente trabajo analizó las representaciones externas que utilizan los docentes en la resolución de problemas, las anticipaciones que proponen y el sentido que ellos atribuyen a los conceptos matemáticos que serán construidos.
A partir del análisis realizado se describieron las representaciones externas que utilizan los docentes. Para responder a las cuestiones planteadas, se consideró el primer problema para el contenido "resolver problemas de reparto en los cuales el resultado puede expresarse usando fracciones".
Acerca de este problema se puede inferir entre otros aspectos, que la mayoría de los docentes emplean el algoritmo de la división e indican el cociente en forma fraccionaria, como registro de representación externa. También el resultado es expresado como fracción o número mixto, en estos casos, la relación es sólo enunciada en términos de equivalencia, "a cada uno le corresponde 5 chocolates y que es una fracción equivalente a ".
Algunos docentes se apoyan en otro sentido de las fracciones, en el significado parte-todo, esta posibilidad es considerada en dos trabajos como único recurso de resolución. Es importante tener en cuenta que en estos casos también es posible -de acuerdo a las particiones realizadas- obtener diferentes escrituras fraccionarias asociadas a las mismas.
También surgieron resoluciones muy particulares, algunas de ellas por su proximidad a las que realizan los alumnos en sus primeros intentos por resolver estos problemas y otras, por utilizar representaciones decimales del cociente obtenido, expresión que no corresponde al sentido del problema analizado. En ambos casos no se identificaron procedimientos que atiendan a la posible evolución de las representaciones empleadas o a la discusión de la pertinencia de los resultados obtenidos.
En una gran parte de los trabajos analizados, los maestros no explicitan los conceptos matemáticos que permiten resolver la situación (conocimiento que sería objeto de enseñanza a partir del problema planteado) o directamente se lo relaciona con la tarea involucrada en el problema (reparto), inclusive se encuentran presentes conceptos que no tienen relación con la situación o directamente no intervienen en la resolución.
Con respecto al juego de marcos en su mayoría prevalecieron las resoluciones en el marco numérico, apoyados en algunos casos en el marco geométrico, sin tener en cuenta que cada forma de representación expresa y pone en juego aspectos y estrategias particulares. Encontrar la solución, o de un principio de solución en un marco puede ayudar a encontrar la solución en otro y a veces a verificar los resultados.
El trabajo en diferentes marcos es una estrategia propia de los expertos -es decir de los matemáticos- en la generación de conocimiento. Según se desprende del trabajo, lo complejo es lograr que los docentes accedan a las estrategias de los expertos, en lugar de encerrarse en un único registro de representación, y que sean capaces de utilizar varios registros, para un mismo marco. Sí el problema lo permite, sería deseable que los alumnos tuvieran la posibilidad de interactuar con diferentes marcos que es un tipo de habilidad, muy difícil de adquirir y es una tarea a largo plazo, que se debería propiciar desde la Educación Primaria.
Los resultados evidencian que muchas de las dificultades que tienen los docentes para anticipar los procedimientos de los alumnos están vinculadas con sus propios reparos para elaborar registros de representaciones de la situación planteada y reconocer las nociones que intervienen.
Aunque desde el Diseño Curricular se propicia el uso e integración de las diferentes formas de representación desde los primeros años de la escolaridad, y se proponen problemas como los utilizados en este trabajo, parece muy lejana la posibilidad de que esto se traslade al aula. Las restricciones que imperan en la formación docente y la tradición escolar dominante conspiran contra esta posibilidad . Así mismo surgen nuevas cuestiones: ¿cómo distingue el docente los conceptos matemáticos y sus representaciones?, ¿cómo se trabaja en el aula para que surjan las distintas representaciones? Se considera de interés continuar con la reflexión iniciada en este trabajo, de modo que se pueda avanzar en el debate por mejorar la enseñanza y aprendizaje de la matemática.
REFERENCIAS
1. Brizuela, B. (2005), "Relaciones entre representaciones: el caso de Jennifer, Nathan y Jeffrey" en Alvarado M. y Brizuela B. Haciendo números. Las notaciones numéricas vistas desde la psicología, la didáctica y la historia", Ed. Paidós, México. [ Links ]
2. Brousseau, G. (1986), Fondements et méthodes de la didactique des mathématiques. Recherches en Didactique des Mathématiques V 7(2) 33-115. [ Links ]
3. Brousseau, G. (2007), Iniciación al estudio de la teoría de las situaciones didácticas, Libros del Zorzal, Buenos Aires. [ Links ]
4. Castro E. y Castro E. (1997), Representaciones y modelización, en Rico L. (coord.) La educación matemática en la escuela secundaria, Ed. Horsori, Barcelona. [ Links ]
5. Contreras de la Fuente A., Luque, L. Ordoñez, L. (2004) Una perspectiva didáctica en torno a los contextos y a los sistemas de representación semiótica del concepto de máximo. Educación Matemática, Vol 16 (1) pp. 59-87. [ Links ]
6. D.G.C. y E. (2008), Diseño Curricular para la educación primaria, D.G.C. y E., Pcia. de Buenos Aires. [ Links ]
7. Douady R. (1984) Relación enseñanza - aprendizaje, Dialéctica Instrumento Objeto, Juego de marcos,en Revista de Didáctica Nº 3, Universidad de París 7, Francia. [ Links ]
8. Duval, R. (1993), Registres de représentation sémiotique et fonctionnement cognitif de la pensée, Annales de Didactique et de Sciences Cognitives, 5, Estrasburgo. [ Links ]
9. Duval, R. (1996), Quel cognitif retenir en didactique des mathématiques. Recherches en Didactique des Mathématiques, Vol 16 (3) pp.349-382. [ Links ]
10. Duval, R. (2006), Quelle sémiotique pour l'analyse de l'activité et des productions mathématiques?, Relime Vol. 9, extra No. 1. [ Links ]
11. Font, V. (2000) "Algunos puntos de vista sobre las representaciones en didáctica de las matemáticas", Documento de didáctica de las CCEE y la matemática de la Universidad de Barcelona, Barcelona. [ Links ]
12. Hughes, M. (1987), Los niños y los números, Ed. Planeta, Barcelona. [ Links ]
13. Panizza, M. (2003), Reflexiones generales acerca de la enseñanza de la matemática, en Panizza M. (comp.), Enseñar matemática en el Nivel Inicial y el Primer Ciclo de la EGB, Ed. Paidós, Buenos Aires. [ Links ]
14. Parra, C. (1994) Cálculo mental en la escuela primaria, en C. Parra e I. Saiz (comps.), Didáctica de matemáticas. Aportes y reflexiones, Paidós, Buenos Aires. [ Links ]
15. Peltier M. L., (2003), Problemas aritméticos. Articulación, significados y procedimientos de resolución en Educación Matemática V 15(3), Ed. Santillana, México. [ Links ]
16. Perrin-Glorian, M.J. (1993) Questions didactiques soulevées à partir de l'enseignement des Mathématiques dans des classes « faibles » Recherches en Didactique des Mathématiques V 13 (1/2) pp. 5-118. [ Links ]
17. Rico, L. (2009), Sobre las nociones de representación y comprensión en la investigación en Educación Matemática APNA, 4 (1), 1-14, España. [ Links ]
18. Rico, L., Castro E. y Romero I. (2000), Sistemas de representación y aprendizaje de estructuras numéricas, Departamento de Didáctica de la Matemática, Universidad de Granada, España. [ Links ]
19. Sadovsky P. (2005), Enseñar matemática hoy. Miradas, sentidos y desafíos, Libros del Zorzal, Buenos Aires. [ Links ]
20. Vergnaud G. (1990) La théorie des champs conceptuels Recherches en Didactique des Mathématiques, V10/2-3, pp.133-170. [ Links ]
21. Vergnaud G. (1991) El niño, la matemática y la realidad, Ed. Trillas, México. [ Links ]
22. Vergnaud G. (2007) Forma operatoria y forma predicativa del conocimiento. Actas I Encuentro Nacional de Educación Matemática, Abril de 2007, UNICEN, Tandil, Argentina. [ Links ]














