Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista electrónica de investigación en educación en ciencias
versión On-line ISSN 1850-6666
Rev. electrón. investig. educ. cienc. vol.7 no.1 Tandil ene./jul. 2012
ARTICULOS ORIGINALES
Conexiones entre los conceptos de dependencia e independencia lineal de vectores y el de solución de sistemas de ecuaciones lineales en R2 y R3 desde el punto de vista de los modos de pensamiento.
Marcela Parraguez González, Jorge Bozt Ortiz
marcela.parraguez@ucv.cl, jabozt@gmail.com
Instituto de Matemática, Pontificia Universidad Católica de Valparaíso, Av. Brasil 2950, Valparaíso, Chile
Resumen
Esta investigación tiene como principal objetivo el comprender y analizar en el marco de la teoría de los modos de pensamiento, el razonamiento a partir de lo teórico o desde lo práctico que evidencian estudiantes universitarios al enfrentarse a los conceptos dependencia e independencia lineal de vectores y solución de un sistema de ecuaciones lineales en R2 y R3, así como las conexiones que establecen esos estudiantes de educación superior entre dichos conceptos.
A lo largo de la investigación se ha evidenciado que los estudiantes tienden a situarse en un mismo modo de pensamiento -el que tiene que ver con las relaciones numéricas y algebraicas que puedan establecer con los conceptos, denominado modo de pensamiento analítico-aritmético- aun cuando el contexto del ejercicio favorezca otro modo de pensamiento, como por ejemplo el sintético- geométrico. Además, se ha podido constatar que la coordinación y el tránsito entre los distintos modos de pensar los conceptos dependencia lineal y solución de un sistema de ecuaciones lineales favorecen conexiones adecuadas entre ambos.
Palabras clave: Dependencia e independencia lineal de vectores; Solución de sistemas de ecuaciones lineales; Modos de pensamiento.
Connection Between The Concepts Linear Dependence And Independence Of Vectors And Solution of Systems Of Linear Equations In R2 And R3 From The Point Of View Of The Modes Of Thinking
Abstract
In this investigation we have adopted as its main objective to understand and analyze in the framework of the theory of modes of thinking, reasoning from the theoretical or practical evidence from the college students to be exposed to concepts of linear dependence and independence vectors and solving a system of linear equations in R2 and R3 and the connections that establish these students in higher education between those concepts.
Throughout the investigation we have shown that students tend to be in the same way of thinking-that has to do with numerical and algebraic relationships that can be established with the concepts, so-called analytic-arithmetic thinking-even when the context otherwise favorable exercise of thought, such as synthetic-geometric. In addition, we found that the coordination and transition between different modes of thinking about linear dependence concepts and solution of a system of linear equations favor right connections between them.
Key words: Linear dependence and independence of vectors; Solving systems of linear equations; Modes of thinking
Liens Entre Les Concepts De Dépendance Et Indépendance Linéaire De Vecteurs Et La Résolution De Systèmes D´Equations Linéaires Dans R2 Et R3, Du Point De Vue Des Modes De Pensée.
Résumé
L'objectif principale de cette recherche est de comprendre et d'analyser dans le cadre de la théorie des modes de pensée, les types de raisonnement dont font preuve, dans un cadre théorique ou pratique, des étudiants du premier cycle universitaire qui abordent les notions de dépendance et indépendance linéaire des vecteurs et la résolution d'un système d'équations linéaires dans R2 et R3, ainsi que les liens qui établissent ces concepts.
Au cours de la recherche, nous avons montré que les étudiants ont tendance à se cantonner à un même mode de pensée - celui relié aux relations numériques et algébriques qu'ils peuvent établir avec les concepts en jeu, dit mode de pensée analytique-arithmétique - même lorsque le contexte de l'exercice favorise une autre mode de pensée, par exemple, le mode synthétique-géométrique. De plus, nous avons constaté que la coordination et la transition entre les différents modes de pensée relatifs aux concepts de dépendance linéaire et la résolution d'un système d'équations linéaires favorisent l´établissement des liens adéquats entre ces concepts.
Mots-clés: Dépendance et indépendance linéaire de vecteurs; Résolution de systèmes d'équations linéaires; Modes de pensée.
Ligação Entre Os Conceitos Dependência E Independência Linear Conceitos De Vetores E Soluçãodes Sistemas De Equações Lineares no R2 E R3 Do Ponto De Vista Dos Modos De Pensar
Resumo
Esta investigação tem como principal objetivo compreender e analisar no âmbito da teoria dos modos de raciocínio de pensar, a partir das evidências teóricas ou práticas dos alunos da faculdade para ser exposto a conceitos de dependência linear e vetores independência e resolver um sistema de equações lineares em R2 e R3 e as conexões que estabelecem esses alunos no ensino superior entre esses conceitos.
Ao longo da investigação, temos mostrado que os estudantes tendem a ser da mesma maneira de pensar, que tem a ver com relações numéricas e algébricas que podem ser estabelecidas com os conceitos, os chamados aritmética-analítico o pensamento, mesmo quando o exercício do contexto outra coisa favorável do pensamento, como o sintético-geométrico. Além disso, descobrimos que a coordenação ea transição entre os diferentes modos de pensar sobre os conceitos de dependência linear e solução de um sistema de equações lineares favor conexões certas entre eles.
Palavras-chave: Dependência e independência linear de vetores; Sistemas de resolução de equações lineares; Modos de pensar.
1. INTRODUCCIÓN
Descripción y justificación de la problemática
La importancia y trascendencia del álgebra lineal -en particular los conceptos de dependencia e independencia lineal- en otras disciplinas de la matemática es indudable: solución de un sistema de ecuaciones lineales, matrices, base y dimensión de un espacio vectorial, solución de ecuaciones diferenciales, aplicaciones en economía e ingeniería, son algunos de los muchos aspectos matemáticos ligados a ella. Particularmente, la problemática de investigación surge al preguntarnos cómo estudiantes universitarios ligan los conceptos de dependencia e independencia lineal de vectores en R2 y R3 y el de solución de un sistema de ecuaciones lineales homogéneo.
Curricularmente esos conceptos se ubican en la enseñanza media chilena (estudiantes de 15-16 años) y se inicia con el estudio de los sistemas de ecuaciones lineales, razón por la cual comenzamos indagando en aquellas investigaciones que dicen relación con los sistemas de ecuaciones lineales y con el concepto de solución que construyen los estudiantes. Respecto a los sistemas de ecuaciones lineales, hay evidencia de que en general se enseñan gráficamente sólo en un contexto bidimensional, y que en un nivel tridimensional son más difíciles de pensar las diferentes condiciones, según reporta Marines y Monroy (1998). Respecto a su solución, en Ochoviet (2009) hay evidencia de que los estudiantes (14-15 años) la identifican con los puntos de intersección de rectas de a pares, teniendo dificultades para identificarla en sistemas rectangulares, como por ejemplo de 3x2.
Respecto a los conceptos de dependencia e independencia lineal, en Dorier (2000) se logra identificar un obstáculo en los estudiantes, que tiene que ver con extender las ideas de R2 y R3, como por ejemplo el pensar que dado que dos vectores en R2 no colineales son linealmente independientes, tres vectores en R3 no colineales también han de serlo. Andreoli (2009) identifica otros obstáculos, de carácter epistemológico, al entrevistar a estudiantes entre 18 y 21 años de Bioquímica, como por ejemplo la necesidad de "n" ecuaciones para resolver un sistema de "n" incógnitas y el condicionar la posibilidad de solución única de un sistema, a que ninguna de las ecuaciones sea la amplificada de otra.
Respecto a los sistemas de ecuaciones lineales, Barrera (2008) concluye que no existen conexiones entre los distintos modos de pensar al abordar un problema de sistemas de ecuaciones lineales homogéneo con dos incógnitas, y que en general tienden a recurrir a un solo modo de pensamiento para resolverlos (no todos al mismo). Monroy (2008) reporta dificultades en estudiantes y profesores al interpretar el concepto solución en relación al de dependencia e independencia lineal. A estos antecedentes agregamos, desde nuestra experiencia, que los conceptos solución de un sistema y dependencia lineal, el primero a nivel escolar y el segundo a nivel universitario, son trabajados en Chile en general desde una mirada algebraica, muy pocas veces geométrica, y sin dar mayor importancia a la conexión entre ambas.
De este modo, interesa indagar el concepto solución de un sistema de ecuaciones lineales homogéneo con dos y tres incógnitas y el de dependencia e independencia lineal de vectores que construyen estudiantes chilenos de educación superior al terminar un curso de álgebra lineal, así como la conexión que establecen entre ambos conceptos, y desde cuál(es) modo(s) de pensar es interpretado. Particularmente, interesa indagar sobre las relaciones que logran establecer los estudiantes entre el conjunto solución de un sistema lineal de ecuaciones homogéneo y el concepto de dependencia e independencia lineal de vectores en subespacios de R2 y R3.
Para indagar en las conexiones que están haciendo los estudiantes universitarios entre los conceptos en estudio, usaremos como marco teórico los modos de pensamiento de Anna Sierpinska (2000), porque brindan tres formas de pensar y entender los objetos matemáticos, donde cada una permite dar una mirada distinta de la conexión en cuestión, logrando una mayor comprensión de esto. Sierpinska distingue tres modos de pensar los conceptos asociados al álgebra lineal: analítico-aritmético (AA), sintético-geométrico (SG) y analítico-estructural (AE). De esta forma, la problemática a la luz del marco teórico se resume como sigue: los modos de pensar los conceptos solución de un sistema de ecuaciones lineales homogéneo con dos y tres incógnitas y dependencia e independencia lineal de vectores en R2 y R3 en estudiantes universitarios, propician conexiones entre ambos conceptos.
Para afrontar esta problemática se han trazado preguntas que guiarán la investigación.
1 ¿Qué elementos matemáticos contribuyen a lograr el tránsito entre los distintos modos de pensamiento al situar juntos los conceptos solución de un sistema de ecuaciones lineales homogéneo con dos y tres ecuaciones, y dependencia e independencia lineal de vectores en R2 y R3?
2 ¿A partir de qué modo de pensamiento se logran conexiones entre los conceptos solución de un sistema de ecuaciones lineales homogéneo y dependencia e independencia lineal de vectores en R2 y R3?
Para dar respuesta a estas preguntas de investigación hemos propuesto los siguientes objetivos:
Objetivo general de investigación
Comprender y analizar desde una postura cognitiva el hecho didáctico de entender los conceptos solución de un sistema de ecuaciones lineales y dependencia e independencia lineal de vectores en los modos de pensamiento SG, AA y AE, para propiciar y orientar la conexión entre ambos conceptos.
Objetivos específicos de investigación
1 Establecer evidencias empíricas con sustento teórico acerca de los modos de pensamiento en que los estudiantes universitarios comprenden los conceptos solución de un sistema de ecuaciones lineales y dependencia e independencia lineal de vectores en R2 y R3.
2 Identificar y comprender los factores matemáticos asociados a la conexión entre los conceptos solución de un sistema de ecuaciones lineales y dependencia e independencia lineal de vectores en R2 y R3.
3 Identificar los elementos matemáticos de conexión entre los tres modos de pensamiento SG, AA y AE.
4 Analizar y contrastar que la conexión entre los conceptos solución de un sistema de ecuaciones lineales y dependencia e independencia lineal de vectores promueve la interacción entre los modos de pensamiento SG, AA y AE.
Una aproximación histórica-epistemológica a los conceptos sistema de ecuaciones lineales y dependencia lineal de vectores
Los sistemas de ecuaciones lineales y el concepto de dependencia lineal están muy relacionados, pues el segundo surge del cuestionamiento sobre cuándo un sistema de ecuaciones lineales tiene solución. Sin embargo, los sistemas de ecuaciones surgen desde mucho antes. Los primeros vestigios sobre resolución de ecuaciones las encontramos en civilizaciones muy antiguas, como lo son la babilónica y la egipcia. En particular, los babilónicos lograron desarrollar técnicas para resolver ecuaciones de grado 1 y 2, la cuales se basaban en razonamientos puramente geométricos (Stewart, 2007). No obstante, fueron los chinos, entre los años 200 y 100 a.C., quienes se acercaron mucho más a las ideas de sistemas de ecuaciones e incluso de determinante y matriz, ya que no sólo planteaban un problema en un sistema de ecuaciones, sino que además proponían al lector instalar los coeficientes del sistema en forma de tabla y luego realizar multiplicaciones en las columnas para restarlas entre ellas, similar al método de escalonamiento de una matriz que se realiza hoy en día.
El concepto de dependencia e independencia lineal aparece mucho más tarde, pero siempre ligado a los sistemas de ecuaciones. Uno de los primeros precursores del concepto es el matemático Leonard Euler, quien en 1750, en el contexto de la paradoja de Cramer relacionada con curvas algebraicas, afirma que "n ecuaciones podrían no ser suficientes para determinar n valores". Para explicar este hecho, Euler argumenta a partir de sistemas de 2x2 de la siguiente forma:
"no es posible determinar las dos incógnitas x e y, pues al eliminar x, la otra desaparece también y queda una ecuación idéntica (identidad 0=0) de la cual no puede ser deducida. La razón para tal incidente es en principio muy obvia. Como la segunda ecuación puede ser descrita de la forma 6x - 4y = 10, que no es más que el doble de la primera 3x - 2y = 5y que de ésta no difiere en nada" (Euler, 1750, p. 219).
Luego continúa su explicación para sistemas de 3x3 y 4x4, extendiéndola al caso nxn y concluyendo que "cuando uno dice que para determinar n incógnitas, es suficiente tener n ecuaciones que dan sus relaciones mutuas, debe ser añadida la restricción que ellas son todas diferentes o que ninguna es combinación de las demás" (Andreoli, 2009; p. 31).
Podemos ver así que en un principio los conceptos de dependencia e independencia lineal, así como el de combinación lineal, eran entendidos más bien desde lo intuitivo, sin una definición formal. Este privilegio por la intuición provocó que se descuidaran los cuestionamientos sobre sistemas incompatibles e indeterminados por casi un siglo, ligando así el concepto de dependencia lineal a una forma más bien intuitiva de pensar una ecuación como dependiente de otra, lo que constituyó un estancamiento en cuanto a al desarrollo de dicho concepto. Ya en el siglo XIX, esta idea intuitiva de dependencia se liga a la de nulidad del determinante principal de un sistema cuadrado de ecuaciones lineales. Es así como el "descubrimiento de Stanley (1861) marca un paso fundamental hacia la conceptualización de dependencia lineal al demostrar que dicho orden máximo está relacionado con el número máximo de soluciones independientes" (Dorier, 1995; p. 231). De esta forma, la idea de dependencia lineal estaba fuertemente ligada a las de sistemas de ecuaciones y determinante y rango de una matriz, pero aun no se contaba con una definición formal del concepto. Fue así como en 1875 Frobenius (Andreoli, 2009; p. 32) logra dar una definición de independencia lineal (la definición moderna del concepto), de ecuaciones y n-uplas, sin uso de determinantes, es decir: "v1,v2,…,vk son linealmente independientes si la única combinación lineal de v1,v2, …,vk que da como resultado el vector cero, es aquella en la que todos los coeficientes son cero" (Kolman & Hill, 2006, p. 294).
Este aspecto es un punto fundamental en la génesis del álgebra lineal, pues la definición formal de dependencia lineal es la que permite entender de la misma manera todos los objetos bajo el foco de sus relaciones lineales. En este sentido, la definición formal de dependencia lineal sería vital para vincular dicho concepto a sus diferentes interpretaciones (geométricas y aritméticas) y al concepto solución de un sistema de ecuaciones lineales, convirtiéndola en un aspecto fundamental para la problemática planteada.
Diferentes contextos de estudio
La problemática apunta a las diferentes formas en que se pueden entender los conceptos dependencia e independencia lineal de vectores y el de solución de un sistema de ecuaciones lineales, los cuales tienen relación con los diferentes contextos (algebraico, geométrico y estructural) en los que pueden presentarse dichos conceptos. Por tanto, son de especial interés para la investigación los diferentes contextos de estudio en los que se sitúan estos conceptos y la forma en que éstos interactúan.
El álgebra lineal, y el álgebra en general, no siempre han sido consideradas el mejor camino para dar una respuesta. Ya en 1679, Leibniz se resistía al estudio puramente algebraico al señalar:
"Todavía no estoy satisfecho con el álgebra porque esto no proporciona los métodos más cortos o las construcciones más hermosas en geometría. Por eso creo que, por lo que a la geometría concierne, necesitamos todavía otro análisis que es claramente geométrico o lineal y que expresará la situación directamente como el álgebra expresa magnitudes" (Leibnitz, 1853, p. 233-234).
Sucede que ambos contextos, el algebraico y el geométrico, han entregado diferentes herramientas de justificación a cuestiones matemáticas. Ejemplos de ello son la validación de los complejos, que llevó a los matemáticos de la época a retornar del álgebra a la geometría. A su vez, los matemáticos Möebius y Bellavitis intentaron generalizar la geometría espacial, constituyendo las bases de lo que hoy se conoce como geometría vectorial.
Otro ejemplo de comunicación entre el álgebra y la geometría tiene que ver con William Hamilton, quien buscó por mucho tiempo ternas dotadas de la adición y la multiplicación que verificara las propiedades de un cuerpo y que extendiera la idea de número complejo a dimensión tres. Sólo un cambio de mirada en las propiedades algebraicas a la naturaleza geométrica de la multiplicación en dimensión dos le permitió darse cuenta que dicha operación en dimensión tres, que representaría finalmente el producto escalar y vectorial al mismo tiempo, debería considerar las longitudes (unidimensional) de vectores, la rotación entre sus dos direcciones (bidimensional) y el ángulo que ellos forman (unidimensional). Esto le permitió llegar más tarde, en 1843, al invento de sus cuaterniones. Todos estos acontecimientos que se han señalado tienen que ver con el desarrollo del álgebra vectorial, el cual tuvo incidencia importante en el desarrollo del álgebra lineal, particularmente en lo que respecta a la interpretación geométrica de sus objetos de estudio. No obstante, este aspecto geométrico no siempre contribuyó a la evolución del álgebra lineal. Por ejemplo, el pensar sólo en "lo posible" constituyó un obstáculo al momento de ampliar los conceptos del álgebra lineal a espacios vectoriales de dimensión superiores a tres. Tanto es así que Möebius, en su Der Barycentriche Calcul definió lo que hoy se conoce como congruencia de figuras en el mismo plano, añadiendo que ello no es verdadero para figuras tridimensionales, lo que explicó bajo el siguiente argumento:
"…para la coincidencia de dos sistemas iguales y similares A, B, C, D y A', B', C', D', … en el espacio de tres dimensiones, en los cuales los puntos D, E… y D', E',… están sobre los lados opuestos de los planos ABC y A'B'C', será necesario, debemos concluir por analogía, que nosotros deberíamos ser capaces de dejar a un sistema hacer media revolución en un espacio de cuatro dimensiones. Pero ya que tal espacio no puede ser pensado, entonces esa coincidencia, en este caso, es también imposible." (Möbius, 1915, p.240).
Vemos así que la constitución del álgebra lineal como disciplina marca un hecho trascendental en la historia y evolución de la matemática, pues no sólo entrega una generalización de los aspectos geométricos en juego sino que da una estructura sólida a los objetos matemáticos presentes y a las relaciones que se pueden establecer entre ellos.
2. MARCO TEÓRICO
Justificación y descripción del marco
La elección del marco teórico con el que afrontamos la investigación se justifica en aquellos aspectos claves que interesa indagar, vale decir: la forma en que los estudiantes piensan y entienden los objetos matemáticos en juego (dependencia e independencia lineal de vectores, solución de un sistema de ecuaciones lineales), cuál de estas formas prevalece en cada estudiante, cuáles son las conexiones que logran establecer los estudiantes entre las diferentes formas de mirar los objetos, cuáles son las conexiones que establecen los estudiantes entre los objetos matemáticos en juego, cuáles formas de mirar estos objetos son las que permiten dichas conexiones y si existe tránsito entre las diferentes formas de pensar un objeto matemático en juego. De acuerdo al propósito de la investigación, elegimos como marco teórico los modos de pensamiento propuestos por Anna Sierpinska (2000). La elección de éste se fundamenta principalmente en base a tres argumentos: primero, el ser un marco teórico que destaca lo que queremos mirar, ya que apunta a las diferentes maneras de pensar o concebir un objeto matemático; segundo, el ser un marco que nace en el álgebra lineal, lo cual permite que se acomode muy bien a los conceptos matemáticos en juego en la presente investigación, ya que son propios del álgebra lineal; tercero, el ser un marco utilizado por otros autores que han realizado investigaciones en temas afines con este, obteniendo resultados muy interesantes e importantes para esta investigación (Monroy, 2008 y Ochoviet, 2009).
Respecto a los modos de pensamiento, Anna Sierpinska (2000) señala que los objetos matemáticos adquieren diferentes significados al ser trabajados en diferentes modos. Además, destaca que los modos de pensamiento no constituyen diferentes etapas del desarrollo del pensamiento algebraico, es decir, todos son igualmente útiles para alcanzar el concepto, cada uno en su propio contexto. En este sentido, cada modo de pensamiento permite una vía de acceso al objeto matemático, por lo que los modos de pensamiento se complementan, ninguno está incluido en el otro, y la coordinación y el tránsito entre ellos amplía el concepto que se tiene del objeto matemático. Sierpinska (2000) distingue tres modos de pensamiento: uno que tiene que ver con el pensamiento práctico (sintético-geométrico) y otros dos que tienen que ver con el pensamiento teórico (analítico-aritmético y analítico-estructural).
Pensamiento Sintético-geométrico (SG): aquí los objetos son presentados mediante una representación geométrica. La visualización matemática (en el sentido de Zimmermann y Cunningham, 1991) que tenga el sujeto del objeto toma un rol fundamental en el entendimiento de dicho objeto. Por ejemplo, una recta sería entendida a través de su gráfica, lo mismo que un plano, un vector puede ser representado mediante una flecha dirigida, la solución de un sistema de ecuaciones lineales en R2 como la intersección común de rectas en el plano (figura 1), la solución de un sistema de ecuaciones lineales en R3 como la intersección común de planos en el espacio (figura 2), etc.
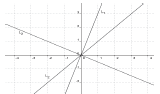
Figura 1: Solución gráfica de un sistema de ecuaciones lineales con dos incógnitas.
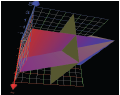
Figura 2: Solución gráfica de un sistema de ecuaciones lineales con tres incógnitas
Pensamiento Analítico-aritmético (AA): aquí los objetos matemáticos son pensados a través de relaciones numéricas. Así, por ejemplo, los vectores aquí son representados por sus componentes (n-uplas), las rectas y planos por sus ecuaciones, los sistemas de ecuaciones lineales son comprendidos y expresados a través de las ecuaciones que los componen (figura 3), las combinaciones lineales de vectores son comprendidas a partir de las coordenadas de cada uno (figura 4), etc.
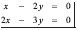
Figura 3: Sistema de ecuaciones lineales en R2.
![]()
Figura 4: Combinación lineal de vectores en R3.
Pensamiento Analítico-estructural (AE): aquí se recurre a las propiedades de los objetos o a los axiomas que permiten explicarlos. Así, por ejemplo, el cero vector es entendido como aquel que deja a todo vector invariante bajo la suma de vectores, las combinaciones lineales de vectores dependen de la estructura del espacio vectorial y de las operaciones que se definan en él, como por ejemplo las operaciones suma ![]() y ponderación
y ponderación ![]() definidas en el espacio vectorial
definidas en el espacio vectorial ![]() por:
por:
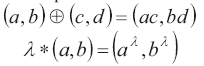
Cabe señalar que en este espacio vectorial ![]() sobre R, con las operaciones
sobre R, con las operaciones ![]() y
y ![]() , el cero vector es el (1,1), y los vectores de
, el cero vector es el (1,1), y los vectores de ![]() sobre R no siempre se corresponden gráficamente con flechas rectilíneas dirigidas, sino que pueden ser representados con flechas curvas (figura 5). En efecto, el vector (1,2) genera una recta vertical, ya que,
sobre R no siempre se corresponden gráficamente con flechas rectilíneas dirigidas, sino que pueden ser representados con flechas curvas (figura 5). En efecto, el vector (1,2) genera una recta vertical, ya que, ![]() , es decir, la primera coordenada siempre es igual a 1 y la segunda toma valores mayores o iguales a 1. Por lo tanto genera la recta x = 1 en
, es decir, la primera coordenada siempre es igual a 1 y la segunda toma valores mayores o iguales a 1. Por lo tanto genera la recta x = 1 en ![]() . En cambio el vector (2,4) genera la función cuadrática, ya que:
. En cambio el vector (2,4) genera la función cuadrática, ya que: 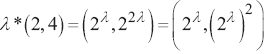 , es decir, la segunda coordenada es siempre el cuadrado de la primera. Por lo tanto genera una parábola y = x2 donde x toma valores mayores o iguales a 1.
, es decir, la segunda coordenada es siempre el cuadrado de la primera. Por lo tanto genera una parábola y = x2 donde x toma valores mayores o iguales a 1.
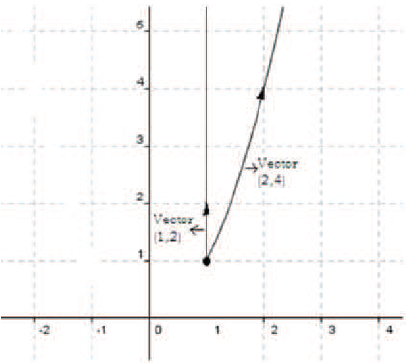
Figura 5: Representación gráfica de los vectores (1,2) y (2,4) en ![]() .
.
Estos modos de pensamiento pueden verse como el resultado de una superación de dos obstáculos o dos posiciones dogmáticas opuestas: una, que rechaza los números dentro de la geometría y la otra, que rechaza que la "intuición geométrica" pueda ser llevada a un dominio puramente aritmético. Estos modos de pensamiento es preferible considerarlos como igualmente útiles, cada uno en su propio contexto, para propósitos específicos y principalmente cuando están interactuando.
Sierpinska en una indagación realizada hace más de una década (Sierpinska, 2000), indica que el desarrollo del álgebra lineal se inició como un proceso de pensar analíticamente el espacio geométrico. Tomando una perspectiva muy general, se podrían distinguir, en este desarrollo, dos grandes pasos referidos a dos procesos. Uno fue la aritmetización del espacio, que tuvo lugar al pasar de la geometría sintética a la geometría analítica en Rn. El otro fue la desaritmetización del espacio a su estructuración, con la que los vectores abandonan las coordenadas que los anclaban al dominio de los números y se convierten en elementos abstractos cuyo comportamiento está definido por un sistema de propiedades o axiomas.
La principal diferencia entre los modos 'sintético' y 'analítico' es que en el modo sintético, los objetos son dados directamente para ser descritos por la mente, la cual trata de describirlos, es decir, de manera natural, mientras que en el modo analítico estos objetos son dados indirectamente, de hecho son construidos solamente por la definición de las propiedades de los elementos (Sierpinska, 2000).
Por ejemplo, en el modo sintético, una línea recta se puede ver como un objeto preestablecido con una cierta forma y que ocupa cierta parte en el espacio. Por un lado se podrá hablar de las propiedades de la línea recta pero por otro lado, estas propiedades sólo la describirán mas no la definirán. Por su parte, el modo analítico hace que la línea recta quede definida de acuerdo a ciertas relaciones específicas entre las coordenadas de los puntos o vectores en un espacio de dimensión dada. Esto muestra que si se piensa en el objeto 'recta' lo primero que se viene a la mente es el objeto representado con la figura correspondiente, pero no necesariamente se tendría que pensar en un principio en la 'ecuación lineal' que la define. También si se presentan 'dos rectas coincidentes' como objeto se viene a la mente una recta que se visualiza de la figura dada, pero no se pensaría en una representación de un sistema de dos ecuaciones equivalentes que la define.
Respecto a la diferencia entre los modos de pensamiento analítico-aritmético y analítico-estructural, es que en el primero un objeto es definido por una fórmula que permite calcularlo, y muchos razonamientos analítico-aritméticos tienen una tendencia de mostrar que dos procesos o métodos conducen al mismo resultado; por otro lado, en el pensamiento analítico-estructural, un objeto es mejor definido por un grupo de determinadas propiedades.
Por ejemplo, "si un estudiante está pensando en las posibles soluciones de un sistema de tres ecuaciones lineales con tres variables por visualización de las posibles posiciones de tres planos en el espacio, él está en el modo sintético-geométrico. Si ahora el estudiante piensa en el mismo problema en términos de los posibles resultados de una reducción por filas de una matriz de él, está en el modo analítico-aritmético. Pensando en términos de matrices invertibles y no invertibles, podría ser un síntoma del modo analítico-estructural" (Sierpinska, 2000).
3. METOLOGÍADesde los objetivos de investigación, ha sido pertinente utilizar un diseño metodológico de estudio de caso, en la medida que son particularmente apropiados para estudiar una situación en intensidad, en un período de tiempo, facilitando la identificación de los distintos procesos interactivos que conforman una realidad (Arnal, Del Rincón y Latorre, 1992). Se refiere a "caso" en la medida que: analiza en concreto realidades específicas y singulares, que adquieren su valor como indagaciones intensivas, y con profundidad en casos particulares; contrasta realidades específicas de las que pueden extraerse problemas comunes y matizaciones singulares, pero de ninguna manera explicaciones genéricas y definitivas sobre la realidad estudiada. De esta estrategia metodológica se deriva, un tipo de conocimiento conceptual, que sirve para comprender realidades concretas, dentro de un contexto global. Permite aproximarse a la complejidad de los múltiples y diferentes procesos que se desencadenan en el transcurso de una situación particular en estudio. Enfatiza tanto en aquellos elementos comunes de los casos, como en aquellos elementos diferenciadores que complejizan, diversifican y especifican cada una de las diferentes experiencias estudiadas.
"...Los estudios de casos son adecuados para un análisis intensivo y profundo de uno o pocos ejemplos de ciertos fenómenos;..." (Goetz y LeCompte, 1988, p. 69). Según Elliot (1994), las relaciones se iluminan mediante la descripción concreta de realidades sociales y personales, a través de leyes causales y de correlaciones estadísticas. Los estudios de casos proporcionan una teoría naturalista de la situación, que en esta investigación pretende aportar a nuestra comunidad en un tema tan relevante como lo es, conexiones entre los conceptos dependencia e independencia lineal de vectores y el de solución de sistemas de ecuaciones lineales.
Con el propósito de indagar en los modos de pensar, SG, AA y AE, la comprensión y conexión de los conceptos en estudio, que muestran estudiantes universitarios, se diseñan instrumentos -cuestionarios- para que den luces de lo que podría estar sucediendo con la coordinación y tránsito entre estos tres modos.
A continuación detallamos algunos de los aspectos más importantes de la metodología y fase de experimentación de esta investigación.
Implementación de la situación
La situación que se implementó en la investigación corresponde a la aplicación de un cuestionario a estudiantes de una Institución de Educación Superior chilena. A continuación algunos de los detalles más importantes de los informantes a los que se aplicaron las 8 preguntas que conformaban el cuestionario.
Población objetivo
La población objetivo corresponde a estudiantes voluntarios de un establecimiento de educación superior chilena, ya que es en este nivel donde se realizan los cursos de álgebra lineal. Los estudiantes voluntarios que conforman los dos casos de estudio son siete. De de estos siete estudiantes, tres que cursan el quinto semestre de Licenciatura en Matemática conforman el caso 1 y cuatro que cursan quinto semestre de Pedagogía en Matemática conforman el caso 2 (ver tabla 1). Todos los estudiantes a los que se les aplicó el cuestionario aprobaron el curso de Álgebra Lineal y se caracterizan por ser estudiantes con buenos resultados académicos.
Tabla 1: Resumen de informantes y técnicas de recogida de información.

Justificación de la población objetivo
Los criterios de selección de estas unidades de estudios trabajadas como "casos", se vinculan con las siguientes categorías e indicadores:
- Estudiantes de educación superior: Los conceptos dependencia e independencia lineal y solución de un sistema de ecuaciones lineales son vistos en conjunto en este nivel.
- Estudiantes exitosos: Esto permite apreciar la relación entre el éxito que tienen los estudiantes en la asignatura Álgebra Lineal y el nivel de logro en el aprendizaje de cada uno de los conceptos matemáticos en juego. Además, consideramos que estudiantes con estas características pueden establecer mejores conexiones entre los conceptos involucrados.
- Estudiantes que aprobaron Álgebra Lineal: Debido a que aprobaron este curso el semestre anterior al que se encuentran actualmente, por lo que tienen mayores posibilidades de acceder a todos los conceptos principales del Álgebra Lineal.
- Estudiantes de Licenciatura en Matemática: Porque es una carrera puramente matemática, por lo que se espera un nivel más completo y acabado de los conceptos que en otras carreras. Con esto también buscamos que el contenido matemático no sea el principal obstáculo al momento de enfrentarse los estudiantes al cuestionario.
- Estudiantes de Pedagogía en Matemática: Porque al igual que en la Licenciatura esta es una carrera relacionada directamente con la matemática y también para indagar en las conexiones de los futuros docentes entre conceptos como vectores, sistema de ecuaciones, etc. Al igual que con los estudiantes de Licenciatura en Matemática, con esto también buscamos que el contenido matemático no sea el principal obstáculo al momento de enfrentarse los estudiantes al cuestionario.
- Accesibilidad: Los investigadores tienen la posibilidad de acceder a estudiantes de esta Institución de Educación Superior.
Toma de datos
La toma de datos consistió en la aplicación del cuestionario a fines de Mayo del año 2011, el cual respondió cada uno de los siete estudiantes que conforman los dos casos de estudio de manera individual, en 120 minutos aproximadamente. Además, para optimizar el espacio y concentración de los estudiantes, así como la observación del investigador, la aplicación del cuestionario se llevó a cabo en dos grupos: el primer grupo compuesto de tres estudiantes de Licenciatura en Matemática y el segundo grupo compuesto de cuatro Estudiantes de Pedagogía en Matemática.
Instrumento
El instrumento que se aplicó corresponde a un cuestionario de ocho preguntas abiertas. A continuación se describen algunos de los detalles más importantes de éste.
Preguntas del cuestionario
Las cuatro primeras preguntas del cuestionario (Anexo), cada una de ellas con partes (a) y (b), relacionan los conceptos dependencia e independencia lineal y solución de un sistema de ecuaciones lineales en R2 con operaciones usuales, enfocadas desde los distintos modos de pensamiento.
Las siguientes tres preguntas del cuestionario, cada una de ellas con partes (a) y (b), relacionan los conceptos dependencia e independencia lineal y solución de un sistema de ecuaciones lineales en R3 con operaciones usuales, enfocadas desde los distintos modos de pensamiento.
La última pregunta del cuestionario, con partes (a) y (b), relaciona los conceptos dependencia e independencia lineal y solución de un sistema de ecuaciones lineales en R2 con operaciones no usuales.
Objetivos generales de las preguntas
- Identificar el (los) modo(s) de pensamiento que predomina(n) en el (los) estudiante(s).
- Promover en el estudiante el tránsito entre los distintos modos de pensamiento
- Indagar algunas conexiones entre los conceptos involucrados (cada pregunta establece conexiones entre los conceptos dependencia e independencia lineal y el de solución de un sistema de ecuaciones).
Validación del instrumento
El instrumento aplicado a los estudiantes fue sometido a diversas instancias de co-evalución por un grupo de didactas con investigaciones relacionadas y no relacionadas con la investigación. Además, la versión final del cuestionario es fruto de una reestructuración y reformulación de diseño de preguntas que buscaban rescatar desde los estudiantes las conexiones que éstos logran establecer entre los conceptos solución de un sistema de ecuaciones lineales en R2 y R3 con los de dependencia e independencia lineal de vectores.
Análisis a priori de las preguntas
A continuación se presenta el análisis a priori de dos de las preguntas del cuestionario (pregunta 4 y 6) aplicadas a los estudiantes, a través de las cuales se obtuvo información importante, la cual será confrontada posteriormente a través del análisis a posteriori.
Pregunta 4: A continuación se presenta la solución gráfica de un sistema de 3 ecuaciones lineales con 2 incógnitas:

a. En R2, con las operaciones suma y ponderación usuales, ¿los vectores generadores de cada una de las rectas del sistema (vistas como subespacios de R2) forman un conjunto linealmente independiente? Justifique su respuesta.
b. ¿Tiene solución el sistema? ¿Cuántas? Justifique su respuesta.
Pregunta 6: Sean ![]() ,
, ![]() y
y ![]() tres vectores en R3, con las operaciones suma y ponderación usuales. Para cualquier combinación lineal de la forma:
tres vectores en R3, con las operaciones suma y ponderación usuales. Para cualquier combinación lineal de la forma:
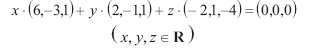
Si se iguala coordenada a coordenada se obtiene un sistema lineal homogéneo de 3 ecuaciones con 3 incógnitas, cuya solución gráfica, vista desde distintas posiciones, es la siguiente:
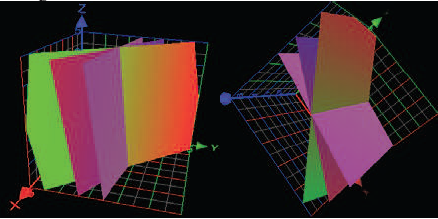
A partir de lo anterior se pregunta:
a. ¿Cuál es el conjunto solución del sistema? Justifique su respuesta
b. ¿El conjuntoes linealmente independiente? Justifique su respuesta
Respuesta experta pregunta 4
a. Como el sistema consta de tres rectas, el conjunto formado por los vectores generadores de cada una de ellas tiene tres vectores. Como en R2 el número máximo de vectores linealmente independiente es 2, este conjunto es linealmente dependiente.
b. Gráficamente se puede ver que las tres rectas del sistema pasan por el origen de coordenadas, que es el único punto común entre ellas. Por lo tanto, el sistema tiene solución única, el (0,0).
Respuesta experta pregunta 6
a. Se puede ver que la solución gráfica del sistema corresponde a tres planos que se intersectan en una recta. Por lo tanto, el sistema tiene una recta solución, es decir, infinitas soluciones.
b. El sistema resuelto en la primera parte de la pregunta proviene de la combinación lineal ![]()
Como el sistema tiene infinitas soluciones, existen infinitas tripletas (x,y,z), distintas de la trivial (0,0,0),que satisfacen la combinación lineal descrita anteriormente, por lo que el conjunto ![]() es linealmente dependiente.
es linealmente dependiente.
Análisis a priori de la pregunta 4 de las posibles respuestas de los estudiantes desde los modos de pensamiento
Si el estudiante relaciona la independencia lineal de vectores con vectores no colineales, puede interpretar la situación mostrada en la gráfica como vectores no colineales y por tanto vectores linealmente independientes (figura 6). Este argumento sitúa al estudiante en un modo de pensar SG, pues es su representación geométrica del concepto independencia lineal de vectores la que lo llevaría a concluir de esa manera. A partir de este argumento pueda darse que el estudiante relacione independencia lineal con solución única del sistema, estableciendo una conexión, errónea en este caso pues el conjunto es linealmente dependiente, entre los conceptos independencia lineal y solución de un sistema de ecuaciones lineales.
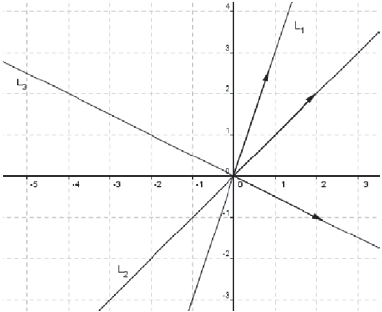
Figura 6: Rectas del sistema de la pregunta 3 y sus vectores generadores
Aquel estudiante que argumenta a partir de la gráfica que el sistema está formado por 3 vectores en R2 y por tanto es linealmente dependiente podría estar situando su pensamiento en el modo AE, ya que si bien la gráfica es lo que le permite observar 3 vectores en R2, es su estructura como espacio vectorial la que le permite concluir.
Se espera que algunos estudiantes continúen situándose en el modo AA para responder las preguntas. En este caso, una respuesta que reflejaría tal hecho sería el determinar las coordenadas de cada uno de los vectores generadores de las rectas y a través de ellas concluir que el conjunto de vectores es linealmente independiente o no.
Para responder la segunda parte de la pregunta, el estudiante puede observar que la única intersección común de las rectas es el (0,0) y concluir que la solución es única. En este caso, el estudiante estaría situado en el modo de pensamiento SG, pues la solución gráfica del sistema le es suficiente para resolverlo.
Es posible que algunos estudiantes determinen las ecuaciones de cada una de las rectas y a partir de ellas resuelvan el sistema mediante algún método algebraico. En este caso, el estudiante no lograría interpretar la gráfica en términos de la solución del sistema y se situaría en el modo de pensamiento AA.
En esta pregunta el estudiante podría incurrir en los siguientes errores:
- Interpretar la no colinealidad de vectores como independencia lineal del conjunto formado por ellos.
- Concluir o reafirmar que, dado que el sistema de ecuaciones tiene solución única, el conjunto de vectores es linealmente independiente debido a que solución única implica independencia lineal de vectores.
Análisis a priori de la pregunta 6 de las posibles respuestas de los estudiantes desde los modos de pensamiento
Para poder identificar la recta intersección de los planos como la solución del sistema de ecuaciones planteado, el estudiante requiere tener una concepción geométrica del concepto solución de un sistema de ecuaciones lineales en R3. Así, el estudiante que responde que el sistema tiene infinitas soluciones debido a que los tres planos se intersectan en una recta evidencia un modo de pensamiento SG, pues las gráficas presentadas en la pregunta son las que le permiten concluir.
Es posible que algún estudiante no logre situarse en un modo de pensamiento SG para resolver el problema, frente a lo cual prefiera obtener las ecuaciones del sistema a partir de la combinación lineal y luego resolver el sistema. En este caso, las ecuaciones del sistema son:
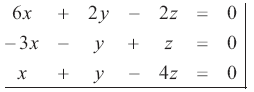
Aquí el estudiante no utilizaría toda la información presentada en el problema y sólo recurriría a aquellos aspectos de la pregunta que le favorecen un modo de pensamiento AA, ya que al no poder interpretar la intersección de planos como la solución del sistema preferiría recurrir a sus ecuaciones y mediante algún método algebraico resolverlo y obtener el conjunto solución.
Si el estudiante logra conectar los conceptos solución de un sistema de ecuaciones lineales homogéneo y el de dependencia lineal de vectores, podrá concluir que el conjunto de vectores es linealmente dependiente debido a que el sistema de ecuaciones proveniente de la combinación lineal formada e igualada al vector nulo tiene infinitas soluciones. Si no logra establecer conexiones, es probable que el estudiante resuelva dos veces el mismo sistema, sin advertirlo.
Si el estudiante concibe la dependencia lineal como vectores colineales, es probable que concluya que el conjunto es linealmente independiente, ya que ninguno es un ponderado del otro. En este caso, si el argumento proviene de las coordenadas de los vectores, diremos que el estudiante muestra un modo de pensamiento AA, mientras que si el argumento es en base a una representación geométrica de los vectores en tres direcciones diferentes diremos que muestra un modo de pensamiento SG.
Es posible que algún estudiante extienda la idea en R2 de relacionar vectores linealmente independientes con vectores no colineales a R3, relacionando planos no coincidentes con la de un conjunto de vectores linealmente independientes, pudiendo concluir que el conjunto de vectores es linealmente independiente. Este razonamiento proviene de la interpretación geométrica que se le puede dar a la dependencia e independencia lineal de vectores en R3, por lo que un argumento así evidenciaría que el estudiante está situado en un modo de pensamiento SG.
Es posible que algún estudiante se base en vectores normales de cada uno de los planos que conforma el sistema. Así, puede concluir que las normales de cada uno de los planos no son colineales y por tanto el conjunto de vectores es linealmente independiente, lo que respondería nuevamente a una extensión errónea de la representación geométrica de dos vectores linealmente independientes en R2 a tres vectores linealmente independientes en R3. En este caso, el argumento se basa en la representación geométrica de vectores en R3, por lo que el modo de pensamiento en el que estaría situado un estudiante bajo esta respuesta es el SG.
4. RESULTADOS
En los análisis los estudiantes del caso 1 son identificados como E1, E2 y E3, y los del caso 2 E4, E5, E6 y E7.
Análisis a posteriori de la pregunta 4
Análisis de las respuestas de los estudiantes parte 4a
Los estudiantes E1 y E5 se basan en la gráfica para señalar que cada una de las rectas tiene un vector generador diferente (sin señalar cuáles son esos vectores generadores). A partir de ello, concluyen que el conjunto formado por estos es linealmente independiente, ya que ninguno es combinación lineal del otro (figura 7). Esto refleja lo que señalamos en el análisis a priori respecto a la interpretación de vectores no colineales como vectores linealmente independientes. El argumento utilizado por estos dos estudiantes se basa en la interpretación de la gráfica presentada en la pregunta, lo que de acuerdo a lo señalado en el análisis a priori sitúa sus pensamientos en el modo SG.

Figura 7: Respuesta pregunta 4.a estudiante 1.
El estudiante E6 nuevamente sitúa su pensamiento en el modo SG, pero su argumento es diferente al de E1 y E5. Considera conjuntos de dos vectores (al parecer, se resiste a tomar conjuntos de tres vectores en R2) y concluye que entre ellos existe independencia lineal ya que todos generan a R2 (ver figura 8), por lo que el conjunto formado por los tres vectores es linealmente independiente.

Figura 8: Respuesta pregunta 4.a estudiante 6.
Los estudiantes E2, E4 y E7 también concluyen que el conjunto de vectores es linealmente independiente. Para ello obtienen las coordenadas de cada uno de los vectores generadores de las rectas y responden que ninguno pertenece a la misma recta (figura 9).

Figura 9: Respuesta pregunta 4.a estudiante 4.
En este argumento podemos apreciar una conexión entre los modos AA y SG, ya que primero determinan las coordenadas de los vectores generadores y luego los asocian a una de las tres rectas, es decir, desde lo aritmético (coordenadas) se sitúan en la gráfica que presenta el problema (un vector para cada recta), concluyendo finalmente que son linealmente independientes por no colinealidad de las rectas. Así, el argumento dado por estos estudiantes los sitúa en un tránsito desde el modo SG al AA, ya que a partir de la gráfica obtienen las coordenadas de cada vector generador, para luego volver a realizar un tránsito desde el modo AA al SG, identificando cada vector como el generador de una recta diferente a la generada por otro. De esta forma, los seis estudiantes que hemos analizado en esta parte de la pregunta 4 evidencian una concepción de independencia lineal de vectores en R2 restringida a la no colinealidad de los vectores.
El estudiante E3 fue el único de los 7 estudiantes, que concluyó que el conjunto de vectores es linealmente dependiente. Para ello obtuvo primero las coordenadas de los vectores generadores de cada una de las rectas. Sin embargo, su argumento no se basa en las coordenadas sino en la dimensión del espacio vectorial R2 y como consecuencia de ello al conjunto maximal de vectores linealmente independientes que se puede tener en él (figura 10). En este caso, el estudiante E3 se sitúa inicialmente en un modo de pensamiento AA (determina las coordenadas de los vectores generadores), pero su argumento se basa en la dimensión de R2, que le entrega el número máximo de vectores linealmente independientes en él. Como esto responde a un argumento elaborado más bien en torno a propiedades de los espacios vectoriales que a operaciones aritméticas, consideramos que este estudiante puede estar situando su pensamiento en el modo AE. No obstante, puede ser muy precipitado afirmarlo, ya que no queda del todo claro si su conclusión es simplemente una aplicación de un teorema o si la pregunta la está analizando desde la estructura del espacio vectorial R2.

Figura 10: Respuesta pregunta 4.a estudiante 3.
Análisis de las respuestas de los estudiantes parte 4b
Los estudiantes E1, E5, E6 y E7 responden que la solución del sistema es el (0,0), ya que es el lugar donde se intersectan las tres rectas (figuras 11 y 12). De acuerdo al análisis a priori de esta parte de la pregunta, estos estudiantes sitúan su pensamiento en el modo SG, ya que la gráfica le es suficiente para concluir su respuesta.

Figura 11: Respuesta pregunta 4.b estudiante 5.

Figura 12: Respuesta pregunta 4.b estudiante 6.
El estudiante E3 identifica como única solución el (0,0), haciendo referencia a que es el único punto que satisface las tres ecuaciones simultáneamente. Como no determina las ecuaciones de cada una de las rectas (figura 13), se infiere una interacción de este estudiante entre los modos SG y AA, ya que identifica la solución del sistema (que responde al modo SG, pues es capaz de responder esto sólo con la información presentada en la pregunta, es decir, la solución gráfica del sistema) con el único par ordenado de R2 que satisface las tres ecuaciones simultáneamente (que responde al modo AA, ya que identifica cada una de las rectas con una ecuación y la pertenencia de un punto a ella como aquel punto cuyas coordenadas satisfacen la ecuación de la recta).

Figura 13: Respuesta pregunta 4.b estudiante 3.
El estudiante E4 determina las ecuaciones de cada una de las rectas y resuelve el sistema sustituyendo una de las variables en las otras ecuaciones. De esta forma, concluye que la solución es única: x = 0 e y = 0 (figura 14). De acuerdo al análisis a priori de esta parte de la pregunta el estudiante sitúa su pensamiento en el modo AA, ya que la gráfica presentada la utiliza sólo para determinar la ecuación de cada una de las rectas, lo que muestra que el estudiante E4 no tiene una concepción geométrica clara de solución de un sistema de ecuaciones lineales, ya que en la pregunta 3 también determinó las ecuaciones de las rectas para resolver el sistema.

Figura 14: Respuesta pregunta 4.b estudiante 4.
El estudiante E2 emplea una estrategia de tipo aritmético diferente a la de los demás estudiantes. Para responder a la pregunta utiliza una especie de teorema que trata sobre "el número de ecuaciones menos el número de incógnitas" (figura 15).

Figura 15: Respuesta pregunta 4.b estudiante 2.
Argumenta que como la diferencia es igual a 1, la solución tiene un parámetro, lo que, se subentiende, apuntaría a un conjunto infinito de soluciones que tiene el sistema. Parece que este argumento puede estar relacionado con la creencia de necesitar "n" ecuaciones para resolver un sistema en el que hay "n" variables. En este caso, la gráfica no le es suficiente para concluir, por lo que prefiere recurrir a un sistema de ecuaciones en términos de ecuaciones y variables. Al igual que el estudiante E4, el estudiante E2 no demuestra tener una concepción geométrica clara del concepto solución de un sistema de ecuaciones lineales, ya que en la pregunta 3 también recurrió a las ecuaciones de las rectas para resolver el sistema.
Por lo tanto, en esta pregunta nuevamente no hay un modo de pensamiento que predomine por sobre otro, ya que algunos estudiantes recurren al modo AA y otros al SG (e incluso es posible de que uno de los estudiantes se esté situando en el modo AE). Además pudimos observar que las sospechas respecto a la relación que establecerían los estudiantes entre la no colinealidad de vectores en R2 y la independencia lineal de los mismos era cierta, ya que al parecer algunos estudiantes extienden el modelo que presenta dos vectores linealmente independientes como colineales en R2 a tres vectores en R2.
Análisis a posteriori de la pregunta 6
Análisis de las respuestas de los estudiantes parte 6a
Sólo los estudiantes E1, E6 y E7 se apoyan en la representación gráfica de la solución del sistema de ecuaciones lineales para responder a la pregunta (figuras 16 y 17). Sin embargo los estudiantes E1 y E6 identifican en la gráfica una infinidad de puntos, ya que los planos se intersectan en una recta, siendo éste el conjunto solución. Para ambos estudiantes la gráfica es suficiente para responder a la pregunta, sin recurrir a operaciones aritméticas, por lo que su pensamiento está situado en el modo SG.

Figura 16: Respuesta pregunta 6.a estudiante 7.
El estudiante E6 obtiene primero el sistema desde la combinación lineal de los vectores y argumenta que resolver el sistema obtenido es equivalente a resolver un sistema en R2 con rectas (figura 17), con la diferencia que en esta ocasión los objetos geométricos son planos. Esto muestra que el estudiante E6 continúa recurriendo al modo SG para resolver las preguntas, con la distinción que a medida que avanza en el cuestionario comienza a transitar cada vez más entre los modos AA y SG.

Figura 17: Respuesta pregunta 6.a estudiante 6.
Los estudiantes E2, E3, E4 y E5 optan por resolver el sistema de ecuaciones a partir de la combinación lineal de los vectores, pero los estudiantes E2, E3 y E5 llevan el sistema a su forma matricial y lo resuelven, concluyendo que tiene infinitas soluciones (figuras 18 y 19).

Figura 18: Respuesta pregunta 6.a estudiante 3.

Figura 19: Respuesta pregunta 6.a estudiante 5.
El estudiante E4 en cambio opta por resolver el sistema sustituyendo variables en términos de otra (figura 20).

Figura 20: Respuesta pregunta 6.a estudiante 4.
En ambos casos los estudiantes prefieren trabajar con las ecuaciones del sistema en lugar de interpretar su solución gráfica, lo que muestra una tendencia y comodidad hacia este tipo de trabajo; situándose en el modo AA.
Análisis de las respuestas de los estudiantes parte 6b
Los estudiantes E1 y E2 responden que el conjunto es linealmente dependiente recurriendo a un argumento geométrico. Por una parte (figura 21), el estudiante E1 argumenta que como el sistema tiene infinitas soluciones, el conjunto es linealmente dependiente; su argumento se basa en la respuesta dada a la primera parte de la pregunta, en donde argumentó que gráficamente se observan infinitos puntos en la intersección de los planos. Por tanto, su pensamiento a lo largo de toda la pregunta se sitúa en el modo SG, ya que sólo recurre a la gráfica y a la interpretación de ésta para responder. Además, establece conexiones adecuadas entre los conceptos solución de un sistema de ecuaciones lineales y dependencia lineal de vectores.

Figura 21: Respuesta pregunta 6.b estudiante 1.
Por otra parte (figura 22), el estudiante E2 establece que ninguna de las rectas pasa por el origen. Esto lleva a pensar que logra establecer conexiones entre los conceptos solución de un sistema de ecuaciones lineales y dependencia lineal de vectores, pero en R3 estas conexiones son erradas, ya que no logra interpretar correctamente la gráfica, fijando su atención en los ejes coordenados en lugar de los planos. Además, este estudiante situó su pensamiento en dos modos, ya que en la primera parte de la pregunta estaba situado en el modo AA, pero su argumento de la segunda parte lleva a situarla en el modo SG. A pesar de ello no se evidencia tránsito entre estos dos modos de pensamiento, ya que ambas preguntas las resuelve por separado.

Figura 22: Respuesta pregunta 6.b estudiante 2.
Los estudiantes E3 y E5 concluyen que el conjunto de vectores no puede ser linealmente independiente, ya que la solución del sistema obtenido en la primera parte de la pregunta es el (0,0,0) (figura 23). Por lo tanto, ambos estudiantes continúan situando su pensamiento en el modo AA para responder a la pregunta y además logran establecer conexiones correctas entre los conceptos solución de un sistema de ecuaciones lineales y dependencia lineal de vectores, ya que la primera es el argumento para responder a la segunda.

Figura 23: Respuesta pregunta 6.b estudiante 3.
Los estudiantes E4 y E7 concluyen erróneamente que el conjunto de vectores es linealmente independiente. Por una parte, el estudiante E4 forma una matriz con los vectores y señala que ninguna de las columnas es igual a 0 (figura 24). Por lo tanto, su argumento depende de las relaciones numéricas que establece a partir de la matriz, lo que sitúa su pensamiento en el modo AA.

Figura 24: Respuesta pregunta 6.b estudiante 4.
Por otro lado, el estudiante E7 argumenta que ninguno de los vectores puede ser expresado como un ponderado de otro vector del conjunto (figura 25). Vemos así que este estudiante establece una equivalencia entre la colinealidad de un par de vectores y la dependencia lineal del conjunto completo. Además, su argumento se fundamenta en las coordenadas de los vectores, por lo que su pensamiento está situado en el modo AA, y no establece conexiones entre los conceptos solución de un sistema de ecuaciones lineales y dependencia lineal de vectores, ya que ambas partes de la pregunta las resuelve por separado.

Figura 25: Respuesta pregunta 6.b estudiante 7.
El estudiante E6 también responde que el conjunto de vectores es linealmente independiente, pero su argumento es del tipo geométrico (figura 26). Por una parte establece que cada vector genera un plano diferente y por otra señala que para que el conjunto fuese linealmente dependiente la gráfica debería corresponder a dos planos (dos de los tres planos coincidentes) o un solo plano (los tres planos coincidentes).

Figura 26: Respuesta pregunta 6.b estudiante 6.
Al basar su argumento sólo en la gráfica, se concluye que el estudiante sitúa su pensamiento en el modo SG. Además, logra establecer conexiones entre los conceptos solución de un sistema de ecuaciones lineales y dependencia lineal de vectores, aunque éstas son incorrectas. Creemos que su conclusión responde a una extensión del concepto que tiene de dependencia lineal de vectores en R2 a R3, ya que en la pregunta 4 del cuestionario argumentó que el conjunto de vectores es linealmente independiente debido a la no colinealidad de éstos, lo que parece generalizar a R3 al concebir el conjunto de vectores de la pregunta 6 linealmente independientes debido a que los planos no son coplanares. En este sentido, se infiere que extiende la idea de colinealidad en R2 a coplanar en R3.
Así se logra mostrar, que la mayoría de los estudiantes se sitúa en el modo de pensamiento AA para responder esta pregunta, evidenciando dificultades para dar una interpretación a la solución gráfica del sistema. La mayoría de los estudiantes prefiere trabajar con las coordenadas de los vectores, a pesar de que ello signifique un trabajo más extenso. Además, 5 de los 7 estudiantes evidenciaron en esta pregunta establecer conexiones entre los conceptos solución de un sistema de ecuaciones lineales y dependencia lineal de vectores en R3. Las conexiones adecuadas se dieron tanto en estudiantes situados en el modo AA como aquellos que evidenciaron un modo de pensamiento SG. No obstante, éstas se dieron principalmente cuando el estudiante se situó en el modo AA ¿y por qué AA? porque no podía dar interpretación geométrica a la solución del sistema de ecuaciones lineales. Por tanto, parece ser que el modo AA propicia de mejor manera conexiones entre ambos conceptos que el modo SG, esto debido a que los estudiantes privilegian el modo AA para responder. Respecto a las conexiones incorrectas, también se dieron en ambos casos, tanto en el modo AA como en el modo SG. No obstante, el origen parece ser el mismo: la idea de concebir la dependencia lineal de vectores exclusivamente como vectores colineales, lo que al parecer extienden a R3 a planos coplanares como condición necesaria y suficiente para que existe dependencia lineal de vectores.
5. CONCLUSIONES Y REFLEXIONES
Conclusiones respecto a los modos de pensamiento
Se ha podido constatar a través de las 8 preguntas del cuestionario, que en general, el modo de pensamiento que prevalece en los estudiantes del caso 1 y caso 2 es el AA. El modo SG aparece sólo en las preguntas que presentan gráfica -a excepción de un estudiante del caso 2 que logra transitar entre los modos AA y SG-. En las preguntas que presentan gráfica los estudiantes de ambos casos estuvieron distribuidos equitativamente en la forma de abordar el problema, ya que a algunos les bastó la gráfica para responder, pero otros prefirieron obtener las coordenadas de los vectores generadores para determinar dependencia e independencia lineal o determinar las ecuaciones de las rectas para resolver un sistema de ecuaciones lineales. Esto muestra que los estudiantes tienen una fuerte tendencia al modo AA para enfrentar los problemas relacionados con sistemas de ecuaciones lineales y los problemas relacionados con dependencia e independencia lineal de vectores.
En general los estudiantes logran transitar desde el modo SG al modo AA. Consideramos que esto se debe a la necesidad de establecer su pensamiento en el modo AA por parte de los estudiantes, ya que en general el tránsito se da frente a la no posibilidad de interpretar la solución gráfica de un sistema de ecuaciones.
La mayoría de los estudiantes presenta grandes dificultades para pensar los sistemas de ecuaciones lineales en el modo SG; algunos estudiantes que habían pensado los sistemas de ecuaciones en R2 en el modo SG cambiaron al modo AA en los sistemas de R3.
La mayoría de los estudiantes de ambos casos no logra situar su pensamiento en el modo AE. Cuando la estructura del espacio vectorial es modificada los estudiantes en su mayoría se sitúan en el modo AA, lo que los lleva a no cuestionarse sobre el concepto del cero vector de un espacio vectorial, asociándolo al par (0,0) o trío (0,0,0) -2-upla nula o 3-upla nula, respectivamente-, independiente de la estructura del espacio. Sólo aquellos estudiantes que acceden al modo AE logran identificar el cero vector de acuerdo a la estructura del espacio.
Cada vez que los estudiantes lograron transitar entre distintos modos de pensamiento el argumento que se puede observar tenía que ver con la definición formal del concepto, tanto de dependencia e independencia lineal de vectores como de solución de un sistema de ecuaciones lineales. Esto trae como consecuencia que el tránsito entre los distintos modos de pensar los conceptos solución de un sistema de ecuaciones lineales y dependencia e independencia lineal de vectores en R2 y R3 por parte de los estudiantes, tendría su origen en las definiciones formales de estos conceptos.
Conclusiones respecto a la conexión entre los conceptos
El concepto solución de un sistema de ecuaciones lineales, en su mayoría se reduce a un par o trío ordenado, dependiendo de si el problema corresponde a R2 o R3. Aproximadamente la mitad de los estudiantes de ambos casos no tiene un concepto geométrico del concepto solución de un sistema de ecuaciones lineales y aquellos que sí lo tienen lo asocian a la intersección común de rectas o planos. Esto tuvo consecuencias en cuanto a la conexión entre los conceptos dependencia e independencia lineal y el de solución de un sistema de ecuaciones lineales, ya que algunos estudiantes concluyen la independencia lineal de un conjunto de vectores argumentando que un vector es un ponderado del otro, pero para encontrar la solución del sistema recurren a las ecuaciones de las rectas y prefieren determinarla resolviendo algebraicamente.
La mayoría de los estudiantes manifestó concebir como equivalentes los conceptos colinealidad y dependencia lineal, así como no colinealidad a independencia lineal. Esta asociación entre ambos conceptos los lleva a establecer relaciones geométricas correctas respecto a la dependencia e independencia lineal sólo entre dos vectores en R2, cometiendo errores en el caso de tres vectores no colineales en R2. Consideramos que este modelo de representación de vectores colineales o no colineales aleja a los estudiantes de los conceptos de dependencia e independencia lineal, situándola por sobre su definición formal.
Algunos de los estudiantes que asociaron la dependencia lineal a vectores colineales en R2 tuvieron dificultades al cambiar la estructura del espacio vectorial. El concebir la dependencia lineal de esta forma los lleva a no considerar la combinación lineal igualada al cero vector y reducir el problema a escribir uno de los vectores como un ponderado del otro, y por tanto a no considerar la definición de la operación suma en el espacio vectorial. Esta idea en general situó a los estudiantes en el modo AA -cuando la colinealidad la explicaron en el sentido de un vector como ponderado de otro- o en el modo SG -cuando la colinealidad la explicaron en el sentido gráfico de vectores coincidentes-, no pudiendo acceder al modo AE.
Otro problema que presentaron los estudiantes a raíz de la representación de vectores linealmente dependientes en R2 como vectores colineales tiene que ver con la dependencia lineal de vectores en R3. Algunos estudiantes extendieron la idea de colinealidad de vectores en R2 a planos coplanares en R3, estableciendo una equivalencia entre vectores linealmente dependientes en R3 y planos coplanares como solución gráfica del sistema de ecuaciones proveniente de la combinación lineal igualada al vector cero. En consecuencia, las representaciones de vectores linealmente dependientes en R2 y R3 asociadas a vectores colineales y planos coplanares lleva a los estudiantes a una limitación, y en algunos casos a errores, en sus conexiones entre los conceptos dependencia e independencia lineal de vectores y el de solución de un sistema de ecuaciones lineales en R2 y R3.
En general los estudiantes de ambos casos no establecen conexiones entre los conceptos solución de un sistema de ecuaciones lineales y el de dependencia e independencia lineal cuando trabajan en R2. La mayoría de ellos resuelve por separado el sistema de ecuaciones lineales y la dependencia lineal de vectores, sin advertir que ambas equivalen a resolver el mismo sistema de ecuaciones. Sin embargo, al trabajar con vectores en R3 la mayoría de los estudiantes logran conectar estos conceptos. Consideramos que esto se debe principalmente a dos aspectos: primero, la estructuración del cuestionario, ya que el estudiante se enfrentó a las preguntas relacionadas con R3 después haberse enfrentado a las preguntas relacionadas con R2 , las que están orientadas precisamente a conectar estos conceptos. En este sentido, pensamos que los estudiantes logran conectar los conceptos solución de un sistema de ecuaciones lineales y el de dependencia e independencia lineal en R3 debido al esfuerzo de intentar conectar con anterioridad estos mismos conceptos en R2 ; segundo, el que los sistemas de ecuaciones presentados en R3 son más evidentes que los presentados en R2 . Además, cuando se cambió la estructura del espacio vectorial, aquellos estudiantes que se situaron constantemente en el modo AA no lograron conectar los conceptos, llegando a identificar el concepto de independencia lineal de vectores con la solución vacía de un sistema de ecuaciones lineales.
Finalmente, señalamos que dentro de las conexiones que lograron establecer los estudiantes entre los conceptos solución de un sistema de ecuaciones lineales y el de dependencia e independencia lineal de vectores, éstas se dieron tanto en estudiantes situados en los modos AA y SG. No obstante, en su mayoría las conexiones se dieron cuando estaban situados en el modo AA, lo cual coincide con el hecho de que en general el modo que prevalece en los estudiantes es el AA, tanto en las preguntas relacionadas con R2 y R3. Dentro de las conexiones que establecieron los estudiantes no todas fueron correctas. En cambio, aquellos estudiantes que lograron situarse en el modo AE lograron establecer conexiones correctas entre los conceptos en juego, lo cual coincide con la hipótesis de que sólo aquellos estudiantes que logran transitar por el modo AE, tanto en los conceptos dependencia e independencia lineal como en el de solución de un sistema de ecuaciones lineales en R2 y R3 pueden llegar a establecer conexiones adecuadas entre ambos conceptos.
Conclusiones didácticas y reflexiones
Respecto a los sistemas de ecuaciones, podemos dar evidencias que no todos los estudiantes tienen un concepto geométrico de la solución de un sistema de ecuaciones lineales, porque la mayoría de las veces se sitúan desde el álgebra para abordar y resolver los problemas, lo que limita no sólo su desenvolvimiento en la disciplina del álgebra lineal, sino que también, su concepción de los objetos matemáticos presentados. Consideramos que esto es consecuencia de la forma en la que se abordan usualmente los sistemas de ecuaciones lineales (con énfasis en lo algebraico en desmedro de lo geométrico) y la importancia que se le dan a los métodos de resolución algebraica. Cabe destacar además que el resolver un sistema por alguno de los métodos algebraicos convencionales no necesariamente constituye un aprendizaje logrado puesto que el estudiante puede estar respondiendo solamente a un algoritmo. Es por esto que consideramos fundamental ser enfático en la solución gráfica e interpretación geométrica de éstos al momento de enseñar los sistemas de ecuaciones, que por lo general es la menos considerada y profundizada de los métodos de resolución. A su vez, los otros conceptos del álgebra lineal que aparecieron en los cuestionarios, tanto en las preguntas propuestas a los estudiantes como en las respuestas de los mismos, son principalmente trabajados desde el álgebra por parte de los estudiantes, en cualquier curso inicial de álgebra lineal. Consideramos que esto también es consecuencia de la enseñanza que han recibido los estudiantes, ya que en general recurren a los mismos argumentos -algebraicos en su mayoría-. En general recurren a la interpretación geométrica del concepto, como un último recurso de argumento, y cuando no son capaces de dar una interpretación algebraica de lo que están haciendo. Por tanto, consideramos fundamental el presentar en la enseñanza del álgebra lineal constantemente la interpretación algebraica en armonía con la geométrica de los conceptos, de manera que el estudiante logre transitar entre los modos AA y SG sin mayor problema.
Uno de los factores importantes y que se identificaron como clave para que el estudiante logre transitar entre los diferentes modos de pensamiento es la forma en que se aproxima a la definición formal de los conceptos. Consideramos que ésta es la que permite al estudiante discernir si lo que piensa es adecuado o no. En este sentido, diferentes aproximaciones a la definición formal del concepto matemático es uno de los principales puentes que permite al estudiante transitar correctamente entre los tres modos de pensamiento. No obstante, para poder lograr esta conexión debe aprender previamente a situarse desde distintas posturas que están presentes en el álgebra lineal: lo geométrico, lo analítico y lo estructural, lo que se logra situando al estudiante frente al concepto en diferentes contextos. Por tanto, consideramos que la definición formal de los conceptos es fundamental y necesaria para poder transitar entre los tres modos de pensamiento, pero en absoluto suficiente.
Una de las representaciones más usuales de vectores linealmente dependientes en el plano son los vectores colineales, lo que se acomoda muy bien al uso común de la palabra dependiente, ya que al ser los vectores colineales dependiente del mismo vector generador. Sin embargo, esta representación, geométrica en el caso de vectores colineales y algebraica en el caso de un vector escrito como un ponderado del otro, lleva muchas veces al estudiante a construir un incorrecto concepto de dependencia e independencia lineal al establecer una equivalencia con el ser colineales o no colineales, en dimensiones más grandes que dos. Por esta razón parece fundamental presentar a los estudiantes distintos modelos de representación geométrica de vectores linealmente dependientes en R2, que consideren más de dos vectores. En particular, presentar a los estudiantes más de dos vectores en R2, todos no colineales, puede contribuir a una restructuración de su concepto de dependencia e independencia lineal de vectores.
Un concepto que debe ser trabajado con más detalles es el del cero vector de un espacio vectorial. Puede ser que el llamarle cero vector incida en que el estudiante lo asocie necesariamente con el (0,0), pero parece que la principal razón es que por lo general los ejercicios a los que se someten los estudiantes trabajan con las operaciones usuales en R2 y R3, lo que dificulta que el estudiante recurra en alguna ocasión a las propiedades que debe cumplir el cero vector en su estructura algebraica de grupo abeliano. Por tanto, consideramos que el incluir entre los ejemplos y la ejercitación espacios vectoriales con operaciones no usuales contribuye a una mejor y más adecuada construcción del concepto cero vector.
Un factor importante que consideramos tiene que ver con la poca conexión que los estudiantes realizan entre los conceptos solución de un sistema de ecuaciones lineales y dependencia e independencia lineal tiene que ver con la forma en la que son enseñados ambos conceptos a la vez. Por una parte, por lo general se presenta el decidir la dependencia e independencia lineal de vectores como el resolver un sistema de ecuaciones lineales homogéneo. En este sentido, los sistemas de ecuaciones pasan a ser una herramienta para resolver el problema de la dependencia lineal. En cambio, para resolver los sistemas de ecuaciones lineales una de las estrategias más usadas por los estudiantes en el cuestionario aplicado, fue el llevarlo a su forma matricial y escalonar la matriz, lo que da cuenta de la relación del tipo de solución de un sistema con la dependencia o independencia lineal de los vectores involucrados. No obstante, consideramos que en general esta estrategia fue utilizada sólo como un algoritmo de resolución y que los estudiantes no logran establecer conexiones. Para contribuir a la conexión entre ambos conceptos consideramos fundamental el situar al estudiante no sólo en el modo AA para resolver los problemas de dependencia lineal y sistemas de ecuaciones, ya que esto puede limitarlo a aplicar un algoritmo y no mirar con profundidad el tema.
ANEXO
Cuestionario Completo
1. Dado el siguiente sistema de ecuaciones:
![]()
a. ¿Tiene solución el sistema? ¿Cuántas?

b. Considere las rectas del sistema como subespacios de R2, con las operaciones suma y ponderación usuales. ¿El conjunto formado por los vectores generadores de cada uno de estos subespacios son linealmente independientes? Justifique su respuesta.

2. Dado el siguiente sistema de ecuaciones:
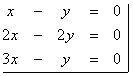
a. Considere las rectas del sistema como subespacios de R2, con las operaciones suma y ponderación usuales. ¿El conjunto formado por los vectores generadores de cada uno de estos subespacios son linealmente independientes? Justifique su respuesta.
b. ¿Tiene solución el sistema? ¿Cuántas?
3. A continuación se presenta la solución gráfica de un sistema de 3 ecuaciones con 2 incógnitas:
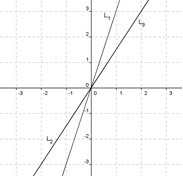
a. ¿Tiene solución el sistema? ¿Cuántas? Justifique su respuesta.
b. En R2, con las operaciones suma y ponderación usuales, ¿los vectores generadores de cada una de las rectas del sistema (vistas como subespacios de R2) forman un conjunto linealmente independiente? Justifique su respuesta.
4. A continuación se presenta la solución gráfica de un sistema de 3 ecuaciones con 2 incógnitas:

a. En R2, con las operaciones suma y ponderación usuales, ¿los vectores generadores de cada una de las rectas del sistema (vistas como subespacios de R2) forman un conjunto linealmente independiente? Justifique su respuesta.
b. ¿Tiene solución el sistema? ¿Cuántas? Justifique su respuesta.

Sean ![]() ,
, ![]() y
y ![]() tres vectores en R3, con las operaciones suma y ponderación usuales. Para cualquier combinación lineal de la forma
tres vectores en R3, con las operaciones suma y ponderación usuales. Para cualquier combinación lineal de la forma
![]()
e igualando coordenada a coordenada se obtiene el siguiente sistema lineal homogéneo:
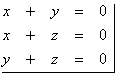
a. ¿Cuántas soluciones tiene el sistema? Justifique su respuesta.
b. ¿El conjunto
es linealmente independiente? Justifique su respuesta.
Sean ![]() ,
, ![]() y
y ![]() tres vectores en R3, con las operaciones suma y ponderación usuales. Para cualquier combinación lineal de la forma
tres vectores en R3, con las operaciones suma y ponderación usuales. Para cualquier combinación lineal de la forma
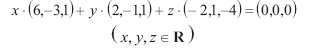
e igualar coordenada a coordenada se obtiene un sistema lineal homogéneo de 3 ecuaciones con 3 incógnitas, cuya solución gráfica, vista desde distintas posiciones, es: la siguiente:
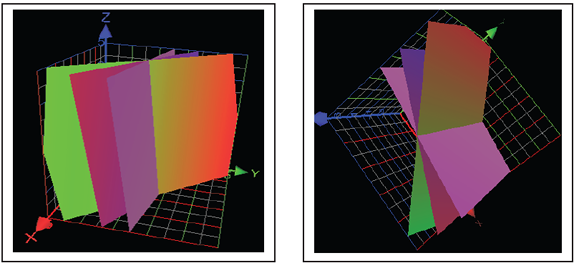
a. ¿Cuál es el conjunto solución del sistema? Justifique su respuesta.
b. ¿El conjunto
es linealmente independiente? Justifique su respuesta.
Sea ![]() , con las operaciones suma y ponderación usuales. Determine justificadamente si el conjunto A es linealmente independiente si al resolver el sistema de ecuaciones lineales homogéneo proveniente de la combinación lineal
, con las operaciones suma y ponderación usuales. Determine justificadamente si el conjunto A es linealmente independiente si al resolver el sistema de ecuaciones lineales homogéneo proveniente de la combinación lineal ![]() se obtiene como solución:
se obtiene como solución:
- a. Tres planos que se intersectan en el cero vector.

b. Tres planos, dos de ellos coplanares.
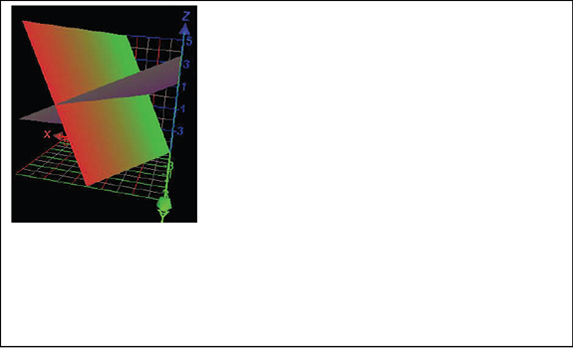
8. En el espacio vectorial ![]() , con las operaciones suma (
, con las operaciones suma (![]() ) y ponderación (
) y ponderación (![]() ) definidas por:
) definidas por:
Suma: ![]()
Ponderación: ![]()
¿Los siguientes conjuntos son linealmente dependientes? Justifique su respuest
a.
b.
REFERENCIAS BIBLIOGRÁFICAS
1. Andreoli, D. (2009). Análisis de los obstáculos en la construcción del concepto de Dependencia Lineal de vectores en alumnos de primer año de la universidad. (Tesis de maestría, no publicada). CICATA-IPN, México. [ Links ]
2. Arnal, J.; Del Rincón, D.; Latorre, A. (1992). Investigación Educativa. Fundamentos y Metodología. Barcelona: Labor. [ Links ]
3. Barrera, J. (2008). Modos de pensamiento en la solución y planteamiento de sistemas de ecuaciones lineales homogéneos con dos incógnitas. (Tesis de Maestría, no publicada). Universidad Autónoma del Estado de Hidalgo, México. [ Links ]
4. Dorier, J.-L. (1995). A General Outline of the Genesis of Vector Space Theory.Historia Mathematica, 22(3), 227-261. [ Links ]
5. Dorier, J.-L. (2000). Recherche en Histoire et en Didactique des Mathématiques sur l'Algèbre linéaire. Perspectives théorique sur leurs interactions. Les cahiers du laboratoire Leibniz, 12, 1-89. [ Links ]
6. Elliott, J. (1994). La investigación-Acción en Educación. España Editorial: Morata. [ Links ]
7. Euler, L., (1750). Sur une contradiction apparente dans la doctrine des lignes courbes. Mémoires de l'Académie des Sciencies de Berlin, 4, 219-223. [ Links ]
8. Goetz, J.P.; Lecompte, M.D. (1988). Etnografía y diseño cualitativo en investigación educativa. España. Editorial Morata. [ Links ]
9. Kolman, B. & Hill, D. (2006). Álgebra lineal. México: Editorial Pearson. [ Links ]
10. Gottfried Wilhelm Leibniz, Leibnizens Mathematische Schriften, ed. C. I. Gerhardt, 2 vols., Berlin: Julius Pressner, 1850; reprint ed., Euvres mathematiques de Leibnitz, Paris: Libraire de A. Frank Editeurs, 1853. [ Links ]
11. Marines, J. & Monroy, J. (1998). Dificultades en la transición del pensamiento sintético y analítico en sistemas de tres ecuaciones lineales con tres variables. (Tesina de Especialidad, no publicada). Universidad Autónoma del Estado de Hidalgo, México. [ Links ]
12. Ochoviet, T. (2009). Sobre el concepto de solución de un sistema de ecuaciones lineales con dos incógnitas. Tesis de Doctorado, no publicada). CICATA-IPN, México. [ Links ]
13. Möbius, A. F. (1915). Gesammelte Werke, R. Baltzer, (ed.), 4 volc., Leipzig: S. Hirtzel KG ; reprint ed., Wiesbaden: Dr. Martin Sändig oHG, 1967. [ Links ]
14. Monroy, A. (2008). Modos de Pensamiento en Solución y Planteamiento de Sistemas de Ecuaciones Lineales Homogéneos con tres o más Variables. (Tesis de Maestría, no publicada). Universidad Autónoma del Estado de Hidalgo, México. [ Links ]
15. Sierpinska A. (2000). On some aspects of student's thinking in linear algebra. Dorier (Eds.), On the Teaching of Linear Algebra (pp. 209-246). Dortrecht/Boston/London: Kluwer Academic Publishers. [ Links ]
16. Stewart I. (2007). Historia de las Matemáticas en los últimos 10.000 años. Barcelona: Editorial Crítica S.L. [ Links ]
17. Zimmermann, W. y Cunningham, S. (1991). Visualisation in Teaching and Learning Mathematics. Washington, DC: Mathematical Association of America. [ Links ]














