Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista electrónica de investigación en educación en ciencias
versión On-line ISSN 1850-6666
Rev. electrón. investig. educ. cienc. vol.7 no.2 Tandil dic. 2012
ARTICULOS ORIGINALES
Significado de las Distribuciones Muestrales en Textos Universitarios de Estadística
Hugo Alvarado1 y Nelson Segura2
alvaradomartinez@ucsc.cl , nsegura@ucsc.cl
1, 2Departamento de Matemática y Física Aplicadas
1, 2Universidad Católica de la Santísima Concepción, Chile
Resumen
En este trabajo se analiza la presentación de las distribuciones muestrales en una muestra de 22 libros de texto de estadística más utilizado en la enseñanza a estudiantes de ingeniería en Chile. Mediante el modelo del significado de un objeto matemático, se han diferenciado los elementos más importantes del tema y revelado la riqueza en las aplicaciones a situaciones de la ingeniería. Los textos muestran, en general, que son cada vez más técnicos en ausencia de la fundamentación de propiedades estadísticas, la forma usual de expresión es simbólica, descuidando las representaciones gráficas y simulaciones. En consecuencia, se deducen algunos criterios para el diseño de futuras propuestas de enseñanza, como la complementación de la experimentación y la generalización de las distribuciones muestrales por medio de variadas formulaciones, representaciones y herramientas de resolución de problemas.
Palabras-clave: Educación; Evaluación del aprendizaje; Física; Enseñanza Secundaria.
Meaning of Sampling Distributions in University Statistics Textbooks
Abstract
In this paper we analyse the presentation of sampling distributions in a sample of 22 statistics textbooks more employed in teaching engineering students in Chile. Our work is based on a theoretical model on the meaning of mathematical objects. The most important elements of the subject revealed a wealth of applications to engineering situations. The texts show, in general, are becoming more technical in the absence of the foundations of statistical properties, the usual form of symbolic expression, neglecting the graphic representations and simulations. As a consequence of such an analysis we infer some criteria for the future designing of teaching proposals, like the complementation of the experimentation and generalization of sampling distributions through various formulations, representations and tools for solving problems.
Keywords: Sampling Distributions; Meaning of mathematical objects; Analysis of textbooks.
Signification des Distributions d'échantillonnage dans les Textes Universitaires de Statistiques
Résumé
Dans ce travail on analyse la présentation des distributions d'échantillonnage dans un échantillon de 22 livres de statistiques les plus utilisés dans l'enseignement des étudiants d´une carrière de ingénierie au Chili. Grâce au modèle du signifié d'un objet mathématique, on a différencié les éléments les plus importants du sujet et relevé leurs richesses dans les applications aux situations de l'ingénierie. Les textes montrent, en général, qu'ils sont à chaque fois plus techniques en absence de fondements des propriétés statistiques; la forme usuelle d'expression est symbolique, en négligeant les représentations graphiques et les simulations. Par conséquent, on en déduit quelques critères pour la conception de futures propositions d'apprentissage, comme la complémentarité de l'expérimentation et la généralisation des distributions d'échantillonnage par moyen de variétés de formulations, représentations et les outils de résolution de problèmes.
Mots clés: Distributions d'échantillonnage; Signifié des objets mathématiques; Analyse des livres de textes.
Significado das Distribuições Amostrais em Textos Universitários de Estatística
Resumo
No presente artigo analisa-se a apresentação das distribuições amostrais em uma amostra de 22 livros de texto de estatística mais utilizados no ensino a engenheiros no Chile. Por meio do modelo do significado de um objeto matemático, foram diferenciados os elementos mais importantes do tema e revelada uma abundância das aplicações a situações da engenharia. Os textos mostram que, em geral, eles são mais e mais técnicos em ausência da fundamentação de propriedades estatísticas, a forma habitual de expressão é simbólico, descuidando-se as representações gráficas e simulações. Por conseguinte, inferem-se alguns dos critérios para a concepção de futuras propostas de ensino, tais como a complementaridade de experimentação e a generalização das distribuições amostrais por meio de diversas formulações, representações e ferramentas de resolução de problemas.
Palavras chave: Distribuições amostrais; Significado de objetos matemáticos; Análise de livros de texto..
1. INTRODUCCIÓN
Las distribuciones muestrales son consideradas la piedra angular de la inferencia estadística (Gardfiel, delMas y Chance, 2004) y tienen como prerrequisitos esenciales para su comprensión apropiarse de la idea de distribución y variabilidad (Pfannkuh y Wild, 2004), y familiarización con distribuciones comunes como la binomial y la normal (Ramírez, 2008). Es un tópico de la estadística considerada difícil para los estudiantes, ya que conjuga muchos conceptos asociados, diversos tipos de lenguaje y representaciones, propiedades, procedimientos y argumentos. Específicamente, las distribuciones muestrales se consideran importantes en el trabajo del ingeniero, al proporcionarles herramientas metodológicas para el desarrollo de su trabajo en situaciones de incertidumbre. Una cuestión general de estudio es la siguiente ¿Los libros de texto de estadística cubren un espectro amplio de las distribuciones muestrales con variadas situaciones a la ingeniería, graduando su nivel de dificultad?
Un curso tradicional de estadística en estudios de ingeniería incluye el estudio de las distribuciones muestrales, considerado un puente entre las distribuciones de probabilidades y la estimación de parámetros (puntual y por intervalo de confianza). Estos tópicos, además de contribuir a la adquisición de conocimientos conceptuales y procedimentales sobre objetos estadísticos variados, permiten generar competencias estadísticas específicas que pueden alcanzarse, tales como: identificar, modelar y resolver problemas que describan fenómenos aleatorios en la práctica de ingeniería; usar paquetes computacionales para resolver problemas del área de estadística; interpretar críticamente información estadística; habilidad para realizar experimentos de simulación en el diseño de procesos, entre otros. Todas estas competencias se deben reforzar para una formación óptima del profesional en las Escuelas de Ingeniería.
En este trabajo se analiza el significado de las distribuciones muestrales en los libros de texto de probabilidad y estadística dirigidos a ingenieros. Se utiliza la metodología de análisis de textos empleadas por investigadores acerca del estudio de otros conceptos estadísticos (Tauber, 2001; Cobo y Batanero, 2004; Alvarado y Batanero, 2008). Como una primera etapa, se lleva a cabo un estudio epistémico acerca del significado de referencia de las distribuciones muestrales, y nos apoyamos en el modelo de la teoría de los significados institucionales y personales de los objetos matemáticos (Godino y Batanero, 2003). Se han obtenido veinticinco situaciones-problemas relacionadas con la distribución de la suma de dos variables aleatorias y su extensión al caso de la media muestral y varianza muestral obtenidas de poblaciones normales, las situaciones que están directamente relacionados con la evolución histórica del teorema central del límite (Alvarado y Batanero, 2006), y las situaciones-problemas indirectas cuyas soluciones llevan a la búsqueda de una distribución que aproxime la suma de variables aleatorias de poblaciones que no son normales (Alvarado y Batanero, 2008). Se describen cuatro tipos de lenguaje y representaciones (Ortiz, 1999) y ocho procedimientos para resolver los problemas. Se establecen catorce proposiciones de la distribución de la suma de variables aleatorias asociada a poblaciones normales; de las cuales seis están en correspondencia con las propiedades de la distribución normal encontradas por Tauber (2001:139 a 144), y siete que tratan aplicaciones del teorema central del límite (Alvarado y Batanero, 2008). Por último se han obtenido cinco tipos de argumentos para comprobar las soluciones de los problemas de aplicación de las distribuciones muestrales.
El análisis de los textos, aunque no sustituye la observación de la enseñanza en el aula, proporciona información para la construcción de instrumentos de evaluación y puede ser un recurso para los profesores, contribuyendo a tomar decisiones sobre cuáles pueden recomendar a sus estudiantes. Además, provee ideas para enriquecer su actividad docente en el aula, atendiendo a las dificultades que podrían tener los estudiantes al estudiar estos textos (Alvarado y Batanero, 2008). Se intenta acercarse a los conceptos de las distribuciones muestrales desde una diversidad de campos de problemas de donde surgen las propiedades. Considerando las investigaciones relacionadas con la enseñanza de las distribuciones muestrales se estudia la hipótesis: es complejo el significado de las distribuciones muestrales presentados en los textos de estadística aplicada a la ingeniería y se encontrarán una variedad de enfoques y aproximaciones.
2. FUNDAMENTO DEL ESTUDIO
2.1. Marco Teórico
Al hacer matemáticas emergen objetos matemáticos que son representados en forma escrita, oral, gráfica o incluso por gestos. Se incluye en la idea de objetos personales las concepciones, esquemas, representaciones internas, etc. La actividad matemática queda modelada en términos de sistemas de prácticas operativas y discursivas. Font, Godino y D`Amore (2007) señalan que de estas prácticas emergen diferentes tipos de objetos matemáticos primarios, que se que denominan "elementos del significado" y corresponden a: situaciones y problemas que inducen actividades matemáticas y definen el campo de problemas asociado al objeto, en nuestro caso las distribuciones muestrales; procedimientos y operaciones que se realiza en distintos tipos de prácticas que pueden llegar a convertirse en objeto de enseñanza; representaciones materiales utilizadas en la actividad de resolución de problemas (términos, expresiones, símbolos, tablas, gráficos); definiciones y propiedades características del objeto y sus relaciones con otros conceptos y proposiciones; demostraciones que empleamos para probar sus propiedades y que llegan a formar parte de su significado. La forma usual de demostración en matemáticas es la deductiva, que es la más extendida en los libros universitarios. Este tipo de argumentación se completa o sustituye por otras como la búsqueda de contraejemplos, generalización, análisis y síntesis, simulaciones con ordenador, demostraciones, etc.
Además, los autores establecen que si las interpretaciones realizadas por los alumnos no son las esperadas por el profesor se produce un conflicto semiótico; entendido como cualquier disparidad entre los significados atribuidos a una expresión por dos sujetos (profesor y alumno). Los elementos de significado están relacionados entre sí formando configuraciones de redes de objetos intervinientes y emergentes de los sistemas de prácticas (Godino, Batanero y Font, 2009). Según los autores, se dirá que un sujeto comprende un determinado objeto matemático cuando lo usa de manera competente en diferentes prácticas. Se considerará para el análisis de las distribuciones muestrales la tipología de objetos matemáticos primarios, y que se organizan en sistemas conceptuales, teorías, etc.
2.2. Investigaciones sobre las Distribuciones Muestrales
Son escasas las investigaciones acerca de la enseñanza de las distribuciones muestrales en la educación superior. A continuación, se presentan los estudios relacionados con la enseñanza de las distribuciones muestrales con apoyo informático, y sobre el análisis de contenido de proposiciones presentes en las distribuciones muestrales. Enseñanza con recursos informáticos. En general, las investigaciones destacan la falta de comprensión del efecto del tamaño de la muestra sobre la variabilidad de la distribución muestral, y tienden a confundir la media de la población (parámetro) y la media muestral. Estas dificultades son observadas por delMas, Garfield, y Chance (2004) mediante una enseñanza basada en la simulación, utilizando un programa de elaboración propia. Los autores sugieren que la tecnología por sí sola no es suficiente para la comprensión, sino que las actividades y la enseñanza de tipo constructivista tienen un rol importante. Otros trabajos recientes relacionados con las distribuciones muestrales son el de Inzunza (2006), que analiza el significado de las distribuciones muestrales en un ambiente de simulación computacional. Concluye, que a pesar que el software Fathom permite evaluar procesos en la manipulación de parámetros y datos en distintas distribuciones de probabilidades, los estudiantes cometen errores frecuentes en el uso de representaciones numéricas, tienen un manejo superficial de los conceptos y propiedades de las distribuciones muestrales y presentan pocos elementos argumentativos. Retamal, Alvarado y Rebolledo (2007) llevan a cabo una enseñanza contextualizada de las distribuciones muestrales con uso del programa @risk en estudiantes de ingeniería. Sugieren para su comprensión desarrollar el lenguaje gráfico en la simulación, seguido de la representación algebraica según la naturaleza de las variables aleatorias.
Los trabajos anteriores confirman la importancia de apropiarse de conceptos previos de las distribuciones muestrales, que según Gardfiel, delMas y Chance (2004) corresponden al análisis de gráficos, medidas de tendencia central y de dispersión, construcción de la distribución normal, cálculo de probabilidades como área bajo la curva, noción de muestreo aleatorio y exploración de la variabilidad. Ramírez (2008) analiza las formas de razonamiento que muestran estudiantes de maestría en el estudio de la distribución normal basado en un enfoque frecuencial y con un desarrollo empírico de la distribución con la simulación en el software Fathom. Concluye que este recurso le permitió erradicar o modificar las conceptualizaciones erróneas que tenían los estudiantes sobre la distribución normal, aunque destaca poner atención al lenguaje y simbología matemática utilizado por los estudiantes, como el uso de datos reales para el estudio de la distribución normal.
Análisis de contenido. Se han efectuado estudios sobre las dificultades de comprensión de la aproximación binomial por la normal y la presentación del teorema central del límite en una muestra de libros de texto de estadística destinados a la formación de ingenieros (Alvarado y Batanero, 2007, 2008). Los autores mostraron que existe una gran riqueza de lenguaje, herramientas de resolución de problemas, conceptos asociados, propiedades y tipos de argumentos que le confieren una gran complejidad y posibilita presentaciones muy diferentes a los alumnos. De la muestra de 16 textos seleccionados varios de ellos comienzan con la aproximación de la distribución normal a la binomial y luego enuncian el teorema central del límite. Sin embargo, otros textos lo abordan enunciando el teorema y posteriormente indicando las condiciones de la bondad de la aproximación para el caso particular de la distribución binomial. En los textos es más común aplicar el teorema para la distribución de muestras de la media muestral. A continuación, se describen los trece campos de problemas, iniciados para el caso especial de la aproximación binomial que dio origen al teorema central del límite y que después se generalizó y formalizó (Alvarado y Batanero, 2008).
SP13. Obtener una aproximación de la distribución binomial para valores grandes de n.
SP14. Determinar la distribución aproximada de la suma de n variables discretas i.i.d.
SP15. Establecer la distribución de la suma de v.a. discretas no idénticamente distribuidas.
SP16. Determinar la distribución aproximada de la suma de variables continuas.
SP17. Estimar el error de aproximación en el teorema central del límite.
SP18. Encontrar condiciones necesarias y suficientes para el teorema central del límite.
SP19. Obtener la distribución aproximada de la suma de variables dependientes.
SP20. Obtener el tamaño adecuado de una muestra de poblaciones desconocidas.
SP21. Obtener la distribución aproximada de los logaritmos de v. a. independientes.
SP22. Obtener la distribución aproximada de diferencias de medias muestrales en dos poblaciones desconocidas.
SP23. Determinar la distribución aproximada de funciones de variable aleatoria.
SP24. Estimar por intervalos de confianza la media y parámetros para muestras grandes.
SP25. Establecer pruebas de hipótesis de la media para muestras grandes.
3. METODOLOGÍA
Se seleccionaron 22 libros texto que se listan en el Apéndice, de manera que se contemplasen distintas categorías y teniendo en cuenta los que aparecen en las bibliografías recomendadas para estudiantes de ingeniería, principalmente en Chile. Para la elección de la muestra, se consideraron diferentes tipos de libros que estuviesen disponibles en la biblioteca de la Universidad: a) 8 textos de estadística para administración y economía; b) 7 textos de estadística para ingeniería y ciencias; c) 4 textos clásicos de probabilidad y estadística de autores de prestigio; d) 2 textos de estadística recientes de enfoque novedoso, y e) un texto de estadística aplicada a las ciencias de la salud, a modo de extender el campo de problemas y ejercicios del tema.
Los pasos a seguir en el análisis de contenidos son los siguientes:
a) Determinar los textos de estadística universitaria a analizar;
b) Seleccionar los capítulos que tratan el tema de las distribuciones muestrales, clasificando y agrupando las diferentes definiciones, propiedades, representaciones y justificaciones prototípicas;
c) Determinar los elementos de significado, como guía para establecer el significado de las distribuciones muestrales que se da en la institución universitaria;
d) Elaborar tablas comparativas que recogen los elementos de significado en los distintos textos seleccionados;
e) Análisis comparativo de contenido, entre lo que los autores de los libros seleccionados consideran más adecuado para este nivel educativo y el análisis del significado de referencia;
f) Presentación de conclusiones, mediante el análisis descriptivo de la información obtenida.
Se considerará para el análisis de las distribuciones muestrales la tipología de los elementos de significado. En primer lugar, se analizarán los campos diferenciados de las situaciones problemas cuya resolución hace surgir la idea de las distribuciones muestrales, como entidades culturales socialmente compartidas; ya que los problemas matemáticos y sus soluciones son compartidos en el seno de instituciones o colectivos específicos implicados en el estudio de ciertas clases de problemas. Un segundo elemento de significado que se estudiará es el conjunto de palabras, notaciones y todas las representaciones de las distribuciones muestrales (objeto de estudio), que sirvan para representar las definiciones y propiedades, así como para describir los problemas y sus datos. Continuaremos con el estudio de los tipos de procedimientos empleados en la solución de problemas, y las descripciones de las propiedades de la distribución de la media de variables aleatorias que provienen tanto de poblaciones normales y que provienen de variables aleatorias que tratan aplicaciones del teorema central del límite (Alvarado y Batanero, 2008). Un quinto elemento de significado a analizar son los argumentos. Todas las situaciones problemas, proposiciones, lenguaje y algoritmos se relacionan entre sí mediante razonamientos o argumentos que se usan para comprobar las soluciones de los problemas o demostrar las propiedades y relaciones.
El análisis de texto sirve para efectuar inferencias mediante la identificación sistemática y objetiva de las características específicas de un texto. Su objeto final es la búsqueda del significado, cuya percepción depende de la existencia de las señales y de las características de los significantes: "Es un proceso complejo, seguramente el que más esfuerzo intelectual requiere de entre todas las técnicas de análisis de datos y es uno de los pocos campos de los comprendidos en las etapas finales del proceso de investigación en la que el investigador desempeña un papel individual y creativo" (Ghiglione y Matalón, 1991). Para Ortíz (1999) si en un texto aparece un significado sesgado, éste puede llegar a transmitirse a los alumnos, debiendo el profesor que los usa mantener una permanente vigilancia epistemológica sobre el contenido de los libros de texto.
Varios investigadores en la línea de didáctica de la probabilidad y estadística (Tauber, 2001; Cobo y Batanero, 2004; Alvarado y Batanero, 2008) señalan la importancia de este recurso didáctico. Pues, la riqueza de esta metodología constituye una base para garantizar la validez de contenido, mediante la construcción y aplicación de un instrumento de evaluación. Así, en nuestro caso, nos permitirá determinar la correspondencia entre el significado de las distribuciones muestrales entregado por el profesor y la comprensión de éste por el estudiante. A continuación, se presentan los resultados y conclusiones de este análisis, proporcionando ejemplos que ayuden a clarificar las diferentes categorías encontradas.
4. RESULTADOS
4.1 Situaciones Problemas
Se analizarán la presencia de las situaciones problemas (SP) en los libros de texto seleccionados. Las situaciones SP1 a SP12 corresponden a la distribución de la suma de dos variables aleatorias y su extensión al caso de la media muestral y varianza muestral obtenidas de poblaciones normales; SP13 a SP19 están directamente relacionados con la evolución histórica del teorema central del límite; y SP20 a SP25 son consideradas situaciones problemas indirectas cuyas soluciones llevan a la búsqueda de una distribución que aproxime la suma de variables aleatorias de poblaciones que no son normales.
SP1. Determinar la distribución de la suma de dos variables aleatorias discretas independientes e idénticamente distribuidas (v.a.d.i.i.d.). Para describir las variables aleatorias discretas asociadas a determinados experimentos basta con determinar la distribución de probabilidad. Presentamos un ejemplo del lanzamiento de dos dados:
En el juego "más o menos que siete" en las ferias, se lanza una vez un par de dados no cargados y la suma obtenida determina si el jugador gana o pierde su apuesta. Por ejemplo, el jugador puede apostar 1.00 dólar a que la suma será menor que 7 (es decir 2, 3, 4, 5 o 6). Para esta apuesta el jugador perderá 1.00 dólar si el resultado es igualar o exceder a 7, o ganará 1,00 dólar si el resultado será menor que 7. De manera similar, el jugador puede apostar 1,00 dólar a que el resultado será mayor que 7 (es decir, entre los números 8 y 12). El jugador gana 1,00 si el resultado es mayor que 7, pero pierde 1,00 dólar si el resultado es 7 o menos. Una tercera forma de jugar es apostar 1,00 dólar al 7. Para esta apuesta el jugador ganará 4,00 dólares si la suma es 7 y perderá 1,00 dólar si es otro número. a) Obtenga la función de distribución de probabilidad que representa los resultados posibles para una apuesta de 1,00 dólar a que la suma es menor que 7. b) Ídem para el caso que la suma es mayor que 7. c) Ídem para el caso que la suma es igual a 7. d) Muestre que el beneficio (o pérdida) esperada a largo plazo son los mismos para el jugador, sin importar qué método de juego use. (Berenson, Levine , Krehbiel 2000: 185)
SP2. Determinar la distribución de la suma de dos variables aleatorias continuas. En estadística aplicada a la ingeniería a menudo se necesita conocer la suma de variables aleatorias perteneciente a una misma familia de distribución aunque con parámetros diferentes. El siguiente ejemplo ilustra la distribución exponencial:
El tiempo que se utiliza para atender a un cliente en la caja registradora de un pequeño supermercado es una variable aleatoria, que tiene una distribución exponencial con parámetro λ. Suponga que X1 y X2 son los tiempos para atender a dos clientes diferentes, los cuales se supone son independientes uno del otro. Consideremos el tiempo total de atención To= X1 +X2 para los dos clientes, como un estadístico.
a) Determine la función de distribución de la variable To.
b) Calcule la media y varianza de la distribución de To (Devore 2001: 223).
SP3. Determinar la distribución de una combinación lineal de variables normales. Considere las variables aleatorias X1,X2,……,Xn independientes con distribución normal de media ![]() y varianza
y varianza ![]() . Si
. Si ![]() y b son constantes para las que al menos uno de los
y b son constantes para las que al menos uno de los ![]() es distinto de cero, entonces las variables
es distinto de cero, entonces las variables ![]() tiene distribución normal con media
tiene distribución normal con media ![]() y varianza
y varianza ![]() (De Groot 1988: 257). El siguiente ejemplo considera este campo que da inicio a la idea de la distribución de una suma de variables aleatorias:
(De Groot 1988: 257). El siguiente ejemplo considera este campo que da inicio a la idea de la distribución de una suma de variables aleatorias:
Cinco automóviles del mismo tipo viajarán 300 millas. Los primeros dos utilizarán una gasolina económica y los otros tres gasolinas de marca. Sean
los valores observados de millas por galón para los cinco automóviles y suponga que estas variables son independientes y normalmente distribuidas con μ1= μ2=20, μ3 = μ4= μ5 =21y σ2= 4 para la económica y σ2 =3.5 para la de marca. Defina una variable aleatoria Y por, Y =
-
De modo que Y es una medida de la diferencia en eficiencia entre la gasolina económica y la de marca. a) Determine la función distribución de Y. b) Calcule P(0≤Y) y P(-1 ≤ Y ≤ 1). (Sugerencia:
, con
) (Devore 2001: 238).
SP4. Determinar la distribución de la suma de n variables aleatorias normales. Este campo es un caso particular del caso anterior, al considerar las constantes de la combinación lineal igual a 1. Se ha encontrado este tipo de problemas situado en el área de la ingeniería:
La manufactura de cierto componente requiere el uso tres máquinas diferentes. El tiempo de uso de las máquinas para cada operación tiene una distribución normal y los tres tiempos son independientes entre sí. Los valores medios son 15, 30 y 20 min., respectivamente, y las desviaciones estándar son 1, 2 y 1,5 min., respectivamente. ¿Determine la función de distribución de manufactura de cierta componente? ¿Cuál es la probabilidad de que tome a lo más 1 hora la manufactura de producir un componente seleccionado al azar? (Devore 2001: 238)
SP5. Obtener la distribución de la media muestral en poblaciones normales. Este campo aparece de manera habitual en los textos para determinar la distribución de la media muestral en poblaciones normales, de la siguiente forma: Supóngase que las variables aleatorias ![]() constituyen una muestra aleatoria de una distribución normal con media
constituyen una muestra aleatoria de una distribución normal con media ![]() y varianza
y varianza ![]() y sea
y sea ![]() la media muestral. Entonces
la media muestral. Entonces ![]() tiene una distribución normal con media
tiene una distribución normal con media ![]() y varianza
y varianza ![]() (De Groot, 1988: 257). Un ejemplo se presenta a continuación:
(De Groot, 1988: 257). Un ejemplo se presenta a continuación:
Se sabe que la dureza Rockwell de pernos, de cierto tipo, tiene un valor medio de 50 y desviación estándar de 1.2. Si la distribución es normal, ¿cuál es la probabilidad de que la dureza muestral media para una muestra aleatoria de 9 pernos sea por lo menos 51? (Devore 2001: 235)
SP6. Determinar la distribución de la diferencia de medias muestrales en poblaciones normales. Las principales características de la distribución de la diferencia ![]() entre las medias muestrales de dos muestras aleatorias simples independientes son: a) La media
entre las medias muestrales de dos muestras aleatorias simples independientes son: a) La media ![]() es µ1 - µ2. Es decir, la diferencia de las medias muestrales es un estimador insesgado de la diferencia de las medias poblacionales; b) La varianza de la diferencia es la suma de las varianzas de
es µ1 - µ2. Es decir, la diferencia de las medias muestrales es un estimador insesgado de la diferencia de las medias poblacionales; b) La varianza de la diferencia es la suma de las varianzas de ![]() y
y ![]() , que es
, que es ![]() +
+ ![]() ; c) Si las dos distribuciones son normales, entonces la distribución de
; c) Si las dos distribuciones son normales, entonces la distribución de ![]() también es normal. Estas características se pueden deducir de forma matemática utilizando los teoremas de probabilidad, o colocar de manifiesto en las simulaciones. La diferencia
también es normal. Estas características se pueden deducir de forma matemática utilizando los teoremas de probabilidad, o colocar de manifiesto en las simulaciones. La diferencia ![]() entre las dos medias muestrales es la base en la construcción de los intervalos de confianza para la diferencia entre las medias poblacionales µ1 -µ2.
entre las dos medias muestrales es la base en la construcción de los intervalos de confianza para la diferencia entre las medias poblacionales µ1 -µ2.
Un especialista en adquisiciones compra 25 resistores del vendedor 1, y 30 del vendedor 2. Sean
las resistencias observadas del vendedor 1, las cuales se supone que están distribuidas de manera normal e independiente, con media 100Ω y desviación estándar 1,5Ω. De manera similar, sean
las resistencia observadas del vendedor 2, las cuales se supone que están distribuidas de manera normal e independiente, con media 105 Ω y desviación estándar 2,0Ω. ¿Cuál es la distribución de muestreo de
? (Montgomery y Runge 1996: 319)
SP7. Obtener la distribución de la varianza muestral en poblaciones normales. Para determinar esta distribución hay que considerar: muestras aleatorias ![]() de una distribución normal con parámetros
de una distribución normal con parámetros ![]() y
y ![]() , entonces, la variable aleatoria
, entonces, la variable aleatoria ![]() tiene distribución de probabilidad Chi-cuadrado (
tiene distribución de probabilidad Chi-cuadrado (![]() ) con n-1 grados de libertad. Un ejemplo es el siguiente:
) con n-1 grados de libertad. Un ejemplo es el siguiente:
En IEEE Transacciones (junio de 1990) se presentó un algoritmo híbrido para resolver problemas de programación matemáticos polinomiales 0 - 1. El tiempo de resolución (en segundos) de un problema escogido al azar empleando el algoritmo híbrido tiene una distribución de probabilidad normal con media μ = 0,8 segundos y σ = 1,5 segundos. Considere una muestra aleatoria de n= 30 problemas resueltos con el algoritmo híbrido. a) Describa la distribución de muestreo de s2 de los tiempos de resolución para los 30 problemas. b) Calcule la probabilidad aproximada que s2 sea mayor que 3,30. (Mendenhall y Sincich 1997: 327)
SP8. Determinar el error de estimación en poblaciones normales. El error estándar es una medición de la dispersión de la media muestral alrededor de la media poblacional. El tamaño del error estándar se ve afectado por dos variables. La primera es la desviación estándar, si la desviación estándar es grande, entonces el error estándar también lo será. La segunda es el tamaño de la muestra, conforme aumenta el tamaño de la muestra el error disminuye; esto indica que hay menos variabilidad en la distribución muestral de la media muestral. Un ejemplo es el siguiente:
Suponga que se estudian varias transacciones de retiro realizada en un cajero automático de un banco en particular durante un año, que representa a la población, y que en ese tiempo, se hicieron 36,500 transacciones. Si la desviación estándar de esta población, considerada normal, de la cantidad de dinero retirado por transacción es 50 dólares, ¿Cuál es el error estándar de la media si se seleccionan muestras de tamaño 400 con reemplazo? (Berenson, Levine y Krehbiel 2000: 256)
SP9. Obtener el tamaño adecuado de una muestra de población normal. Para realizar cualquier trabajo de investigación estadístico se necesita un tamaño de muestra adecuado para verificar las hipótesis. Al obtener suficientes observaciones puede ocurrir un nivel de confianza elevado y un error de estimación pequeño, pero en la práctica determinar los datos cuesta tiempo y dinero. Puede ocurrir que un tamaño de la muestra ideal sea inviable por razones económicas (Moore, 1995). Este campo de problemas es uno de los principales en ingeniería, aunque suponemos que no se refuerza su relevancia en el aula. La obtención del tamaño de muestra adecuado requiere conocer el error de estimación, la variabilidad y un nivel de confianza, como se muestra en el siguiente ejemplo:
Un grupo de consumidores desea estimar el monto de las facturas de energía eléctrica, distribuida de forma normal, para el mes de julio para las viviendas unifamiliares en una ciudad grande. Con base en estudios realizados en otras ciudades, se supone que la desviación estándar es 25 dólares. El grupo desea estimar el monto promedio para julio dentro de ±5 dólares del promedio verdadero con 99% de confianza. a) ¿Qué tamaño de muestra necesita? b) Si desea 95% de confianza, ¿qué tamaño de muestra requiere? (Berenson, Levine y Krehbiel 2000: 289)
SP10. Estimar parámetro de forma puntual. Cuando tenemos una población conocida pero desconocemos algún parámetro de ella, entonces se puede estimar dicho a través de datos muestrales. Un estimador es puntual cuando se obtiene un solo valor del parámetro. En el ejemplo siguiente se pide estimar el parámetro puntual de la media de una población.
El departamento de vida silvestre proporciona alimentación especial a las crías de trucha arcoíris en un estanque. Una muestra del peso de 40 truchas reveló que la media de la muestra es 402.7 gramos y la desviación estándar de dicha muestra es 8.8 gramos. ¿Cuál es el peso medio estimado de la población? ¿Cómo se le llama a esta estimación? (Lind, Mason y Marchal 2000: 249)
SP11. Obtener intervalo de confianza para la media muestral de poblaciones normales. Rara vez los estimadores puntuales coincidirán con el parámetro, debido a que depende de la muestra que se escoge. La estimación por intervalos considera estimadores puntuales insesgados para parámetros tales como p, µ, µ1- µ2, p1-p2 con base en una muestra aleatoria bajo algunos supuestos (condiciones que deben existir para aplicar correctamente un procedimiento estadístico). Se presenta un ejemplo de precisión de los intervalos en el contexto de resistencia de materiales:
Un ingeniero civil analiza la resistencia a la compresión de concreto. Esta se distribuye aproximadamente en forma normal con varianza σ2 =1000 (psi)2. Una muestra aleatoria de 12 especimenes tiene una resistencia media a la compresión de
= 3250 psi. a) Construya un intervalo de confianza de 95% con respecto a la resistencia media de compresión. b) Construya un intervalo de confianza de 99% con respecto a la resistencia media de compresión. Compare el ancho de este intervalo con el encontrado en (a) (Wisniewski 2001:231)
SP12. Establecer pruebas de hipótesis de la media muestral de poblaciones normales. En la práctica con frecuencia tenemos que tomar decisiones relativas a una población sobre la base de la información proveniente de una muestra. Para ello, es útil plantear hipótesis estadísticas (conjeturas o afirmaciones) de lo que creemos sobre los parámetros de la población. En general se refiere a parámetros de la población de la cual se requiere hacer la afirmación. Se presenta el siguiente ejemplo:
Una operación en una línea de producción debe llenar cajas con detergente hasta un peso promedio de 32 onzas. Periódicamente se selecciona una muestra de cajas llenas, que se pesan para determinar si están faltas o sobrante de llenado. Si los datos de la muestra, que provienen de poblaciones normales, llevan a la conclusión de que les faltan o sobran detergente, se deben parar la línea de producción, y hacer los ajustes necesarios para que el llenado sea correcto. a) Formule las hipótesis nula y alternativa que ayuden a decidir si es conveniente parar y ajustar la línea de producción. b) Comente la conclusión y la decisión cuando no se puede rechazar H0. (Anderson, Sweeney y Willians 2001: 332)
La Tabla 4.1.1 indica que los campos de problemas comunes en los 22 textos fueron la estimación por intervalos de confianza de la media y las pruebas de hipótesis de parámetros, ya sea para poblaciones normales como para muestras grandes (SP11, SP12, SP24 y SP25). Lo siguen los casos del teorema central del límite de la aproximación binomial por la normal (SP13) y estimar el error de aproximación (SP17). En cambio, casi inexistente fueron la obtención de las distribuciones de la suma de dos variables aleatorias discretas (SP1) y continuas (SP2). También, se observa que los textos no contemplan la secuencia de la historia del teorema central del límite, aunque es comprensible para este nivel educativo que no utilicen de la estadística matemática avanzada. Sin embargo, los libros de texto aplicado a las ciencias de la ingeniería carecen de problemas de variables discretas, por ejemplo la distribución Poisson que es un modelo de importancia en la ingeniería. También, indicamos que los siguientes libros de texto contienen la mayoría de las situaciones problemas, De Groot (1988) [Nº17] con 14 campos seguido de los textos Milton (1998), Meyer (1992) y Canavos (1992) [Nº 16, 18 y 19] con 13 campos.
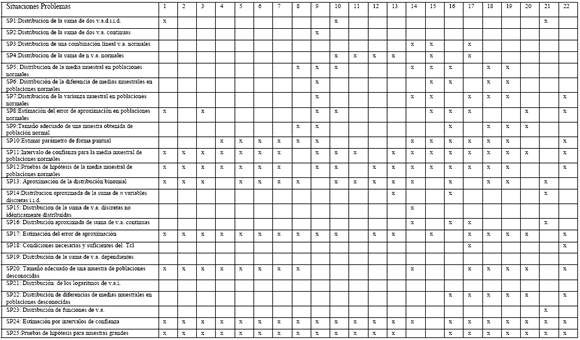
Tabla 4.1.1 Situaciones problemas que presentan los libros seleccionados.
En los textos de estadística para la administración y economía (Apéndice [1 al 8]), las situaciones que realzan los autores son el de la inferencia de intervalos y pruebas de hipótesis, además de la estimación del error de aproximación del teorema central del límite (SP17) y obtener el tamaño adecuado de una muestra de poblaciones desconocidas (SP20). En los libros de estadística para ingeniería y ciencias [Del 9 al 15] se añaden a los campos mencionados el de determinar la distribución de la suma de n variables aleatorias normales (SP4) y obtener una aproximación de la distribución binomial para valores grandes de n (SP13). La presencia de los campos en los textos seleccionados se encuentra entre 7 y 14 situaciones. El texto de Milton y Arnold (2004) satisface sólo 11 campos de problemas. Los libros de textos clásicos y recientes de probabilidad y estadística aplicada [17 al 22] son los que contienen más campos de problemas con un promedio de 11 situaciones. Se suman a estos textos la presencia de los campos de estimar parámetro de forma puntual (SP10) y obtener el tamaño adecuado de una muestra de poblaciones desconocidas (SP20).
En general, los libros carecen de fundamento matemático y trabajan más el factor de simulación a partir de una distribución binomial con apoyo informático. Es conveniente presentar una variedad de ejercicios de aplicación para el estudio del comportamiento de la suma de variables aleatorias tanto de poblaciones normales como desconocidas, que pensamos tiene consecuencias en las aplicaciones de los intervalos de confianza y las pruebas de hipótesis. Además, es deseable presentar ejemplos contextualizados a la profesión, como los presentan los textos de administración, a objeto de valorar el uso de las distribuciones muestrales como herramienta estadística para la toma de decisiones. Cabe señalar, que las variables más tratadas son para el caso continuo, aunque señalamos su conveniencia de iniciar el estudio del tema con el caso de variables discretas a través de la simulación en dos y más variables con dispositivos manipulativos (dados, fichas, monedas, urnas) y posteriormente para muestras mayores con apoyo informático. Finalmente, se observa en muchos textos la falta de rigurosidad en las justificaciones de procedimientos en los diversos ejemplos, y carencias de ejercicios sobre la obtención de tamaños de muestra adecuados en el ámbito de la ingeniería, para establecer el diálogo con el estudiante sobre cuantificar el error de estimación de parámetros, elementos fundamentales en la comprensión de la inferencia estadística.
4.2. Lenguaje y Representaciones
El lenguaje matemático-estadístico utilizado es el segundo elemento de significado, considerando las palabras, notaciones y las representaciones gráficas y de simulación. Se señalan cuatro tipos de lenguaje y representaciones utilizadas en relación a las distribuciones muestrales:
Términos y expresiones verbales. El vocabulario de las palabras y frases para describir los conceptos, sus operaciones y transformaciones son las que debe tener en cuenta el profesor para asegurar la comprensión por parte de los estudiantes. Se diferencian tres subtipos (Ortiz, 1999):
1) Palabras o expresiones matemáticas específicas, que normalmente no forman parte del lenguaje habitual. Por ejemplo: distribución muestral, axiomas, teoremas, error de estimación, factor de corrección por población finita, error estándar, etc.
2) Palabras que aparecen en la matemática y el lenguaje común, aunque no siempre con el mismo significado entre los dos contextos. Por ejemplo: media, esperanza, población, muestra grande, simulación manipulable, modelo, etc.
3) Palabras que tienen significados iguales o muy próximos en ambos contextos. Por ejemplo: promedio, moda, central, muestras moderadamente grandes, etc.
En estos tres subtipos existen un gran número de expresiones asociadas a las distribuciones muestrales, debido a los diversos elementos relacionados con el tema. Por lo tanto, los tres subtipos están presentes en todos los textos seleccionados, siendo la más frecuente la categoría de palabras específicas. En particular, Tauber (2001) presenta una gama de elementos de significados específicos relacionado con la distribución normal y Alvarado y Batanero (2008) establecen los múltiples significados del teorema central del límite.
Notaciones y símbolos. Las notaciones simbólicas, características del lenguaje matemático, permiten trabajar a un alto nivel de complejidad en el sistema de operaciones de las distribuciones muestrales. Por tanto, consideramos importante el uso de símbolos en el aprendizaje de las distribuciones muestrales. Algunas de las expresiones encontradas fueron x1, x2,.., xn para referirse a una muestra aleatoria, ![]() para enunciar la media aritmética,
para enunciar la media aritmética,![]() para describir la varianza muestral,
para describir la varianza muestral, ![]() denota la variable aleatoria Y tiene distribución Chi-cuadrado con n-1 grados de libertad, etc.
denota la variable aleatoria Y tiene distribución Chi-cuadrado con n-1 grados de libertad, etc.
Representaciones gráficas. Además, del lenguaje y los símbolos, encontramos diversos tipos de representaciones gráficas. El más usual son los histogramas, presentes en textos como Canavos (1992), Hanke y Reitsch (1997), Hildebrand y Lyman, Newbold (1997), Berenson, Levine y Krehbiel (2000). Lo siguen los gráficos de barras para representar las distribuciones de frecuencias relativas.
Simulaciones. La simulación es una representación en el sentido que sustituye un experimento estocástico por otro y su empleo es especialmente útil en la enseñanza de conceptos y propiedades de las distribuciones muestrales. Los siguientes textos proponen ejercicios para generar muestras aleatorias con simulaciones manipulables: Hildebrand y Lyman (1997), Berenson, Levine y Krehbiel (2000), Lind, Mason y Marchal (2000), Anderson, Sweeney y Willians (2001), Mendenhall y Sincich (1997), Devore (2001), Meyer (1992), Johnson y Kuby (2004). Otros textos, como Hildebrand y Lyman (1997), usan para la simulación software estadístico tales como Minitab, SAS o la planilla electrónica Excel.
En la Tabla 4.2.1 se muestra un resumen de las expresiones y representaciones de las distribuciones muestrales. Las notaciones y símbolos es el más común en los textos, y presente mayoritariamente en los textos clásicos y modernos [N° 17 al 22]. En los textos aplicados a la administración y economía utilizan también el lenguaje gráfico. La simulación, como apoyo didáctico a la comprensión de las distribuciones muestrales, está presente sólo en ocho textos. Cabe destacar que los textos Devore (2001), Johnson y Kuby (2004), Hildebrand y Lyman (1997), Berenson, Levine y Krehbiel (2000), Lind, Marchal y Wathen (2008), Anderson, Sweeney y Williams (2001) conducen al lector desde la simulación manual a la simulación con uso del computador, transferencia de secuencia didáctica que consideramos importante. Mientras que es débil la presencia de la simulación en los textos para ingeniería civil.

Tabla 4.2.1 Lenguaje y representaciones de las distribuciones muestrales.
4.3 Procedimientos
Las situaciones problemas relacionadas con las distribuciones muestrales se pueden resolver mediante las siguientes técnicas:
AP1: Cálculo de estadístico de variables aleatorias discretas acotadas. Este algoritmo se observa en el cálculo de la media muestral y la varianza muestral obtenidas de variables discretas acotadas. Se presenta el siguiente ejemplo para el caso del cálculo de los estadísticos de la media muestral y del rango en muestras de tamaño 2.
Sea X el número de paquetes que envía por correo un cliente seleccionado al azar, en cierta oficina de envíos. Suponga que la distribución de X es como sigue:
X 1 2 3 4
P(x) 0.4 0.3 0.2 0.1
a) Considere una muestra aleatoria de tamaño n = 2 (dos clientes) y seael número medio muestral de paquetes enviados. Obtenga la distribución de probabilidad de
. b) Consulte en inciso a) y calcule P (
≤ 2.5)
c) Otra vez considere una muestra aleatoria de tamaño n = 2, pero ahora concéntrese en la estadística R = rango muestral (diferencia entre los valores máximos y mínimos de la muestra). Obtenga la distribución de R. [Sugerencia: calcule el valor de R para cada resultado y utilice las probabilidades del inciso a)] (Devore 2001:228).
AP2: Cálculo de estadístico para datos agrupados en clases. Este tipo de cálculo para datos agrupados es poco frecuente en los textos analizados. Aparece en los textos Anderson, Sweeney y Williams (2001), Miller, Freund y Johnson (1992) y Canavos (1992).
AP3: Cálculo algebraico de variables aleatorias normales con calculadora y/o tablas estadísticas. Este procedimiento aparece en diez textos de los 22 analizados, y se presentan generalmente para el caso del cálculo algebraico de la media muestral obtenidas de distribuciones normales. No obstante, las situaciones no son explícitas en separar el algoritmo de cálculo, primero para la suma de variables aleatorias y luego para la media aritmética, lo que puede ser una dificultad de aprendizaje del tema en los estudiantes.
AP4: Cálculo de probabilidades en poblaciones normales para obtener una muestra aleatoria adecuada. El cálculo algebraico de la media muestral de variables aleatorias con distribución normal es el más típico y presente en la mayoría de los libros de texto analizados. El siguiente ejemplo conduce a encontrar un tamaño de muestra adecuado.
La longitud de las barras de metal producidas por una cadena de producción es una variable aleatoria con distribución normal y desviación estándar 1.8 milímetros, cuya longitud a cada lado de la media muestral no sea superior a 0.5 milímetros. ¿Cuántas observaciones debe tener la muestra para construir tal intervalo? Utilice un nivel de significancia 0.01. (New Bold 1997: 274)
AP5: Cálculo algebraico y transformación de n variables aleatorias. Esta técnica se presenta principalmente en los textos de estadística para ingeniería y los textos clásicos de estadística, para el cálculo algebraico de la media muestral de variables aleatorias.
AP6: Cálculo de probabilidades aproximada para obtener una muestra aleatoria adecuada. Este procedimiento se presenta en nueve textos de estadística para administración e ingeniería. Scheaffer y Mc Clave (1993:236) presentan un ejemplo de una máquina de llenado de botellas, donde se requiere encontrar un tamaño de muestra adecuado a partir de la información de la varianza de las cantidades de llenado, error de estimación y una probabilidad dada.
AP7: Cálculo de probabilidades referidas al teorema central del límite con calculadora, tablas de distribución o programa computacional. De Groot (1988:262) exhibe la situación del lanzamiento de una moneda 900 veces y se pretende determinar la probabilidad de obtener más de 495 caras. Para ello, el estudiante puede utilizar el cálculo algebraico aplicando el teorema central del límite para el caso particular de la aproximación de la distribución binomial por la normal, obteniendo una probabilidad aproximada. Cabe señalar, que para muestras grandes es útil la experimentación con el ordenador, obteniendo el cálculo del estadístico a partir de la obtención de los números aleatorios, por ejemplo, con la planilla Excel. De los textos considerados menos de la mitad plantean problemas con ordenador.
AP8: Cálculo de probabilidades referidas al teorema central del límite a partir de simulaciones con materiales manipulables. Hanke y Reitsch (1997:211) presentan una población de las edades 10, 20, 30, 40 y 50, para la que puede elaborarse la distribución de la media muestral de todas las muestras posibles de tamaño 2 con reemplazo. Mediante el algoritmo de resolución se establecen diferentes propiedades del teorema central del límite.
Se observa en la tabla 4.3.1 que la estrategia más común para resolver problemas es el cálculo algebraico de probabilidades en poblaciones normales para obtener una muestra aleatoria adecuada (AP4), presente en diecisiete de los textos seleccionados. Por el contrario, el algoritmo menos empleado es el cálculo del estadístico para datos agrupados en clases (AP2). Pocos textos plantean problemas con ordenador, sin atender a los nuevos enfoques de la enseñanza de la estadística basados en actividades que sean significativas para los estudiantes con datos reales y uso de recursos informáticos. Los textos que presentan cinco técnicas para resolver problemas son: Canavos (1992), Johnson y Kuby (2004), Montgomery y Runger (1996), Aderson, Sweeney y Willian (2001).

Tabla 4.3.1 Algoritmos y procedimientos que presentan los libros seleccionados.
4.4 Proposiciones
Las propiedades encontradas son de dos tipos:
Propiedades de la distribución de la suma o media de variables aleatorias que provienen de poblaciones normales. Se han obtenido catorce propiedades, de las cuales, las primeras seis están en correspondencia con las propiedades de la distribución normal encontradas por Tauber (2001:139 a 144), que clasificó en geométricas, estadísticas y algebraicas.
P1. La media de la distribución de una combinación lineal de variables aleatorias es la suma de las medias por sus respectivas constantes numéricas.
P2. El valor esperado de la distribución de la media aritmética es la media de la población.
P3. La varianza de la distribución de una combinación lineal de variables aleatorias independientes es la suma de las varianzas por sus constantes numéricas al cuadrado.
P4. La varianza de la distribución de la media aritmética es la varianza de la población sobre el tamaño de la muestra de variables aleatorias independientes.
P5. El valor esperado de la distribución de la varianza muestral es la varianza de la población.
P6. La varianza de la distribución de la varianza muestral de poblaciones normales es la varianza de la población por una constante.
P7. La combinación lineal de variables aleatorias independientes normales sigue una distribución normal.
P8. La media aritmética de una muestra aleatoria de población normal tiene distribución normal.
P9. La suma de cuadrados de variables aleatorias independientes normales estándar tiene una distribución Chi-cuadrado.
P10. La suma de cuadrados de las desviaciones medias sobre la varianza de la población normal sigue una distribución Chi-cuadrado.
P11. La distribución de la media muestral de la población normal con varianza desconocida sigue una distribución t-student.
P12. La distribución de la diferencia de medias muestrales en poblaciones normales con varianzas conocidas sigue una distribución normal.
P13 La distribución de la diferencia de medias muestrales en poblaciones normales con varianzas desconocidas sigue una distribución t-student.
P14. El cuociente de varianza muestrales sobre las varianzas poblaciones normales sigue una distribución de Fisher.
Propiedades de la distribución de la suma o media de variables aleatorias que tratan aplicaciones del teorema central del límite (Alvarado y Batanero, 2008).
P15. La media aritmética de una muestra aleatoria de tamaño suficientemente grande sigue una distribución aproximadamente normal.
P16. La aproximación mejora conforme crece el número de variables aleatorias.
P17. Las diferencias de medias muestrales en dos poblaciones siguen una distribución aproximadamente normal.
P18. Aproximación de una distribución discreta a la distribución normal.
P19. Aproximación de una distribución continua a la distribución normal.
P20. Los estimadores de máxima verosimilitud tienen distribución asintótica normal.
P21. Los estimadores de los momentos tienen distribución asintótica normal.
P22. Corrección por continuidad.
La Tabla 4.4.1 indica que las propiedades más frecuentes en los textos son el valor esperado y varianza de la media muestral (P2, P4), la distribución de la media aritmética según sea conocida o no la varianza (P8, P11). Lo siguen las propiedades de la diferencia de medias muestrales en poblaciones normales con varianzas conocidas (P12), la distribución Fischer (P14) y la distribución aproximada de la media aritmética a la normal en muestras grandes (P15). En cambio, son escasas las propiedades de los métodos de estimación puntual (P19, P20) y de la varianza muestral (P5, P6). Se observa que los libros de estadística para negocios y administración ([1 al 8]), usan la propiedad de corrección por continuidad, que no es el caso de los textos de estadística para ingeniería ([9 al 15]). No obstante, los primeros textos presentan las propiedades como definiciones, en cambio los otros textos de estadística clásicos y de ingeniería consideran las propiedades en términos de proposiciones o teoremas, algunos con su demostración. Los textos donde aparecen gran parte de las propiedades son: Miller, Freund (1992) con 19 propiedades, seguido de los textos Montgomery y Runge (1996), Walpole, Myres y Myers (1999), Devore (2001) y Mendenhall y Sincich (1997).

Tabla 4.4.1 Proposiciones que presentan los libros seleccionados.
4.5 Argumentos
A continuación, se señalan los tipos de argumentos relacionados con las distribuciones muestrales:
A1. Demostraciones formales algebraicas y/o deductivas. Para validar un teorema o una proposición, como el teorema central del límite, usualmente se procede a la demostración matemática mediante la función generadora de momentos. Los textos clásicos que la utilizan son: De Groot (1988), Walpole, Myers y Myers (1999), Mendenhall, Wackerly y Scheaffer (1994), Meyer (1992) y Canavos (1992).
A2. Presentación de casos particulares de un resultado general. La mayoría de los textos presentan ejemplos o ejercicios como un caso particular de un resultado general. Se presenta un ejemplo de aproximación de la distribución normal a la distribución binomial.
Un vendedor contacta telefónicamente con clientes potenciales para estudiar si merece la pena una visita a domicilio. Su experiencia le indica que el 40% de sus contactos por teléfono vienen seguidos de una visita a domicilio. Si contacta con 100 personas por teléfono ¿Cuál es la probabilidad de que se realicen entre cuarenta y cinco y cincuenta visitas como resultado? Newbold (1997:180)
A3. Simulaciones manipulables de distribuciones en el muestreo. Algunos textos presentan como argumentos la simulación con dispositivos manipulativos en pequeñas poblaciones para validar alguna proposición; aunque no representa una demostración matemática sino más bien una verificación. Los textos que tienen este tipo de situaciones son: Hanke, Reitsch (1997), Hilebrand, Lyman (1997), Lind, Mason y Marchal (2000), Lind, Marchal y Wathen (2008), Milton y Amold (2004), Meyer (1992), Johnson y Kuby (2004) y Triola (2004).
A4. Simulación gráfica con el computador. Otra forma de verificación es la simulación con un ordenador para observar tendencias de distintos gráficos de histogramas al variar los tamaños de muestras. Los textos que presentan esta argumentación son: Hanke, Reitsch (1997), Hilebrand, Lyman (1997), Berenson, Levine y Krehbiel (2000), Lind, Mason y Marchal (2000), Lind, Marchal y Wathen (2008), Mendenhall y Sincich (1997), Devore (2001), Mendenhall, Wackerty y Sheaffer (1994), Johnson y Kuby (2004) y Triola (2004). El texto Anderson, Sweeney y Willians (2001: 265) muestra la aplicación del teorema central del límite para tres poblaciones distintas a la distribución normal. Sin embargo, se observa para muestras de tamaño 5 que la distribución muestral de obtenida en cada población comienzan con una apariencia acampanada. Cuando el tamaño de la muestra es de 30 las tres distribuciones muestrales tienen una distribución aproximadamente normal.
A5. Comprobación de ejemplos y contraejemplos, sin pretender generalizar. Algunos textos utilizan ejemplos para verificar las propiedades de las distribuciones muestrales. El siguiente ejemplo muestra uno de los casos más utilizados de aproximación de la distribución normal a la distribución binomial.
Una moneda legal se lanza 300 veces. Empleando la aproximación normal a la distribución binomial, encuentre la probabilidad de obtener: a) entre 155 y 165 caras, inclusive, b) Exactamente 150 caras, c) Menos de 140 o más de 160 caras. Wisnieswski y Velasco (2001, pp. 214).
En la Tabla 4.5.1 se establece los argumentos presentes en los textos, que se relacionan con los elementos de significado a través de las propiedades. Se observa que son pocos los textos de estadística que utilizan la demostración formal para validar los teoremas o proposiciones de las distribuciones muestrales.
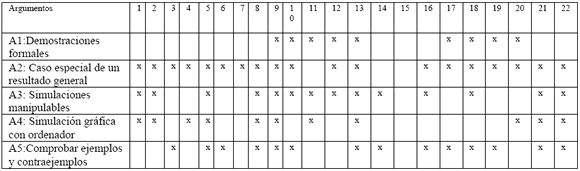
Tabla 4.5.1 Argumentos que presentan los libros seleccionados.
En casi todos los textos analizados presentan el ejemplo de aproximación de la distribución normal a la binomial como un caso particular de un resultado general. Son pocos los textos que usan las simulaciones manipulables de distribuciones en el muestreo, las cuales consideramos contribuyen a comprender de mejor forma la utilización de las propiedades, a pesar que no es una demostración formal. Las demostraciones algebraicas de los teoremas de las distribuciones muestrales tienden a desaparecer en los libros de textos más actuales tales como Lind, Marchal y Wathen (2008), Levin, Balderas (2004), Triola (2004), Johnson y Kuby (2004) Velasco y Wisniewski (2001) y Berenson, Levine y Krehbiel (2000).
Los textos de estadística matemática son los más completos en las demostraciones aunque no trabajan la simulación. En general, las demostraciones formales están ausentes en los textos para administración, que al parecer no es el propósito de los autores para este nivel educativo. Su presencia están en los textos para ingenieros Miller, Freund y Johnson (1992) Montgomery Runge (1996), Walpole, Myres y Myres (1999) y Devore (2001). No obstante, los textos para administración y economía destacan las aplicaciones del teorema central del límite mediante la simulación gráfica con el ordenador; encontrados en textos como Berenson, Levine y Krehbiel (2000), Lind, Mason y Marchal (2000), Anderson, Sweeney y Willians (2001). Mientras que en los libros de ingeniería presentan una mayor cantidad de argumentos de demostraciones formales algebraica y/o deductiva, presentación de casos particulares de un resultado general y mayor argumentación para poblaciones normales, en Miller, Freund y Johnson (1992), Walpole, Myers y Myers (1999), Montgomery y Runge (1996) y Devore (2001).
5. CONCLUSIONES
Se ha establecido una aproximación del significado de las distribuciones muestrales; mediante la descripción de 12 campos de problemas asociado a poblaciones normales y 13 relacionados con el teorema central del límite, 4 tipos de representaciones, 8 procedimientos de solución de problemas, 22 propiedades y 5 formas de razonamientos de comprobación de soluciones. Esto nos permitirá elaborar una secuencia de enseñanza de las distribuciones muestrales por caminos diversos. El diseño de actividades de aprendizaje puede contemplar un rango de dificultad, variedad de procedimientos y formas de exploración bastante mayor que la forma tradicional presentada en textos de estadística para ingenieros. Así también tenemos la base para la construcción de los instrumentos de evaluación y la interpretación de las respuestas de los estudiantes de ingeniería, identificando los posibles errores y dificultades.
El análisis de contenido ha mostrado múltiples aplicaciones de las distribuciones muestrales en las Ciencias de la Ingeniería y su implicación en la inferencia estadística, aunque no todos los libros de texto destinados a los estudiantes le asignan la misma importancia, por las orientaciones específicas de cada texto. En relación a los textos de estadística para administración y economía, otorgan escasa importancia a la demostración formal para validar los teoremas o proposiciones de las distribuciones muestrales. En sus capítulos no se estudia la distribución de la suma de variables aleatorias y no aparecen la construcción de variables aleatorias con distribuciones Chi-Cuadrado, T-Student y de Fisher, utilizadas comúnmente en los intervalos de confianza y las pruebas de hipótesis. Consideramos que a un mayor rigor matemático ayudará a la comprensión de las propiedades más significativas de las distribuciones muestrales y a apreciar su alcance de aplicación en temas importantes como los métodos de estimación, errores de estimación y aproximaciones a las distribuciones de probabilidades clásicas. Los textos carecen de rigurosidad en los enunciados de ejercicios, por ejemplo no se expresa literalmente que para muestras de tamaño menor que 30 dicha muestra es extraída de una de distribución normal o aproximadamente normal cuando se aplica el teorema central del límite. En pocos textos se hace presente las representaciones manipulativa y de simulación, y el planteamiento de problemas con datos reales con salidas de software, que consideramos un recurso indiscutible de apoyo a la enseñanza de las distribuciones muestrales. La tendencia de los textos apuntan a ser más técnicos en ausencia de la fundamentación de propiedades estadísticas, y el procedimiento usual de resolver los ejercicios es mediante la representación manipulativa con su respectiva gráfica de barras. En cuanto a los textos de estadística para ingeniería, aparecen en las distribuciones muestrales argumentos de tipo algebraico, la forma usual de expresión es simbólica, y en varios textos deducen las variables de distribuciones clásicas de probabilidad por medio de la suma de variables aleatorias independientemente e idénticamente distribuidas. Por ejemplo, para la variable con distribución T de Student la presentan como el cociente entre una variable normal estándar sobre la raíz cuadrada de la variable Chi-Cuadrado dividida por sus grados de libertad. Sin embargo, no se observa en los autores que enfaticen las representaciones manipulables y la simulación gráfica con el ordenador; situación que se presenta también en los textos clásicos de estadística, en que predomina la argumentación y fundamentación de las proposiciones.
La información proporcionada por los libros ha permitido establecer un significado de referencia para diseñar una propuesta didáctica específica de enseñanza de las distribuciones muestrales. Se sugiere contextualizar los diferentes elementos de significado en actividades relacionadas con la ingeniería en orden de dificultad progresiva en base al tiempo disponible. También, implementar las configuraciones manipulativa y computacional para ampliar la parte algebraica, mediante la simulación gráfica y conectando los modelos de probabilidades con su experimentación. De este modo, el estudiante inicia su trabajo con dispositivos manipulativos (dados, fichas,…) sin utilizar notación o cálculo algebraico. Los procedimientos serán empíricos y gráficos en papel y lápiz, y aparecerán conceptos básicos como el de experimento aleatorio para obtener la suma de dos variables aleatorias. Mediante la implementación de recursos computacionales (G-Numeric, applet, plataforma virtual,..) se amplían notablemente el lenguaje, la dinámica de las representaciones gráficas y aparecen algunos conceptos como aproximación y calidad de aproximación. Se incorpora como procedimiento la simulación y el argumento es inductivo y la generalización según la sensibilidad de los parámetros de las distribuciones de probabilidades. Estas representaciones se complementan con la configuración algebraica, caracterizada por el lenguaje simbólico con procedimientos analíticos, uso de tablas de distribuciones para calcular probabilidades. El proceso de estudio se puede organizar mediante una secuencia de sesiones agrupadas en dos lecciones: Distribución de estimadores (media y varianza) obtenidos de poblaciones normales, y la Distribución de estimadores obtenidos de poblaciones que no son normales, en que se determinan las condiciones de aproximación de distribuciones por la distribución normal. Así, la utilización de experimentos aleatorios hace posible explorar los distintos valores de los parámetros de las distribuciones, que esperamos contribuya a la implicación de los estudiantes en las actividades de aprendizaje de las distribuciones muestrales.
Agradecimientos: Fondo Nacional de Desarrollo Científico y Tecnológico, mediante el Proyecto de Iniciación Fondecyt Nº 11080071.
APENDICE
Libros de textos incluidos en el análisis:
1. Hanke, J. y Reitsch, A. (1997). Estadística para Negocios. Segunda edición. Madrid: McGraw Hill- Interamericana.
2. Hildebrand, D. y Lyman, R. (1997). Estadística aplicada a la administración y a la economía. Delaware: Addison-Wesley
3. NewBold, P., Berenson, M. y Levine, D. (1997). Estadística para los negocios y la economía. México: Prentice Hall.
4. Krehbiel, T. (2000). Estadística para administración. México: Pearson Educación.
5. Lind, D., Mason, R. y Marchal, W. (2000). Estadística para administración y economía. México: McGraw-Hall.
6. Anderson, R. Sweeney, D. y Willians, T. (2001). Estadística para administración y economía. México: Thomson.
7. Levin, R., Balderas, D. y Gómez, R. (2004). Estadística para administración y economía. Sèptima edición. México: McGraw-Hall.
8. Lind, D., Marchal, W. y Wathen, S. (2008). Estadística aplicada a los negocios y la economía. México: McGraw-Hall.
9. Miller, I. y Freund, J. (1992). Probabilidad y Estadística para Ingenieros. México: Hispanoamérica.
10. Montgomery, D. y Runger, G. (1996). Probabilidad y Estadística Aplicadas a la Ingeniería. México: McGraw Hall.
11. Mendenhall, W. y Sincich, T. (1997). Probabilidad y Estadística para Ingeniería y Ciencias. Cuarta edición. México: Prentice Hall.
12. Walpole, R., Myers, R. y Myers, S. (1999). Probabilidad y Estadística para Ingenieros. Sexta edición. México: Prentice Hall, Pearson.
13. Devore, J. (2001). Probabilidad y Estadística para Ingeniería y Ciencias. Quinta edición. México: Thompson.
14. Velasco, G. y Wisniewski, P. (2001). Probabilidad y estadística para Ingeniería y Ciencias. México: Thompson.
15. Milton, S. y Arnold, J. (2004). Probabilidad y Estadística con Aplicaciones para la Ingeniería y Ciencias Computacionales. (2004). México: McGraw Hall.
16. Milton, J. (1998). Estadística para Biología y Ciencias de la Salud. Segunda edición. Madrid: McGraw-Hall - Interamericana.
17. De Groot, M. (1988). Probabilidad y Estadística. Wilmington: Addison-Wesley.
18. Meyer, P. (1992). Probabilidad y Aplicaciones Estadística. Segunda Edición. México: Addison-Wesley.
19. Canavos, G. (1992). Probabilidad y Estadística. México: McGraw Hill.
20. Mendenhall, W., Wackerly, D. y Sheaffer, R. (1994). Estadística Matemática con Aplicaciones. Segunda edición. México: Grupo Editorial Iberoamericana.
21. Johnson, R. y Kuby, P. (2004). Estadística Elemental. Tercera edición. México: Thompson.
22. Triola, M. (2004). Probabilidad y Estadística. Novena Edición. México: Pearson Educación.
REFERENCIAS
1. Alvarado, H. y Batanero, C. (2006). El significado del teorema central del límite: Evolución histórica a partir de sus campos de problemas. En A. Contreras, L. Ordoñez y C. Batanero (Eds.). Investigación en Didáctica de las Matemáticas/ Congreso Internacional sobre Aplicaciones y Desarrollos de la Teoría de las Funciones Semióticas (pp. 257-277). Jaén: Universidad de Jaén, España. [ Links ]
2. Alvarado, H. y Batanero, C. (2007). Dificultades de comprensión de la aproximación normal a la distribución binomial. Números, 67. [ Links ]
3. Alvarado, H. y Batanero, C. (2008). Significado del teorema central del límite en textos universitarios de probabilidad y estadística. Estud. pedagóg. Vol. 34 (2), pp. 7-28. [ Links ]
4. Cobo, B. y Batanero, C. (2004). Significados de la media en los libros de texto de secundaria. Enseñanza de las ciencias, 22(1), 5-18. [ Links ]
5. delMas, R., Garfield, J., & Chance, B. (2004). "Using assessment to study the development of students` reasoning about sampling distributions", Trabajo presentado en el American Educational Research Association. Annual Meeting. California. [ Links ]
6. Font, V., Godino, J. D. & D`amore, B. (2007). An ontosemiotic approach to representations in mathematics education. For the Learning of Mathematics, 27 (2), 2-7. [ Links ]
7. Garfield, J., delmas, R. & Chance, B. (2004). Reasoning about sampling distributions. En D. Ben-Zvi & J. Garfield (Eds), The Challenge of developing Statistical Literacy, Reasoning and Thinking. Netherlands: Kluwer Academic Publishers. [ Links ]
8. Ghiglione, R. y Matalón, B. (1991). Les enquêtes sociologiques. Théories et practique. París: Armand Colin. [ Links ]
9. Godino, J. D. y Batanero, C. (2003). Semiotic functions in teaching and learning mathematics. En M, Anderson, A. Sáenz-Ludlow, S. Zellweger y V,V, Cifarelli (Eds.), Educational perspectives on mathematics as semiosis: From thinking to interpreting to knowing (pp. 149-168). New York: LEGAS. [ Links ]
10. Godino, J. D., Batanero, C. Y Font, V. (2009). Análisis de procesos de instrucción basado en el enfoque ontológico-semiótico de la cognición matemática. Extraído el 06 Noviembre, 2011, de http://www.ugr.es/~jgodino/funciones-semioticas/sintesis_eos_10marzo08.pdf [ Links ]
11. Inzunsa, S. (2006). Significados que estudiantes universitarios atribuyen a las distribuciones muestrales en un ambiente de simulación computacional y estadística dinámica, Tesis doctoral, Departamento de Matemática Educativa del Centro de Investigación y de Estudios Avanzados del IPN (CINVESTAV). [ Links ]
12. Moore, D. S. (1995). Estadística aplicada básica. España: Antoni Bosch. [ Links ]
13. Ortiz, J. J. (1999). Significado de los conceptos probabilísticos elementales en los textos de Bachillerato. Tesis Doctoral. Universidad de Granada. [ Links ]
14. Pfannkuch, M. & Wild, C. (2004). Towards and understanding of statistical thinking. En D. Ben-Zvi & J. Garfield (Eds). The challenge of developing statistical literacy, reasoning and thinking (pp. 17-46). Dordrecht, the Netherlands: Kluwer Academic Publisher. [ Links ]
15. Ramírez, G. (2008). Formas de razonamiento que muestran estudiantes de maestría de matemática educativa sobre la distribución normal mediante problemas de simulación de fathom. Revista electrónica de investigación en educación en ciencias. Vol. 3 (1), pp. 10-23. [ Links ]
16. Retamal, L., Alvarado, H. y Rebolledo, R. (2007). Understanding of sample distributions for a course on statistics for engineers. Ingeniare, Vol. 15, pp. 6-17. [ Links ]
17. Tauber, L. (2001). Significado y comprensión de la distribución normal a partir de actividades de análisis de datos,Tesis doctoral, Universidad de Sevilla. [ Links ]














