ARTICULOS ORIGINALES

Modelación en la enseñanza de las matemáticas: Matemáticos y profesores de matemáticas, sus estrategias

 

Guerrero-Ortiz, Carolina ; Mena-Lorca, Jaime

c_cguerrero@yahoo.com.mx ; mena.jaimemena@gmail.com

Instituto de Matemáticas, Pontificia Universidad Católica de Valparaíso, Blanco Viel, 596, Cerro Barón, Valparaíso, Chile

 

---

Resumen

Presentamos los resultados de un estudio comparativo entre las trayectorias y estrategias de modelización movilizadas por matemáticos y profesores de matemáticas al abordar una situación hipotética que implica la construcción de un modelo matemático. La investigación se desarrolló dentro de un enfoque cualitativo con un grupo de profesores de matemáticas y estudio de casos de investigadores matemáticos. Los resultados muestran que el proceso de construcción de un Modelo Matemático difiere principalmente por el tipo de procesos cognitivos desarrollados en ambos grupos de estudio y las trayectorias de modelización son dependientes de las representaciones gráficas que los individuos utilizan para abordar el problema.

Palabras clave. Matemáticas; Modelización; Registros de representación; Profesores; Trayectorias de modelación.

Modeling in mathematics education: Mathematicians and Math Teachers, their strategies

Abstract
We present the results of a comparative study between the trajectories and modeling strategies mobilized by mathematicians and math teachers to address a hypothetical situation that involves the construction of a mathematical model. The research was conducted within a qualitative approach with a group of math teachers and case study research mathematicians. The results show that the process of building a mathematical model differ primarily by the type of cognitive processes performed in both study groups and paths modeling are dependent of graphical representations that individuals use to address the problem.

Keywords: Modelling; Registers of representation; Mathematicians; Math teachers; Ways of modeling.

Modélisation dans l'enseignement des mathématiques: professeurs de mathématiques et mathématiques, leurs stratégies

Résumé
Nous présentons les résultats d'une étude comparative entre les trajectoires et les stratégies de modélisation mobilisées par les mathématiciens et professeurs de mathématiques qui ont été confrontés à une situation qui implique la construction d'un modèle mathématique. La recherche a été menée dans une approche qualitative et concerne un groupe de professeurs de mathématiques du lycée et une étude de cas avec des chercheurs en mathématiques. Les résultats montrent que le processus de construction d'un modèle mathématique diffère principalement par le type de processus cognitifs développés dans les deux groupes d'étude et les trajectoires de modélisation dépendent des représentations graphiques que les individus utilisent pour résoudre le problème.

Mots-clés. Mathématiques ; Modélisation ; Registres de représentation ; Professeurs ; Trajectoires de modélisation.

---

 

1. INTRODUCCIÓN

La modelización es un término empleado en distintos contextos y con distintos objetivos, una buena clasificación de las investigaciones en el área se puede encontrar en los trabajos de Blomhøj (2009). Modelizar en el ambiente de educación matemática refiere al proceso que involucra la representación de la realidad¹ por medio de un modelo matemático. Suele hacerse una distinción entre las aproximaciones a la modelización, por un lado tenemos las aplicaciones y la modelización para el aprendizaje de las matemáticas y, por el otro, el aprendizaje de las matemáticas para desarrollar habilidades en la construcción de modelos matemáticos. La primera vertiente considera el uso de actividades de modelización como un vehículo para la construcción de conceptos matemáticos. Y la segunda vertiente involucra la aplicación de las matemáticas para construir modelos matemáticos (Niss, Blum, & Galbraith, 2007), aunque estas dos vertientes no son disjuntas sí involucran una diferencia en el énfasis que se pone en el desarrollo de actividades en el aula. Al hablar de actividades en el aula, necesariamente tenemos que hacer referencia a la triada profesor-alumno-tarea, donde indiscutiblemente el profesor de matemáticas tiene un gran peso, cumpliendo el  rol de modelador y participando en la confección y/o selección de las tareas, es por esta razón que la atención se dirige hacia las habilidades que el profesor domina. Nuestra investigación da cuenta, de algunas estrategias que los matemáticos encargados de la formación de profesores y profesores de matemáticas en formación continua activan al modelizar una situación.

Diversas investigaciones han buscado identificar las estrategias de modelización que se ponen en juego cuando modeladores expertos y novatos se enfrentan a la resolución de un problema (Crouch & Haines, 2004; Bransford, et. al., 2000), en ellas se reporta, entre otras cosas, que los modeladores novatos generalmente no se toman el tiempo suficiente para comprender la situación planteada. También se reportan las dificultades que tienen los novatos al seleccionar la información relevante y utilizarla en la construcción de un modelo matemático adecuado. Los obstáculos en la construcción e interpretación de modelos matemáticos se relacionan con las dificultades en el acceso a conceptos y procedimientos matemáticos apropiados para determinar la solución. Se ha observado, en el proceso de modelización de los novatos que tienden a usar estrategias lineales más que estrategias cíclicas y, que la validación de los modelos obtenidos no constituye un elemento relevante para ellos, como consecuencia encuentran dificultades al reconocer el tipo de modelo asociado a determinada situación y no logran relacionar los resultados del modelo matemático con la situación que le da lugar. Por otro lado, los modeladores expertos logran tener acceso a los conocimientos necesarios de forma más eficiente. Algunos autores mencionan que es posible que sean necesarios muchos años de práctica para llegar a ser un experto. Estas investigaciones no dan cuenta de los procesos y estrategias que novatos y expertos evidencian al modelizar una situación, lo que justifica el desarrollo de investigaciones que nos permitan comprender aquellos aspectos implicados en la construcción de un modelo que ambos grupos (expertos y novatos) movilizan y los elementos que favorecen el tránsito por el ciclo de modelización de una manera eficiente. En el contexto del empleo de la modelización como medio de aprendizaje de las matemáticas cabe preguntarse si los profesores transmiten a sus estudiantes las estrategias que utilizan para modelar una situación, en el sentido que algunas de las etapas que constituyen una trayectoria de modelización suceden de manera interna (en la mente) como se verá más adelante.

En nuestra investigación consideramos, por una parte, matemáticos experimentados quienes realizan actividades de investigación en matemática pura, además de dar clase a profesores en formación, y que no necesariamente están involucrados en actividades de modelización (entendido como el estudio de fenómenos reales). Por otra parte consideramos, profesores de matemáticas que se desempeñan desde nivel básico hasta universitario, quienes durante sus estudios universitarios contaron con una formación robusta en matemáticas y que generalmente cuentan con poca experiencia en el desarrollo de tareas de modelización en el aula. Enfatizamos que no pretendemos de ninguna manera realizar una comparación en cuanto a la competencia de modelización entre los profesores de matemáticas y los matemáticos, más bien trataremos de identificar aquellas herramientas y representaciones que utilizan como estrategias de modelización ambos grupos, atendiendo a la idea de que este conjunto de conocimientos puede servir de guía para identificar aquellos aspectos que sería conveniente desarrollar en profesores en formación y en los estudiantes.

Centramos la atención en la forma en que los resolutores trasladan un problema hipotético a un contexto matemático, esto es, observamos y analizamos las estrategias que se hacen presentes en la matematización horizontal. La comprensión de los procesos desarrollados por los dos grupos de observación adquiere relevancia debido a que es en ésta etapa cuando deben tomarse decisiones sobre la identificación de los aspectos más importantes de la situación, la organización de la información con base en sus relaciones para construir el modelo matemático y los procesos matemáticos que serán utilizados para llegar a la solución.

Las dificultades que se presentan en la modelización están en parte relacionadas con los procesos de abstracción y la descontextualización de la situación que dio lugar al problema, así como a la poca experiencia de los resolutores novatos, por esta razón es necesario investigar en profundidad los aspectos que permiten que los modeladores novatos se conviertan en expertos (Haines & Crouch, 2007). En el contexto educativo, una manera de enfrentar esta problemática es conociendo cuáles son las estrategias que utilizan los matemáticos e intentar desarrollar en los estudiantes este tipo de herramientas y habilidades, más aún si muchos matemáticos participan ampliamente en la formación de los profesores de matemáticas. Es claro que el conocimiento gestado en la interacción entre estos dos grupos es el que finalmente será transmitido a los estudiantes, es por eso que las preguntas que dirigen nuestra investigación son: ¿Qué estrategias son puestas en juego al modelizar una situación? ¿Existen diferencias entre las estrategias de los matemáticos y los profesores de matemáticas?

Con el objetivo de dar respuesta a nuestras preguntas de investigación, presentamos los resultados de analizar las rutas de modelización (Borromeo-Ferri, 2007) desarrolladas por dos grupos de observación, tomando en consideración las estrategias y herramientas matemáticas a las que recurren. Tiene sentido mencionar que el estudio de la modelización desde el punto de vista cognitivo es una rama de la investigación en la cual no se ha profundizado lo suficiente, así pretendemos contribuir a los resultados que se han reportado mostrando algunas características de los matemáticos y profesores de matemáticas cuando modelan una situación en un contexto hipotético.

2. MARCO CONCEPTUAL

Los principales retos que se presentan al modelizar una situación, no están precisamente relacionados con los procesos matemáticos, sino con la transición de la realidad al mundo de las matemáticas y, en sentido contrario, habiendo obtenido el modelo de la situación y su solución, con la reinterpretación en términos de la realidad. Mientras que para un experto la reinterpretación puede resultar trivial, no es así para los novatos (Crouch & Haines, 2004). En relación con el tránsito de la realidad al modelo matemático, Borromeo-Ferri (2006) ha identificado algunas etapas involucradas en un proceso de modelización, profundizando principalmente en el análisis de los procesos cognitivos. En este nivel distingue las fases: (RS) Situación Real, (MRS) Representación Mental de la Situación, (RM) Modelo Real y (MM) Modelo Matemático (figura 1).

Figura 1. Procesos cognitivos

La autora profundiza en el estudio de las interacciones que suceden entre las fases señaladas anteriormente, que en la figura 2 se ubican en el lado derecho (Reality). Los distintos ciclos de modelización identifican generalmente los aspectos procedimentales que suceden entre el mundo real y el mundo matemático (Blum, 1993; Blomhøj & Jensen, 2003). Borromeo-Ferri hace énfasis en los aspectos cognitivos dentro del ciclo de modelización, en su trabajo del 2006 reconstruye empíricamente las fases del proceso y presenta una descripción detallada del tránsito entre estas fases:
La Situación Real (RS), representa la situación dada en el problema, puede ser una imagen o un texto. Al transitar de la RS a la Representación Mental de la Situación (MRS) el individuo comprende más o menos el problema, reconstruye mentalmente la situación, aun cuando no lo comprenda completamente puede comenzar a trabajar en él.

La Representación Mental de la Situación (MRS) en cada individuo puede ser diferente, dependiendo de su estilo de pensamiento², por ejemplo, puede ser visual en relación con la experiencia; o la atención puede centrarse en datos numéricos y relaciones dadas en el problema, depende de las asociaciones que el individuo elija mientras comprende la tarea. La autora señala dos aspectos que hacen la diferencia entre la Situación Real (RS) y la Representación Mental de la Situación (MRS): 1) simplificaciones inconscientes de la tarea y 2) la elección individual del cómo abordar el problema. En el paso de la MRS al Modelo real (RM),  tienen lugar simplificaciones e idealizaciones más conscientes en el individuo, debido a que en la fase de MRS el individuo ya ha tomado decisiones que influyen en el filtrado de la información, el proceso de transición puede requerir de conocimiento extra-matemático dependiendo del tipo de tarea.

La fase de Modelo Real (RM) está fuertemente relacionada con la fase de MRS, debido a que el RM es prácticamente construido a nivel interno y las representaciones externas representan al Modelo Real dependiente de las declaraciones que el individuo hace al externalizar el modelo. Al transitar del RM al Modelo Matemático (MM), se hace presente un progreso individual de matematización, donde podría ser necesario también recurrir a conocimiento extra-matemático.

La fase de Modelo Matemático (MM) consiste de representaciones externas, expresiones matemáticas o dibujos. Las expresiones del individuo están más relacionadas con hechos matemáticos y en menor grado con la realidad. Esta fase completa el proceso de transición hacia las matemáticas. Con esta fase se concluye el proceso de matematización horizontal.

Las transiciones que suceden alrededor de estas fases resultan determinantes puesto que las externalizaciones que el individuo expresa por medio de imágenes, lenguaje matemático y afirmaciones son representaciones de las actividades mentales que suceden en él, dependientes también de la experiencia y conocimientos previos del resolutor (La figura 1 muestra el proceso descrito).

En el tránsito del MM a los resultados matemáticos (etiquetado 4 en la figura 2), se ponen en juego las competencias matemáticas del individuo, tales como recursos matemáticos y estrategias para analizar, explorar el modelo y obtener resultados o conclusiones. La fase de resultados matemáticos constituye la escritura de los resultados obtenidos del modelo. El tránsito de los Resultados Matemáticos a los Resultados Reales (etiquetado 5) se da mediante la reinterpretación de la solución en términos del problema planteado. Borromeo-Ferri (2006), señala que los individuos frecuentemente realizan esta transición de manera inconsciente.

En la fase de Resultados reales, se discute su correspondencia con la situación. Al validar los resultados, el individuo busca relaciones entre sus resultados y la MRS, dependiendo esto de la forma de validación que elija: Validación intuitiva o validación basada en el conocimiento.

La siguiente imagen (fig. 2) muestra la sucesión entre las fases que se han descrito.

Figura 2. Ciclo de modelización con una perspectiva cognitiva (Borromeo-Ferri, 2006)

Los elementos anteriormente descritos juegan un papel fundamental en la constitución de nuestro marco conceptual, en tanto que matemáticos y profesores de matemáticas no transitan por la misma ruta de modelización, ya que ésta será determinada por su experiencia, conocimientos en el tema y estilo de pensamiento. Cuando hablamos de conocimientos en el tema, no nos referimos únicamente al conocimiento matemático, sino a la capacidad de ver el problema y sus relaciones matemáticas como un conjunto de elementos interrelacionados, puesto que la manera en que los individuos enfrentan la solución de un problema no está únicamente determinada por sus conocimientos matemáticos (Bransford, et. al., 2000).

Conocer los aspectos cognitivos y procedimentales que se ponen en juego en los procesos de modelización, nos brindará herramientas para conjeturar sobre la evolución de las habilidades matemáticas y de razonamiento de acuerdo a la experiencia de los individuos, tal como la capacidad para identificar aquellos elementos relevantes de la información, sus propiedades y las relaciones que permiten organizar la información en una estructura que conduce al planteamiento de un modelo matemático para representar una realidad. Además, nos ofrecerá información sobre las habilidades reflexivas de los participantes con relación a las reglas de comportamiento y limitaciones de un modelo, lo cual supone también la capacidad de contrastar y validar dicho modelo en términos del contexto que le dio lugar. Nos interesamos en documentar los procesos matemáticos que tienen lugar cuando nuestros dos grupos de observación abordan la modelización de una situación hipotética.

3. METODOLOGÍA

 Se trata de una investigación de corte cualitativo, descriptivo e interpretativo, en el sentido que nuestro objetivo se dirige al análisis de las características de la actividad matemática de los participantes cuando modelizan una situación (Miles & Huberman, 1994). El análisis de la información se apoya en la observación del trabajo individual de los participantes y en sus argumentaciones mientras resolvían la tarea propuesta. Nuestros datos principales consisten de observaciones, entrevistas y material escrito.

Debido a que los procesos cognitivos generalmente no son expresados, pusimos especial atención en evidenciar los procesos mentales de los participantes, mediante el análisis de las rutas individuales de modelización:

"Una ruta de modelización describe un proceso individual a nivel interno o externo... Para ser más preciso desde el punto de vista cognitivo, uno debe hablar de las rutas de modelación visibles, ya que sólo se puede hacer referencia a expresiones verbales o representaciones externas para la reconstrucción del punto de partida y la trayectoria de una ruta de modelación" (Citado en Borromeo-Ferri 2010, pp. 112)

Participantes
Participaron en nuestra investigación tres matemáticos: Roger, Hugo y Evan, quienes se dedicaban a la docencia e investigación, los consideramos como "expertos", aunque su campo de investigación no está necesariamente relacionado con la modelización. También participaron 20 estudiantes de magister en didáctica de las matemáticas, quienes durante su formación académica a nivel universitario habían cursado asignaturas relacionadas con la matemática formal y al momento de la investigación eran profesores de matemáticas en servicio.

Los matemáticos resolvieron la tarea de manera individual, se les pidió que expresaran verbalmente lo que pensaban y se les entrevistó respecto a procedimientos que no quedaban claros. Los profesores resolvieron la tarea, también de manera individual y expresaron su razonamiento y procesos de solución ante el resto de sus compañeros. Se video-grabó a los participantes mientras resolvían la tarea y durante la entrevista, al final de la resolución de la tarea se recogió el material escrito y se analizó de acuerdo a los bloques que se muestran en la sección 4.

La tarea
Se eligió una tarea con un contexto, relativamente conocido para los participantes. La cual podía ser resuelta únicamente de forma gráfica o haciendo uso de conocimientos de geometría plana y/o geometría analítica. Esta tarea fue presentada originalmente en Vasíliev & Gutenmájer (1980). Para efectos de la investigación se adaptó ligeramente la redacción del problema quedando de la siguiente manera:

Considere la siguiente situación:
Una escalera se encuentra apoyada en un muro, sobre la escalera, en medio de ella hay un gato sentado. La escalera comienza a deslizar sobre el suelo, sin despegarse del muro.
¿Cuál es la trayectoria que describe el gato? Justifique su respuesta.
¿Cuál sería la trayectoria si el gato no está en medio de la escalera? Justifique su respuesta.
Nota: en ambos casos suponga que el gato no se baja de la escalera.

El proceso de solución de este problema ya ha sido estudiado con el uso de herramientas digitales, mostrando algunas dificultades relacionadas con la visualización del lugar geométrico (Planchart, 2009), y más recientemente se han hecho algunas propuestas para abordarlo de manera efectiva con el uso de software de geometría dinámica (Santos-Trigo, 2012). Sin embargo, nuestra investigación no se enfoca en la observación de las dificultades, tampoco constituye una propuesta de enseñanza, más bien el interés se dirige hacia la observación de las estrategias de modelación y argumentos desarrollados por matemáticos y profesores de matemáticas.

4. DISCUSIÓN Y ANÁLISIS DE LA INFORMACIÓN

 El análisis de la información se organizó en 4 bloques: 1) Comprensión del problema - primeras ideas e impresiones, 2) Búsqueda de estrategias para abordar el problema, 3) Construcción del modelo y 4) Obtención de resultados y conclusiones. La estructura de análisis de información es consistente con las fases del ciclo de modelización presentado en los fundamentos conceptuales de este trabajo, en el sentido que, el primer bloque agrupa el tránsito de RS a RM de la figura 1. El bloque dos, profundiza en las externalizaciones que realizan los individuos derivadas del tránsito de la MRS al RM. El tercer bloque considera el proceso de matematización etiquetado con 3 en la figura 2. Y el cuarto bloque, incluye las transiciones 4, 5 y 6.

La información obtenida del proceso de modelización de los participantes se organizó y analizó de acuerdo a los bloques señalados debido a que difícilmente se puede visualizar el tránsito entre las fases que aparecen del lado derecho en la figura 2, ya que éstas suceden de manera interna y sólo podemos establecer conjeturas sobre ellas de acuerdo a lo que los individuos expresan.

Para analizar simultáneamente el trabajo de los participantes, en cada bloque describimos primero el trabajo de los matemáticos y posteriormente algunos fragmentos del trabajo de los profesores, por cuestión de espacio seleccionamos los trabajos que nos parecieron más representativos.

4.1 Comprensión del problema -primeras ideas e impresiones

 Identificamos de inicio que se trata de una tarea que condiciona el proceso de solución al uso de esquemas pictóricos, en algunos casos para explicarse la situación y en otros casos únicamente para representar el problema como es el caso de los matemáticos. Se observó que los matemáticos de manera casi inmediata trasladaron el problema a una representación matemática (Fig. 3.a y 3.b) y posteriormente se enfocaron en la búsqueda del formalismo matemático en el proceso de solución. Mientras que la mayoría de los profesores comenzaron con el análisis del contexto del problema mediante el bosquejo de diferentes gráficos que les pudieran sugerir alguna idea de la dinámica de la situación y permanecieron en esta etapa durante un tiempo considerable. Esto no significa que los matemáticos no hayan realizado dibujos para comprender la situación, sólo que el proceso fue mucho más rápido para dar paso al análisis de la situación y búsqueda de herramientas más formales que les permitieran demostrar sus conjeturas. Describimos a continuación estos aspectos.

La forma de abordar el problema de Roger y Hugo evidenció, en primera instancia, el traslado de la situación a una representación matemática, como se muestra en las figuras 3.a y 3.b.

Figura 3.a. Roger traslada la situación a una representación matemática

Figura 3.b. Representación del problema hecha por Hugo

Figura 3.c. Representación pictórica de Evan

Roger después de leer el problema dibujó el esquema de la figura 3.a y etiquetó los puntos señalados en la figura, no expresó argumentos sobre el lugar geométrico. En el caso de Hugo, se observó que mientras realizaba la construcción mostrada en la figura 3.b, estaba reconstruyendo mentalmente el lugar geométrico del punto medio de la escalera (así lo expresó al momento de bosquejar la situación), a diferencia de Roger quien primero trasladó el problema a una situación geométrica y después analizó las propiedades. Al entrevistar a Hugo sobre sus primeras ideas del comportamiento de la situación esto es lo que expresó:
  Inv- en este caso. ¿En qué pensaste (fig. 3.b)?
Hugo-creo que la primera vez he pensado que iba a ser un segmento, pero después he visto que todos
estos son iguales [segmentos OM y OC], porque son       la mitad de esto [segmento AB],
Inv- ¿Por qué?
Hugo-Porque es un teorema, este se llama mediana [segmento OM], la mediana es la mitad de la hipotenusa.

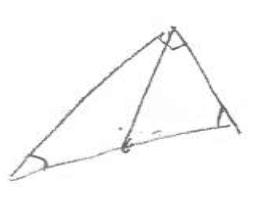
Por otro lado, Evan, realizó un dibujo de la situación (fig. 3.c), después de manera similar a Roger, trasladó el problema a un planteamiento geométrico (fig. 4) y conjeturó que el movimiento del gato describiría una trayectoria en línea recta. Adelante se muestra un segmento de la transcripción.

Figura 4. Representación geométrica de Evan

Evan - Esto es un triángulo rectángulo, entonces, llego al punto medio [a], y...  ese ángulo [ángulo en b]  respecto a esto ¿hay una propiedad que me diga algo?
Evan -¿Qué es lo que me gustaría?, me gustaría que la trayectoria fuera una línea recta [segmento cd]. Entonces para probar que es una línea recta, como yo creo que es, ¿Qué es lo que tiene que pasar?, tiene que pasar que...
Inv- ¿tu hipótesis es que el gato se va mover en una línea recta?
Evan -si, o también tendría que hacer un curvita así. [Dibuja en el aire una curva cóncava] 
Por otra parte, el trabajo de los profesores reveló que todos se apoyaron en el uso de esquemas para estudiar el movimiento del gato y posterior a ello introdujeron elementos matemáticos (fig. 5.a). Se encontraron también algunas dificultades en la representación de la situación, por ejemplo en la figura 5.b, donde al no respetar la longitud del segmento y la posición del punto medio confundieron la posición de dicho punto con las intersecciones de los segmentos de línea. En la figura 5.c al no considerar el movimiento del segmento cuando se aproxima a la vertical, determinaron que el desplazamiento del punto sería en línea recta vertical como se muestra. No entraremos en el estudio de estas dificultades, otros investigadores ya lo han hecho. Aunque cabe señalar que la representación del movimiento de la escalera mediante segmentos constituye una unidad de visualización que llama mucho la atención, lo que provoca que los individuos cambien de tarea, de representar la trayectoria del gato a representar el movimiento de la escalera.

Figura 5.a

Figura 5.b

Figura 5.c
Representaciones de los profesores

Comentarios. Las transcripciones dan evidencia de la simplificación e idealización que realizan los profesores, por ejemplo, señalan que el gato se considera como un punto, que no tiene peso, que no hay fricción entre la escalera y el piso, etc., aspectos que nos muestran el tránsito entre la Representación Mental de la Situación (MRS) y el Modelo Real (RM), donde destacan las simplificaciones que el individuo realiza conscientemente. Mientras que los matemáticos no ofrecen explicaciones sobre las características del fenómeno o sobre aquellos elementos que son idealizados al construir el modelo correspondiente, es decir, sólo nos permiten observar el tránsito entre las fases del Modelo Real (RM) y el Modelo Matemático (MM).

Al parecer los profesores establecen mayores conexiones con la realidad y los matemáticos se desvinculan más rápidamente de ella. En términos de los estilos de pensamiento descritos por Borromeo-Ferri (2010; 2012), podríamos adelantar que Roger y Hugo poseen un estilo de pensamiento analítico, Evan un pensamiento integrado y los profesores evidencian un pensamiento más visual, sin embargo no tenemos elementos para caracterizar los estilos de pensamiento en adultos.

4.2 Búsqueda de estrategias para abordar el problema

 4.3

Es difícil identificar el momento exacto en que los participantes comienzan a buscar estrategias de solución, ya que éstas en muchos casos pueden ser operaciones mentales que no es posible observar hasta que el individuo las externalice de forma verbal o escrita. Para Hugo un primer paso representar matemáticamente la idea que tenía sobre la trayectoria que describía el movimiento del punto medio, así lo demostró cuando trazó los segmentos OM y OC, y posteriormente cuando etiquetó algunos puntos (ver figura 3.b). En el caso de Roger quien inició representando el problema en forma geométrica y asignando una etiqueta a los puntos, la entrevista nos ayudó a obtener información sobre su estrategia para encontrar el modelo algebraico (ver figura 3.a):
Inv- ¿En qué pensaste primero?
Roger- La primera hipótesis que hice.
Roger - En ver si la distancia de este punto [d] a algún  punto de los que dibujé [puntos c y e] se mantenía constante, por ejemplo, ver si eso era constante [segmento cd], pero no tenía cara de ser así, luego o sea bueno sospechaba, tuve la impresión de que era así, pero no me era muy claro, después traté de completar esta figura así, ver si la simetría me ayudaba.

Evan, bosquejó la figura mostrada en 6.a y comenzó a estudiar la congruencia entre triángulos, al no encontrar elementos que le sirvieran intentó analizar el problema de manera diferente (Fig. 6.b), así representó el triángulo rectángulo que forma la escalera, el muro y el suelo, e identificó los ángulos, de manera que la figura 6.c le servirá para resolver el problema, este cambio de estrategia lo expresa como sigue: "el gato siempre está en la mitad, entonces ahora estoy fijando la escalera y estoy viendo como se mueve el ángulo"

Figura 6.a

Figura 6.b

Figura 6.c
Evan pasa de estudiar la congruencia de triángulos a la representación de la situación mediante el teorema de Tales

Tal como se puede observar, los argumentos de los matemáticos están basados en el análisis de la representación matemática del problema obtenida en el bloque anterior. Los profesores en este bloque no se habían desprendido completamente de las representaciones pictóricas de la situación, en muchos casos sus estrategias mostraron que constantemente recurrían a los trazos que realizaron para comprender la situación, por ejemplo las figuras 5.a, 5.b y 5.c.
Por otro lado, después que los profesores analizaron el problema e intuyeron la trayectoria del punto medio, manifestaron diferentes estrategias para resolver la situación. Con respecto a la figura 5.a un profesor escribió "se quiere demostrar que la distancia de A a M es siempre la misma, o sea, es un radio", con esas ideas construyó el esquema mostrado en la figura 7  e identificó algunas relaciones:

Figura 7. Estrategia mostrada por un profesor, centrada en propiedades geométricas

Otro profesor decidió abordar el problema situándolo en un sistema de coordenadas (Fig. 8), donde llamó k a la longitud del segmento AB y P al punto medio, con estos datos recurrió al cálculo de la distancia con herramientas de geometría analítica y propuso una relación entre las
distancias AP = PB = k/2, las cuales representó y operó como se muestra en la figura, pero ésta estrategia de solución le llevó a introducir nuevas variables (x₁ y y₁), no notó que para el caso en que P es el punto medio, las distancias dadas por (x-x₁) y (y-y₁) son iguales a x y y, respectivamente.

Figura 8. Estrategia mostrada por un profesor, apoyada en la geometría analítica

Una profesora también situó el problema en el plano cartesiano, pero a diferencia del caso anterior recurrió a la geometría plana observando la congruencia entre los triángulos, como se muestra en la figura 9.

Figura 9. Proceso de solución considerando la congruencia

Comentarios. En el bloque anterior los profesores invirtieron mucho tiempo en el estudio del movimiento de la situación, razón por la que en este bloque ya conocían la trayectoria, aun así volvían constantemente a los trazos realizados para verificar la forma de la curva en cuestión. Se enfocaron en buscar diferentes estrategias para determinar el modelo algebraico, la mayoría de ellas se dirigió al planteamiento del problema en un sistema de coordenadas. Muchas de sus estrategias no les ayudaron a construir el modelo algebraico (como el caso mostrado en la figura 8) y tuvieron que redefinir su camino de solución. En cuanto a los matemáticos, observamos que dos ellos (Roger y Hugo) pareciera que reconstruyeron el lugar geométrico conforme leían el problema,  mientras que Evan en el intento de visualizar el lugar geométrico que describe el movimiento del punto reconstruye el teorema de Tales.

4.4 Construcción del modelo.

La búsqueda de estrategias y la construcción del modelo están sumamente relacionadas, en el sentido que el individuo al elegir una estrategia de solución y no hallar un modelo que considere pertinente, tiende a proponer una nueva estrategia generándose así un proceso cíclico entre la comprensión del problema, la búsqueda de estrategias de solución y la construcción del modelo, este tránsito es más fácil de observar en los profesores, no así en los matemáticos quienes procedieron directamente con la representación matemática del problema.
En seguida se muestra cómo Roger después de identificar las características geométricas del problema, ubicó la situación en un sistema de referencia, localizando las coordenadas del punto P y recurriendo a herramientas de geometría plana como el teorema de Tales para obtener la solución.

El siguiente extracto de la conversación confirma el empleo de herramientas geométricas para obtener la expresión algebraica:
Roger- Como esto se va moviendo, el lado a y el lado b, finalmente no vi ningún método geométrico visual, entonces dije bueno, escribo las ecuaciones y ya está.
Inv- Y para escribir las ecuaciones, ¿qué estás usando?
Roger - Teorema de Pitágoras, o sea digo, cuando el gato está en medio, si este lado vale a y este vale b, entonces este punto [punto p] tendrá coordenadas... la coordenada x va ser b/2 y la coordenada y va ser a/2...
Roger - ...entonces esta ecuación en términos de  e  me queda así [fig. 10. b], que es la ecuación de una circunferencia.
Inv- ¿Y el otro caso?
Roger - Bueno es lo mismo, y te va dar la ecuación de una elipse.

Figura 10.a

Figura 10.b
Roger ubica el problema en un sistema de coordenadas

Hugo determinó el lugar geométrico de las dos situaciones, primero el caso en que el gato se encuentra en medio de la escalera y después el caso en que se encuentra en otra posición de la escalera, así cuando construyó el modelo algebraico ya contaba con una idea del lugar geométrico que debería obtener, resolviendo primero el segundo caso y después el primero. Su procedimiento también mostró estar relacionado con argumentos geométricos, además del empleo de estrategias matemáticas más formales. Por ejemplo, la siguiente transcripción refiere a la obtención del modelo algebraico de la elipse (fig.11) ubicando la situación en un sistema de coordenadas

Figura 11. Hugo determina el modelo algebraico

Hugo –; ... si el gato no está en la mitad. Cuál es la trayectoria?...Puede ser una elipse probablemente, pero cómo se puede demostrar sin cálculos? Sin cálculos es difícil de demostrar, con cálculo es fácil porque las coordenadas son tx y (1-t)y, t entre 0 y 1...a²+b²=l²  entonces es una elipse con los ejes (1-t)l  y tl . En este caso es la elipse. Cuando  es ½, es una circunferencia.

La figura 12 junto a la transcripción ilustra la demostración algebraica en el caso del punto medio, haciendo uso de las propiedades geométricas del triángulo (teorema de la mediana relativa a la hipotenusa).
Hugo - bueno para escribir la solución acá... OAB tiene el ángulo de 90 grados. AM=MB=OM, OM=AB/2, entonces M está en el círculo de radio C, entre 0 y AB/2. {x>=0, y>=0}
Inv- ¿Podrías describir tu proceso para resolver el problema?
Hugo - buscar algo común para todos los puntos, una característica común para todos los puntos, para diferentes posibilidades.
Hugo - después he pensado en algunas cosas que se conocen en el triángulo cuando un punto está a la mitad, hay diferentes teoremas, por ejemplo ese teorema... También he pensado si alguno se aplica acá y he visto que ese se aplica.

Figura 12. Operaciones realizadas con referencia a la figura 3.b

Evan recurrió también a la geometría del problema. Tomando como apoyo la figura mostrada en 6.c construyó la figura 13.a y determinó los ángulos que se muestran, al ver que esto no le ofrecía ningún resultado cambió de estrategia, construyendo diferentes representaciones de la situación (figuras 13.b y 13.c), hasta que logró visualizar el lugar geométrico del punto medio: "Este de acá es igual a este... ahora me dio que es una circunferencia, una semicircunferencia, no... que raro (se refiere a los segmentos etiquetados con r en la figura 13.b)."

Figura 13.a

Figura 13.b

Figura 13. c
Esquemas utilizados por Evan para determinar el lugar geométrico

Al abordar la segunda pregunta, Evan bosquejó el dibujo de la figura 14, señalando en los ejes lo que él llamó movimiento al límite, es decir, cuando la escalera está posicionada de forma vertical y cuando está en el suelo en forma horizontal. Lo expresó de la siguiente manera: "... estos son los movimientos al límite. Si el gato está aquí, vamos a ver el punto medio, parte aquí y baja, parte aquí y esto empieza a crecer.  Pero eso es lo que saco, me dan puras circunferencias, ¿si está bien?", en este fragmento de la transcripción Evan hace referencia al punto mostrado en el eje horizontal y en una primera aproximación al estudio del caso en que el punto no está en medio de la escalera menciona que su movimiento podría describir circunferencias.

Figura 14. Conjetura de Evan

Al no encontrar argumentos que le permitieran verificar su respuesta trató de emplear el método usado para el caso del punto medio, suponiendo que en lugar de una semicircunferencia tendría una elipse manteniendo un ángulo recto sobre la elipse (Fig. 15). Aunque en este momento Evan ya tenía una idea del lugar geométrico que describiría el movimiento del punto en cuestión, el método de solución empleado le impidió obtener la ecuación correspondiente.

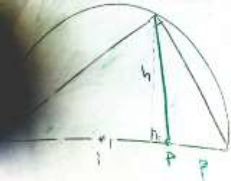
Figura 15. Evan intenta resolver el caso en que el punto no es el punto medio

El proceso de construcción del modelo desarrollado por los profesores se caracteriza por la amplia presencia de procedimientos algebraicos, basados en la congruencia de triángulos y el cálculo de distancias. En algunos casos, la argumentación expresada al obtener el lugar geométrico carece de precisión. Un ejemplo es el de un profesor quien concluyó que se trataba del lugar geométrico de una circunferencia con centro en el origen, pero al justificar sus resultados se expresa de manera confusa al referirse a la distancia que permanece constante (segmento AM en la figura 7): "al cambiar la escalera de posición, las diagonales siempre se dividían, por lo tanto, el gato situado en medio de la escalera sigue la trayectoria de ¼ de circunferencia".

Para el caso en que el gato se encuentra en una posición distinta, este profesor inicialmente señaló que la trayectoria del punto describiría un comportamiento similar al mostrado en la figura 5.b. Pero al construir el modelo algebraico, determinó la ecuación de la elipse con centro en el origen 1=(x²/a²)+(y²/b²)  (identificando también que cuando a=b se trata de una circunferencia), no logró establecer relaciones entre los resultados derivados de su procedimiento algebraico y la idea que tenía sobre la trayectoria. Este ejemplo ilustra cómo el razonamiento de algunos profesores se desarrolló de manera aislada, por un lado estudiaron el comportamiento de la situación con la construcción de un modelo gráfico y, por el otro lado, construyeron el modelo algebraico. Al final no lograron establecer conexiones entre estos modelos.

Comentarios. En el caso de los profesores, al inicio se puso en juego la identificación de las propiedades cualitativas de la situación, hecho influenciado por la percepción del movimiento, posteriormente la mayoría recurrió al uso de herramientas geométricas y la ubicación del problema en un sistema de coordenadas, buscando obtener las expresiones algebraicas que tradicionalmente son asociadas a un lugar geométrico (ecuación canónica de la elipse y circunferencia). En el caso de Roger y Hugo, el inicio de la solución del problema mostró estar asociado a la representación mental del lugar geométrico construida en la comprensión de la situación. Posteriormente movilizaron sus recursos matemáticos para la construcción del modelo matemático, entre ellos sus conocimientos sobre geometría plana y geometría analítica, mostrando preferencia por el uso de conceptos asociados a la geometría plana y como último recurso herramientas de geometría analítica. Llama la atención el caso de Evan, ya que los caminos que desarrolla están plasmados de una amplia gama de representaciones, en algunos momentos representaciones dinámicas, por ejemplo, la figura 14 que corresponde a las trayectorias de los puntos medios para segmentos con diferente longitud.
Podemos identificar dos momentos en la construcción del modelo matemático: uno relacionado con la identificación visual del lugar geométrico, y el otro momento, que se presenta posterior a la visualización, relacionado con la construcción del modelo algebraico. Ambos momentos se manifiestan en el tránsito de la Representación de la Situación (RS) al Modelo Matemático (MM).

4.5 Obtención de resultados y conclusiones.

La visualización del lugar geométrico. Todos los participantes identificaron la trayectoria del objeto en cuestión. Observamos algunas particularidades entre nuestros participantes, por ejemplo, Roger aunque conocía el lugar geométrico esperado no hizo referencia a él, sino hasta que trasladó la situación a una representación geométrica, Hugo lo hizo durante la construcción del modelo geométrico, Evan conjeturó que la trayectoria era una línea recta, y los profesores sólo fueron conscientes de que se trataba del lugar geométrico de una circunferencia y una elipse después de que dibujaron la situación para diferentes casos, similar a la figura 5.a.
Como se mostró anteriormente, Evan al visualizar el lugar geométrico de una semi-circunferencia (diferente a la hipótesis que había propuesto inicialmente), trató de explicar la situación de diferentes maneras. A continuación se muestra un fragmento de la transcripción de sus argumentos (continua de las figuras 13.a, 13.b y 13.c)
Evan - aquí, es una semicircunferencia, ¿no? Pero, ¿es o no es?,... es que es muy raro, no puede ser.
Inv- ¿dónde lo observas? [Refiriéndose a la figura 13.c]
Evan - Que ese lado es igual a ese. ... este lado está fijo [etiquetado (a)], es el tamaño medio y este está fijo [etiquetado (b)], entonces en el fondo son dos palitas que se abren del mismo tamaño. Entonces te da una semicircunferencia o un cuarto de circunferencia, no sé, pero es muy raro eso. ¿Es una semicircunferencia, o no?
Evan - Lo que digo es lo siguiente... voy a mirar la escalera así, aquí está el punto medio, entonces esto mide r, es como si fuera el radio de una circunferencia. Entonces ayuda a fijar cuanto mide este de aquí, que mide r, y si yo fijo r aquí, me interesa saber como se mueve este punto respecto de este, si?, bueno pero en realidad no depende del triángulo que yo dibujé, esto siempre pasa, así que si estoy a radio r, el punto medio se tiene que mover dentro de los puntos de radio r, es una semicircunferencia. Está dentro de una semicircunferencia y lo peor que puede pasar es que la escalera este parada y este aquí a distancia r y que la escalera este acostada y entonces está a distancia r.

Las expresiones de Evan reflejan un conflicto entre la imagen mental que tenía del comportamiento de la situación y los resultados obtenidos, incluso podríamos decir que la imagen inicial es persistente y por ello la insistencia de Evan al explicar su solución de maneras diferentes. 
La solución como modelo algebraico. Roger asumió que en el caso diferente al punto medio, obtendría el lugar geométrico de una elipse, pero no realizó operaciones para comprobarlo. Al preguntar a Hugo respecto a la comprobación de sus resultados, recurrió  a sus conocimientos sobre las propiedades de la elipse y la circunferencia, más que a comprobaciones algebraicas. Aquí se muestra un fragmento de la entrevista, discusión desarrollada alrededor de la figura 11.

Inv- y ¿estás seguro de tu respuesta?
Hugo - si
Inv- si no fuera así, pensarías en la validación?
Hugo - probablemente si, pero estoy seguro! Vale, esa es una validación pero es otro método que da también el caso  ½, es exactamente lo mismo.
Inv- A que te refieres?
Hugo - cuando este t=1/2 eso significa que el punto está a la mitad, entonces el cálculo dice que los puntos tienen esa forma, entonces va a ser el círculo.
Hugo - En la segunda he intentado hacer algo similar, he pensado que debería ser una elipse porque es la generalización natural y he intentado usar caracterizaciones de la elipse. Sabia que iba a funcionar si lo hacia con geometría analítica, calcular coordenadas y eso,  pero he intentado también hacerlo geométricamente como acá, pero no sé si es fácil o no! He pensado un poco, he visto que no es fácil y entonces he hecho los cálculos y he visto que es la fórmula de una elipse.

En relación con los profesores, todos ellos obtuvieron una idea de la trayectoria del punto después de probar para diferentes posiciones de la escalera, posterior a ello se enfocaron en la obtención del modelo algebraico, ninguno de ellos consideró la validación del modelo obtenido.

5. CONCLUSIONES

 Tal como se observó en las primeras fases, matemáticos y profesores recurrieron al trazo de esquemas como una estrategia para abordar la resolución del problema. Estos esquemas fueron utilizados por los participantes de manera diferente, los matemáticos como una manera de relacionar sus conocimientos matemáticos con el fenómeno en estudio. Antes de proceder con la prueba analítica, visualizaron casi inmediatamente la trayectoria del desplazamiento, razón por la que su trabajo, después de haber comprendido la situación se centró en la realización de cálculos y búsqueda de herramientas más formales para justificar sus conjeturas (Roger y Hugo). Los profesores utilizaron sus esquemas como un medio para comprender la situación que les era planteada, necesitaron realizar varios esquemas para imaginar la trayectoria que se les había pedido localizar, posterior a esto destaca la extensa variedad de cálculos realizados para determinar el modelo algebraico. En otras palabras, mientras que Hugo y Roger apoyados en las propiedades de lugar geométrico lo reconstruyeron mentalmente, los profesores no fueron capaces de imaginarlo sin el apoyo de la representación pictórica de la situación, para ellos la idea de lugar geométrico estaba constituida también por la escritura de la expresión analítica del mismo. El trabajo de los profesores, en el primer bloque, se caracterizó por el trazo de esquemas similares a los mostrados en las figuras 5.b y 5.c, aproximadamente el 50% de ellos construyeron esquemas que les conducían al trazo de curvas que no les permitieron visualizar el desplazamiento real, dificultades similares a las que reporta Planchard (2009). Este hecho ofrece evidencia de algunas diferencias en la representación mental de la situación (MRS) y el modelo real (RM) que cada individuo construye, las cuales como en el caso de algunos de nuestros participantes pueden ser equivocadas y mediadas en gran medida por la intuición que tienen sobre el comportamiento de la situación. Tall (1994) investigó las imágenes mentales que matemáticos y estudiantes de matemáticas construyen e identificó tres aspectos importantes que están implicados en la comprensión del conocimiento en las matemáticas: representar la información visualmente, usar símbolos para representar la información y cuando un proceso es demasiado largo utilizar la práctica, en la modelización estos elementos se ponen en acción durante todo el proceso. Añadimos a lo anterior que en el caso de tareas que implican una visualización geométrica-dinámica las imágenes mentales pueden volverse persistentes, como lo muestra el caso de Evan.

El hecho que matemáticos y profesores evidencien diferentes maneras de abordar el proceso de modelación puede ser asociado a su experiencia y al dominio de los conocimientos matemáticos involucrados. Mientras que dos de los matemáticos pudieron integrar propiedades matemáticas y características del problema en una primera aproximación a la construcción del modelo, el resto de los participantes tuvo la necesidad de recurrir al uso de variados esquemas para comprender la situación y después proceder a construir el modelo algebraico. Estos aspectos constituyen un eslabón que determina el tránsito de los participantes por el ciclo de modelización de manera eficiente.

En relación con los profesores, destaca el uso de procedimientos que les son conocidos (herramientas de geometría analítica y geometría plana), más que un intento por comprender las relaciones entre las variables, esto les impidió al inicio identificar la trayectoria como un cuarto de circunferencia. Crouch & Haines (2004), señalan que este tipo de dificultades también son provocadas por el contexto escolar en el sentido que la enseñanza se dirige hacia el desarrollo de una mayor capacidad de abstracción, generalmente en ambientes descontextualizados, por lo que no se favorece el desarrollo de habilidades para establecer relaciones entre los conocimientos adquiridos y situaciones de tipo extra-matemático.

De los esquemas pictóricos que realizaron los profesores podemos inferir que, parte de las dificultades que se presentan al interpretar la situación, están relacionadas con un cambio en la tarea, es decir, pasan de localizar la trayectoria del punto a localizar la trayectoria descrita por el movimiento de la escalera, situación que puede ser generada debido a que la unidad de visualización que representa la posición del segmento sobresale por encima de la representación del movimiento del punto, lo que genera una asociación con un modelo geométrico equivocado, esto hace una diferencia con los matemáticos esencialmente por su capacidad de abstracción.

Al validar los resultados se identificaron maneras distintas de proceder, para Hugo y Roger la validación se encuentra asociada al conocimiento previo del lugar geométrico y en menor grado con la verificación del procedimiento matemático. Para Evan, la validación se apoya en la comprensión de la dinámica de la situación y la confrontación de los resultados con la idea previa que tenía sobre el comportamiento. Y para los profesores la validación se apoya en la asociación del modelo algebraico con su representación gráfica, además de la revisión de las operaciones algebraicas realizadas.

En relación con la tarea propuesta, los resultados de esta investigación sugieren que su diseño determina la forma de proceder en la resolución, donde el camino de solución puede estar influenciado por la experiencia y las herramientas matemáticas de quien resuelve, más que por una preferencia en la elección de un registro de representación.

Finalmente, señalamos que las fases de modelización difícilmente se pueden pesquisar en los matemáticos, en particular aquellas involucradas entre el tránsito de la situación real al modelo matemático debido a que éstas suceden de manera interna y muy rápidamente (proceso de abstracción), de forma que al responder a los cuestionamientos del investigador el individuo puede estar en una fase superior. En este sentido, el dialogo establecido entre la representación del problema y el matemático sucede de manera interna, y las representaciones utilizadas constituyen una herramienta para expresar las ideas. Los profesores manifestaron la necesidad de trabajo con un par así sus representaciones fueron utilizadas como medio de comunicación y expresión, y fue posible observar algunos indicios del tránsito entre las fases mencionadas. Al no hallar congruencia entre las representaciones, el trabajo en pares entre los profesores favoreció la fase de matematización debido al dialogo establecido entre los individuos a partir de una representación del problema.

En el contexto pedagógico, creemos que es necesario concientizar a los docentes sobre la capacidad de abstracción (caracterizada por el tránsito contiguo entre las fases RS y MM) que poseen algunos individuos a manera de que logren hacer esfuerzo racional por transmitir a sus estudiantes el proceso interno de pensamiento desarrollado al modelizar una situación. Con estas ideas nos hemos planteado como futuro trabajo la investigación en el proceso de enseñanza sobre las interacciones que se establecen entre las fases RS-MM en los docentes y la manera en que los profesores logran trasmitirlas a sus estudiantes.

Notas al pie

¹Entendiendo por realidad aquellas situaciones que se presentan en un contexto no matemático y que puedan llegar a ser reales en la imaginación de los estudiantes.

²Estilo de pensamiento matemático es definido como: "el camino a través del cual un individuo prefiere presentar, entender y pensar, hechos matemáticos y establecer conexiones entre determinadas imaginaciones internas y/o las representaciones externalizadas (Borromeo-Ferri, 2012, pg. Abcde+3)". En individuos con una edad entre 15 y 16 años se han identificado tres estilos de pensamiento diferentes: Pensamiento visual, analítico e integrado.

BIBLIOGRAFÍA

1. Blomhøj, M. & Jensen, T. H. (2003). Developing mathematical modeling competence: conceptual clarification and educational planning. Teaching Math and its applications: An international Journal of the IMA, 22(3), pp. 123-139.         [ Links ]

2. Blomhøj, M. (2009). Different perspectives in research on the teaching and learning mathematical modelling—Categorising the TSG21 papers. In M. Blomhøj & S. Carreira (Eds.), Mathematical applications and modelling in the teaching and learning of mathematics: Proceedings from TSG21 at the ICME11 (pp. 1–;17). IMFUFA-text no. 461, Department of Science, Systems and Models, Roskilde University.         [ Links ]

3. Blum, W. (1993). Mathematical modelling in mathematics education and instruction. Descargado el 19-11-10 de http://oai.bibliothek.uni-kassel.de/bitstream/urn:nbn:de:hebis:34-2009051227366/1/BlumModelling1993.pdf        [ Links ]

4. Borromeo Ferri, R. (2006). Theoretical and empirical differentiations of phases in the modelling process. Zentralblatt für Didaktik der Mathematik, 38 (2), 86-95.         [ Links ]

5. Borromeo Ferri, R. (2007). Modeling from a cognitive perspective: Individual modeling routes of pupils. In C. Haines, P. Galbraith, W. Blum, & S. Khan (Eds.), Mathematical modeling (ICTMA 12): education, engineering and economics (pp. 260–;270). Chichester: Horwood.         [ Links ]

6. Borromeo Ferri, R. (2010). On the influence of mathematical thinking styles on learners' modelling behaviour.  Journal für Mathematikdidaktik, 31 (1), 99-118.         [ Links ]

7. Borromeo Ferri, R. (2012). Mathematical thinking styles and their influence on teaching Rogerand learning mathematics. In the 12th International Congress on Mathematical Education. 8 July –; 15 July, 2012, COEX, Seoul, Korea        [ Links ]

8. Bransford, J., Brown, A., & Cocking, R. (Eds.) (2000). How People Learn: Brain, Mind, Experience, and School. Expanded Edition. Committee on Developments in the Science of Learning with additional material from the Committee on Learning Research and Educational Practice, National Research Council. Washington, D.C. National Academies Press. Downloaded from http://www.nap.edu/catalog/9853.html        [ Links ]

9. Crouch, R. & Haines, C. (2004). Mathematical modelling: transitions between the real world and the mathematical model, International Journal of Mathematical Education in Science and Technology, 35:2, 197-206        [ Links ]

10. Haines, C. & Crouch, R. (2007). Mathematical Modelling and applications: ability and competence frameworks. In W. Blum, P. L. Galbraith, H. Henn, & M. Niss (Eds.), Modelling and applications in mathematics education. The 14th ICMI study (pp. 417–;424). New York: Springer.         [ Links ]

11. Miles, M. B. & Huberman, A. M. (1994). Qualitative Data Analysis: An Expanded Sourcebook. California: Sage. 2ª Edición.         [ Links ]

12. Niss, M., Blum, W., & Galbraith, P. (2007). Introduction. In W. Blum, P. L. Galbraith, H. W. Henn & M. Niss (Eds.), Modelling and Applications in Mathematics Education (pp. 3-32). New York: Springer.         [ Links ]

13. Planchart, O. (2009). Estudio de un problema: El gato en la escalera. El lugar geométrico. Revista 360ο, 4. Descargado el 6 de Nov de 2013 de http://cremc.ponce.inter.edu/360/revista360/Documents/Edicion%204/Matematica/Estudio%20de%20un%20problema%20El%20gato%20en%20la%20escalera.%20El%20lugar%20geom%C3%A9trico.pdf

14. Santos-Trigo, M. (2012). El estudio de fenómenos de variación y el empleo de herramientas digitales. Downloaded from https://itunes.apple.com/us/book/estudio-fenomenos-variacion/id547065928?mt=11.         [ Links ]

15. Tall, D. (1994). Understanding the Processes of Advanced Mathematical Thinking. Invited talk given at the International Congress of Mathematicians, Zurich. Edited version published in L'Enseignement Mathématiques, 1996, 42, 395-415. Descargado el 22-11-13 de http://homepages.warwick.ac.uk/staff/David.Tall/pdfs/dot1996i-amt-icm.pdf        [ Links ]

16. Vasíliev, N. B. y Gutenmájer, V. L. (1980). Rectas y Curvas (Trad. Margarita Gómez). Moscú         [ Links ]: