ARTICULOS ORIGINALES

Elaboración de orientaciones didácticas desde la reflexión docente: el caso del enfoque funcional del álgebra escolar

 

Horacio Solar, Francisco Rojas

hsolar@uc.cl , frojass@uc.cl

Facultad de Educación, Pontificia Universidad Católica de Chile, Av. Vicuña Mackenna 4860, Macul, Santiago de Chile.

 

---

Resumen

Nuestra investigación se focaliza en la elaboración de orientaciones didácticas que emerjan del proceso reflexivo del profesor a partir del diseño e implementación de una unidad didáctica. La elaboración de orientaciones didácticas en conjunto con el docente lo destacamos como el eje central de la investigación, ya que permite promover un rol más activo del profesorado en los procesos de innovación didáctica, específicamente en los relativos al desarrollo del álgebra escolar. A partir de esta visión colaborativa, se presenta el caso de la profesora Marta, cuyas reflexiones permitieron elaborar orientaciones didácticas para el trabajo de patrones crecientes para los niveles de 5° y 6° básico (10-12 años). Como resultado principal, se ha podido observar que la elaboración de las orientaciones didácticas es producto de una interrelación entre diferentes dimensiones del Conocimiento Matemático para la Enseñanza (MKT: mathematical knowledge for teaching): entre ellos el conocimiento especializado del contenido, los conocimientos del contenido y de los estudiantes y del contenido y de la enseñanza. La Metodología de Trabajo Docente (MTD)  que se ha utilizado para la formación de los profesores en álgebra escolar ha sido un enfoque que ha evidenciado ser muy potente para que emerjan reflexiones profundas de los profesores, y que ha permitido generar orientaciones didácticas propicias para el trabajo algebraico escolar desde una perspectiva funcional.

Palabras clave: Álgebra temprana; Reflexión docente; Orientaciones didácticas; Conocimiento matemático para enseñar.

Development of teaching guidelines from teacher reflection: the case of the functional approach of school algebra

Abstract

Our research focuses on the development of teaching guidelines that emerge from the teacher reflective process through the design and implementation of a teaching sequence. The development of teaching guidelines in conjunction with the teacher is highlighted as the focus of our research, as it allows the promotion of a more active role of teachers in educational innovation processes, specifically those related to the development of school algebra. From this collaborative approach, the case of Marta is presented, whose reflections helped to develop teaching guidelines for the work in growing patterns for levels 5 and 6 of elementary education (10-12 years). As a main result, it has been observed that the development of teaching guidelines is the product of the interrelation between different dimensions of mathematical knowledge for teaching (MKT): specialized knowledge of content, knowledge of content and students, and content and teaching. The methodology used for the development of these guidelines has been a tool that has shown to be very powerful to promote the emergency of teacher's deep reflections and has generated appropriate teaching guidelines for working in school algebra from a functional perspective.

Keywords: Early algebra; Teaching reflection; Teaching guidelines; Mathematical knowledge for teaching.

Élaboration des orientations didactiques de professeur de réflexion: le cas de l'approche fonctionnelle de l'algèbre à l'école

Résumé

Notre recherche se concentre sur l'élaboration des orientations didactiques qui émergent du processus de réflexion du professeur lors de la conception et la mise en œuvre d'une séquence didactique. Nous plaçons l'élaboration d'orientations didactiques en commun avec l'enseignant comme axe central de notre recherche, au sens où elle permet de développer un rôle plus actif du professeur dans les processus d'innovation didactique, spécifiquement dans ceux relatifs au développement de l'algèbre scolaire. À partir de ce point de vue collaboratif, nous présentons le cas de la professeur Marta, dont les réflexions ont permis d'élaborer des orientations didactiques pour le travail des séquences croissantes pour les grades 5 et 6 (10-12 ans). Notre principal résultat est d'avoir pu observer que l'élaboration d'orientations didactiques pour le travail des séquences croissantes est le résultat d'une inter-relation entre différentes dimensions des connaissances mathématiques pour enseigner (MKT) : entre la connaissance spécialisée du contenu, la connaissance du contenu et des élèves et du contenu et de l'enseignement. La méthodologie utilisée pour l'élaboration de ces orientations s'est avéré être un outil très puissant pour faire émerger des réflexions profondes des professeurs, et qui a permis de générer des orientations didactiques propices pour le travail algébrique scolaire dans une perspective fonctionnelle.

Mots clés: Algèbre début; Professeur de réflexion; Orientations didactiques; Connaissances mathématiques pour l'enseignement.

Elaboração de orientações didácticas a partir da reflexão de professores: o caso da abordagem funcional da álgebra escolar

Resumo

Nossa pesquisa se foca na elaboração de orientações didáticas que emergem do processo reflexivo do professor a partir do desenho e implementação de uma sequência didática. A elaboração de orientações didáticas em conjunto com o docente é destacada como o eixo central da pesquisa, já que permite promover um papel mais ativo do professorado nos processos de inovação didática, especificamente nos relativos ao desenvolvimento da álgebra escolar. A partir desta visão colaborativa, apresenta-se o caso da professora Marta, cujas reflexões permitiram elaborar orientações didáticas para o trabalho de padrões crescentes para os níveis de 5º e 6º básico (10-12 anos). Como resultado principal, se observou que a elaboração das orientações didáticas é produto de uma interrelação entre diferentes dimensões do conhecimento matemático para ensinar (MKT): entre o conhecimento especializado do conteúdo, os conhecimentos do conteúdo e dos estudantes, e do conteúdo e do ensino. A metodologia utilizada para a elaboração destas orientações tem sido uma ferramenta que tem se mostrado muito potente para gerar profundas reflexões por parte dos professores, e que tem permitido desenvolver orientações didáticas propicias para o trabalho algebraico escolar desde uma perspetiva funcional.

Palavras-chave: Álgebra cedo; Reflexão professor; Orientações didáticas; Conhecimento matemático para o ensino.

---

1. INTRODUCCIÓN

En los últimos años, ha habido una nueva mirada al álgebra escolar, en la cual se ha dado relevancia a los procesos de generalización y pensamiento inductivo (Iztcovich, Ressia, Novembre y Becerril, 2012; Castro, Cañadas y Molina, 2010), por ejemplo, a través del estudio de patrones crecientes. Este enfoque ha sido desarrollado por lo que se denomina Early Algerbra o Álgebra Temprana (e.g. Blanton y Kaput, 2005; Molina, 2009), que promueve el estudio del álgebra desde los primeros años de escolaridad, basado en un modelo funcional del álgebra. Esto se ha visto reflejado en la incorporación de esta perspectiva en currículums de matemáticas de varios países (NCTM, 2003; Ministerio de Educación Nacional, 2006; Departament d'Educació, 2007; Mineduc, 2012) en los primeros años de primaria. Sin embargo, para los profesores de los niveles iniciales, la incorporación de esta área de trabajo matemático no es trivial, y se hace compleja su aplicación en aula. Por ello, consideramos que es necesario dar relieve a las orientaciones didácticas para el desarrollo del álgebra temprana, es decir, sugerencias para el profesor de matemáticas de cómo gestionar actividades enfocadas al desarrollo del álgebra desde una visión funcional.

Dicha elaboración la hemos enfocado desde una perspectiva de trabajo colaborativo con los docentes, ya que creemos que los procesos de reflexión de la práctica, en conjunto con los de preparación de la enseñanza, son los que permiten al docente adquirir un conocimiento que sea conducente a la implementación de nuevas propuestas curriculares. Y es este conocimiento que se genera a partir de la reflexión el que puede constituir lo que Shulman (1987) define como el Conocimiento Didáctico del Contenido, o lo que en matemáticas Ball y su equipo han denominado Conocimiento Matemático para la Enseñanza (MKT, por sus iniciales en inglés) (Hill, Ball y Schilling, 2008; Ball, Thames y Phelps, 2008; Hill, Rowan y Ball, 2005). Tanto los nuevos conocimientos en las áreas de relaciones, patrones y cambio que se trabajan con esta nueva perspectiva de Álgebra Temprana, como los conocimientos didácticos respecto de cómo preparar y gestionar el conocimiento matemático en el aula, constituye un conocimiento matemático específico para enseñar, que el profesor debe dominar para una enseñanza efectiva del álgebra escolar. En otras palabras, el profesor debe tener un conocimiento especializado sobre los patrones repetitivos y crecientes, y cómo conducen hacia las funciones; debe tener conocimiento sobre cómo desarrollar en los estudiantes el pensamiento relacional por medio de los patrones. Este conocimiento matemático y didáctico se debe ver reflejado en una planificación de la enseñanza que cautele una visión funcional del álgebra y anticipe los razonamiento de los estudiantes.

Por lo general, los profesores de educación primaria, cuya formación inicial no es exclusiva en matemáticas, a su egreso no tienen un dominio profundo del conocimiento matemático escolar y, habitualmente, desarrollan este tipo de conocimiento matemático para enseñar a través de la experiencia docente (Avalos y Matus, 2010).  No obstante, consideramos que ese conocimiento que se genera en la propia experiencia no suele ser transmitido a otros profesores, ya que muchas veces no cuentan con la oportunidad ni de racionalizarlo ni de compartirlo. En este sentido, la investigación que presentamos aquí se focaliza en la elaboración de orientaciones didácticas para la enseñanza del álgebra temprana, que emergen del proceso reflexivo del profesor a partir del diseño e implementación de una unidad didáctica, ya que la manera de elaborar dichas orientaciones se puede considerar como base para estudiar el conocimiento matemático para la enseñanza del profesor.

Racionalidad de la investigación y objetivos

En las últimas propuestas del currículo de matemáticas chileno (Mineduc, 2009; 2012), el álgebra ha estado presente en los cursos de educación básica o primaria. En el ajuste curricular (Mineduc, 2009), se determinan como eje de contenido matemático el eje de álgebra, a partir de 5° año de educación básica (10 a 11 años). Posteriormente, se establecen las nuevas Bases Curriculares (Mineduc, 2012), acorde al proceso de implementación de la nueva Ley General de Educación. En dichas bases, el álgebra toma un papel sustancial al proponerse desde primer año de educación primaria, y evolucionando en complejidad en los cursos siguientes. En este nuevo currículum, el aspecto funcional del tratamiento algebraico se introduce en los primeros años por medio del trabajo con patrones, figurativos o numéricos, el cual permite desarrollar una serie de procesos propios del álgebra tales como la conjetura, predicción, generalización y creación de modelos, por nombrar algunos. El acercamiento al álgebra por la vía del estudio de patrones la consideramos adecuada, ya que permite introducir la noción de variable, el uso de gráficas para estudiar la dependencia entre ellas, y el estudio de modelos algebraicos tales como proporcionalidad directa e inversa. Estos temas en su conjunto permiten el desarrollo del pensamiento variacional (Díaz, 2005), y es precisamente dicho tipo de pensamiento el que busca desarrollar el álgebra temprana, entendiéndola como el estudio del cambio.

Para los profesores, esta visión del álgebra y su incorporación a la escolaridad temprana no es trivial. Nombramos dos antecedentes que alertan de las dificultades que puede tener un profesor al promover esta visión del álgebra en la escuela. En primer lugar, los profesores de educación básica en Chile que ya tienen varios años de experiencia, se han acostumbrado a trabajar con un currículo de matemáticas en que lo algebraico está inserto en el eje de números y operaciones. Si bien en el currículum tradicional (Mineduc, 2002) se estudiaban patrones repetitivos y crecientes, se hacía de forma puntual privilegiando la representación numérica de los patrones por sobre  el uso de figuras para representarlos, sin destacar los procesos de conjeturación y generalización propios del carácter algebraico. En segundo lugar,  consideramos que tradicionalmente ha existido una tendencia por los profesores a asociar el álgebra con una manipulación de expresiones, que se materializa en la generalización de la aritmética y estudio de ecuaciones, pero no así con la visión funcional, en que se estudia el cambio, tema relativo a las funciones y que además es propio de educación secundaria.

Las investigaciones sobre el álgebra temprana son relativamente recientes (Blanton y Kaput, 2005; Molina, 2009) y aún falta tiempo para que repercuta a las prácticas en el aula de matemáticas. Además, existe una carencia de libros de texto para primaria que consideren la visión funcional del álgebra. Por ello, y ante la falta de literatura, en el estudio se ha contemplado un aspecto de innovación que consiste en la creación de materiales para la enseñanza del álgebra en primaria. El material contempla dos aspectos fundamentales: una secuencia de enseñanza y unas orientaciones didácticas para su desarrollo. La secuencia de enseñanza es diseñada en forma conjunta con el profesorado, en base al modelo de planificación utilizado por el docente, y se implementa para su evaluación; posteriormente el profesor describe la experiencia que permite la elaboración de las orientaciones didácticas para dicho material.

En la elaboración de orientaciones didácticas por parte del profesor, es muy relevante el papel que juega la reflexión profesional, en este caso la reflexión de la práctica (Shön, 1998). Estos procesos reflexivos permiten al docente cuestionar su conocimiento profesional relativo al conocimiento matemático para enseñar. Este proceso permite indagar sobre su percepción de la gestión de las actividades realizadas de la unidad didáctica y así evaluar la pertinencia y adecuación del material implementado. En este sentido, el proceso analítico de las reflexiones docentes sobre aspectos del álgebra escolar en niveles medios de la educación primaria nos ha permitido, en colaboración con los profesores, elaborar las orientaciones didácticas para la secuencia de enseñanza del álgebra, desde la perspectiva funcional, en donde se estudian temas tales como patrones, proporcionalidad y funciones por medio de la interpretación de gráficas.
De hecho, la elaboración de orientaciones didácticas en conjunto con el docente lo destacamos como el eje central de la investigación, pues éstas representan la intención de promover un rol más activo del profesorado en el desarrollo del álgebra escolar y de los procesos de innovación didáctica.

Para dar respuesta a la problemática presentada, se han establecido tres objetivos específicos:

• Elaboración colaborativa de situaciones de aprendizaje del álgebra desde una perspectiva funcional.
• Implementación de la unidad didáctica para elaborar de forma colaborativa las orientaciones didácticas de las situaciones de aprendizaje.
• Descripción de la reflexión del profesor en el proceso de discusión de las orientaciones didácticas.

2. MARCO TEÓRICO

Hemos considerado que hay cuatro dimensiones que son esenciales en la problemática de nuestra investigación: una descripción del álgebra temprana y su visión funcional, estudiar la reflexión del profesor, caracterizar el conocimiento matemático para enseñar, y hacer una conceptualización inicial sobre orientaciones didácticas. A continuación se presenta una revisión de la literatura de cada una de estas dimensiones.

2.1. Álgebra temprana y su visión funcional

Actualmente, en diversas propuestas curriculares se hace constar la necesidad de considerar el desarrollo del pensamiento algebraico desde los primeros niveles de enseñanza primaria (Solar y Rojas, 2011). Una de las propuestas que responden a dicha necesidad es el enfoque de la Early Algebra (o Álgebra temprana), en el cual se promueve fuertemente el estudio de patrones y de relaciones entre cantidades, y también de estructuras algebraicas y propiedades aritméticas (Blanton y Kaput, 2005; Molina, 2009).

Asimismo, Godino, Castro, Aké y Wilhelmi (2012) que han traducido Early Algebra como Razonamiento Algebraico Elemental, señalan que la incorporación del álgebra en el currículo en primaria debe promover tareas con diversos grados de algebrización. Estas ideas nos permiten sostener que la incorporación de un álgebra tempana promueve el desarrollo conceptual de matemáticas más profundas y complejas.

Por otra parte, varios autores han señalado los diversos usos de la variable en el álgebra (Schoenfeld y Arcavi, 1988; Socas, Camacho, Palarea y Hernández, 1996; Ursini, Escareño, Montes y Trigueros, 2005), en donde se desprenden cuatro interpretaciones de álgebra: aritmética generalizada, resolución de ecuaciones, funcional y estructural. En estas interpretaciones del álgebra, el sentido funcional permite interpretarla como el estudio de las relaciones entre cantidades, a la vez que la variable se entiende en su sentido más amplio de variabilidad, a diferencia de las otras interpretaciones en que la variable tiene valor único como en el caso de las ecuaciones (incógnitas), o son letras como en el caso de estudio de las propiedades de conmutatividad, asociatividad, etc., (aritmética generalizada) o también en el caso de los polinomios (estructural).
En particular, en el sentido funcional del álgebra, el estudio de patrones es significativo. La búsqueda de patrones es vista como una forma de abordar el establecimiento de la generalización, que es la esencia de las matemáticas (Barbosa, Vale, y Palhares, 2012). Estos mismos autores señalan que en un contexto de niños de 6° de primaria (11-12 años) si bien hay experiencias en que los estudiantes prefieren enfoques numéricos sobre los visuales para resolver problemas de patrones, hay estudios relacionados con la visualización en que han evidenciado la importancia de las representaciones en el desarrollo conceptual. Por lo tanto, es importante proporcionar tareas que estimulen a los estudiantes a usar y entender el potencial de las estrategias visuales, y a relacionar contextos numéricos con los contextos visuales para comprender el significado de números y variables. En nuestra investigación hemos considerado que la noción de patrón es central para orientar el álgebra que conocen los profesores, la cual se asocia comúnmente a las interpretaciones de aritmética generalizada y resolución de ecuaciones. Con ello, se espera hacer una transición hacia una visión funcional del álgebra.

Existen varias organizaciones curriculares en que la interpretación funcional del álgebra está presente de diferentes maneras tanto en primaria como en secundaría. En el currículo español, desde el nivel equivalente a 7º año de educación primaria, además del eje de álgebra aparece el eje "Funciones y gráficas" (Ministerio de Educación y Ciencia, 2006). En particular, en el currículo de la Comunidad Autónoma de Cataluña, ya desde el primer año de primaria se introduce el eje llamado "Relaciones y cambio" (DOGC, 2007), organización curricular que destaca el Pensamiento Variacional. Otro caso es el que presentan los Estándares Básicos de Competencias en Matemáticas de Colombia (Ministerio de Educación Nacional, 2006), en el cual uno de los cinco ejes propuestos se denomina "Pensamiento Variacional y Sistemas Algebraicos y Analíticos", en que se amplía evidentemente la visión del álgebra. Asimismo, en la propuesta curricular del NCTM¹ (2003) de EEUU, el estándar de contenido Álgebra se refiere a las relaciones entre cantidades incluyendo las funciones, las formas de representación de relaciones matemáticas y el análisis del cambio. En las nuevas Bases Curriculares chilenas para los cursos de 1º a 6º de primaria (MINEDUC, 2012), contexto donde se sitúa esta investigación, aparecen dos cambios relevantes en torno al álgebra respecto al currículo anterior: por una parte, al eje se le denomina "Patrones y Álgebra" en vez de "Álgebra" y, por otra, comienza a desarrollarse en 1º de primaria, en vez de en 5º de primaria. Estos cambios han tenido como consecuencia una mayor importancia al estudio de patrones desde el primer año de primaria. Estos currículos, en su conjunto, promueven visiones del álgebra que son más amplias que las tradicionales, al ir más allá de la asociación tradicional con el estudio de estructuras matemáticas y manipulación de expresiones algebraicas.

2.2. Reflexión docente

Desde los trabajos de Schön (1998), la reflexión del profesor en el desarrollo de su práctica ha tomado un importante rol en los procesos de formación permanente del profesorado. En este sentido, consideramos que es sustancial implicar a los docentes, durante el proceso de capacitación, en procesos intensos e intensivos de reflexión sobre la práctica, tanto sobre aquella realizada por otros profesores, como la realizada por ellos mismos, ya que esto permite comprender y mejorar la propia práctica profesional (Zeichner, 1993). Como profesional reflexivo, el profesor ha de dirigir sus acciones, previniéndolas y planeándolas de acuerdo con los fines que tenga en perspectiva. Por ello, se esperaría que un profesional reflexivo exhiba múltiples operaciones sobre un tema; por ejemplo, ser capaz de definirlo, explicarlo, compararlo con otros elementos, sacar inferencias y conclusiones, resolver problemas de la vida cotidiana en que aplica ese conocimiento e, incluso, inventar y crear a partir de ese dominio (Beas, Santa Cruz, Thomsen, y Utreras, 2000).

Para llegar a construir conocimiento profesional, en nuestro caso un conocimiento matemático para enseñar, Schön (1998) sostiene que es necesaria tanto la reflexión sobre la acción (aquel proceso reflexivo que se desarrolla antes y después de la acción) como la reflexión en la acción (aquel diálogo reflexivo del profesional con su entorno de acción, en el cual encuadra y resuelve los problemas sobre la marcha). Los docentes muchas veces no son conscientes del conocimiento que producen al realizar su práctica, y una vía para ello es hacer presente y ostensible este conocimiento tácito por medio de la reflexión de la enseñanza. Explicitar estos conocimientos profesionales (disciplinares, didácticos, pedagógicos, etc.,) permite criticarlos, examinarlos y perfeccionarlos, evidenciando así los aspectos más sutiles y complejos de las prácticas pedagógicas. Del mismo modo, permite cambiar las creencias u orientaciones (orientations) de los profesores en el sentido planteado por Schoenfeld (2011), ya que el conocimiento explicitado se constituye como un recurso (resources), cuyo uso permite el logro de unas determinadas metas (goals) de aprendizaje.

La construcción del conocimiento matemático en el contexto escolar, en nuestro caso sobre el álgebra temprana, requiere de interpretar de manera completa la práctica docente. Una reflexión centrada solo en algunos aspectos, puede conducirnos a considerar que es posible reflexionar sobre la práctica sin necesidad de incorporar una reflexión profunda sobre el conocimiento mismo que es construido en el aula. Proceder de esta forma, ignoraría que no sólo lo enseñado depende de la herramienta con la que se pretende conseguir su aprendizaje, sino al revés, que las Organizaciones Didácticas (Bosch, Espinoza y Gascón, 2003), se configuran de manera estrechamente vinculada a la estructura dada a lo que hay que enseñar. Por lo tanto, no es factible realizar procesos de formación y desarrollo profesional centrados o bien en el conocimiento disciplinar o bien en cuestiones generales sobre la enseñanza, ya que esta separación desvirtúa la esencia misma del aprendizaje matemático. El aprendizaje del álgebra temprana, y en particular de la generalización y estudio del cambio por medio de patrones crecientes, solo puede ocurrir de forma efectiva por medio de un modo particular de gestionar la enseñanza, en unas condiciones institucionales determinadas. De este modo, en los procesos de formación docente se debe profundizar en conocimientos matemáticos para la enseñanza, en su dimensión didáctica y disciplinar, a la vez que reflexionar sobre cuestiones pedagógicas generales que constituyan condiciones que faciliten o dificulten el aprendizaje (Espinoza, Barbé, y Gálvez, 2009).

Para indagar en la reflexión de los docentes, Van Es y Sherin (2007) proponen estudiar los cambios que se producen en ella respecto de los análisis que éstos hacen de las prácticas, tanto propias como de otros. Los autores proponen tres aspectos a tener en cuenta: el actor involucrado en el análisis realizado por el docente, el tema y el tipo de análisis realizado (Tabla 1).

Tabla 1: Categorías de análisis de la reflexión (Van Es y Sherin, 2007, p. 161)

La primera de estas categorías busca examinar sobre quién se hacen los comentarios cuando el docente realiza un análisis de la práctica. Estos posibles actores no sólo incluyen al profesor y a los alumnos (que son quienes aparecen en los videos que se utilizan como medio de análisis), sino también agentes externos, como por ejemplo desarrolladores curriculares. Además, se contempla un indicador que dé cuenta de los momentos que el docente habla de sí mismo, en tanto el desarrollo de su propia práctica.

La segunda categoría, aborda aquellos temas sobre los que hablan los profesores, que incluye el pensamiento matemático, aspectos pedagógicos, clima de clase, la gestión, u otros aspectos. El pensamiento matemático se refiere a las ideas matemáticas y a la comprensión expresada en la clase (por ejemplo, "Él estaba usando sus dedos para contar los grupos de diez"); los aspectos didácticos se refieren a las técnicas y estrategias para la enseñanza (por ejemplo, "¿Qué método se utiliza para enseñar a sumar números de dos dígitos?''); el clima de la clase se refiere al entorno social de la misma (por ejemplo, "Esa fue una lección divertida"); y la gestión se refiere a las declaraciones sobre la mecánica de la clase (por ejemplo, "El profesor maneja muy bien las interrupciones").

La tercera categoría se centra en cómo los profesores analizan la práctica: a nivel descriptivo, evaluativo e interpretativo. El nivel descriptivo se refiere a las declaraciones que relatan los hechos ocurridos (por ejemplo, "Los estudiantes tenían las manos en alto. El maestro llamó a una alumna para ir a la pizarra"); el nivel evaluativo se refiere a las declaraciones en las que los profesores comentan sobre lo que consideran bueno o malo, o sobre aquello que debería haber sido hecho de manera diferente (por ejemplo, "Me gusta mucho cómo fue hecha la clase". "Eso fue genial"); y el nivel interpretativo se refiere a las declaraciones en las que los profesores hacen inferencias sobre lo que observan. Es decir, usan sus observaciones de lo que sucede en el video para hacer hipótesis acerca de por qué estos acontecimientos ocurren.

A partir de este trabajo, en Solar, Espinoza, Rojas, Ortiz, González y Ulloa (2011) desarrollamos tres niveles de análisis, que varían en función de la presencia de causalidad en los argumentos dados por los profesores al analizar su práctica y la de otros. La figura 1 esquematiza los niveles definidos.

Figura 1: Niveles de Reflexión Docente (adaptado de Solar et al., 2011, p. 171).

En el nivel descriptivo, hay una ausencia de relaciones de causalidad, en cambio, en el nivel relacional, dichas relaciones son puntuales, y solo en el nivel interpretativo, se evidencian relaciones sustanciales de causalidad. Por otra parte, el paso de un nivel a otro se ve reflejado por cambios en el tema de análisis: en un nivel descriptivo existe una tendencia a considerar aspectos de carácter pedagógicos, en cambio en los siguientes niveles se empiezan a considerar aspectos de carácter didáctico, es decir, estrictamente relacionados con la enseñanza y aprendizaje matemáticos. Un segundo criterio de transición son los actores: en un nivel descriptivo puede centrarse en el alumno, profesor u otros actores, en cambio en un nivel interpretativo estos actores aparecen articulados y mutuamente dependientes. Finalmente, un tercer foco es el grado de explicitación de las reflexiones, es decir, cuan explícito era el argumento que fundamentaba la explicación de los hechos sobre los cuales se reflexionaba, tal que en un nivel interpretativo se esperaba que las relaciones de causalidad se expresen de manera clara y explícita.

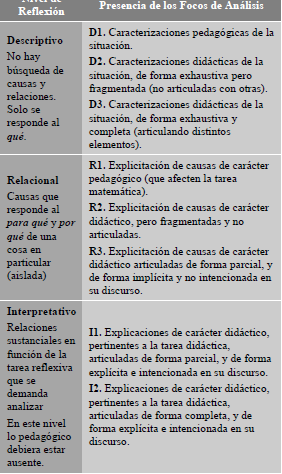
En la tabla 2, se presenta una graduación de cada nivel de reflexión en función de los criterios y focos descritos. Esta propuesta analítica es acorde con la intención de obtener adecuadas orientaciones didácticas, ya que para ello se requiere diseñar, implementar y reflexionar las propuestas de enseñanza (Rojas y Solar, 2012). Por otra parte, permite identificar trayectorias reflexivas, a partir del análisis de las distintas instancias en que los docentes participan, señalando el nivel reflexivo en el que se sitúa, y relacionándolo a la tarea didáctica que se resuelve, obteniendo una descripción robusta del discurso que el docente pone en juego.

Tabla 2: Niveles y focos de reflexión docente (adaptado de Solar et al., 2011, p. 171)

2.3. Conocimiento matemático para enseñar
A partir de la noción de "Conocimiento pedagógico del contenido" (PCK) acuñada por Shulman (1987), Ball et al. (2008) han propuesto una teorización más completa de este tipo de conocimiento profesional, cuya línea de trabajo ha apuntado a la problemática de la determinación y medición de tal conocimiento.

Al dirigir su mirada hacia los procesos de instrucción, Ball et al. (2008) plantean la problemática de determinar cuál es el conocimiento matemático para la enseñanza. Esta mirada supone que el conocimiento matemático per se no garantiza un buen desempeño en la ejecución de una tarea profesional específica, sino que se debe seleccionar y representar el conocimiento técnico profesional que permite emprender tales tareas. La problemática se suscitó en particular debido a que, aun reconociendo la trivialidad de la afirmación "el conocimiento matemático de un profesor es relevante para enseñar matemática", la evidencia empírica que apoyaba esta afirmación era bastante elusiva, en particular, producto del desconocimiento del tipo de conocimiento matemático que se debía observar en las investigaciones (Ball et al., 2008).

Los modelos iniciales de Ball centraron la atención en hacer la distinción entre conocimiento matemático y conocimiento sobre la matemática (Ball, 1990). No obstante, los aportes teóricos de Shulman permitieron redefinir el problema hacia el estudio del conocimiento matemático para la enseñanza, el cual se compone del conocimiento matemático propiamente tal, así como del conocimiento pedagógico del contenido (Ball, et al., 2008; Delaney, Ball, Hill, Schilling y Zopf., 2008). El modelo de Ball extiende, por tanto, el concepto de PCK hacia el concepto de conocimiento matemático para la enseñanza (MKT, por sus siglas en inglés), el cual es también propuesto como el conocimiento que los profesores deben saber.

En la figura 2, se puede ver el modelo propuesto por Ball y sus colaboradores, en donde se presenta la organización del MKT en términos de tipos de conocimientos, delimitados por la relación entre el conocimiento matemático y los distintos actores o instituciones asociadas (profesor, alumno y disciplina; currículo y disciplina).

Figura 2. Organización del MKT, adaptado de Hill, Ball y Schilling (2008, p. 377).

Estas dimensiones del MKT han sido descritas en varias publicaciones y comentadas por otros autores:

La distinción entre el conocimiento común del contenido (CCC) y el conocimiento especializado del contenido (CEC) consiste en que, mientras el primero refiere al conocimiento puesto en juego para resolver problemas matemáticos, para lo cual un matemático, o incluso un sujeto adulto con suficiente conocimiento, está capacitado; el segundo refiere, por ejemplo, a realizar un ordenamiento de las secuencias con que podrían desarrollarse los diferentes aspectos de un contenido específico. Para esta última acción, es posible que un sujeto adulto, o inclusive un matemático, no tenga necesariamente la competencia ni la posibilidad de llevarla a cabo (Godino, 2009, p.16).

Ball et al. (2008) señalan que el conocimiento en el horizonte matemático (CH) se asocia a tener conciencia de cómo se conectan los temas matemáticos y la duración de las matemáticas en el currículo. Este conocimiento ha sido uno de los más complejos de comprender por los diferentes énfasis que se le puede dar, aunque algunos autores (Figueiras, Ribeiro, Carrillo Fernández y Deulofeu, 2011; Carrillo, Contreras y Flores, 2013) lo asocian con un tipo de conocimiento en términos de conexiones entre conceptos e ideas matemáticas.

El aporte de Ball y su equipo radica en la propuesta de un modelo del conocimiento que el profesor debe sostener para emprender la implementación de currículos matemáticos en educación primaria. Este modelo es reconocido como teórico, por cuanto no habría suficientes datos que permitan sostener que los profesores tengan conocimiento pedagógico del contenido en forma independiente del conocimiento del contenido en sí mismo (Hill et al., 2008).

No obstante lo anterior, Ball reconoce que el conocimiento del contenido y de los estudiantes sí permite hacer una distinción respecto de los otros tipos de conocimiento matemático para la enseñanza, y lo individualiza como un tipo de conocimiento relevante, que tiene evidencia empírica que sustenta su existencia, y que por tanto tiene potencial de correlacionar con el rendimiento de los alumnos. El conocimiento del contenido y de los estudiantes (CCE) es definido por Ball como el conocimiento que posee el profesor sobre cómo los estudiantes piensan, conocen y aprenden determinado contenido (Hill et al., 2008; Delaney et al., 2008). Según estos autores, el CCE se construye en torno a evidencia empírica, y por tanto, tendría cierto grado de sistematicidad u organización que le permita constituir un conocimiento.

El modelo está en pleno desarrollo en la actualidad, y la investigación ha apuntado a determinar criterios y modos de medir el conocimiento matemático para la enseñanza. En particular, el CCE, como categoría de análisis del modelo, ya ha demostrado empíricamente una fuerte multidimensionalidad que sugiere que el estudio de éste requiere del apoyo de aproximaciones cualitativas que permitan arrojar luces respecto de las dimensiones y direcciones de trabajo futuro (Hill et al., 2008).

2.4. Desarrollo de orientaciones didácticas
En niveles intermedios de concreción del currículum se suelen encontrar orientaciones didácticas para la gestión de actividades de aula, teniendo éstas un carácter instruccional, con sugerencias de cómo desarrollar de mejor manera las actividades propuestas. En Chile, los nuevos programas de estudio (Mineduc, 2012) presentan, para cada una de las unidades propuestas, una sección de observaciones al docente en que se indican fuentes de material de apoyo (vínculos web), material de consulta para el docente (fuentes y libros), y estrategias para tratar conceptos, habilidades y actitudes. Esta visión de las orientaciones didácticas se puede entender como un conjunto de sugerencias instruccionales, en un status de producto.

Ante la pregunta de cómo los profesores pueden elaborar orientaciones didácticas, en primer lugar es necesario considerarlas como un proceso a desarrollar. En este sentido, nuestra propuesta está basada en la idea que las orientaciones van más allá de sugerencias instruccionales (producto), y que se asocian al conocimiento que el profesor construye en su elaboración (proceso). A partir de esta forma de entender las orientaciones, y tomando en cuenta tres dimensiones fundamentales en la formación de profesores: matemáticas, aprendizaje, y diseño y desarrollo de la enseñanza (Azcárate, 1998), podemos entenderlas como contenedoras de las dimensiones del conocimiento profesional del profesor de matemáticas. Estos conocimientos del profesor se pueden implementar y evidenciar en diversos momentos de la práctica, tales como el estudio de las matemáticas, la planificación de situación de enseñanza y, en particular, la gestión de estas situaciones en el aula. Bajo esta lógica, las dimensiones del MKT propuestos por Ball y colaboradores se pueden entender como las diferentes dimensiones que se pueden asociar a orientaciones didácticas.

En proyectos anteriores (Solar et al., 2011; Solar y Ortiz, 2014), se ha diseñado una Metodología de Trabajo Docente (MTD) para la formación permanente de profesores con un énfasis en la gestión del aula de matemáticas. La MTD se caracteriza por problematizar situaciones de enseñanza por medio de análisis de episodios de aula, e incentivando la reflexión permanente del profesor, teniendo como objetivo que el docente profundice en las reflexiones que puede hacer de las prácticas, tanto de sus compañeros como de otros. Dicha metodología se lleva a cabo por medio de un ciclo de formación continua con profesores, que más que avanzar linealmente por fases, supone un trabajo en espiral, en que la ejecución de cada fase permite remirar y profundizar en las fases anteriores. Las fases consideradas son las siguientes (Solar et al. 2011, p. 48):

• Estudio de una temática matemático -; didáctica² específica, que incluye la puesta en práctica en aula de algunas propuestas de enseñanza elaboradas expresamente para su análisis y reflexión en términos de la experiencia vivida por algunos profesores al implementarlas.
• Elaboración propia de una secuencia de enseñanza en torno a un contenido matemático afín a las situaciones anteriores, y que sea coherente con los principios didácticos que propone esta metodología.
• Implementación de dicha secuencia de enseñanza con apoyo y seguimiento en el aula, y con retroalimentación inmediata por parte del equipo investigador que acompaña al docente en sus clases.
• Análisis y reflexión colectiva sobre las distintas experiencias vividas, determinando sus fortalezas y debilidades y, en función de ello, ajustar y mejorar tanto la secuencia de enseñanza como su gestión en el aula.

En base a los antecedentes mencionados en cada una de las cuatro dimensiones, consideramos que la MTD de formación de profesores puede ser viable para elaborar orientaciones didácticas del álgebra desde una visión funcional sobre las dimensiones del MKT, por estar basado en el conocimiento matemático por medio del estudio de las situaciones de enseñanza, y el conocimiento pedagógico del contenido por la vinculación con la práctica docente. En la discusión de los resultados abordaremos el vínculo entre estas dimensiones.

3. METODOLOGÍA

Dado que nos interesan los procesos de construcción de orientaciones didácticas ligadas a la reflexión de la práctica docente, la perspectiva metodológica de este trabajo se enmarca en un enfoque cualitativo interpretativo, orientado a describir, interpretar y entender el significado de los fenómenos sociales, intentando darles sentido desde el significado que las propias personas les atribuyen a dichos fenómenos (Merriam, 1998; Bryman, 2004). En el trabajo colaborativo con los docentes, el desarrollo de orientaciones didácticas se ha diseñado en tres etapas: una primera etapa de formación de profesores, una segunda etapa en el seguimiento de un caso en la implementación de una unidad didáctica, y una tercera etapa en la elaboración de las orientaciones didácticas a partir de la experiencia.

En la primera etapa, se seleccionaron 5 profesores de 5º y 6º básico (10-12 años) para participar en un proceso de formación basado en la Metodología de Trabajo Docente (MTD) sobre la visión funcional del álgebra.  Como criterio de selección, se consideró que los profesores hubieran tenido una experiencia de formación continua en matemáticas y que no tuvieran una formación del álgebra escolar desde una visión funcional. Los profesores pertenecían a establecimientos educacionales de la ciudad de Concepción (Chile) y alrededores. La formación se organizó en un seminario de 4 sesiones cada 15 días, llevado a cabo durante el primer semestre del 2011 cuyas sesiones se centraron en un análisis curricular en el eje de álgebra y en analizar situaciones algebraicas con una visión funcional,  orientaciones para su gestión en el aula. Posteriormente, se desarrolló en conjunto una unidad didáctica para el tratamiento funcional del álgebra escolar, a ser aplicada en los niveles de 5º o 6º básico (10 a 12 años).

La segunda etapa de la investigación consistió en el seguimiento de un caso. De los cinco profesores, se seleccionó a la profesora Marta para hacer el seguimiento en la implementación de la unidad didáctica, dado que fue una de una de las profesoras que mostró mayor nivel de reflexión en el seminario. Esto se vio reflejado en un diseño de la unidad didáctica muy enmarcado en la visión funcional del álgebra, diseño que fue realizado por Marta y revisado por el formador. Para el análisis, se seleccionaron los temas nucleares de la unidad didáctica diseñada junto a la profesora, y dentro de estos temas, actividades representativas y matemáticamente relevantes según la visión funcional del álgebra escolar. La unidad didáctica se implementó al final del año académico, en los meses de noviembre y diciembre de 2011, con una duración de 14 sesiones. Mediante una observación no participante se registró con una cámara de video todas las sesiones. La estrategia de análisis de las clases observadas se describe en los apartados siguientes.

En una tercera etapa, se ha considerado que la producción de orientaciones didácticas requiere de los procesos que vive el docente y de su reflexión de la práctica, ya que ésta es una perspectiva analítica sobre las actividades diseñadas y su implementación, y es una visión que no posee el investigador. Por ello, se realizaron entrevistas semi-estructuradas a la profesora Marta en las cuales se les pedía analizar los episodios de clase que rescataban las actividades representativas, enfatizando tres aspectos puntuales: análisis matemático de las actividades, dificultades y errores que presentan los estudiantes, y gestión de la propia práctica. Con ello, se caracterizó el nivel de reflexión a partir de los criterios de Solar et al. (2011) de manera tal de observar hasta qué punto el trabajo realizado en conjunto ha ido impactando en su concepción didáctica de la enseñanza y aprendizaje del álgebra escolar.

En las tres etapas se consideró como información relevante las decisiones y problemáticas vividas por profesores, y en particular las de Marta, ya que éstas permiten ahondar en las herramientas, conocimientos y experiencias que necesitaban para diseñar e implementar situaciones de aprendizaje matemáticamente relevantes.

4. RESULTADOS

En este artículo, mostramos el caso la profesora Marta, quien ha diseñado, implementado y analizado su unidad didáctica en 5º básico (10-11años) en una escuela municipal de la comuna de Chiguayante, cercana a la ciudad de Concepción (Chile). En los resultados que exponemos a continuación, mostramos el recorrido de Marta por las tres etapas: la elaboración de la unidad didáctica, la observación de sus clases en que se seleccionaron actividades claves y las entrevistas en que Marta analiza episodios de sus clases.

El primer paso en la elaboración de la unidad didáctica realizada por Marta, fue establecer un lugar dentro de la temporalización curricular para trabajar el álgebra desde la visión funcional desarrollada en los seminarios. Marta decidió realizarla a continuación de la unidad de estadística dado que en dicha unidad haría un primer estudio de la interpretación de gráficas estadísticas, ya que esto serviría de antecedente para el estudio posterior de la interpretación de gráficas funcionales. La selección de contenidos fue establecida por la docente, según dos criterios articulados: los contenidos considerados por los programas oficiales para la unidad de álgebra en el nivel correspondiente, y los temas que se habían estudiado en el seminario, todo ello apoyado por el equipo investigador. De ese proceso, la profesora seleccionó 4 grandes temas a abordar: Patrones, Variables, Proporcionalidad e Interpretación de gráficas. En la tabla 3 se representa un esquema de la unidad.

Tabla 3: Esquema de la unidad didáctica elaborada por Marta.

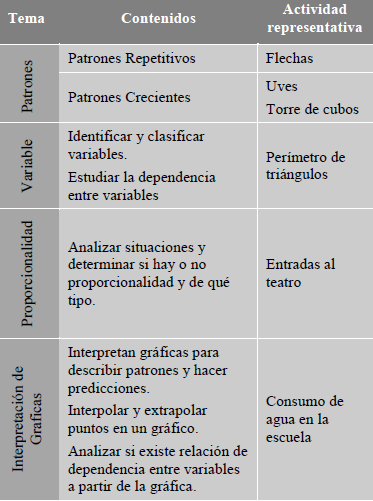
Para el análisis de la implementación de la unidad didáctica, junto a la profesora se seleccionó una actividad representativa en cada uno de los cuatro temas tratados (tabla 3), entre todas las que había diseñado. Para el tema de patrones repetitivos se escogió la actividad flechas, dado que sistematiza los procedimientos estudiados en este tema. Para patrones crecientes se seleccionaron dos actividades, por una parte la actividad Uves, que representan los números impares, ya que su gestión en clase produjo reflexiones y preguntas a los investigadores que se deseaban contrastar con la docente, y por otra, la actividad Torre de cubos, por ser una actividad representativa de este tema en que se promueve el uso de la tabla para encontrar la regularidad. Para el tema de Variables, se escogió la actividad Perímetro de triángulos, por ser una actividad que permitió en clases un estudio de dependencia de variables. Para Proporcionalidad, se escogió la actividad Entradas al teatro por ser una actividad que permitía estudiar situaciones proporcionales y no proporcionales. Para Interpretación de gráficas se seleccionó la actividad Consumo de agua, dado que hubo una participación activa de los estudiantes.

4.1. Gestión y análisis de dos actividades basadas en patrones crecientes.
A partir de los datos recopilados, que dicen relación con la unidad didáctica y su implementación (gestión de la actividad), y de la reflexión que hace Marta de ello (entrevistas semi estructuradas ), los resultados en cuanto a Orientaciones Didácticas para trabajar el álgebra escolar desde una perspectiva funcional, así como a los esquemas reflexivos de esta docente, permiten ver si las recomendaciones o críticas a la propuesta y su implementación provienen desde perspectivas pedagógicas generales, o bien de análisis centrados en lo didáctico de manera interrelacionada y robusta.

A continuación se presenta el proceso de recoger orientaciones didácticas para dos actividades nucleares asociadas al tema de patrones: Uves y Torre de cubos. Estas actividades corresponden a patrones crecientes, es decir, secuencias de elementos que aumentan en una cantidad constante de elementos entre un término de la secuencia y el inmediatamente siguiente. Cuando la secuencia es numérica se denomina patrón numérico. En los patrones crecientes se da una relación que matemáticamente es muy importante: se puede obtener una expresión para cualquier término, relacionando la posición con la cantidad de elementos. Esta relación puede ser usada para introducir a los estudiantes en la noción de función.

En la implementación realizada por Marta, este tema consideró una parte importante del tiempo destinado a la unidad didáctica: 6 sesiones (desde la 3ª hasta la 8ª).
4.1.1. Actividad Uves
En la actividad de las Uves, descrita en la figura 3, la tarea consiste en determinar el patrón con que se forman las "uves", según la posición que ocupan en la secuencia. Esta actividad presenta un patrón creciente, que se modela con los números impares, por lo que se piensa sería abordable por los estudiantes.

Figura 3: Actividad de las "Uves"

Gestión de la actividad
En la clase de Marta, los estudiantes llegaron a establecer la secuencia de uves hasta la sexta posición. En la figura 4 se aprecia como Marta escribe la secuencia de las Uves, y en la figura 5 como una estudiante reconoce el patrón.

Figura 4: Imagen profesora Marta en el desarrollo de la actividad de las "Uves".

Figura 5: Imagen de una estudiante reconociendo el patrón en la actividad de las "Uves".

El siguiente episodio muestra las acciones discursivas realizadas por la profesora para que lleguen a descubrir el patrón de la secuencia. Los alumnos trabajan, respondiendo a la primera pregunta: ¿Cuántos puntos tendrá el séptimo término de la secuencia? El propósito de Marta al plantear esta pregunta fue que los estudiantes definieran la cantidad de puntos que tendría la uve de la séptima posición, pero sin tener que dibujar los puntos que conforman las uves.

Marta: ¿cuántos puntos tendrá el 7º término?
Alumnos: 15 puntos [varios alumnos]
Marta: ¿y cómo lo supieron?
Alumnos: porque se iban agregando 2 [varios alumnos]
Marta: a ver 1,2, 3, 4, 5, 6, 7 ya 15 [señala las figuras en la guía proyectada en la pizarra y asocia el 7 al 15 y pone un visto bueno de correcto] perfecto. ¿Y si yo no hago esto de sumar 2?
Alejandra: multiplico
Marta: ya, multiplico qué.
Alejandra: 2×1 + 1
Marta: [la profesora escribe 2×1 + 1] 2 × 1 y le agrego 1. Perfecto.
Rodrigo: o la posición... ah no, que es lo mismo.
Marta: escucharon lo que está diciendo él. 2, me dice, por la posición + 1 [escribe (2×n) + 1] ¿sería esta la regla?
Alumnos: sí. Igual podía ir (2 × 1) + 1 [varios alumnos]
Marta: pensemos. Yo escribo 2×2 y le agrego 1. Esta es la posición 2. 2 por 2 son 4, más 1 [escribe (2×2) + 1 debajo de la segunda figura]. ¿A qué le estoy agregando 1?
Alumnos: a la multiplicación [varios alumnos]
Marta: esto es la multiplicación, a este producto agregue 1 y así hay que escribirlo, porque si yo lo escribo de esta manera, miren [escribe (2×2) + 1 en la pizarra] ¿qué tengo que hacer primero ahí? ¿Qué hubiera sido siempre primero?
Alumnos: la multiplicación [varios alumnos]
Marta: ya y después el 1, paréntesis dice esto primero y después agrega. Perfecto. ¿Qué tipo de número es el 3, 5, 7, 9, 11, 15?
Alumnos: números impares [varios alumnos]
Marta: entonces miren cómo se escribe un número impar, así se escribe un número impar, así 2n+1, esa es la representación algebraica de un número impar [escribe impar en la pizarra y lo asocia con el 2n+1 escrito anteriormente] ¿se lo habían imaginado así?
Alumnos: no [varios alumnos]

En este episodio, se puede apreciar que ante la intervención de Marta de preguntar por la relación multiplicativa, Alejandra responde con la expresión aritmética 2×2 + 1. Después, Rodrigo menciona la posición, que da pie para que Marta escriba la expresión algebraica (2×n) + 1, que relaciona la posición con la cantidad de puntos. Marta sigue trabajando las relaciones multiplicativas con el caso de la segunda figura 2×2 + 1 = 5, para acordar con el grupo curso cómo funciona la regla de formación. Posteriormente, Marta pregunta por la naturaleza de los números de la secuencia, frente a lo cual los alumnos son capaces de asociarlos con los números impares. Es interesante destacar que los estudiantes antes de la intervención de Marta reconocen que no habían asociado la secuencia con los números impares.

Entrevista a Marta
El episodio descrito sirvió de base para elaborar la entrevista, en que se analizó la gestión de la actividad con la profesora. En la tabla 4, para cada una de las preguntas de la entrevista, se han extraído las intervenciones de Marta que permiten la elaboración de orientaciones didácticas. Las palabras en negrita señalan las palabras clave que sustentan las orientaciones descritas más adelante.

Tabla 4: Preguntas de la entrevista a Marta y extracto de sus intervenciones.

Del análisis de las respuestas de Marta en la entrevista, se han podido inferir las siguientes orientaciones didácticas:

A1 Las actividades de patrones tienen el propósito de que los niños descubran la regularidad en la secuencia. En la actividad de las uves, el profesor debería promover que los estudiantes, sin tener que dibujar, puedan establecer una relación entre la posición de la figura y la cantidad de puntos.
A2 Si se requiere encontrar el patrón, los estudiantes pueden necesitar que el profesor los guie, haciendo énfasis en que los estudiantes encuentren regularidades
A3 Los estudiantes pueden tener dificultad en dar el salto de una posición concreta, 2 o 3, a la expresión de una posición cualquiera, simbolizada con "n", ya que comprender la generalización requiere de un nivel de abstracción mayor.
A4 Se ha de cautelar de ser organizado en la gestión de la actividad, por ejemplo, desglosar las preguntas.
A5 Se ha de adaptar el uso de guías con las actividades según las dificultades que pueden tener los estudiantes.
A6 Se ha de incentivar que los compañeros se expliquen entre ellos sus procedimientos.
A7 Que sean los propios estudiantes que descubran la regularidad, sin forzarlos. Si no obtienen el patrón será en otro momento.
A8 Los estudiantes no están familiarizados con este tipo de actividades, en particular con actividades tales como las uves permiten resignificar los números impares y pares que los estudiantes conocen desde los cursos anteriores, pero que solo habían tenido oportunidad de estudiarlo desde un punto de vista aritmético.
A9 Seguir el razonamiento de los estudiantes. Nos puede sorprender como docentes hasta donde son capaces de llegar en el estudio de los patrones.

4.1.2. Actividad Torre de cubos

En la unidad didáctica que ha diseñado e implementado Marta, el tema de Patrones termina con el uso de tablas para su desarrollo. En la actividad "Torre de cubos", la regla del patrón es más compleja que en el caso anterior, y por lo tanto se promueve el uso de una tabla como apoyo para obtener el patrón. En la figura 6 se puede apreciar cómo se presentó la actividad a los estudiantes.

Gestión de la actividad

En la clase de Marta, en el desarrollo de este problema, los estudiantes tuvieron algunas dificultades en encontrar el patrón. En este episodio se muestra como Marta guía el proceso.

Figura 6: Preguntas e imágenes presentadas en la actividad Torre de Cubos.

Marta: veamos si yo tengo 1 sólo cubo, cuál será el área del cubo?
Alumnos: ¿2?
Alumnos: 10
Marta: si tengo solamente 1 cubo
Alumnos: lo de arriba lo de abajo...
Marta: ¿cuántas caras son?
Alumnos: 6
Marta: y 1 × 1 es 1 ¿Cuánto es ahí?
Alumno: ¿10?
Marta: no
Alumno: 6
Marta: ya, ¿cuándo tengo 2?
Alumno: 10
Marta: ¿10? ¿Cuándo tengo 3?
Alumno: 14
Marta: ¿cuándo tengo 4?
Alumno: 18
Marta: ¿cuándo tengo 5?
Alumno: 22
Marta: ¿cuándo tengo 6?
Marta: 26
Marta: ¿qué van haciendo ustedes ahí? ¿ir de 4 en 4?, van agregando 4, agregan 4 y qué pasa con eso ahora.

En el episodio se aprecia que los alumnos no tienen seguridad en el número de caras a considerar, ante lo cual Marta es quien finalmente establece las relaciones y los estudiantes solo van contando los números. Los estudiantes presentan dificultades y Marta guía de forma unidireccional la conversación con los estudiantes para establecer el patrón.
En el diseño de esta actividad, si bien se preveía que los estudiantes tuvieran más dificultades por ser un patrón más complejo que los anteriormente presentados (4n+2), se consideró que introduciendo la tabla los estudiantes tendrían un apoyo suficiente para poder establecer el patrón. Pero en la práctica la tabla no representó el andamiaje esperado para los estudiantes. En la entrevista a la profesora se profundiza en la gestión de la actividad y en las posibles causas que originaron estas dificultades en los estudiantes.

Entrevista a Marta

De igual modo que en la actividad anterior, de cada una de las preguntas de la entrevista se han extraído los párrafos que permiten dar cuenta de algunas orientaciones didácticas. En la tabla 5 se han puesto en negrita las palabras clave que sustentan las orientaciones descritas.

Tabla 5: Preguntas de la entrevista a Marta y extracto de sus intervenciones.

Del análisis de las respuestas de Marta en la entrevista, se han podido recoger las siguientes orientaciones didácticas:
B1 El uso de material concreto facilita la visualización de los cubos en las torres.
B2 Trabajar el concepto de variable al establecer la relación entre el número de cubos y él área de la torre.
B3 Los estudiantes si bien cuentan las caras tienen dificultades en encontrar la relación entre la cantidad de cubo y el número de caras
B4 La tabla permite visualizar los datos con otra representación y tiene la ventaja de permitir ver cuánto va a aumentar o cuánto va disminuir la otra variable.
B5 Generar preguntas en clase que permitan guiar a los estudiantes a predecir el área.

4.1.3. Tipos de orientaciones didácticas

A partir del análisis anterior, es decir, de lo que la profesora Marta da como respuesta a las preguntas sobre la realización de sus actividades, se obtuvieron cuatro dimensiones que recogen, en su conjunto, todas las orientaciones didácticas obtenidas de las actividades de Uves y Torres de cubos (orientaciones A y B, respectivamente):

Propósito de la actividad o de la clase: exponer razones que vinculen la actividad con el conocimiento matemático en juego, o con las expectativas de aprendizaje.
Variables didácticas: condiciones de realización que se establecen para la gestión de la actividad (uso material concreto, representaciones adecuadas, ámbito numérico, relación entre los números, entre otros.). El término proviene de la teoría de situaciones didácticas de Brousseau (1997), en que la complejidad de las técnicas que utiliza un resolutor depende de las condiciones de realización -o valores de la variable- de una tarea matemática.

Dificultades y errores: dificultades que pueden tener los estudiantes, o errores esperados en la realización de las actividades.

Gestión de aula: se contempla dos aspectos asociados a la gestión del aula por parte del profesor: (1) gestión del aprendizaje (del error y dificultades, u otros aspectos asociados al aprendizaje); (2) gestión de competencias matemáticas, tales como la resolución de problemas o argumentación matemática.

Estas cuatro dimensiones tienen la ventaja de caracterizar en cuatro grandes temas las orientaciones didácticas, que si bien han surgido del análisis de dos actividades de patrones crecientes, consideramos que dada su naturaleza podrían ser extensibles a otros contenidos. En la tabla 6 se ha agrupado el listado de orientaciones didácticas para el tema de patrones crecientes en las cuatro dimensiones.

Tabla 6: Clasificación orientaciones didácticas obtenidas de la entrevista con Marta.

4.2. Niveles de Reflexión

Para dar cuenta de los niveles de reflexión de Marta, se ha vinculado su reflexión a dos aspectos centrales de esta forma de trabajo. Por una parte, se han considerado las reflexiones en el marco de la actividad que se desarrolla, ya que las configuraciones y complejidades del conocimiento matemático implican unos determinados niveles de análisis de lo que ocurre en la enseñanza y aprendizaje de los mismos. Por otra parte, se ha vinculado las reflexiones a los tipos de pregunta que se le realizan a la docente, ya que los énfasis de las mismas (análisis didáctico matemático de las actividades (ADM), dificultades y errores que presentan los estudiantes (DE), gestión de la actividad (GA)), impactan no solo en lo que la profesora puede decir, sino sobre todo en la demanda que se le hace respecto del nivel de profundidad que requiere la explicación o respuesta que pueda dar. En la tabla 7 se puede apreciar cómo está distribuida la entrevista en términos de los focos de las preguntas y las actividades.

Tabla 7: Preguntas según foco y actividad

Teniendo estas consideraciones, se siguió la siguiente estrategia de análisis. En primer lugar se clasificaron las preguntas de las entrevistas según las intenciones de cada una de ellas, y se señalaron los episodios (actividades matemáticas) a los que están vinculados. En segundo lugar, se realizó la clasificación de las respuestas de la profesora por pregunta según los niveles de reflexión, y los focos de éstos. Finalmente se realizó un estudio de la trayectoria reflexiva de Marta, vinculada al tipo de actividad matemática de cada etapa de la propuesta didáctica, y al tipo de pregunta que se le realizó.

En la tabla 8 se describe la codificación de las respuestas de Marta en las actividades de Uves y Torres. Como se puede apreciar, la profesora no alcanza niveles extremos de reflexión (D1 e I2), siendo puntual la presencia del nivel interpretativo, lo que hace que su reflexión sea de tipo descriptiva relacional, en su mayoría con relaciones causales de tipo didáctico. Además, los niveles reflexivos de la profesora son relativamente homogéneos en tanto su aparición en la reflexión sobre sus clases. Por otra parte, en la tabla 9 se puede apreciar la frecuencia por tipo y nivel de reflexión.

Tabla 8: Codificación de las respuestas de Marta según foco de la pregunta y nivel reflexivo.

Tabla 9: Frecuencia por tipo de reflexión y nivel reflexivo.

Respecto de la trayectoria reflexiva de la profesora, a medida que transcurre la entrevista, primero respecto de la actividad de las Uves y después con la actividad de las Torres, se aprecia una disparidad entre la primera actividad y la segunda, tal como muestra el gráfico 1.

El nivel reflexivo de la profesora en lo referido a la actividad de las "Uves" no presenta ningún tipo de tendencia, tanto en su evolución como en el nivel, ya que la cantidad de respuestas de tipo descriptivo y relacional es casi la misma. Respecto del tipo de caracterizaciones son en su mayoría de tipo didáctico, es decir, están directamente relacionadas a la actividad matemática que se está desarrollando. Por otro lado, en la actividad "Torres de cubos" se aprecia una tendencia a la baja en el nivel de reflexión que va presentando la profesora. Igual que en la actividad anterior, la mayoría de sus reflexiones son de corte didáctico. Es interesante destacar que la profesora, en ambas actividades, realiza tanto descripciones como relaciones, sean estas puntuales o complejas.

Al relacionar las variables de foco de la pregunta, actividad y nivel reflexivo, se pueden observar ciertas concentraciones. A la luz de los niveles de reflexión, en el gráfico 2 se puede apreciar que son las respuestas a las preguntas ADM las que alcanzan mayor nivel reflexivo, concentrándose en los niveles relacionales. En cambio, las preguntas GA, aun teniendo algunas respuestas de alto nivel relacional, se concentran en niveles descriptivos. Aunque solo se presentan dos preguntas DE, se puede apreciar que entre una actividad y otra hay una transición de niveles descriptivos a relacionales.

Desde el punto de vista de las actividades, en el gráfico 2 se puede observar que las respuestas a preguntas de tipo ADM y relativas a la actividad "Uves" llegan a menores niveles de reflexión, de tipo descriptivo y relacional pedagógico, que las respuestas a preguntas sobre la actividad "Torre de cubos", las cuales se concentran en niveles relacionales e incluso interpretativos. Por otra parte, de acuerdo a las preguntas de tipo GA, solo las respuestas a preguntas relativas a la actividad "Uves" alcanzan niveles altos de reflexión, siendo las respuestas a preguntas sobre la actividad "Torre de cubos" solo de tipo descriptivo. Según esta diferencia en la profundidad de la reflexión según la actividad analizada, se observa una influencia de esta variable (tipo de tarea matemática) en la capacidad para relacionar causalmente las explicaciones sobre lo que sucede en el aula.

Gráfico 1: Niveles de reflexión según episodio

Gráfico 2: Niveles de reflexión según tipo de pregunta.

5. DISCUSIÓN

En este estudio, se ha abordado cómo caracterizar orientaciones didácticas obtenidas de la reflexión de una profesora al diseñar y poner en práctica una unidad didáctica asociada con una visión funcional del álgebra escolar, en particular de patrones crecientes. A continuación se comentarán algunos aspectos clave de los temas nucleares de este trabajo.

5.1. Orientación del álgebra desde una visión funcional

La experiencia que se ha descrito, muestra de qué manera una unidad didáctica de álgebra asociada a un enfoque funcional para un quinto año básico (10-11años), se corresponde con una visión amplia del álgebra, en que la orientación dada por la profesora que diseñó la unidad didáctica, tiene características que Molina (2009) señala sobre Early Algebra. En efecto, los temas estudiados en la unidad didáctica: Patrones, variable, proporcionalidad e interpretación de gráficas, y en particular el caso expuesto sobre patrones crecientes, se asocian con el estudio de las relaciones funcionales, de la generalización de patrones y relaciones numéricas. Este enfoque se condice el sentido funcional del álgebra que permite interpretarla como el estudio de las relaciones entre cantidades, a la vez que la variable se entiende en su sentido más amplio de variabilidad. (Socas et al., 1996).

Esta visión funcional del álgebra que le ha dado la profesora Marta a la Unidad didáctica, tiene relación con el seminario de formación en que participó Marta y con el acompañamiento en el diseño de la unidad didáctica. Por medio de este proceso de formación se logró que Marta plantee una propuesta que, no solo ampliaba su perspectiva anterior, sino también ampliaba la visión del álgebra que el propio currículum chileno proponía en aquel entonces (MINEDUC, 2009). Actualmente las bases curriculares 1º a 6º de primaria (MINEDUC, 2012) sí se corresponden con esta visión amplia del álgebra con una perspectiva de Early algebra, del mismo modo que otras propuestas curriculares (NCTM, 2003; Ministerio de Educación Nacional, 2006; DOGC, 2007)

Tal como señalan Barbosa et al. (2012) es necesario proponer tareas específicas que estimulen a los estudiantes a usar estrategias visuales asociado a un desarrollo del pensamiento funcional. Las dos actividades de patrones crecientes analizadas- uves y torres de cubos- han sido seleccionadas por Marta con una finalidad específica. La actividad de las uves tiene el propósito de que los propios alumnos puedan establecer la relación entre la posición de la figura y la cantidad de puntos sin tener que dibujar los puntos, y en caso del actividad torres de cubos, se promueve utilizar la tabla para visualizar dicha relación. Para la actividad Torre de cubos se observaron dificultades en los estudiantes que no estuvieron previstas por Marta, por lo que tuvo que guiar de forma unidireccional a los estudiantes, en comparación a la actividad de las Uves. Las orientaciones didácticas que emergieron dan cuenta de cómo hacerse cargo de las dificultades visualizadas: entre ellas el uso de material concreto, trabajar el concepto de variables, generar preguntas que permitan guiar a los estudiantes a predecir el área.

Dado el cambio de enfoque que implica este tipo de actividades, en que los profesores no están habituados con esta visión del álgebra escolar, no es trivial pensar en la necesidad de contar con orientaciones didácticas para que el profesor pueda mediar en el aprendizaje de este tipo de actividades que hasta ahora no eran habituales para alumnos y que actualmente están siendo incorporados dado las nuevas directrices de los currículum de matemáticas.

5.2. Conocimiento Matemático para Enseñar en el proceso de elaboración de unidades didácticas

En base a la organización del conocimiento matemático para enseñar mostrada en la figura 2 (Hill et al., 2008), la elaboración de orientaciones didácticas que han emergido de las reflexiones de Marta se pueden asociar a dos tipos de conocimiento: del contenido y de los estudiantes (CCE), y del contenido y de la enseñanza (CCEn). Las orientaciones didácticas de la dimensión variable didáctica se asocian al CCEn, mientras que las orientaciones didácticas de la dimensión dificultades y errores se asocian al CCE; las orientaciones didácticas de las dimensiones propósito y gestión del aprendizaje se asocian a ambos tipos de conocimiento (CCEn y CCE). El hecho de que las orientaciones didácticas revelen conocimientos pedagógicos del contenido no quiere decir que no estén presentes los conocimientos disciplinares. De hecho varias de las orientaciones didácticas descritas (A1, A3, A8, B2, B4) incorporan un conocimiento disciplinar que puede ser entendido, inclusive, como conocimiento especializado del contenido (CEC). Si bien es coherente que el enfoque de una orientación didáctica sea en referencia al conocimiento pedagógico del contenido puesto que si tendiera a los conocimientos disciplinares podría denominarse "orientaciones disciplinares", resulta interesante que las orientaciones didácticas descritas contengan conocimiento disciplinar, y más aún, que sea especializado del contenido. De hecho en las entrevistas con Marta los conocimientos disciplinares y pedagógicos del contenido se manifestaban de forma articulada, coincidiendo con lo señalado por Hill et al. (2008), en que estos dos tipos de conocimientos no se muestran de forma independiente. Por tanto se podría establecer un nuevo criterio de construcción que contemple vincular el conocimiento especializado del contenido (CEC) en los tipos de orientaciones didácticas descritas en el apartado 4.1.3.

5.3. Reflexión del profesor

Los resultados que se han presentado en términos de los niveles reflexivos alcanzados por la profesora participante se han visto fuertemente influenciados por la combinación de dos variables: la actividad o tarea matemática que se ha desarrollado en aula, y el foco de la reflexión demandada. La gráfica 2 nos permitió ver que la profesora fue capaz de llegar a relaciones causales de carácter didáctico en el análisis didáctico matemático de actividades más complejas para los estudiantes, como la "Torre de cubos". Sin embargo, pareciera ser que el análisis de la gestión de este tipo de actividades más complejas se vuelve confuso para ella y no llega a pasar más allá de la descripción didáctica de las mismas. Ahora bien, respecto de actividades más sencillas como la actividad de las "Uves", la profesora es capaz de analizar la gestión de ellas a niveles relacionales, sin embargo el análisis didáctico matemático de las mismas se vuelve descriptivo.
A partir de estas relaciones, se observa un comportamiento, que podríamos llamar inverso, respecto de la reflexión de la profesora según el foco de la misma y la complejidad de la tarea matemática analizada. Cuando se analiza lo realizado en aula según actividades de diferente nivel de complejidad, desde el foco de análisis didáctico matemático (ADM), se observa que actividades más complejas producen reflexiones de mayor profundidad en términos de causalidad didáctica. A su vez, cuando se analizan estas tareas más complejas desde el foco de la gestión de aula (GA), se producen reflexiones de carácter descriptivo. Por otra parte, las actividades de baja demanda analizadas desde la perspectiva ADM, parecieran no producir reflexiones de tipo relacional, pero analizadas desde la perspectiva GA, se logra niveles reflexivos de tipo descriptivo y relacional.

Según lo anterior, podemos sostener que es factible para un docente describir potentemente las características de una actividad matemática compleja para los estudiantes, pero no necesariamente establecer relaciones didácticas causales sobre la gestión de aula de la misma. Si consideramos los componentes del conocimiento matemático para la enseñanza (Ball et al., 2008), podríamos inferir que la profesora tiene elementos del conocimiento especializado del contenido (CEC) que le permiten describir y analizar lo ocurrido en aula con actividades didáctico matemáticas complejas planteadas por ella a los estudiantes. Sin embargo, cuando se le demanda analizar la gestión de aula de ese tipo de actividades, faltarían herramientas propias del conocimiento del contenido y los estudiantes y la enseñanza (CCE y CCEn) que le permitan llegar a nivel de mayor profundidad reflexiva, estableciendo relaciones didácticas causales estructuradas.

En términos del levantamiento de orientaciones, resulta relevante que para actividades más complejas para los estudiantes, la profesora muestre elementos de conocimiento especializado del contenido (CEC), ya que con esas reflexiones se pueden construir sugerencias para el desarrollo y mejora de la actividad, sobre todo en lo relativo a orientaciones sobre el propósito de la actividad y de las variables didácticas en juego. Sin embargo, aun siendo descriptivas las reflexiones sobre actividades complejas en cuanto a la gestión del aula, estas reflexiones establecen una base para la elaboración de este tipo de orientaciones. En definitiva, para la elaboración de orientaciones ricas en contenido, es necesario al menos los componentes didácticos en las reflexiones docentes, con componentes de causalidad para aquellas que son catalogadas como más complejas para los estudiantes.

6. CONCLUSIÓN

Por medio de este estudio, hemos visto que la elaboración de orientaciones didácticas, que si bien puede ser una tarea compleja desde una visión colaborativa entre investigador y docente, reporta una serie de evidencias que analizadas desde la reflexión del profesor permite generar orientaciones ricas en contenido y con múltiples dimensiones.

La visión funcional detrás del álgebra escolar que actualmente está presente en el currículum chileno de matemáticas requiere de un proceso de formación del profesorado con el cual se puedan apropiar de este nuevo enfoque. La profesora participe del estudio, que hemos llamado Marta, no estaba familiarizada con el álgebra desde una mirada funcional. A raíz de su participación en el seminario, tuvo que diseñar una unidad didáctica en que ella misma tomó las decisiones de cómo sería dicha propuesta, mostrando autonomía para seleccionar, secuenciar y proponer actividades. Esto pone de manifiesto que Marta consiguió cierta apropiación de la visión funcional del álgebra. Dicha dinámica en que la profesora tiene un rol protagónico desde el primer momento, ha permitido que las orientaciones didácticas que se han ido recogiendo sean desde sus propias sugerencias y no de la interpretación de los investigadores.

Frente a la carencia presente en la literatura sobre cómo elaborar orientaciones didácticas y qué aspectos considerar, este estudio propone cuatro dimensiones: propósito, variables didácticas, dificultades y errores, y gestión del aprendizaje. La dimensión propósito expone las razones que vinculan la actividad con el conocimiento matemático en juego, o con las expectativas de aprendizaje; orientaciones que no consideran estos aspectos difícilmente podrán profundizar en el sentido que tienen las actividades escogidas en una planificación. La dimensión variables didácticas que establecen las condiciones de realización para la gestión de la actividad, es un aspecto recogido de la teoría de situaciones de Brousseau (1997), en que la evolución de los procedimientos que utilizan los alumnos depende de las condiciones de realización de la actividad. Si bien no es muy usual por los profesores planificar los procedimientos matemáticos en una clase, sí es frecuente considerar de manera implícita o explícita las condiciones en que la actividad se realiza tales como el tipo de materiales, las representaciones, o el ámbito numérico; por ello es relevante que estos aspectos estén presentes en las orientaciones didácticas. La dimensión dificultades y errores describe las posibles dificultades que pueden tener los estudiante y los errores esperados en la realización de las actividades; si bien es cada vez más frecuente encontrar orientaciones didácticas que se hagan cargo de esta dimensión, usualmente dichas orientaciones son generales y se elaboran desde el punto de lo que piensa el profesor, sin registrar evidencias de posibles respuestas de los estudiantes. Un desafío es que las orientaciones didácticas en una planificación consideren ejemplos de respuestas (correctas e incorrectas); investigaciones como la presentada en este artículo contribuye a recolectar evidencias para ello. La dimensión gestión de aula contempla dos aspectos: gestión del aprendizaje y gestión de las competencias. Siguiendo con el razonamiento anterior, es cada vez más frecuentes encontrar indicaciones de gestión en una planificación, pero éstas suelen ser generales sin apoyarse en las posibles respuestas de los estudiantes. Al contar con evidencias es factible dejar registro de preguntas específicas que puede hacer el profesor para gestionar una dificultad o error. Si bien los procesos matemáticos tales como la representación, modelización o argumentación actualmente están considerados en los currículos de matemática (NCTM, 2003; MINEDUC, 2012) en que se proponen ejemplos de tareas matemáticas para el desarrollo de los procesos matemáticos, no se cuenta con criterios para la gestión de dichos procesos y por tanto las prácticas de planificación se siguen centrando el desarrollo de los aprendizajes en términos de los contenidos matemáticos. Es por ello que considerar orientaciones didácticas sobre la gestión de los procesos matemáticos es una herramienta fundamental para que el profesor pueda efectivamente desarrollar los procesos en el aula de matemáticas y no centrarse solo en el estudio de contenidos.

Por otra parte, hemos encontrado que la riqueza de algunas orientaciones didácticas se puede justificar por el Conocimiento matemático para enseñar del profesor (Ball at al., 2008): la elaboración de las orientaciones didácticas es producto de una interrelación entre el conocimiento especializado del contenido (CEC) y los conocimientos del contenido y de los estudiantes (CCE) y de la enseñanza (CCEn). Esta relación contribuye al argumento de que las planificaciones deben basarse en las evidencias de aprendizaje de los estudiantes, y las orientaciones didácticas den respuestas ante estas evidencias.

Para observar el impacto que ha tenido este proceso de formación permanente de profesores, que hemos denominado Metodología de Trabajo Docente (MTD), en su concepción didáctica de la enseñanza y aprendizaje del álgebra escolar, se han utilizado criterios de reflexión de la práctica (Solar et al., 2011) que han permitido que los docentes reflexionen sobre sus propias clases con un foco en la causalidad y con criterios didáctico-matemáticos. Para ello, la utilización de entrevistas semi-estructuradas en que los docentes analizan los episodios de sus propias clases, ha sido una herramienta que ha evidenciado ser muy potente para que emerjan reflexiones profundas de los profesores, y que ha permitido generar orientaciones didácticas propicias para el trabajo algebraico escolar desde una perspectiva funcional, tanto para las actividades como para la gestión de las mismas. En investigaciones futuras sería relevante seguir perfeccionando la utilización de la MTD para la elaboración de orientaciones didácticas.

Notas al Pie

¹National Council of Teacher of Mathematics.

²La temática matemático-didáctica hace referencia a un conocimiento del profesor de matemáticas ligado a la matemática, su enseñanza y el aprendizaje, en el caso de esta investigación, la temática es el álgebra temprana.

AGRADECIMIENTO

Este trabajo es producto del proyecto de investigación "Elaboración de orientaciones didácticas para el enfoque funcional del álgebra desde la reflexión docente" (DIN08/2011), financiado por la Facultad de Educación de la Universidad Católica de la Santísima Concepción, Chile. Y Agradecemos a la profesora Mercedes Huerta quien colaboró en la investigación.

BIBLIOGRAFÍA

1. Avalos, B. y Matus, C. (2010). La Formación Inicial Docente en Chile desde una Perspectiva Internacional. (Informe Nacional del Estudio Internacional IEA TEDS M). Santiago: Ministerio de Educación de Chile.         [ Links ]

2. Azcárate, P. (1998). La formación inicial del profesor de matemáticas: análisis desde la perspectiva del conocimiento práctico professional, Revista Interuniversitaria de Formación del Profesorado, 32, 129-142.         [ Links ]

3. Ball, D. L. (1990). The mathematical understandings that prospective teachers bring to teacher education. Elementary School Journal, 90, 449-466.         [ Links ]

4. Ball, D. L., Thames, M. H. y Phelps, G. (2008). Content Knowledge for Teaching: What Makes it Special?, Journal of Teacher Education, 59(5), Dec. 2008, 389-407.         [ Links ]

5. Barbosa, A, Vale, I. y Palhares, P. (2012). Pattern tasks: Thinking processes used by 6th grade students, Relime 15(3) 273-293.

6. Beas, J., Santa Cruz, J., Thomsen, P., y Utreras, S. (2000). Enseñar a pensar para aprender mejor. Santiago: Ediciones Universidad Católica.         [ Links ]

7. Blanton, M. L. y Kaput, J. (2005). Characterizing a classroom practice that promotes algebraic reasoning. Journal for Research in Mathematics Education, 36(5), 412-446.         [ Links ]

8. Bosch, M., Espinoza, L. & Gascón, J. (2003). El profesor como director de procesos de estudio: análisis de organizaciones didácticas espontáneas. Recherches en didactique des mathématiques, 23(1), 79-135.         [ Links ]

9. Brousseau, G. (1997). Theory of Didactical Situations in Mathematics. The Netherlands: Kluwer Academic Publishers.         [ Links ]

10. Bryman, A. (2004). Social Research Methods. Second Edition. Oxford: Oxford University Press.         [ Links ]

11. Carrillo, J., Contreras, L. C. y Flores, P. (2013). Un modelo de conocimiento especializado del profesor de matemáticas. En L. Rico, M. C. Cañadas, J. Gutiérrez, M. Molina e I. Segovia (eds.), Investigación en didáctica de la matemática. Libro homenaje a Encarnación Castro (pp. 193-200). Granada, España: Comares.         [ Links ]

12. Castro, E., Cañadas, M. C. y Molina, M. (2010). El razonamiento inductivo como generador de conocimiento matemático. Uno Revista de Didáctica de las Matemáticas, 57, 55-67.         [ Links ]

13. Delaney, S., Ball, D. L., Hill, H., Schilling, S. y Zopf, D. (2008). "Mathematical knowledge for teaching": Adapting U.S. measures for use in Ireland. Journal of Mathematics Teacher Education, 11(3), 171-197.         [ Links ]

14. Departament d'Educació (2007). Currículum educació primària. Catalunya: Servei de Ordenació Curricular.         [ Links ]

15. Diaz, L. (2005). Profundizando en los entendimientos estudiantiles de variación. RELIME, 8 (2), 45-168.         [ Links ]

16. DOGC. (2007). 4915 Decret 142/2007 de 26 de juny, d'ordenació dels ensenyaments de l'educació primària.         [ Links ]

17. Espinoza, L., Barbé, J. y Gálvez, G. (2009). Estudio de fenómenos didácticos vinculados a la enseñanza de la aritmética en la educación básica chilena. Enseñanza de las Ciencias, 27(2), 157-168.         [ Links ]

18. Figueiras, L., Ribeiro, M., Carrillo, J., Fernández, S., y Deulofeu, J. (2011). Teachers' advanced mathematical knowledge for solving mathematics teaching challenges: a response to Zazkis and Mamolo. For or the Learning of Mathematics 31(3), 26-28.         [ Links ]

19. Godino, J. (2009). Categorías de Análisis de los conocimientos del Profesor de Matemáticas, Unión, 20- 13-31.         [ Links ]

20. Godino, J., Castro, W., Aké, L. y Wilhelmi, M. (2012). Naturaleza del Razonamiento Algebraico Elemental. Bolema, 26, (42), 483-511.         [ Links ]

21. Hill, H., Rowan, B., Ball, D.L. (2005). Effects of Teachers' Mathematical Knowledge for Teaching on Student Achievement. American Educational Research Journal. 42(2), 371-406.         [ Links ]

22. Hill, H., Ball, D. L., y Schilling, S. (2008). Unpacking "pedagogical content knowledge": Conceptualizing and measuring teachers' topic-specific knowledge of students. Journal for Research in Mathematics Education, 39(4), 372-400.         [ Links ]

23. Iztcovich, H., Ressia de Moreno, B., Novembre, A. y Becerril, M. M. (2012). La matemática escolar. Las prácticas de enseñanza en el aula. Buenos Aires: Aique Educación.         [ Links ]

24. Merriam, S. B. (1998). Qualitative research and case study applications in education. San Francisco: Jossey-Bass Publishers.         [ Links ]

25. MINEDUC. (2002). Marco Curricular de la Educación Básica. Objetivos Fundamentales y Contenidos Mínimos Obligatorios de la Educación Básica. Santiago de Chile: Ministerio de Educación.         [ Links ]

26. MINEDUC. (2009). Objetivos Fundamentales y Contenidos Mínimos Obligatorios de la Educación Básica y Media, Actualización 2009. Santiago de Chile: Ministerio de Educación.         [ Links ]

27. MINEDUC. (2012). Bases Curriculares de Matemática para Educación Básica. Santiago de Chile: Ministerio de Educación.         [ Links ]

28. Ministerio de Educación Nacional. (2006). Estándares básicos de competencias en Lenguaje, Matemáticas, Ciencias y Ciudadanas. Bogotá. Disponible en: www.mineducacion.gov.co/cvn/1665/articles-116042_archivo_pdf2.pdf        [ Links ]

29. Ministerio de Educación y Ciencia. (2006). Real decreto 1631/2006 de 29 de diciembre, por el que se establecen las enseñanzas mínimas correspondientes a la Educación Secundaria Obligatoria. BOE, 5, 677-773.         [ Links ]

30. Molina, M. (2009). Una propuesta de cambio curricular: integración del pensamiento algebraico en educación primaria. PNA, 3(3), 135-156.         [ Links ]

31. NCTM (National Council of Teachers of Mathematics). (2003). Principios y Estándares para la Educación Matemática. España: Sociedad Andaluza de Educación Matemática Thales.         [ Links ]

32. Rojas, F. y Solar, H. (2012). Elaboración de orientaciones didácticas para el estudio del algebra escolar desde el diseño, la implementación y la reflexión docente. Presentado en XXI COMCA Congreso de Matemática Capricornio. Antofagasta, Chile.         [ Links ]

33. Schoenfeld, A. H. (2011). Toward professional development for teachers grounded in a theory of decision making. ZDM Mathematics Education, 43, 457-469.         [ Links ]

34. Schoenfeld. A. H. y Arcavi, A. (1988). On the meaning of variable. Mathematics Teacher, 81(6), 420-; 427.         [ Links ]

35. Schön, D. A. (1998). El profesional reflexivo: cómo piensan los profesionales cuando actúan. Barcelona: Paidos Iberica.         [ Links ]

36. Shulman, L. S. (1987). Knowledge and Teaching: Foundations of the New Reform. Harvard Educational Review, 57(1), 1-22.         [ Links ]

37. Socas, M., Camacho, M., Palarea, M. y Hernández, J. (1996). Iniciación al álgebra. Madrid: Síntesis.         [ Links ]

38. Solar, H., Espinoza, L., Rojas, F., Ortiz, A., González, E. y Ulloa, R. (2011). Propuesta metodológica de trabajo docente para promover competencias matemáticas en el aula, basadas en un Modelo de Competencia Matemática (MCM). ProyectoFONIDE511091. Santiago: MINEDUC.         [ Links ]

39. Solar, H. y Rojas, F. (2011). Una mirada más amplia del álgebra. Presentado en I Congreso Internacional de Enseñanza de las Ciencias y la Matemática, Tandil (Argentin).

40. Solar, H. y Ortiz, A. (2014). Generación de casos clínicos para la línea de Educación Matemática en la carrera de Educación Básica con Mención. Informe FAD 01. Concepción (Chile): UCSC.         [ Links ]

41. Ursini, S., Escareño, F., Montes, D. y Trigueros, M. (2005) Enseñanza del álgebra elemental: un enfoque alternativo. México: Trillas.         [ Links ]

42. Van Es, E. A., y Sherin, M. G. (2007). Mathematics teacher' "learning to notice" in the context of a video club. Teaching and Teacher Education, 24(2), 244-276.         [ Links ]

43. Zeichner, K. M. (1993). El maestro como profesional reflexivo. En D. Liston y K. M. Zeichner (Eds.), La formación del profesorado y las condiciones sociales de la enseñanza. Madrid: Morata.         [ Links ]