ARTICULOS ORIGINALES

Engenharia Didática no contexto da Transição Complexa do Cálculo – TCC: o caso da série de Laurent

 

Francisco Regis Vieira Alves¹, Monique Rafaela Monteiro Marinho²

fregis@ifce.edu.br , monick15marinho@yahoo.com.br

¹Instituto Federal de Educação, Ciência e Tecnologia do Estado do Ceará. Mestrado Acadêmico em Ensino de Ciências e Matemática – PGECM.

²Instituto Federal de Educação, Ciência e Tecnologia do Estado do Ceará. Mestrado Acadêmico em Ensino de Ciências e Matemática – PGECM.

 

---

Resumo

Este artigo apresenta uma Engenharia Didática – ED, tendo em vista o ensino da noção de série de Laurent. O citado assunto se apresenta como um estudo compulsório em muitas cursos de graduação em Matemática no Brasil, no interior da disciplina de Introdução à Variável Complexa. Assim, como constituidor de um quadro assumido como referência na ED, considera a perspectiva de uma análise proporcionada pelo contexto da Transição Complexa do Cálculo – TCC, tendo em vista a identificação e registro de elementos de transição e elementos de ruptura, condicionados pelo contato de um grupo de cinco estudantes e um professor, com a Teoria das funções na variável complexa. Desenvolvido no Instituto Federal de Educação, Ciência e Tecnologia do Estado do Ceará – IFCE, no ano de 2015, o trabalho relata um perspectiva de complementaridade, na adoção de um design de investigação, tendo em vista o uso da Teoria das Situações Didáticas – TSD, com o escopo de descrever e estruturar situações de ensino, ancoradas numa mediação que buscou acentuar a visualização como processo impulsionador e mobilizador de conhecimentos tácitos e intuitivos dos alunos participantes da investigação. No rol dos dados coligidos e apresentados, como consequência do desenvolvimento de todas as fases prevista por uma ED, são evidenciados: a mediação do professor participante do experimento se mostrou afetada/modificada pelo uso da tecnologia (uso do software Geogebra); os estudantes manifestaram interpretações intuitivas e heurísticas, tanto na fase de análise cognitiva, bem como na etapa de experimentação, relacionadas com a noção de série de Laurent; os estudantes manifestaram um entendimento, por intermédio da visualização dinâmica da representação da série de Laurent. Ademais, os dados indicam a apropriação de certos conceitos da teoria por intermédio da língua materna e a mobilização de conhecimentos (ações gestuais e o emprego de metáforas) que extrapolam a natureza formal e estrurante do modelo matemático em discussão.

Palavras chave: Engenharia Didática; Transição Complexa do Cálculo; Ensino; Série de Laurent.

Didactical Engineering in the Complex Calculus´ Transition: the Laurent series case

Abstract

This article presents a Didactical Engineering – DE, in view of the teaching of the Laurent serie´s notion. The aforementioned subject is presented as a compulsory study in many undergraduate mathematics´courses in Brazil, within the discipline of Introductory to Complex Variable. Thus, as constitutor a frame taken as reference in the DE considers the perspective of analysis provided by the Complex Transition of Calculus – CTC, in order to identify and register some transition elements and breaking elements, conditioned by a contact of five students´group and a teacher with the Theory of functions in complex variable. Developed at the Federal Institute of Education, Science and Technology of Ceara ´IFCE, in 2015. The paper reports a complementary perspective about the adoption of a research design in order to use the Theory of Didactical Situations – TSD, with the goal of describing and desiging teaching situations, anchored in a mediation that sought to accentuate the visualization as the catalyst and mobilizing process of a tacit and intuitive knowledege of the students participating of the investigation. In the list of the data collection presented, as a result of the development of all phases planned by DE, are highlighted: the mediation of the experiment participant teacher is really affected and modified by the technology´s use (the software Geogebra); the students expressed some intuitive and heuristic interpretations, both in cognitive analysis phase, and the experimentation´s phase, related to the Laurent´s series, they expressed an kind of understanding, through a dynamic visualization of the representation of Laurent´s series. Moreover, the data indicates the appropriation of a certain concept of the theory through the mother langue and the mobilization of knowledge (gestural actions and the use os methaphors) that go beyond the formal and mathematical structural model into discussion.

Keywords: Didactical Engineering; Complex Calculus Transition; Teaching; Laurent´s series

Engienerie Didactiques

Résumé

Cest article présent un ingénièrie didactique – ID, compte tenu de l´enseignement de la notion de serie de Laurent. Le sujet mentionné ci-dessus est présenté comme une étude obligatoire dans le nombreux cours de premier cycle en Mathématiques au Brésil, dans la discipline de L´Introduction a la variable complexe. Ainsi, comme centre sur an cadre pris comme référence dans le ID, considére le point de vue de l´analyse fournie par le perspective de la Transition Complexe du Calcul – TCC afin d´identifier et d´enregistrer les élèments de transition et des élèments de rupture, conditionnés par le contact d´un groupe de cinq étudiants et le professeur devant la Théorie des fonctions de variable complexe. La recherche a se develloppé a L`Institut Féderal de L`Éducation, Science et Technologie de l´État de Ceará – IFCE, en 2015. L´article presente une perspective complementaire de l´adoption d´une conception de la recherche afin d´utilizer la Théorie des Situations didáctiques – TSD, avec le but de décrire et concevoir des situations d´enseignement, supporté dans une médiation qui a cherché et accentuer le processus mobilizateur de connaisssance tacite et intuitive des étudiantes participant à l´enquête de investigation. Dans la liste des donnés recueillies et présentées, en raison du développment de toutes les phases prévue das une ED, ils son mis en évidence: la mediation de l´enseignement participant de l´expérience se montré modifié par l´uitilisation de la technologie (l´utilisation de logiciel GeoGebra); les étudiants ont expremimé interprétations intuitives et l´heuristiques, tant en phase d´analyse congnitive et la phase d´experimentation, liée à la notion de série de Laurent, ils ont exprimé la compreéhension grâce à l´éficacité dynamique de la répresentation des séries de Laurent. En outre, les donnés indiquent l´appropriation de certains concept de la théorie à trávers de la langue maternelle et la mobilisation des connaissances (actions gestuelles et l´utilisation de métaphores) qui vont au delá du formel et le modele structurant mathématiques dans la discussion.

Mots clés: Engienierie Didactiques; Transition do Calcul Complexe; L´enseignement; Serie de Laurent.

---

1. INTRODUÇÃO

Indubitavelmente, inúmeros trabalhos desenvolvidos a partir da década de 80, sobretudo na França, proporcionaram a obtenção e o acúmulo de conhecimentos científicos, didáticos e metodológicos, relacionados a determinados conhecimentos matemáticos clássicos, correspondentes ao contexto do ensino acadêmico (ARTIGUE, 1984a; 1984b; 1989; BROUSSEAU, 1989; DOUADY, 1984; 1993; 2008; MARGOLINAS, 1995; ROBERT, 1986, 1988). No rol dos estudos desenvolvidos, acentuamos àqueles que se detiveram, de modo particular, aos conteúdos do Cálculo Diferencial e Integral, bem como, aos conteúdos de Análise (GRENIER & LEGRAND, 1986; ROBINET, 1986; 1992; ROBERT, 1982; 1983).

A tônica geral desses últimos estudos, consistiu em considerar o binômio ensino-aprendizagem, a partir da constatação de determinados entraves e obstáculos recorrentes, identificados no sistema de ensino francês, ainda por decorrência do vies formalista e estruturalista (CHOQUET, 1963) e a perspectiva de ensino propugnada pela corrente policéfala bourbaki (BOURBAKI, 2006; DOUADY, 1995a; 1995b), cuja maioria de seus membros eram franceses (MARGOLINAS & DRIJVERS, 2015, p. 895).

Assim, a sinergia de um grupo de especialistas didatas franceses evoluiu, com o desenvolvimento de uma pratica sistemática de organização, preparação e experimentação de sessões de ensino investigativo, capaz de desenvolver um corpus científico e, que, permitiu a identificação de inúmeros obstáculos (epistemológicos) e a superação de quadros indefectíveis ou realidades de ensino marcadas pela obsolescência e anacronismo das pespectivas e/ou concepções vinculadas ao saber matemático.

Desse modo, de modo inconteste, por cerca de 20 anos, os escritos em torno do uso da Engenharia Didática – ED, da Teoria dos Campos Conceituais, da Teoria das Situações Didáticas – TSD, da Teoria dos Registros de Representação Semiótica – TRRS, da Teoria Antropológica do Didático – TAD e da Teoria dos modelos CkC produziram a robustez científica para a demarcação da área de pesquisa e investigação, denominada de Didática da Matemática (ARTIGUE, 1984b; BROUSSEAU, 1986a; 1986b; BOLON, 1996; BROUSSEAU, 1986a; 1986b; 1994; 1998; LABORDE, 1997).

Não obstante, quando nos atemos aos prolongamentos e implicações dessas perspectivas, tomando como referencia outros corpus teóricos matemáticos, a partir de uma análise cuidadosa, podemos depreender que, alguns assuntos específicos permaneceram num oblívio total, até os días de hoje (ALVES, 2011; ALVES, 2014a; 2015; HENRIQUES, 2006).
Senão, vejamos o caso do Cálculo em Várias Variáveis ou da Teoria das funções em varias variáveis. Diante da profusão de estudos sobre a noção de limite, sobre o processo de derivação e de integração produzidos na década de 80 (GRENIER & LEGRAND, 1986; ORTON, 1983a; 1983b), registramos a aparente escassez e as correspondentes repercussões de certas teorías, como a TRRS, ou como a dialética do instrumento-objeto (DOUADY, 1983), para o caso de implicações para os limites de funções em varias variáveis, ou ainda o processo de derivação e integração de funções em varias variáveis.

No Brasil, assinalamos a tese de Alves (2011), que propugnou a manifestão de obstáculos, semelhantes aos registrados no caso de uma variável real, agora, no contexto da Teoria das funções em varias variáveis. De modo geral, Alves (2011) leva em consideração um extenso periodo de estudos compulsórios dos estudantes na academia, que podem durar de dois até tres anos. Formalmente, os estudantes mantêm contato com a Teoria das funções em uma variável real e, algum tempo depois, com a Teoria das funções em varias variáveis (ALVES; BORGES NETO & DIAS, 2012; LIMA, 2017). Dessa forma, os fenômenos relacionados com o ensino e aprendizagem no referido lapso temporal de estudos exigem vigilancia constante. E, deste modo, Alves cunhou o termo Transição Interna do Cálculo – TINC.

Segundo a perspectiva do autor, determinados elementos, quer sejam de ordem metodológica, psicológica, epistemológica, histórica, podem atuar no sentido de facilitar/impulsionar o acumulo e sistematização de saberes dos estudantes, ao decurso do contato com a Teoria das funções em uma variável real, para a Teoria das funções em varias variáveis, em duas ou três variáveis, por exemplo.

Por outro lado, a partir de uma perspectiva epistemológica barchelariana , outros elementos de ordem metodológica, psicológica, epistemológica ou histórica podem atuar no sentido de dificultar, retardar, impedir e, mesmo, causar lentidões ao conhecimento a ser adquirido pelo estudante.

De modo prosaico, Alves (2011) nomeou os primeiros elementos como elementos de transição, enquanto que, o segundo grupo se relaciona e faz referencia aos elementos de ruptura. Em outros manuscritos, Alves (2014; 2015) desenvolveu uma discussão que permite a consideração de um lapso temporal acadêmico ainda mais extenso, que tem seu início com o estudo da Teoria das funções na variável real, passando pela Teoria das funções em varias variáveis, até findar com a Teoria das funções na variável complexa.

A despeito da escassez de trabalhos no Brasil com tal temática, Alves (2015) cunhou o termo Transição Complexa do Cálculo – TCC, para demarcar um periodo de estudos, e os fenômenos identificáveis a partir da interação alunos – professor – saber matemático, quando consideramos a passagem da variável real para a variável complexa, que simbolizamos .

De modo preliminar, acentuaremos dois elementos comentados por Alves (2015) que podem, em decorrência da mediação ou ação metodológica assumida, atuar como elementos de ruptura. Com efeito, reconhecemos quase como um conhecimento matemático legítimo, determinados argumentos explicativos (e metafóricos) no contexto de ensino do Cálculo em uma variável real. Assim, na figura abaixo, ao lado esquerdo, Tall (2009, p 5) recorda certos gestos dinâmicos capazes de transmitir o significado matemático da noção de declividade de uma curva e o comportamento de uma reta tangente ao seu gráfico no plano (ver figura 1).

Por outro lado, ao lado direito, Tall (2009, p. 6) acentua uma espécie de sensação física aliada a ideia de comportamento da declividade ao longo do gráfico, pois um estudante pode compreender e apreender uma ação gestual dinâmica correspondente ao comportamento de crescimento, declividade nula e, logo em seguida, decrescimento. Observamos na figura 1, um cenário que proporciona, por intermédio da visualização e relações estabelecidas entre o sujeito e o objeto. Em relação a tal intenção metodológica, Tall (2009, p. 10) assinala que “isto produz uma versátil abordagem para o cálculo combinando a personificação e simbolismo aos quais a noção de limite surge naturalmente no processo, não formalmente no início do processo, em que os estudantes manifestam dificuldades neste tópico”.

A discussão de Tall pode ser demarcada no contexto da teoria do Pensamento Matemático Avançado (TALL, 2002). O aspecto diferenciado de sua perspectiva reside no fato de conceber um corpus teórico capaz de explicar os fenômenos de ensino e aprendizagem condicionados por objetos matemáticos pertencentes a teorias abstratas.

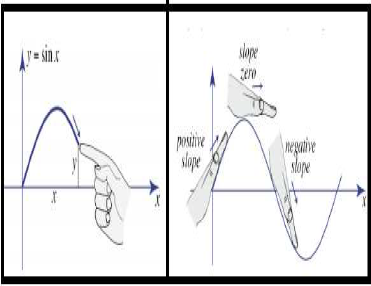
Figura 1. Tall (2009; 2011) evidencia o papel imprescindível de recurso gestuais e metafóricos para o ensino do Cálculo.

Na Teoria do Pensamento Matemático Avançado, registramos uma preocupação constante com a visualização, afim de proporcionar outras posibilidades de apreensão intuitiva dos objetos matemáticos do Cálculo e Análise, predominantemente. Por outro lado, com origem na influência da perspectiva de Needham (2000), Polya & Latta (1979) e Wegert (2012), Alves (2015) assinalou os entraves e obstáculos (MARINHO, 2017) que enfrentamos, na medida em que, no contexto da Teoria das funções na variável complexa, buscamos explorar a visualização (ver figura 2) ou, ainda, inserir, no ritual acadêmico de ensino, elementos alternativos (ações gestuais e metáforas intuitivas), afim de proporcionar um entendimento ou uma compreensão tácita e intuitiva para os estudantes.

Na figura 2 divisamos uma espécie de “vulcão” ou “pico” de duas montanhas, identificadas por intermédio de nossa capacidade perceptual (ALVES, 2012).

Figura 2. Visualização de “vulcões” que designam um sentido/significado metafórico para a noção de singularidades de funções, na perspectiva de Needham (2000, p. 66).

Nesse sentido, na figura 2, Needham (2000) referencia o gráfico de algumas funções na variável complexa, que simbolizamos por , aonde, o termo  designa a parte real de uma função f(z), enquanto que  constitui sua parte imaginária. Ora, um dos entraves à capacidade cognitiva dos estudantes reside no fato de que, seu gráfico é um subconjunto do . Assim, via de regra, não existe uma abordagem standard e precisa que proporcione a visualização de certos conceitos na variável complexa (WEGERT & SEMMLER, 2011; WEGERT, 2010; 2012).

Por outro lado, outros problemas específicos podem ser identificados. Com efeito, pontuamos abaixo a mudança notacional envolvendo a noção de sequências de números reais para a noção de sequência de números complexos. Logo em seguida, identificamos a noção de séries de números reais que admitem sua generalização, quando estudamos a noção de séries de números complexos.

E, na última implicação indicada '=>', quando escrevemos , fazemos referência a uma série de potências, na variável real. E, algum tempo depois, os estudantes entram em contato com as noções que indicamos por  (série de Taylor) ou  (série de Laurent).

Figura 3. Quadro sistemático envolvendo a mudança notacional no caso de sequências, séries e séries de potências (elaboração do autor).

Com origem em uma apreciação açodada, poderíamos inferir que a única mudança significativa notacional na figura 3 envolve, tão somente, a substituição da letra “x” pela letra “z”. O que não se mostra evidente se insere num bojo de inúmeros alterações, em decorrência da introdução da variável complexa. Por exemplo, quando deparamos a decomposição  E, a convergência da série  ocorre se, e somente se, contarmos com a convergência de .

Por outro lado, o registro de concepções inadequadas ou mal formuladas possui sua história inicial, desde o primeiro contato com a noção de sequências e séries de números reais. Com efeito, na tese de Robert (1982), deparamos um estudo sobre a aquisição da noção de convergência de sequências e séries de números reais. De modo geral, a pesquisadora constatou a manifestações de concepções estáticas (como condicionadas pela definição formal ou simbologias lógicas) relacionadas com ambos os conceitos, assim como, registrou a manifestação de concepções dinâmicas (envolvendo a descrição verbal dos objetos), relacionadas com a noção de convergência/divergência. Robert (1982, p. 437) adverte que “não se mostra fácil a tarefa de propor uma imagem mental correspondente a tradução da definição de ”.

E, nas conclusões de sua tese, Robert assinala:

Ademais, temos constatado que a imagem cinemática usual da noção, uma das mais antigas (devido a D´Álembert) e a mais vulgarizada, não se mostra propriamente eficaz. E, dentre a produção dos estudantes, tendo exprimido o modelo dinâmico existem, quase sempre, respostas incorretas ou ambíguas, do que respostas corretas. Tal constatação não envolve apenas as tarefas correspondentes ao modelo de convergência, como podemos constatar em certos exercícios, mobilizamos uma representação para a convergência.

No excerto acima, deparamos elementos investigados pela autora, que evidenciam um caráter imprescindível do entendimento da noção de convergência/divergência, do ponto de vista dinâmico (e não apenas estático) e, correspondendo a uma produção de representações adequadas pelos estudantes participantes do estudo. Ora, de imediato, podemos depreender entraves semelhantes, quando passamos a considerar outros contextos de ensino (BRIDOUX, 2012; GHEDAMSI, 2009) e com outras teorias de base fundante, como no caso das funções na variável complexa (BRADEN, 1985; CARTIN, 1995; CHAVEZ, 2014; GLUCHOFF, 1993; MARQUES & SOUZA, 2016; PEREZ, 2012; SANTOS, 1998; TIROSH & ALMOG, 1989; TOMASIUNAS, 2012).  

Por exemplo, o processo de integração de funções na variável complexa representa a generalização de certos elementos que costumeiramente deparamos na teoria das funções de uma variável real (BOTTAZZINI, 1986; GRAY, 2015). Shokranian (2011, p. 143) esclarece nossa ilação:

Na teoria das funções reais, originalmente, a integração foi usada para calcular a área de uma figura geométrica ou o volume de um sólido. Diferentemente, na variável complexa, a teoria da integração é uma ferramenta para estudar funções analíticas, tais como os Teoremas de Cauchy e outros que mostraremos. Por outro lado, uma das aplicações fundamentais das integrais das funções complexas é também o cálculo das integrais definidas de uma variável real [...]

A proeminência histórica e a mudança de perspectiva implementada pelos matemáticos profissionais é comentada por Bottazzini, quando observa que:

Quase a metade do Cours D´Analyse é devotado aos conceitos de Análise Complexa, que constitui uma das mais fundamentais obras de Cauchy em Matemática e, talvez, a mais importante. Em suas mãos, o cálculo de quantidades complexas se tornou um instrumento indispensável de análise, perdendo a áurea de mistério e inexplicabilidade que acompanhou os números complexos desde seu surgimento na solução de equações algébricas do terceiro grau. (BOTAZZINNI, 1986, p. 127).

E, pouco mais adiante, comenta ainda que:

Tal incerteza, dominante no final do século, retrata o testemunho de Gauss e sua relutância em tornar público sua posição em 1799. Defendeu posição de que a interpretação geométrica dos números complexos e sua demonstração do Teorema Fundamental da Álgebra se tornaria incompreensível sem os primeiros. (BOTAZZINNI, 1986, p. 127).

Ora, o excerto acima indica de modo claro o apelo aos métodos matemáticos geométricos, aliados ao formalismo, no sentido de disserminar determinadas ideias da Teoria das funções na variável complexa. Assumimos, pois, posição concorde com Needham (2000), Krantz (1990; 2007), Wegert (2012) e, sobretudo, com a perspectiva de Polya & Latta (1974). Esses últimos autores desenvolvem uma abordagem geométrica, com apelo a determinados elementos e fenômenos, relativamente ao processo de integração de funções na variável complexa, manifestando uma interpretação diferenciada para a seguinte simbologia , aonde f  é uma função na variável complexa e y designa um caminho no plano complexo.  

Por outro lado, a partir de uma intenção metodológica que entendemos ser diferenciada, Polya & Latta (1974) fazem agregar significados físicos para o processo de integração. Nesse sentido, com o escopo de descrever uma interpretação física para a classe de funções do tipo  estabelecem:

Vamos focar nossa atenção num ponto em um rio largo, fluindo de forma constante. Muitas partículas passam por tal ponto, sempre partículas diferentes passam, porém, todas passam com a mesma velocidade se o fluido for realmente estável. Todavia, uma certa velocidade pertence a tal ponto, representada por um vetor possuindo uma magnitude definida e direção. De modo geral, a cada ponto da corrente fazemos corresponder um vetor, representando a velocidade do fluxo no ponto. O fluxo constante de um rio nos sugere um importante conceito de campo de vetores. (POLYA & LATTA, 1974, p. 61)

O expediente dos autores acima evolui, com o cuidado matemático necessário e com o escopo que pensamos ser o mais importante e vinculado ao nosso assunto na direção de uma interpretação física de uma integral de linha, para funções de variável complexa. Com efeito, com arrimo do apelo mnemônico que vislumbramos na figura 4, compreendemos o esforço metodológico dos autores no sentido de uma transposição didática (CHEVALLARD, 1991), de cunho intuitivo e interpretativo. De modo simbólico, fornecemos uma tradução correspondente como segue

(ver figura 4), aonde tomamos f(z)=w.

Figura 4. Polya & Latta (1974, p. 146) propugnam uma significação física para a noção de integral de linha

Para concluir nossa seção preliminar, acentuamos os seguintes elementos: (i) o caráter abstrato de varios conceitos na Teoria das funções na variável complexa proporciona entraves ao ensino e à aprendizagem semelhantes ao caso da Teoria das funções da variável real, todavía, pouco conhecidos e discutidos na literatura; (ii) o caráter abstrato de varios conceitos na Teoria das funções na variável complexa dificulta a exploração heurística, intuitiva dos conceitos, por intermédio da visualização e percepção de propriedades gráfico-geométricas.

Ora, a partir das considerações anteriores, realizamos um primeiro passo para deflagarmos um processo investigativo e perquiridor, que deter-se-á ao âmbito da Transição Complexa do Cálculo – TCC. Ademais, no extenso repertorio de conceitos fundantes da Teoria das funções na variável complexa, restringir-nos-emos ao caso da série de Laurent (figura 3, ao lado direito), que prevê a descrição de uma função analítica, em termos de um desenvolvimento em séries de potências (BRADLEY & SANDIFER, 2009; CONWAY, 1978; KRANTZ, 2008; 2009; GONG, 2001; GLUCHOFF, 1993; SCHWERDTFEGER, 1979).

Assim, na próxima seção, elegeremos o percurso investigativo a ser seguido e, portanto, estabeleceremos os pressupostos necessários para sua realização. Por conseguinte, diante do quadro descritivo anterior elegeremos a seguinte pregunta norteadora da investigação: De que forma a visualilização e a exploração sistemática da intuição, no contexto de ensino de série de Laurent, pode concorrer para a evolução de aprendizagens que não se mostrem restritivas ao quadro de representações algorítmicas e a um trato eminentemente formalista?

2. SOBRE A ENGENHARIA DIDÁTICA – ED

Como consequência da organização científica e a sinergia implementada na França, sobretudo no final dos anos 60 e, com maior proeminência, entre as décadas de 80 e 90, constatamos a demarcação e a evolução, graças a um processo cumulativo de escritos científicos, da pesquisa em Didática da Matemática (BROUSSEAU, 1986; 1988; 1994). Tal vertente de estudos adquiriu um substrato científico em decorrência, originalmente, do interesse em torno dos fenômenos relacionados com o ensino e a aprendizagem em Matemática, em seus diversos níveis (ARTIGUE, 1989; 1995; BOSCHET & ROBERT, 1983; DOUADY, 1995a; 1995b).

Sendo assim, uma profusão de trabalhos permitiu a consolidação e a demarcação de um campo de estudos, bem como a evolução de um design de investigação cientifica, que se apoiou numa metáfora que remete a um planejamento sistemático de um engenheiro, tendo em vista a concepção e ajuste de um projeto preciso. Desse modo, a terminologia Engenharia Didática – ED foi usada para designar um modus operandi de investigação ou ainda como “uma metodologia para o análise de situações didáticas” (BRUM & SCHUHMACHER, 2013) e, também

Trata-se de etiquetar, de certa forma, uma forma de trabalho didático, comparável ao do engenheiro, para realizar um projeto preciso, se apoia sobre diversos conhecimentos científicos de seu domínio, aceita a se submeter a um controle do tipo científico e, ao mesmo tempo, se encontra obrigado a trabalhar com objetos mais depurados da ciência [...] (ARTIGUE, 1996, p. 243)

A constatação da ED como metodologia de pesquisa se caracteriza como um esquema experimental baseado num conjunto de experimentações e realizações didáticas em sala de aula. Artigue (1996, p. 247) indica as seguintes etapas: concepção, realização, observação e a análise de sequências de ensino. Mas, do ponto de vista da ação experimental e tempo investigativo, Artigue distingue ainda: (1) fase de análises preliminares; (2) fase de concepção e análise a priori das situações didáticas; (3) experimentação e, por fim, (4) análise a posteriori e validação de todo aparato teórico construído.

Por outro lado, a vertente francófona se distinguiu a partir de uma tradição, no âmbito da pesquisa, envolvendo um caráter de complementaridade entre varios quadros teóricos. Dessa forma, adotaremos a Teoria dasSituações Didáticas – TSD (BROUSSSEAU, 1986a; 1986b), tendo em vista a elaboração de situações-didáticas que proporcionem as interações desejadas envolvendo a tríade sujeito – professor – conhecimento matemático e seus resultados excelentes no campo experimental (MARGOLINAS & DRIJVERS, 2015, p. 901).

Temos, pois, o interesse no controle, previsão, predição e replicação dos elementos identificáveis da tríade há pouco mencionada. Nesse sentido, Brousseau fornece a indicação de elementos essenciais à práxis do professor, ao mencionar que é necessário “poder comparar, não apenas os resultados, mas também as condições nas quais eles foram obtidos e de modo que tais condições sejam reprodutíveis.”. (BROUSSEAU, 1986, p. 3). Outrossim, o pesquisador esclarece a possibilidade de “reprodução” no ensino de Matemática, quando acrescenta ainda que

Esta reprodutibilidade implica uma descrição, não ingênua, de todas as condições observadas, mas seletivas e que repousam sobre uma escolha pertinentes às variações possíveis de efeitos reconhecidos. A reprodutibilidade repousa, então, na compreensão dos fenômenos fundamentais, isto é, do tecido de relações atestadas, constituindo a teoria e permitindo se escolher as condições de ensino, de explicar seus efeitos e de prevê-los. (BROUSSEAU, 1986, p. 3).

O excerto anterior, inaugura uma preocupação sui generis com um olhar sistematizado e cientificizado para os fenômenos relacionados com o ensino e aprendizagem em Matemática. Para finalizar a seção atual, antecipamos o propósito do porvir abordado no próximo segmento. Com efeito, a primeira fase da ED, nomeada de análises preliminares, possui como um dos objetivos (e escopo) a “identificação dos problemas de ensino e de aprendizagem do objeto de estudo e delinear de modo fundamentado as questões, as hipóteses, os fundamentos teóricos e metodológicos da pesquisa” (ALMOULOUD, 2007, p. 172).

3. ANÁLISES PRELIMINARES

Artigue (1995, p. 38) explica que uma investigação de ED, na fase preliminar de concepção, se baseia em um quadro teórico didático geral e em conhecimentos adquiridos no campo de estudo. Os elementos mais frequentes considerados nas analises preliminares, são apontados por Artigue como: análise epistemológica dos conteúdos contemplados no ensino; análise do ensino tradicional e seus efeitos; análise das concepções dos estudantes, as dificuldades e obstáculos que determinam sua evolução; análise do campo de restrições de onde devemos situar a realização didática efetiva. Todos os elementos anteriores são desenvolvidos em termos dos objetivos de trabalho adotados na presente investigação.

De um ponto de vista macro, podemos afirmar que “a primeira fase se estrutura em torno de uma análise do funcionamento do sistema […]” (ARTIGUE, 1995, p. 39). Não obstante, nos parecem pouco identificáveis os elementos de nosso interesse. Assim, acentuamos o papel das concepções dos estudantes participantes do estudo, bem como uma análise epistemológica dos conteúdos e do ensino atual, representado pelas abordagens presentes no compêndios de livros (CECÍLIA & BERNADEZ, 2008; LINS NETO, 1996; SOARES, 2014)

Nesse sentido, Laborde (1997) fornece uma explicação pormenorizada para esses dois elementos. Com efeito, Laborde (1997, p. 104) indica três categorias de interesse em tais estudos produzidos, sobretudo, no final dos anos 80 para o início dos anos 90, a saber: a dimensão epistemológica, a dimensão cognitiva e a dimensão didática. A primeira dimensão adquire proeminência natural, tendo em vista que, a vigilância do pesquisador no que concerne aos conteúdos matemáticos de uma sequência de ensino e de que modo pode atuar/modificar sua transmissão em situação.

A dimensão cognitiva é constatada por “alguns trabalhos que procedem uma análise fina das concepções preliminares dos aprendizes antes da aplicação de uma sequência” (LABORDE, 1997, p. 105), o que pode ocorrer de modo interno (ao cabo das primeiras situações relativamente às quais os estudantes são confrontados), ou de modo externo (a partir da comparação e apreciação de outras investigações que fornecem dados sobre concepções possíveis dos sujeitos).

Ademais, desde que assumimos uma posição concorde com Artigue (1989; 1995), levamos em consideração o campo de restrições e identificação do campo matemático de nosso interesse. Desse modo, no que concerne ao nosso terreno epistemológico de consideração, advertimos que a simples mudança da variável real para a variável complexa proporciona ao estudante um quadro de injunção que estabelece uma diversidade de links conceituais no contexto do estudo de séries de potências (ALVES, 2014d). .

Por exêmplo, sabemos que o símbolo matemático  é a variável, representa uma série de potências. “Na variável complexa, a situação é semelhante, de modo que a série de potência é uma série infinita indicada por ” (SHOKRANIAN, 2009, p. 229).

Uma interpretação pouco cuidadosa da ilação do autor no parágrafo passado pode transmitir a impressão de que são poucas as mudanças conceituais em questão. Não obstante, aparentemente, o foco do mesmo foi direcionado apenas para a notação standard empregada no trato desses objetos. Por outro lado, podemos nos ater a outros elementos, nomeadamente, àqueles de ordem topológica (SCHWERDTFEGER, 1979) e que permitem divisar outros aspectos que extrapolam um simples sistema matemático notacional particular (figuras 5 e 6).

Com efeito, outro elemento que merece atenção e representa papel de destaque no contexto do estudo de séries, diz respeito à noção de convergência. Neste sentido, assinalamos que “um problema principal é a determinação da convergência e a analiticidade das séries de potencias. O mesmo foi considerado como um problema principal para as series de potencias reais em Cálculo” (SHOKRANIAN, 2009, p. 230).

Nas figuras 5 e 6 trazemos alguns desenhos (figuras) sugeridos por Needham (2000), em seu livro intitulado Visual Complex Analysis, afim de significar um comportamento previsto e esperado para as reduzidas de ordem ‘k’, denotadas por , de uma série de potência, na medida em que aguardamos sua convergência (visto que tendem a se acumular num disco, centrado em um ponto ‘p’, de raio pequeno).

Figura 5. Needham (2000, p. 227) fornece uma interpretação geométrica para a noção de convergência de uma série de potência na variável complexa por intermédio de suas reduzidas

E, quando nos atemos aos elementos de ordem histórica em torno do nascedouro e da evolução da noção de convergência, compreendemos os inúmeros percalços e obstáculos enfrentados por matemáticos profissionais ao decurso de séculos (BOTTAZZINI & GRAY, 2013; DEBNATH, 2015; HAIRER & WANNER, 2008; MEDVEDEV, 1991; ROBINET, 1984).

Figura 6. Needham (2000, p. 67) evidencia o caráter geométrico das séries de potências.

Nos parágrafos anteriores, referenciamos a dimensão epistemológica do interesse de nosso estudo. Reparemos, todavía, que ocorrem varios elementos da dimensão didática que se mostram íntimamente relacionados com os elementos que indicamos há pouco, atinentes à dimensão epistemológica. Ademais, quando buscamos compreender o ensino atual, se torna preemente, a consideração e apreciação dos compêndios atuais, publicados em nosso idioma (ou o exemplos de outros países). Dessa forma, enunciaremos um teorema e um criterio de convergência de séries de números complexos, que prevêem a descrição de uma série de potências em termos do desenvolvimento de Laurent e que possui lugar invariante nas obras do gênero.

Teorema²(de Laurent): Suponhamos que f é uma função analítica em um anel , onde . Então, f tem uma representação em série de Laurent centrada em z, que é válida para todo . Além disso, os coeficientes são dados por , onde ‘r’ é qualquer número em .
Não tencionamos desenvolver sua demonstração formal aquí, não obstante, com arrimo na figura 7, acentuamos a única figura, recorrentemente explorada pelos autores de livros, em sua demonstração formal.

Figura 7. Figura explorada para a demonstração do teorema de Laurent. (CECÍLIA & BERNADEZ, 2008, p. 151)

Critério de Cauchy: Uma condição necesária e suficiente para que a série  seja convergente, é que, para todo , então (LINS NETO, 2012, p. 28; FLANIGAN, 1972, p. 209).

Por outro lado, a última dimensão a ser tomada nas análises preliminares, diz respeito a dimensão cognitiva. Dessa forma, recordamos mais uma vez os ensinamento de Laborde (1997, p. 105), sobre o carater imprescindível do nosso conhecimento sobre às possíveis manifestações das concepções (dimensão cognitiva) do sujeitos participantes do estudo atual.

Artigue (1995, p. 40) esclarece ainda que a dimensão cognitiva é “associada as características cognitivas do público alvo, o qual, se dirige o processo de ensino”. Isto é, em dependencia do nosso público de interesse, se torna imprescindível uma análise preliminar das concepções e habilidades dos sujeitos envolvidos no experimento.

Isso posto, declaramos que nosso estudo foi desenvolvido no Instituto Federal de Educação, Científica e Tecnológica do Estado do Ceará – IFCE, em 2015. Participaram do estudo um grupo de seis anos, todavía, os dados a serem discutidos de todas as seções envolvem a produção dos alunos 1, 2, 3, 4 e 5, com dois encontros, com duração de duas horas para cada encontro.

E, tomando como referencia a perspectiva da TINC e da TCC, buscamos identificar na mediação de um professor, determinados elementos que concorrem para a aprendizagem da noção de série de Laurent, assumindo a visualização como fator impulsionador e mobilizador de conhecimentos que extrapolam os saberes formais e estruturais da Teoria das funções na variável complexa.

Diante disto, definiremos a seguinte questão de investigação: Em se considerando o contexto da Transição Complexa do Cálculo – TCC, que elementos concorrem ou atuam, como elementos de transição e como elementos de ruptura, numa mediação de ensino que evidencia a visualização como elemento imprescindível no ensino e na aprendizagem para a noção de série de Laurent?

Ora, com origem no questionamento anterior, definiremos ainda: (a) Que elementos de transição e elementos de ruptura sao identificáveis numa mediação que a assume a visualização como imprescindível? (b) Que elementos de ordem intuitiva, relacionados com a série de Laurent, se manifestam, ao decorrer das atividades dos estudantes?

Em nosso caso, o modelo matemático condiciona, fortemente, todas as estratégias, ações e decisões dos aprendizes em torno do estudo de série de Laurent. Essa variável didática é prevista, de modo geral, por Brousseau (1986, p. 412). Por isso, as variáveis micro-didáticas que apontaremos (responsáveis por uma análise local na experimentação) são correlatas ao que Brousseau (1986) nominada de situação-didática³. Além disso, nas situações didáticas abordadas nas análises preliminares que buscamos apresentar, desejamos que “elas permitam adaptações dos alunos, na medida em que tomam decisões e as modificam” (BROUSSEAU, 1986, p. 440). Doravante, os dados apresentados foram analísados tendo em vista a identificação de elementos de transição e elementos de ruptura. Observamos que, os momentos registrados da mediação do professor participante do estudo ficou restrito ao caso da noção de limite de funções na variável complexa, a noção de funções deriváveis na variável complexa e um caso preliminar envolvendo a noção de convergencia de uma série de potência.

Certamento, os dados abordados constituem parte de um conjunto maior e, os que discutiremos logo na sequência servem para responder, pelo menos provisoriamente, na seção atual, aos questionamentos indicados há pouco (ítem (a) e (b)).

Assim, antes de iniciarmos uma discussão sobre uma apreciação preliminar das concepções dos estudantes, acentuamos a perspectiva de Bolon (1996, p. 75), quando recorda que:

A organização da sequência repousa sobre a hipótese de que a criança constrói novos conhecimentos a partir dos conhecimentos anteriores, na necessidade e em condições de reestruturá-los. O papel do professor se insere em favorizar a articulação entre os antigos saberes e os novos, proporcionando um novo procedimento de resolução, procedimento que resultará num novo conhecimento.

Na figura abaixo, registramos um momento da mediação em que o professor explorou ações gestuais e a produção de conjecturas explicativas relacionadas com a noção de derivabilidade. Na figura 8, o aluno 1, buscou significar, por intermédio de ações gestuais (elementos de ordem intuitiva), a existencia de uma reta tangente ao gráfico de uma função, no caso de funções de uma única variável real.

Figura 8. Na análise preliminar, registramos uma mediação do professor que buscou fortalecer os elementos de transição, no que concerne à noção de diferenciabilidade.

Ainda com referência ao aluno 1, registramos o momento da mediação que buscou explorar alguns elementos de transição, na medida em que, no caso da Teoria das funções em uma variável real, os alunos esperam a existencia de uma reta tangente ao gráfico da função.

Já na Teoria das funções em varias variáveis, o aluno 2 (ver figura 9) designou um modelo dialógico e gestual, pelo uso de uma folha de papel e do apagador, tendo em vista a existencia esperada de um plano tangente à superficie de uma função em duas variáveis reais. Na figura 9, registramos os momentos didáticos que envolveram aspectos cognitivos mobilizados na abordagem do professor investigador.

Nesse caso, percebemos que a intenção didático-metodológica do professor não se restringiu àqueles elementos de ordem formal e estruturante, peculiar ao estilo ortodoxo da Matemática, no âmbito acadêmico. Os elementos de transição, nesse caso, são identificáveis, na medida em que, a ação intencional de ensino buscou relacionar, reinterpretar e readaptar os saberes (conhecimentos) institucionalmente veiculados em etapas anteriores, ao momento atual do grupo de aluno, matriculados na disciplina de Introdução à variável complexa.

Divisamos nas quatro e sucessivas imagens e apelo ao lado gestual e metafórico, com o escopo de interpretar e transmitir o sentido da noção de diferenciabilidde de funções em uma variável real (reta tangenge ao gráfico) e em varias variáveis (plano tangente). Paulatinamente, o aluno 2, com o auxílio próximo do professor, manifestou sua interpretação tácita e individual sobre o progressivo processo da noção matemática de diferenciabilidade, quando nos atemos ao contexto da teoría das funçõe em uma variável real, passando pela teoría das funções em varias variáveis e, por fim, exemplificando com um apelo gestual conjunto, inclusive com o auxílio do professor, o caso da teoría das funçõe na variável complexa (ver figura 10). Vejamos nas figuras 9 e 10.

Figura 9. Na análise preliminar, o aluno 2, desenvolveu uma atividade conjectural explicativa do fenômeno da diferenciabilidade para uma variável e em varias variáveis.

Na mediação didática desenvolvida pelo professor participante do estudo, com base na figura 8, deparamos um momento em que houve a exploração intuitiva de elementos que proporcionam a transição das concepções elaboradas e construidas pelos sujeitos no caso da variável real em direção à variável complexa. Nessa imagem (figura 10), tanto professor e aluno 1 participaram de uma ação gestual conjunta que buscou representar a identificação de dois planos tangentes correspondentes às partes real e imaginária de uma função.

Figura 10. Ainda no caso do aluno 1, o professor participante do estudo auxiliou o estudante na obtenção de uma ação gestual que corresponde à existencia de dois planos tangentes para funções na variável complexa.

Mas, desde que encontramos alguns relatos indicando as limitaçoes do software Geogebra (ALVES, 2015), no tocante à descrição de funções reconhecidamente complexas, a mediação do professor envolveu, assim, o uso em caráter de complementaridade, de dois softwares. Na figura 9, observamos o momento em que o professor buscou transmitir ao aluno 4, a significação gráfico-geométrica da noção de derivabilidade da seguinte função  , com  (ALVES, 2015),
No contexto de discussão da figura 11, registramos o diálogo entre o professor e o aluno 3:

Professor: Eu peguei essa função e separei a parte real e parte imaginária. Agora, qual seria a interpretação possível. Por exemplo, essa função, que valores complexos ela assume?

Aluno 3: Isso aquí é o cosseno hiperbólico….Acho que o plano…acho que a superficie….designada…pode ser uma superficie no espaço.

Professor: Repare que a aquí temos a parte real. Nesse ponto, desejamos determinar um plano, como você vê ai no computador. Feita a construção, quero saber se, no ponto, podemos determinar um plano. Pergunta: a parte real da função na variável complexa é diferenciável?

Aluno 3: Há, nesse ponto é diferenciavel, pois se aproxima por um plano tangente na superficie. A ideia é retirada de um teorema desde que aprendi nos Cálculos…

Nas declarações anteriores, constatamos uma mediação e a mobilização de conhecimentos a partir da interação visual dos objetos matemáticos em discussão. Até aquí, observamos o estimulo do professor sobre a atividade de produção de conjecturas do aluno 3. E, dando continuidade, registramos ainda:

Professor: Geometricamente, o que isto significa?

Aluno 3: Geometricamente, no plano existe uma reta. Mas, no espaço, conseguimos determinar um plano que tangencia e superficie. Indica, aquí, se esse plano for tangente, a diferenciabilidade…

Professor: Você tem certeza disso? Temos um indicio da diferenciabilidade?

Aluno 3: Certeza disso não…se tiver um plano é apenas um indício. Tem que ver se podemos determinar em todo ponto da superficie. E, quando consideramos a parte imaginária….pelo mesmo principio, se determinarmos um plano na parte imaginária da função…

Professor: Agora, você pode relacionar a definição de derivabilidade na variável complexa?

Aluno 3: No plano se diferenciável admite uma reta. Em varias variáveis, teremos um plano. E, no caso da variável complexa, teremos dois planos. E, assim, ela vai ser diferenciável na parte real e na parte imaginária e, não necessáriamente teremos o mesmo plano. Serão dois planos, um para parte real e outro para a parte imaginária.

No trecho anterior, registramos a ocasião da atividade de produção de conjecturas, por parte do aluno 3 e, em meio de suas declarações, identificamos um elemento de transição correspondente, no contexto da Teoria das funções na variável complexa. Reparemos o argumento sobre a existencia de doiss planos tangentes (ALVES, 2016), no cenário de aprendizagem que vislumbramos na figura 11.

Figura 11. Em algumas situações, o professor explorou o CAS Maple afim de proporcionar a visualização de determinadas funções e o entendimento da noção de diferenciabilidade, do ponto de vista geométrico.

Agora, com origem na figura 11, registramos a discussão desencadeada a partir da inspeção do gráfico da função . Quando questionado sobre seu caráter de diferenciabilidade, o aluno 2 respondeu:

Aluno 2: A representação do CUV consiste em obtermos um certo ponto, em que a função é derivável nesse ponto, e daí consigo traçar uma reta que tangencia esse ponto. Nesse caso está no espaço IRxIRxIR.

Assim, com origem nas declarações anteriores, o fragmento do registro do diálogo estabelecido entre os alunos 3 e 2, e o professor, observamos a exploração de um elemento de transição correspondente à noção de diferenciabilidade, na medida em que o professor buscou recontextualizar os conhecimentos anteriores do estudante, para o âmbito das funções na variável complexa.

Por outro lado, ainda no contexto das análises cognitivas, se mostra imprescindível, tendo em vista nosso interesse declarado nas seções iniciais, pela ação do estudante estimulada pela visualização da noção de limite , podemos constatar, na figura 12, um momento de sensibilização e introdução da tecnología na mediação proposta pelo professor ao decurso da disciplina Introdução à Variável Complexa.

Figura 12. Registramos na mediação do docente a exploração dos recursos tecnológicos tendo em vista a visualização da noção de limite, com o uso do software Geogebra.

Com arrimo nas informações registradas na figura 8, podemos depreender que foram mobilizadas concepções adequadas, a partir da exploração do software Geogebra. De fato, em várias ilações produzidas pelos alunos 1, 2, 3, 4 e 5, divisamos a mobilização de um saber que extrapola os limites logicizantes da própria Matemática.

Vale assinalar que, no âmbito da perspectiva da Transição Complexa do Cálculo –TCC, Alves (2014) acentua o caráter imprescindível da exploração de elementos tácitos, intuitivos, que questionam o papel da hegemônico da certeza matemática. Ora, a manifestação subjetiva da certeza pode ser reforçada numa mediação de ensino que negligencia, por exemplo, o papel dos contraeexemplos.

Para exemplificar nossa ideia, na figura 13, ao lado esquerdo, Needham (2000) explora a visualização da região do plano complexo correspondente ao caráter de convergência de uma série de potência. Em contrapartida, ao lado direito, na mesma figura (figura 9), divisamos a região de convergência e outra de divergência.

Needham (2000, p. 69) adverte a possível identificação de uma região, na qual, o sujeito não consegue afirmar ou infirmar nada sobre o caráter de convergência. Divisamos sua representação correspondente à região do plano complexo em que pode ocorrer o “anel da dúvida”. (ver figura 13).

Figura 13. Needham (2000, p. 69) discute a identificação da região de convergencia de uma série de potencias, bem como a possível identificação do “anel da dúvida”.

Podemos agora confrontar as informações exibidas nas figuras 13 e 14. Dessa forma, registramos a ação investigativa do aluno 3, que buscou compreender e determinar uma região correspondente ao “anel da dúvida”. Na figura abaixo, o aluno verbalizou, gesticulou e produziu uma atividade conjectural relacionada com o comportamento de incerteza da série de potencias explorada com o software GeoGebra.

Figura 14. O aluno 3 desenvolveu uma atividade investigativa de determinação do “anel da dúvida” correspondente a uma série de potencias.

Na figura 15, registramos uma tarefa (situação de devolução⁴), que envolveu a determinação gráfico-geométrica do anel de convergencia de uma série de potencias segundo a descrição de Laurent (teorema). Na referida tarefa, observamos que o professor estimulou o aluno da determinação/discriminação, de uma região no plano complexo em que podemos esperar a convergencia, de acordo com certos teoremas institucionalizados pelo professor.

Não obstante, a construção explorada com o software GeoGebra, buscou acentuar o comportamento do desenvolvimento de Laurent na frontera da região anelar, assim, o efeito metodológico final, consistiu em criar um ambiente de incerteza e de discusão com os estudantes, posto que, nenhum estudante conseguiu determinar, de forma precisa, a região de convergencia no plano.

Com efeito, na figura 16, registramos a interação entre o prefessor e o aluno 4. Reparemos que, na figura 16, ao lado esquerdo, o aluno 4 observou o comportamento dinâmico da divergencia da representação correspondente à série de Laurent. Por outro lado, ainda na figura 16, agora na imagem do meio, o aluno 4 começou a acompanhar e descrever, por intermédio de uma relação visual, estabelecida com o objeto matemático (série de Laurent), seu comportamento progressivo de convergencia. E, por fim, todo o processo manipulativo dinâmico que vislumbramos na figura 15, culminou com a identificação do comportamento de convergencia, fato que se mostra inexequível sem o suporte computacional (ALVES, 2015).

Figura 15. Com a exploração do software Geogebra, o professor proporcionou a visualização e uma atividade investigativa em torno do “anel da dúvida” relacionado com a noção de série de Laurent e um processo dinâmico de convergencia/divergencia.

No fragmento abaixo, constatamos que o estudante desenvolveu uma atividade investigativa guiada por sua capacidade perceptual e visualização para o entendimento dinâmico das relações matemáticas em jogo. Aquí, deparamos, de maneira inequívocada, concepções dinâmicas sobre a noção de convergência.

Aluno 3: Aí, é nesse momento que ela passa de divergente para convergente….eassa região aí é de divergencia…aparentemente divergente…

Figura 16. O aluno 3 buscou confrontar o modelo matemático formal (ao lado esquerdo), previsto pelo teorema com o modelo computacional explorado com o software (ao lado direito).

Trazemos, logo em seguida, alguns trechos do audio envolvendo a discussão entre o professor e os alunos 3 e 4. O episódio envolveu a introdução, por parte do professor, do “anel da dúvida” (ver figura 16). De fato, observamos que a intenção didática do professor envolveu uma introdução do termo ou terminología que sofreu apreciação, análise e julgamento da turma.
Todas as ações foram apoiadas na visualização tendo como escopo o debate entre o grupo dos alunos. Todavia, os dados mais representativos (ndicadores de nossas hipóteses) foram produzidos apenas pelos alunos 3 e 4.

Professor: Se eu souber que ela converge…

Aluno: Eu já sei que essa é a lei de formação dela….

Professor: Não…muito forte. Para cada variação do número complexo, eu vou somar de acordo com essa fórmula. E, estou somando um número complexo, um vetor. Aí, voce vai indicar aonde você acha que converge ou acha que diverge. Se existe uma região no plano aonde sempre converge ou diverge. Se nesse disco aquí converge ou diverge. Ou ainda, uma outra em que não podemos afirmar nada….Por exemplo, você sabe o que é ponto de sela?

Professor: Você sabe o que é ponto de sela?

Aluno 3: É um ponto em que não há nem máximo e nem mínimo…o ponto possui derivada…

Aluno 4: Eu sugiro o termo ponto de sela…

Professor: Vocês acham que o termo ponto de sela representa bem a ideia do comportamento dela….tem ponto ela converge né…Você acha que ela diverge ou converge? Marque os pontos!

Aluno 4: Aparentemente sim…acho que ela diverge aquí. E diverge aquí também.

Aluno 3: É como você falou, aparentemente sim. Esta convergindo, divergindo e depois converge….

Professor: Você consegue traçar um anel e nele a série sempre converge? Dois círculos concéntricos?

Aluno 4: Não sei se diverge…só digo que parece….Aqui, é nesse momento que ela passa de convergente para divergente…Aparentemente divergente e, agora, está convergindo.

Aluno 3: […] há vejo que nessa região o vetor tende a se acumular, logo imagino que ela deve convergir, isso em uma certa vizinhança, já em outro momento percebo que o vetor resultante explode, nesse caso, acho que a série diverge.

No trechos apresentados há pouco, registramos a adoção de uma terminología por parte do professor que atuou como elemento de transição. Com efeito, o professor recordou o termo “ponto de sela”, para significar um comportamento matemático impreciso. E, nesse caso, deparamos uma situação de ensino em que os alunos não podem afirmar ou infirmar nada sobre as propriedades percebidas.

Outrossim, em contraposição das terminologías preferidas pelos autores de livros que tendem a tornar hegemónico um quadro de concepções formais e estruturais, no trecho acima detectamos o trecho “[…] há vejo que nessa região o vetor tende a se acumular”, do aluno 3, evidenciando uma concepção dinâmica (ROBERT, 1983) do processo acarretado pela visualização e representação vetorial proporcionada pelo software (ALVES, 2013, 2014d).

Nesse caso, quando registramos a fala do aluno 4 que declarou “aparentemente sim…acho que ela diverge aquí. E diverge aquí também”, evidenciando a mobilização de um conhecimento, a partir da interação com o software e que evitou o emprego precipitado de notações simbólicas ou fórmulas para a conclusão da tarefa damandada.

Outra ação explorada pelo professor buscou confrontar a ideia da região anelar prevista pelo teorema de Laurent, com a região anelar buscada nas imagens 10, 11 e 12. Nessas situações, nenhum aluno conseguiu concluir a tarefa e determinar, posto que se mostrava impossível, a região do plano complexo correspondente.

Por fim, como resultado do debate da turma diante da tarefa proposta pelo professor, a turma cunhou o termo “anél da dúvida”, fato que se mostrou correlacionado e em consonância com o termo previsto e discutido por Needham (2000, p. 69), figura 9, ao lado esquerdo.  

Antes de finalizarmos a fase atual, recordamos que Artigue (1995, p. 40) adverte sobre “a larga predominância do quadro algébrico e o desenvolvimento da teoría, a dificuldade na identificação dos problemas relacionados ao nascimento da teoría no quadro geométrico”. Assim, no sentido de desenvolver um controle das possíveis estratégias dos sujeitos participantes (etapa de experimentação) definiremos os elementos considerados no quadro analítico de nossa situação problema.
Por exemplo, vamos considerar a função meromorfa⁵  e descrever seu desenvolvimento em série de Laurent na região .
No quadro analítico, decompomo-la do seguinte modo:  e ai, podemos considerar os seguintes casos: (a) 1<|z|; (b)|z|<3; (c) |z|>3. Ora, de acordo com o item (a), teremos . De modo similar, no item (b), empregaremos o seguinte expediente: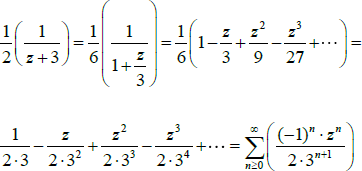

Assim, na região da coroa circular 1<|z|<3 escrevemos o seguinte desenvolvimento da função anterior como série de Laurent dada pela seguinte expressão analitica f(z)= .
Por fim, podemos ainda verificar seu comportamento no complementar do disco de raio 3. Mas, para o item (c) teremos |z|>3>1 e assim, vemos que:

Finalmente, inferimos que a função  é descrita pela série de potências . Tal modelo (da expansão de Laurent) nos permite a previsão/predição das estratégias dos estudantes, no quadro analítico.
Vale comentar que, nas estratégias anteriores, assumimos como pré-requisito o conhecimento sobre o comportamento da série geométrica, cuja condição é caracterizada por 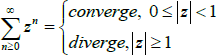 (SOARES, 2014, p. 132).

Para concluir a etapa de análises preliminares, recordamos o caráter imprescindível de determinarmos nossas variáveis macro-didáticas (concernentes à organização global da engenharia), bem como as variáveis micro-didáticas (responsáveis pela organização local da engenharia).

Antes, porém, recordamos que:

Na análise a priori, devemos conceber uma análise de controle dos significados. Isto, quer dizer que, de forma muito esquemática, que a teoría construtivista se assenta no principio da participação do estudante na construção de seus conhecimentos através da interação com um meio determinado.

E, a partir da perspectiva propugnada no excerto anterior, Artigue (1995, p. 44), justifica a relevancia da Teoria das Situações Didáticas – TSD, que se fundamenta em determinados pressupostos da teoría construtivista e “serve como referência para a metodología da engenharia, desde que, se constitui ume teoría de controle das relações e significados das situações” (ARTIGUE, 1995, p. 44). Não obstante, tendo em vista os dados empíricos discutidos na presente seção, afim de prosseguirmos, elegemos as seguintes hipóteses, consubstanciadas na síntese dos dados empíricos coletados na seção atual:

(c) Uma mediação envolvendo o uso do softwares para o ensino de série de Laurent proporciona a aquisição de concepções sobre a noção de convergência e divergência de um ponto de vista dinâmico e não estático; (d) A tecnología permite ao professor acentuar o papel dos elementos de transição e evitar ou, pelo menos, suavizar a ação dos elementos de ruptura; (e) A exploração da visualização possibilita a mobilização de um conbecimento dos estudantes que extrapola os limites e a natureza do conhecimento matemático formal e estruturante.

O ítem (c) se fundamenta, na medida em que, inúmeros estudos (ALVES, 2014a; TOMASIUNAS, 2012; WINSLOW, 2003) apontam para as potencialidades do software GeoGebra (e do CAS – Computer Algebraic System) no sentido de proporcionar um entendimento dinâmico e heurístico dos processos matemáticos (convergência/divergencia de séries). Já os elementos assumidos no ítem (d) são corroborados por elementos oriundos da TINC (ALVES, 2011). Enquanto que, o item (e) se fundamenta, também, na perspectiva de Artigue (2003; 2013).

4. ANÁLISE A PRIORI E CONCEPÇÃO DA SITUAÇÃO DIDÁTICA

Na fase atual, manifestamos um profundo interesse pela “determinação e seleção dos elementos que permitem os comportamentos dos estudantes e seu significado” (ARTIGUE, 1995, p. 45). Assim, de modo sistemático, e seguindo a tradição dos estudos dessa vertente, descreveremos uma parte descritiva e outra parte preditiva, posto que, se mostra condicionada pelas caracteristicas das situações ou da situação-didática ora considerada.

Diante disto, indicaremos três elementos: a descrição local das caracteristicas da situação problema; os elementos que podem entrar em jogo em função das possibilidades de ação, seleção, decisão, controle e validação dos sujeitos 1, 2, 3, 4 e 5. Bem como a previsão dos campos de comportamentos dos sujeitos, o controle dos significados dos conhecimentos mobilizados pelos sujeitos em situação.
Para efeito de maior sistematização, assumiremos que uma situação-problema envolvendo “a escolha de questões abertas e/ou fechadas numa situação matematizada ou menos matematizada, vinculada a um campo de problemas colocados em um ou vários domínios de saber.” (ALMOULOUD, 2007, p. 174).

Cabe esclarecer/distinguir um conjunto de elementos predominantemente considerados nas etapas dialéticas de ensino previstas (e modelizadas) pela TSD, a saber:
Situação dialética de ação.

O aluno é confrontado com uma situação de onde se origina um problema. No âmbito de busca por uma solução, ele produz ações que podem concorrer para a elaboração de um conhecimento na prática (em ação). Em maior ou menor substância poderá explicitar suas razões, todavia, a situação não exige. (DOUADY, 1984, apud ARTIGUE, 1984, p. 7).

Situação dialética de formulação.
Condições diferentes produzem a necessidade da mudança de informações e a criação de uma linguagem para assegurar/permitir tal mudança. Na situação de formulação, o estudante pode justificar suas ações, todavia, a situação não exige. (DOUADY, 1984, apud ARTIGUE, 1984, p. 7).

Situação dialética de validação.
As mudanças não concernem apenas com a informação, mas, também, com o conjunto de declarações. Se torna necessário provar o que foi realizado por meio de uma ação na etapa passada. (DOUADY, 1984, apud ARTIGUE, 1984, p. 7).

Situação dialética de institucionalização.
Se caracterizam pelo momento de fixação ou convenção explícita do estatuto cognitivo de um conhecimento ou saber. (BROUSSEAU, 1981, p. 17).

Ainda sobre a situação de institucionalização, Artigue (1984) acentua o papel principal do professor de Matemática, no sentido da mudança do estatuto do conhecimento matemático científico, ao pontuar que:

 [...] o conhecimento matemático que o expert deverá convencionar ou fixar, seguindo os rituais acadêmicos, com estatuto de um novo saber, rico em relações conceituais (ARTIGUE, 1984, p. 8).

Na situação-problema que abordaremos na presente seção, assumiremos os pressupostos e a sistemática de ação prevista pela ED. Ademais, tendo em vista a consideração de uma perspectiva de influência de caráter metodológico, assinalaremos a dialética dos momentos de ação, formulação, validação (BROUSSEAU, 1986a) e a fase de institucionalização (ALMOULOUD, 2007, p. 23) de acordó com as características da mediação prevista pela TSD.  

Ademais, “as situações-problema devem ser concebidas de modo a permitir ao aluno agir, se expressar, refletir e evoluir por iniciativa própria, adquirindo assim novos conhecimentos.” (ALMOULOUD, 2007, p. 174). Por fim, na etapa da análise a priori, de acordo com as características de cada situação proposta, podemos prever o comportamento dos alunos, o que se coaduna com o que prevê Artigue (1995).
Situação-problema I: Decidir⁶ a região do plano complexo em que podemos contar com a convergência da expansão associada a seguinte função .
Comentários: Vamos agora retomar a questão anterior, em que já verificamos sua descrição .  Adotaremos uma sistemática de verificação o comportamento de convergência/divergência de cada parte desta soma formal. Ao lado esquerdo, em cor rosa (ver figura 17), divisamos um vetor bem pequeno que representa a soma das contribuições das parcelas presentes na seguinte reduzida indicada por  (CRITÉRIO DE CAUCHY).
Com origem em seu comprimento, é fácil inferir que na fronteira do disco de raio unitário, observamos um comportamento que sugere a convergência, na medida em que arrastamos um ponto móvel (discriminado com o software) no complementar do disco de raio 3.  Por outro lado, ao lado direito, na mesma região (ver figura 17), a soma resultante (indicada por um vetor em cor verde) da expressão  indica e/ou sugere sua divergência, dado que seu comprimento é visivelmente muito maior e supera o diâmetro do disco raio 3.
Nesse caso, podemos conjecturar ou prever que a soma formal pode divergir, dado que as reduzidas da segunda expressão podem ser tornar ilimitadas as reduzidas, quando crescemos .
Daí, na figura 17, depreendemos que a expressão final  deve divergir (comprimento final do vetor é muito grande), tendo em vista o comportamento da soma .

Figura 17. Visualização do comportamento das reduzida de série uma série de Laurent na região complementar do disco de raio 3. (Elaboração do autor) para |z|<1 .

Agora, com arrimo na figura 18, com auxílio de um ponto móvel (na cor verde) no plano complexo, observamos agora que o comprimento do vetor rosa resultante manifesta um comportamento imprevisto (de crescimento rápido). Ao lado direito, todavia, visualizamos que o comportamento da soma parcial (reduzida) , relativamente ás contribuições de cada vetor, é bem menor do que a soma anterior (manifestam comportamento controlado).

Por outro lado, na janela ao lado esquerdo, podemos explorar um comportamento dinâmico para o vetor (na cor rosa) e conjecturar que o controle da soma formal das potências, correspondentes aos índices inteiros negativos, presentes na expansão de Laurent, se mostra ilimitada. Portanto, as possíveis conclusões sobre seu comportamento deverá ser um indicativo de divergência (ao lado esquerdo) da soma correspondente, enquanto que, ao lado direito (ver figura 18), sua soma resultante final se mostra controlada.

Dessa forma, quando exploramos o comportamento da seguinte soma , apenas a segunda parcela deverá convergir, portanto, o resultado final produz uma série divergente.

Figura 18. Visualização do comportamento dos termos da série de Laurent no interior do disco de raio 1 com recurso ao software GeoGebra (elaboração do autor).

Na figura 19, divisamos o rastro proveniente da verificação de seu comportamento (de convergência) na coroa . Mais uma vez, desenvolveremos um exercício de, por intermédio da visualização, prever e conjecturar o comportamento final da soma formal , por intermédio de suas reduzidas.

Figura 19. Visualização do comportamento dos termos de uma série de Laurent em uma região anelar 1<|z|<3. (Elaboração do autor) conforme previsto pelo teorema.

Como discutido e evidenciado em parágrafos anteriores e, a idéia do teorema de Laurent, sabemos sobre sua convergência na região anelar .
Deste modo, podemos conjecturar a convergência da expressão formal , visto que a contribuição de cada parcela, em termos de comprimentos dos vetores resultantes é controlável em 1<|z|<3. Seu comportamento geométrico pode ser visualizado na figura 19 e, percebemos que o comprimento dos vetores resultantes de cada soma parcial se mostra controlado, a despeito de uma exploração que podemos realizar com um ponto móvel (vetor), na cor verde.
Como indicamos na seção passada, a expressão de Laurent  diz respeito à sua descrição na região anelar (Teorema de Laurent).
Ao lado esquerdo confirmamos o comportamento que sugere a divergência da reduzida atinente às potencias pertencentes à expansão de Taylor (ver figura 19). Por outro lado, na figura 19, salientamos o vetor resultante da soma de todas as contribuições dos vetores.
Deste modo, quando movemos o ponto móvel na coroa |z|<1, verificamos que todas suas partes presentes na série de Laurent podem possuir um comportamento ilimitado. O que é um indicativo de sua divergência e que corrobora com nossas informações extraídas do quadro analítico, posto que a expansão inicial converge apenas no anel (Teorema de Laurent).

Por outro lado, quando realizamos uma inspeção do comportamento desta expressão no interior do disco unitário, visualizamos o comportamento que mostramos abaixo. Grosso modo, não podemos expressar a convergência da série de Laurent. O fato de seu comportamento que sugere a divergência é originada da parte (ao lado esquerdo). Enquanto que a outra parcela, do ponto de vista da contribuição de suas reduzidas, apresenta um comprimento arbitrariamente pequeno e não influencia decisivamente no resultado final.
Semelhantemente ao que fizemos há pouco, buscaremos divisar quais parcelas da soma formal de Laurent  é responsável pela não convergência na região fora da coroa anelar. Ora, na figura 20, ao lado esquerdo, depreendemos que as contribuições da parcela envolvendo potencias negativas permanecem pequenas, diante das variações fornecidas ao número complexo móvel. Não obstante, ao lado direito, observamos que o comprimento do vetor resultante da soma de uma reduzida é maior do que o raio. Fato que sugere seu caráter ilimitado (portanto, a divergência).

Figura 20. Visualização do comportamento de uma reduzida da série fora do disco de raio 3 e, portanto, a visualização dinámica do comportamento de divergencia. (Elaboração do autor).

As informações anteriores, condicionadas por intermédio de uma exploração do software, permitem prever, ajustar e conduzir o processo investigativo. Antes, porém, recordamos que a situação problema anterior envolve uma tarefa inicial para os estudantes. E, “sua resposta inicial deve permitir, somente, ao aluno colocar em ação uma estratégia de base, com auxílio de seus conhecimentos anteriores mas, rápidamente, tal estratégia deve se revelar razoavelmente ineficaz, obrigando o estudante a realizar acomodações, para responder ao questionamento proposto” (BROUSSEAU, 1988, p. 15).

5. EXPERIMENTAÇÃO E ANÁLISE A POSTERIORI

 Almouloud (2007, p. 177) adverte que a análise a posteriori não se constitui como uma crônica da classe, todavia, uma análise feita à luz da análise a priori, dos fundamentos teóricos assumido, das hipóteses de trabalho, de investigação e da problemática da pesquisa atual.

Vale recordar que o termo “análise a priori” indica o tratamento de dados que, do ponto de vista temporal, ainda se mostram independentes de uma realidade e ambiente em que transcorrerá a experimentação, bem como a efetiva aplicação de uma sessão estruturada de ensino (com duração de 3 (três) horas. De outro lado, na fase atual, passaremos a discutir e analisar os dados originados a partir das interações entre o grupo de alunos participantes do estudo (alunos 1, 2, 3, 4 e 5), do professor responsável pela condução de uma situação didática envolvendo a noção de série de Laurent e, certamente, o conhecimento matemático em jogo.

Afim do controle do nosso aparato conceitual de investigação, os dados que buscamos evidenciar aquí, se mostram os mais próximos e diretamente relacionados aos nossos objetivos declarados e hipóteses de investigação. Ademais, os esquemas usuais de validaçao estatística (ARTIGUE, 1995, p. 48) não são considerados e muito pouco associados aos dados empíricos de nossa presente experimentação.

Recordamos que "uma análise a priori, devido a sua extensão, se tratando de um trabalho de macro-engenharia, se mostra praticamente incomunicável em toda sua extensão” (ARTIGUE, 1995, p. 49). Dessa forma, os dados apresentados aquí constituem os mais representativos de uma parte de nossa investigação.

Assumimos como pressuposto de que “a constituição do sentido, tal como entendemos, implica numa interação constante dos alunos com situações problemáticas, interações dialéticas (caso o sujeito antecipe, finalize suas ações) [...]” (BROUSSEAU, 1998, p. 117). Assim, de modo preliminar, os alunos manifestam uma ação em situação, na condição em que a situação problema manifeste um sentido e desperta o interesse dos mesmos.

Adotaremos uma apresentação dados coletados ao decorrer das fases dialéticas previstas por Brousseau (1986) e Almouloud (2007). Dessa forma, na situação de ação, registramos uma mediação do professor⁷ que buscou evidenciar o papel da software, no sentido de impulsionar/mobilizar conhecimentos tácitos e intuitivos, com arrimo na vizualização e exploração das construções dinâmicas com o software GeoGebra.

De maneira semelhante ao destacado por Artigue (2008, p. 4-5), em nosso caso, o uso da ED e da TSD, na fase de experimentação, deve proporcionar uma prática controlada na intervenção em sala de aula, de modo que, o pesquisador-professor, em consonância das variáveis micro-didáticas eleitas nas duas fases iniciais da ED, consiga predizer as reações dos aprendizes e interpretar os sentidos produzidos pelo grupo controle.

Ademais, recordamos que num processo de ensino, “o professor coloca em jogo um meio relativamente ao qual o aluno deve interagir. Tal interação é produtora de conhecimentos” (MARGOLINAS, 1995, p. 344). E, ainda, em todas as fases dialéticas previstas pela TSD, registraremos a presença do professor, no sentido do reinvestimento necessário para o progresso da situação-didática (BROUSSEAU, 1986; 1988; 1998).
Dessa forma, no que concerne a atividade desenvolvida pelo aluno 3, registramos sua interpretação dinâmica do processo de convergencia/divergência de série de Laurent, que indicamos por .
De modo sistemático, na figura 16, ao lado esquerdo, o aluno 3 comentou o comportamento da expressão . Na figura 21, o aluno buscou transmitir ao pesquisador a ideia e o comportamento gráfico-geométrico correspondente ao comportamento de divergência. Nesse caso, o sujeito, por meio de uma ação gestual, o descreveu por meio de uma paulatina abertura da sua mão direita, como podemos divisar na figura.

Dessa forma, procedemos uma interpretação conjunta das imagens produzidas nas figuras 21 e 22, posto que, retratam uma idiossincrasia local do aluno 3, correspondentemente ao entendimento da representação produzida pelo software. Reparemos que, quando restrito ao quadro analítico, a atividade conjectural e as habilidades depuradas e exigidas na visualização e compreensão do objeto representado se mostram consideravelmente reduzidas e, mesmo, inexistem, como constatamos na extratégia analítica do seu desenvolvimento.

Figura 21. Na situação de ação o aluno 3 desenvolveu argumentos gestuais e manifestou a produção de conjecturas com origem na visualização da série de Laurent e sua divergência.

Figura 22. Na situação de ação o aluno 3 desenvolveu argumentos gestuais e manifestou a produção de conjecturas com origem na visualização da série de Laurent e sua convergência (seção de experimentação).

Almouloud (2007, p. 38) esclarece que, neste momento, a troca de informações e mensagens entre os aprendentes é imprescindível. Ademais, o resultado do debate a dialética “permite criar um modelo explícito que pode ser formulado com sinais e regras comuns”.

Dessa forma, registramos e acompanhamos uma sistemática de discussão (debate) com os estudantes, envolvendo uma exploração das construções proporcionadas pelo software Geogebra (ver figuras 21, 22 e 23), tendo sido realizado em sala de aula a discussão da teoría formal sobre a série de Laurent.

Em determinados momentos, o professor estimulou aos estudantes um retorno ao modelo formal, sobretudo na fase de validação e, por fim, na fase de institucionalização. Na figura 18, registramos uma ação do aluno 3, que buscou comparar os dados produzidos pelo software GeoGebra com as propriedades extraidas e indicadas pelo modelo formal matemático subjacente. A intenção metodológica estimulada pelo professor atuou no sentído de reforçar o retorno das estratégias anteriores e conjecturas produzidas nas fases de ação e de formulação da TSD.

Acompanhamos um movimento dialético do professor, na medida em que, a tecnología assumiu um papel de ponto de partida e estímulo para a discussão do modelo da série de Laurent. E, logo em seguida, as estratégias dos estudantes foram incentivadas. Alguns argumentos formais foram captados na fase de validação da TSD, em torno do debate do grupo de estudantes, tendo em vista a determinação de criterios de validade (MARGOLINAS, 2014, p. 32).

Figura 23. Na fase dialética de validação, o aluno 3 desenvolveu uma atividade formal buscando discutir os argumentos formais da demonstração do teorema.

E, por fim, como apreciamos na figura 19, um retorno ao modelo computacional, tendo em vista sua agregação ao conhecimento social a ser incorporado ao patrimônio de saberes do grupo de estudantes, em uma instituição de ensino de referência.

Brousseau (1986, p. 342) comenta que “a produção no ensino de conhecimento matemático demanda um esforço de transformação de um conhecimento em saber matemático [...]”, Assim, ele indica que a epistemologia do professor atuará no sentido de não personalização e não contextualização, e que buscará eliminar os traços históricos que determinaram sua aparição.

Ora, a distinção de Brousseau é clara, no sentido de pontuar um conhecimento mobilizado, localizado e particular, pertencente a um grupo de alunos e, gradualmente, receberá status de maior generalidade, pois, enquadrado num corpus teórico formal, cujo viés estruturalista/formalista se mostra evidenciado e distinguido na academia.

Figura 24. Registro de ações e gestos dinâmicos do aluno 1 que buscou significar e descrever um comportamento de convergencia /divergência da série de Laurent.

Todavia, os dados produzidos nas fases dialéticas de ação e formulação possuem elementos marcadamente de natureza particular do grupo, posto que foram originados do debate em sala de aula. Na figura 24, acompanhamos ações gestuais, corporais e dinâmicas do aluno 1, acompanhadas de suas explicações.

Assinalamos que nas argumentações anteriores, uma série de ilações podem ser produzidas pelos estudantes, com um caráter local e provisório. Alguns dos argumentos empregados podem ser formalmente respondidos pelo professor ou, de outra forma, o debate em sala de aula poderá/deverá continuar e o expert conduzi-los a um estádio mais elevado de compreensão/entendimento das ideias matemáticas e propriedadess envolvidas na fase anterior.

Almouloud (2007, p. 40) esclarece que “uma vez construído e validado, o novo conhecimento vai fazer parte do patrimônio da classe embora não tenha ainda o estatuto de saber social”. Desse modo, tendo em vista tornar oficial determinado saber e indicar a relevância de incorporá-lo ao patrimônio cultural da classe, alguns argumentos (formais) e trechos do teorema de Laurent foram rediscutidos pelo grupo (ver figura 25), uma vez que, “as verdades matemáticas são estabelecidas por intermédio dos teoremas” (OTTE, 2002, p. 348).

Figura 25. Na fase dialética de validação, o aluno 4 desenvolveu uma atividade formal buscando discutir os argumentos formais da demonstração do teorema de Laurent com o restante de seus pares.

Para concluir, registramos que a ação do professor acentuou a intenção didática de transformar o conhecimento produzido pelo grupo de alunos em um patrimonio do saber cultural e local, a ser incorporado pelo grupo e que, tal conhecimento, resultante da interação estudantes – professor – saber matemático, não se restringiu ao formalismo standard e recorrentemente acentuado pelos autores de compêndios especializados sobre tal assunto (ALVES, 2014d; 2015). .

Para exemplificar, no excerto abaixo, o aluno 2 manifestou uma entendimento da noção sobre o “anel da incerteza” que se contrapôs ao anel ou região anelar da certeza, em que contamos, nas condições do teorema de Laurent, com a convergência da série.

Aluno 2: hum percebo que nessa região a série converge, pois o vetor resultante esta se concentrando nessa região. Mas como assim? O ponto quando se movimenta em pouco percurso, torna a serie divergente, e isso tudo na mesma região anelar. Há então, meu ponto de vista é que nesse anel, está ocorrendo uma incerteza, pois ora a serie diverge, outro momento converge. Logo classifiquemos como ‘‘anel da incerteza’’.

O trecho anterior envolve a manifestação de uma concepção tácita e intuitiva, produzida a partir da interação e visualização proporcionada pelo software. O cenário de investigação do aluno 2 é apontado nas figuras 26 e 27. Ademais, assumimos posição concorde com Margolinas (2004, p. 24), quando comenta que “o professor é responsável sobre o ponto de vista do conhecimento que circula em classe”. Ora, constatamos o esforço didático do professor participante do estudo, no sentido de sensibilizar no grupo, um ponto de vista que, recorrentemente, aliou/agregou aos modelos formais, um pensamento heurístico e intuitivo. Tal fenômeno se enquadra no pensamento de Margolinas (2004).

Figura 26. Debate entre o grupo de alunos participantes envolvendo o entendimento do “anel da incerteza” no contexto da convergência/divergencia de série de Laurent.

Assim, registramos que, a partir das interações do grupo de alunos, estimuladas pelo professor, relações modificadas, por intermédio do uso da tecnología, foram observadas a partir da aparição de concepções, cuja natureza não se restringiu ao quadro analítico usualmente explorado numa mediação que desconsidera a tecnología atual (ALVES, 2016). Sua natureza pode ser enquadrada no que Robert (1983) denomina de concepções dinámicas sobre às noções de sequências e séries.

Figura 27. Debate entre o grupo de alunos participantes envolvendo o entendimento do “anel da incerteza” no contexto da convergência/divergencia de série de Laurent.

Por fim, realizamos uma discussão geral com os estudantes sobre toda a teoría discutida e aprendida ao decurso da disciplina. Nesse sentido, o aluno 1, se manifestou como segue:

Aluno 1: Na minha opiníão, a variável complexa é mais abstrata do que os quadro Cálculos, pois, nos últimos, temos aplicações bem mais imediatas […]

Quando questionado, o aluno 2 recordou que:

Aluno 2: No Cálculos não tivemos que observar a parte real e imaginária. Além disso, os números complexos é um conjunto semi-ordenado e o plano complexo é bastante diferente do plano IRXIR.

Cabe registrar, que o fator apontado pelo aluno 2 se mostra recorrente dentro da teoría, como por exemplo, no caso de séries de números complexos, que indicamos simbolicamente por .
E, por fim, quando consultado, o aluno 4, se manifestou seu entendimento quanto às modificações no contexto da TCC:

Aluno 3: Sim, na variável complexa generalizamos os conceitos de sequências e séries […] Os conceitos de derivada e integral que, além de generalizados, temos propriedades muito diferentes, como as equações de Cauchy-Riemann […]

No sentido de descrever as mudanças percebidas pelo mesmo. O aluno 4 forneceu na figura abaixo, o sentido de retratar o comportamento de uma função na variável complexa. Depreendemos que o seu pensamento envolveu o entendimento/distinção de que o gráfico final da função f(z) se mostra como um subconjunto do IR⁴, como assim esclarece Needham (2000).

Figura 28. O aluno 4 buscou fornecer um desenho explicativo para a noção de funções contínuas no caso da variável complexa.

Em nosso caso, recordamos que “o término da Engenharia Didática designa um conjunto de sequências de classes concebidas, organizadas e articuladas no tempo, de maneira coerente por um professor-engenheiro, com o fim de realizar um projeto de aprendizagem para um população determinada de alunos” (DOUADY, 1995, p. 62). Assim, no próximo segmento, passaremos ao processo de validação de nosso aparato de investigação.

6. DISCUSSÃO E VALIDAÇÃO INTERNA

 Laborde (1997, p. 105) evidencia um elemento imprescindível ao decurso de uma ED, quando analisa o relato de uma pesquisa que pode ser entendida como uma ação intencional em que:
O autor fornece ao leitor uma narração comentada do desenvolvimento, estruturado pelo tempo (cronologicamente) ou pelos temas escolhidos de análise. Em ambos os casos, o leitor se apropria das “lunetas” do autor, com exceção de passagens transcritas pelo sujeito da crônica, para um expediente de análise crítica.

No final do excerto anterior, sublinhamos o carater de imprescindibilidade, da tarefa de deixar a cargo do leitor, a emissão de um juizo (ou parecer) sobre as passagens transcritas ipsis litteris ao decurso do manuscrito. Sublinhamos ainda, no bojo das preocupações de Laborde que, com as respectivas produções dos estudantes são previstas, num estudo de ED, uma validação interna da sequência didática, bem como uma validação externa. A primeira envolve “uma descrição genérica da classe ou das condutas e tipos de produção majoritárias na classe, estudo de sua evolução e verificação de sua adequação no que concerne ao esperado dos estudantes” (LABORDE, 1997, p. 105).

Laborde (1997, p. 105) explica que a validação externa envolve uma comparação das produções dos estudantes antes ou ao longo da sequência, ou ainda após experimentação em sala, o que pode ocorrer por meio de entrevistas individuais ou em grupo, bem como por meio de questionários. E, também, por meio da comparação de produções externas, vinculando outros alunos não submetidos à mesma sequência estruturada de ensino.

Dessa forma, assumimos aquí apenas um processo de validação interna, tendo como referência preliminar, os objetivos (itens a e b) declarados nas seções anteriores, bem como nossas hipoteses (itens c, d e e) da investigação e, por fim, as produções individuais e coletivas dos alunos submetidos ao processo de experimentação.

Isso posto, declaramos que, no conjunto dos dados empíricos coletados nas análises preliminares e experimentação, encontramos indicios de concepções dos estudantes, mobilizadas em situação, que apresentavam vinculo com um conjunto de concepções e ideias peculiares ao Cálculo em uma variável real e ao Cálculo em varias variáveis. Tal fato, proporcionou que comprovássemos a readaptaçao/reutilização de concepções locais e ideias provisórias, o que passa a atuar, segundo a perspectiva do TCC, como elementos de transição facilitadores da evolução do pensamento.

Ademais, em consonância com o nosso segundo questionamento declarado na etapa de análise preliminar, registramos varios elementos de natureza tácita e de ordem intuitiva, vinculados/determinados pela atividade de visualização e busca do entendimento das noções de convergência e divergência da soma formal abordada na situação didática, a partir da “soma visual” das informações apropriadas com o software GeoGebra.
Com efeito, a manifestação de ações gestuais (e movimentos corporais), como assim explica Tall (2009), traz num bojo de significados e percepções locais, a mobilização de conhecimentos, cuja natureza extrapolou os limites lógico-formais em Matemática Pura e revelam indicios do desenvolvimento e evolução do significado do pensamento matemático (TALL, 2007, p. 13).

No que concerne ao efetivo alcance de nossas hipóteses de trabalho, cabe observar que nosso conjunto de três hipóteses investigativas foram cunhadas a partir dos elementos mais proeminentes, identificados nas análises preliminares. Desse modo, não lidamos com hipóteses distanciadas de noso quadro de referência investigativa, nem muito menos, com elementos que exigissem extenso periodo (de tempo) de experimentação (em sala de aula) e acompanhamento dos grupo dos alunos 1, 2, 3, 4 e 5.

O caráter insofismável da proposta de uma ED, reside na possibilidade de geraçao de conhecimemtos didáticos-metodológicos acerca de determinado assunto matemático particular, a ponto de que, os resultados apontados na etapa de validação da ED, admitam replicação e modelização controlada, bem como, o possivel aperfeiçoamento do modelo concebido em outras situações e realidades de ensino acadêmico.
Dessa forma, Artigue (1984a) alerta para o fato de que determinados aspectos relacionados com a replicabilidade assumem papel importante nos estudos envolvendo o uso da ED.  Com efeito, a autora menciona a existencia de modelos implícitos e explícitos que carecem de atenção e acompanhamento por parte do professor-pesquisador.

Ora, Artigue (1984b) comenta que no transcurso de experimentações repetidas, podemos encontrar as seguintes características: os mesmos procedimentos devem parecer (ao menos os que não sao marginais) hierarquias compraráveis; a historia da classe pode ser descrita com um número reduzido de órbitas (trajetórias); as regularidades observadas em nível dos procedimentos deve ser em essencia o resultado de regularidades individuais. E, essas não devem depender de ações repetidas de deslocalização e desbloqueio que realiza o professor; as perturbações leves que não deixam de se manifestar numa classe ou em outra não devem tender a amplificar-se numa outra.

Dessa forma, diante dos elementos apontados por Artigue (1984b), cabem ainda algumas constatações e indicações finais. De modo preliminar, quando comparamos os dados produzidos pelos estudantes na fase de análise preliminar e experimentação, constatamos a regularidade, no que concerne às estratégias identifícáveis recorrentes, do apelo não marginal da capacidade de visualização (e apreensão perceptual das propriedades de convergência/divergência), tendo em vista o entendimento de propriedades e a configuração computacional para a noção de convergência ou divergência para a série de Laurent proposta na atividade em sala com o um único grupo controle.

Ademais, os dados obtidos no conjunto das análises cognitivas dos estudantes (análises preliminares), apontaram que: a visualização e exploração dos softwares CAS Maple e GeoGebra proporcionou a manifestação de elementos de transição (ALVES, 2011), no que concerne aos conceitos de limite e diferenciabilidade, na medida em que os estudantes, por intermédio dos questionamentos do investigador, explicitaram modelos cognitivos tácitos, de natureza idiossincrásica, revelados no âmbito da Teoria das funções em uma variável real, ainda no contexto do estudo das funções na variável complexa.

CONCLUSÕES E FUTURAS INVESTIGAÇÕES

Para concluir, não podemos desconsiderar as advertências de Artigue (1995, p. 49) quando explica que “na maioria dos textos publicados concernentes às engenharias, a confrontação das análises, a priori e a posteriori, permite a aparição de distorções”. E, pouco mais adiante, a autora aponta a ocorrência da formulação de hipóteses demasiadamente globais, “que colocam em jogo processos de aprendizagem demorados”, fato que impossibilita uma sintonia pretendida com a amplitude da ED proposta.

Em nosso caso, quando nos debruçamos nas três hipóteses aqui formuladas (final da terceira seção), notamos que parte delas possuem uma caraterística de adequação e não envolvem processos demorados de aprendizagem, segundo preconiza Artigue (1995, p. 49). Entretanto, outras envolvem e exigem a proposição de outras investigações que ultrapassam os limites de nossa discussão, não obstante, com as características aqui discutidas, nosso projeto de engenharia deverá levar em consideração “os registros dos estudos de caso, nos quais, a validação é essencialmente interna” (HADDAD, 2012, p. 19).

Vale recordar um momento de relativo antagonismo a ser enfrentado pelo expert. De fato, Margolinas (1995, p. 342) recorda que as ações envolvendo a “devolução”, designam “as ações do professor que visam encarregar os estudantes com responsabilidade de elaboração de estratégias de resolução para situações dadas”. Por outro lado, a mediação do professor investigado se mostrou afetada pelo uso da tecnologia (ARTIGUE, 2003; 2009; 2012; 2013), de modo que, em cada fase correspondente da TSD (ação, formulação, validação), que antecedem o momento de institucionalização, deparamos a ocorrência de uma ação de devolução, consubstanciada por uma intenção de ensino que reformula as variáveis em jogo e acentua a responsabilidade do aluno no retorno da tarefa. Tal fenômeno é preconizado, por exemplo, por Margolinas (2004).

Ou seja, em cada fase dialética, ocorreu o reinvestimento da tarefa do estudante, por parte do professor, como garantidor que a ação do grupo não ficasse restrita ao quadro analítico e que adotasse, de modo efetivo, a visualização como elemento primário, facilitador e imprescindível em cada etapa de investigação (fato que auxilia para a apreciação de nossa questão de investigação). Ademais, afim de não provocarmos pertubações no funcionamento da classe, como previsto na tese de Artigue (1984b, p. 83), deixamos ao cargo do professor investigado, predominantemente, na condução da tarefa proposta em sala de aula.

Para concluir, recordamos que Brousseau forneceu a indicação de elementos essenciais à práxis do professor, ao mencionar que é necessário “poder comparar, não apenas os resultados, mas também as condições nas quais eles foram obtidos e de modo que tais condições sejam reprodutíveis.”. (BROUSSEAU, 1986, p. 3). Outrossim, o pesquisador esclarece/indica a possibilidade de “reprodução” ou replicação no ensino de Matemática, quando acrescenta ainda que

Esta reprodutibilidade implica uma descrição, não ingênua, de todas as condições observadas, mas seletivas e que repousam sobre uma escolha pertinentes às variações possíveis de efeitos reconhecidos. A reprodutibilidade repousa, então, na compreensão dos fenômenos fundamentais, isto é do tecido de relações atestadas, constituindo a teoria e permitindo se escolher as condições de ensino, de explicar seus efeitos e de prevê-los. (BROUSSEAU, 1986, p. 3).

Ora, as reflexões de Brousseau permitem extrair implicações e ensinamentos imediatos para o conhecimento produzido aquí, a partir das interações acompanhanadas entre a tríade estudantes – professor – conhecimento matemático, para o caso da série de Laurent. Outrossim, desde que, seu enquadramento teórico, consequencia de sua natureza multiifacetada, se evidencia complexo, a análise das concepções dos estudantes (tanto no bojo das análises cognitivas, bem como nas tarefas instadas aos sujeitos a decorrer da tarefa) indicou a ocorrência de concepções que se relacionam com elementos de transição, bem como outras vinculadas a determinados elementos de ruptura (que precisam ser evitadas ou suavizados).

No bojo dessa constatação, declaramos a verificação de nossas hipóteses de trabalho, tendo em vista que:

• Apresentamos dados empíricos que acentuam um entendimento dinâmico do processo de convergência/divergencia da noção de série de Laurent (questão de investigação (a), e a hipótese (c)), tendo em vista o arrimo do software.
• Apresentamos dados que apontam, em nosso curso intervalo de experimentação, concepções atinentes ao Cálculo que foram readaptadas/ressignificadas ao contexto da Teoria das funções na variável complexa (questão de investigação (b), e hipótese (d)) (ver figura 23);
• Apresentamos dados que apontam roteiros para uma mediação capaz de impulsionar maior ênfase nos elementos de transição (com maior papel para a visualização e emprego de metáforas⁸), e maior concientização da propagação, no contexto da Teoria das funções na variável complexa, de concepções mal adaptadas ou inadequadas (ver figura 24);
• Segundo Otte (2006, p. 36), em Matemática, “fatos são explicados por intermédio de provas”. Mas, com o auxílio da tecnología atual, diversos eventos foram explicados/significados por intermédio de outras rotinas de ensino e, assim, o percurso reducionista apontado por Otte (2006, p. 36) pode ser assumido para nâo ser o único para a mediação da noção de série de Laurent.

De modo sistemático, indicamos elementos que podem atuar como elementos de ruptura, na medida em que, nossa mediação desconsidere e/ou negligencie aprendizagens anteriores dos estudantes. Certamente que, a tecnología possibilita a superação do quadro hegemônico das representações analíticas que registramos nos compêndios consultados (ver figura 29), não obstante, tal ilação ainda exige futuras investigações aprofundadas com tal interesse.

Figura 29. Quadro resumido das concepções envolvendo um elemento de transição correspondentes ao caso da noção de diferenciabilidade de funções na variável complexa (ALVES, 2015).

Por fim, de modo inconteste, deparamos um quadro de excassez e um quadro de conhecimentos científicos, no que concerne ao ensino e a aprendizagem da Teoria das funções na variável complexa, ainda de modo deficitário no Brasil. Ora, do ponto de vista institucional, sabemos do extenso lapso temporal de contato dos estudantes, desde o início dos cálculos até a variável complexa. Assim, se evidencia a relevância de um acompanhamento atencioso e próximo da evolução das aprendizagens no referido periodo de estudos compulsórios.

De modo semelhante ao relato dos estudo tendo em vista o contato com outras teorias matemáticas abstratas (ÁVILA, 2002; ARSLAN, 2005; BLOCH, 2006), perspectivamos a persistência de uma abordagem, por parte dos autores de livro do assunto, que tendem a tornar hegemônico um trato eminetemente formalista e estruturalista (BALACHEFF & GAUDIN, 2002; CHOQUET, 1963; ROGALSKI, 1990) o que, na prática, pode precipitar os momentos de uma mediação centrada nas fases dialéticas de validação e institucionalização dos conhecimentos matemáticos.

Finalmente, a presente proposta de uma ED detém o potencial de aplicação empírica em sala de aula, sua predição, reprodução e replicação, tendo em vista o extenso repertório de elementos abordados e sistematizados até aqui, com o escopo de proporcionar o acúmulo de conhecimentos didáticos e metodológicos sobre o ensino de Análise Complexa, com atenção particular ao objeto série de Laurent.

Não desconsiderando, portanto, o quadro de transição que vislumbramos na figura 30 e, um extenso repertório de entraves que não podem prescindir de uma atenção por parte dos estudiosos, uma vez que, como distinguimos em nosso intróito, alguns assuntos (ou tópicos particulares) específicos em Matemática têem permanecido numa situação de oblívio total.

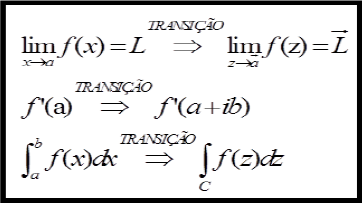
Figura 30. Quadro sistemático de transição simbólica da Teoria das funções na variável real para a Teoria das funçõesx na variável complexa (elaboração dos autores).

Notas al pie

¹Introduzido por G. Barchelard em 1938, no campo da Didática da Matemática, a ideia original é adaptada por Brousseau, em 1976. Assim, o mesmo descreve as noções de obstáculos no ensino de Matemática de ordem ontogenética, de ordem didática e, por fim, epistemológica.

²Pierre Alphonse Laurent (1813 – 1854) empregou algumas ideias fundamentais de A. Cauchy, para a descrição do teorema que leva seu nome (BOTTAZZINNI & GRAY, 20144, p. 171).

³Em sua tese, Brousseau (1986, p. 297) lembra que a acepção moderna de ensino, busca exigir do professor a provocação de mudanças e alterações desejáveis no estudante. Ademais, diante das tarefas, o aluno deve aceitar a demanda da tarefa colocada pelo professor (devolução). Nesse contexto, uma situação didática envolve um processo investigativo, com a presença e coordenação do professor. Por outro lado, numa situação em que identificamos a ausência de uma ação pedagógica intencional, é nomeada por situação a-didática.

⁴Segundo Margolinas (1995, p. 342) envolvem ações do professor visando encarregar o aluno da responsabilidade da elaboração das estratégias de resolução para uma situação dada.

⁵Na teoria das funções na variável complexa, função meromorfa é caracterizada pelo quociente de duas funções polinomiais, portanto, uma quantidade finita de pólos, nesse caso, nos pontos -1 e -3.

⁶Logo de início, o enunciado da situação transfere/indica a responsabilidade de resolução da tarefa para o estudante.

⁷Margolinas (2009, p. 16) recorda que “no caso das engenharias longas, o pesquisador participa da colocação de tarefas dos estudantes, e o pesquisador assume uma parte do papel do professor [...]”.

⁸Polya (1967, p. 172) assinala o papel decisivo do uso de metáforas no ensino ao declarar que “Em todo caso, existe uma vasta família de metáforas que possuem duas coisas em comum: elas são sempre concernentes à atividade do homem que consiste na resolução de problemas e todas sugerem a mesma representação geométrica”.

BIBLIOGRAFÍA

1. Almouloud, Ag Saddo. (2007). Fundamentos da Didática da Matemática São Paulo: Editora UFPR.         [ Links ]

2. Alves, F. R. V. (2011). Aplicações da Sequência Fedathi na promoção das categorias intuitivas do Cálculo a Várias Variáveis (tese de doutorado). Fortaleza: Universidade Federal do Ceará – UFC, 339f.

3. Alves, F. R. V. (2012). INSIGHT: descrição e possibilidades de seu uso no ensino do Cálculo. Revista VYDIA Educação, 32(2), 149 – 148.

4. Alves, F. R. V. (2013). Viewing the roots of polynomial functions in complex variable: the use of GeoGebra and the CAS Maple. Acta Didactica Naposcencia. 6(4).         [ Links ]

5. Alves, F. R. V. (1014a). Engenharia Didática para o Teorema da Função Implícita: análise preliminares e a priori. Revista Brasileira de Ensino de Ciência e Tecnologia, 7(3), 148 – 168.

6. Alves, F. R. V. (2014b). Técnica Computacional para o Ensino de Matemática Computational Technique for Teaching Mathematics –  . EM TEIA: Revista de Educação Matemática e Tecnológica Iberoamericana, 5(2), 1 – 9.

7. Alves, F. R. V. (2014c). Aplicações no Ensino de Variável Complexa: uma discussão sobre o uso dos softwares Geogebra e CAS Maple. Revista do Instituto GeoGebra Internacional de São Paulo, 3(2).         [ Links ] 

8. Alves, F. R. V. (2014d). Visualizing the behavior of infinite series and complex power series with the GeoGebra. GeoGebra International Journal of Romania. 4(1), 1 – 10.

9. Alves, F. R. V. (2015). Visualização de Teoremas em Análise Complexa: exemplos no contexto da Transição Complexa do Cálculo TCC. Revista Sinergia - IFSP, 16(1), 65 – 76.

10. Alves, F. R. V. (2016). Engenharia Didática: implicações para a pesquisa no ensino no ámbito da Análise Complexa – AC. Ciência & Natura, 38(1), 567 – 575.

11. Alves, F. R. V. & Borges Neto, H. (2011). Transição interna do cálculo em uma variável para o cálculo a várias variáveis: uma análise de livros. Educação Matemática Pesquisa, 13(3), 598 – 625.

12. Alves, F. R. V; Borges Neto, H. & Alves Dias, M. (2012). Implicações e aplicações da Teoria das Representações Semióticas no ensino do Cálculo. Jornal Internacional de Estudos em Educação Matemática, 5(1), 54 – 84.

13. Arslan, S. (2005). L´approche qualitative des équations differentielles en classe terminal´s: est-elle viable? Quels sont les enjeux et les consequences? (these en didactiques de mathématiques). Grenoble: Université Josephe Fourier.         [ Links ]

14. Artigue, M. (1984a). Modélisation et reproductibilité en didactique des Mathématiques. Le Cahiers Blancs. 8 (1), 1-39.         [ Links ]

15. Artigue, M. (1984b). Contribuition à l´étude de la reproductibilité des situations didactiques – divers travaux de mathématiques et des didactiques des mathématiques. (Thése d´état). Paris: Université Paris VII. 264f.

16. Artigue, M. (1989). Épistèmologie et Didactiques. Le Cahiers Rouges. 3 (1), 1-28.         [ Links ]

17. Artigue, M. (2003). Qué se Puede Aprender de la Investigación Educativa en el Nível Universitário? Boletín de La Asociatíon Venezolana, 10(2), 117-134.         [ Links ]

18. Artigue, M. (2009). Didactical design in Mathematics Education. Carl Winslow (eds). NORMA08, Copenhaguen: Sense Publishers, Denmark, 7 – 16.

19. Artigue, M. (2012). L´éducation mathématiques comme champ de recherché et champ de pratique: resultats et défis. EM TEIA: Revista de Educação Matemática e Tecnológica Iberoamericana, 3(3), 1 – 18.

20. Artigue, M. (2013). L´impact curriculaire des Technologies sur L´Éducation Mathématiques. EM TEIA: Revista de Educação Matemática e Tecnológica Iberoamericana, 4(1), 1 – 15.

21. Ávila, G. (2002). O ensino de Cálculo e da Análise. Matemática Universitária, 33(1), 83-94.         [ Links ]

22. Balacheff, N. & Gaudin, N. (2002). Students conceptions: an introduction to a formal characterization. Les Cahier du Laboratoire Leibniz. 65(1), December, 1 – 25. 

23. Bolon, J. (1996). Comment les enseignants tirent-ils parti de recherche faites en Didactiques des mathématiques? Le cas de l´enseignement des décimaux a la chárnière écolle-collegue (Thése de doctorat). Paris: Université Paris VII, 319f.         [ Links ]

24. Bloch, I. (2006). Quelques apports de la Theorie des Situations a la didactique des Mathematiques dans l´enseignement secondaire et superieure. (Habilitation de recherché). Aquitaine: IUFM.         [ Links ]

25. Boschet, F. & Robert, A. (1983). Ingénierie Didactiques sur les suítes numeriques après le baccallauréat. Publications Mathématiques et Informatiques des Rennes, 2(2), 1 – 26.

26. Braden, B. (1985). Picturing Functions of a Complex Variable. The College Mathematics Journal, 16(1), 63-72.         [ Links ]

27. Bridoux, S. (2012). Enseignement des premieres notions de topologie à L´Université. (thése de doctorat). Paris: Paris VII.         [ Links ]

28. Bradley, R. E. & Sandifer, C. E. (2009). Cauchy´s cours d´Analyse: an annoted translation, New York: Springer.         [ Links ]

29. Brousseau, G. (1988). Les différents rôles du maître. Bulletin de l’A.M.Q. Montréal., 1988, 14-24.

30. Brousseau, G. (1989). Les obstacles épistémologies, problêmes et ingéniere didactiques. In: Brousseau, G. (1989). Théorie des Situations Didactiques, 115 – 160.

31. Brousseau, G. (1986a). Fondements et methodes de la Didactiques des Mathématiques. Recherche en Didactiques des Mathématiques. 7(2), 33 – 115.

32. Brousseau, G. (1986b). Théorisation des phénomènes d´enseignement des Mathématiques (these de doctorat). Bourdeaux: Université Bourdeaux I, 905f.         [ Links ] 

33. Brousseau, G. (1994). Perspective pour la didactique des mathématiques: vingt ans de didactique des mathématiques en France. Paris: La Pensée Sauvage, 5 – 66.

34. Brousseau, G. (1998). Les obstacles épistémologiques, problèmes et ingénierie didactique. G. Brousseau, (org.) (1998). Théorie des situations didactiques. Grenoble La Pensée Sauvage, 115 – 160.

35. Bottazzini, U. (1986). The Higher Calculus: a history of real and complex analysis from Euler to Weierstrass. New York: Springer-Verlag.         [ Links ]

36. Bottazzini, U. & Gray, J. (2013). Hidden Harmony – geometric fantasies: the rise of complex functions, New York: Springer-Verlag.

37. Bourbaki, N. (2006). Élèment d´histoires de mathématiques. New York: Springer-Verlag.         [ Links ]

38. Brum, W. P. & Schuhmacher, E. (2013). A Engenharia Didática como campo metodológico para o planejamento de aula de matemática: análise de uma experiência didática para o estudo de geometria esférica. Jornal Internacional de Estudos em Educação Matematica, 6(2), 60 – 84.

39. Cartin, H. (1995). Théorie elementaires des fonctions analytiques d´une ou plusieurs variables. Paris: Hermann editeurs des scinces et des arts.         [ Links ]

40. Cecília, S. F. & Bernadez, N. C. (2008). Introdução às funções de uma variável complexa. Rio de Janeiro: SBM.         [ Links ]

41. Chavez, E. (2014). Teaching Complex Numbers in High School. (Dissertation in Natural Sciences). Louisiana: Louisiana State University. 66f.         [ Links ]

42. Chevallard. Y. (1991). La Transposition Didactique. Paris: La Pensée Sauvage Édition.         [ Links ]

43. Choquet, G. (1963). What is Modern Mathematics? England: Educational Explorers Limited.         [ Links ]

44. Conway, J. B. (1978). Functions of One Complex Variable. Second Edition. New York: Springer Verlag.         [ Links ]

45. Debnath, L. (2015). A brief history of the most remarkable numbers e, i and γ in mathematical sciences with applications. International Journal of Mathematical Education in Science and Technology. 46(6), March, 853 – 878.

46. Douady, R. (1983). Rapport enseignement apprentissage: dialectique outil-objet, jeux de cadre. Le Cahiers Blancs 3(1), 1 – 23.

47. Douady, A. (1984). De la didactiques des Mathématiques à l´heure actuelle. Le Cahiers Blancs. 6 (1), 1-22.         [ Links ]

48. Douady, A. (1993). L´Ingénierie Didactiques. Le Cahiers Rouges. 19 (1), 1-52.         [ Links ]

49. Douady, R. (1995a). La ingeniería didáctica y la evolución de su relación con el conocimiento. Gomez, P. (org.) Ingenieria Didactica en Educación Matemática. Bogotá: Grupo Editorial Iberoamericano, 1 – 7.

50. Douady, R. (1995b). Nacimiento y desarrollo de la didáctica de las matemáticas en Francia: rol de los IREM.         [ Links ]

51. Douady, R. (2008). Géométrie, graphiques, fonctions au collège. Revista Electrónica de investigación en educación e ciencias. 1, 1-7.         [ Links ]

52. Flanigan, F. J. (1972). Complex Variables: harmonic and analytic functions. California: San Diego State University.         [ Links ]

53. Gray, J. (2015). The Real and the Complex: A History of Analysis in the 19th Century, New York: Springer.         [ Links ]

54. Krantz, S. G. (1990). Complex Analysis: the geometric view. New York: American Mathematical Society.         [ Links ]

55. Krantz, S. G. (2009). A guide to real variables. Washington: Washington University.         [ Links ] 

56. Krantz, S. G. (2008). A guide to complex variables. Washington: Washington University.         [ Links ] 

57. Krantz, S. G. (2007). Complex Variables: a phisical approach with applications and Matlab tutorials. London: Chapman and Hall/CRC.         [ Links ]

58. Ghedamsi, I. (2009). Enseignement du d´ebut de l’analyse réelle à l’entrée `a l’université: Articuler contrôles pragmatique et formel dans des situations à dimension a-didactique. (These de doctorat), Bourdeux: Université Bourdeux II.

59. Gong, S. (2001). Concise Complex Analysis. New Jersey: World Scientific.         [ Links ]

60. Gluchoff, A. D. (1993). Complex Power Series-A Vector Field Visualization. Mathematics Magazine, 66(3), 189 – 191, 1993.

61. Grenier, D. & Legrand, M. (1986), Une séquence d´enseignement sur l´intégrale en DEUG, a première année. Le Cahiers Blancs. 22 (1), 1-90.         [ Links ]

62. Haddad, Sassi. (2012). L´enseignement de L´intégrale en classe terminale de l´enseignement tunisien. (These de doctorat). Paris: Université Paris VII.         [ Links ]

63. Hairer, E. & Warner, G. (2008). Analysis by Its History, New York: Springer.         [ Links ]

64. Henriques, A. (2006). L´enseignement et l´apprentissage des integrales multiples: analyse didactique integrant l´usage du logiciel Maple (Thèse de Doctorat), Grenoble: Université Joseph Fourier, IMAG, 320p.         [ Links ]

65. Lima, Maria. V. M. Integrais generalizadas e Integrais Dependentes de Parâmetros: um contributo da Engenharia Didática. (Dissertação de mestrado em Ensino de Ciências e Matemática). Fortaleza: Mestrado em Ensino de Ciências e Matemática PGECM – IFCE. 2017. 188f.

66. Lins Neto, A. (1996). Funções de uma variável complexa. Rio de Janeiro: SBM.         [ Links ]

67. Laborde, C. (1997). Affronter la complexité des situations didátiques d´apprentissage des mathématiques en classe: défis et tentatives. DIDASKALIA, 10(1), 97 – 112.

68. Margolinas, C. (1995). D´evolution et institutionnalisation: deux aspects antagonistes du rôle du maître. Didactique des disciplines scientifiques et formation des enseignants, Paris: Maison Édition, 342-347.         [ Links ]

69. Margolinas, C. (2004). Points de vues de l´élève et du professeur : essai de développement de la théorie des situations didactiques (Habilitation de recherche). Provence: Université de Provence. 160f.         [ Links ]

70. Margolinas, C. & Drijvers, P. (2015). Didactical Engineering in France ; an insider’s and an outsider’s view on its foundations, its practice and its impact. ZDM Mathematics Education. 47(6), 893 – 903.

71. Marinho, Monique. R. M. Categorias intuitivas no ensino do teorema de Laurent: um contributo da Engenharia Didática Clássica. (Dissertação de mestrado em Ensino de Ciências e Matemática). Fortaleza: Mestrado em Ensino de Ciências e Matemática PGECM – IFCE. 2017. 193f.

72. Marques, E. M. R. & Souza, A. R. (2016). A complementary approach to study the real and imaginary roots of a quadratic function. Geogebra International Journal of Romania, 5(1), 1 – 11.

73. Medvedev, F. (1991). Scenes from the History of Real Functions. Boston: Birkäuser-Verlag.         [ Links ]

74. Orton, A. (1983a). Students´ understanding of Differentation. In: Educational Mathematical Studies. Netherlands: Reidel Publishing Company, 235-250.         [ Links ]

75. Orton, A. (1983b). Student´s understanding of integration. Educational Studies in Mathematics, 1-18.         [ Links ]

76. Otte, M. (2002). Proof-Analysis and the Development of Geometrical Thought. (Eds.) Hitt, F. (2002). Representation and Mathematical visualization. Work group of PME, 337 – 368.

77. Otte, M. (2006). Proof and Explanation from a Semiotical Point of View. Revista Latinoamericana de Investigación en Matemática Educativa. Número especial, 23 – 45.

78. Perez, Alicia. M. (2012). Visualizing Complex Solutions of Polynomials. (Master of Arts). Austin: University of Texas.         [ Links ]

79. Polya, G. (1967). Le découverte des Mathématiques. Paris: DUNOD Editeurs.         [ Links ]

80. Robert, A. (1982). Acquisition de la notion de convergence des suites numériques dans l´enseignement supérieur. (Thése de doctorat). Paris: Université Paris VII,         [ Links ]

81. Robert, A. (1983). Ingénierie didactiques sur les suites après le baccalaureat. Le Cahiers Blancs. 4 (1), 1-25.         [ Links ]

82. Robert, A. (1986). Didactique dans l´enseignement supérieur: une démarche. Le Cahiers Blancs. 28 (1), 1-41.         [ Links ]

83. Robert, A. (1988). Une introduction a la Didátiques de Mathématiques. Le Cahiers Blancs. 50 (1), 1-66.         [ Links ]

84. Robinet, J. (1984). Histoire de la convergence uniforme. Le Cahiers Blancs. 9 (1), 1-20.         [ Links ]

85. Robinet, J. (1986). Les réels: Quels modèles en ont les élêves? Le Cahiers Blancs. 21 (1), 1-48.         [ Links ]

86. Robinet, J. (1992). Le pouquoi et le comment d´une ingénierie (la convergence uniforme). Le Cahiers Rouges. 12 (1), 1-26.         [ Links ]

87. Robinet, J. (1983). De L´ingenierie Didactiques. Les Cahiers Blancs. 1(1), 1 – 11.

88. Rogalski, M. (1990). Enseigner des Méthodes des Mathematiques. Recherche em Didactiques des Mathématiques, nº 1, 1 – 10.

89. Rudin, Walter. (1986). Real and Complex Analysis. New York: McGrall-Hill Book Company.         [ Links ]

90. Santos. L. Claumir. (1998). Funções complexas de uma variável complexa: uma abordagem via software Mathematica. (Dissertação de mestrado). Campinas: Universidade de campinas.         [ Links ]

91. Schwerdtfeger, H. (1979). Geometry of Complex Numbers. New York: Dover Publications.         [ Links ]

92. Shokranian, S. (2011). Uma introdução à Variável Complexa, Sao Paulo: Editora Moderna.         [ Links ]

93. Soares, M. G. (2014). Cálculo em uma Variável Complexa. Rio de Janeiro: SBM.         [ Links ]

94. Tall, D. (1991). Advanced Mathematical Thinking. London: Klumer Publishers.         [ Links ]

95. Tall, D. (2007). Embodiment, Symbolism, Argumentation and Proof. Proceedings on Reading, Wrinting and Argumentation. National Changhua University, Taiwan. 1 – 13.

96. TALL, D. Dynamic Mathematics ant the blending of knowledge structures in the Calculus. ZDM Mathematics Education. v. 41. 481 – 492. 2009.

97. TALL, D. Perceptions, operations and proof in undergraduate mathematics. The Morgan Journal. v. 1, nº 1, 19 – 27. 2011.

98. Tirosh, D. & Almog, N. (1989). Conceptual adjustments in Progressing from Real and Complex Numbers. 13 th. Proceedings of Psychology of Mathematics Education - PME, 221 – 227.

99. Tomasiunas, R. (2012). Visualizing complex integration with the GeoGebra. GeoGebra International of Romania, 2(2), 77 – 84. 

100. Vergnaud, G. (1981). Quelques orientation théoriques eet methodoloiques des recherches française en Didactiques des Mathématiques. Recherche en Didactiques des Mathématiques. 2(2), 215 – 231.

101. Wegert, Elias & Semmler, Günter. (2011). Phase Plots of complex functions: a journey in illustration. AMS, 58(6). 768-780.         [ Links ]

102. Wegert, E. (2010). Phase Plots of Complex Functions: a Journey in Illustration. Notices in Americal Mathematical Society, July, 1 – 18.

103. Wegert, E. (2012). Visual Complex Functions: an introduction with the phase portrait. New York: Birkhäuser.         [ Links ]

104. Wegert, E. & Semmler, G. (2011). Phase Plots of complex functions: a journey in illustration. AMS, 58(6). 768-780.         [ Links ]

105. Winslow, C. (2003). Semiotic and discursive variables and CAS-Based Didactical Engineering. Educational Studies in Mathematics, 52, 271 – 288.