ARTICULOS ORIGINALES

Fomentando la indagación en estudiantes de secundaria mediante la resolución de problemas, una estrategia para articular matemática y ciencias: Un estudio de caso

 

Miguel Alejandro Rodriguez Jara

mrodriguez@upla.cl

Facultad de Educación y Centro de Estudios Avanzados de la Universidad de Playa Ancha

 

---

Resumen

El presente artículo reporta el desempeño que mostraron estudiantes de secundaria en condición de vulnerabilidad al abordar tres problemas. Uno de ellos se propuso en el marco de tres talleres de matemática y ciencias y, los otros dos, en un cuestionario que incluyó problemas de la prueba PISA. Metodológicamente interesaba indagar en los argumentos, procedimientos y la influencia del conocimiento científico que estuvo a la base para abordar dichos problemas, los que su vez hicieron referencia a un contexto común para los participantes. Los hallazgos muestran una desarticulación entre la información que provee cada problema y lo que realizan efectivamente los estudiantes, junto con la aparición de procedimientos auténticos cuando el enunciado del problema no hace referencia a una forma determinada de proceder.

Palabras clave: Indagación; Resolución de problemas; Estadística implicativa

Encouraging inquiry in high school students through problem solving, a strategy for articulating math and science: A case study

Abstract

This article reports on the performance of vulnerable high school students whilst addressing three issues. One of these was proposed in the framework of three math and science workshops, and the other two in a questionnaire that included problems from the PISA test. Methodologically, we were interested in investigating the arguments, procedures and the influence of scientific knowledge that was at the base while addressing these problems, which in turn referred to a common context for the participants. The findings show a disarticulation between the information provided by each problem and what the students actually do, along with the appearance of authentic procedures when the statement of the problem does not refer to a particular way of proceeding.

Keywords: Inquiry; Problem solving; Implicative statistics.

Favoriser l'enquête chez les élèves du secondaire par la résolution de problèmes, une stratégie pour articuler les mathématiques et les sciences: une étude de cas

Résumé

Cet article rend compte des performances des élèves du secondaire vulnérables lorsqu'ils ont abordé trois problèmes. L'un d'eux a été proposé dans le cadre de trois ateliers de mathématiques et de sciences et les deux autres dans un questionnaire qui comprenait des problèmes du test PISA. Sur le plan méthodologique, il était intéressant d'étudier les arguments, les procédures et l'influence des connaissances scientifiques qui étaient à la base pour résoudre ces problèmes, qui à leur tour faisaient référence à un contexte commun pour les participants. Les résultats montrent une désarticulation entre les informations fournies par chaque problème et ce que les élèves font réellement, ainsi que l'apparition de procédures authentiques lorsque l'énoncé du problème ne fait pas référence à une certaine manière de procéder.

Mots clés: Enquête; Résolution de problèmes; Statistiques implicatives.

---

 

1. INTRODUCCIÓN

En Chile desde el año 2009 se viene aplicando un ajuste curricular a los distintos subsectores del aprendizaje, particularmente en matemática y ciencias (Ministerio de Educación, MINEDUC, 2009). En el año 2017 el MINEDUC convocó a distintos actores del mundo escolar y académico para que evaluaran una propuesta de innovación curricular dirigida a estudiantes de entre 16 a 18 años. El foco de dicha iniciativa fue desarrollar distintos tipos de pensamiento y promover el trabajo interdisciplinar, todo ello en correlato con la formación ciudadana (MINEDUC, 2017). En el año 2018, por disposición gubernamental se sugirió incorporar nuevos contenidos al currículo escolar con problemáticas asociadas al cambio climático —desertificación, falta de lluvia y aumento de las temperaturas, entre otras— (MINEDUC, 2017). Para los próximos años el MINEDUC se ha comprometido a que todos los estudiantes chilenos tomen conciencia de su rol con el medio ambiente natural y social, en atención a los distintos escenarios que se viven a nivel mundial como son el cambio ambiental global, la migración y las pandemias, ente otros.

Lo anterior viene a subsanar dos aspectos que son relevantes para el desarrollo de un país, el aumento en el interés de los jóvenes por estudiar ciencia y tecnología y, a su vez, que exista una comprensión real de la importancia que aprender ciencias a nivel escolar para así poder vincular temas como la salud personal y pública, el cuidado del medio ambiente y la conservación de la energía desde edades tempranas. Por lo tanto, interesa avanzar hacia metodologías que propicien mayores y mejores procesos comprensivos de la ciencia en el sistema escolar (Minner et al., 2010).

En el marco de lo que hemos planteado, cabe preguntarse cómo se están gestionando y promoviendo —desde una perspectiva transdiciplinar— los aprendizajes de los estudiantes al interior de las aulas, considerando cada uno de los requerimientos de la política educativa y los desafíos que la modernidad nos demanda como sociedad.

2. PROBLEMÁTICA Y ANTECEDENTES

2.1.- Articular matemática y ciencias

A nivel internacional existen instancias donde se evalúa las competencias que han adquirido los escolares tanto en ciencias como en matemática (Pajares, 2005). Los bajos resultados que obtienen los participantes de algunos países refleja las dificultades que enfrentan sus sistemas educativos para desarrollar habilidades de pensamiento y promover aprendizajes contextualizados, fenómeno del cual no están exentos los países de América Latina y el Caribe (Valverde y Näslund-Hadley, 2010; Pajares, 2005).

A nivel escolar se mantiene esa tendencia de enseñar algoritmos y técnicas sin un adecuado sustento que refuerce el conocimiento que subyace a dichos procedimientos y, menos aún, que dicho conocimiento se aborde considerando contextos más específicos como los que afectan a un ciudadano en su desenvolvimiento diario (Fernández, 2005). A modo de ejemplo, cabe indicar que el excesivo énfasis en la enseñanza de algoritmos en la asignatura de matemática instala fenómenos como La edad del capitán, el que ha sido documentado en diferentes países. Fenómeno que se manifiesta con la estrategia de identificar datos numéricos para realizar operaciones aritméticas, sin que la respuesta tenga sentido en el contexto del mismo (D’Amore, 2011). Lo anterior incide negativamente en el desarrollo de habilidades de pensamiento, en el sentido de lo que se plantea en las pruebas PISA y TIMSS (OCDE, 2016).

Respecto de la enseñanza de las ciencias en espacios educativos europeos es posible advertir un cambio de perspectiva en su enseñanza, tanto en primaria como secundaria (Osborne y Dillon, 2008; Rocard et al., 2007; Campanario y Moya, 1999). En particular, se está desplazando el enfoque academicista —aquel cuya premisa es que todos los estudiantes son potenciales científicos— por uno constructivista —donde el estudiante es quien construye su propio aprendizaje—, siendo el profesor un mediador y facilitador de las tareas de aprendizaje.

En García-Carmona, Criado y Cañal (2014) se presenta un análisis crítico de la educación científica en España para primaria. Los autores plantean que los estudiantes deben desarrollar actividades que les permita utilizar sus conocimientos previos y, a la vez, vivir la experiencia de hacer ciencia. En Lupión y Prieto (2014), se reporta una propuesta para secundaria que incluye problemas en contexto, es decir, situaciones que afectan al ciudadano en su desenvolvimiento cotidiano. En dicha instancia se evidencia una mejor calidad de los aprendizajes, más allá de lo que los programas de estudio proponían.

En relación a experiencias masivas y exitosas se puede mencionar un programa que nace en México, el cual logra externalizarse a países como Perú, Bolivia y Argentina, por nombrar algunos. El foco de dicha iniciativa es la enseñanza y aprendizaje de la matemática y las ciencias. En dicho programa se ha privilegiado el uso de metodologías de corte constructivista, poniendo de relieve el método científico (Bosch, 2014). Cabe mencionar que las distintas actividades son diseñadas por especialistas en la materia y, en la ejecución de los talleres, se involucra a los profesores y profesoras de aula que atienden a los estudiantes que participan de dicha instancia. La ciencia en tu escuela ha mostrado tener buenos resultados en su implementación, articulando de manera efectiva el trabajo de ambas disciplinas (Campanario y Moya, 1999).

Esta idea de integrar ciencia y matemática no tan solo contribuye a los aprendizajes de los estudiantes —en el sentido de activar en ellos conocimientos previos mediante problemas en contexto que estimulen un trabajo colaborativo—. Además provee de una instancia para que los profesores y profesoras de matemática y ciencias planifiquen en conjunto actividades integradas, permitiéndoles validar su conocimiento desde una mirada inter o transdiciplinar (Treacy y O’Donoghue, 2014).

En el año 2003 se implementó en distintas escuelas de Chile el programa Enseñanza de las Ciencias Basado en la Indagación(ECBI). El propósito de dicha iniciativa es que los niños y niñas desarrollen habilidades, actitudes y conceptos asociados con las ciencias. Para ello, el ECBI promueve la comprensión en ciencias utilizando problemas que hacen referencia a un contexto a través de la interacción con el mundo real (Abell, Smith y Volkmann, 2006).

La implementación de ECBI en los establecimientos educacionales ha mejorado la visión de la enseñanza y aprendizaje de las ciencias tanto en profesores como estudiantes. Ello ha impactado favorablemente en el clima del aula, fundamentalmente en las relaciones colaborativas, la tolerancia y el respeto. A lo anterior se suma al aumento de la motivación por aprender ciencias y, en particular, ha propiciado la inclusión de estudiantes con dificultades de aprendizaje (Devés y López, 2012).

2.2.-Resolución de problemas como un articulador

La Resolución de Problemas (RP) en matemática cobra fuerza desde un punto de vista educativo con los planteamientos de Polya (1990), quien propone cuatro fases para abordar un problema, a saber: (a) comprender el problema, (b) idear un plan, (c) ejecutar dicho plan y (d) mirada en retrospectiva. Cabe indicar que dichas fases no son necesariamente secuenciales, es decir, se puede ir de una fase a otra indistintamente durante el proceso de resolución. En la dinámica de dichas fases, destaca el uso de estrategias como un elemento articulador de éstas (Polya, 1990).

Es importante hacer notar que la RP no es una tarea exclusiva del subsector de matemática, ya que hay propuestas en ciencias que están inspiradas en el modelo de Polya. Éstas definen sus propias fases y también ponen de relieve el uso de estrategias (Pozo, Pérez y Domínguez, 1994). Cabe indicar que, independiente del área donde se aborde la RP, se debe tener en cuenta que una estrategia hace referencia a un patrón de decisiones al utilizar información para el logro de determinados objetivos (Bruner, 1990).

Desde un punto de vista educativo, los trabajos de Bruner son pioneros en la conceptualización de lo que hoy entendemos por estrategia (Bruner, 1990). Para Olave (2005) una estrategia es una acción dirigida de manera consciente y anticipada cuya finalidad es asegurar el logro de objetivos. En otras palabras, es vista como un conjunto de actividades y procedimientos hacia un fin. Por otro lado, Escoriza (2003) plantea que una estrategia es un conocimiento procedimental que direcciona una acción. Dichos conocimientos son espontáneos, controlados y dirigidos hacia un objetivo. Dados los matices que dicho concepto ha ido tomando, actualmente se la considera como una herramienta de análisis en la RP,

De las investigaciones que se enfocan en la interpretación de estrategias en RP podemos mencionar el trabajo de Rodríguez y Parraguez (2014), quienes analizan el desempeño de estudiantes chilenos de secundaria en una olimpiada de RP en matemática. Los autores hacen uso del concepto imagen y concepto definición de Vinner (1991) para identificar los elementos cognitivos que intervienen en el proceso de resolución. Como principal hallazgo se menciona que el concepto imagen y concepto definición no siempre dialogan favorablemente cuando se aborda un problema, imposibilitando que un estudiante pueda hacer un uso efectivo de una estrategia o un procedimiento matemático al intentar dar respuesta a un problema (Rodríguez y Parraguez, 2014).

Por otro lado, en Rodríguez, Gregori, Riveros y Aceituno, (2018) analizan las estrategias y procedimientos matemáticos que utilizaron estudiantes chilenos de 12 a 14 años en un programa de talento académico. Valiéndose de la estadística implicativa los investigadores clasificaron jerárquicamente los procedimientos y obtuvieron relaciones de implicación entre éstos. Como principal resultado, mencionan que el uso de determinadas estrategias no es exclusivo de los estudiantes talentosos, la diferencia radica más bien en la manera como dichos recursos son administrados por este tipo de estudiantes durante el proceso de resolución.

2.3.- Preguntas de investigación

Considerando los antecedentes del apartado anterior y el deseo de contribuir a la articulación de los subsectores de matemática y ciencias, mediante el uso de problemas, nos propusimos abordar las siguientes preguntas de investigación.

¿Cuál es el rol de los problemas contextualizados para promover la articulación entre matemática y ciencias?

¿Qué estrategias, procedimientos matemáticos y argumentos despliegan estudiantes de entre 14 a 16 años al abordar problemas de la Prueba PISA que hacen referencia a un contexto?

3. MARCO CONCEPTUAL

A continuación presentamos nuestro marco conceptual que nos provee de los elementos teóricos para diseñar talleres que estimulen la articulación entre matemática y ciencias mediante la activación del método científico. A su vez, nos provee de elementos cognitivos para evaluar la incidencia de un concepto en la resolución de problemas.

3.1. El método indagatorio

El método indagatorio, desde un punto de vista educativo, es visto como una estrategia de enseñanza aprendizaje, cuya piedra angular es la indagación, la cual es entendida por el National Research Council (NCR), como un conjunto de actividades cuyo objetivo es permitir a los estudiantes comprender fenómenos naturales y, cuyas explicaciones se sustentan en los hallazgos que se obtienen a partir de la experimentación y la exploración (Bosch, 2014; Harlen, 2013; NCR, 1996). Las fases que sigue el método indagatorio, como se aprecia en la Figura 1, son las siguientes: (1) Focalización, momento en el cual los estudiantes describen y clarifican sus ideas; (2) Exploración, instancia en la cual los estudiantes trabajan con materiales concretos o información específica de manera conjunta; (3) Reflexión, período en el cual los estudiantes organizan, comparten, analizan y defienden sus datos, para finalmente pasar a la (4) Aplicación, oportunidad donde el estudiante es capaz de utilizar lo aprendido en nuevos contextos y situaciones de la vida real (Dyasi, 2015).

Figura 1. Diagrama sobre las fases del método indagatorio

3.2.-El concepto imagen y concepto definición

Tall y Vinner (1981) definen los constructos concepto imagen y concepto definición para explicar el nivel de comprensión que un aprendiz tiene de un concepto matemático. Dichos constructos configuran un sistema cognitivo que permite modelar la adquisición de un concepto y su respectivo uso cuando se aborda un problema. El concepto imagen corresponde a las representaciones y mecanismos mentales que permiten evocar un concepto y dar cuenta de su funcionamiento en un contexto específico. En cambio, el concepto definición son aquellas invariantes que caracterizan al objeto matemático como tal (Tall y Vinner, 1981).

En la enseñanza de la matemática ha prevalecido la idea de que los estudiantes deben comenzar el aprendizaje matemático mediante el concepto definición y, a partir de esa imagen conceptual deben avanzar hacia un desarrollo cognitivo mediante la ejercitación y la realización de actividades que le den una carga de significado a dicho concepto, como se expresa en el diagrama de la Figura 2 (Vinner, 1991:71).

Figura 2: Desarrollo cognitivo de la definición formal de un concepto.

Una vez adquirido el concepto, como se sugiere en la Figura 3, ambas imágenes conceptuales coexisten en la mente del sujeto, pudiendo haber contradicciones (Tall y Vinner, 1981). Dichas contradicciones se manifiestan cuando el individuo intenta resolver algún problema matemático. A modo de ejemplo, es posible que un aprendiz determine que un cuadrado no es un rectángulo, prevaleciendo en ese caso el concepto imagen por sobre el concepto definición. En cambio un estudiante puede afirmar que el número 0,999… es menor que 1, aunque el concepto definición lo lleve a establecer lo contrario.

Figura 3: Desarrollo cognitivo de la definición formal de un concepto.

En términos generales, es deseable que el concepto imagen y concepto definición interactúen favorablemente para producir una respuesta adecuada en una determinada tarea o problema, como se ilustra en el diagrama de la Figura 4, aunque ello no siempre es posible (Vinner, 1991: 72).

Figura 4: Interacción entre concepto definición y concepto imagen.

En la práctica el sistema cognitivo al que hemos hecho referencia puede manifestarse de distintas maneras, de acuerdo a la interacción que se dé entre las dos imágenes conceptuales que conforman dicho sistema. En la Figura 5 se muestra la posibilidad de que un aprendiz dé respuesta a un problema siguiendo una deducción puramente formal, al hacer referencia sólo a la imagen conceptual del conocimiento matemático que está en juego (Vinner, 1991: 172).

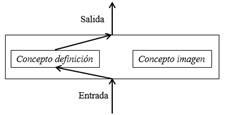
Figura 5: Deducción puramente formal en RP.

En cambio como se ilustra en la Figura 6, un estudiante puede evocar, mediante una representación, algún aspecto de la imagen conceptual que le permite dar una respuesta a un problema que trata de resolver (Vinner, 1991:172).

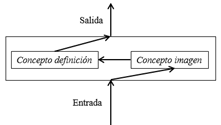
Figura 6: Deducción siguiendo un pensamiento intuitivo.

Por último habrá problemas donde se manifieste una respuesta intuitiva sin hacer referencia al concepto definición, como se expresa en la Figura 7. Tales problemas son poco habituales en la enseñanza, como es el caso de los problemas no rutinarios. Cuando se les propone este tipo de problemas a los estudiantes, éstos los suelen considerar alejados de los objetivos tradicionales de un curso de matemática. Por lo tanto, “no parece haber nada que tienda a cambiar los hábitos comunes de enseñanza que son, en principio, inadecuados para contextos técnicos” (Vinner, 1991: 73).

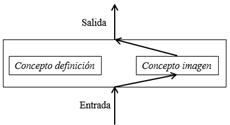
Figura 7: Respuesta intuitiva a un problema.

Para cerrar este apartado, hacemos notar que los constructos concepto imagen y concepto definición vienen a complementar las distintas fases del método indagatorio, ya que en cada una de ellas un estudiante puede recurrir a un concepto ya adquirido para dilucidar algún aspecto asociado a la problemática que está abordando.

4. METOLOGÍA

La investigación fue de carácter mixto, ya que utilizamos un estudio de caso y un método estadístico con un enfoque interpretativo para analizar los datos. La elección de un estudio de caso obedece fundamentalmente a la necesidad de precisar evidencias de un comportamiento específico que se observa en un contexto determinado (Rodríguez, Gil y García 1999).

Participaron de la investigación 47 estudiantes de un establecimiento educacional con un alto índice de vulnerabilidad, el cual está subvencionado por el estado chileno y se ubica en la región de Valparaíso, Chile. Las edades de los estudiantes fluctuaron entre los 14 y 16 años, los que fueron individualizados con una letra E y un número correlativo (E1 a E47).

4.1.- Sobre los talleres y el método estadístico

Para llevar a cabo nuestro estudio implementamos tres talleres de matemática y ciencias relacionados con las algas. Recurso que está presente en casi toda la costa de Chile, constituyendo un elemento contextual de fácil reconocimiento por los estudiantes. Además resulta ser un recurso muy versátil, ya que sus extractos son utilizados tanto en la cosmética como en la alimentación y, por sobre todo, es un buen bio-indicador del estado ambiental de las aguas del mar.

Los talleres fueron planificados vía una metodología de codiseño entre los investigadores y la profesora de biología a cargo del grupo de estudiantes. Ello favoreció la validación de la propuesta a partir de elementos curriculares emanados por el MINEDUC.

Tabla 1.
Sobre los distintos aspectos del programa de matemática y ciencias naturales

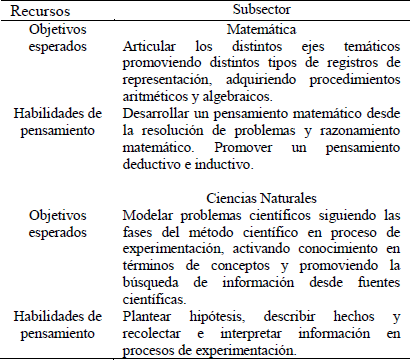
A continuación, una descripción general de cada taller.

Taller 1: Determinar las características biológicas y ambientales de tres especies de algas. Paralelamente se dio a conocer una técnica de secado mediante el uso de paños secos sobre una superficie de papel y el respectivo prensado, a partir de un ejemplar fresco. Paralelo a ello, la bióloga marina y la profesora de ciencias, procuraron que los estudiantes describieran las características observables de las algas y, luego, una descripción más detallada de su morfología, mediante el uso de un microscopio y textos científicos.  

Taller 2: Cuantificar el contorno de un alga representada en una hoja de papel, emulando a aquellas que se secaron mediante un prensado en el taller 1. Los materiales utilizados fuero un lápiz, una regla y un trozo de hilo. Sumado a ello tuvieron que determinar la desviación media y promedio de las distintas medidas que obtuvo cada grupo. El propósito de ello fue comparar dichos indicadores para establecer la pertinencia de las mediciones individuales y grupales. 

Taller 3: Cuantificar el peso de un alga fresca y luego seca tras el secado en estufa a 60 º C por 48 horas. Para ello, cada grupo pesó el alga fresca y luego el alga seca. Con ese dato pudieron determinar finalmente el porcentaje de agua presente cada alga.

Una vez concluidos los tres talleres, la profesora de biología aplicó a sus estudiantes un cuestionario con dos problemas de la prueba PISA. Posteriormente se analizaron las estrategias, procedimientos matemáticos y argumentos que los estudiantes desplegaron al resolverlos. El propósito del cuestionario no fue correlacionar el desempeño de los estudiantes en ambas instancias, sino más bien analizar el conocimiento elemental, los distintos procedimientos y argumentos que se utilizaron en ambos problemas.

Para analizar los datos del cuestionario, se recurrió a la estadística implicativa (en adelante ASI [Analyse Statistique Implicative] por su sigla en francés) (Gras, Susuki, Guillet y Spagnolo, 2008; Orús, Zamora y Gregori, 2009), y el uso del software CHIC (Coherive Hierarchical Implicative Classification) versión 6.0 (Couturier, 2008). Una de las características de ASI es que combina dos tipos de análisis estadísticos multivariantes: un análisis de conglomerados (cluster analysis), para descubrir grupos homogéneos de variables, y un análisis de reglas de asociación (association rules), para explorar relaciones no-simétricas que permiten establecer relaciones de causa y efecto entre las variables analizadas. La otra característica es que ASI basa sus cálculos en la probabilidad de encontrar una coincidencia entre dos variables (o respectivamente un contraejemplo a una regla) para medir la similitud entre esas dos variables (o la intensidad de una regla que relaciona las dos variables) (Gras et al., 2008; Orús et al., 2009).

El árbol jerárquico de similaridad (dendrograma) se forma de la manera habitual, esto es, comienza con cada variable formando una única clase y agrupando, a cada paso, las dos clases más similares sucesivamente, hasta obtener una única clase que agrupa todas las variables, siendo la interpretación de los grupos hallados el aspecto más importante. Adicionalmente, el árbol de similaridad destaca algunas clases como significativas, por la relación preponderante de los índices de similaridad entre las variables que se hallan reunidas en dicha clase (Orús, 2009). Cuando se forma cada clase de variables similares, se puede calcular un índice de contribución de cada informante a la formación de esa clase. Con esos índices, se destaca el grupo de los informantes que más la ha manifestado. Una inspección detallada de ellos, permite ahondar aún más en la descripción de la clase, así como indagar el posible efecto de otras variables (asociadas a las categorías de análisis) en la formación de dicha clase de variables similares.

El grafo implicativo es la representación gráfica de las reglas de asociación entre parejas de variables. La fuerza de las reglas de asociación se suele medir mediante un índice llamado confianza, esto es, el porcentaje de individuos que cumple la regla de entre los que la podrían cumplir (por verificar el antecedente de la regla), en el sentido clásico de una implicación. Este indicador es útil para predecir si un individuo presenta el rasgo del consecuente, una vez se sabe que presenta el rasgo del antecedente. No obstante, cuando el rasgo consecuente es muy abundante en los informantes, no es evidente que su presencia se deba a un efecto causado por el antecedente de la regla. Así, el grafo implicativo representa las reglas cuyas intensidades superan un umbral (elegido por los investigadores, y que suele ser del 90%, 95% o 99%), y se deben interpretar como asociaciones implicativas estadísticamente significativas. A partir de estas asociaciones inesperadas, se deben distinguir relaciones de causa y efecto que se justifican a la luz de las categorías del análisis a priori, y otras relaciones que no se podrían aprovechar si no hay una justificación adecuada por parte del investigador.

4.2. Análisis a priori de la actividad del taller 2 y los problemas de la prueba PISA

A continuación se presenta el análisis a priori de los tres problemas que seleccionamos para mostrar los resultados de este estudio. Comenzamos con el problema del taller 2, haciendo referencia al modelo cognitivo de nuestro marco conceptual dado los aspectos conceptuales que implica medir una figura cuyo contorno es irregular.

Problema
Obtengan la media del contorno del alga que se representa por el dibujo de la derecha (ver hoja anexa). Una vez obtengan individualmente la medida del contorno, mediante el trozo de hilo y la regla, determinen el promedio y la desviación media del grupo. Luego comparen sus resultados con los de los otros grupos.

Respuesta esperada

En primer lugar se espera que cada estudiante segmente la figura a medida que utilicen el trozo de hilo para luego sumar todas las medias que realice e indicar la longitud del contorno de la figura. Se espera que haya dificultades para hacer coincidir el trozo de hilo con el contorno de la figura. Además, el uso de la fórmula de la desviación media requiere estar familiarizado con el valor absoluto. En la Figura 8 se propone la respuesta ideal considerando la interacción entre ambas imágenes conceptuales asociadas al concepto de medir.

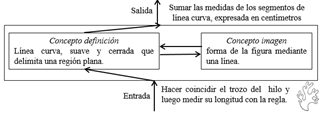
Figura 8. Respuesta ideal según modelo cognitivo.

A continuación se presenta el análisis a priori de las dos preguntas de la prueba PISA (OCDE, 2016), el que incluye una respuesta esperada y las respectivas categorías de análisis socializadas en el codiseño.

Pregunta 1
Para la realización de un concierto de rock se reservó para el público asistente un terreno rectangular con unas dimensiones de 100 m por 50 m. Se vendieron todas las entradas y el terreno se llenó de fans, todos de pie. ¿Cuál de las siguientes cifras constituye la mejor estimación del número total de asistentes al concierto? Encierra en un círculo la alternativa que creas correcta. Justifica tu respuesta.

A. 2 000       B.  5 000    C.  20 000    D.  50 000     E. 100 000

Respuesta esperada
Un estudiante puede asumir que la longitud promedio del pie de una persona chilena puede ser 25cm. El área de la zona circular donde se pueda ubicar una persona es de unos 2.000cm2. Como el área de la superficie donde se realiza el concierto es de 50.000.000 cm2, el número de personas que pueden estar de pie se puede estimar mediante 50.000.000 ¸ 2.000 = 25.000. Por lo C es tanto la alternativa.

En la Tabla 2 presentamos las estrategias (e), procedimientos matemáticos (p) y argumentos (a), que validamos con la profesora de biología, quien además participó activamente en ambas instancias.

Tabla 2.
Categorías de análisis pregunta 1

Pregunta 2
Contextualizando:
A continuación, se muestra una foto de las estatuas llamadas Cariátides, las que fueron erigidas en la Acrópolis de Atenas hace más de 2.500 años. Las estatuas están hechas de un tipo de roca llamada mármol. El mármol está compuesto de carbonato de calcio. En 1980, las estatuas originales fueron trasladadas al interior del museo de la Acrópolis y fueron sustituidas por copias. Las estatuas originales estaban siendo corroídas por la lluvia ácida.

Pregunta 2.1
La lluvia normal es ligeramente ácida porque ha absorbido algo del dióxido de carbono del aire. La lluvia ácida es más ácida que la lluvia normal porque además ha absorbido gases como óxidos de azufre y óxidos de nitrógeno. ¿De dónde vienen los óxidos de azufre y los óxidos de nitrógeno que hay en el aire?

Pregunta 2.2
Una astilla de mármol tiene una masa de 2,0 gramos antes de ser sumergida en vinagre durante toda una noche. Al día siguiente, la astilla se extrae y se seca. ¿Cuál será la masa de la astilla de mármol seca?

A. Menos de 2,0 gramos       B. Exactamente, 2,0 gramos 
C. Entre 2,0 y 2,4 gramos     D. Más de 2,4 gramos

Respuesta esperada
Para la pregunta 2.1 se pueden considerar diferentes fuentes de contaminación: Actividad industrial que conlleve el uso de combustibles fósiles como el petróleo y/o el carbón o los gases de volcanes. Para la pregunta 2.2 se considera que el vinagre es un ácido y como el mármol está compuesto por carbonato de calcio va a reaccionar con el vinagre, luego el peso de la astilla debería ser menor a dos gramos.

En la Tabla 3 presentamos las posibles estrategias y argumentos que se espera en la respuesta esperada.

Tabla 3.
Categorías de análisis pregunta 2

5.-RESULTADOS

A continuación, en una primera etapa, presentamos un análisis de algunas respuestas al problema del taller 2 recurriendo a los constructos concepto imagen y concepto definición. Luego, en una segunda etapa, nos enfocamos en algunas respuestas a los problemas del cuestionario recurriendo a los recursos que el software CHIC nos provee.
 
5.1.-Análisis a las respuestas del problema taller 2

En la figura 9 se aprecia la respuesta de E18 quién utilizó el procedimiento que se esperaba para medir el contorno del alga, haciendo uso del trozo de hilo y la regla.

Figura 9. Respuesta de E18 al medir el contorno del alga.

1) “Con el hilo recorrer toda la línea negra o la orilla del alga”

2) Luego medir con una regla en centímetros el largo del hilo y el resultado será el contorno del alga. X=58cm (app)
Perímetro o contorno del alga es 48cm.

En atención lo que indica E18 se puede decir que sigue un pensamiento intuitivo pues se enfoca en los atributos de la figura para recurrir luego al concepto de medida y así dar respuesta al problema, como se grafica en la Figura 10.

Figura 10. Interpretación de la respuesta de E8 según el modelo cognitivo.

En cambio, como se aprecia en la Figura 11, la estrategia que utilizó E46 consistió en trazar un polígono para luego obtener su perímetro. Llama la atención que no haya indicado que su respuesta era una aproximación del contorno de la figura, independiente de la medida que haya obtenido. Por otro lado, E46 calcula sin dificultad la desviación media de los datos de su grupo pero no repara en el valor extremo al calcular el promedio. Tampoco interpreta el resultado de la desviación media en función de las medidas de los integrantes de su grupo.

Figura 11. Respuesta de E46 a la actividad de medir.

“Para sacar el contorno de esta figura, medí todos los extremos (los que más sobresalen de la figura) en escala de cm y luego sumé los resultados de cada extremo y llegué al resultado de 24,5 cm de contorno.

En la respuesta de E46, como se describe en la Figura 12, interactúa el concepto definición y concepto imagen de perímetro.

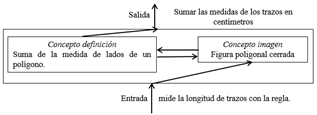
Figura 12. Respuesta de E46 donde interactúan ambas imágenes conceptuales de perímetro.

En las respuestas de E15, como se aprecia en la Figura 13, se observan dos procedimientos. El primero fue seguir trazos con el pedazo de hilo y luego determinar el perímetro del polígono que logró generar. El segundo procedimiento fue hacer coincidir el trozo de hilo con el contorno de la figura. Además llama la atención la necesidad de determinar el largo y ancho de la figura, probablemente con la idea de aplicar alguna fórmula de algún polígono conocido. Finalmente declara dos medidas sin justificar el por qué se inclina por una de ellas.

Bueno el largo es 9,3 L
El ancho 6,4 A
El contorno es 55 C
“Primero el contorno lo medí dos veces con hilo alrededor así con ángulos medí 27 y con el hilo de a poco me dio 55”

Figura 13. Respuesta de E15 al medir el contorno del alga.

En la respuesta de E15, como se grafica en la Figura 14, prevalece una deducción puramente formal desde la noción de contorno y medida, haciendo uso del trozo de hilo y la regla.

Figura 14. Respuesta de E15 haciendo referencia al concepto definición de contorno y perímetro.

A la luz de las respuestas de estos tres estudiantes se observa la necesidad de asociar un polígono a la figura y, por otro lado, utilizar el trozo de hilo con la regla para estimar la medida de su contorno, como se esperaba. Con lo que declara E18 y E15 se puede ver la tensión que se da entre las noción de contorno y perímetro.

En la Tabla 7, presentamos los diferentes procedimientos que fueron utilizados por los estudiantes para dar respuesta al problema.

Tabla 7.
Procedimientos que utilizaron los estudiantes para determinar el contorno de un alga

5.2.-Análisis de las respuestas a los problemas del cuestionario

En la Figura 15 presentamos el árbol de similaridad que obtuvimos con CHIC mediante una matriz que se configuró al tabular la presencia o ausencia de cada una de las categorías previstas en el análisis a priori y las respuestas de cada uno de los estudiantes al cuestionario, asignando un 1 ante la presencia de una categoría y un 0 en la ausencia de ésta.

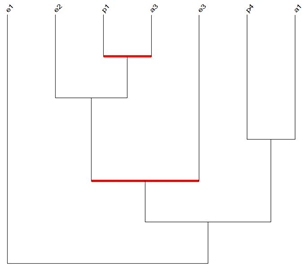
Figura 15. Árbol de similaridad para la pregunta 1

Destacan en dicho árbol dos clases significativas, la clase (p1, a3) en el nivel 1 arrojó un índice de similaridad de 1 y la clase ((e2 (p1 a3)) e3) en el nivel 4 un índice de similaridad de 0,9761. El alto índice de similaridad de ambas clases se explica por el hecho que la mayoría de los estudiantes asoció el área de la región con el número de asistentes al evento. Cabe mencionar que los estudiantes E32 y E34 contribuyeron para que ambas clases significativas se configuraran, siendo E34 quien muestra una respuesta adecuada al problema. 

En la respuesta de E34, como se aprecia en la Figura 16, éste asume explícitamente un número de personas por metro cuadrado. Ello evidencia que hay una interacción entre el concepto imagen y concepto definición área en una región rectangular. Es decir, E34 entiende que el metro cuadrado es una unidad de medida y a la vez un espacio que le permite ubicar un número de personas para así proyectar el número de asistentes al concierto de manera proporcional.

Figura 16. Respuesta de E32 al problema 1

“50m ´ 100m = 5.000m2     
5.000 ´ 4 = 20.000”
“5000 por el área del terreno multiplicado por 4 porque en 1 m2 caben 4 personas aprox.”.

Por otro lado, E32 razona de manera similar a E34 describiendo el procedimiento que utilizó pero no indicando la cantidad de personas que asumió por metro cuadrado, como se puede apreciar en la Figura 17.

Figura 17. Respuesta de E32 al problema 1

“Saqué la cantidad aproximado de personas que puede haber en un m2 y luego multipliqué con el área del terreno”.

En la Figura 18 se aprecia la respuesta de E15, quien no logra abordar adecuadamente el problema. Según él, no identifica una operación aritmética que le dé sentido a lo que se le pide. Para E15, el concepto imagen área de una región rectangular no interactúa con el concepto definición. Es decir, no logra establecer que el metro cuadrado, la unidad para expresar el área de la cancha de fútbol, es a su vez una porción de terreno que le permite distribuir un número adecuado de personas y, con ello, estimar el número de asistentes en función del área total.

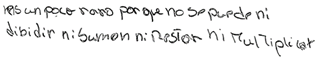
Figura 18. Respuesta de E15 al problema 1

“Es un poco raro porque no se puede ni dividir ni sumar ni restar ni multiplicar”

En cambio, en la respuesta de E16 como se observa en la Figura 19, éste asume que el área de la cancha de fútbol corresponde al número de personas que pueden asistir al concierto. Con la respuesta de este estudiante, se puede ver que prevalece el concepto imagen de área por sobre el concepto definición. Es decir, aplica el procedimiento multiplicar el largo por el ancho sin analizar el sentido que dicha respuesta tiene en el contexto del mismo.

Figura 19. Respuesta de E16 al problema 1

En la Figura 20, se aprecia el grafo implicativo donde destaca sólo la implicación a1 Þ p4, con una intensidad de implicación del 99%. La fuerza de implicación se explica en parte, pues la mayoría de los estudiantes asoció el área del terreno con el número de asistentes al evento. Hubo una tendencia a utilizar los datos que proporcionaba el problema para aplicar el procedimiento estándar para el cálculo del área de una región rectangular. Lo anterior, constituye una evidencia de que los estudiantes no comprendieron el problema. Cabe mencionar que ninguno de ellos mencionó experiencias personales relacionadas con la asistencia a eventos musicales, como referirse al número de personas que desde esas vivencias puede evocar el número de personas en un metro cuadrado, como un punto de referencia.

Figura 20. Grafo implicativo asociado a la pregunta 1

En la Figura 21 se presenta el árbol de similaridad asociado al problema 2. En él se aprecian dos clases significativas de las cuales (e4, a6) arrojó un índice de similaridad de 0,86, la otra clase no fue considerada para el análisis pues obtuvo un índice muy bajo. Los estudiantes E15, E18, E28, E42 y E45 contribuyeron para que la primera clase se configurara, donde las categorías e4 y a6 son representativas del desempeño que tuvieron los estudiantes en el problema. En general, los estudiantes no logran relacionar la información que se hace en la contextualización y los encabezados del mismo. En particular no logran extrapolar el efecto que tiene la lluvia ácida en las estatuas de mármol a la situación de la astilla y el vinagre mediante el pH, para argumentar de esa manera que el peso de la astilla disminuye.

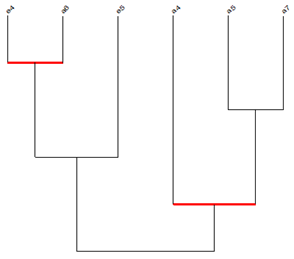
Figura 21. Árbol de similaridad asociado al problema 2

En la respuesta de E15, como se aprecia en la Figura 22, éste recurre a información primaria del encabezado, sin hacer referencia a algún proceso natural o artificial que contribuya a la formación de lluvia ácida. Para el segundo apartado, si bien elige la alternativa correcta no relaciona el vinagre con el de la lluvia ácida mediante el pH.

Figura 22. Respuesta de E15 al problema 2

“Porque el dióxido de carbono del ambiente reacciona con el vapor de agua”.
“Pesa menos de 20 porque el vinagre ataca el mármol. Acetato de calcio soluble”.

En la respuesta de E18, como se aprecia en la Figura 23, se hace mención a la quema de combustible, aunque no da ejemplos ni tampoco hace referencia a la composición de los gases en dicho proceso, en atención a la información que entrega el primer apartado del problema. Por otro lado, E18 logra dar una característica del vinagre que le permite elegir la respuesta correcta, sin hacer mención al dato que se entrega de la lluvia ácida y las estatuas de mármol.

Figura 23. Respuesta de E18 al problema 2

“El dióxido de azufre viene del CO2 y el óxido nitrógeno también. Por la quema de combustible”.
“El vinagre es una sustancia ácida que deteriora y/o oxida el mármol. Ya que el mármol es débil con los ácidos”

En la respuesta de E42, como se aprecia en la Figura 24, es muy similar a la respuesta de E18 con la diferencia que éste asocia el nivel de temperatura en la quema de combustible para explicar la emisión de dióxido de carbono y de los óxidos, los que aportan a la lluvia ácida.

Figura 24. Respuesta de E42 al problema 2

“El óxido de azufre se produce cuando quemamos combustible o autos y óxido de nitrógeno es lo mismo pero a más temperatura”.
“Es porque el vinagre desintegra la sustancia al igual que la lluvia ácida cuando cae”

DISCUSIÓN

Para dar respuesta al problema del taller 2 era necesario que los estudiantes siguieran el contorno de la figura con el trozo de hilo y, luego, usando la regla, midieran la longitud de éste para obtener una aproximación del contorno de la figura. Dicha estrategia se utilizó adecuadamente, aunque se observaron dificultades por parte de algunos estudiantes para utilizar dicho procedimiento. En relación a eso último se puede mencionar la respuesta de E15, quien hace mención a dos procedimientos. Uno de ellos fue seguir una poligonal con el trozo de hilo, probablemente evocando el cálculo del perímetro de alguna figura conocida. Lo anterior se puede relacionar con la influencia que tiene la enseñanza de la matemática cunado se enfoca en el uso de algoritmos y fórmulas sin ahondar en sus fundamentos (Fernández, 2005).   

Por otro lado, destaca la estrategia de E46 quien trazó un polígono asociado a la figura y luego calculó su perímetro para dar respuesta al problema (Olave, 2005; Escoriza, 2003). Además, E46 pudo calcular la desviación media aplicando la fórmula con la que disponían, sin cuestionar la existencia de un valor atípico cuando consideró las medidas de sus compañeros de grupo, como se observa en la Figura 11. Esa forma de proceder posiciona al estudiante en el concepto definición desviación media y muestra que no logra activar el concepto imagen, ya que E46 no visualiza en la recta real la distancia de las tres medidas respecto del promedio. Con lo anterior se refuerza la idea de que en la enseñanza de la matemática prevalece el calcular en desmedro de otras habilidades de pensamiento (Fernández, 2005).

En relación al problema del taller 2, se evidencia que en algunos estudiantes prevaleció el concepto imagen medida por sobre el concepto definición (Vinner, 1991), esa falta de interacción entre ambas imágenes conceptuales explica en parte porque algunos estudiantes no logran activar el procedimiento que consiste simplemente en seguir la figura con el trozo de hilo y luego medir con la regla para dar una respuesta, que además no es única.
 
Para el problema 1 de la prueba PISA, determinar el número de asistentes a un concierto de rock, prevaleció la estrategia identificar datos numéricos para luego aplicar el procedimiento estándar para calcular del área de una región rectangular, sin hacer un cuestionamiento a dicho número como representante del número de asistentes al concierto, salvo que se establezca que en un metro cuadrado se pueda ubicar una sola persona en cualquier concierto de rock. Lo anterior está estrechamente relacionado con lo que ocurre en el fenómeno de la edad del capitán (D’Amore, 2011).

Siguiendo con el problema 1, se observa que en algunos estudiantes prevalece el concepto definición área y, ante la ausencia de más datos, no logra activar el concepto imagen para poder visualizar una porción de espacio más pequeña, como lo que le ocurrió a E18. Por otro lado, hay evidencias del uso de la estrategia reducir el problema a otro más simple, al hacer referencia a un terreno de un metro por un metro. Además se observa el uso de la estrategia asumir resuelto el problema, cuando se asume un determinado número de personas por metro cuadrado, como se evidenció en las respuestas de E32 y E34. 

Respecto del problema 2.1 de la prueba PISA, si bien hacen mención a un conocimiento general sobre las fuentes de contaminación, no logran asociar, por ejemplo, que la quema de algún tipo de combustible fósil, dados sus componentes, se relaciona con la lluvia ácida. Al parecer están conscientes de que ese fenómeno ocurre en su entorno, pero no son conscientes de las fuentes de emisión que las provocan y, menos aún, de los procesos químicos que intervienen, lo que se condice con los resultados de la prueba PISA (OCDE, 2016). Respecto de las respuestas al problema 2.2, se observa que los estudiantes no logran relacionar la información de la contextualización del problema 2 con las características similares del vinagre con la lluvia ácida, en cuanto a su pH. Evidenciándose además dificultades en la lectura comprensiva y escasa evidencia del desarrollo de habilidades de pensamiento. 

En relación a la primera pregunta de investigación podemos indicar que al utilizar problemas que hacen referencia a un contexto específico, en nuestro caso la medición, se activan procedimientos y se obtienen datos para realizar cálculos o hacer uso de estadígrafos estimulando conjeturas y argumentos respeto de la problemáticas que se generan al momento de medir. También es posible extrapolar la problemática a situaciones similares, como por ejemplo, pensar en las medidas del contorno del tronco de un árbol para obtener el diámetro de éste y su respectivo volumen, asumiendo porciones del tronco de árbol con forma cilíndrica. De esa manera se contribuye gradualmente con la articulación entre matemática y ciencias, mediante la indagación.

Cabe mencionar que, en general, no se evidenció la utilización de conocimiento explícito de los programas de estudio, excepto el manejo de las operaciones aritméticas y la familiaridad que hay en el uso de fórmulas, en el sentido de reemplazar y calcular, como ocurrió en el problema del taller 2. En general, los estudiantes se limitaron sólo a calcular o bien a utilizar información del enunciado del problema sin un mayor análisis.

En atención a la segunda pregunta de investigación, se evidenció una baja frecuencia en el uso de estrategias como: hacer un dibujo, crear una lista, asumir resuelto el problema o reducir el problema a otro más simple. Tampoco se consideraron medidas antropomórficas para hacer estimaciones. En relación a los argumentos, estos se reducen a descripciones superficiales que dan cuenta sobre la forma de proceder.  

A MODO DE CONCLUSIÓN

En primer lugar, destacamos, a la luz de los resultados obtenidos, la necesidad de articular los distintos subsectores de aprendizaje a través de actividades curriculares —talleres con base en problemas que hagan referencia a algún contexto— para activar conocimientos previos y fomentar en los estudiantes el desarrollo de habilidades de pensamiento a través de la indagación. No basta con proponer un conjunto de actividades aisladas, es necesario procurar que los distintos aspectos asociados a un problema que hace referencia a un contexto se puedan activar. Ello es clave para que los estudiantes puedan explorar procedimientos y levantar argumentos que promueven la discusión y el trabajo en equipo.

Las actividades de los talleres 1 y 3 se llevaron a cabo siguiendo el método indagatorio, dando oportunidad a los estudiantes de confrontar y compartir sus aprendizajes. Pero desde los resultados del cuestionario se puede ver que ello no es suficiente, es necesario incorporar dicha metodología al proceso de enseñanza aprendizaje, por lo menos de manera intermitente e integrando los distintos subsectores del aprendizaje. No es suficiente proponer instancias aisladas que buscan articular matemática y ciencias, es necesario instaurarlo como una política en el currículo escolar.

En tareas de aprendizajes que son cercanas a los contextos de los estudiantes, es posible advertir competencias asociadas al querer aprender y trabajar colaborativamente, enfatizando en el error como una instancia de aprendizaje. Cuando se define un recurso de aprendizaje pertinente a la realidad de los estudiantes, es posible advertir mayor nivel de discusión respecto a las estrategias o requerimientos para resolver una tarea o una situación problema, integrando la matemática y ciencias en dicha resolución.

Hacemos notar la importancia que tuvo para nuestra investigación la estadística implicativa, dado que nos permitió seleccionar informantes en función de la contribución que éstos hicieron en la configuración de una clase significativa.

Para finalizar, como una proyección a la actividad de medir, se puede pensar en talleres que se enfoquen en las medidas anatómicas como el contorno de la cintura para abordar conceptos como índice de masa corporal, peso promedio, entre otras, con la finalidad de reflexionar sobre la salud personal y la importancia de una dieta equilibrada. En dichos talleres se pueden involucrar a profesionales del área de la salud, entre otros.

BIBLIOGRAFÍA

1. Abell, S.; Smith, D. y Volkmann, M. (2006). Inquiry in Science Teacher Education. In Flick, L y N. Lederman (Eds.). Scientific inquiry and the nature of science: Implications for teaching, learning, and teacher education (pp. 389-425). Netherlands: Springer.         [ Links ]

2. Bosch, C. (2014). Un vistazo al programa Ciencia en tu escuela. Revista Educación Matemática, especial 25 años.         [ Links ] 

3. Bruner, J. (1990). Acts of Meaning. Cambrige, Massachusetts: Harvard University Press.         [ Links ]

4. Campanario, J. y Moya, A. (1999). ¿Cómo enseñar ciencias? Principales tendencias y propuestas. Revista Enseñanza de las Ciencias, 17(2), 179-192.         [ Links ]

5. D’Amore, B. (2011). Didáctica de la Matemática. Bogotá:Cooperativa Editorial Magisterio. 

6. Devés, R. y López, P. Inquiry based science education and its impact on school improvement: The ECBI Program in Chile. Recuperado 18 de mayo del 2019 desde http://www.ecbichile.cl/wp-content/uploads/2012/05/Handbook_Deves-7-041.pdf        [ Links ]

7. Dyasi, H. (2015) La enseñanza de la Ciencia basada en la indagación; Razones por las que debe ser la piedra angular en la enseñanza y el aprendizaje de la ciencia. En Gutiérrez, R., Everaert, C., Robles, C. (Eds) La enseñanza de la ciencia en la enseñanza de la ciencia. Antología sobre Indagación (pp. 9-18). Innovación en la enseñanza de la ciencia, A.C.: México.         [ Links ]

8. Escoriza, J. (2003). Evaluación del conocimiento de las estrategias de comprensión lectora. España: Edicions Universitat.         [ Links ]

9. Fernández, J. (2005). Avatares y estereotipos sobre la enseñanza de los algoritmos en matemáticas. Revista Iberoamericana de Educación Matemática, 4 , 31-36.         [ Links ]

10. García-Carmona, A.; Criado, A. y Cañal, P. (2014). ¿Qué educación científica se promueve para la etapa de primaria en España? Un Análisis para las prescripciones oficiales de la LOE. Revista Enseñanza de las Ciencias, 32(1), 139-157.         [ Links ]

11. Gras, R.; Susuki, E.; Guillet, F. y Spagnolo F. (2008). Statistical Implicative Analysis. Theory and applications. Studies in Computational Intelligence 127. Berlin: Springer-Verlag.         [ Links ]

12. Harlen, W. (2013). Evaluación y Educación en Ciencias Basada en la Indagación: Aspectos de la Política y la Práctica. Trieste: Global Network of Science Academies.         [ Links ]

13. Lupión, T. y Prieto, T. (2014). La contaminación atmosférica: Un contexto para el desarrollo de competencias en secundaria. Revista Enseñanza de las Ciencias, 32(1), 159-177.         [ Links ]

14. MINEDUC (2009). Objetivos Fundamentales y Contenidos Mínimos Obligatorios de la Educación Básica y Media. Actualización 2009. Santiago de Chile: Ministerio de Educación.         [ Links ]

15. MINEDUC (2017). Propuesta Curricular para 3° y 4° medio. Documento consulta pública. http://basesdelfuturo.educarchile.cl/wp-content/uploads/2017/03/Propuesta_Curricular-Consulta-P%C3%BAblica.pdf.         [ Links ]

16. Minner, D; Levy A y Century, J. (2010). Inquiry-based science instruction –what is it and does it matter? Results from a research synthesis years 1984-2002. Journal of Research in Science Teaching, 47(4), 474-496.

17. Olave, M. (2005). Un estudio sobre las estrategias de los estudiantes de bachillerato al enfrentarse al cálculo del área bajo una curva. Tesis de maestría no publicada. Centro de Investigación en Ciencia Aplicada y Tecnología del Instituto Politécnico Nacional. México.         [ Links ]

18. Osborne, J. y Dillon, J. (2008). Science Education in Europe: Critical Reflections. London: Nuffield Foundation.         [ Links ]

19. Orús, P.; Zamora, L. y Gregori, P. (2009). Teoría y aplicaciones del análisis estadístico implicativo: primera aproximación en lengua hispana. Pilar Orús, Larisa Zamora, Pablo Gregori (Editores). Castellón: Universitat Jaume I, Departamento de Matemáticas; Santiago de Cuba: Facultad de Matemática y Computación. Universidad de Oriente de Santiago de Cuba, 2009. 516 p. ISBN 978-84-692-3925-4.         [ Links ]

20. OECD (2016). Resultado PISA 2015. https://www.oecd.org/pisa/pisa-2015-results-in-focus-ESP.pdf. Accessed 25.04.17.         [ Links ]

21. Pólya, G. (1990). Cómo plantear y resolver problemas. México: Trillas.         [ Links ]

22. Pozo, J.I., Pérez, M. y Domínguez, J. (1994). La solución de problemas. España: Ediciones Siglo XXI.         [ Links ]

23. Pajares, R. (2005). Resultados en España del estudio PISA 2000: Conocimientos y destrezas de los alumnos de 15 años. España: Ministerio de Educación.         [ Links ] 

24. Rocard, M.; Csermely, P.; Jorde, D.; Lenzen, D.; Walberg, H. y Hemmo, V. (2007). Science Education Now: A Renewed Pedagogy for the Future of Europe. Brussels: Directorate General for Research, Science, Economy and Society.         [ Links ]

25. Rodríguez, G. y García, E. (1999). Metodología de la investigación cualitativa. Málaga: Aljibe.         [ Links ]

26. Rodríguez, M.; Gregori, P.; Riveros, A. y Aceituno, A. (2017). Análisis de las estrategias de resolución de problemas en matemática utilizadas por estudiantes talentosos de 12 a 14 años. Revista Educación Matemática, 29(2), 159-186.         [ Links ]

27. Rodríguez, M. y Parraguez M. (2014). Interpretando estrategias en resolución de problemas desde dos constructos teóricos: Un estudio de caso. Revista electrónica de investigación en educación en ciencias, 9(2), 1-12.         [ Links ] 

28. Tall, D. y Vinner, S. (1981). Concept image and concept definition in mathematics, with particular reference to limits and continuity. Educational Studies in Mathematics, 12(2), 151-169.         [ Links ]

29. Treacy, P. y O’Donoghue, J. (2014). Authentic Integration: A model for integrating mathematics and science in the classroom. International Journal of Mathematical Education in Science and Technology, 45(5), 703-718.

30. Valverde, G. y Näslund-Hasley, E. (2010). La condición de la educación en matemáticas y ciencias naturales en América Latina y el Caribe. Consultado el 02 de septiembre del 2017 desde https://publications.iadb.org/handle/11319/2757#sthash.uBt7NAvb.dpuf.         [ Links ]

31. Vinner, S. (1991). The Role of Definitions in the Teachingand Learning of Mathematics, in D. Tall (Ed.): Advanced mathematical thinking (pp. 65-81). Dordrecht: Kluwer A. P.         [ Links ]