ARTÍCULOS ORIGINALES

Comparison of heat-unit methods to predict tomato anthesis

Comparación de métodos que utilizan unidades de calor para predecir la antesis de tomate

 

Bouzo CA & JC Favaro

Departamento de Producción Vegetal, Facultad de Ciencias Agrarias, Universidad Nacional del Litoral. Kreder 2805. C.P. 3080. Esperanza, Santa Fe, Argentina.
Address Correspondence to: Dr. Carlos Alberto Bouzo, Fax 054-03496-426400; Phone 054-03496-420639 Int. 161; e-mail: cbouzo@fca.unl.edu.ar

Recibido / Received 30.IX.2013.
Aceptado / Accepted 15.X.2013.

 

---

Abstract. The aim of this work was to compare methods to predict the time of anthesis in tomato (Solanum lycopersicum L.). Two independent experiments were carried out using seeds of the Tauro commercial hybrid. Daily maximum and minimum air temperatures were measured by means of an electronic thermometer with data storage; the photoperiod was calculated using a mathematical procedure. The moment at which each inflorescence presented 50% of its flowers in anthesis was recorded. The use of calendar days (CD) had a high dispersion, which was measured with a variation coefficient (VC) higher than 3.70% for all inflorescences. The method that considered both a base temperature and the photoperiod allowed the highest prediction uniformity for the conditions of this assay, since its VC was lower than 0.30%.

Keywords: Solanum lycopersicum L.; Ontogeny; Flowering; Simulation; Development; Temperature.

Resumen. El objetivo de este trabajo fue comparar algunos métodos para predecir el momento de la floración en el cultivo de tomate (Solanum lycopersicum L.). Se realizaron dos experimentos independientes utilizando semillas del híbrido comercial Tauro. La temperatura del aire se midió con frecuencia horaria mediante un termómetro electrónico con almacenamiento de datos, y el fotoperíodo se calculó mediante un procedimiento matemático. Se realizó un registro para establecer el momento en que cada inflorescencia presentaba el 50% de sus flores en antesis. La utilización de días calendarios (DC) tuvo una alta dispersión, medida con un coeficiente de variación (CV) mayor a 3,70% para todas las inflorescencias. El método que consideró una temperatura base y el fotoperíodo fue el que permitió tener la mayor uniformidad de predicción para las condiciones de este ensayo, debido a que su CV fue menor a 0,30%.

Palabras clave: Solanum lycopersicum L.; Ontogenia; Floración; Simulación; Desarrollo; Temperatura.

---

 

INTRODUCTION

Predicting the development of horticultural crops is of great importance for technical decision-making. In tomato, the possibility of having a reliable calculation method would allow producers, technologists and breeders to employ a useful tool to predict the anthesis moment of the crop with higher certainty.
The employment of methods relating plant phenology to some environmental variables, e.g. temperature, would allow to obtain a more accurate precision than those based on calendar day calculations. The methodology to calculate the accumulation of heat units has been applied in numerous crops to predict harvest date and, consequently, determine planting date (Mc-Master & Wilhelm, 1997). However, there are different calculation methods of heat units (UC) that take into account the response of the development rate to air temperature.
Each phase or expression of plant development is determined by characteristic or cardinal temperature values such as minimum or base temperature (TB) and maximum or 'ceiling' temperature (TC) below or above which, respectively, the crop arrests its development. Another characteristic temperature value is the optimum temperature (TO), at which the process reaches its maximum intensity (Charles-Edwards et al., 1986). The duration of a phase usually decreases as temperature increases from TB to TO, and increases above the latter (Squire, 1990).
Values between 4.3 °C and 10.0 °C have been proposed as TB for tomato. These differences might be due to various factors such as the varieties employed, locality and handling conditions of the crop (Perry et al., 1997). The TO value goes from 15 °C to 18 °C at night, and from 18 to 27 °C during daytime; the TC value goes from 30 to 36 °C (Perry et al., 1997). Procedures other than the canonical way of calculating degreedays (GD), consisting in subtracting the TB value from the medium daily temperature (TM), have been proposed. These new procedures incorporate the following parameters: (1) maximum temperature or higher threshold temperature (TC) (McMaster & Smika, 1988); (2) photoperiod, transforming GD in photothermal units (FT); (3) optimum temperature (TO), calculating units as 'tautochrones' (Norero, 1987), or (4) different values of TB for day- and nighttime (Brown & Bootsma, 1997). The aims of this work were to compare some of these methods to predict development, and establish the most reliable one, for fresh-tomato consumption.

MATERIALS AND METHODS

Two independent experiments were carried out consisting in sowing tomato seeds (Solanum lycopersicum L.) of the 'Tauro' commercial hybrid on two dates: 5 and 19 January, 2012. Multicell packs filled with substrate with a volume of 70 cm³ per cell were employed. The substrate consisted of a mixture of perlite 20% and a pre-mixture based on peat moss 80% (Sunshine Premix N° 6, SUNGRO-Horticulture, Canada). During the nursery phase, a parabolic greenhouse was employed covered with polyethylene LDT 150 µm thick. Microsprinkling was used for irrigation using a total of 5 mm distributed twice a day. Fertilization started on day seven after seeding with a solution of 300 ppm N, 100 ppm P, 100 ppm K, 95 ppm Ca and 30 ppm Mg. The transplant was performed on February 8. Plants were 35 and 21 days old for the first and second experiment, respectively. They were placed on a typical Argiudol soil located at Angel Gallardo (Santa Fe) (31° 30' S, 60° 43' W), in separate rows leaving 1.40 m or 0.35 m between plants, which represented a density of about 20400 plants/ha. Tomato plants were pruned to one stem by removing all lateral shoots, and the crop was conducted in trellising with the plants staked individually.
The plants were drip-irrigated and fertilized with a total of 250 kg/ha N, 80 kg/ha P and 350 kg/ha K. During the experiment, rainfall was 590 mm and crop evapotranspiration of 640 mm; irrigation provided an extra 70 mm. The experimental design consisted of complete blocks at random with five repetitions per seeding date. The time at which inflorescences had 50% of the flowers in anthesis was recorded to relate it to the indices calculated by the different study mathematical methods. Daily maximum and minimum air temperatures were recorded at each plot by using thermocouples connected to multiplexers and a datalogger (Cava-Logger, Mod. LM35/01). The photoperiod was calculated according to the procedure proposed by Goudriaan & Van Laar (1994) (Fig. 1). The mean relative humidity during the experiment was 69% (±10%). Initially, it was 61% and at the end of the experiment (and early autumn) it was 71%.

Fig. 1. Variation in the measured maximum (Tmax) and minimum (Tmin) temperatures, and calculated photoperiod during the experiments.
Fig. 1. Variación durante los experimentos de las temperaturas medidas máxima (Tmax) y mínima (Tmin), y del fotoperíodo calculado.

The methods employed were the following:

Method 1 (conventional):

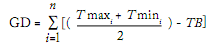
Method 2 (Perry et al., 1997):

Method 3 (Perry et al., 1986):

Method 4 (Owens & Moore, 1974):

Method 5 (Tyldesley, 1978):

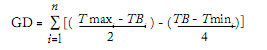
Method 6 (Masle et al., 1989):

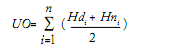
Method 7 (Brown & Bootsma, 1997)

Hd_i = 3.33 . (T max_i - TBd) - 0.084 . (T max_i - TBd)²
Hn_i = 1.8 . (T min_i - TB_n)

where TB is Base Temperature (TB = 6.1 °C); Tmax_i and Tmin_i, daily maximum and minimum temperatures, respectively; TC, 'ceiling' temperature (TC = 27.0 °C); LD, day length (hours); TB_d and TB_n, base temperatures during day- and nighttime, respectively (TB_d = 10.0 °C and TB_n = 4.0 °C); LD, duration of the daytime period; Hd_i and Hn_i: auxiliary variables for day- and nighttime, respectively; UO: Ontario Units; GD: Degree Days; UFT: Photothermal Unit.

RESULTS AND DISCUSSION

Using calendar days (DC) to predict anthesis caused a high dispersion of the data measured through the variation coefficient (CV), with values higher than 3.7% for all inflorescences (Table 1). Method 6 showed the best prediction for the conditions of this assay with a CV lower than 0.30%. These results confirm those obtained by Perry et al. (1997) who reported that the inclusion of day length improves prediction (Table 1). In this case, day length was applied in combination with the GD conventional method. It is highly likely that its application to methods also containing a higher threshold temperature (TC) could improve the predictive value even further. Method 7, whereby Ontario Units were calculated, was another method which provided a low coefficient of variation (CV). The results obtained are comparable with those of Gray et al. (1980), even though these authors worked with tomato genotypes for industry. All the remaining methods evaluated had higher CV values. However, these results should not be taken as defnitive for the case of fresh-tomato consumption, since these methods should be compared with a greater number of varieties and localities. Even for the same locality, it would be necessary to perform the evaluation of methods during two different seasons, as proposed by Perry et al. (1993) for chili pepper.

Table 1. Values resulting from the evaluated methods for obtaining 50% of anthesis in each inflorescence for the first and second experiment (Exp. 1 and Exp. 2, respectively), where DC are calendar days. For each inflorescence, the first column shows the mean value (MV), and the second column shows the variation coefficient (VC) in percentage.
Tabla 1. Valores obtenidos para el primer y segundo experimento (Exp. 1 y Exp. 2, respectivamente) de los métodos evaluados para el 50% de antesis en cada inflorescencia, donde DC son los días calendarios. Para cada inflorescencia, en la primer columna se presentan los valores medios (MV), y la segunda columna muestra el coeficiente de variación (VC) en porcentaje.

For example, a useful comparison for tomato would be to consider the prediction ability of the methods in the same locality for spring and summer seedings. However, the results obtained with Method 6 and the low dispersion of results from the two experiments and the three inflorescences evaluated afford a higher level of reliability to this method. All the other methods had a variability twice as high as the one obtained with Method 6 (Table 1). The methods employed have been proposed to simulate the development of a great number of crops. In this process, it is the temperature plants reach which really regulates the rate of crop development (Wheeler et al., 2000). In this vein, and although air temperature is a good indicator of the cultivar temperature, there are other meteorological variables that modify plant temperature by impinging on the energy and mass balance of the cultivar, e.g., air humidity, intensity of solar radiation, or wind velocity (Bouzo, 1998). However, the incorporation of these variables might not allow obtaining a simple, fast method to estimate the anthesis moment of a crop. Our preliminary results indicate (1) the little reliability of calendar days (DC), and (2) the possibility of improving the predictive value of the conventional procedure (Method 1) through the incorporation of day length, according to the results obtained with Method 6.

CONCLUSIONS

Seven methods were analyzed to predict the development of tomato employing reference temperatures characteristic of this species, and simple meteorological variables such as maximum and minimum temperatures and daily photoperiod.
The method which appeared as the most reliable one, given the low variation coefficient calculated, was that which included day length (photoperiod) in the normal calculation of daily heat units.

REFERENCES

1. Angus, J.F., R.B. Cunningham, M.W. Moncur & D.H. Mackenzie (1980). Phasic development in field crops I. Termal response in the seedling phase. Field Crops Research 3: 365-378.         [ Links ]

2. Bouzo, C.A. (1998). Modelo mátemático para simular la demanda máxima de agua de los cultivos. Tesis M. Sc. Biblioteca Pontifica Universidad Católica de Chile. 121 p.         [ Links ]

3. Brown, D.M. & A. Bootsma (1997). Crop heat units for corn and other warm-season crops in Ontario. Ontario Ministry of Agriculture, Food and Rural Affairs. Agdex 111/31. 5 p.         [ Links ]

4. Charles-Edwards D.A., D. Doley & G.M. Rimmington (1986). Modelling Plant Growth and Development. Academic Press. Australia. 235 p.         [ Links ]

5. Goudriaan, J. & H.H. Van Laar (1994). Modelling Potential Crop Growth Processes. Textboook with Exercises. Kluwer Academic Press. Dordrecht. The Netherlands. 239 p.         [ Links ]

6. Gray, D., J.A. Ward & J.R.A. Steckel (1980). Growth and development of bush tomatoes in relation to temperature. The Journal of Agricultural Science 95: 285-292.         [ Links ]

7. Masle, J., G. Doussinalut, G.D. Farquhar & B. Sun (1989). Foliar stage in wheat correlates better to photothermal time than to thermal time. Plant, Cell and Environment 12: 235-247.         [ Links ]

8. McMaster G.S. & W.W. Wilhelm (1997). Growing degree-days: one equation, two interpretations. Agricultural and Forest Meteorology 87: 291-300.         [ Links ]

9. McMaster, G.S. & W.W. Smika (1988). Estimation and evaluation of winter wheat phenology in the central Great Plains. Agricultural and Forest Meteorology 43: 1-18.         [ Links ]

10. Norero, A.L. (1987). El tautocrón: un concepto biomatemático para definir la longevidad de cultivos anuales. Ciencia e Investigación Agraria 14: 195-214.         [ Links ]

11. Owens Jr., T.O. & E.L. Moore (1974). A comparison of various methods of calculating heat unit requirements of tomato. Technical Bulletin No. 70, Mississippi Agric. and Forestry Experiment Station, Mississippi State University. 7 p.         [ Links ]

12. Perry, K.B., T.C. Wehner & G.L. Johnson (1986). Comparison of 14 methods to determine heat unit requirements for cucumber harvest. HortScience 21: 419-423.         [ Links ]

13. Perry, K.B., D.C. Sanders, D.M. Granberry, J.T. Garrett, D.R. Decoteau, R.T. Nagata, R.J. Dufault, K.D. Batal & W.J. McLaurin (1993). Heat units, solar radiation and daylength as pepper harvest predictors. Agricultural and Forest Meteorology 65: 197-205.         [ Links ]

14. Perry, K.B., W. Yihua, D.C. Sanders, J. T. Garret, D.R. Decoteau, R.T. Nagata, R.J. Dufault, K.D. Batal, D.M. Granberry & W.J. McLaurin (1997). Heat units to predict tomato harvest in the southeast USA. Agricultural and Forest and Meteorology 84: 249-254.         [ Links ]

15. Squire, G.R. (1990). The Physiology of Tropical Crop Production. CAB International, Wallingford, UK. 236 p.         [ Links ]

16. Tyldesley, J.B. (1978). A method of evaluating the efect of temperature on an organism when the response is non-linear. Agricultural Meteorology 19: 137-153.         [ Links ]

17. Wheeler, T.R., P.Q. Craufurd, R.H. Ellis, J.R. Porter & P.V. Vara Prazad (2000). Temperature variability and the yield of annual crops. Agriculture, Ecosystems and Environment 82: 159-167.         [ Links ]