Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Análisis filosófico
versión On-line ISSN 1851-9636
Anal. filos. vol.23 no.1 Ciudad Autónoma de Buenos Aires mayo 2003
ARTÍCULOS
Confirmación hipotetico-deductiva y confirmacion bayesiana
Alejandro Cassini
Universidad de Buenos Aires - CONICET
Resumen
En este trabajo hago una comparación sistemática entre las dos teorías de la confirmación más populares en la actualidad: el método hipotético-deductivo y el bayesianismo. En primer lugar, enumero los cinco problemas fundamentales de la teoría hipotético-deductivista. Estos son el problema de las hipótesis estadísticas, el del grado de confirmación, el de la conjunción irrelevante, el del holismo epistemológico y el de las hipótesis alternativas. Luego, hago una presentación general de la epistemología bayesiana y muestro de qué manera estos problemas resultan tratables en el marco bayesiano. Finalmente, concluyo que los tres primeros admiten una solución satisfactoria, sobre la base de algunos supuestos razonables. Los dos últimos, en cambio, todavía son problemas abiertos para la teoría bayesiana de la confirmación.
PALABRAS CLAVE: Filosofía de la ciencia; Confirmación; Bayesianismo.
Abstract
Bayesians often affirm they have produced the best available theory of confirmation. In particular, they claim to have superseded the venerable hypothetico-deductive method. In this paper I intend to assess that claim by making a systematic comparison between both theories of confirmation. I begin by listing the main problems of hypothetico-deductive confirmation. I then show that this conception is incompatible with Hempel's conditions of adequacy for qualitative confirmation. I expound the Bayesian theory of confirmation with some detail in order to show that this theory is able to solve three out of the five fundamental problems of hypothetico-deductive confirmation. largue that the remaining two problems (alternative hypotheses and epistemological holism) are still open questions for the Bayesians.
KEY WORDS: Philosophy of science; Confirmation; Bayesianism.
1. Introducción
El método hipotético-deductivo (en adelante H-D) es, desde hace más de un siglo, la concepción más popular del método cientí fico en las ciencias fácticas, tanto entre los científicos como entre los filósofos1. Numerosos críticos, sin embargo, señalan que es un método incompleto porque no proporciona, entre otras cosas, una teoría satisfactoria de la confirmación de las hipótesis y teorías científicas. Los bayesianos, en particular, sostienen que su propia teoría de la confirmación puede reemplazar exitosamente a la idea de confirmación implícita en el viejo método de la hipótesis. En este trabajo me propongo evaluar esta afirmación, es decir, comparar las virtudes y defectos de estas dos concepciones de la confirmación de teorías. Hay muchas otras críticas que pueden hacerse al método H-D, pero aquí sólo me ocuparé del problema de la confirmación2.
A veces se concibe al bayesianismo como una teoría de la confirmación alternativa al método H-D, como un rival inductivista del tradicional método de la hipótesis, que es esencialmente deductivista. Contra esta interpretación argumentaré que la teoría bayesiana de la confirmación conserva algunas de las ideas fundamentales del método H-D. Ciertamente, no es una extensión conservativa de este método, puesto que rechaza algunos de los supuestos básicos de la teoría de la confirmación H-D. Por otra parte, propone un marco conceptual diferente, sobre todo en la manera de interpretar el grado de confirmación de las hipótesis. No obstante, en este marco conceptual pueden plantearse esencialmente los mismos problemas que aquejan al método H-D. La diferencia es que muchos de ellos pueden resolverse de manera exitosa en el programa bayesiano, o al menos tienen una respuesta razonable, mientras que carecen de solución dentro del contexto hipotético-deductivista. La teoría bayesiana de la confirmación también permite justificar algunas de las ideas de Popper acerca del valor epistemológico de las "conjeturas audaces"; aunque, en mi opinión, estas ideas no están necesariamente ligadas al método H-D en general.
Comenzaré por exponer de manera muy sintética el método H-D. No presentaré la versión falsacionista de Popper, sino la versión confirmacionista formulada por Hempel y muchos otros auto res3. Luego, enunciaré los problemas principales que debe enfrentar la idea hipotético-deductivista de confirmación, y analizaré las posibles soluciones que podrían ofrecerse dentro del marco conceptual del método H-D. Concluiré que en la mayoría de los casos no hay soluciones satisfactorias. Seguidamente, haré una presentación de las condiciones de adecuación de la teoría cualitativa de la confirmación de Hempel y mostraré que dicha teoría es incompatible con la definición de confirmación H-D. En la parte principal de este trabajo intentaré exponer la teoría bayesiana de la confirmación, en su versión más ortodoxa, de manera sumaria, pero completa y autocontenida. Mostraré, en primer lugar, cuáles son los elementos de la confirmación H-D y de la teoría cualitativa de Hempel que el bayesianismo retiene. Luego, dedicaré la mayor parte del espacio disponible a analizar la manera en que los problemas del método H-D pueden resolverse en un marco conceptual bayesiano. Finalmente, señalaré cuáles son los problemas todavía no resueltos por la teoría bayesiana de la confirmación.
El objetivo de este trabajo se limita a realizar una comparación sistemática entre las teorías de la confirmación H-D y bayesiana. No pretendo dar cuenta del estado actual de las teorías generales de la inducción y la confirmación, entre las que hay numerosas concepciones no bayesianas y no probabilistas. Tampoco intento hacer una evaluación del bayesianismo frente a otras teorías rivales de la confirmación. La conclusión que extraigo al final es que la teoría bayesiana de la confirmación es superior al método H-D en la resolución de problemas epistemológicos. La teoría bayesiana retiene muchas de las virtudes del método H-D y, a la vez, consigue solucionar algunos de sus principales problemas, aunque no todos. El análisis de las dificultades de la propia teoría bayesiana de la confirmación, que son numerosas, está más allá de los límites de este trabajo.
2. El método hipotético-deductivo
El método H-D es tan bien conocido que no es necesario presentado con todo detalle. Se lo puede describir, sintéticamente, de esta manera. Primero se parte de la identificación de un problema para el cual el conocimiento vigente no tiene una solución. Luego se propone una nueva hipótesis o conjetura que, en caso de ser verdadera, constituiría una solución al problema en cuestión. Después se deducen hipótesis derivadas de la hipótesis propuesta, generalmente con la ayuda de hipótesis auxiliares, hasta conseguir la deducción de alguna consecuencia observacional (es decir, un enunciado singular de observación). Las consecuencias observacionales deducidas de la nueva hipótesis se contrastan empíricamente mediante observaciones o experimentos. Si resultan verdaderas, la hipótesis queda confirmada y puede aceptarse provisionalmente. Si las consecuencias observacionales resultan falsas, la hipótesis es refutada y debe abandonarse4.
La conocida asimetría entre verificación y refutación muestra que ningún número finito de consecuencias observacionales verdaderas prueba la verdad de una hipótesis, pero una sola consecuencia observacional falsa prueba que dicha hipótesis es falsa. En efecto, si H |= E (pero no a la inversa) y E es verdadero, no se deduce la verdad de H; pero si E es falso, se deduce ¬H (donde H es una hipótesis cualquiera y E es un enunciado observacional o una conjunción finita de tales enunciados). Así, por razones puramente lógicas, nunca es posible verificar una hipótesis mediante el método H-D, pero en principio, siempre es posible falsaria o refutada.
En la mayoría de los casos, este esquema simplificado es insuficiente para dar cuenta del proceso de la investigación científica. Las teorías e hipótesis teóricas generalmente no implican consecuencias observacionales por sí mismas, sino en conjunción con diversas hipótesis auxiliares, pertenecientes a una o más teorías diferentes. Así, si (H & A) |= E y E es verdadero, la conjunción H & A ha quedado confirmada como un todo, pero la confirmación no se distribuye a cada uno de sus componentes (donde A es una conjunción finita de hipótesis auxiliares). Si, en cambio, E es falso, la conjunción H & A está refutada, pero de allí no se sigue que una determinada hipótesis sea falsa. Lo único que puede concluirse es ¬H ⅴ ¬A, es decir, que uno de los dos conyuntos (o ambos) es falso; pero no es posible determinar, por medios puramente lógicos, cuál de ellos. Este es el bien conocido problema del holismo de la contrastación empírica, que Pierre Duhem fue el primero en advertir claramente (Duhem, 1894 y 1906).
Todavía este modelo más sofisticado resulta excesivamente simple para dar cuenta de una situación de contrastación empírica. Generalmente una teoría o hipótesis teórica, incluso en conjunción con un conjunto de hipótesis auxiliares, no implica una determinada consecuencia observacional E, sino un condicional de la forma C →E, donde C es un enunciado observacional que describe ciertas condiciones iniciales. Podemos afirmar, entonces, que (H & A & C) |= E, o bien, que (H & A) |= (C → E). Ambas expresiones son equivalentes (por el teorema de la deducción). Por lo general, se considera que los enunciados de condiciones iniciales no pertenecen al sistema de hipótesis que se contrasta, de modo que se prefiere la segunda formulación, que expresa una predicción condicional5. La evidencia total que confirma o refuta H & A está formada por la conjunción C & E. Obviamente, si C es falsa, la predicción condicional C → A es verdadera y el sistema teórico H & A queda confirmado. Pero nadie está interesado en esta clase de confirmación trivial. Nos interesa contrastar H & A cuando C es verdadero. En tal caso, la confirmación o refutación de H & A depende de la verdad o falsedad de E. De aquí en adelante llamaré E al condicional C → A, cuyo antecedente asumo como verdadero, y H a la conjunción H & A, donde A es un conjunto, no necesariamente no vacío, de hipótesis auxiliares.
Ahora podemos enunciar la condición general de confirmación del método hipotético-deductivo:
Confirmación H-D: E confirma a H si y sólo si, H |= E.
En esta definición se expresa un deductivismo estricto, de acuerdo con el cual sólo los enunciados observacionales deducidos de un sistema de hipótesis pueden confirmado. Los críticos del método H-D, tanto bayesianos como no bayesianos6, han señalado que la noción de confirmación H-D que acabamos de definir es excesivamen te estrecha y posee numerosas limitaciones. Sin pretensión de ser exhaustivos, podemos resumir las principales dificultades del método H-D mediante el enunciado de cinco problemas fundamentales:
1. Hipótesis estadísticas: el método H-D no se puede aplicar a la contrastación de hipótesis estadísticas o probabilísticas porque éstas no implican consecuencias observacionales (ni aisladamente, ni en conjunción)7. Por consiguiente, tales hipótesis no son confirmables ni refutables desde el punto de vista del método H-D.
2. Grado de confirmación: el método H-D es puramente cualitativo y no puede emplearse para calcular el grado de confirmación de una hipótesis respecto de la evidencia disponible, ni tampoco para decidir cuándo una hipótesis está mejor confirmada que otras hipótesis rivales que también han sido confirmadas.
3. Holismo de la contrastación: cuando se emplea un conjunto de hipótesis auxiliares A, si (H & A) |= E y E es falso, no puede deducirse ¬H, sino sólo ¬(H & A), es decir, ¬H ⅴ ¬A. Por consiguiente, el método H-D no permite determinar cuál es la hipótesis que ha sido refutada o disconfirmada.
4. Conjunción irrelevante: si E confirma a H, entonces, también confirma a H & B, donde B es un enunciado cualquiera. Ello es así en razón de la monotonía de la deducción, ya que si es verdadero que H |= E, también lo es que (H & B) |= E. Por tanto, si una evidencia confirma a una determinada hipótesis, también confirma a infinitos conjuntos de hipótesis que contienen a dicha hipótesis como elemento.
5. Hipótesis alternativas: si una evidencia E confirma a una determinada hipótesis H1, también confirma a un número indefinido de hipótesis incompatibles con H1. Desde el punto de vista lógico; si H1 |= E, existe al menos una H2 tal que |= ¬(H1 & H2) y H2 |= E. En consecuencia, el método HD no permite determinar cuál es la hipótesis que ha sido confirmada.
Cualquier teoría aceptable de la confirmación debería solucionar estos cinco problemas o, al menos, ofrecer una respuesta razonable a cada uno de ellos. Consideremos qué soluciones puede dar el propio método H-D.
Respecto de las hipótesis estadísticas no es posible extender la condición de confirmación H-D de modo que abarque la confirmación de teorías probabilistas. Consecuentemente, el método H-D sólo resulta aplicable a las teorías deterministas, entendidas como aquellas que no contienen hipótesis estadísticas o probabilistas. Sin embargo, es posible apelar a los métodos de la estadística clásica (de Fisher o Neyman-Pearson), que, si bien se desarrollaron de manera independiente, son compatibles con el método H-D. Esto, sin embargo, equivale a admitir una limitación insuperable en el alcance del método H-D y conduce a adoptar dos métodos de confirmación diferentes, uno para las teorías deterministas y otro para las probabilistas. De esta manera, se termina por dar la razón a los críticos que afirman que el método H-D es incompleto8. Por otra parte, dada la importancia que tienen las teorías probabilísticas en la ciencia contemporánea, la teoría fundamental de la confirmación resulta ser la inferencia estadística y no el método H-D.
Respecto del grado de confirmación, el método H-D podría en principio extenderse a una teoría cuantitativa de la confirmación. Es cierto que tal como ha sido formulado sólo contiene una teoría cualitativa de la confirmación, o más bien, una parte de tal teoría, pero nada impide que se la complete y extienda. Popper, por ejemplo, construyó una teoría del grado de corroboración que trata de evitar el compromiso con la probabilización de las teorías y, a la vez, intenta formular cuantitativamente su versión falsacionista del método H-D9. Hasta el momento no se ha probado que sea imposible cons truir una teoría cuantitativa de la confirmación que recoja todas las intuiciones básicas del método H-D, pero la empresa parece difícil de llevar a cabo. Si fuera posible medir el grado de confirmación de una hipótesis o teoría respecto de toda la evidencia disponible, se podría determinar cuál hipótesis está mejor confirmada que otras. También se podría esperar por esta vía una solución al problema de las hipótesis alternativas. Por ahora éstos son problemas abiertos, pero es un hecho que no disponemos de una teoría cuantitativa satisfactoria de la confIrmación H-D, esto es, no tenemos manera de medir el grado de confirmación en el contexto del método H-D.
Respecto del holismo de la contrastación el método H-D no provee ninguna solución. En verdad, el holismo epistemológico representa un desafío para toda teoría de la confirmación y no es claro que haya sido resuelto de manera satisfactoria en alguna teoría existente, como veremos más adelante.
Por último, no hay manera de solucionar el problema de la conjunción irrelevante en el método H-D, a menos que se introduzca explícitamente una condición ad hoc como la siguiente: si E confirma a H1 y H2 |= H1, entonces, E no confirma a H2 (suponiendo que H2 no es lógicamente equivalente a H1). En verdad, la definición de confirmación H-D satisface la negación de esta condición, es decir, si E confirma a H1 y H2 |= H1, entonces, E confirma a H2. Sin embargo, si se admite esta condición, que Hempel llamó condición conversa de consecuencia, se producen resultados paradójicos. Esta es una cuestión que debemos analizar inmediatamente.
3. La confirmación hipotético-deductiva y las condiciones de Hempel
En su artículo clásico sobre la confirmación de hipótesis Hempel (1945) presenta la primera teoría cualitativa de la confirmación desarrollada de manera completa y precisa. Antes del trabajo de Hempel sólo se disponía del concepto H-D de confirmación, que no es suficiente para obtener una teoría aceptable de la inferencia científica. Hempel se propuso evitar algunas de las dificultades del método H-D, pero a la vez, conservar algunas intuiciones cualitativas implícitas en el concepto de confirmación H-D. Sin embargo, el resultado de su trabajo es una teoría de la confirmación muy diferente del método H-D, puesto que, como veremos, su teoría es incompatible con la definición de confirmación H-D.
La confirmación, según Hempel, es una relación entre oraciones o conjuntos de oraciones que satisface ciertas condiciones de adecuación. Las condiciones de adecuación son las siguientes:
Condición de implicación: Si E |= H, entonces, E confirma a H.
Condición conversa de consecuencia: Si E confirma a H y G |=H, entonces, E confirma a G.
Condición especial de consecuencia: Si E confirma a H y H |= G, entonces, E confirma a G.
Condición de equivalencia: Si E confirma a H y |= (H ↔ G),entonces, E confirma a G.
Condición de consistencia: SiE confirma aH y también a G, entonces, |≠ ¬(H & G).
Hempel construyó una definición de confirmación que satisface todas sus condiciones de adecuación, excepto la condición conversa de consecuencia. Aunque todas las condiciones de adecuación parecen intuitivamente razonables cuando se las considera de manera individual, tomadas conjuntamente producen resultados paradójicos o completamente inaceptables. El más importante es la paradoja de que cualquier evidencia confirma a cualquier hipótesis. En efecto, sean H y G dos hipótesis cualesquiera y E una evidencia que se ha verificado:
1. Si E |= H, entonces, E confirma a H [Condición de implicación]
2. E |= (E v G) [por lógica proposicional]
3. E confirma a (E ⅴ G) [De 1 y 2]
4. G |= (E v G) [por lógica proposicional ]
5. Si E confirma a H y G |= H,entonces, E confirma a G [Condición conversa]
6. E confirma a G [De 3, 4 y 5] •
El resultado al que hemos llegado es que, si se aceptan todas las condiciones de adecuación de Hempel, entonces, cualquier evidencia E confirma a cualquier hipótesis arbitraria G. Para evitar esta paradoja Hempel opta por rechazar la condición de consecuencia conversa y mantener las restantes condiciones. De allí resulta un beneficio adicional porque se elimina el supuesto que produce uno de los problemas fundamentales del método H-D, la paradoja de la conjunción irrelevante, que amenazaba también a la teoría de Hempel. Si no se acepta la condición conversa de consecuencia, ya no se produce la paradoja de que si E confirma a H, también confirma a H&B.
La definición de confirmación H-D satisface la condición conversa de consecuencia de Hempel, pero no satisface las de consistencia y de consecuencia especial. En efecto, supongamos que H |= E y E es verdadero. En ese caso, E confirma a H. Luego, por la condición conversa de consecuencia, E confirma tanto a H & G como a H & ¬G, ya que ambas hipótesis compuestas implican a E. Sin embargo, esas dos hipótesis son lógicamente incompatibles, lo cual viola la condición de consistencia. Por otra parte, si E confirma a H y H |= G, no se sigue que E confirme a G. Sólo la confirmará en el caso de que G |= E, pero esto no es verdadero en general. No todas las consecuencias lógicas de H implican a E. La condición de implicación sólo vale en el método H-D cuando E y H son lógicamente equivalentes, pero no en general, es decir, cuando H no implica E. Por último, la confirmación H-D satisface la condición de equivalencia, ya que si E confirma a H y H es lógicamente equivalente a G, E también confirma a G, dado que G |= E.
La comparación entre la confirmación H-D y la teoría cualitativa de Hempel arroja los siguientes resultados. La confirmación HD satisface la condición conversa de consecuencia, que Hempel rechaza, mientras que viola las condiciones de implicación, de consecuencia especial y de consistencia, que Hempel acepta. La única condición que se cumple en ambas teorías es la de equivalencia. Esto muestra que la teoría de la confirmación de Hempel y el método HD son claramente incompatibles.
Hempel nunca proporcionó una justificación de sus condiciones de adecuación, porque parece consideradas como evidentes, o al menos intuitivamente razonables. La condición de equivalencia se basa en la idea de que la confirmación que una hipótesis recibe de una determinada evidencia depende exclusivamente del contenido de esa hipótesis y no de la manera en que la hipótesis está formula da. Dos hipótesis lógicamente equivalentes no son en realidad dos hipótesis diferentes, sino sólo dos formulaciones de una misma hipótesis. Por tanto, no parece aceptable decir que la misma evidencia confirma a una hipótesis y no confirma a su equivalente. Ello sería semejante a decir que una hipótesis resulta confirmada por la evidencia cuando dicha hipótesis está escrita en español, pero no cuando está escrita en inglés. La condición de equivalencia parece, entonces, altamente razonable ya que nos asegura que la confirmación es una relación entre proposiciones y no entre las oraciones que las expresan.
La condición de consistencia afirma que una misma evidencia no puede confirmar hipótesis lógicamente incompatibles. Sin embargo, la historia de la ciencia parece generosa en contraejemplos. En determinada época, las teorías corpuscular y ondulatoria de la luz resultaban ambas confirmadas por los mismos fenómenos ópticos, es decir, por idénticas evidencias. Por su parte, las condiciones de consecuencia especial y conversa no parecen en absoluto evidentes y razonables. De hecho, Hempel mismo tuvo que eliminar la condición conversa de consecuencia, como ya hemos visto. Carnap, por su parte, sometió a un análisis riguroso todas las condiciones de adecuación de Hempel y concluyó que, salvo la condición de equivalencia, las restantes tienen contraejemplos y deben ser rechazadas10. La misma conclusión se obtiene en el contexto de la teoría bayesiana de la confirmación, excepto para la condición de implicación, como veremos enseguida.
4. La teoría bayesiana de la confirmación
La lógica inductiva tiene como una de sus finalidades principales la de construir una teoría general de la confirmación de hipótesis científicas11. Antes de 1945 la lógica inductiva prácticamente no existía y el concepto mismo de confirmación apenas había sido elucidado12. Ese año tanto Carnap como Hempel publicaron una serie de artículos pioneros en los cuales analizaban el concepto cualitativo de confirmación y proponían diferentes métodos para medir el grado de confirmación de las hipótesis científicas13. En 1950 Carnap publicó Logical Foundations of Probability, que se considera habitualmente como la obra fundacional de la lógica inductiva. El programa de Carnap, basado en la interpretación lógica de las probabilidades, pronto encontró limitaciones de alcance y dificultades técnicas que lo hicieron poco viable. Aunque algunas de esas dificultades se solucionaron posteriormente, cuando Carnap murió, en 1970, su programa de lógica inductiva ya había sido abandonado por la mayoría de los filósofos de la ciencia. Mientras tanto, se produjo la emergencia de la lógica inductiva bayesiana, que aplicó a la teoría de la confirmación diversos elementos de la inferencia estadística bayesiana, desarrollada, entre otros, por H. Jeffreys, J. I. Good, L. Savage y D. V. Lindley. La teoría bayesiana de la confirmación es un programa de investigación en desarrollo que, como tal, tiene éxitos y anomalías. Una evaluación global de este programa es tema de todo un libro14. Aquí sólo puedo dar un esbozo de algunos aspectos positivos de la teoría bayesiana de la confirmación, aquellos que son relevantes para la comparación con el método H-D15.
Las lógicas inductivas cuantitativas, como la bayesiana, tienen el objetivo de encontrar una medida del grado de confirmación de una hipótesis o teoría respecto de la evidencia disponible. Esto es, buscan definir una función confirmación C que asigne un número real a cada hipótesis o teoría (o, más precisamente, a cada tríada 〈H, E, K〉) que represente el grado en el cual una hipótesis se encuentra confirmada por determinada evidencia. Sea H una hipótesis o conjunto de hipótesis, E un enunciado observacional que describe una determinada evidencia y K el conocimiento aceptado en un momento dado. La expresión C(H, E & K) = r afirma que el grado de confirmación de la hipótesis H respecto de la evidencia E y el conocimiento antecedente K es igual al número real r. Todas las lógicas inductivas probabilistas se caracterizan por la afirmación de que el grado de confirmación es una medida probabilística del apoyo empírico. Se basan, por consiguiente, en la siguiente identidad:
C(H, E & K) = P(H / E & K)
Esta ecuación afirma que el grado de confirmación de H respecto de E y K es igual a la probabilidad condicional de H dados E y K. Puesto que H, E y K son proposiciones, o conjuntos de proposiciones, otra manera de leer la ecuación es la siguiente: el grado de confirmación de H respecto de E y K es igual a la probabilidad de que H sea verdadera dado que E y K son verdaderas. La función confirmación C se identifica, entonces, con la función probabilidad P tal como es usualmente caracterizada en el cálculo axiomático de probabilidades, ya sea en la formulación de Kolmogorov o en alguna otra axiomatización diferente. La teoría bayesiana de la confirmación pertenece a esta clase de lógicas inductivas probabilistas.
El sistema axiomático de Kolmogorov está formulado en el lenguaje de la teoría de conjuntos, pero la lógica inductiva bayesiana requiere que se lo formule en el lenguaje de la lógica proposicional clásica. Ambas formulaciones son equivalentes y sus respectivos lenguajes son intertraducibles. Aquí adoptaré una formulación axiomática diferente de la de Kolmogorov, introduciendo la noción de probabilidad condicional como término primitivo mediante un axioma16.
Sea ξ un conjunto de proposiciones cerrado respecto de las combinaciones finitas veritativo-funcionales. La probabilidad P es una aplicación de ξ en el conjunto de los números reales (P: ξ → R) que satisface los siguientes axiomas:
Axioma 1: para toda proposición α ∈ ξ, 0 ≤ P(α) ≤ 1.
Axioma 2: para toda proposición α ∈ ξ tal que |= α,P(α) = 1.
Axioma 3: para cualesquiera proposiciones α, β ∈ ξ tales que |= ¬ (α & β), P(α ∨ β) = P(α) +P(β).
Axioma 4: para cualesquiera proposiciones α, β ∈ ξ, P(α & β) = P(β) x P(α / β).
Los axiomas 3 y 4, de aditividad y multiplicación, respectivamente, se pueden escribir de una manera más general para cualquier secuencia finita de proposiciones. Se obtiene, así, la teoría de la probabilidad con aditividad finita. Para los fines de este trabajo, sin embargo, no resulta necesario apelar a esta formulación general17.
En el curso de nuestra argumentación necesitaremos emplear tres teoremas de la teoría de la probabilidad que son bien conocidos y no demostraremos aquí. Son los siguientes:
Teorema 1: P(¬α) = 1 - P(α).
Teorema 2: P(¬α / β) = 1 - P(α / β).
Teorema 3: P(α) = p(α) x P(β / α) + P(¬α) x P(β / ¬α).
Los dos primeros son los teoremas del complemento para probabilidades absolutas y condicionales, respectivamente. El tercero es el teorema de probabilidad total. El célebre teorema de Bayes se deduce exclusivamente del Axioma 4:

Reemplazando en el denominador P(β) por su equivalente según el Teorema 3 se obtiene otra formulación del teorema de Bayes:

Todos los teoremas sobre probabilidades que se deduzcan de los axiomas de la teoría de la probabilidad son también teoremas acerca del grado de confirmación de hipótesis. Por otra parte, toda interpretación verdadera de la teoría de la probabilidad, también será una interpretación verdadera, un modelo, de la teoría de la con firmación. Una lógica inductiva probabilista no está necesariamente ligada, como a veces se cree, a una determinada interpretación del cálculo de probabilidades, sino que, como la propia teoría abstracta de las probabilidades, admite, en principio, múltiples modelos.
La teoría bayesiana de la confirmación, en su versión ortodoxa, adopta la interpretación subjetiva o personal de las probabilidades elaborada por Bruno De Finetti (1937). Se debe advertir, sin embargo, que no todos los bayesianos son personalistas, de modo que bayesianismo no es sinónimo de subjetivismo probabilista En este trabajo emplearé la teoría bayesiana ortodoxa, con la advertencia de que todos los resultados acerca de la confirmación que se deduzcan exclusivamente de los axiomas 1-4 de la teoría de la probabilidad también admiten interpretaciones no subjetivistas.
En la teoría bayesiana personalista las probabilidades se interpretan como los grados de creencia de cada sujeto individual. La expresión P(α/ K) = r debe leerse como si afirmara que r es el grado de creencia de un determinado individuo en la verdad de la proposición a dadas las creencias contenidas en K, que acepta como verdaderas. De Finetti probó en 1937 que esta interpretación satisface los axiomas del cálculo de probabilidades (con aditividad finita). Se acepta desde entonces que la interpretación en términos de grados de creencia es un modelo de la teoría matemática de la probabilidad18.
La epistemología bayesiana ortodoxa se basa en los supuestos de que la creencia admite grados y de que los grados de creencia de un sujeto se pueden representar mediante números reales. Esta representación numérica es una idealización, que incluso puede tomarse como una ficción útil. A estos supuestos le agrega dos principios fundamentales. El primero es que un sistema racional de grados de creencia debe ser coherente, es decir, satisfacer todos los teoremas de la teoría matemática de la probabilidad. El segundo es que los grados de creencia deben actualizarse a la luz de la experiencia mediante la regla de condicionalización. La justificación de estos dos principios ha sido objeto de una enorme bibliografía que no puede comentarse aquí19. Los bayesianos ortodoxos consideran que estos dos principios son condiciones necesarias y suficientes para la racionalidad de un sistema de grados de creencia20.
La regla de condicionalización es una regla de inferencia inductiva que determina cómo actualizar la función probabilidad cuando se adquiere información proveniente de nuevas evidencias empíricas21. Sea P la función probabilidad de un sujeto antes de que se conozca la evidencia E y P' la función probabilidad del mismo sujeto después de que E se ha conocido. La regla de condicionalización estricta determina cómo se relacionan estas dos funciones de probabilidad, bajo los supuestos de que E se ha verificado (y tiene, por tanto, probabilidad 1) y de que las proposiciones a las que se aplica la función inicial P son inciertas (es decir, no tienen probabilidad 0 ni 1). La regla de condicionalización estricta se puede enunciar, entonces, de esta manera:
P'(α / K) = P(α / E & K), dado que P'(E/ K) = 1.
La aplicación de esta regla de condicionalización garantiza la conservación de la coherencia de un sistema de grados de creencia.
El componente específicamente bayesiano de esta lógica inductiva aparece en relación con esta regla. De acuerdo con la teoría de la probabilidad, P'(α / E & K) = P(α / K) x P(E / α & K) / P(E / K). Este no es más que el teorema de Bayes (el número 4 de nuestra lista). La regla de condicionalización es, entonces, una aplicación del teorema de Bayes para actualizar la función probabilidad de un sujeto individual. Muestra de qué manera la adquisición de nueva evidencia afecta a los grados de creencia de cada sujeto produciendo nuevos grados de creencia.
El uso de la regla de condicionalización presupone el proceso no inferencial en el cual se pasa de una probabilidad inicial P(E / K) < 1 a la probabilidad final P(E / K) = 1. En términos menos formales, este es el proceso por el cual se verifica la evidencia E. La lógica inductiva bayesiana no se ocupa del proceso epistemológico de verificación del conocimiento observacional. Simplemente, presupone que la evidencia es cierta o está verificada y forma parte del conocimiento aceptado. A nadie se le escapa que los datos de que se dispone en la práctica científica son falibles y rara vez se encuentran verificados. Para manejar los casos en que la evidencia es incierta, la regla de condicionalización se puede generalizar de esta manera:
![]()
Para el caso más simple, en el que la partición de los Ei = {E,↓E}, la regla adopta la siguiente forma: P'(α / K) = P(α / E & K) x P'(E / K) + P(α / ¬E & K) x P'(¬E / K). Esta generalización de la regla de condicionalización la propuso Richard Jeffrey en 1965 y tiene, entre otras, la virtud de que se reduce a la regla de condicionalización simple o estricta cuando P'(E / K) = 122. La regla de Jeffrey permite la condicionalización cuando la evidencia es incierta, es decir, cuando 0 < P'(E / K) < 1. Además, el cambio de la función probabilidad de P(E / K) a P'(E / K) resulta reversible, mientras que en el caso de la condicionalización bayesiana estricta es irreversible (puesto que P'(E / K) = 1).
La teoría bayesiana de la confirmación emplea el teorema de Bayes para calcular el grado de confirmación de una hipótesis o teoría. La lógica inductiva bayesiana es aplicable tanto a teorías deterministas como a teorías probabilistas o estadísticas. En el caso de hipótesis deterministas el uso de este teorema está sujeto a los siguientes requisitos: a) (H & K) |= E; b) 0 > P(H / K) < 1; y c) 0 < P(E / K) < 1. El primero afirma que la evidencia se deduce de la hipótesis H y el conocimiento antecedente K tomados conjuntamente. El segun do y el tercer requisito afirman que respecto del K tanto H como E son inciertas, es decir, no se conoce con certeza si son verdaderas o falsas. El tercer requisito implica que ni E ni ¬E se deducen de K.
Con el fin de simplificar los puntos específicos que quiero mostrar, ignoraré por ahora el uso de hipótesis auxiliares y supondré que las hipótesis y teorías que consideramos tienen por sí mismas consecuencias observacionales, es decir, implican una determinada evidencia E. El teorema de Bayes, aplicado a la confirmación de una única hipótesis o conjunción de hipótesis H adopta la siguiente forma:

Aquí P(H / K) es la probabilidad previa de la hipótesis H, relativa a la evidencia disponible K, esto es, la probabilidad de H antes de que se conozca que E es verdadero. P(H / E & K) es la probabilidad posterior de H, es decir, la probabilidad de H después que se ha verificado E. Por su parte, P(E / H & K) se conoce como likelihood, y representa la probabilidad de E suponiendo que H es verdadera. Finalmente, P(E/ K) es la llamada esperabilidad, o sea, la probabilidad de que E sea verdadero independientemente de que H sea verdadera o falsa. Usualmente, se la reemplaza por la fórmula de probabilidad total enunciada en el Teorema 3, de modo que la forma más utilizada es:

El teorema de Bayes también se puede aplicar de forma generalizada a la confirmación de dos o más hipótesis diferentes, que por lo general son hipótesis rivales. Para un número finito de hipótesis mutuamente excluyentes H1 ... Hn, el teorema toma la siguiente forma:

De aquí en adelante me limitaré al caso más simple en el que se calcula el grado de confirmación de una única hipótesis o conjun to de hipótesis H. Además, para simplificar la notación, suprimiré el conocimiento antecedente K toda vez que no sea indispensable hacerlo explícito.
5. Hipótesis equivalentes
Ante todo, comencemos por demostrar que la teoría bayesiana de la confirmación permite justificar la condición de equivalencia de Hempel, que también se cumple en la confirmación H-D. Es posible probar que si una determinada evidencia confirma a una hipótesis H, también confirma a todas las hipótesis que son lógicamente equivalentes a H; y las confirma en el mismo grado o medida. Esto es una consecuencia de un teorema de la teoría de la probabilidad que afirma que dos proposiciones lógicamente equivalentes tienen la misma probabilidad. Por tanto, dos hipótesis lógicamente equivalentes tienen el mismo grado de confirmación respecto de la misma evidencia y, el mismo conocimiento antecedente. Esto es, para toda evidencia E y todo conocimiento antecedente K, |= (H ↔G) →P(H / E & K) = P(G/E & K). Para demostrarlo necesitamos probar un teorema previo, según el cual, si una proposición implica a otra, la probabilidad de la primera no es mayor que la de la segunda.


Finalmente, podemos probar que dos proposiciones lógicamente equivalentes tienen la misma probabilidad.

A partir de este teorema se demuestra el que realmente nos interesa probar, que expresa la condición de equivalencia en términos bayesianos:


6. Confirmación por implicación
Cuando una hipótesis H implica a una determinada evidencia E, resulta obvio que P(E / H & K) = 1. Por consiguiente, si H es una hipótesis universal o determinista, el teorema de Bayes se simplifica y toma la forma:
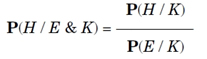
Antes de proseguir debemos probar que efectivamente si una hipótesis implica una determinada evidencia) la probabilidad de la evidencia dada esa hipótesis es igual a 1. Este es un caso específico de un teorema más general según el cual, si una proposición implica a otra, la probabilidad de la segunda dada la primera es igual a 1. La prueba, para las proposiciones H y E, es como sigue:


La noción bayesiana de confirmación consiste en el incremento del grado de confirmación de una hipótesis o teoría cuando se descubre una nueva evidencia. Se la define habitualmente del siguiente modo:
Confirmación incremental: La evidencia E confirma incrementalmente a la hipótesis H respecto del conocimiento antecedente K si y sólo si, P(H / E & K) > P(H / K).
La teoría bayesiana de la confirmación incorpora algunas de las ideas cualitativas fundamentales del método H-D. Esencialmente, la idea de que una hipótesis se confirma cuando se verifica alguna de sus consecuencias observacionales. Esto es, si la hipótesis H implica lógicamente a la evidencia E, entonces, E' confirma a H. La noción bayesiana de confirmación incremental permite justificar esta intuición. Siempre que una hipótesis implica una determinada evidencia, la verificación de esa evidencia aumenta el grado de probabilidad de la hipótesis. Podemos probarlo como un teorema:

Como ya señalamos antes, este resultado se sigue bajo el supuesto de que) < P(H / K) < 1 y ) < P(E / K) < 1. Estas son las dos condiciones que se requieren en general para aplicar de manera útil o no trivial el teorema de Bayes, dado que la regla de condicionalización bayesiana no puede elevar ni disminuir las probabilidades previas iguales a 0 o iguales a 1. Por otra parte, es obvio que si P(H / K) = 1, no es posible la confirmación incremental de H. Esto ocurre, por ejemplo, cuando H es una verdad lógica o cuando, no siendo una verdad necesaria, H se deduce de K.
La teoría bayesiana no acepta la noción de confirmación HD, sino sólo una parte de ella, que llamaré confirmación por implicación. Esto es, si H |= E, entonces, E confirma incrementalmente a H. La conversa no es necesariamente verdadera. Desde el punto de vista bayesiano, una hipótesis puede estar confirmada por evidencias que no se deducen de ella. Esto se refleja en el hecho de que P(H / E & K) > P(H / K) → (H & K |= E) no es un teorema de la teoría de la probabilidad. La teoría bayesiana de la confirmación no sostiene el deductivismo estricto de la confirmación H-D. Por esta razón, como veremos, puede dar cuenta de la confirmación de hipótesis estadísticas.
7. Refutación de hipótesis
La otra idea fundamental del método H-D es la de refutación. De acuerdo con ella, cuando una hipótesis tiene al menos una consecuencia observacional falsa, dicha hipótesis está refutada desde un punto de vista lógico. La teoría bayesiana de la confirmación recoge este resultado de manera cuantitativa porque prueba que si una hipótesis implica una evidencia falsa, su grado de confirmación se reduce a 0. Podemos demostrarlo en el siguiente teorema:

La evidencia ¬ E refuta a la hipótesis H porque P(H / ¬E & K) = 0. La refutación es el caso de disconfirmación máxima de una hipótesis por la evidencia. Una vez que una hipótesis ha sido refutada no puede adquirir ningún grado positivo de confirmación mediante condicionalización bayesiana. Ello es así porque si P(H / E & K) = 0, entonces, P(H / E & E' & K) = 0 para cualquier nueva evidencia E'. La única manera de salir de esta situación es o bien eliminar la evidencia refutadora ¬E, o bien modificar el conocimiento antecedente K de modo tal que no se cumpla la condición a). En cualquiera de esos dos casos es posible que el grado de confirmación de H vuelva a ser mayor que O. Ambas estrategias implican la contracción del conjunto de proposiciones K, lo cual no puede hacerse dentro de un marco exclusivamente bayesiano (puesto que K contiene sólo conocimiento aceptado, esto es, P(K) = 1).
Eliminar la evidencia refutadora ¬E consiste en revisar las observaciones o experimentos que suponemos que la han verificado, de manera que se encuentre algún error en esa verificación. Revisar el conocimiento antecedente K para evitar la refutación consiste en desactivar la implicación de la consecuencia E. Esto es, si (H & K) |=E, se debe encontrar un conjunto K' tal que (H & K) |≠ E. De este modo, ↓E deja de ser una evidencia refutadora para H. En los casos típicos en ciencia teórica, E se deduce de H, K y un conjunto de hipótesis auxiliares A. En tal situación, por lo general se buscará desactivar la implicación de E modificando alguno de los elementos de A, esto es, reemplazando A por otro conjunto de hipótesis auxiliares A'. Si ninguna de estas estrategias resulta exitosa, entonces, será necesario reemplazar H, ya que ninguna evidencia ulterior podrá elevar su grado de confirmación por sobre 0.
8. La condición de implicación
La condición de implicación de Hempel también es válida en la teoría bayesiana de la confirmación. Esto es, si E implica H, entonces, E confirma incrementalmente a H. Para ello es necesario que la probabilidad previa de H sea menor que 1. Esta es una condición general para cualquier caso de confirmación incremental, ya que es obvio que si P(H / K) = 1, entonces, para cualquier evidencia E, P(H / E & K) ″ P(H / K). Esto no es más que decir que no se puede incrementar la probabilidad de una hipótesis que ya tiene la probabilidad máxima. La condición de Hempel vale siempre que se cumpla la condición 0 < P(H / K) < 1. Como ya hemos señalado, la idea bayesiana de confirmación incremental presupone que las hipótesis que se confirman no son verdades necesarias ni están implicadas por el conocimiento antecedente K23. Bajo esa condición, la prueba del siguiente teorema es casi inmediata.

9. La conjunción irrelevante
Veamos ahora de qué manera la teoría bayesiana soluciona el problema de la conjunción irrelevante. Sabemos que si (H & K) |= E, en razón del carácter monótono de la deducción, también ocurre que (H & B & K) |= E, donde B es un enunciado cualquiera, posiblemente irrelevante para H. De acuerdo con la definición de confirmación H-D, E confirma a la vez a H y a H & B. La teoría bayesiana de la confirmación acepta la confirmación por implicación y, por tanto, debe admitir que E confirma incrementalmente tanto a H como a H & B (suponiendo que P(H & B / K) > 0). Así, es verdad tanto que P(H / E & K) > P(H / K) como que P(H & B/ E & K) > P(H & B/ K). Sin embargo, esto nada dice acerca del incremento en los respectivos grados de confirmación. La solución bayesiana del problema consiste en probar que, en general, el grado de apoyo que E da a H & B es mucho menor que el grado de apoyo que E da a H. La razón de ello es que, bajo la condición de que 0 < P(B / K) < 1, siempre ocurre que P(H & B / K) < P(H / K). Por tanto, dada la desigualdad de las probabilidades previas, y dada la misma evidencia E, las probabilidades posteriores mantendrán la desigualdad, es decir, P(H & B / E & K) < P(H / E & K). Para probar este resultado es necesario admitir que H y B son probabilísticamente independientes, lo cual es indudablemente cierto si B es un enunciado irrelevante para H. La prueba es la siguiente:

De este resultado se deduce que el grado de apoyo de E a H es mayor que el grado de apoyo de E a H & B. Es decir, (P(H / E & K) - P(H / K) > (P(H & B / E & K) - P(H & B / K)). La prueba de este resultado es evidente a partir del teorema anterior y de las siguientes igualdades, que se deducen del teorema de Bayes:
P(H / E & K) - P(H / K) = P(H / K) x ((l / P(E / K) -1))
P(H & B / E & K) - P(H & B / K) = P(H & B / K) x ((l / P(E / K)) - 1)).
Siempre que se agregue a una hipótesis H un enunciado irrelevante B (cuya probabilidad sea mayor que 0 y menor que 1) la confirmación incremental que E provee a H & B será menor que la que provee a H sola. El grado de apoyo de H resultará igual al de H & B solamente en el caso de que P(B / K) = 1. Este resultado es completamente razonable, porque si B es una verdad lógica, naturalmente esperamos que, cualquiera sea la evidencia E, P(H / E & K) = P(H & B / E & K). Es decir, la conjunción de una tautología con una hipótesis empírica no afecta al grado de confirmación de esta última. Por otra parte, si B es una hipótesis empírica, tendrá el mismo efecto que una tautología sólo si está completamente verificada. Ninguna hipótesis empírica puede alcanzar mediante condicionalización bayesiana una probabilidad posterior igual a 1, si tiene una probabilidad previa menor que 1. Por tanto, el único caso en el que la conjunción de una hipótesis empírica irrelevante no disminuye el grado de confirmación del sistema total ocurre cuando dicha hipótesis ya ha sida previamente aceptada con probabilidad 1.
10. La improbabilidad de la evidencia
Popper ha señalado a lo largo de toda su obra que las predicciones más audaces de una teoría son aquellas que tienen mayor valor epistemológico para la contrastación de dicha teoría. Según Popper, las predicciones más improbables proporcionan contrastaciones más severas de una teoría. Más precisamente, la corroboración de una consecuencia improbable aumenta más el grado de corroboración de una hipótesis que la corroboración de una consecuencia observacional de probabilidad alta. No me parece que esta idea sea una parte esencial del método H-D, pero, en cualquier caso, puede justificarse en el contexto de la teoría bayesiana de la confirmación. Para ello basta con interpretar que las predicciones más audaces de una teoría son las consecuencias observacionales que tienen menor probabilidad respecto del conocimiento antecedente K. En términos bayesianos, cuanto menor sea P(E / K), tanto mayor será el grado de apoyo que E confiera a una hipótesis H24.
En el marco de la teoría bayesiana de la confirmación esta tesis encuentra una justificación más rigurosa que en la teoría de la corroboración de Popper. En efecto, si se satisfacen las condiciones a), h) y c) (enunciadas en la sección 4), se sigue del Teorema de Bayes que el incremento en el grado de confirmación de H producido por E es inversamente proporcional a la probabilidad de E dado K:

Es decir, cuanto más improbable sea la evidencia respecto del conocimiento antecedente, mayor es el incremento en el grado de confirmación de la hipótesis que implica a esa evidencia. Esto justifica la idea intuitiva, sostenida tanto por Popper como por otros partidarios del método H-D, según la cual cuanto menos probable sea una predicción, mayor es el grado de apoyo que proporciona a la hipótesis de la cual se deduce25.
En general, el grado de apoyo que la evidencia E confiere a una hipótesis H es igual al cociente P(H / E & K) / P(H / K). Esto se sigue directamente del teorema de Bayes, donde:

El primer miembro de la ecuación es la definición del grado de apoyo que E confiere a H. La probabilidad de H dada E aumentará en caso de que el cociente P(E / H & K) / P(E / K) sea mayor que 1.
Una manera diferente de probar este resultado es a través del uso de la regla de condicionalización estricta. Como ya hemos dicho, el primer paso para utilizar esta regla es de tipo no inferencial y consiste en el cambio de la probabilidad previa P(E / K) < 1 a la probabilidad posterior P(E / K) = 1. El aumento en el grado de confirmación es, entonces, proporcional a la diferencia P(E / K) - P(E / K). Esto, a su vez, es igual a 1 - P(E / K). Cuanto más cercana a 1 sea esta diferencia, tanto mayor será el aumento en el grado de confirmación que E produce en H. Es decir, mayor será la diferencia entre P(H / E & K) - P(H / K). Si ocurre que P(E / K) = 1, la diferencia P(E / K) - P(E / K) = 0, y, por tanto, E no aumenta el grado de confirmación de H. La evidencia conocida con certeza no tiene valor confirmatorio26.
11. El retorno decreciente de las contrastaciones repetidas
Popper ha afirmado que cuando se incrementa el número de repeticiones de una determinada experiencia, disminuye la severi dad de la contrastación y, por consiguiente, disminuye el apoyo evidencial que cada una de esas experiencias proporciona a una determinada hipótesis. Sostuvo que este hecho es una suerte de "ley del retorno decreciente de las contrastaciones repetidas" (Popper, 1963, p. 240). La razón de tal retorno decreciente es que los resultados previos de una contrastación se incorporan al conocimiento antecedente. Por tanto, un nuevo resultado del mismo tipo de contrastación resulta cada vez más probable a la luz del conocimiento antecedente. Dado que el grado de corroboración de una hipótesis es proporcional a la improbabilidad de la evidencia que la apoya, el grado de corroboración de esa hipótesis se elevará cada vez menos a medida que la contrastación se repite.
Popper (1963, p. 240) sostuvo que esta idea es difícil de explicar en una teoría inductivista de la ciencia, pero Grünbaum (1976) señaló al respecto que encuentra también una justificación natural en un contexto bayesiano. Desde el punto de vista bayesiano, la repetición de una observación o experimento de la misma clase eleva siempre el grado de confirmación de una hipótesis, pero no en la misma cantidad. El retorno epistémico es cada vez menor a medida que aumenta el número de pruebas repetidas que proporcionán evidencia del mismo tipo. La prueba de ello es simple. Sean E1, E2, ..., En diferentes enunciados que expresan diferentes instancias de la misma clase de evidencia E. Cada una de ellas, una vez conocida, se incorpora al conocimiento antecedente K. Entonces, si H implica a E1, E2, ..., En,
P(H/E1 & K) < P(H/E2 & K & E1) < ... < P(H/En & K E1 & ... & En-1).
Las probabilidades de las evidencias El, E2, ..., En son probabilidades previas y, como tales, no pueden calcularse mediante el teorema de Bayes, sino que deben tomarse como dadas. Esto abre la puerta, como siempre, a asignaciones subjetivas diferentes. Sin embargo, parece razonable aceptar que P(E1 / K) < P(E2 / K & E1) < ... < P(En / K & E1 & ... & En-1). Es necesario, pues, un acuerdo acerca de las probabilidades previas, pero no respecto de valores numéricos determinados. Diferentes individuos pueden asignar diferentes valores a las probabilidades de E1, E2, ..., En. Sólo se requiere que todos los diferentes valores satisfagan la desigualdad anterior. En tal sentido, el acuerdo es mínimo y parece razonable. Por otra parte, la razón que justifica el consenso sobre esas probabilidades previas es la misma que invoca Popper. Una vez conocidos los primeros resultados de un experimento, los resultados posteriores se vuelven cada vez más probables a la luz de ese mismo conocimiento.
De lo anterior se sigue una justificación de la idea tradicional según la cual una evidencia más variada proporciona (ceteris paribus) más apoyo a una determinada hipótesis que una evidencia menos variada o de una sola clase. Si E y E' son dos evidencias de especies diferentes, en general hemos de suponer que son probabilísicamente independientes, de modo que la ocurrencia de una no disminuye la probabilidad de la otra. Es decir, lo razonable será suponer que P(E / K & E) = P(E / K). En suma, la evidencia más variada tendrá una menor probabilidad previa que la evidencia menos variada y, por tanto, mayor poder confirmatorio para una determinada hipótesis27.
12. Las hipótesis estadísticas
Finalmente, la teoría bayesiana de la confirmación, a diferencia del método H-D, se puede aplicar a hipótesis estadísticas. La regla de condicionalización y el teorema de Bayes se usan exactamente de la misma manera que en el caso de las hipótesis deterministas. La única diferencia es que si H es una hipótesis estadística y E una determinada evidencia, H no implica lógicamente a E. Por consiguiente, P(E/ H & K) no será siempre igual 1, sino, generalmente, menor que 1. En la fórmula de Bayes, entonces, la probabilidad previa P(E / H & K) no es eliminable, sino que será necesario asignarle un valor mayor que 0 y menor que 1. H resultará incrementalmente confirmada por E, a pesar de no implicar a E, cuando P(E / H & K) > P(E / ¬ H & K). Este es un resultado general que vale también para el caso en el que E implica a H. Podemos probarlo de la siguiente manera (suprimiendo K para abreviar las fórmulas):

La conversa de este teorema también es un teorema (que se prueba de manera análoga al anterior pero remontando la prueba de abajo hacia arriba), de modo que, escribiendo la fórmula de manera completa, podemos afirmar que (P(H / E & K) > P(H / K)) ↔ (P(E /H & K) > P(E /¬H & K)).
Se sigue de este teorema que el cambio en el grado de confirmación de una hipótesis H es proporcional a la diferencia entre las likelihoods: P(E / H & K) - P(E / ¬H & K). Cuando esta diferencia es un número positivo, el grado de confirmación de H aumenta; si la diferencia es negativa, el grado de confirmación disminuye; y si es nula, el grado de confirmación permanece sin cambios. En el caso de las hipótesis deterministas que implican a la evidencia E, el grado de confirmación de una hipótesis H dada la evidencia E no puede disminuir. Ello es así porque P(E / H & K) = 1, de modo que la diferencia P(E / H & K) - P(E / ¬H & K) nunca puede ser negativa. Por tanto, (H & K |= E) → P(H / E & K) ≥ P(H / K). Esta es una generalización del Teorema 9 que se obtiene cuando se admite que 0 < P(E / K) ≤ 1. Con las hipótesis estadísticas, en cambio, dado que H no implica a E, en general ocurrirá que P(E / H & K) < 1. Consiguientemente, la diferencia entre las likelihoods puede ser negativa, y en ese caso, la evidencia E disminuye el grado de confirmación de la hipótesis H.
13. Problemas no resueltos
La teoría bayesiana de la confirmación resuelve satisfactoriamente tres de los problemas que aquejan al método H-D, el del grado de confirmación, el de la conjunción irrelevante y el de la confirmación de hipótesis estadísticas. Sin embargo, no ofrece, en mi opinión, una solución razonable a los otros dos problemas, el del holismo epistemológico y el de las hipótesis alternativas compatibles con la evidencia. Una discusión detallada de estos dos problemas está más allá de los límites de este trabajo, por lo que me limitaré a hacer algunas observaciones esquemáticas.
Comencemos por el problema de las hipótesis alternativas. Supongamos que dos hipótesis rivales H y H' implican a la misma evidencia E. En tal caso, P(E / H & K) = 1 = P(E / H' & K). Se sigue, por tanto, del teorema de Bayes que las probabilidades previas y posteriores de las dos hipótesis se relacionan de la siguiente manera:
![]()
Esta igualdad entre cocientes implica que P(H / E & K) ≠ P(H'/ E & K) si y sólo si, P(H / K) ≠ P(H' / K). En particular, P(H / E & K) > P(H' / E & K) si y sólo si, P(H / K) > P(H' / K). Esto es, las probabilidades posteriores de las dos hipótesis son diferentes únicamente cuando las respectivas probabilidades previas son diferentes. En tal caso, la evidencia E parece no desempeñar ningún papel significativo para discriminar entre los grados de confirmación de ambas hipótesis. El problema se traslada a la asignación de las probabilidades previas de cada hipótesis. Pero dado que esas son probabilidades subjetivas, es posible que diferentes científicos discrepen en sus asignaciones de modo tal que para algunos P(H / K) > P(H' / K), mientras que para otros P(H / K) < P(H' / K). En esas circunstancias, ninguna evidencia E que sea implicada por ambas hipótesis es capaz de resolver el desacuerdo inicial. El grado de confirmación que se obtenga condicionalizando sobre la evidencia no hará otra cosa que reflejar en las probabilidades posteriores el desacuerdo en las probabilidades previas de cada hipótesis. Muchos bayesianos confían en que este problema podrá resolverse una vez que se obtenga alguna solución satisfactoria al problema más general de la objetividad de la inferencia científica, o, más específicamente, al problema de cómo asignar racionalmente probabilidades previas y cómo obtener consenso acerca de tales asignaciones. Por el momento éste es un problema abierto, cuya solución está pendiente28.
La respuesta bayesiana ortodoxa a este problema es que la aplicación reiterada de la regla de condicionalización (y, por tanto, del teorema de Bayes) hace converger los valores de las probabilidades posteriores de las hipótesis. Las probabilidades previas no se borran, pero sí se "decoloran" cuando se condicionalizan respecto de la nueva evidencia adquirida. De esta manera, la divergencia inicial en las probabilidades previas tiende a hacerse cada vez menor a medida que la evidencia se acumula. Si bien los diferentes grados de confirmación de una determinada hipótesis continúan siendo diferentes después de cualquier número finito de aplicaciones de la regla de condicionalización, los valores tienden a ubicarse en un intervalo real cada vez menor. Se han probado diversos teoremas generales acerca de la fusión de las opiniones y la convergencia de las probabilidades bajo ciertas condiciones muy generales29. Tales teoremas muestran que, bajo el supuesto de que la probabilidad previa que se asigne a una hipótesis sea siempre 0 < P(H / K) < 1, todas las diferentes probabilidades posteriores convergen hacia el valor P(H /K) = 1 cuando se aplica reiteradamente la regla de condicionalización estricta. El único requisito general es que todos los sujetos estén de acuerdo en cuáles son las hipótesis que tienen una probabilidad previa igual a 0. Si un sujeto asigna P(H / K) = 0 y otro P(H / K) > 0, sus probabilidades posteriores nunca convergen por el simple hecho de que P(H / K) = 0 no puede cambiar por condicionalización bayesiana.
La convergencia de las probabilidades previas no soluciona, sin embargo, el problema de las hipótesis alternativas. En primer lugar, porque no puede garantizarse la convergencia en el corto plazo. Por ejemplo, si un científico asigna a una hipótesis dada una probabilidad previa muy cercana a 0 y otro le asigna una probabilidad previa muy cercana a 1, la convergencia de las respectivas probabilidades posteriores será extremadamente lenta. Los dos científicos no lograrán alcanzar ningún acercamiento significativo en sus probabilidades posteriores a lo largo de sus vidas. Después de cualquier número humanamente realizable de condicionalizaciones, tales probabilidades todavía serán cercanas a 0 y a 1, respectivamente. La convergencia de las probabilidades posteriores se produce más o menos rápidamente si las probabilidades previas no son cercanas a los valores extremos. Pero el bayesianismo ortodoxo no dispone de ningún procedimiento que limite de esta manera la elección de las probabilidades previas.
Por otra parte, si dos científicos parten de asignaciones diferentes de probabilidades previas para dos hipótesis rivales, de modo que uno de ellos satisfaga la desigualdad P(H / K) > P(H' / K) y el otro no, después de cualquier número finito de aplicaciones de la regla de condicionalización las probabilidades posteriores de cada uno de ellos todavía mantendrán la divergencia inicial respecto de la desigualdad. En el caso límite en que las probabilidades converjan hacia 1, nos encontraremos con dos hipótesis rivales con el mismo grado de confirmación respecto de toda la evidencia disponible. La elección entre ambas hipótesis estará, entonces, subdeterminada por la evidencia, de modo que el problema de las hipótesis alternativas quedará irresuelto.
El problema del holismo epistemológico es mucho más difícil de tratar. La solución mayoritariamente admitida por los bayesianos es la propuesta por Dorling (1979)30, En lo esencial, la solución de Dorling es la siguiente. Si (H & A.) |= E, y ¬E, entonces, desde un punto de vista lógico, sólo puede inferirse ¬H v ¬A. ¿Cómo puede saberse si hay que revisar H o A? La respuesta bayesiana es que debe revisarse la hipótesis o conjunto de hipótesis cuyo grado de confirmación se vea afectado en mayor medida por la evidencia negativa ¬E. El teorema de Bayes permite mostrar que la evidencia que refuta un sistema de hipótesis no afecta a las partes de ese sistema de la misma manera. En algunos casos ¬E puede bajar drásticamente el grado de confirmación de H y en otros casos el de A. Ello depende de cuáles sean las probabilidades previas y las likelihoods de las correspondientes hipótesis.
La hipótesis H se debe mantener cuando la evidencia negativa ¬E, que refuta al sistema S = (H & A), tiene el efecto de disminuir el grado de confirmación de A mucho más que el de H. En caso contrario, se debe mantener A y revisar H.
Las condiciones que deben cumplirse para que ocurra el primero de los casos son las siguientes. 1) H y A son probabilísticamente independientes, de modo que P(A / H & K) = P(A / K). 2) Las dos hipótesis tienen probabilidades previas diferentes, de modo que P(H / K) > P(A / K). 3) Las likelihoods son muy desiguales: P(E / ¬H & A & K) << P(E/ H & ¬ A & K); y P( E / ¬H & ¬A & K) << 1. Si se dan estas condiciones, resulta que P(H / ¬E & K) >> P(A / ¬E & K)31.
Hay dos dificultades fundamentales para esta solución bayesiana, La primera es el viejo problema de la subjetividad de las probabilidades previas y likelihoods involucradas. Dado que se trata de probabilidades personales, no hay nada que obligue a un sujeto a asignar valores de probabilidad que cumplan con las desigualdades especificadas en las condiciones 2) y 3). Consiguientemente, diferentes científicos o grupos de científicos podrían obtener resultados totalmente discordantes para las probabilidades posteriores de H y de A. La solución bayesiana requiere que en la comunidad científica se alcance un consenso acerca de las probabilidades previas y likelihoods de H y de A. Como en otros casos, no es necesario que el acuerdo se haga sobre valores numéricos específicos, sino sólo sobre las desigualdades expresadas en las condiciones 2) y 3). Histórica mente, puede constatarse que de hecho tal consenso se alcanzó en algunos casos, pero esto es contingente. Nada en la metodología bayesiana implica que tal consenso se alcance siempre o incluso pueda alcanzarse. En suma, la solución bayesiana depende de que se cumplan ciertas condiciones que no pueden explicarse mediante el método bayesiano. Earman (1992, pp. 84-85) advierte este problema y sostiene que una solución satisfactoria depende de que se resuelva el problema de la objetividad de la inferencia científica. Pero éste, como ya vimos, constituye una de las dificultades principales del programa bayesiano.
Otra dificultad, que no parece haberse advertido hasta ahora, es el propio holismo epistemológico. La solución bayesiana presupone una estrategia no holista, según la cual, los componentes de un sistema de hipótesis son separables, esto es, se les puede asignar grados de confirmación a cada uno de ellos de manera aislada. Esto es precisamente lo que el holista epistemológico niega, o debería negar, si es que su posición ha de ser coherente. Supongamos, por ejemplo, que el sistema S se compone de una única hipótesis H y una sola hipótesis auxiliar A, de modo que (H & A) |= E, pero H |≠ E y A |≠ E. En ese caso E confirma globalmente al sistema S, de la misma manera que ¬E lo refuta globalmente. Así como, dado ¬E, no es posible concluir que una determinada hipótesis de S es falsa, tampoco es posible, dado E, concluir que alguna de las hipótesis de S ha sido confirmada. La confirmación de un sistema de hipótesis es global y no se distribuye a sus componentes32. En particular, no puede asignarse a H o a A, tomadas aisladamente, ningún grado de confirmación. Desde el punto de vista holista, no es posible determinar si la evidencia ¬E, que refuta a S como un todo, disminuye más el grado de confirmación de A que el de H. Esta estrategia es imposible desde la perspectiva holista porque no existen tales grao dos de confirmación para hipótesis aisladas. En todo caso, sólo puede asignarse a S un grado de confirmación global. La solución bayesiana, en suma, simplemente ignora el holismo epistemológico y procede de una manera no holista. Esto no resuelve el problema de Duhem, como pretenden muchos bayesianos, porque, tal como yo lo entiendo, éste consiste precisamente en la cuestión del holismo epistemológico.
14. Conclusión
El esquema del método H-D que tomamos como punto de partida constituye un modelo tan general del proceso de la investigación científica que, prácticamente, ningún filósofo de la ciencia lo cuestiona en la actualidad. Como esquema general, el método H-D es indudablemente adecuado. Sin embargo, incluso en sus versiones más complejas, resulta excesivamente simple e incompleto. La teoría de la confirmación H-D, que sólo está implícita en el esquema general del método H-D, tiene un alcance limitado porque no puede aplicarse a las teorías probabilistas, que son posiblemente las más importantes de la ciencia contemporánea. Por otra parte, dentro de su dominio de aplicación, el de las teorías deterministas, deja sin resolver muchos problemas fundamentales. El método H-D, en suma, no proporciona una teoría satisfactoria de la confirmación.
Los bayesianos no rechazan el esquema general del método HD, pero sostienen que la teoría H-D de la confirmación es notoriamente incompleta y limitada. Los críticos bayesianos de la teoría HD de la confirmación no la rechazan completamente, puesto que aceptan que captura correctamente algunos de los rasgos generales de la inferencia científica como, por ejemplo, la idea de confirmación por implicación. La teoría bayesiana de la confirmación puede verse como un intento por conservar los aciertos generales del método H-D y superar las limitaciones de la teoría H-D de la confirmación. Un éxito indudable del programa bayesiano es la extensión del dominio del método al campo de las hipótesis estadísticas. La teoría bayesiana de la confirmación proporciona un esquema unificado que puede aplicarse a la contrastación de hipótesis deterministas y probabilistas por igual. Otro de los méritos del bayesianismo es que proporciona una teoría cuantitativa de la confirmación que, en principio, resuelve el problema de la conjunción irrelevante y ofrece un algoritmo general para calcular el grado de confirmación de cualquier teoría o hipótesis.
La teoría bayesiana de la confirmación retiene tres de las condiciones fundamentales del concepto de confirmación H-D: la confirmación por implicación, la refutación de una hipótesis general mediante un contraejemplo y la condición de equivalencia de Hempel. Además, incorpora algunas de las ideas originales de Popper acerca del valor epistemológico de las conjeturas audaces, tales como el retorno decreciente de las contrastaciones repetidas y el valor confirmatorio de las predicciones improbables. Sin embargo, la teoría bayesiana de la confirmación no es una simple extensión del método HD, ni de la teoría cualitativa de Hempel, ni de la teoría de la corroboración de Popper. Hay al menos alguna tesis de cada una de estas teorías de la inferencia científica que el bayesianismo no acepta. Entre ellas, la conversa de la condición de confirmación por implicación, es decir, el deductivismo estricto del método H-D; todas las condiciones de adecuación de Hempel, excepto la de equivalencia y la de implicación; y toda la teoría del grado de corroboración de Popper (de la que no nos hemos ocupado aquí).
El bayesianismo representa, en mi opinión, una teoría de la confirmación completa, tanto respecto de su alcance como de su capacidad de resolver muchos problemas epistemológicos tradicionales. No obstante, ya hemos señalado que no es capaz de resolver todos los problemas del método H-D. El holismo epistemológico y el problema de las hipótesis alternativas todavía esperan una solución satisfactoria. En tanto teoría general de la inferencia científica, el bayesianismo tiene multitud de problemas y anomalías, entre las cuales no es menor el problema de la subjetividad de los grados de confirmación, que representan sólo los grados de creencias de cada individuo. No es éste el lugar para tratar estas dificultades33. En última instancia, el programa bayesiano, como todo programa de investigación en pleno desarrollo, tiene que ser juzgado a largo plazo haciendo una evaluación global (y comparativa) de todos sus éxitos y fracasos. Posiblemente todavía sea prematuro sacar conclusiones generales o definitivas. Creo que lo único que puede decirse con certeza es que constituye un programa de investigación que ha hecho grandes progresos en teoría de la confirmación. Comparativamente, representa un avance considerable respecto de la noción de confirmación del método H-D. Sin embargo, sus anomalías son lo suficientemente importantes como para erigirse en serias amenazas potenciales para el futuro del programa.
La tarea de construir una teoría de la confirmación completamente satisfactoria todavía está pendiente. Si en el futuro el programa bayesiano no consigue superar sus dificultades, tarde o temprano será abandonado. En principio, cualquier otra teoría probabilista de la confirmación (en la que sean demostrables los teoremas 1-13) podría capitalizar los éxitos del bayesianismo que hemos reseñado. La pregunta fundamental en la situación actual es si la teoría de la probabilidad es adecuada para dar cuenta de la inferencia científica, como suponen los bayesianos y muchos de sus rivales, o si es necesario construir una teoría no probabilista de la confirmación. En este último caso, ya sabemos, al menos, dos cosas importantes: primero, que tal teoría no podrá ser una teoría. cualitativa y simple como el método H-D, y segundo, que deberá retener la mayor parte de los aspectos exitosos de la teoría bayesiana de la confirmación34.
1 La denominación tradicional es "método de la hipótesis", que algunos autores todavía emplean (por ejemplo, Achinstein 1985; y a veces también Popper 1983, p. 332). Los orígenes del método hipotético-deductivo se remontan hasta el siglo XVII, pero sólo se vuelve dominante en la segunda mitad del siglo XIX. Lalande (1929) es una obra ya antigua, pero todavía útil, sobre la historia del tema.
2 Para otras críticas al método cfr. Achinstein (1985) y Lipton(1991), pp. 18. 19 y 88.89.
3 Hempel (1966) contiene una formulación elemental, pero rigurosa, del método H-D en su versión confirmacionista. Braithwaite (1953) es una obra más antigua que ofrece una presentación más extensa, aunque no tan clara, de la misma versión.
4 Esta es una descripción muy resumida y simplificada, pero suficiente para los fines de este trabajo. Una exposición mucho más detallada del método hipotético-deductivo se puede encontrar en Klimovsky (1994), caps. 9-14.
5 Así lo hace, por ejemplo, Hempel (1966), p. 19.
6 Entre las críticos no bayesianos se cuentan Barker (1957), cap. VIII; Glymour (1980), pp. 29-48; y Miller (1987), cap. V. La crítica de Glymour ha sido la más influyente y algunos bayesianos, como Earman (1992, pp. 63-64 y 239n), la consideran definitiva. Para otros ejemplos de críticas bayesianas al método hipotético-deductivo cfr. Salmon (1967), pp. 21-27 y 114-116; Horwich (1982), pp. 11-12; Y Earman y Salmon (1992), pp. 48-49.
7 Salvo que se introduzcan hipótesis auxiliares ad hoc, tales como H →E (donde H es una hipótesis estadística y E un enunciado observacional cualquiera). El sistema formado por H y H → E implica la consecuencia observacional E, que H por sí sola no implica.
8 Popper, por ejemplo, comenzó por admitir que las hipótesis y teorías probabilistas no son científicas, sino metafísicas, puesto que no son falsables (Popper, 1959, p. 262). Pero inmediatamente revisó esta idea posición insostenible. Sostuvo que es posible encontrar alguna convención o "decisión metodológica" (Popper, 1959, p. 191) que haga falsables a las hipótesis estadísticas, aunque nunca propuso una regla metodológica precisa. Gillies (1971 y 1973, caps 8-10) fue el primero en hacerlo y Popper le prestó su apoyo enseguida (Popper 1959, p. 419, Addendum de 1972).
9 Popper (1959), Apéndice *IX y (1983) §§ 27-32. Popper sostiene que una hipótesis está corroborada cuando ha resistido todos los intentos de falsación sin haber sido refutada. Popper emplea el término "corroboración" en vez de "confirmación" con el fin de evitar las connotaciones probabilistas que tiene este último término en la lógica inductiva. Aquí no me ocuparé de la teoría popperiana del grado de corroboración. Es una teoría que tiene muchas dificultades técnicas y que, en general, ha teni do muy escasa aceptación (Diez y Moulines, 1997, pp. 426-430, contiene un buen sumario de las críticas principales a la teoría de Popper).
10 Carnap (1950), § 87. Para otras críticas a la teoría cualitativa de Hempel cfr. Salmon (1975) y Earman (1992), pp. 65-69. Aquí sólo he presentado una parte de la teoría de la confirmación de Hempel. El resto no es relevante a los fines de este trabajo.
11 Por cierto, ése no es el único objetivo. En sentido amplio la lógica inductiva se ocupa de estudiar todas las inferencias que no son deductivamente válidas pero proporcionan algún tipo de apoyo a sus conclusiones (cfr. Skyrms 2000, que es la mejor introducción elemental al tema). Muchos autores incluyen a la inferencia estadística en el campo de la lógica inductiva (por ejemplo, Baird 1992 y Hacking 2001).
12 Una excepción notable es el trabajo de Hossiason-Lindenbaum (1940), que contiene, entre otras cosas, el primer intento de solución de las paradojas de la confirmación cualitativa.
13 Hempel (1945); Hempel y Oppenheim (1945); Carnap (1945).
14 Como, por ejemplo, el de Earman (1992).
15 Conviene advertir que no todos los bayesianos piensan que su objetivo es construir una teoría de la confirmación. Horwich (1993), por ejemplo, mantiene una concepción terapéutica del bayesianismo. Considera que la finalidad principal del programa bayesiano es resolver problemas y perplejidades filosóficas, pero no proporcionar una teoría completa de la inferencia científica.
16 La axiomatización de Kolmogorov contiene solamente los axiomas 1-3 e introduce la noción de probabilidad condicional mediante la siguiente definición: si P(β) > 0, entonces, p(α / β) = def P(α & β) / P(β). El axioma 4 no requiere la restricción P(β) > O. Sobre las ventajas de emplear este axioma cfr. Gillies (2000), pp. 59 y 65-66.
17 La formulación generalizada más habitual emplea el concepto de espacio de probabilidad. Un espacio de probabilidad finito es una estructura X = ( ξ, P) que cumple los siguientes axiomas:

18 Para mayores detalles véase Gillies (2000), cap. 4, que ofrece una prueba elemental, pero completa, del llamado teorema de Ramsey-De Finetti.
19 Cfr., por ejemplo, Earman (1992) cap. 2; Howson y Urbach (1993), caps. 5 y 6; y Maher (1993), caps. 4 y 5. La discusión ha girado en torno a la validez de los llamados Dutch books arguments, de tipo sincrónico para la justificación del principio de coherencia, y de tipo diacrónico para la justificación del principio de condicionalización.
20 Esta es ciertamente una tesis muy discutible. Hay un amplio espectro de posiciones bayesianas no ortodoxas que la rechazan porque consideran que los grados de creencia de un agente deben estar sujetos a restricciones adicionales. Ejemplos de tales restricciones son las dos siguientes. Una es la llamada coherencia estricta, que es la conversa del Axioma 2, y afirma que sólo las verdades necesarias tienen probabilidad 1. Otra es la llamada función de probabilidad experta, que se define así Q es una función experta de probabilidad para P, si y sólo si, para toda proposición a, P(α / Q(α) = r) = r. La función Q puede representar simplemente la opinión de un experto en un tema determinado, pero también puede representar probabilidades objetivas, por ejemplo, la frecuencia relativa o el azar objetivo. De este modo, se pueden introducir probabilidades objetivas en el marco conceptual bayesiano. Por supuesto, los bayesianos ortodoxos, subjetivistas intransigentes, no admiten este tipo de restricciones.
21 Aquí me atengo a la interpretación bayesiana usual de la regla de condicionalización. Levi (1980) Cap. 10, adopta una interpretación diferente, que distingue entre un uso sincrónico y uno diacrónico de esta regla. En este trabajo no recogeré esa distinción.
22 Ctr. Jeffrey (1983), cap. 11, donde se presentan varios ejemplos de aplicación de esta regla.
23 Carnap (1950), p. 473, presenta el siguiente contraejemplo a la condición de implicación (también admitido por Salmon 1975, p. 7): si H = ( ∃ x) (Fx), E = Fa y K = Fb, entonces, P(H / E & K) = 1 = P(H / K). El contraejemplo no es aceptable desde el punto de vista bayesiano porque es un caso en el que K implica a H y, por consiguiente, P(H / K) = 1. En ese caso no hay confirmación incremental posible. En esas circunstancias tampoco es válida, por ejemplo, la confirmación por implicación del método H-D.
24 Popper mismo se expresa en estos términos: "Podemos decir, entonces, que, si tomamos e como una contrastación de h, la severidad de esta contrastación interpretada como apoyo evidencial, será tanto mayor cuanto menos probable sea e, dado b solo (sin h); esto es, cuanto menos sea p(e, b), la probabilidad de e dado b" (Popper, 1963, p. 390). Aquí b es el conocimiento antecedente, ahora usualmente representado como K.
25 Cfr. Jeffrey (1992), pp. 58-59, para una prueba gráfica de esta afirmación.
26 Esta es la llamada paradoja de la old evidence, formulada por Glymour (1980, pp. 85-93) y largamente discutida por los bayesianos (ctr. Earman, 1983, y, especialmente, Earman 1992, cap. 5, para un análisis equilibrado).
27 No es posible responder en general cuándo dos evidencias son de la misma clase y cuándo no lo son. La variedad es relativa al conocimiento aceptado en un determinado momento. Como señala Earman (1992, p. 79), después de Newton el movimiento de los proyectiles terrestres y el de los planetas se consideran evidencias del mismo tipo, mientras que antes de la revolución científica eran fenómenos de dos clases completamente diferentes.
28 Howson y Urbach (1993), pp. 161-164, reconocen esta dificultad y admiten que la teoría bayesiana no tiene una solución a la cuestión de cuándo elegir una hipótesis frente a otras rivales que también implican la evidencia. Sin embargo, es un hecho que los científicos se enfrentan a esta clase de problema y lo resuelven tomando decisiones bien definidas.
29 Earman (1992), cap. 6, contiene una buena exposición de este tema. Earman es especialmente escéptico acerca de la utilidad de los teoremas de convergencia para resolver el problema de la objetividad de la inferencia científica.
30 Tanto Earman (1992), pp. 83-85, como Howson y Urbach (1993), pp. 136-142, siguen las líneas generales de la solución de Dorling. Strevens (2001) es un reciente refinamiento de las ideas de Dorling.
31 Dorling (1979 y 1982) analiza varios casos históricos. En uno de ellos, por ejemplo, muestra que si los valores son, respectivamente, los siguientes: 0.9 y 0.6 para las probabilidades previas, y 0.001; 0.5 y 0.5 para las likelihoods, las probabilidades finales resultan P(H / ¬E & K) = 0.8976 y P(A / ¬E & K) = 0.003. En esa situación, argumenta, lo razonable es retener H sin cambios y modificar A.
32 En su discusión general del holismo, Laudan (1990, p. 70) ha expresado muy claramente este punto: "Cuando un sistema pasa un test, no podemos asignar un nivel específico de confianza a las hipótesis individuales componentes del sistema".
33 El libro de Earman (1992) es todavía la exposición más honesta y detallada de los problemas del bayesianismo. Shimony (1993), caps. 9 y 10, contiene también una revisión del programa bayesiano en una dirección menos subjetivista, la de un personalismo moderado completado con principios metodológjcos a posteriori. Aquí no me he ocupado de las ideas de Shimony, porque me limité al marco del bayesianismo ortodoxo, es decir, subjetivista. Salmon (1990) intenta conciliar el bayesianismo con algunas ideas de Kuhn. Las críticas al bayesianismo formuladas desde posiciones no bayesianas son muy abundantes y de muy diferente calidad. Por ejemplo, Miller (1987), cap, 7; Miller (1994), caps. 6-8; Mayo (1996), caps. 3, 4 y 10.
34 Agradezco a Eleonora Cresto por ayudarme a mejorar las demostraciones de algunos de los teoremas, También agradezco al anónimo autor del referato de Análisis Filosófico por sus detallados comentarios a la primera versión de este trabajo.
Bibliografía
1. Achinstein, P. (1985), "The Method of Hypothesis: What Is It Supposed to Do, and Can it Do It?", en: P. Achinstein y O. Hannaway (eds.), Obseruation, Experiment, and Hypothesis in Modern Physical Science, Cambridge, MA, The MIT Press, 1985, pp. 127-145. [ Links ]
2. Baird, D. (1992), lnductiue Logic: lnferring the Unknown, Upper Saddle River, NJ, Pearson Custom Publishing. [ Links ]
3. Barker, S. F. (1957), lnduction and Hypothesis: A Study ofthe Logic of Confirmation, New York, Cornell University Press. [ Links ]
4. Braithwaite, R. B. (1953), Scientific Explanation, Cambridge, Cambridge University Press. [ Links ]
5. Carnap, R. (1945), "On Inductive Logic", Philosophy of Science, 12, pp. 72-97. [ Links ]
6. Carnap, R. (1950), Logical Foundations of Probability, Chicago, University of Chicago Press. [ Links ]
7. De Finetti, B. (1937), "La prevision: ses lois logiques, ses sources subjectives", Annales de l'lnstitut Henri Poincaré, 7, pp. 1-68. (Traducción inglesa: "Foresight: Its Logical Laws, Its Subjective Sources", en: Kyburg, H. y H. Smokler (eds.), Studies in Subjectiue Probability, New York, Krieger, 1980, pp. 53-118). [ Links ]
8. Diez, J. A. y C. U. Moulines (1997), Fundamentos de filosofía de la ciencia, Barcelona, Ariel. [ Links ]
9. Dorling, J. (1979), "Bayesian Personalism, the Methodology of Scientific Research Programmmes, and Duhem's Problem", Studies in History and Philosophy of Science, 10, pp. 177-187. [ Links ]
10. Dorling, J. (1982), "Further Illustrations of the Bayesian Solution of Duhem's Problem" (Manuscript). [ Links ]
11. Duhem, P. (1894), "Quelques réflexions au sujet de la physique expérimentale", Revue des Questions Scientifiques, 36, pp.179-229. [ Links ]
12. Duhem, P. (1906), La théorie physique: son object, sa structure, Paris, M. Riviere. [ Links ]
13. Earman, J. (ed.) (1983), Testing Scientific Theories, Minneapolis, University of Minnesota Press. [ Links ]
14. Earman, J. (1992), Bayes or Bust? A Critical Examination of Bayesian Confirmation Theory, Cambridge, MA, The MIT Press. [ Links ]
15. Earman, J. y W. Salmon (1992), "The Confirmation of Scientific Hypotheses", en: M. Salmon y otros (eds.) Introduction to the Philosophy of Science, Inglewood Cliffs, NJ, Prentice Hall, 1992, pp. 42-103. [ Links ]
16. Gillies, D. (1971), "A Falsifying Rule for Probability Statements", British Journal for the Philosophy of Science, 22, pp. 231-261. [ Links ]
17. Gillies, D. (1973), An Objective Theory of Probability, London, Methuen. [ Links ]
18. Gillies, D. (2000), Philosophical Theories of Probability, London-New York, Routledge. [ Links ]
19. Glymour, C. (1980), Theory and Evidence, Princeton, Princeton University Press. [ Links ]
20. Grünbaum, A. (1976), "Is Falsifiability the Touchstone of Scientific Rationality? Karl Popper versus Inductivism", en: R. S. Cohen y otros (eds.), Essays in Memory of Imre Lakatos, Dordrecht, Reidel, 1976, pp. 213-250. [ Links ]
21. Hacking, I. (2001), An Introduction to Probability and Inductive Logic, Cambridge,. Cambridge University Press. [ Links ]
22. Hellman, G. (1997), "Bayes and Beyond", Philosophy of Science, 64, pp. 191-221. [ Links ]
23. Hempel, C. G., (1945), "Studies in the Logic of Confirmation", Mind, 54, pp. 1-26 y 97-121. [ Links ]
24. Hempel, C. G., (1965), Aspects of Scientific Explanation, New York, The Free Press. [ Links ]
25. Hempel, C. G., (1966), Philosophy of Natural Science, Upper Saddle River, NJ, Prentice Hall. [ Links ]
26. Hempel, C. G., y Oppenheim, P., (1945), "A Definition of 'Degree of Confirmation"', Philosophy of Science, 12, pp. 98-115. [ Links ]
27. Horwich, P. (1982), Probability and Evidence, Cambridge, Cambridge University Press. [ Links ]
28. Horwich, P. (1993), "Wittgensteinian Bayesianism", Midwest Studies in Philosophy,vol. 18, pp. 62-77. [ Links ]
29. Hossiason-Lindenbaum, J. (1949), "On Confirmation", Journal of Symbolic Logic, 5, pp. 133-148. [ Links ]
30. Howson, C. y P. Urbach (1993), Scientific Reasoning: The Bayesian Approach, 2ª ed., La Salle (Ill.), Open Court (1ª ed. 1989). [ Links ]
31. Jeffrey, R. (1983), The Logic of Decision, 2ª ed., Chicago, University of Chicago Press (1ª ed. 1965). [ Links ]
32. Jeffrey, R. (1992), Probability and the Art of Judgment, Cambridge, Cambridge University Press. [ Links ]
33. Klimovsky, G. (1994), Las desventuras del conocimiento científico: Una introducción a la epistemología, Buenos Aires, A-Z Editora. [ Links ]
34. Lalande, A. (1929), Les théories de l'induction et l'expérimentation, Paris, Boivin. [ Links ]
35. Laudan, L. (1990), Scienceand Relativism: Some Key Controversies in the Philosophy of Science, Chicago-London, University of Chicago Press. [ Links ]
36. Levi, I. (1980), The Enterprise of Knowledge: An Essay on Knowledge, Credal Probability, and Chance, Cambridge, MA, The MIT Press. [ Links ]
37. Lipton, P. (1991), lnference to the Best Explanation, London, Routledge. [ Links ]
38. Maher, P. (1993), Betting on Theories, Cambridge, Cambridge University Press. [ Links ]
39. Mayo, D. G. (1996), Error and the Growth of Experimental Knowledge, Chicago and London, The University of Chicago Press. [ Links ]
40. Miller, D. (1994), Critical Rationalism: A Restatement and Defence, Chicago and La Salle, Open Court. [ Links ]
41. Miller, R. W. (1987), Fact and Method: Explanation, Confirmatian and Reality in the Natural and the Social Sciences, Princeton, Princeton University Press. [ Links ]
42. Popper, K. R. (1959), The Logic of Scientific Discovery, London, Routledge. [ Links ]
43. Popper, K. R. (1963), Conjectures and Refutations: the Growth of Scientific Knowledge, London, Routledge. [ Links ]
44. Popper, K. R. (1983), Realism and the Aim of Science, London, Routledge. [ Links ]
45. Salmon, W. (1967), The Foundations of Scientific lnference, Pittsburgh, University of Pittsburgh Press. [ Links ]
46. Salmon, W. (1975), "Confirmation and Relevance", en: G. Maxwell y R. Anderson Jr. (eds.), lnduction, Probability, and Confirmation, Minneapolis, University of Minnesota Press, 1975, pp. 3-36. [ Links ]
47. Salmon, W. (1990), "Rationality and Objectivity in Science or Tom Kuhn Meets Tom Bayes", en: C. Wade Savage (ed.), Scientific Theories, Minneapolis, University of Minnesota Press, 1990, pp. 175-204. [ Links ]
48. Shimony, A. (1993), Search for A Naturalistic World View. Volume I: Scientific Methodology and Epistemology, Cambridge, Cambridge University Press. [ Links ]
49. Skyrms, B. (2000), Choice and Chance: An lntroduction to Inductive Logic, 4a ed., Belmont, CA, Wadsworth. [ Links ]
50. Strevens, M. (2001), "The Bayesian Treatment of Auxiliary Hypotheses", British Journal for the Philosophy of Science, 52, pp. 515-537. [ Links ]














