La afirmación “todos los triángulos son isósceles” es obviamente falsa; sin embargo, una supuesta “demostración” de tal aserto ha devenido muy popular. Al parecer, la autoría de dicha argumentación se debe a Rouse Ball (Rouse Ball, ¹⁹⁰⁵, pp. 38-39). Diversos autores han calificado aquella “prueba” como “falacia” o “sofisma”. Por ejemplo: Rouse Ball (¹⁹⁰⁵, p. 38), E. A. Maxwell (¹⁹⁶³, p. 13), Ya. S. Dubnov (²⁰⁰⁶, p. 2) ¹ , Jesse Norman (²⁰⁰⁶, p. 2), Marvin J. Greenberg (²⁰⁰⁸, p. 25), K. Manders (²⁰⁰⁸, p. 94). En su ya canónica obra, Hamblin enseña que un argumento falaz es, desde el punto de vista de una larga tradición que se remonta a Aristóteles, un argumento que no es válido, pero lo parece (Hamblin, ¹⁹⁷⁰, p. 12) ² . Aunque se ha objetado la validez histórica de esta tesis (Hansen, ²⁰⁰²), la caracterización propuesta posee la innegable virtud de ofrecer (en forma estilizada) una agenda neta para aquel que procure evaluar si una argumentación particular es falaz. Siguiendo pues tal perspectiva, si se pretende afirmar que un argumento dado es una falacia, dos cuestiones resultan esenciales: ¿por qué el argumento es incorrecto?, ¿por qué luce como si fuera correcto? Podría quizá objetarse que tal agenda depende críticamente de una caracterización obsoleta de falacia; no obstante, con inesenciales variaciones terminológicas (a los fines presentes) podría formularse ambas cuestiones apoyándose en definiciones actuales y reconocidas del fenómeno —véase, por ejemplo, Vega Reñón (²⁰¹³, p. 31)—.

Como es bien conocido, existen falacias que se apoyan en estrategias implementables en contextos muy diversos; por ejemplo, la denominada “falacia del hombre de paja” puede encontrarse en el debate político o académico —véase, por ejemplo, Tindale (²⁰⁰⁷, pp. 19 y ss.)—. Pero también hay falacias propias de un ámbito específico por el tipo de recursos argumentales a los que apelan; así se habla de “falacias filosóficas” —véase, por ejemplo, Nelson (²⁰¹⁶)— o de “falacias matemáticas” —véase, por ejemplo, Maxwell (¹⁹⁶³)—. Convengamos en llamar a las primeras “falacias globales” y a las segundas, “falacias locales”. En ocasiones, el esfuerzo por dar cuenta de aquellas interrogantes tradicionales antes anotadas enriquece la percepción de la estructura de la falacia en cuestión y, en particular, resalta o subraya ciertos aspectos relevantes del campo en que ocurre —contribuyendo así, si correspondiera, a una mejor comprensión de su filiación local—. El objeto de este artículo es, precisamente, responder aquellas persistentes interrogantes, respecto de la alegada falacia geométrica que concluye que todos los triángulos son isósceles. Tal exploración permite obtener cierta ganancia en su comprensión estructural y funcional y, a la vez, resaltar ciertos relevantes aspectos del denominado “razonamiento geométrico tradicional basado en diagramas”.

El itinerario expositivo es el siguiente. En el apartado 1 se expone el argumento en cuestión; en los apartados 2 y 3 se aluden a dos diagnósticos diversos de su incorrección (Dubnov, ²⁰⁰⁶; Manders, ²⁰⁰⁸), estudiándose con cierto detalle la propuesta de Manders; este examen permite extraer algunas importantes conclusiones sobre la naturaleza (geométrica) de esta falacia. El apartado 4 ofrece una conjetura (justificada en forma detallada) acerca del origen de su pertinaz capacidad persuasiva; aunque, en términos generales, esta falacia sigue en este respecto una metodología frecuente, su implementación es original e informativa (desde el punto de vista geométrico). Finalmente, el último apartado sugiere un rasgo que la coloca en una suerte de segundo orden y muestra cómo, entenderla en tal ubicación, contribuye a dar relieve a algunas cuestiones importantes del razonamiento geométrico basado en diagramas.

1.

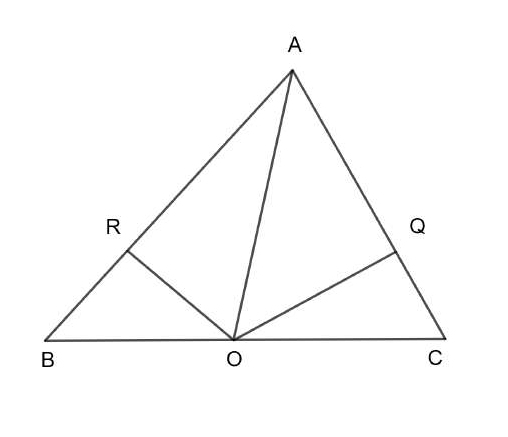
Se trata de “demostrar” que todos los triángulos son isósceles. El argumento es el siguiente. Sea ABC un triángulo (cualquiera)

Diagrama 1 

Siguiendo la exposición de Norman (2006, pp. 3-5), puede dividirse la prueba en cuatro bloques. Primero, se prueba que OB es igual a OC. Para ello, se demuestra, aplicando el criterio lado-ángulo-lado, que los triángulos ODB y ODC son congruentes, ya que DO es trivialmente igual a DO, DB es igual a DC, por bisección de BC, y, como OD es perpendicular a BC, los ángulos ODB y ODC son congruentes. Segundo, se prueba que AR es igual a AQ y OR es igual a OQ. Para ello basta demostrar que los triángulos ARO y AQO, por el criterio ángulo-lado-ángulo, son congruentes —AO es igual a AO, por bisección del ángulo BAC, los ángulos RAO y QAO son congruentes, y los ángulos ARO y AQO son congruentes pues OR es perpendicular a AB y OQ es perpendicular a AC—. Tercero, se prueba que RB es igual a QC. Para lograrlo, se demuestra, apelando al criterio ángulo recto-hipotenusa-lado, que los triángulos ORB y OQC son congruentes —pues ORB y OQC son rectos, porque OR es perpendicular a AB y OQ es perpendicular a AC, y ya se ha probado que OB es igual a OC y OR es igual a OQ—. Luego, el cuarto bloque, puede describirse así (como literalmente lo hace Norman):

1) AB = AR + RB

2) AB = AQ + QC

3) AB = AC

Luego el triángulo ABC es isósceles.

Norman destaca especialmente que las igualdades 1 y 2 están respaldadas en la lectura de la figura: así aísla perfectamente (en su interpretación) la contribución diagramática a la trama argumentativa.

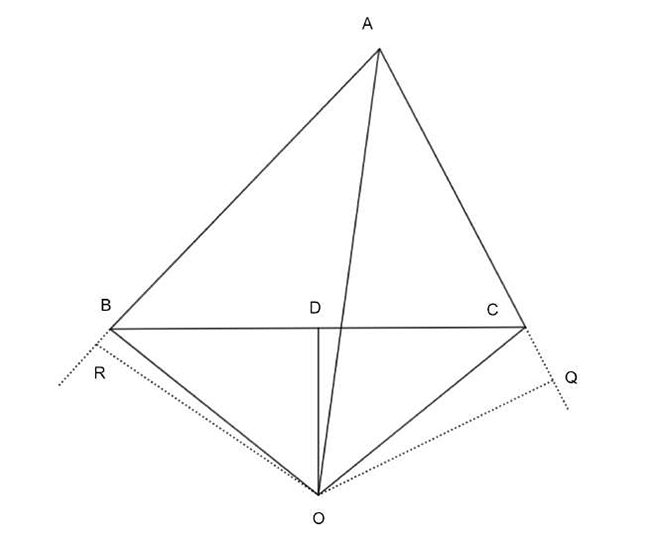
Esta argumentación inicial puede fortalecerse. Siguiendo a dicho autor, podría agregarse el tratamiento de otros dos casos, correspondientes a los diagramas siguientes:

Diagrama 2 

Diagrama 3 

Los diagramas 2 y 3, en la línea de Greenberg (2008, pp. 26-27), podrían tratarse así. En 2, por la misma argumentación anterior del caso 1, ARO es congruente con AQO y, luego, OR es igual a OQ y, por bisección de BC, OB es igual a OC, de modo que, por el criterio ángulo recto-hipotenusa-lado, los triángulos ORB y OQC son congruentes. Luego, RB es igual a QC. Por el mismo argumento del caso 1, se obtiene el resultado. En 3, por el mismo argumento, los triángulos ARO y AQO son congruentes, es decir, AR es igual a AQ y RO es igual a OQ. Un argumento igual al caso 1, basado en el criterio lado-ángulo-lado, permite afirmar la congruencia de BOD y COD, luego BO es igual a OC. Luego, dado que la longitud de las respectivas hipotenusas (BO, OC) son iguales y los respectivos lados (RO, OQ) son iguales, los triángulos OBR y OQC son congruentes. Luego BR es igual a CQ. Así

1’) AB = AR - BR

2’) AB = AQ - CQ

3’) AB = AC.

Como se ve aquí 1’ y 2’ se apoyarían en el diagrama (al igual que 1 y 2); la diferencia es que ahora la operación es la sustracción.

¿Por qué se ha hablado arriba de “fortalecimiento” de la argumentación? Porque esta discriminación en tres diagramas podría lucir como una adecuada y exhaustiva caracterización del “espacio lógico” del cual aquella debe dar cuenta. La “demostración”, dicho rápidamente, exhibiría la estructura de una argumentación por casos y los casos arriba considerados agotarían el espacio lógico.

2.

La conclusión de la anterior “demostración” es manifiestamente falsa; luego, algo debe andar mal en tal argumentación. Como se detalló, una lista de autores prestigiosos la reputan como una falacia geométrica. ¿Por qué geométrica? Sirviéndose de la caracterización resaltada por Hamilton, la respuesta podría constar de dos partes: porque el error reside en el uso de estrategias específicamente geométricas de razonar y la capacidad persuasiva del argumento falaz se apoya en la fiabilidad general de ciertos procedimientos inferenciales específicamente geométricos. No se trata de una estructura argumental falaz general que se instancia en un caso particular (alojado en una teoría específica), sino la concreción de una estructura argumental falaz local (i.e. geométrica). Además, como oportunamente se discutirá, la capacidad suasoria del argumento se apoya en, por así decirlo, razones específicamente geométricas. Luego es esta, propiamente, una falacia geométrica, no meramente una falacia en geometría. Ahora bien, justificar esta adscripción en una acepción clásica, como se adelantó, supone una doble tarea justificativa. Empecemos pues por el primer desafío: ¿por qué es erróneo el argumento?

La respuesta de Dubnov se inclina por una suerte de falla en la definición del espacio lógico a considerar: se habría omitido un caso; precisamente aquel que desmiente el resultado. Según este autor “No han sido examinados todos los casos posibles” (Dubnov, ²⁰⁰⁶, p. 24) y, precisamente, el caso no considerado es el que bloquea la supuesta prueba, luego: “Establecer este vacío en la prueba es suficiente para desacreditarla” (Dubnov, ²⁰⁰⁶, p. 24). Quizá merezca acentuarse que, desde la perspectiva de Dubnov, el diagnóstico que permite reputar este argumento particular como falacia no es sino una instancia más de una suerte de patrón “falacioso” general o común. Así lo describe:

A veces se requieren varios dibujos para un solo teorema, porque la demostración puede variar con las posiciones relativas de las partes de una figura. Por ejemplo, la demostración de un teorema sobre un ángulo inscrito en un círculo generalmente involucra tres posibilidades: el centro del círculo se encuentra sobre un lado del ángulo, dentro del ángulo o fuera de él. Es importante agotar todos los arreglos posibles de las partes de la figura; la omisión de cualquier arreglo al que no se pueda aplicar el razonamiento expuesto, por supuesto, invalida toda la demostración; puede ser precisamente por ese arreglo que el teorema resulta ser falso. (Dubnov, ²⁰⁰⁶, pp. 1-2)

La perspectiva de Manders parece alejarse explícitamente de tal diagnóstico. Según este autor, la estrategia de casos consiste en “buscar variantes diagramáticas que satisfagan las condiciones establecidas en el texto” (Manders ²⁰⁰⁸, p. 124) ³ . Avanza en este sentido una distinción entre caso y objeción, denominando “…caso a aquella variante que se reconoce que surge de explorar el control de la ramificación de casos; y objeción a la variante que surge de explorar el control de la apariencia” (Manders, ²⁰⁰⁸, p. 124). E inmediatamente agrega el autor

Por ejemplo, las variantes en el argumento de que todos los triángulos son isósceles surgen de explorar el control de la apariencia, no el control de la ramificación de los casos, pues pretenden apartarse de las mismas opciones métricas iniciales mediante una construcción completamente determinada; cualquier incapacidad de nuestra parte para distinguir cuál es la apropiada es una falla de control de la apariencia (Manders, ²⁰⁰⁸, p. 124)

Esto fundamenta su veredicto:

A partir de este criterio, Dubnov caracteriza equivocadamente su respuesta al desafío: lo que se pide no es que “consideremos todos los casos” (p. 24) sino que, dado uno de los diagramas, exploremos a fin de dar cuenta de su apariencia adecuada. (Manders, ²⁰⁰⁸, p. 124)

La línea argumental de Manders es clara. En cierta forma, su posición se sustenta en el contraste caso/objeción. Se está frente a un caso cuando se trata de una construcción que responde a una variante diagramática de las condiciones impuestas por el texto; una objeción aparece en la búsqueda por diseñar adecuadamente el diagrama correspondiente. Las diversas figuras consideradas arriba ejemplifican una labor del último tipo, que concluye con (esencialmente) el diagrama siguiente:

Diagrama 4 

Así pues, el problema residiría, según este autor entonces, en una falla en el diseño del diagrama o, expresado en su terminología, revelaría una dificultad en “el control de la apariencia” diagramática (Manders, ²⁰⁰⁸, pp. 94 y ss.). El problema no consiste en un error en la exhaustividad de una ramificación necesaria, como al parecer piensa Dubnov, sino en una incapacidad de producir la topología diagramática adecuada. El diagrama 4, para decirlo en la terminología de Manders, representa una objeción, no un caso.

El contraste entre ambos autores reside así en la explicación de la naturaleza del error (desde el punto de vista de la práctica diagramática). Parece difícilmente discutible la riqueza del punto de vista de Manders (más allá de su propia problematización de la distinción caso/objeción). Examinémosla con cierto detalle. Según su punto de vista, como se recuerda, es necesario distinguir entre atributos exactos y coexactos. Esta larga cita es elocuente:

Considérense todos los diagramas (imperfectos) que razonablemente se pudieran trazar con ciertas especificaciones dadas; algunos de ellos se pueden considerar relacionados por deformación o variación. Los atributos coexactos son aquellas condiciones que no se ven afectadas por algún espectro de todas las variaciones continuas de un diagrama especificado; de manera paradigmática que una región incluya a otra (la cual no se ve afectada independientemente de cómo se muevan y deformen hasta cierto punto los límites), o la existencia de puntos de intersección como los que se requieren en Euclides I.1 (que no se ve afectada independientemente de cómo se deformen hasta cierto punto las circunferencias). Los atributos exactos son aquellos que, para al menos alguna variación continua del diagrama, se mantienen solo en casos aislados; de manera paradigmática, la rectitud de las líneas o la igualdad de ángulos (ninguna de las cuales sobrevive ningún tipo de deformación salvo excepciones, por pequeña que sea). La distinción es del todo evidente para cualquiera que haya hecho suficientes diagramas y entienda qué se puede controlar y qué no en un diagrama razonablemente sencillo. (Manders, ²⁰⁰⁸, p. 92)

Los atributos exactos son aquellos que “desde el tiempo de Descartes, pueden expresarse por ecuaciones” y, en la práctica geométrica tradicional son expresados por “igualdades o proporcionalidades” (Manders, ¹⁹⁹⁶, p. 392); estos son extremadamente sensibles a la variación diagramática, pues “se mantienen solo en casos aislados”. Ejemplos de ellos son la igualdad de segmentos, la igualdad de ángulos, la congruencia de triángulos, la propiedad “recto” respecto de un ángulo, la propiedad “círculo” respecto de una curva... Es precisamente su alta sensibilidad a la “perturbación” de los diagramas, la que ubica a los atributos exactos fuera de “nuestro control”, tanto en lo que respecta al producir los diagramas como al “juzgarlos por la vista” (Manders, 1996, p. 392). Por tal razón, la práctica diagramática como tal es incapaz de proveer los medios para resolver las discrepancias entre los practicantes, en relación con la producción así como en la decodificación de los diagramas. Por ello, cuando se trata de atributos exactos, su justificación solo puede hacerse apelando al texto, no al diagrama. Por el contrario, los atributos coexactos o no exactos son aquellos que se mantienen firmes para “algún espectro de todas las variaciones continuas de un diagrama especificado”. “Podemos decir que expresan la topología del diagrama.” (Manders, ¹⁹⁹⁶, p. 393). Algunos ejemplos de ellos son regiones planas delimitadas no vacías: triángulos, cuadrados, círculos, ángulos… Las discrepancias respecto a los atributos coexactos puede tramitarse exitosamente y es esta la razón por la cual su justificación puede hacerse en forma consistente y estable apelando al diagrama. Dicho brevemente:

la distinción de atributos exactos/coexactos se relaciona directamente con los recursos que la práctica tiene para controlar la producción de diagramas y ofrecer una resolución de desacuerdos entre juicios con base en sus apariencias. La práctica tiene recursos para limitar el riesgo de desacuerdo en torno a atribuciones coexactas (explícitas) a partir de un diagrama; pero carece de tales recursos para las atribuciones exactas, y por consiguiente no podría permitirlas sin caer en un desorden de juicios en conflicto sin posibilidad de ser resuelto. (Manders, ²⁰⁰⁸, pp. 91-92)

Según este autor, muchas falacias se originan en asumir la lectura en el diagrama de una atribución exacta que visualmente parece darse, pero que es falsa. Ahora bien, este no es el caso de la falacia en consideración. Tal rasgo la hace especialmente interesante: la apelación al diagrama respeta la “regla de oro” impuesta por la distinción exacto-coexacto. La información que se lee en el diagrama es perfectamente legítima. ¿Cuál es esa información? La recogida en los pasos numerados como 1-2 y 1’-2’ —por supuesto, también queda cubierta la correspondiente a la información diagramática relevante para el tratamiento del diagrama 2—. Es decir: la génesis del error no se encuentra en la naturaleza de la información extraída de los diagramas. ¿Dónde se ubica entonces?

Quizá podría conjeturarse que, dado que las atribuciones exactas se expresan como igualdades y las atribuciones coexactas como desigualdades estrictas, un “diagrama inapropiado respecto de un rasgo coexacto” no debería acarrear “ninguna conclusión exacta inapropiada” (Manders, 2008, p. 94); desdichadamente la situación no es así. Para empezar, atributos coexactos no necesariamente dan lugar a desigualdades estrictas: en el caso que nos ocupa, como lo ilustra la notación de 1-2 y 1’-2’, aquí se tienen ecuaciones y de allí buena parte de su fortaleza inferencial:

Ciertas relaciones de ecuaciones son coexactas y se leen apropiadamente a partir de las relaciones topológicas en el diagrama: las inclusiones en un diagrama autorizan la aseveración de que el todo (región, ángulo, línea) es igual a la suma de sus partes separadas. (Manders, ²⁰⁰⁸, p. 94)

Y, como lo evidencia esta falacia, se obtiene una “conclusión exacta inapropiada”. El origen del error está, precisamente, en el “carácter inapropiado” del diagrama. O, usando la terminología de Manders, en un fallo en el control de la apariencia del diagrama. Su diagnóstico se expresa así:

Los recursos de la geometría tradicional para hacer frente a argumentos de esta naturaleza consisten en el control del diagrama; con exploración del comportamiento del diagrama como respaldo. Para triángulos que no se aproximan a ser isósceles, todo excepto la apariencia inicial dada se podría eliminar por refinamiento del diagrama sometido a la “disciplina de diagramas” […] de modo que podríamos bloquear la atribución de las otras apariencias que condujeran a la conclusión no deseada. Pero la capacidad del argumento geométrico para explotar esto se ve restringida por la sensibilidad ilimitada, para los triángulos próximos a isósceles, de la apariencia del diagrama construido. (Manders, ²⁰⁰⁸, p. 96)

Así pues, se trata del “control del diagrama”; para obtener ese control es necesario “explorar” cómo se comporta. En particular, en relación a la variación coexacta producida a partir de la asunción de ciertas condiciones exactas iniciales, es decir, cómo repercuten (en términos coexactos) las variaciones (en términos exactos) del diagrama en cuestión. Si se aproxima o se desvía el diagrama (en este caso) respecto del diagrama de un triángulo isósceles (ajuste exacto), cómo se comporta el diagrama (desde el punto de vista coexacto). Esta exploración es la que permite apreciar la sensibilidad del diagrama (como artefacto demostrativo de esta práctica matemática) a la fidelidad representacional exacta relevante; esta exploración permite así identificar los aspectos “eliminables” y por “refinamiento del diagrama” obtener el artefacto adecuado. Adviértase que no se trata este de un ejemplo de necesidad de demostrar una proposición para diversos casos; se trata más bien de refinar adecuadamente el diagrama antes que de evitar una falla en la exhaustividad del tratamiento de todos los casos relevantes. No obstante, la última observación de la cita de Manders revela el reconocimiento de una dificultad importante.

Este caso particular contrasta con aquellas falacias geométricas (tal cual se advirtió arriba) que se originan en extraer información exacta del diagrama; como es obvio, en tales argumentaciones la génesis del error residiría precisamente en tal operación. Esta diferencia entre falacias quizá pudiera alentar un contraste genérico entre aquellas que se originan en errores en la lectura del diagrama y aquellas cuya explicación se encuentra en fallas en la producción del diagrama. En cualquier caso, por supuesto, el error se manifestará en la trama argumental correspondiente, pero la génesis es diversa: en las primeras, el problema surge de una deficiencia en la interpretación de una cierta estructura gráfica; en las segundas, el déficit proviene de una inadecuada confección de una estructura gráfica específica. ¿Por qué es inadecuada? Según la interpretación de Dubnov, por incompletud. Según la interpretación de Manders, por error de diseño o fracaso en el control de la apariencia diagramática. Nótese que, independientemente de cuál interpretación se considere correcta, ambas comparten la locación de la equivocación en la actividad de confección o elaboración del dispositivo diagramático, es decir, en el desafío (esencial para la argumentación geométrica basada en este recurso) del control de la producción diagramática. Dicho en forma rápida, quizá la clasificación sugerida por la observación de Manders podría resumirse en falacias geométricas de interpretación y falacias geométricas de figuración —en ambos tipos o clases le corresponde al diagrama un papel estelar—.

La anterior clasificación posee interés además en un sentido más general. Ilustra en forma indirecta pero vívida la existencia de un mecanismo doble de control de la práctica geométrica tradicional respecto de la contribución diagramática. Por una parte, se tiene aquel control basado en la distinción exacto-coexacto y, por otra, el asociado a la disciplina diagramática (con sus componentes de exploración y refinamiento). Como era de esperar, estos mecanismos no funcionan en forma inconexa. En especial, el estudio del origen del error de esta falacia revela (como, por supuesto, apunta Manders) las implicancias desestabilizadoras de cierta información coexacta codificada y legítimamente extraíble del diagrama. Pero, además, revela una suerte de “dependencia” de rasgos coexactos de rasgos exactos en el diagrama original y esta es una importante clave exploratoria a fines de refinarlo.

3.

¿Cómo, a pesar de su incorrección, logra el argumento persuadir? —esta es, como se dijo, la segunda cuestión a responder—. ⁴ Una pista general para enfrentar este desafío es cierto rasgo general de las falacias: frecuentemente estos argumentos persuaden por su similitud estratégica superficial o aparente con argumentos correctos. En ese sentido, Vega Reñón ha señalado que algunos autores apelan a “la semejanza estructural con pautas de inferencia acreditadas” (Vega Reñón, ²⁰¹³, p. 100). Si se procura una explicación de esta naturaleza, pueden encontrarse aquí elementos de juicio que la apoyen.

En primer término, la consideración del doble control inferencial del recurso diagramático en el argumento geométrico tradicional promete prestar un servicio importante. El hecho de que este argumento falaz respete la “regla de oro” de la lectura de los diagramas podría decirse que lo dota de una capacidad suasoria muy importante; brevemente expresado: este uso de la figura satisface uno de los dos criterios de aquel control doble referido. En segundo lugar, su formulación más desarrollada corre como una argumentación por casos. Y esta estructura de ramificación de casos es, por supuesto, usada fiablemente en el razonamiento geométrico. Si se repara en la exposición del argumento falaz por parte de Dubnov se advertirá que apunta, directamente, a una decodificación por parte de la lectora, el lector de esta naturaleza:

Sea ABC un triángulo arbitrario (Fig. 5, 6 o 7); construya la bisectriz del ángulo C y la bisectriz perpendicular del lado AB. Consideraremos las diferentes posiciones relativas de estas líneas. (Dubnov, ²⁰⁰⁶, p. 9) ⁵

En tercer lugar, la determinación o definición del “espacio lógico” que supone la argumentación falaz parece respaldarse en una forma muy natural en el diagrama: podría decirse que o bien el punto O se encuentra al interior del triángulo ABC, o sobre la base BC o es externo al triángulo. Se trata de tomar en cuenta todos los “arreglos posibles de las partes de la figura” (para usar la terminología de Dubnov). Netz ha llamado la atención, en su ya clásica obra, sobre lo que él denomina “starting-points” (Netz, ¹⁹⁹⁹, pp. 169 y ss.). ⁶ Estos “puntos de partida” son, esencialmente, aserciones que se asumen como necesariamente verdaderas, sin ofrecerse justificación. Existen, según dicho autor, un tipo de puntos de partida denominado “intuiciones”; en una formulación rápida, se trata de aserciones “obviamente verdaderas”. Escribe Netz

The most important intuition, perhaps, is yet another relative of ‘decomposition’ intuitions, only here the whole of logical space is decomposed. [La intuición más importante es quizá otra emparentada con las intuiciones de “descomposición”, solo que aquí el espacio lógico es descompuesto en su totalidad.] (Netz, ¹⁹⁹⁹, p. 184)

Estas operaciones de descomposición del espacio lógico juegan un papel crítico en la demostración euclidiana. Netz refiere a la estrategia argumental que explota tal descomposición como “grid”. Luego un punto relevante es cómo se define la red o cuadrícula:

A certain grid is laid over the logical space, and everything is said to fall under it. The grid is exhaustive, hence the necessity it conveys. After all the options have been surveyed, no alternative should be left open. [Una cierta cuadrícula se aplica al espacio lógico y todo cae bajo ella. La cuadrícula es exhaustiva y de allí la necesidad que transmite. Después de que todas las opciones han sido examinadas, ninguna alternativa debería dejarse abierta.] (Netz, ¹⁹⁹⁹, p. 184)

Este autor advierte que, en algunos casos, tal delimitación o estructuración del espacio lógico es producto de una intuición más bien lógica, pero, en otros, se trata de una intuición más espacial (Netz, ¹⁹⁹⁹, p. 184). Un ejemplo elocuente de preeminencia diagramática en la definición de la descomposición pertinente (siguiendo a Netz) es IV.5. Se lee en Euclides

Divídanse en dos partes iguales las rectas AB, AГ, por los puntos ∆, E [I, 10], y a partir de los puntos ∆, E trácese ∆Z, EZ formando ángulos rectos con AB, AГ; entonces coincidirán o bien dentro del triángulo ABГ o sobre la recta BГ o fuera de BГ

La figura es

A primera vista, si se repara en la estrategia descripta en el texto euclidiano y se inspecciona el diagrama, la similitud con la partición del espacio lógico de la argumentación falaz resulta evidente. Por supuesto, la falacia en discusión contribuye a esclarecer que tal partición es, por decirlo en forma rápida, más profundamente heterogénea de lo que luce a primera vista: no alcanza la pura inspección del diagrama para asegurar su corrección. Pero, a los fines presentes, el aspecto que se desea resaltar es que evidencia un indiscutible nivel de “semejanza estructural” (para decirlo con las palabras de Vega Reñón).

Una coda sintética de estas consideraciones quizá podría formularse así: siguiendo la perspectiva del control doble arriba aludido, la semejanza o similitud discutida hundiría sus raíces en este caso tanto en el plano de la lectura del diagrama (en virtud de su respeto a la “regla de oro”) como en el plano de su producción (en virtud de su fina semejanza estructural). Luego, no debiera sorprender su fortaleza suasoria.

Como es obvio, el contraste entre falacias de lectura y falacias de figuración impacta sobre la naturaleza de la capacidad suasoria correspondiente y las correspondientes políticas de evitación del error argumental. En los casos de las primeras, el potencial engañador deviene de una cierta indistinción o ambigüedad en los atributos legítimamente predicables del diagrama (cuyo esclarecimiento teórico lo aportaría la neta distinción entre atributos exactos y coexactos). En ausencia de tal clarificación, el uso ilegítimo resultaría difícilmente distinguible del legítimo y la semejanza entre uno y otro devendría de tal ambigüedad —aunque la práctica geométrica virtuosa habría encontrado mecanismos exitosos de evitación del error—. Tal similitud sería la responsable entonces de los errores de lectura y, consecuentemente, del poder persuasivo del argumento falaz (qua argumento geométrico). La incorporación (implícita o explícita) de tales criterios normativos de lectura del diagrama a la práctica geométrica en cuestión resultaría el antídoto correspondiente.

En los casos de las falacias de figuración, lo que enseña al menos el ejemplo discutido es que la semejanza estructural es poderosa y la política de corrección se apoya en un proceso de exploración o refinamiento diagramático sofisticado (si se simpatiza con la perspectiva de Manders) o en una exigente comprensión de la distinción de casos (si se opta por la óptica de Dubnov).

4.

Una exploración como la desarrollada hasta aquí puede deparar beneficios en términos de una mejor comprensión de la falacia local y, eventualmente, resaltar algunos aspectos relevantes del campo en el cual esta se inserta. Empecemos por el primer punto. Maxwell, en su obra Fallacies in Mathematics, sugiere distinguir entre equivocaciones (“mistakes”), errores de poca monta y sin consecuencias, una metida de pata (“howler”) que es un error que “inocentemente” conduce a un resultado válido y una falacia (“fallacy”) que caracteriza, contrastándola con aquel, así: “Por contraste, la FALACIA conduce mediante engaño a una conclusión errónea pero plausible” (Maxwell, ¹⁹⁶³, p. 9).

Como se advierte, la caracterización de Maxwell no se aleja en demasía de la propuesta aristotélica resumida por Hamblin (aunque no se explicite la comprensión argumental del fenómeno, el contexto es elocuente). En particular, parecen estar presentes en la definición del matemático las dos tradicionales dimensiones exhibidas en la del filósofo. Una observación interesante, sin embargo, es que la falacia que hemos discutido arriba parece no encajar (estrictamente) con esta caracterización. Pues, difícilmente, alguien consideraría “plausible” la evidentemente falsa afirmación que todos los triángulos son isósceles.

El necesario ajuste correctivo no es mayor, pero posee algún interés resaltarlo. En el caso estudiado, la conclusión no es el objeto del engaño de la estrategia argumentativa falaz: tal objeto parece limitarse al propio argumento. Dubnov, en tal sentido, aísla perfectamente el problema (aunque no se refiera directamente al ejemplo aquí considerado):

Entre estas proposiciones hay algunas cuya falsedad será inmediatamente evidente para el lector, por ejemplo, “Un ángulo recto es igual a un ángulo obtuso”. Aquí nuestra tarea es descubrir el error en la prueba. Tales pruebas de afirmaciones deliberadamente incorrectas se conocen desde la Antigüedad como “sofismas”. (Dubnov, ²⁰⁰⁶, p. 2)

Pero, entonces, ¿cuál es el objeto de tal operación? A diferencia de las falacias tradicionales, el objetivo del agente aquí no sería “contrabandear” la conclusión, una tarea, por lo demás, imposible en este caso, sino, dada la evidencia de su falsedad, “contrabandear” la estrategia argumental (como legitimada en el contexto del razonamiento geométrico basado en diagramas, es decir, como demostración). ¿Qué resultado se perseguiría a través de esa operación? Desacreditar en forma contundente la fiabilidad del razonamiento geométrico basado en diagramas. Puede, por ejemplo, leerse en la clásica obra de Klein (luego de la afirmación de la relevancia de establecer los axiomas para la relación “estar entre”):

Ellos [los axiomas referidos] son precisamente tan importantes como cualquier otro axioma, si deseamos desarrollar la geometría como una ciencia realmente lógica, que, luego de seleccionados sus axiomas, no haya ya necesidad de recurrir a la intuición y a las figuras para deducir sus conclusiones. Tal recurso es, sin embargo, estimulante y, por supuesto, siempre permanecerá como una ayuda necesaria en la investigación. Euclides, quien no cuenta con estos axiomas, siempre tiene que considerar diferentes casos con la ayuda de figuras. Como él le concedió tan poca importancia al dibujo geométrico correcto, hay un peligro real que un estudiante de Euclides pueda, a partir de una figura falsamente dibujada, llegar a una conclusión falsa. Es así que surgen numerosos sofismas llamados geométricos. Ellos son pruebas formalmente correctas de teoremas falsos, que se apoyan en figuras equivocadamente dibujadas, i. e., que contradicen los axiomas de “estar entre”. Como un ejemplo, daré uno de tales sofismas, que es ciertamente conocido por algunos de ustedes, aquel que “prueba” que todos los triángulos son isósceles. (Klein, ²⁰¹⁶, p. 228)

Lo que resultaría aquí plausible, en la terminología de Maxwell, no sería la conclusión: sería la argumentación (qua demostración). La falacia sigue poseyendo como función “pasar gato por liebre”, la diferencia está aquí en que el gato es la calidad de la estructura argumentativa misma, no la conclusión. “Ejemplificar” la debilidad de la demostración basada en diagramas es la motivación que lleva a Klein a incluirla en su texto.

Existirían así falacias que poseen un propósito o una funcionalidad de primer orden (incidir en el tema del argumento a través de la aceptación de la conclusión) y falacias que procuran un objetivo de segundo orden (por ejemplo: incidir en la reflexión metaargumental a través de la aceptación de cierta propiedad o calidad del argumento). Es precisamente este rasgo (en este caso) el que la hace apta para la función con que a veces se esgrime, a saber: evidenciar las limitaciones del razonamiento geométrico diagramático. ⁷ Aunque no comparte tal punto de vista, el modo cómo Norman introduce su exposición de este argumento falaz es elocuente ⁸ :

Consideremos un ejemplo específico de la naturaleza aparentemente poco confiable y engañosa de los diagramas en la geometría de Euclides: un argumento falaz bien conocido destinado a respaldar que todos los triángulos son isósceles. (Norman, ²⁰⁰⁶, p. 2)

En general, ¿qué nos enseña esta falacia sobre aquella forma de razonamiento? La explicación de Manders es una réplica satisfactoria y contundente acerca de cómo la práctica geométrica tradicional lidió con este tipo de desafíos; por otra parte, la evidencia de la estabilidad histórica de un cuerpo teórico como el euclidiano parece no permitir dudas al respecto. Si se asume una perspectiva afín a la legitimidad de la inferencia heterogénea (o, aún más estrictamente, al caso particular de práctica inferencial heterogénea constituido por el que se ha denominado “razonamiento geométrico tradicional basado en diagramas”), un aspecto importante sobre el que este argumento llama la atención es la relevancia, en este contexto, del control sobre la fidelidad representacional del diagrama en relación a atributos exactos. Podría pensarse ingenuamente que, como la información extraíble legítimamente del diagrama es coexacta, debiera ser la fidelidad a esta la única relevante. Así mismo un fenómeno presente en el contexto euclídeo podría incluso abonar ese prejuicio, a saber: la ambigüedad interpretativa (Seoane, ²⁰²¹). Es decir, muchas veces, en momentos distintos de una demostración, desde el texto, se atribuyen diversos atributos exactos a una misma porción o zona de un diagrama. Estos exámenes demuestran que aquella conjetura ingenua es falsa. El estudio de esta falacia muestra que solo una reflexión atenta a las relaciones de fidelidad/infidelidad representacional diagramática respecto de aspectos exactos ofrece la clave para identificar la fuente del error: los procesos de exploración y refinamiento diagramático se apoyan en consideraciones de esta índole. Esta observación general supone así mismo otra lección relevante: la cooperación visual-lingüística es más sustantiva que lo que podría sospechar una mirada superficial y, en particular, no se deja captar por un patrón o modalidad simple y única en la relación entre texto y gráfico. Incluso resulta aleccionador este ejemplo para (tal como sugiere Manders) intentar diferenciar diversos objetivos productivos diagramáticos: aquellos orientados a la fijación del espacio lógico de aquellos guiados a controlar la apariencia del diagrama. Quizá una enseñanza profunda que revela esta falacia sea la necesidad de entender la producción (no solo la lectura) diagramática en clave heterogénea.