Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO
Related links
-
 Similars in
SciELO
Similars in
SciELO  uBio
uBio
Share
BAG. Journal of basic and applied genetics
On-line version ISSN 1852-6233
BAG, J. basic appl. genet. vol.18 no.1 Ciudad Autónoma de Buenos Aires Jan./June 2007
ARTÍCULOS ORIGINALES
Comparación de ordenaciones de muestras a nivel de secuencias de aminoácidos, nucleótidos y marcadores RFLP
1Bruno C., 1Arroyo A., 2Giménez Pecci M. P. y 3Balzarini M.
1Becaria doctoral de CONICET.
2Investigador del Instituto de Fitopatología y Fisiología Vegetal IFFIVE-INTA.
3Investigador de CONICET. Profesor de la UNC.
Estadística y Biometría. Facultad de Ciencias Agropecuarias. Universidad Nacional de Córdoba. Av. Valparaíso s/n Ciudad Universitaria. 5000. CC 509. Córdoba. Argentina. cebruno@agro.uncor.edu
RESUMEN
Las distancias entre muestras obtenidas a partir de datos de secuencias de nucleótidos, aminoácidos y de marcadores moleculares son frecuentes en Biología Molecular. El Escalamiento Multidimensional (MDS) es una técnica estadística que permite conocer la estructura subyacente entre muestras vía representación gráfica de su matriz de distancias. Con m muestras evaluadas en p nucleótidos, p aminoácidos o p marcadores, el MDS comienza con una matriz de distancia Dm×m y obtiene un nuevo sistema de coordenadas para ordenar las muestras en un plano. En este trabajo se ordenan muestras de cDNA viral mediante MDS aplicado sobre distintas matrices de distancia: Jones-Taylor-Thornton (distancia entre secuencias de proteínas), Felsenstein84 (distancia entre secuencias de nucleótidos), raíz cuadrada del complemento a uno de los valores de identidad obtenidos durante el alineamiento múltiple de secuencias de aminoácidos y nucleótidos y raíz cuadrada del complemento a uno de los coeficientes de similitud de Dice y Emparejamiento Simple entre perfiles de datos de marcadores RFLP. Una nueva versión de MDS es propuesta para mostrar simultáneamente ordenaciones de diferentes tipos de datos genómicos. Las ordenaciones bidimensionales de las muestras virales, obtenidas bajo diferentes modelos de distancia, fueron comparadas por rotación procrustes y se obtuvo una ordenación de consenso.
Palabras Clave: Distancia euclídea; Escalamiento multidimensional métrico; Rotación procrustes; Virus del Mal de Río Cuarto.
ABSTRACT
Between-sample distances obtained from nucleotide and aminoacid sequences as well as from DNA marker data are frequent in Molecular Biology. Multidimensional Scaling (MDS) is a statistical technique that allows to explore the underlying relationship among samples via graphical representation of the matrix containing the distances among samples. With m samples evaluated at p nucleotide, p aminoacids or p molecular markers, MDS uses a distance matrix Dm×m as input, providing a system of new axes so as to order the m samples in planes. We ordered four viral cDNA samples through MDS applied to different distance matrixes: Jones-Taylor-Thornton (distance among protein sequences), Felsenstein84 (distance among nucleotide sequences), square root of complement to one of the identity scores obtained during multiple alignment of aminoacid and nucleotide sequences, and square root of complement to one of Dice´s and Simple Matching similarity coefficients among RFLP profiles. A new version of MDS is proposed to simultaneously show ordinations from different types of genomic data. The bidimensional ordinations of the viral samples obtained from different distance models were compared by Procrustes rotation and a consensus ordination was obtained.
Key Words: Euclidean distance; Metric multidimensional scaling; Procrustes rotation; Mal de Río Cuarto virus.
Introducción
El explosivo crecimiento de bases datos construidas a partir del desarrollo de métodos para obtener información genómica, demanda nuevas estrategias de análisis de datos. La obtención de secuencias de nucleótidos y/o aminoácidos es frecuente en investigaciones en Biología Molecular. Ésta información es utilizada para encontrar patrones diagnóstico que permiten caracterizar familias de proteínas, detectar o demostrar homología entre nuevas secuencias y familias de secuencias existentes, ayudar a predecir estructuras secundarias y terciarias de nuevas secuencias así como para sugerir cebadores iniciales de oligonucleótidos para PCR (Thompson et al., 1994). Frecuentemente estos estudios se completan con datos de marcadores moleculares. Aún cuando los datos de aminoácidos, nucleótidos y marcadores moleculares se producen sobre las mismas muestras, rara vez se realiza un análisis integrado de la información. El Escalamiento Multidimensional (MDS) (Gower, 1975) es una técnica multivariada con un alto potencial para su aplicación en el análisis de datos genómicos. Esta herramienta permite explorar la estructura de relaciones entre las muestras y representarlas en uno o más planos (espacio de baja dimensión). Se supone que las relaciones entre pares de muestras se pueden representar mediante una medida de similitud o de distancia. Cuando la medida de proximidad entre las entidades i y j se expresa en términos de distancia (dij), la técnica se conoce como escalamiento multidimensional métrico o análisis de coordenadas principales (Johnson and Wichern, 1998). Las matrices de distancia, sobre las cuales se estudia la estructura de relaciones, presentan la característica de ser simétricas, i.e., dij =dji, tener elementos no negativos, i.e., dij > 0 si i¹j, y ceros en la diagonal (i.e., dii =0). Una matriz de distancia se considera euclídea si representa muestras en algún espacio euclídeo tal que la distancia dij entre las muestras i y j, cumple con la desigualdad triangular, i.e., dij £ dji + dki.
EL MDS aborda el problema de representar el conjunto de muestras multidimensionales (cada muestra es analizada en p dimensiones - p nucleótidos, p aminoácidos o p marcadores) en algún espacio euclídeo de menor dimensión (preferentemente un plano) tal que la matriz de distancia en ese espacio reducido, llamémosla A, se aproxime lo mejor posible a la matriz de distancia en el espacio multidimensional, llamémosla D.
Para realizar un MDS clásico se parte de las distancias dij, se definen la matriz A={aij}, donde aij es la mitad de la distancia al cuadrado entre dos muestras, es decir, y la matriz B={bij}, donde bij=(aij-ai.-a.j+a..). La matriz B, es llamada matriz producto interno, si ésta es semidefinida positiva entonces puede concluirse que los elementos de la matriz D son distancias euclídeas. El MDS se basa en la descomposición espectral de la matriz B, se obtienen los autovalores y autovectores de B. La suma de los autovalores representa la varianza total en la matriz D, y la proporción de los autovalores asociados a los ejes (autovectores) que conforman un plano, provee una medida de la proporción de las interdistancias entre muestras explicadas por ese plano. La coordenada principal (CP) de la muestra i sobre el eje k es calculada como.
Es importante notar que la variación de las coordenadas principales dependen de la escala de la medida de distancia usada . En este trabajo, se propone usar una versión escalada de estas componentes para representar las interdistancias observadas a partir de datos geonómicos de distinta naturaleza en sistemas de coordenadas con igual rango de variación en sus ejes. La versión escalada denotada como MDS* se obtiene dividiendo los elementos de B por la suma de sus autovalores (traza) previo a su descomposición espectral.
El objetivo de este trabajo es ilustrar los resultados producidos por MDS clásico y por MDS* (previo escalado de la matriz de entrada) a través de su aplicación sobre un conjunto de muestras de cDNA del virus del Mal de Río Cuarto (MRCV) que fueron sometidas a secuenciación de nucleótidos, secuenciación de aminoácidos y a la restricción por endonucleasas para obtener datos de marcadores RFLP.
Material y Métodos
Datos
Se trabajó con datos moleculares provenientes del genoma viral del Mal de Río Cuarto, para aislamientos provenientes de cuatro localidades, Río Cuarto (RC), Pergamino (P), Jesús María (JM) y Tafí del Valle (TV). El Mal de Río Cuarto es la enfermedad viral más importante del maíz en Argentina. Su agente causal es un reovirus cuyo genoma está compuesto de 10 segmentos de doble cadena de RNA; particularmente los datos provenientes de los segmentos S1 y S10, son de importancia biológica. El segmento S1, es el mayor de todo el genoma del virus (aproximadamente 4500bp), codifica para una proteína de 168kDa, cuya posible función es ser la RNA polimerasa RNA dependiente, enzima necesaria para la síntesis y replicación viral. El S10, es el segmento de menor tamaño, se estima que codifica para la proteína mayoritaria exterior del capsidio viral, proteína de la cubierta del virus con la cual se relaciona dándole la apariencia superficial. Esta proteína es la responsable de las relaciones con el medio y de las principales características biológicas y sexológicas del virus. La comparación de datos de secuencias de nucleótidos, aminoácidos y de marcadores moleculares entre aislamientos de distintas procedencias permite inferir aspectos biológicos relacionados con la mayor o menor conservación/variabilidad del genoma (Giménez Pecci et al., 2001; 2005).
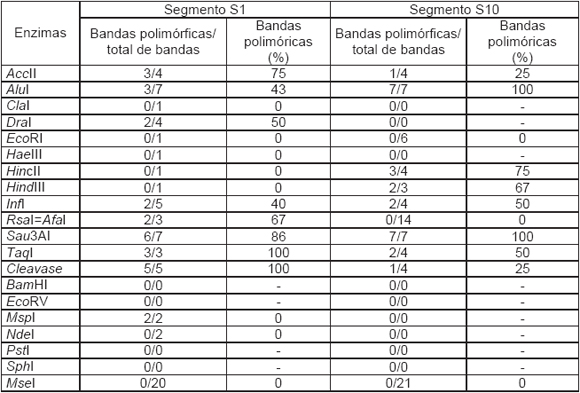
Para ilustrar la implementación de MDS, se usaron datos de los segmentos S1 y S10. La secuencia observada del S1 corresponde aproximadamente al 46% del total del segmento ( ≅ 2200bp), mientras que la del segmento S10 corresponde al 92% del total del segmento ( ≅ 1800bp). El RNA viral se transcribió a DNA empleando RT-PCR con la enzima SuperScript II (BRL). Para los RFLP se utilizó el producto amplificado por PCR, mientras que para la secuenciación, los productos amplificados se clonaron en el vector pGEM-T Easy (Promega). Se utilizaron 19 endonucleasas de restricción y la enzima Cleavase para los RFLP obteniéndose los datos que se muestran en la Tabla I (Giménez Pecci et al., 2005).
Tabla I. Polimorfismo producido por enzimas de restricción en los segmento S1 y S10 de muestras de cDNA del genoma viral del Mal de Río Cuarto.
Obtención de matrices de distancias
Distancias basadas en valores de identidad entre secuencias de nucleótidos y entre secuencias de aminoácidos
Los coeficientes de similitud basados en valores de identidad constituyen el punto de partida de los alineamientos múltiples automáticos de secuencias de nucleótidos y/o aminoácidos. Estos alineamientos pueden ser llevados a cabo con programas como ClustalW (Thompson et al., 1994) los cuales producen una tabla de “acuerdos” y “desacuerdos” entre secuencias que, penalizados por la inserción o delección de secuencias de diferentes longitudes, resulta en una matriz de “valores de identidad”. Para calcular estos valores se contabiliza el número de K segmentos de nucleótidos o aminoácidos coincidentes entre el par de secuencias que se están comparando y se le aplica una penalización fija por cada ausencia de nucleótido o aminoácido (gap). El valor de identidad es calculado como el número de identidades dividido por el número de segmentos comparados después de excluir las posiciones que corresponden a ausencias de bases (gaps) y es expresado en porcentaje (homología). estos valores pueden ser convertidos a distancias dividiendo por 100 y restando desde 1. Las matrices conteniendo los valores de identidad entre cada par de secuencia pueden ser obtenidas, directamente, a partir de los programas PROTDist para secuencias de aminoácidos (Felsenstein, 1993a) y DNADist para secuencias de nucleótidos (Felsenstein, 1993b) o bien con el programa BioEdit (Hall, 2001).
Distancias entre secuencias de aminoácidos basadas en la métrica de Jone, Taylor y Thornton
Las matrices de distancias a partir de secuencias de aminoácidos pueden ser obtenidas bajo diferentes modelos de reemplazo de aminoácidos. Por ejemplo: a) modelo de Jones, Taylor y Thornton (Jones et al., 1992), b) modelo de matrices de probabilidad desde bloques (Veerasamy et al., 2004), c) modelo empírico PAM (Dayhoff, 1979) y d) modelo de Kimura (Kimura, 1983), entre otros. Particularmente, el modelo de Jones, Taylor y Thornton (JTT) es usado por defecto por los programas PROTDist y BioEdit. Este modelo es similar al modelo PAM, uno de los más difundidos para comparar secuencias de aminoácidos, pero es especialmente recomendado para secuencias largas por el reconteo que realiza del número de cambios observados en aminoácidos. La distancia es escalada por la fracción esperada de aminoácidos cambiados, y por tanto se expresa como unidades de dicha fracción.
Distancias entre secuencias de nucleótidos basada en la métrica Felsenstein84
Las distancias entre secuencias de nucleótidos también pueden obtenerse a partir de diferentes modelos de sustitución, por ejemplo: a) modelo de Jukes y Cantor (Jukes and Cantor, 1969), b) modelo de Kimura (Kimura, 1980), c) modelo Felsenstein84 (F84) (Kishino and Hasegawa, 1989; Felsenstein and Churchill, 1996) y d) modelo de distancias LogDet (Barry and Hartigan, 1987; Lake, 1994; Steel, 1994; Lockahart et al., 1994). El modelo de Kimura 2-parámetros, al igual que el modelo de Jukes-Cantor, asume que las mutaciones o sustituciones de nucleótidos ocurren aleatoria e independientemente en cada sitio de comparación. Debido a que la tasa de transiciones es generalmente mayor que la tasa de transversiones, el modelo de Kimura incluye dos parámetros distintos, uno para la tasa de transición y otro para la tasa de transversión, para indicar que no todos los cambios se realizan con igual probabilidad, como lo hace el modelo Jukes-Cantor. El modelo F84, es similar al de Kimura 2-parámetros pero permite, además, incorporar distintas frecuencias para las bases; cuando las bases están en equilibrio el modelo F84 produce los mismos resultados que el modelo Kimura 2-parámetros. La diferencia entre tasas de transición y transversión se indica mediante el cociente transición/ transversión (usualmente se supone que este cociente es dos). Las distintas frecuencias para los cuatro nucleótidos pueden obtenerse directamente desde los datos (i.e., frecuencias empíricas). La distancia F84 es la métrica utilizada por defecto por los programas DNAML para filogenia (Felsenstein, 1993c), DNADist y Bioedit.
Distancias entre perfiles de marcadores RFLP
Los datos de marcadores moleculares RFLP pueden disponerse en una matriz de datos binarios, donde cada fila representa una banda y cada columna una muestra. Así, diremos que es una matriz de datos p×m considerada como un arreglo de las observaciones registradas sobre p marcadores en m muestras, donde el elemento de la fila i, columna j, es 1 o 0 según la muestra j presente o no una “banda” para el marcador i. Los valores registrados sobre el conjunto de p marcadores, para una misma muestra, conforman el perfil molecular de la muestra. Las métricas usadas para expresar la distancia entre dos perfiles moleculares deben respetar la estructura binaria de los datos. Gower (1985) y Jackson et al., (1989) propusieron índices que permiten cuantificar la similitud entre dos observaciones multidimensionales de variables binarias. Mediante transformación de los índices de similitud es posible obtener medidas de distancias entre las muestras. Para inferir sobre distancia genética es necesario suponer que el número de loci del marcador analizado es suficientemente alto, que los loci son bialélicos y que los marcadores se encuentran distribuidos uniformemente sobre el genoma de los individuos que se comparan.
Al comparar los perfiles moleculares provenientes de dos muestras, para cada posición donde podría localizarse una banda, existen cuatro eventos disjuntos posibles: (1) en los dos perfiles se observa la presencia de la banda, denotado como evento (1,1); (2) ninguno de los perfiles presenta banda, evento denotado como (0,0); (3) el primer perfil presenta banda, evento denotado como (1,0) y (4) no existe banda en el primer perfil pero si en el segundo, denotado como evento (0,1). La frecuencia con que ocurre cada uno de estos eventos cuando se comparan dos patrones de bandas se denominarán a, b, c, y d según correspondan a los eventos (1,1), (1,0), (0,1) y (0,0) respectivamente (Tabla II). Para el caso de RFLP, el “evento” es la restricción (corte) del cDNA amplificado por la presencia de una secuencia específica sobre la que actúa la endonucleasa.
Tabla II. Frecuencias de eventos cuando se comparan dos muestras mediante marcadores binarios.
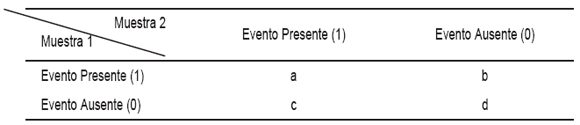
Las frecuencia de polimorfismos representados por los eventos (1,0) y (0,1), de co-presencia (1,1) y de coausencia (0,0) contienen toda la información relevante para la construcción de índices de similitud entre perfiles individuales, i.e. los índices pueden ser expresados como función de dichos recuentos (Bruno et al., 2003). Dos índices comúnmente usados son: a) índice de similitud de Dice [Sij=2a/(2a+b+c)] y b) índice de similitud de Emparejamiento Simple [Sij=(a+d)/(a+b+c+d)]. La transformación raíz cuadrada del complemento a uno de la similitud, sqrt(1-Sij), es recomendada para obtener la distancia entre muestras cuando se pretende producir ordenamientos. Estas distancias pueden ser obtenidas directamente desde programas tales como Info-Gen (Balzarini y Di Rienzo, 2003), Diplomo (Weiller and Gibbs, 1995), RAPDist (Armstrong et al., 1994), Philip (Felsenstein, 1993c), Biosys (Swofford and Selander, 1989) y NTSYS (Rohlf, 1993).
Implementación de técnicas de escalamiento multidimensional
Se realizó un MDS métrico sobre las matrices de distancias entre aislamientos del virus del Mal de Río Cuarto, para dos segmentos del genoma (S1 y S10). Las distancias usadas fueron: datos de secuencias de nucleótidos (distancias F84 y distancias basadas en el valor de identidad obtenidas durante el alineamiento múltiple de secuencias de nucleótidos producido por ClustalW), datos de secuencias de aminoácidos (distancias JTT y distancias basadas en el valor de identidad obtenidas durante el alineamiento múltiple de secuencias de aminoácidos producido por ClustalW), y datos de marcadores RFLP (distancias basadas en el los índices de similitud de Dice y Emparejamiento Simple o ES). En todos los casos donde se obtuvieron similitudes, las mismas fueron transformadas a distancias usando la función sqrt(1-Sij) donde Sij representa la similitud entre las muestras i y j. Cada matriz contiene las distancias entre los pares de aislamientos en el espacio original p-dimensional, donde p es el número de unidades de secuencias de nucleótidos, aminoácidos o marcadores comparados. Para realizar el MDS clásico se usó el software Info-Gen, la implementación del MDS* se logró previo escalado de la matriz B.
En ambos casos, se evaluó el consenso entre cada par de ordenaciones producidas por las primeras dos coordenadas principales (CP) del MDS mediante el coeficiente de rotación procrustes (Johnson and Wichern, 1998). Este coeficiente, se expresa como:
PR2=Tr(XX') + Tr(YY')-2 Tr(diag(l))
donde X es la matriz conformada por las CP1 y CP2 resultantes de una métrica de distancia e Y es la matriz conformada por las coordenadas obtenidas por una segunda métrica. PR2 varia entre 0 y 1, mientras más cercano a 0 sugiere mayor parecido entre los ordenamientos. También se representó la configuración de consenso mediante Análisis Procrustes Generalizado (Gower, 1975) de las ordenaciones obtenidas por MDS*.
Resultados y Discusión
En la Tabla III, se presentan las matrices de distancias obtenidas para cada métrica de proximidad en cada tipo de datos genómicos. Los valores de identidad, complemento a uno de las distancias en matrices b y d (Tabla III), sugieren que todas las secuencias son muy similares (más de 83% de homología). Cuando la homología (medida a través de los valores identidad) entre dos secuencias es menor a 35%, Thompson et al. (1994) reportan baja homología. Aún cuando las matrices de distancia son de pequeña dimensión, ordenar las muestras e interpretar relaciones directamente desde los valores de interdistancias no es simple y por ello es importante aplicar una técnica que permita representar gráficamente las relaciones entre muestras como el MDS.
Tabla III. Matrices de distancia entre cuatro aislamientos del virus del Mal de Río Cuarto obtenidas a partir de datos de secuencias de nucleótidos (a: F84, b: valor de identidad), aminoácidos (c: JTT, d: valor de identidad) y marcadores RFLP (e: Dice, f: Emparejamiento Simple) para dos segmentos del genoma (S1 y S10).
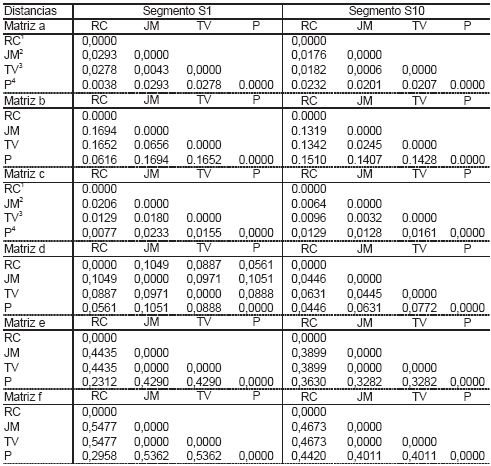
Procedencia de aislamientos: 1RC: Río Cuarto, 2JM: Jesús María, 3TV: Tafí del Valle, 4P: Pergamino.
Todas las métricas de distancias usadas, tanto en la comparación de secuencias de nucleótidos, de aminoácidos como de perfiles de marcadores RFLP, produjeron matrices de distancias Euclideas (i.e., B fue siempre semidefinida positiva). Esta propiedad confirma que las métricas seleccionadas son apropiadas para realizar ordenamientos mediante MDS. En el conjunto de datos de los segmentos S1 y S10 del virus del MRC el valor de p es alto, mientras que el número de muestras (m) es pequeño, consecuentemente las dimensiones del menor espacio que contiene las observaciones también es pequeño (esta no puede ser superior al mínimo entre p y m). Para este conjunto de datos, siempre fue posible visualizar el ordenamiento de las muestras de interés en el plano conformado por las dos primeras coordenadas con un alto porcentaje de variación total explicada (mayor a 90%).
Las magnitudes de las distancias obtenidas desde distintos tipos de datos genómicos no se encuentran en la misma escala, observar que las distancias obtenidas a partir de datos de marcadores moleculares son bastante mayores que las distancias obtenidas a partir de datos de secuencias (Tabla III).
Dado que por construcción, el rango de variación de la primera coordenada principal (CP1) es siempre mayor que el de la segunda coordenada principal (CP2), es conveniente construir un plano donde las dos ejes (CPs) tengan los mismos valores mínimos y máximos (mín-máx) para evidenciar que las diferencias a nivel del eje CP1 (usualmente el eje de las abscisas) son mayores a las que se presentan a nivel del eje CP2 (ordenada). Si cada eje se ajusta a los mín-máx de la CP que representa, y no se presentan los porcentajes de variación explicado, se podrían sobreestimar las diferencias entre muestras que se visualizan a nivel de CP2. Cuando se tienen varios gráficos proveniente de aplicar MDS sobre matrices de distinta escala, los rangos de variación de los ejes podrían ser muy diferentes y por tanto dificultar la presentación de todos ellos con los mismos mín-máx en cada eje. Por ello se hace necesario el escalamiento.
Para los datos del S1, se muestran en la Fig.1 los ordenamientos obtenidos en el plano de las dos primeras coordenadas del MDS clásico y en la Fig. 2 los ordenamientos obtenidos luego del escalamiento de la matriz B por su traza (MDS*). En ambas Figuras, los autovalores asociados a cada eje representan la variabilidad total explicada sobre dicho eje. En la Fig.1, se usaron idénticos mín-máx para las CP1 y CP2 de los datos provenientes de secuenciación pero diferentes a aquellos de datos de perfiles RFLP debido a las diferencias de escala de las matrices de distancias respectivas (Tabla III). El hecho de presentar los ejes con los mismos mín-máx obstaculiza la visualización de diferencias en Fig.1a y 1c. En la Fig. 2 se obtienen idénticas configuraciones que en la Fig. 1 (i.e., el escalamiento por la traza de B no modifica los autovectores usados para construir los ejes), pero todos los gráficos pueden presentarse con los mismos mín-máx.
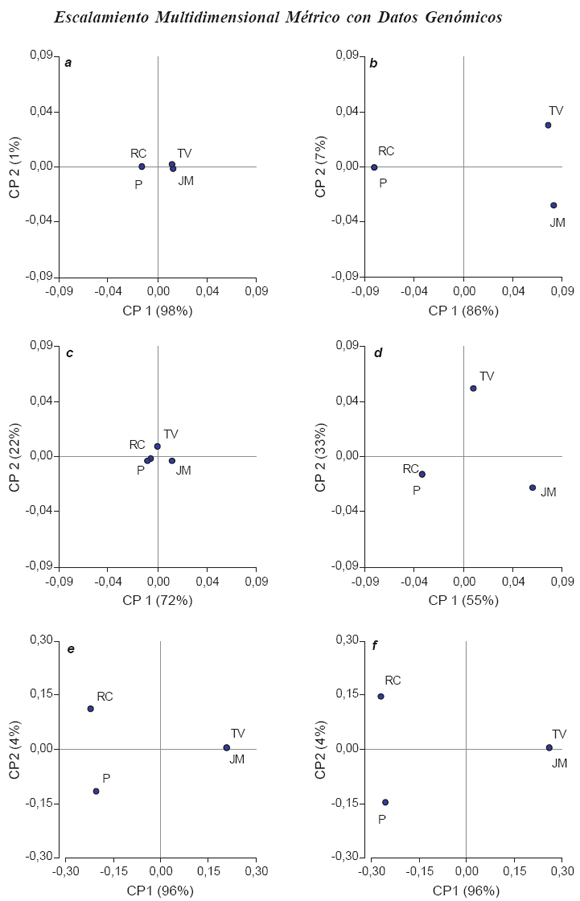
Figura 1. Ordenamiento de cuatro muestras del Segmeno S1 del genoma del virus del Mal de Río Cuarto procedentes de RC: Río Cuarto, JM: Jesús María, TV: Tafí del Valle y P:Pergamino. Distancias basadas en la comparación de secuencias nucleótidos (a: F84, b: valor de identidad), de aminoácidos (c: JTT, d: valor de identidad) y en marcadores RFLP (e: Dice, f: Emparejamiento Simple). Coordenadas sin escalar.
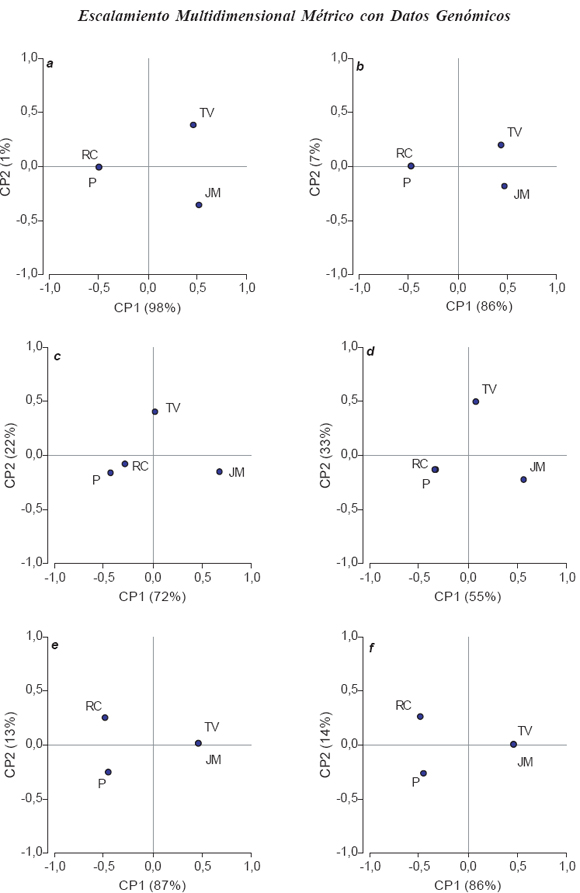
Figura 2. Ordenamiento de cuatro muestras del Segmeno S1 del genoma del virus del Mal de Río Cuarto procedentes de RC: Río Cuarto, JM: Jesús María, TV: Tafí del Valle y P:Pergamino. Distancias basadas en la comparación de secuencias nucleótidos (a: F84, b: valor de identidad), de aminoácidos (c: JTT, d: valor de identidad) y en marcadores RFLP (e: Dice, f: Emparejamiento Simple). Coordenadas escaladas.
Los datos de secuenciación de nucleótidos sugieren, para el segmento S1, dos grupos de aislamientos, uno conformado por los aislamientos RC y P, y el otro grupo formado por TV y JM, independientemente de la métrica de distancia utilizada (Fig.2 a y b). Las altas diferencias en los porcentajes de variación total explicados por CP1 respecto a CP2 ponen en evidencia que la diferencia detectada entre TV y JM, son de menor importancia que las diferencias detectadas entre el grupo RC-P respecto a TV-JM, que se separan a nivel de la CP1. Los ordenamientos logrados a partir de datos de secuenciación de aminoácidos, tanto con la distancia JJT (Fig. 2 c) como con la distancia basada en los valores de identidad (Fig. 2 d), vuelven a mostrar una alta homología entre los aislamientos RC y P diferenciándolos principalmente del aislamiento JM. El porcentaje de varianza explicado sobre CP1 (Fig.2 c y d) es menor que para el caso de datos de nucleótidos (Fig. 2 a y b), lo que permite concluir que a nivel de las secuencias de proteínas parecieran existir diferencias más importantes entre JM y TV que a nivel de nucleótidos.
Para datos de marcadores el eje CP1 obtenido tanto con el coeficiente de similitud de Dice como con el ES (Fig. 2 e y f), permiten diferenciar los mismos dos grupos de aislamientos que los datos de secuencias (i.e., RC-P vs TV-JM), pero no muestran las diferencias entre TV y JM sugeridas por la secuenciación y marcan diferencias entre RC y P. Se observan pequeñas diferencias entre Dice y ES tanto en la Fig. 1 (a nivel de la separación vertical de RC y P) como en la Fig. 2 (a nivel del % de varianza explicado por CP2), las muestras RC y P parecieran más similares para Dice que para ES. Esta diferencia se atribuyó al mayor peso con que el índice de similitud de Dice pondera el evento (1,1) respecto a los eventos (0,1) o (1,0). En estos perfiles RFLP hubo más eventos (1,1) que (0,0) porque las enzimas no produjeron alto grado de polimorfismo, situación común con secuencias de alta homología. El número de eventos (0,0), contemplado por ES y no por Dice, es bajo cuando los marcadores son contabilizados por la restricción de las enzimas.
En la Fig. 3 se presentan los ordenamientos para el Segmento S10 del genoma viral logrados a partir de MDS* para las mismas procedencias de aislamientos. Nuevamente aparecen TV y JM como muestras “cercanas” o parecidas, no obstante existe menos separación de éstos respecto a RC a nivel de los datos de secuenciación. Las diferencias entre P y RC son mayores que las observadas para S1 ya que P y RC se encuentran en distintas mitades del plano según CP1 y/o son separadas por una CP2 con un valor de % de varianza explicado por esta última relativamente alto. El mayor % de variabilidad total explicado por la CP2 para el S10 con respecto al S1, podría sugerir que existen mayor variabilidad entre los aislamientos a nivel de S10. Se supone biológicamente que la proteína codificada por el segmento S10, interactúa durante los proceso de reconocimiento patógeno/hospedante y patógeno/vector. Ambas interacciones son fundamentales en esta familia de virus que sólo se transmite y disemina a través de su vector, dándole probablemente la especificidad al virus. (Giménez Pecci et al., 2005)
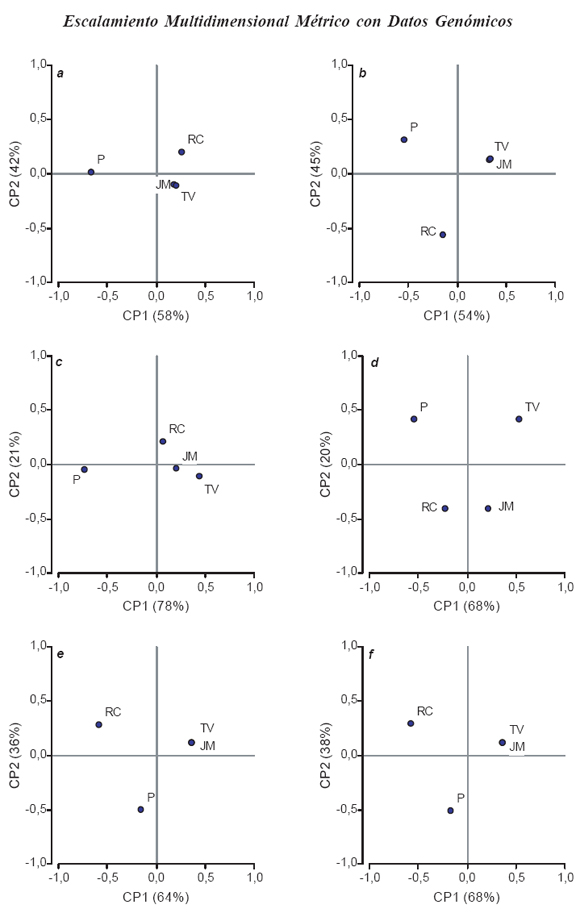
Figura 3. Ordenamiento de cuatro aislamientos procedentes de RC: Río Cuarto, JM: Jesús María, TV: Tafí del Valle y P:Pergamino para el Segmeno S10 del genoma del virus del Mal de Río Cuarto. Distancias basadas en la comparación de secuencias de nucleótidos (a: F84, b: valor de identidad), de aminoácidos (c: JTT, d: valor de identidad), y marcadores RFLP (e: Dice, f: Emparejamiento Simple). Coordenadas escaladas.
Los coeficientes PR2, evidenciaron que los ordenamientos producidos entre distintos modelos de distancia para un mismo tipo de datos fueron altamente congruentes. Para datos del S1, PR2 fue 0,0195 entre secuencias de nucleótidos, 0,0072 entre secuencias de aminoácidos y 0,0122 entre ordenamientos desde datos de marcadores. Para el segmento S10, la congruencia fue alta para datos de marcadores (PR2=0,072) pero menor entre los ordenamientos producidos desde las secuencias de nucleótidos (PR2=0,2007) y desde secuencias de aminoácidos (PR2=0,4923) cuando se compararon los modelos de distancia F84 y JTT versus aquellos provenientes de los valor de identidad.
Thompson (1994) cita que con el programa 1,0 ClustalW, se puede obtener información sobre alineamiento de cualquier conjunto de secuencias, pero el éxito del alineamiento dependerá del número de se-0,5cuencias disponibles, de su relación evolutiva y también de decisiones que deben tomarse en el procedimiento de alineación múltiple (parametrización). Las ordenaciones obtenidas desde los modelos F84 y JTT, para S10, fueron parecidas (PR2=0.00011). Los resultados sugieren que para datos de secuenciación debieran preferirse los ordenamientos basados en modelos de distancia como F84 y JTT antes que aquellos basados en el valor de identidad. Para ambos segmentos las mayores diferencias entre ordenaciones se produjeron al comparar aquellas provenientes de secuenciación con las derivadas desde datos de restricción. Para el S1, los coeficientes PR2 estuvieron entre 0,0961 y 0,2995 (en promedio, PR2=0,1975) y para S10 los valores de PR2, entre datos de secuencias y datos de RFLP, se encontraron en el rango 0,0601 y 0,2266 (en promedio, PR2=0,1430). En la Fig. 4 se presentan los ordenamientos de consenso entre las ordenaciones MDS* provenientes de las 6 matrices de distancia para cada segmento. Para el S1 (Fig. 4 a) el consenso general fue 5,321/6=0,886, y el ordenamiento de las muestras según el segmento S10 mostró un grado de consenso también alto, 5,340/6=0,890 (Fig. 4 b). Las ordenaciones de consenso ponen en evidencia los dos grupos de muestras (RC-P vs TV-JM) según datos del S1, mientras que a nivel del S10 se visualizan las diferencias entre TV-JM respecto a P en primera instancia (CP1) y recién a nivel de CP2 se separa TV-JM de RC, sugiriendo mayores diferencias entre P y RC a nivel de este segmento que a nivel de S1.
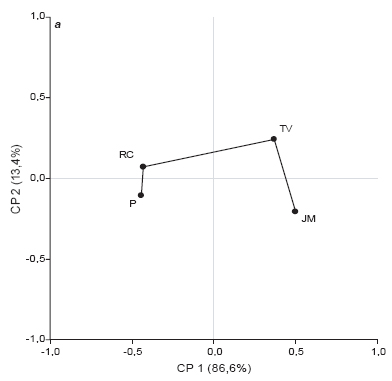
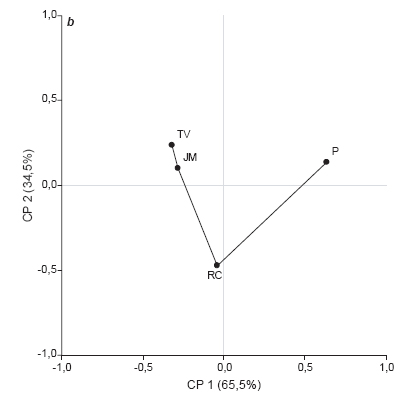
Figura 4. Ordenamiento de consenso de cuatro muestras de virurs (RC: Río Cuarto, JM: Jesús María, TV: Tafí del Valle, P: Pergamino) a partir de las dos primeras coordenadas principales obtendias por escalamiento multidimensional. Segmentos S1 (a) y S10 (b) del genoma del virus del Mal de Río Cuarto.
Comentarios Finales
El MDS métrico facilitó el ordenamiento de los aislamientos en un plano factorial óptimo para la representación de sus interdistancias según distintos modelos de distancia para datos provenientes de secuenciación de nucleótidos, de aminoácidos y datos de marcadores RFLP. La aplicación de MDS previo escalado por la varianza total asociada a cada combinación de tipo de datos genómicos y modelo de distancia permitió comparar los ordenamientos y analizar las variaciones genómicas entre muestras de distinta procedencia. Las ordenaciones no fueron iguales para los segmentos S1 y S10 del genoma del virus del Mal de Río Cuarto, encontrándose mayor variabilidad entre muestras a nivel de S10. La importancia biológica de este segmento es asignada justamente a su mayor variabilidad genética.
Agradecimientos
Este trabajo fue realizado en el marco del proyecto de investigación en estadística genómica subsidiado por la Agencia Nacional de Promoción Científica y Tecnológica y gracias a una beca doctoral subsidiada por CONICET.
Referencias
1. Armstrong, J. S., Gibbs,A., Peakall, R. and Weiller, G. (1994).The RAPDistance Padkage [on line].Availableat http://life.anu.edu.au/molecular/software/RAPDistance/ (Verified November 2003). [ Links ]
2. Balzarini, M. y Di Rienzo, J. (2003). Info-Gen: Software para análisis estadístico de datos genéticos. Facultad de Ciencia Agropecuarias. Universidad Nacional de Córdoba. Argentina. [ Links ]
3. Barry, D. and Hartigan, J.A. (1987). Statistical analysis of hominoid molecular evolution. Statistical Science, 2(2): 191-207. [ Links ]
4. Bruno, C., Balzarini, M. y Di Rienzo, J. 2003. Comparación de medidas de distancais entre perfiles RAPD. Journal of Basic & Applied Genetics, 15:69-78. [ Links ]
5. Dayhoff, M. O. (1979). Atlas of Protein Sequence and Structure, Volume 5, Supplement 3, 1978. National Biomedical Research Foundation, Washington, D.C. [ Links ]
6. Felsenstein, J. (1993a). PROTDIST version 3.5c - Program to compute distance matrix from protein sequences. [ Links ]
7.Felsenstein, J. (1993b). DNADIST version 3.5c - Program to compute distance matrix from nucleotide sequences. (c) Copyright 1986-1993 by Joseph Felsenstein and by the University of Washington. Written by Joseph Felsenstein. [ Links ]
8. Felsenstein, J. (1993c). Phylogeny Inference Package (PHYLIP). Version 3.5. University of Washington, Seattle. [ Links ]
9. Felsenstein, J. and Churchill, G.A. (1996). A Hidden Markov model approach to variation among sites in rate of evolution. Mol. Biol. Evol. 13: 93-104. [ Links ]
10. Giménez Pecci, M. P., Conci, L. R., Truol, G.A., Nagata, T., Kanematsu, S., Laguna, I. G. and Resende, R. O. (2005). Diversity of ecologically distinct Mal de Río Cuarto virus (MRCV) isolates based on RFLPs and genome sequences of S1, S7, S9, S10. Archives Virology (in press). [ Links ]
11. Giménez Pecci, M. P., Laguna, I. G., Conci, L. R., Truol, G.A., Nagata, T. and Resende, R. O. (2001). Diversity of Mal de Río Cuarto virus (MRCV) isolates maintained in greenhoyse based on nucleotide homology virus. Reviews and Research 6(2) Supp 1:156. [ Links ]
12. Gower, J. C. (1975). Generalizad procrustes analysis. Psychometrika. 40:33-51. [ Links ]
13. Gower, J. C. (1985). Measures or similarity, dissimilarity and distance, p. 397 - 405. In Kotz, S. and N. L. Jonhson (eds). Encyclopedia or statistical science. Vol. 5. Wiley, New York. [ Links ]
14. Hall, T. (2001). BioEdit. Version 5.0.6. North Carolina State University, Department of Microbiology. [ Links ]
15. Jackson, D. A., Somers, K. M. and Harvey, H. H. (1989). Similarity coefficients: measures of cooccurrence and association or simply measures or occurrence?. Amer. Nat. 133: 436-453. [ Links ]
16. Johnson, R. A. and Wichern, D. W. (1998). Applied multivariate statistical analysis. Cuarta Edición. Prentice Hall. Upper Saddle River. NJ. [ Links ]
17. Jones, D. T., Taylor W. R. and Thornton, J. M. (1992). The rapid generation of mutation data matrices from protein sequences. CABIOS 8:275-282. [ Links ]
18. Jukes, T. H., and Cantor, C. R. (1969). Evolution of protein molecules, pp. 21-32 in Mammalian Protein Metabolism, edited by H. N. MUNRO. Academic Press, New York. [ Links ]
19. Kimura, M. (1980). A simple model for estimating evolutionary rates of base substitutions through comparative studies of nucleotide sequences. Journal of Molecular Evolution 16: 111-120. [ Links ]
20. Kimura, M., (1983) The Neutral Theory of Molecular Evolution. Cambridge University Press, Cambridge. [ Links ]
21. Kishino, H. and Hasegawa, M. (1989). Evaluation of the maximum likelihood estimate of the evolutionary tree topologies from DNA sequence data, and the branching order in Hominoidea. Journal of Molecular Evolution 29:170- 179. [ Links ]
22. Lake, J. A. (1994). Reconstructing evolutionary trees from dna and protein sequences: Paralinear distances. Proceedings of the National Academy of Sciences of the USA, 91: 1455-1459. [ Links ]
23. Lockahart, P. J., Steel, M. A., Hendy, M. D. and Penny, D. (1994). Recovering evolutionary trees under a more realistic model of sequence evolution. Molecular Biology and evolution, 11: 605-612. [ Links ]
24. Rohlf, F.J. (1993). NTSYS-pc. Numerical Taxonomy and Multivariate Analysis version 1.80. Applied Biostatistics Inc [ Links ]
25. Steel, M. A. (1994). Recovering a tree from the markov the leaf colourations it generates under a markov model. Applied Mathematics Letters, 7(2): 13-23, [ Links ]
26. Swofford D. and Selander, R. (1989). BIOSYS-1. A Computer Program for the Analysis of Allelic Variation in Population Genetics and Biochemical Systematics. Release 1.7. Illinois Natural History Survey Press. 43p. [ Links ]
27. Thompson, J.D., Higgins, D.G. and Gibson, T.J. (1994). CLUSTAL W: improving the sensitivity of progressive multiple sequence alignment through sequence weighting, position specific gap penalties and weight matrix choice. Nucleic Acids Research 22:4673-4680. [ Links ]
28. Veerassamy, S., Smith A. and Tillier, R. M. (2004). A Transition Probability Model for Amino Acid Substitutions from Blocks. Ontatario Cancer Institute. University Health Netword. Toronto, Ontario. Canadá. [ Links ]
29. Weiller G. F and Gibbs A. (1995). DIPLOMO: the tool for a new type of evolutionary analysis. Comput Appl Biosci. (5):535-40. [ Links ]
30. Wilbur,W.J. and Lipman, D.J. (1983). Rapid similarity searches of nucleic acid and protein data banks. Proc. Natl. Acad. Sci. U.S.A. 80:726-730. [ Links ]














