Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Geoacta
versión On-line ISSN 1852-7744
Geoacta v.34 n.2 Ciudad Autónoma de Buenos Aires jul./dic. 2009
Digital terrain model evaluation and computation of the terrain correction and indirect effect in South America
Denizar Blitzkow, Ana C. Oliveira Cancoro de Matos, Jorge Pimentel Cintra
Escola Politécnica da Universidade de São Paulo
EPUSP-PTR, Postal Code 61548, CEP:05424-970, São Paulo, São Paulo, Brazil
E-mail: dblitzko@usp.br, acocmatos@hotmail.com, jpcintra@usp.br;
ABSTRACT
The main objectives of this paper are to compare digital terrain models, to show the generated models for South America and to present two applications. Shuttle Radar Topography Mission (SRTM) produced the most important and updated height information in the world. This paper addresses the attention to comparisons of the following models: SRTM3, DTM2002, GLOBE, GTOPO30, ETOPO2 and ETOPO5, at the common points of the grid. The comparisons are limited by latitudes 60o S and 25 o N and longitudes 100 o W and 25 o W. All these data, after some analysis, have been used to create three models for South America: SAM_1mv1, SAM_1mv2 (both of 1 grid spacing) and SAM_30s (30 grid spacing). Besides this effort, the three models as well as STRM were evaluated using Bench Marks (BM) in Brazil and Argentina. This paper also shows two important geodesy and geophysics applications using the SAM_1mv1: terrain correction (one of the reductions applied to the gravity acceleration) and indirect effect (a consequence of the reduction of the external mass to the geoid). These are important at Andes for a precise geoid computation.
Keywords. Radar altimetry; Height; Digital Terrain Model
RESUMEN
Los objetivos principales de este documento son comparar modelos digitales del continente; enseñar los modelos generados para Sudamérica y presentar dos aplicaciones. Shuttle Radar Topography Mission (SRTM) produjo la información más importante y más actualizada de las altitudes del mundo. Este trabajo centra su atención en las comparaciones de los modelos siguientes: SRTM3, DTM2002, GLOBO, GTOPO30, ETOPO2 y ETOPO5, en los puntos comunes de la rejilla. Las comparaciones son limitadas por las latitudes 60o S y 25 o N y longitudes 100 o W y 25 o W. Todos estos datos, después de los análisis, se han utilizado para crear tres modelos para Sudamérica: SAM_1mv1, SAM_1mv2 (1' de espaciamiento de la rejilla) y SAM_30s (30 de espaciamiento de la rejilla). Los tres modelos bien como el STRM fueron evaluados usando puntos de referencia de nivel (BM) en Brasil y Argentina. Este trabajo también muestra dos aplicaciones importantes del SAM_1mv1: corrección del terreno (una de las reducciones aplicadas a la aceleración de la gravedad) y efecto indirecto. (una consecuencia del proceso de reducción de la masa exterior al geoide). Éstos son muy importantes en la región de los Andes para computar el geoide con exactitud.
Palabras claves. Altimetria de Radar; Altura; Modelo Digital del Terreno
INTRODUCTION
This paper addresses the attention to the following six global Digital Terrain Models (DTM): ETOPO5, GTOPO30, GLOBE, ETOPO2, DTM2002 and the radar mission SRTM3 version 1. ETOPO5 is a model constructed by National Oceanic and Atmospheric Administration/National Geophysical Data Centre (NOAA, 1988). It was derived from terrestrial and oceanic data in a grid of 5. In South America the model has used data digitized from 1:1,000,000 maps. GTOPO30 (Global Topographic Data), constructed by EROS Data Centre (EDC), involves only the terrestrial part of the Earth in a grid of 30. The minimum and maximum elevations are 407m and 8,752m. The data sources were: Digital Terrain Elevation Data (DTED), the Digital Chart of the World (DCW), maps printed by Army Map Service (AMS); see U.S. Geological Survey (1997). The grid was created using the Australian National University Digital Elevation Modelling (ANUDEM) developed by Hutchinson (1989). GLOBE (Global Land One-kilometer Base Elevation), version 1.0, constructed by NOAA/ National Geophysical Data Center (NGDC), has a grid spacing of 30 with default value of -500 on the oceans. The data sources for South America were: DCW, AMS 1:1,000,000 maps digitized by Geographical Survey Institute (GSI), IBGE 1:1,000,000 maps in Amazon, 1:1,000,000 maps of the Defence Ministry in Peru and several DTEDs of different versions (Hasting and Dunbar, 1999). ETOPO2 has a grid spacing of 2 and was constructed by NOAA (2001). The continental part of this model has used GLOBE regridded for 2 by bicubic interpolation. DTM2002 is a model with a resolution of 30, constructed by Raytheon ITSS Corporation. It combines data from GLOBE and from Altimeter Corrected Elevation (ACE); see Saleh and Pavlis (2002). ACE, from Earth and Planetary Remote Sensing Laboratory, University of Montfort, UK, is a global model derived from altimetry data (Johnson et al., 2001).
These models have the grid position, latitude and longitude, referred to World Geodetic System 84 (WGS84). The grid values represent height in meters above Mean Sea Level. Finally, SRTM, the most updated height information in the world, is a joint project undertaken by National Aeronautic and Space Administration (NASA), Deutsches Zentrum für Luft- und Raumfahrt (DLR) and Agenzia Spatiale Italiana (ASI) carried out with a special radar system on board of Endeavour, placed into orbit on February 11th, 2000 and returned to the Earth on the 22nd. Data have been collected on a global basis, from 60º N to 56º S. One of the results is a Digital Terrain Elevation (DTE) named SRTM3 version 1 with a resolution of 3. It may represent the best available global terrain elevation model, with accuracies in different regions of the world subjected to evaluation, but in general the prescribed error is of ±16m (90% of confidence). It is expected that the error in the position is on the order of 15m. The heights are in meters referred to the geoid implied by EGM96/WGS84 and the grid is referred to WGS84 ellipsoid (Lemoine et al., 1998a; Lemoine et al., 1998b; Hensley et al., 2001; JPL, 2004).
COMPARISON AMONG MODELS
The models SRTM3, DTM2002, GLOBE, GTOPO30, ETOPO2 and ETOPO5 were compared among themselves. The comparisons are limited by the latitudes 60o S and 25 o N and longitudes 100o W and 25o W. This is the area of interest for the geoid in South America. The differences were grouped in classes of 10 meters in elevation, allowing a more concise visualization of the differences. The value of 10 meters was selected because SRTM3 was used as reference for the comparison and its prescribed vertical accuracy is ±16 meters with 90% of confidence level, which corresponds to 1.5σ (σ is the standard deviation), and, therefore, 1σ is nearly 10 meters. The differences between the models are shown up to 50 meters because this is the absolute vertical accuracy of the scale of the maps digitized. Greater values are considered as discrepant outliers (|Δ| > 50 m), see Table 1. The comparison of the heights between the models was accomplished only with null or positive values because SRTM3's negative heights do not have physical meaning. In other words, the study was done only in continental area. This condition allowed a more homogeneous comparison between the models.
Table 1 – Comparison among models for the continental area.

Table 1 shows that DTM2002, GLOBE, GTOPO30 and ETOPO2 have many common information. This comes directly from the logic on how they have been created. They have few points with smaller or equal difference to 10 meters relatively to SRTM. ETOPO5 is the most discrepant of the models. This occurs due to the quality of the data source used in the construction of these models (U.S. Geological Survey, 1997; Hasting and Dunbar, 1999; NOAA, 2001; Saleh and Pavlis, 2002; Matos, 2005).
Table 2 shows the statistic results of this comparison. Root Mean Square Error (RMSE) of the comparison between DTM2002 and GLOBE, DTM2002 and GTOPO30, GLOBE and GTOPO30 is approximately 50 meters, confirming that the information source of these models is mostly the same for South America. The difference of 50 meters is within the absolute vertical accuracy of the models data source. All of the models have the positive and negative maximum differences with high values.
Table 2 – Statistics of comparison among models for the continental area.


HISTORICAL DEVELOPMENT OF THE WORK IN SOUTH AMERICA
At the beginning of the 90´s, Surveying and Geodesy Laboratory of the University of São Paulo (LTG/EPUSP) started collaboration with Geophysical Exploration Technology (GETECH), at that time with the Leeds University, through the South American Gravity Project (SAGP). The aim of the project was to obtain public and private gravimetric information of South America, for geophysical applications (Green; Fairhead, 1991). LTG, together with Brazilian Institute of Geography and Statistics (IBGE), obtained gravimetric and altimetric data of Brazil and South America through cooperation agreements with other institutes, mostly militaries of South America. Thus, it was possible to obtain topographical data through digitization of 1:100,000 and 1:50,000 maps for the establishment of a DTM more representative for South America. Until the 20th century, the global DTM used information obtained from 1:1,000,000 maps, the majority of the studied region. SAM model started to be built in 2000, with the information in the continental part obtained during the 90´s. The version 1.0 of GLOBE model was used where SAM did not get elevation information at that time. In the year of 2001, through an agreement with the Brazilian navy, LTG obtained 111 nautical maps in digital form and 20 files with bathymetric data of the project LEPLAC; this means that an effort towards the acquisition of bathymetric information for SAM was started. At the end of the year 2002, LTG initiated the process for digitizing 31 Boarding Maps (the graphic representation of the hydrographic survey). Another 7 files of maps digitized at EPUSP's Hydraulic Department were also added. In 2004, 26 nautical maps of the Argentine coast were also included after digitizing. In 2003, SRTM3's information on elevation became available. At this moment, LTG decided to create three models to evaluate the information obtained during the last ten years, for the study area:
SAM_30s: this model consists of SRTM3 information with spacing of the grid collected every 30. For the continental and the oceanic areas, where no information was available, DTM2002 has been used. SAM_30s has the original height of the point, not the mean value for the area.
SAM_1mv1: this model was generated in the same way as the previous model, except that the spacing of the grid was changed to 1.
SAM_1mv2: this model uses the maps digitized in the continental and oceanic areas of South America. In the areas where no maps were available, the model is the same as the previous one (Figure 1).

Figura 1. Areas of digitalized maps for SAM_1mv2.
The choice of 1 for the grid in South America model is due to the following reasons: 1) it was the resolution conceived originally as a consequence of the scale of the maps and of digitizing interval; 2) the grid of 3 of SRTM3 produces an excessive quantity of information. Thus, the applications with that resolution in continental dimension need to foresee the subdivision in smaller areas with independent processing. The grid of 30 is due to the fact that some global models have this resolution. The first point facilitates the comparison with SRTM3.
MAPS DIGITIZED FOR THE CONTINENTAL AREA
Topographic maps of Brazil were digitized: by GETECH for the Northern region; by IBGE for the center-west and northeast regions and by Petrobras for the southeast and south parts. The maps had two different cartographic reference systems, Córrego Alegre and SAD69. So, the coordinates were transformed from the original reference system to the WGS-84.
The digitizing grid spacing was 1 and 2, according to the map scale. The data digitized in 2 passed by two interpolation processes: the first one transformed them into a grid of 1 and the second resampled the grid for the model SAM_1mv2. The method of interpolation was the nearest neighborhood algorithm assigning an average value to each node that has one or more points within a radius centered on the node (Wessel and Smith, 1991). This method allows the removing of interpolation errors with the data situated in the border of the file.
Servicio Geográfico Militar (SGM) of Uruguay carried out an effort to obtain a DTM for the country using topographic maps. The coordinates are referred to the so called geodetic system Rouusams (International Ellipsoid of Hayford 1930). The horizontal coordinates, after digitizing, were transformed into WGS-84. The spacing of the grid was originally 1. These data were resampled for SAM_1mv2' grid by nearest neighborhood algorithm too. Argentina area used information derived from topographic maps of 1:250,000 produced by Military Geographic Institute (IGM). The data was resampled for 1 using the nearest neighborhood algorithm. For the other countries of South America SRTM3 data were used directly.
Comparisons
SAM_1mv2 (only maps digitized area) was compared with the models SRTM3, DTM2002, GLOBE, GTOPO30, ETOPO2 and ETOPO5. The differences in elevation between the SAM_1mv2 with six other models were grouped in classes of 10 meters (Table 3). Tables 3 and 4 and Figures 2 and 3 show the comparisons of the regions where data of topographic maps are available (Brazil, Argentina and Uruguay). SRTM3 presents more height values similar to SAM_1mv2 than the others (Table 3). Figure 2 shows the histograms of the differences between SAM_1mv2 and SRTM3 for Brazil, Argentina and Uruguay. Most of the discrepancies occur in Argentina and are due to a strong variation in height (Andes) and the aliasing effect of the resample process of the data. Moreover, the data were derived from 1:250,000, with 100 meters spacing of the level curves, therefore without great topographical accuracy. Figure 2 shows that the histograms are skewed: negatively for Brazil and Uruguay, and positively for Argentina. The kurtoses of the three curves are positive therefore they are leptokurtic (Table 5).
Table 3 - Comparison among SAM_1mv2 with global models for the continental area.

Table 4 - Comparison among SAM_1mv2 with global models for the continental area.

Table 5 - Statistic of the three countries.


Figure 2 Histogram of heights differences between SAM 1mv2 and SRTM3.

Fig. 3 - Histogram of heights differences between SAM_1mv2 and SRTM3 in interval of -50 to +50 meters.
Figure 3 is similar to Figure 2, with the study interval limited to -50 to +50 m. Uruguay is the country that presents the biggest consistency between models with the highest frequency in interval of -10 to +10 m: the country has a smooth topography. Brazil and Argentina histograms show that the first has percentages smaller than the second, near zero. In the Andean region, Argentina presents large discrepancies between models; for the rest of the country the topography is smooth with the possibility of a larger consistency. Brazil does not have mountains as high as Andes, but there are topographical irregularities in several regions of the country. These facts explain the behavior of the histograms. Table 4 shows that the mean and RMSE in the comparison SAM_1mv2 with SRTM3 are smaller than the other models. It is important to note that the positive maximum difference for the five first comparisons occurs at the same coordinates. To determine which of the models is closer to the real it is necessary to search for these points in the original topographical map that generated this information.
EVALUATION OF GLOBAL MODELS USING BENCH MARKS
The classical levelling network in Brazil (Figure 4) and Argentina (Figure 5), as a source extremely precise, was used for the validation of SRTM3, SAM_30s, SAM_1mv1 and SAM_1mv2. The majority longitudes and latitudes of the Bench Marks (BM) were derived from maps on 1:50,000, 1:100,000 and 1:250.000 scales, so that the accuracy of the position is compatible with the maps. An error of 50m in horizontal position can be expected. The precision of the spirit leveling network is less than 10 cm. The method of interpolation can introduce an error on the order of meters.

Figure 4 - Distribution of the BMs over Brazil.

Figure 5. Distribution of the BMs over Argentina.
In order to estimate the height of the BM from the grid, bilinear interpolation was used for SRTM3 and the bicubic one for the others. SRTM3 presents many points with no information and for this reason the bilinear interpolation estimates the height in more BM points than the bicubic. The reason is that the bicubic method needs a neighbourhood complete in terms of points (Matos, 2005). The horizontal coordinates of the BM in Brazil were originally in SAD69, subsequently transformed into WGS84; in Argentina the coordinates of the BM are truncated to minutes and the Campo Inchauspe reference was maintained. There are available 62,030 BMs in Brazil and 13,723 in Argentina. The comparison of the height was restricted to intervals of 10m up to 50m. Tables 6 and 7 show comparison of heights of the Brazilian and Argentine BM with SRTM3 and the three SAM models, respectively.
Table 6. Comparison of the Brazilian BM valúes with the estimated ones by SRTM3 and three models SAM

Table 7.Comparison of the Argentine BM valúes with the estimated ones by SRTM3 and three models SAM.

Table 6 (for Brazil) shows that SRTM3 has a more precise data, that is, a greater quantity of points with an error minor than 10m. Table 7 (for Argentina) shows a similar quantity of points for all models. The models have the same quality of data but they show the influence of the spacing of the grid in the result.
Concerning SAM_1mv2 model, the percentages of the differences (Table 6 and 7) show that this model is a slightly less consistent with BMs than the three others. This can be a result of the interpolation process and the accuracy of maps in different scales.
APLICATIONS IN GEODESY AND GEOPHYSICS Terrain Correction
The gravitational effect of the topographical masses, located above geoid, needs to be considered in some applications of physical geodesy, as in the calculation of the anomalies of the gravity and the geoid undulation. The geoid determination through gravimetry data involves the solution of the Geodetic Boundary Value Problem and assumes two conditions (Heiskanen and Moritz, 1967; Gemael, 1999):
1. the gravity measurements have to be made on the geoid itself; and
2. no masses exist outside the geoid.
The first requirement can be accomplished by the use of free air correction to reduce the observed value of gravity to the geoid. The second requirement involves the mathematical removal of the topographic masses followed by their condensation onto the geoid. This can be achieved through Helmert´s second method of condensation (Lambert, 1930), whereby the masses are removed (Bouguer plateau) and subsequently restored as a surface layer of specified density on the geoid. The Bouguer plateau has a constant thickness equivalent to the station height, and the removal of the plate involves the masses above the plate that are not considered in the correction and masses below the plate considered incorrectly. This problem is solved with the addition of one component known as the Terrain Correction (TC) (Hammer, 1939).
Hayford and Bowie (1912) were the first researchers to study the need to use a correction for the gravitational attraction resulted of the terrain undulations around the station. Bullard (1936) used the terrain correction and a correction term for the curvature of the plateau. For this first time, Cassini et al. (1937) used tables up to the distance of 166.735 km (1.5o) from the station. Hammer (1939) modified the system considered by Hayford and Bowie (1912) and a higher precision was obtained for distances greater than 22 km of the station. This method was applied in gravity field research. The Hammer method (1939) for the TC considers the area around the station divided into zones and compartments chart, though a cylindrical model. The height difference between the computation point and each compartment is estimated. The classic formula for TC is given by (Heiskanen and Moritz, 1967):
 (1)
(1)
where
G is Newton gravitation constant;
ρ is the density of the topographic masses assumed constant and equal to 2.67 g cm-3;
R is the radius of a sphere approximating the global geoid;
(x, y) are the coordinates of the DTM grid;
(xp, yp) are the coordinates of the computation point;
h is the height of the point above of the mean sea level;
E denotes the area of integration on the surface;
l (xp-x, yp-y) is a kernel defined as the distance between the points (xp, yp) and (x, y):
![]() (2)
(2)
The TC in Equation 1 is identical to that used by Hammer method (1939). However, the process of calculating the TC in each compartment for each gravity station from topographic maps and Hammer chart is extremely time consuming and it is also subject to human error. A faster alternative to compute this correction, applicable to Equation 1, as it is a convolution integral, together with a DTM regular grid, is the Fast Fourier Transform (2D-FFT):
F{a*b} = F{a}F{b} (3)
where a*b is called convolution of the functions a and b, and F{a} and F{b} are Fourier Transform of a and b, respectively {Spiegel,1977). The Equation 3 is applied to Equation 1, where the function a is the term [h (x, y) - h (xp, yp)f and function b corresponds to l'3(xp-x, yp-y). The details of the development of convolution integral are given in Schwarz et al. (1990). Sideris (1985) and Li and Sideris (1994) use this method, the program called TC2DFTPL, and it was applied in the South América using SAM_lmvl model and result in the valúes of Figure 6 in grayscale.
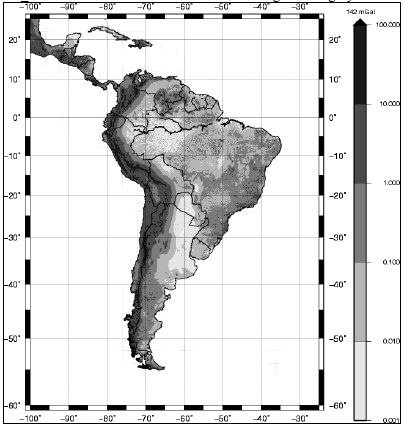
Figure 6.Terrain Correction for South America computed with SAM_1mv1.
TC calculation for South America considered mass-prism topographic model (Li and Sideris, 1994). For this paper integration radius of 166 km was used, due to the Andes region. For heights lower than 2,500 meters it is possible to compute TC with a radius of 50 km due to smaller values (Kirby and Featherstone, 1999). The maximum correction is 142mGal (latitude= -12.2667o and longitude= -72.0333o) and the mean value is 0.4mGal for South America. Figure 6 shows the TC distribution in South America when using SAM_1mv1. The program TC2DFTPL doesnt produce better results in terms of accuracy than MDTs with higher resolution as presented in (Matos, 2005) and (Kirby and Featherstone, 1999).
Indirect Effect
The gravimetric reduction of the external masses into geoid due to the second method of Helmert's condensation of the topography gives origin to the indirect effect on the geoid undulation. As a consequence, this effect generates a fictitious geoid. Thus, the geoid height value derived from the Stokes formula represents the separation between the reference elipsoid and a fictitious one, called co-geoid (Gemael, 1999). The separation between geoid e co-geoid (Nind) is computed by the Bruns formula (Heiskanen and Moritz, 1967; Martinec and Vanicek, 1994):
 (4)
(4)
where δW is the residual gravity potential and γ is the gravity acceleration of normal Earth over the ellipsoid.
The residual potential δW depends on the gravimetric reductions used. For each gravimetric reduction corresponds a different co-geoid. The geoid heights is finally computed by
N = NC+Nmd (5)
where Nc is the co-geoid height.
In this paper, the calculation of the indirect effect on the geoid heights due to Helmert condensation used the following formula (Wichiencharoen, 1982):

where p is the mean density; Hn(P), Hn are the heights of the points of calculation and movable, respectively; Hm is the mean height of the computation área.
The term Nind0 (Equation 7) is the regular part and Nindl + Nind2 (Equations 8 and 9) is the irregular part of the Equation 6. The regular part doesnt need to consider the irregularity of the topography; the irregular part considers the mass above and inexistence of mass below the station.
The integráis had been calculated by FFT technique and the DTM used was SAMlmvl. The Figure 7, also in grayscale, shows the indirect effect distribution in South América. The máximum and minimum values are 0,3m (latitude= -20.4667o and longitude= -28.85o) and –1.9m (latitude= -27.15o and longitude= -68.55o). The mean value is –0.07m for South America.

Figure 7. Indirect Effect for South America computed with SAM_1mv1.
Evaluation of the highest Andean peaks
For the evaluation of these two important applications (Terrain Correction and Indirect Effect), the coordinates of the highest Andean peaks were used. The Figure 8 shows the position of these peaks with the coordinates at Table 8. The points have been obtained choosing the highest values at SRTM grid with the respective coordinates. The column 6 shows the heights of SAM_1mv1 at the same coordinates. The last two columns present the Terrain Correction and Indirect Effect. When the gradient around the peak is big, the TC value is high (e.g. Aconcágua and Chimborazo). The error in the geoid heights at Andes region can read the order of 2 meters (absolute) if the Indirect Effect is neglected, e.g., at Bonete peak the corrections is –1.86m.
Table 8. Andean peaks



Figure 8. Andean peaks
CONCLUSION
ETOPO5, ETOPO2, GTOPO30, GLOBE, DTM2002 models present, in comparison with common points of the SRTM3, a high percentage of values with difference higher than 50 m (Tables 1 and 2), showing a inconsistency between them. SRTM3 performs better than the other five models when data from digitized map are used for comparison (Tables 3 and 4). Nevertheless, SRTM has areas without information where the other models may be used to complete or it is possible to interpolate. However, it will involve a loss of quality in these regions, but the resolution of 3 will be always an advantage of SRTM3. The comparison of the model with heights in BMs shows differences compatible with the precision specified for the model. The differences greater than 50 m (Tables 6 and 7) are due whether to the uncertainty in BM coordinates or the quality of the model. The BMs horizontal coordinates have to be checked. This paper shows the results related of terrain correction and indirect effect for the model SAM_1mv1. The TC2DFTPL program provides results with higher values than expected in some regions of high height variations (e.g., Andes) in models with 30" grid, in particular the SAM_30s, because it has more details of the topography. In general, the models DTM2002, GLOBE and GTOPO30 showed results similar to ETOPO2. This is because they use the same sources of information, mostly maps obtained on the scale of 1:1,000,000, presenting results not better than the SAM's. The indirect effect is not influenced by the topographic structure as much as TC, so the results are similar among the models (Matos, 2005).
The SAM_1mv1 for South America on a 1 (~2km) grid has enabled to the computation of gravimetric terrain correction allowing the computation of complete Bouguer anomalies across the continent. This was done through a two-dimensional FFT algorithm applied to a planar approximation of the terrain-correction formula, and, with a constant topographic density of 2670 kg.m-3. The integration radius was 166 km. This program shows good results for the 1 grid terrain model. The other important application is the indirect effect; the program employed the planar approximation of the geoid and assumed a constant density of all the topographical masses.
Acknowledgements
The authors acknowledge IBGE, the Instituto Geográfico Militar (IGM) of Argentina, Dr. Maria Cristina Pacino of the Universidad Nacional de Rosário, the Engineer Federico Mayer of Servicio de Hidrografia Naval for supplying the Argentina nautical maps. The authors acknowledge also to the Navy Hydrograph Center by the receptivity, orientation and the supply of the Boarding Maps, nautical maps and data of the LEPLAC project. Finally, our gratefulness to GETECH of the Leeds University, especially Dr. J. Derek Fairhead and Graham Gifford.
REFERENCES
1. Blitzkow, D., A.C.O.C. Matos, J.P. Cintra, 2007. SRTM Evaluation in Brazil and Argentina with Emphasis on the Amazon Region. Dynamic Planet - Monitoring and Understanding a Dynamic Planet with Geodetic and Oceanographic Tools. Conference of the International Association of Geodesy 22-26 August 2005, Cairns, Australia.Series: International Association of Geodesy Symposia, Vol. 130. Rizos, Chris; Tregoning, Paul (Eds.), Springer, cap 40, pp 266-271. [ Links ]
2. Bullard, E. C. Gravity measurements in East Africa. Philosophical Transactions of the Royal Society, v. 235, p. 445–534, 1936. [ Links ]
3. Cassini, G.; Dor, P.; Ballarin, S., 1937. Tovole fondamentali per la riduzione dei osservati della gravita. [S.l.]: Publicazione dell Istituto di Geodesia. [ Links ]
4. Gemael, C., 1999. Geodésia física. [S.l.]: UFPR. [ Links ]
5. Green, and Fairhead, 1991. The South American Gravity Project. In: Recent Geodetic and Gravimetric Research in Latin America. Edited by W. Torge. Springer-Verlag. Berlin. [ Links ]
6. Hasting, D.A., and P.K. Dunbar, 1999. Global Land One-kilometer Base Elevation (GLOBE) Digital Elevation Model, Documentation, Volume 1.0. Key to Geophysical Records Documentation (KGRD) 34. National Oceanic and Atmospheric Administration, National Geophysical Data Center, 325 Broadway, Boulder, Colorado 80303, U.S.A. [ Links ]
7. Hammer, S., 1939. Terrain corrections for gravimeter stations. Geophysics, v. 4, p. 184 -194. [ Links ]
8. Hayford, J. F.; Bowie, W., 1912. The effect of topography and isostatic compensation upon the intensity of gravity. [S.l.]: U.S. Coast and Geodetic Survey Special Publication, n. 10. [ Links ]
9. Heiskanen, W. A.; Moritz, H., 1967. Physical geodesy. San Francisco: Freeman and Co. [ Links ]
10. Hensley, S., R. Munjy, P. Rosen, 2001. Interferometric synthetic aperture radar. In: Maune, D. F. (Ed.). Digital elevation model techonoligies applications: the DEM users manual. Bethesda, Maryland: ASPRS (The Imaging & Geospatial Information Society), cap. 6, pp. 142–206. [ Links ]
11. Hutchinson, M.F., 1989. A new procedure for gridding elevation and stream line data with automatic removal of spurious pits. Journal of Hydrology, 106, pp. 211–232. [ Links ]
12. JPL, 2004. SRTM – The Mission to Map the World. Jet Propulsion Laboratory, California Inst. of Techn., Available online at: http://www2.jpl.nasa.gov/srtm/index.html. [ Links ]
13. Johnson, C.P., P.A.M. Berry, and R.D. Hilton, 2001. Report on ACE generation, Leicester, UK. Available online at: http://www.cse.dmu.ac.uk/geomatics/ace/ACE_report.pdf. [ Links ]
14. Kirby, J. F.; Featherstone, W. E., 1930. Terrain correcting australian gravity observations using the national digital elevation model and the fast fourier transform. Australian Journal of Earth Sciences, v. 46, p. 555–562, 1999. [ Links ]
15. Lambert, W. D. The reduction of observed values of gravity to sea level. Bulletin Géodésique, v. 26, p. 107–181. [ Links ]
16. Lemoine, F.G., N.K. Pavlis, S.C. Kenyon, R.H. Rapp, E.C. Pavlis, and B.F. Chao, 1998a. New high-resolution modle developed for Earth' gravitational field, EOS, Transactions, AGU, 79, 9, March 3, No 113, 117-118. [ Links ]
17. Lemoine, F.G., S.C. Kenyon, J.K. Factor, R.G. Trimmer, N.K. Pavlis, D.S. Chinn, C.M. Cox, S.M. Klosko, S.B. Luthcke, M.H. Torrence, Y.M. Wang, R.G. Williamson, E.C. Pavlis, R.H. Rapp and T.R. Olson, 1998b. The development of the joint NASA GSFC and the National Imagery and Mapping Agency (NIMA) geopotential model EGM96, NASA/TP-1998-206861. National Aeronautics and Space Administration, Maryland, USA. [ Links ]
18. Li, Y.C., Sideris, M., 1994. Improved gravimetric terrain correction. Geophysical Journal International 119, 740–752. [ Links ]
19. Martinec, Z.; Vanicek, P., 1994. The indirect effect of topography in the stokes-helmert technique for a spherical aproximation of the geoid. Manuscripta Geodaetica, v. 19, p. 213–219. [ Links ]
20. Matos, A.C.O.C., 2005. Implementação de modelos digitais de terreno para aplicações na área de Geodésia e Geofísica na América do Sul. PhD thesis - Escola Politécnica, Universidade de São Paulo, São Paulo, 355 p. Available online at: http://www.teses.usp.br/teses/disponiveis/3/3138/tde-10102005-104155. [ Links ]
21. Matos, A.C.O.C., D. Blitzkow, 2005. Geração e Avaliação do Modelo Digital de Terreno SAM na Região Costeira do Oceano Atlântico Sul. In: XXII Congresso Brasileiro de Cartografia, Macaé. [ Links ]
22. NOAA (1988). Data Announcement 88-MGG-02, Digital relief of the Surface of the Earth. NOAA, National Geophysical Data Center, Boulder, CO. Available online at: http://www.ngdc.noaa.gov/mgg/global/etopo5.html. [ Links ]
23. NOAA, 2001. 2-minute Gridded Global Relief Data (ETOPO2). NOAA, National Geophysical Data Center, Boulder, CO. Available online at: http://www.ngdc.noaa.gov/mgg/fliers/01mgg04.html. [ Links ]
24. Saleh, J., and N.K. Pavlis, 2002. The development and evaluation of the global digital terrain model DTM2002, 3rd Meeting of the International Gravity and Geoid Commission, Thessaloniki, Greece. [ Links ]
25. Schwarz, K.P.; Sideris, M. G.; Forsberg, R., 1990. The use of fft techniques in physical geodesy. Geophysical Journal International, v. 100, p. 485–514. [ Links ]
26. Sideris, M. G., 1985. A fast fourier transform method of computing terrain corrections. Manuscripta Geodaetica, v. 10, p. 66–73. [ Links ]
27. U.S. Geological Survey, 1997. GTOPO30 Global 30 Arc Second Elevation Data Set. Available online at: http://edcwww.cr.usgs.gov/landdaac/gtopo30/gtopo30.html. [ Links ]
28. Wichiencharoen, C., 1982. The indirect effects on the computation of geoid undulations. [S.l.]: The Ohio State University, Department of Geodetic Science and Surveying (Report no. 336). [ Links ]
29. Wessel, P., W. H. F Smith, 1991. Free software helps map and display data. EOS, Transactions, American Geophysical Union, v. 72, n. 41, p. 441, 445–446. [ Links ]














