Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Geoacta
versión On-line ISSN 1852-7744
Geoacta v.34 n.2 Ciudad Autónoma de Buenos Aires jul./dic. 2009
On the path of plumes of the Río De La Plata Estuary main tributaries and their mixing scales
Claudia G. Simionato1,2, Virna L. Meccia1,2 and Walter C. Dragani2,3,4
1 Centro de Investigaciones del Mar y la Atmósfera (CIMA/CONICET-UBA), Ciudad Universitaria Pabellón II Piso 2 (C1428EHA) Ciudad Autónoma de Buenos Aires,
2 Departamento de Ciencias de la Atmósfera y los Océanos, FCEN, Universidad de Buenos Aires, Ciudad Universitaria Pabellón II Piso 2 (C1428EHA) Ciudad Autónoma de Buenos Aires, Argentina.
3 Servicio de Hidrografía Naval (SHN) and Escuela de Ciencias del Mar (ESCM-INUN) del Ministerio de Defensa. Av. Montes de Oca 2124 (C1270ABV), Ciudad Autónoma de Buenos Aires, Argentina.
4 Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET). Av. Rivadavia 1917 (C1033AAJ), Ciudad Autónoma de Buenos Aires, Argentina.
ABSTRACT
With a length of 300 km and a width that narrows from 220 km at its mouth to 40 km at its upper end, the Río de la Plata is one of the largest estuaries of the world. Its three main tributaries -contributing to a total mean runoff of 22,000 m3 s-1- have different properties and are object of diverse environmental impact due to dissimilar development conditions on their shores. The knowledge of the paths of the plumes of those tributaries along the estuary and their mixing scales is necessary for management purposes. In this paper, advection-diffusion equations for passive tracers are coupled to the three-dimensional Hamburg Shelf Ocean Model and validated by means of a case study. Then, simulations in which each tributary is characterized by a different dye tracer are done for scenarios resulting of the combination of diverse characteristic atmospheric forcing and runoff conditions. The impact of bathymetry and Earths rotation on plumes paths and mixing is also evaluated. Results indicate that, for mean to low discharge conditions, the path of the waters of the tributaries is in the form of two main plumes. The different water speeds of both tributaries, the presence of a bend immediately after their confluence and the varying geometry and bathymetry of the estuary favor a rapid mixing between the Uruguay and Paraná Guazú-Bravo waters, which then flow along the northern portion of the upper estuary channel. The Paraná de las Palmas waters, instead, occupy the southern shallow region of Playa Honda in the upper estuary and then flow following the southern coast. Downstream Colonia, at the intermediate estuary, the occurrence of another large bend and a change in bathymetric features force the flow to concentrate in the central part of the estuary and favor further mixing between the plumes. For high discharge conditions the northern part of the upper estuary is divided into two regions, one with a larger concentration of Uruguay waters between Oyarvide and Martín García islands and the coast and another with a larger concentration of Paraná Guazú-Bravo waters south of the islands. In this case there is a much larger concentration of Uruguay waters along the northern coast, which might be enhanced if a peak runoff occurs for the Uruguay but not for the Paraná River. These conclusions are consistent with what can be inferred from the conductivity field observed at the intermediate estuary, the bottom sediments distribution and satellite images. Results indicate that even though strong winds can favor the mixing of the plumes, especially along Argentinean coast, they preserve their pattern and the effect of the storms only persists for a few days. For mean runoff, the elapsed time to the arrival of the leading edge of the Paraná de las Palmas, Paraná Guazú-Bravo and Uruguay tracer clouds at Buenos Aires is of around 3, 5 and 7 days, respectively. The elapsed time to the peak concentration of the tracer cloud for a typical mean runoff scenario is of around 20 days at Buenos Aires. For that condition, the flushing times of the upper and upper intermediate estuary are of around 10 and 60 days, respectively. Nevertheless, mixing scales can be half (twice) those values for high (low) runoff conditions.
Keywords: Upper and Intermediate Río de la Plata; Plumes; Tributaries; Mixing scales.
RESUMEN
Con una extensión de 300 km y un ancho que varía entre 220 km en su boca y 40 km en su parte superior, el Río de la Plata es uno de los mayores estuarios del mundo. Sus tres tributarios –que contribuyen con una descarga media total de 22.000 m3 s-1- tienen diferentes propiedades y son objeto de distinto impacto medioambiental debido a condiciones disímiles de desarrollo en sus costas. El conocimiento del camino de las plumas de esos tributarios y sus escalas de mezcla es necesario para propósitos de gestión. En este trabajo, se acoplan ecuaciones de advección-difusión para trazadores pasivos al modelo tridimensional Hamburg Shelf Ocean Model y se las valida por medio de un estudio de casos. Luego se realizan simulaciones en las cuales cada tributario es caracterizado por un trazador diferente para escenarios que resultan de combinar las diversas condiciones características del forzante atmosférico y la descarga. El impacto de la batimetría y la rotación de la Tierra en el camino de las plumas y su mezcla también es evaluado. Los resultados indican que, para condiciones de descarga media a baja el camino de las aguas de los tributarios es en la forma de dos plumas principales. La diferente velocidad del agua en ambos tributarios, la presencia de una curva inmediatamente después de su confluencia y la geometría y batimetría variables del estuario favorecen una rápida mezcla entre las aguas del Uruguay y el Paraná Guazú-Bravo, que luego fluyen a lo largo de la parte norte del estuario superior. Las aguas del Paraná de las Palmas, en cambio, ocupan la región somera de Playa Honda en la porción sur del estuario superior y luego fluyen a lo largo de la costa sur. Aguas abajo de Colonia, en el estuario medio, la ocurrencia de una gran curva y un cambio en las características batimétricas fuerzan al flujo a concentrarse en la parte central del estuario y favorece mayor mezcla entre las plumas. Para condiciones de descarga alta la porción norte del estuario se divide en dos regiones, una con mayor concentración de aguas del Uruguay entre las islas Oyarvide y Martín García y la costa, y otra con mayor concentración del Paraná Guazú-Bravo al sur de dichas islas. En este caso, hay una concentración mucho mayor de aguas del Uruguay a lo largo de la costa norte, característica que podría incrementarse si un pico de descarga ocurre en el Río Uruguay pero no en el Paraná. Estas conclusiones son consistentes que lo que puede inferirse del campo de conductividad observado en el estuario intermedio, con la distribución de sedimentos de fondo y con imágenes satelitales. Los resultados indican que aunque vientos fuertes pueden favorecer la mezcla de las plumas, especialmente a lo largo de la costa argentina, ellas mantienen su estructura y el efecto de las tormentas sólo persiste unos pocos días. Para descarga media, el tiempo de arribo del borde de las nubes de trazadores de los ríos Paraná de las Palmas, Paraná Guazú-Bravo y Uruguay a Buenos Aires es de aproximadamente 3, 5 y 7 días, respectivamente. El tiempo hasta el alcance de la concentración pico de la nube de trazadores para un escenario típico de descarga media es de alrededor de 20 días para Buenos Aires y 60 días para el estuario medio. Para esa condición, el tiempo de lavado en el estuario superior y medio superior es de alrededor de 10 y 60 días. No obstante, las escalas de mezcla pueden ser la mitad (el doble) de esos valores para condiciones de descarga alta (baja).
Palabras claves: Río de la Plata superior e intermedio; Plumas; Tributarios; Escalas de mezcla.
1. INTRODUCTION
The Río de la Plata, located on the eastern coast of southern South America at approximately 35° S (Fig. 1 and 2), is one of the largest estuaries of the world (Shiklomanov 1998). It has a northwest to southeast oriented funnel shape approximately 300 km long that narrows from 220 km at its mouth to 40 km at its upper end (Balay 1961). The estuarine area is 35,000 km2 and the fluvial drainage area is 3.1×106 km2 (Depetris and Griffin 1968). This system is of great social, ecological and economical importance for the countries on its shores, Argentina and Uruguay. The Capital cities of those countries (Buenos Aires and Montevideo), the most important harbors of the region and many industrial poles and resorts are located on its coasts. The estuary is the main source of drinking water for the millions of inhabitants in the hinterlands and has the unusual feature of being an area of both spawning and nursery for a number of coastal species, several of them of economic importance (Macchi et al. 1996; Acha et al. 1999; Acha and Macchi 2000; Berasategui et al. 2004; Rodrigues 2005).
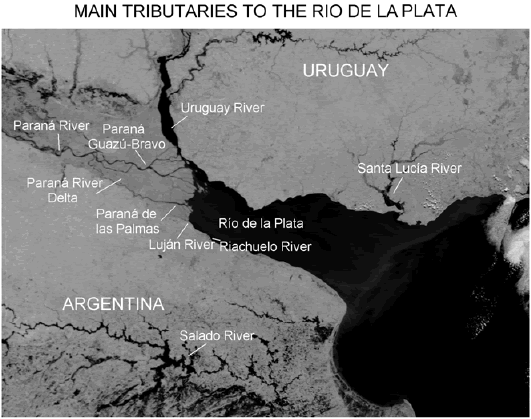
Figure 1. Gray scale color image collected by the Moderate Resolution Imaging Spectroradiometer on board of Terra satellite (MODIS-TERRA) in April, 2002. The image shows the Río de la Plata Estuary and its main tributaries. Adapted from Visible Earth, http://visibleearth.nasa.gov.

Figure 2. Model domain and Río de la Plata bathymetry (in m) in a 1.5 km × 1.5 km resolution, as seen by the model, together with the main geographic and topographical features
Fresh water reaches the estuary through a number of tributaries, being the two major the Paraná and Uruguay. These two rivers, with mean discharges of 16,000 and 6,000 m3 s-1, respectively (Nagy et al. 1997) form the second largest basin of South America. The Paraná River flows into the estuary forming a large delta; the two main branches are Paraná Guazú-Bravo (Fig. 1), transporting approximately 77% of the runoff, and Paraná de las Palmas, transporting the remaining 23% (Jaime et al. 2002). The mean transport of the minor tributaries is several orders of magnitude smaller. For example, the annual average discharge of the Salado River and its system of channels to the Samborombón Bay has been estimated as 26 m3 s-1 (Consejo Federal de Inversiones 1969) and the runoff of the Riachuelo and Luján rivers as 72 and 192 m3 s-1, respectively (Jaime et al. 2001). Therefore, the average continental discharge to the estuary can be evaluated as the result of the transport of the two major tributaries in around 22,000 m3 s-1 (Framiñan et al. 1999). Nevertheless, large variability is observed in inter-annual time scales and peaks as large as 75,000 m3 s-1 and as low as 8,000 m3 s-1 have been recorded in association to El Niño and La Niña events, respectively (Jaime et al. 2002).
The waters of the three main tributaries have different properties (Jaime et al. 2001) and are object of diverse environmental impact due to dissimilar development conditions on their shores. The possibility of a contaminant being spilled upstream the water supply for Buenos Aires and other coastal cities is a constant concern. Traveltime and mixing of water within the estuary are basic flow characteristics that water resources managers and planners need in order to predict the rate of movement and dilution of pollutants that may be introduced into the stream. Mixing processes have a major impact on the biology, chemistry, ecology and water quality of the estuarine environment. Nevertheless, only hypotheses have been suggested about the water paths of the main tributaries along the broad upper and intermediate Río de la Plata estuary and discrepancies are found in the scarce literature regarding the subject. From an analysis of bottom sediments, Parker et al. (1987) inferred that the waters of the tributaries would flow through the upper and intermediate estuary in the form of two differentiated plumes. The southernmost one would be associated to the Paraná de las Palmas, whereas the waters coming from the Paraná Guazú-Bravo and Uruguay rivers would flow as a second branch to the north, along the Uruguayan coast. On the other hand, Jaime et al. (2001) postulated the occurrence of flow corridors in the estuary. According to this hypothesis, the waters of the three main tributaries of the Río de la Plata would flow in well differenced plumes, that the authors called corridors, transporting the corresponding waters with almost no lateral mixing. Classically, lateral mixing in rivers was considered as a slow process that is usually complete within 100–300 river widths. Under ideal conditions an instantaneous input of a pollutant should result in a Gaussian spatial, and skewed temporal (fixed observer) concentration profile; however, case studies show that in general the observed plumes deviate significantly from theory (Hellweger 2005). Several processes, as the difference in speed of rivers waters at their confluence, the varying geometry and bathymetry and channel curvature can strongly increase lateral mixing (Biron et al. 2004; Jamali et al. 2005). As all these features are observed at the confluence of the tributaries to the Río de la Plata, it seems unlikely that a flow in the form of corridors occur in this estuary.
The aim of this paper is, therefore, to study the paths of the plumes of the main tributaries of the Río de la Plata and their mixing scales in the upper and upper intermediate estuary. In this context, numerical models constitute a valuable tool; passive tracers can be coupled to simulate the transport and dispersion of solutes in surface waters because they have virtually the same physical characteristics as water (Feurstein and Selleck 1963; Smart and Laidlaw 1977; Jobson 1996) and have been widely applied to other estuaries (see, for example, Shen et al. 1999; Wanga et al. 2000; Hellweger et al. 2003, 2004; Liu et al. 2004; Koutitonsky et al. 2004; Banas and Hickey 2005). In this paper, advection-diffusion equations for passive tracers are coupled to three-dimensional Hamburg Shelf Ocean Model (HamSOM) developed at the University of Hamburg (Backhaus 1983, 1985) and validated by means of a case study. Afterwards, simulations that include the tidal forcing are done for scenarios resulting of the combination of different characteristic winds and runoffs. The effect of the most frequent extreme atmospheric events associated to strong winds on mixing and deformation of the plumes is also studied, and the persistence of the introduced signal is quantified. Besides permitting the estimation of pollutants release impact on the estuarine waters at different locations, our simulations allow the estimation of useful mixing time scales for the Río de la Plata. The elapsed time to the arrival of the leading edge of the tracers cloud at a location, the elapsed time to the peak concentration of the tracers cloud and the flushing times are calculated.
THE NUMERICAL MODEL AND ITS VALIDATION
Characteristics of the model and simulations
The model applied in the simulations discussed in this paper is the Hamburg Shelf Ocean Model (HamSOM), a widely used three-dimensional primitive equation ocean model developed at the University of Hamburg by Backhaus (1983, 1985). It has been applied to many shelf seas worldwide (see, for example, Backhaus and Hainbucher 1985; Rodríguez et al. 1991; Stronach et al. 1993) having demonstrated to be very robust for studying shelf sea dynamics. In several applications of the model to the Río de la Plata, Simionato et al. (2001, 2004a, 2004b, 2006) showed that it is appropriate to reproduce the observed heights, currents and salinity fields at the estuary. The model characteristics, so as its equations and parameterizations can be found in a number of papers (Backhaus 1983, 1985; Backhaus and Hainbucher 1985; Rodríguez and Alvarez 1991; Rodríguez et al. 1991; Stronach et al. 1993; Alvarez et al. 1997; Simionato et al. 2004a).
HamSOM includes advection-diffusion equations for temperature and salinity. To characterize the path of the tributaries plumes in the estuary, similar advection-diffusion equations for passive tracers -that do not have an effect on density- were coupled to the model. This coupling was done following Harms (1997) and Harms and Povinec (1999) who used HamSOM for tracers dispersión studies in other coastal áreas. Passive tracers are substances which are not influenced by chemical reactions and/or biological processes; consequently, their concentration is only modified by advection and mixing. As these tracers do not have an influence on circulation they act as dye and, therefore, are extremely useful to characterize water masses and to study mixing processes. Additionally, tracers can be used to estimate mixing time scales, as the flushing time (Delhez et al. 2004).
For each tracer, the coupled equation has the form:
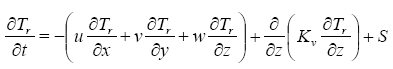
where Tr is the tracer concentration, (u,v,w) the velocity vector, Kv the vertical turbulent diffusion coefficient and S the source term, which takes a valué different from zero only at the tracer source. Advection (the first term in the right hand side of the equation) is calculated with a numerical upstream algorithm, that is based on the previously simulated flow (u,v,w) and tracer (Tr) fields (Harms 1997; Harms and Povinec 1999). Horizontal diffusion was omitted due to a high amount of numerical (artificial) diffusion caused by this method (Harms, 1997). In spite of this disadvantage, the upstream scheme proves to be a rather robust algorithm that avoids over-shootings even if strong releases into clean environments are performed (Harms 1997). Following the eddy viscosity analogy, the vertical diffusive stresses are parameterized as functions of the layer velocities; the vertical eddy mixing coefficients are updated using a mixing length expression (Pohlmann 1996) that accounts for turbulent effects in a local equilibrium way. The bottom stress is parameterized by means of a quadratic law in terms of the current velocity:
![]()
where ![]() stands for the horizontal velocity vector at the bottom layer of the model and
stands for the horizontal velocity vector at the bottom layer of the model and![]() is the vertically averaged horizontal velocity in a frictional layer cióse to the bottom. Cb is the non-dimensional drag or bottom friction coefficient. For stability reasons, this term is treated semi-implicitly, being
is the vertically averaged horizontal velocity in a frictional layer cióse to the bottom. Cb is the non-dimensional drag or bottom friction coefficient. For stability reasons, this term is treated semi-implicitly, being![]() computed in the future time and uL in the present.
computed in the future time and uL in the present.
Model domain spans the región shown in figure 2 and is large enough to ensure that, for the time span of the simulations, boundary effects do not affect results in the upper and upper intermedíate parts of the estuary which are the focus of this paper. The horizontal resolution was set to 1.5 km, fine enough to properly describe the bathymetry and coast line details in the area of interest, so that 301 points were used in longitude and 201 in latitude. As in this region water is essentially fresh and horizontal temperature gradients are very small (Guerrero et al. 1997) temperature and salinity variations were not taken into account. In the simulations for mean seasonal winds 13 vertical layers with lower boundaries at 1, 2, 3, 4, 5, 7, 9, 12, 15, 20, 25, 30 and 55 m were used. When strong winds associated to storms were considered as a forcing, in order to avoid the first layer to become dry its depth was incremented to 3 m and, therefore, only 11 layers were used. An advantage of using a multi-layer model even when density is constant is to allow for a better representation of the bottom friction. The bottom friction factor was reduced to 3/5 of the exterior value (2.5×10-3) at every point where depth is shallower than 10 m; this approach allows for a reproduction of the observed tidal amplitudes and phases (Simionato et al. 2004a). In the momentum equations, the horizontal eddy viscosity has been set to 25 m2 s-1 and the vertical eddy viscosity is model computed following Pohlmann (1996). The time step was of 150 s in compliance with the Courant Friedrich and Lewy (CFL), criterion (Courant et al., 1928).
High resolution bathymetric data (Fig. 2) were obtained from digitalization of nautical charts (SHN 1992, 1999a and 1999b). A complete description of the Río de la Plata morphology and sedimentology can by found in Ottman and Urien (1965; 1966), Urien (1966; 1967; 1972), Depetris and Griffin (1968), Parker et al. (1986 a and b) and López Laborde (1987). The estuary is divided into two regions by the Barra del Indio shoal, a shallow area that crosses the estuary between Punta Piedras and Montevideo (Fig. 1). The upper and intermediate regions -upstream the shoal- are mainly occupied by fresh water. The upper part is characterized by Playa Honda and Ortíz Bank -very shallow areas with depths of between 1 and 4 m- separated from the coast by the Northern, Oriental and Intermediate channels -with depths ranging 5-8 m-. Whereas the Paraná de las Palmas and the Paraná Guazú-Bravo are only a few hundred of meters wide at their confluence to the estuary and can be, therefore, considered as single point sources in the model, the Uruguay river is approximately 10 km wide at its confluence with the Paraná Guazú-Bravo (Fig. 3a). A 20 km long channel of that width, in which head the Uruguay runoff was input, was used in the simulations to better reproduce the flow in that region and the confluence between the rivers.

Figure 3: Surface specific conductivity contours (μS cm-1) from direct observations collected between November 22nd and 23rd, 1982 (a); the dots show the sites where data were gathered. Specific conductivity contours (μS cm-1) as derived from numerical simulations including the conductivity sources at the three main tributaries of the Río de la Plata (b) and adding the Luján and Riachuelo rivers (c).
To introduce the effect of the tides in the simulations, a boundary condition that represents the evolution of the principal semidiurnal lunar (M2) tidal constituent coming from a larger scale model (Simionato et al. 2004a) was imposed to the sea surface elevation. M2 is the main constituent in the area, accounting for most of the tidal variance (DOnofrio et al. 1999).
The atmospheric data were the 6-hourly fields of wind components at 10 m and sea level pressure from NCEP/NCAR reanalysis on a 2.5° × 2.5° latitude-longitude grid. Full details of the NCEP/NCAR project and the dataset are given in Kalnay et al. (1996), references about their quality in the Southern Hemisphere are provided by Simmonds and Key (2000) and a discussion about reanalyzed 10 m wind capability to represent observed variability in the Río de la Plata region can be found in Simionato et al. (2006). Data, available at 0:00, 6:00, 12:00 and 18:00 GMT, were linearly interpolated to model time step. Local winds exhibit a marked seasonal cycle. Offshore winds (westerlies to north-westerlies) prevail in winter, whereas onshore winds (easterlies to north-easterlies) are more frequent in summer (Guerrero et al. 1997; Simionato et al. 2005).
Validation of the advection-diffusion equations for passive tracers: a case study
Unfortunately, there are no direct observations of passive tracers covering the totality of the Río de la Plata estuary to validate the model and its capability to properly represent mixing and transport processes in the region. The best available data for the upper and intermediate estuary, fulfilled of fresh water, correspond to a set of conductivity observations collected by the Servicio de Hidrografía Naval (SHN) of Argentina between November 22nd and 23rd 1982 (Quirós and Senone, 1985), when 24 locations were sampled between the Colonia-Buenos Aires and Montevideo-Punta Piedras lines (Fig. 3a). Conductivity is a measure of the capability of a solution to transport electricity. It depends on the presence of ions, on their total concentration, mobility and balance and, mainly, on temperature (Jaime et al. 2001). The use of specific conductivity, the conductivity normalized to temperature of 25 ºC, eliminates this complication and allows valuable comparisons to be made. Specific conductivity is very useful for identifying in a simple way the various sources of water responsible for flow at a particular site and has been used for the study of mixing rates by many authors (see, for instance, Jaime et al. 2001; Alen-King and Keller 2001; Menendez et al. 2002; Biron et al. 2004).
Figure 3a shows that, due to the influence of sea water, in the exterior part of the estuary specific conductivity is high; there a pattern of isolines transversal to the estuary axis with a large gradient is observed. Nevertheless, at the upper and central parts of the estuary contours display a northwest to southeast -along estuary axis- orientation with larger values on the Argentinean (southern) coast. On the other hand, even though along this coast specific conductivity gradient is relatively high, on the Uruguayan (northern) coast it is lower and the specific conductivity field is more homogeneous, with characteristic values of between 75 and 80 μS cm-1 (micro-Siemens per centimeter). Those patterns seem to be a consequence of the different conductivities that characterize the diverse tributaries. Even though specific conductivity displays variability, it is known that it is larger for the Paraná de las Palmas -with a mean value of 137 μS cm-1- than for the Uruguay river -with mean values of between 50 and 60 μS cm-1- and the specific conductivity of the Paraná Guazú-Bravo has been estimated in 90-100 μS cm-1 (Jaime et al. 2001). Those values suggest that the southern coast of the estuary is mostly dominated by the discharge of the Paraná de las Palmas, with higher specific conductivity, whereas the northern portion is influenced by the low specific conductivity waters of the Uruguay river (50-60 μS cm-1). Nevertheless, the fact that the specific conductivity observed along the northern coast of the estuary (75-80 μS cm-1) is higher than the one that characterizes the Uruguay river waters suggests mixing with the Paraná Guazú-Bravo. On the other hand, the presence of highly contaminated secondary tributaries -as the Riachuelo and Luján rivers- might affect conductivity along the Argentinean (southern) coast (Jaime et al. 2001).
A numerical case study was done with the aim of reproducing the pattern shown in Fig. 3 (left panel). During the observation period, Uruguay river runoff was exceptionally high -20,000 m3 s-1-whereas the discharges of the Paraná Guazú-Bravo and Paraná de las Palmas were of around 12,300 and 3,700 m3 s-1, respectively, closer to November mean values. Those runoffs were included in the simulation in the points of confluence of each of the three tributaries to the estuary. Water specific conductivity at those sources was set to 60, 100 and 137 μS cm-1 for the Uruguay, Paraná Guazú-Bravo and Paraná de las Palmas rivers, respectively. To simulate the oceanic conductivity source and to allow the model to freely develop gradients in the estuary, specific conductivity was initialized with a constant value of 900 μS cm-1 over the entire domain; this value was kept constant at the open boundaries of the model during the simulation. The model was spun-up during one month forced by the tributaries discharges, tides and mean winter winds and sea level pressure. Conductivity was released after the first month of simulation, when also the four-daily observed winds and sea level pressure were included as forcing. The solution for November 22nd, 1982 (after 2 month of tracer simulation) is shown in figure 3b. A comparison of the numerical solution to observations (Fig. 3a) shows that the model has captured the most outstanding features of the observed specific conductivity field. Both the transversal pattern of isolines observed at the intermediate part of the estuary and the longitudinal structure at its upper part, are well represented. The numeric solution reproduces the mixed zone along the Uruguayan coast with specific conductivities below 80 μS cm-1 so as the cross-estuary gradient observed along the Buenos Aires-Colonia line. Nevertheless, along the Argentinean coast, downstream La Plata, the numeric solution displays values which are lower than observations, suggesting that the additional specific conductivity sources associated to the secondary tributaries along this coast can be significantly affecting the total conductivity balance. To evaluate this possibility, an additional simulation was done in which the two most important secondary tributaries, Luján (with a runoff of 192 m3 s-1 and a specific conductivity of 256 μS cm-1, Jaime et al. 2001, 2002) and Riachuelo (with values of 72 m3 s-1 and 1000 μS cm-1, Jaime et al. 2001, 2002) rivers were included. The solution for this case is shown in figure 3c, where it can be observed that -when compared to the former one (Fig. 3b)-specific conductivity along the southern coast has increased downstream La Plata, better resembling the observations. Particularly, the shape and position of the 100 and 150 μS cm-1 isolines are better represented than in the first numerical experiment.
Even though the lack of observations does not allow for a validation of the model upstream the line Colonia-Buenos Aires, results in the rest of the domain are highly satisfactory. The model can capture both the pattern and values of the observed conductivity field, what validates the appropriate functioning of the numerical scheme implemented for tracers dispersion, at least at the intermediate estuary.
RESULTS
The path of plumes of the Río de la Plata tributaries
A set of numerical simulations was carried out with the aim of studying the path of plumes of the main tributaries of the Río de la Plata. To simulate those plumes, the incoming waters of the Uruguay, Paraná Guazú-Bravo and Paraná de las Palmas rivers were characterized at their source by different tracers, with a concentration of 100 (%) in all the cases.
To determine the summer and winter characteristic patterns the model was forced with the mean seasonal NCEP/NCAR 10 m winds and sea level pressure for the period 1972-2001 corrected by speed following Simionato et al. (2006). To evaluate the impact of discharge natural variability on the plumes path, simulations were repeated for mean summer, mean winter, high and low runoff conditions. Continental discharges for those conditions were taken from Jaime et al. (2002) and are shown in Table 1.
Table 1: Runoff (m3 s-1) of the main tributaries of the Río de la Plata estuary for (summer and winter) mean and extreme (low and high) discharge conditions.

To help on the interpretation of the results, sensitivity experiments to bathymetry and Earths rotation were also done. In the first case, estuary depth was artificially set to 7 m everywhere in its upper and intermediate parts, and in the second case, the Coriolis parameter was simply set to zero during the simulation. In every case the hydrodynamic model was spun-up during one month including runoff, wind, atmospheric pressure and tides, but tracers were released at the beginning of the second month of simulation. Then, the model was run for other two months, after what the solution was stable.
Results for mean summer and winter wind and runoff conditions are shown in figures 4a and b. As concentrations at the confluence of the tributaries to the estuary were set to 100%, values at every location represent percentage concentration of the considered tracer at that position. Simulation results (Figs. 4a and b) show two main paths for the tributaries waters in the upper estuary. The Uruguay and Paraná Guazú-Bravo waters (upper and intermediate panels) mainly occupy the northern and central portions of the estuary with abundant mixing between them, whereas the Paraná de las Palmas waters (lower panel) flow to the south, along the Argentinean coast.

Fig. 4: Surface concentration contours (%) of the dye tracers characterizing the Uruguay (upper panels), Paraná Guazú-Bravo (central panels) and Paraná de las Palmas (lower panels) rivers as derived from simulations forced by mean winter runoff and atmospheric forcing (left, a), mean summer runoff and atmospheric forcing (central, b) and mean summer atmospheric forcing and mean winter runoff (right, c).
Even though differences in the concentrations of the tracers are observed at the upper and central portions of the estuary from winter (Fig. 4a) to summer (Fig. 4b), sensitivity experiments demonstrate that they are due to the differences in the mean runoffs from one to other season more than to the difference in the atmospheric forcing. This feature can be clearly appreciated when comparing figures 4a and b to figure 4c, that shows the results of an experiment in which summer winds and atmospheric pressure and winter characteristic runoffs were considered. It can be seen in figure 4 that when the discharge is maintained constant (Figs. 4a and 4c), the effect of a change in the winds is only observed at the exterior part of the estuary. A similar conclusion results from a winter wind-atmospheric pressure/summer discharge simulation (not shown).
Figure 5 shows a detail of the simulations for mean winter atmospheric forcing and runoff conditions corresponding to two instants six hours apart, representing the tide flood (upper panels) and ebb (lower panels). According to the simulations, the waters of the Uruguay and Paraná Guazú-Bravo rapidly and turbulently mix after their confluence. A plume forming a relative maximum and a water lens whose formation is associated to the tidal flood and ebb, respectively, are observed northward Oyarvide and Martín García islands. Hellweger et al. (2004) and Hellweger (2005) demonstrated that those secondary peaks result of a process called tidal trapping (Okubo 1973). As the main plume moves up and down the river with the tide, a mass of tracer can get temporarily trapped. This is illustrated in the upper panels of figure 5, which show plumes of water with high tracer concentration trapped near the Uruguay River mouth during the flood.
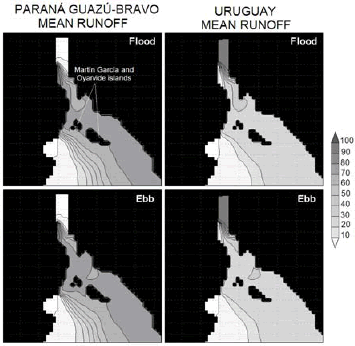
Figure 5: Detail of the surface concentration contours (%) at the upper estuary of the dye tracers characterizing the Uruguay (right panels) and Paraná Guazú-Bravo (left panels) as derived from a simulation forced by mean winter runoff and atmospheric forcing for the flood (upper panels) and ebb (lower panels) tide.
The rapid mixing of the Uruguay and Paraná Guazú-Bravo waters after their confluence observed in figures 4 and 5 is favored by the convergence at the region of a number of features: 1) the different water speeds of both tributaries at their confluence, 2) the presence of a bend immediately after it and 3) the varying geometry and bathymetry of the estuary. The Paraná Guazú-Bravo is narrow and is characterized by a high runoff, whereas the Uruguay is much broader and its discharge is about one third of the Paraná Guazú-Bravos one (Table 1). As a result, when the waters of the Paraná River enter to the Uruguay their speed is much higher, pushing the Uruguay waters laterally and originating a lateral mixing layer.
These transition zones between contiguous flows of different velocity intensify the lateral exchange of material and momentum (Booij and Tukker, 2001). The effect of bends or meanders on dispersion has been studied by several authors (see, for example, Overstreet and Galt, 1995 and Boxall et al. 2003). As water moves around a bend a secondary flow occurs which slightly deflects the streamlines in the flow and helps move particles across the shear boundaries with great increase in the dispersion of pollutants in the downstream direction. Finally, when cross-channel bathymetry profiles are irregular, this either accelerates or decelerates the average flow downstream. These irregularities will cause tracer distributions to speed up or slow down and contribute to the shear in the current pattern. Dispersion is greatly enhanced by an increase in width and depth (Jamali et al., 2005) as those observed in the Río de la Plata.
The sensitivity to bathymetry experiment (shown for the summer atmospheric forcing and runoff case in figure 6a) shows how the geometry and bathymetry condition the path of the plumes along the estuary. For realistic bathymetry, even though only a small portion of the total runoff reaches the estuary through the Paraná de las Palmas, the waters of this tributary fully occupy the shallow region of Playa Honda (Figs. 4 a and b, lower panels), whereas most of the discharge -related to the other two tributaries- is guided through the deeper channels of the north (Figs. 4 a and b, upper and central panels) with abundant mixing. Note that when bathymetry in the upper estuary is kept constant, due to the larger depth, the waters of the Uruguay and Paraná Guazú-Bravo tend to follow more differenced paths (Fig. 6 a and b, upper and central panels). Downstream Colonia, approximately, the geometry of the coast -that acquires an east-west orientation- and the presence of the Intermediate Channel, force the flow to concentrate in the central part of the estuary, favoring mixing and broadening of the dye plumes.

Figure 6: Surface concentration contours (%) of the dye tracers characterizing the Uruguay (upper panels), Paraná Guazú-Bravo (central panels) and Paraná de las Palmas (lower panels) rivers as derived from simulations forced by mean summer runoff and atmospheric forcing when bathymetric features are ignored (left, a) and when the Earth’s rotation is ignored (right, b).
Figure 6b shows the results of a simulation for the case when bathymetry is realistic but the rotation of the Earth is ignored. The effect of the Earths rotation (compare figures 4 and 6) is evident even at the intermediate part of the estuary, consistently with the (barotropic) Rossby radius of deformation that, for the characteristic depth of the upper and central estuary is less than 100 km. The effect of this deflecting force is to deviate the flow to the left (Uruguayan coast) in the Southern Hemisphere. As a result, when rotation is considered (Figs. 4a and b) the plumes of the Uruguay and Paraná Guazú-Bravo rivers have a more elongated and narrow structure along the northern estuarine coast, and the plume of the Paraná de las Palmas leaves the southern coast downstream Punta Piedras, instead of following the coast to Samborombón Bay (Fig. 6b). Note that this feature is not typical of estuaries but a result of the large extension of this particular system that tends to behave as a semi-enclosed basin.
Solutions for lower and higher than normal runoffs (shown in figure 7 for the mean summer wind and atmospheric pressure cases) do not exhibit qualitative significant differences with the mean discharge case above discussed at the intermediate part of the estuary. The main differences are the change in the relative concentrations of the waters of the different tributaries due to the changes in the runoff and an increase (reduction) in the transit time of the waters through the estuary associated to a reduction (increment) in the discharge.

Figure 7: Surface concentration contours (%) of the dye tracers characterizing the Uruguay (upper panels), Paraná Guazú-Bravo (central panels) and Paraná de las Palmas (lower panels) rivers as derived from simulations forced by mean summer atmospheric forcing and high (a) and low (b) runoff.
Figure 8 shows details of those simulations for the upper part of the estuary. When the runoff is low (lower panels) as the speed of the water entering the estuary is lower, the flow results less turbulent and the formation of water lenses by tidal trapping is not observed, but the other features described for mean discharge are conserved. For higher than normal runoff conditions (Fig. 8, upper panels), a change in the path of the plumes at the upper estuary occurs. In this case, due to the huge volume of water discharged by the tributaries and the relative increase in the Uruguay river runoff, the Paraná Guazú-Bravo waters are forced to enter the estuary further south, flowing south Oyarvide and Martín García islands (black in the figure). As a result, the upper part of the estuary is divided into two regions, one with a larger concentration of Uruguay waters northward the islands and along the Uruguayan coast, and other with a larger concentration of Paraná Guazú-Bravo waters at the central part of the estuary and southward the islands. Note that in this case, due to the deviation of the Paraná Guazú-Bravo waters southward and the relative increase in the Uruguay River discharge, the concentration of the waters of this last river along the northern coast significantly increases with respect to the mean and low discharge case (Fig. 4), being three times the one observed in the low discharge case. In nature, as the Paraná and Uruguay rivers drain the waters of different basins, their maxima do not necessarily occur simultaneously. If the Uruguay River discharge is high, but that of the Paraná is normal or low, the described features could be much enhanced and the influence of Uruguay River waters along the northern coast of the estuary might be much larger.

Figure 8: Detail of the surface concentration contours (%) at the upper estuary of the dye tracers characterizing the Uruguay (right panels) and Paraná Guazú-Bravo (left panels) as derived from simulations forced by mean summer atmospheric forcing and high (upper panels) and low (lower panels) runoff for the ebb tide.
Sensitivity to extreme wind conditions
The effect of the most frequent extreme atmospheric events associated to strong winds on the deformation of the plumes, so as the persistence of the signal introduce by them was evaluated. The two typical situations related to intense winds in the Río de la Plata result from local cyclogenesis and cold fronts, respectively (Vera et al. 2002). When cyclogenesis occurs northeastward the Río de la Plata, intense southeasterly winds with speeds of 35-80 km h-1 often blow over the estuary (Seluchi and Saulo 1996). These events, known as Sudestadas, have a typical duration of 48 hours and are associated to flooding on the southern coast of the upper estuary. During the first 36 hours wind speed increases, and then rapidly decays over the next 12 hours. The second situation occurs when cold fronts reach the estuary from the southwest. During these events, known as Pamperos, southwesterly winds which can also be very strong occur, but the time scale of these storms is of only 24 hours.
To study the signal introduced by those events and its persistence, simulations where done in which the initial conditions were the mean wind and runoff scenarios after 60 days of tracers integration discussed in the former section (Fig. 4a and b). The Sudestada was simulated in a simple even realistic way for the small region of interest. A southeasterly wind whose speed increases up to 11 m s-1 (approximately 40 km h-1) during the first 36 hours and then rapidly decays during the next 12 hours, according to the (nondimensional) time function shown in figure 9, was applied. Likewise, the Pampero (not shown) was simulated as a southwesterly wind of similar speed, which grows and decays in time scales of 12 hours. Once the storms have decayed, simulations were continued for an additional period of 20 days under mean winds in order to study the persistence of the signal introduced by them. Even though experiments were repeated for summer and winter conditions, conclusions do not essentially differ for the region of interest.

Figure 9: Nondimensional time function used to modulate wind speed for the simulation of the Sudestada onset and offset.
The maximum sea surface anomaly introduced by the Sudestada (after 42 hours) in the winter case is shown in the upper panel of figure 10. A strong sea surface elevation increment occurs in the upper estuary that reaches its maximum over the Argentinean coast, in the area of Playa Honda. The anomaly in the tracers concentration for that instant can be seen in figure 11a in which, for reasons of clarity of interpretation, only anomalies larger than 5 (%) have been contoured. It can be observed in this last figure that, excepting the frontal zone where tracers meet the ocean and our solution might not be realistic due to having neglected salinity effects, maximum anomalies occur along the Argentinean coast, between La Plata and the estuary head. Anomalies are large, with values of ±25 on the Argentinean coast. The concentration anomalies observed are consistent with the sea surface elevation pattern associated (Fig. 10, upper panel). Along the southern coast, between La Plata and the estuary head, a reduction in the concentration of the Paraná de las Palmas tracer and an increment in the corresponding to the other two tributaries is observed. This can be explain by the inflow of water from the outer estuary (with a lower concentration of tracers) that increases sea surface elevation and inhibits the offshore progress of the Paraná de las Palmas waters.
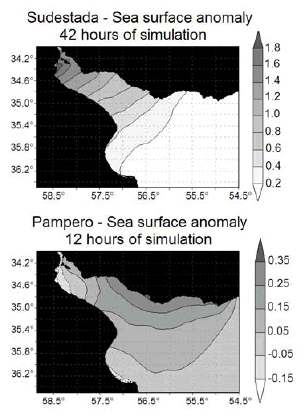
Figure 10: Free surface high (m) anomaly introduced by the Sudestada (upper panel) and Pampero (lower panel).

Fig. 11: Surface concentration anomaly contours (%) of the dye tracers characterizing the Uruguay (upper panels), Paraná Guazú-Bravo (central panels) and Paraná de las Palmas (lower panels) rivers introduced by the Sudestada (a) and Pampero (b).
Time series of the tracers concentration at diverse points of Argentinean and Uruguayan coasts are shown in figure 12, where it is evident that the coastal effect of this kind of storms is mainly manifested on the estuarys southern coast. Note that, as the tributaries enter the estuary at its head, even though the intensity of the response to the storm increases in that direction, the opposite occurs with the persistence of the signal (or the time it takes to return to mean values). In Buenos Aires, all signature of the storm has disappeared 48 hours after it has ended, whereas it persists several more days in La Plata.

Figure 12a: Surface concentration anomalies (%) of the dye tracers characterizing the Uruguay (UR), Paraná Guazú-Bravo (PGB) and Paraná the las Palmas (PP) rivers introduced by the Sudestada at several coastal locations of the Río de la Plata estuary.

Figure 12b: Idem Figure 12a but for the Pampero.
Sea surface anomalies for the Pampero case after 12 hours of simulation for the winter case are shown in the lower panel of figure 10. Southwesterly winds produce an increment in the sea surface elevation over the Uruguayan (northern) coast and a reduction near Buenos Aires but, due to the shorter time span of the storm, the amplitude of the signal is much smaller than for the Sudestada. Tracers anomalies fields after 12 hours are shown in figure 11b.
Maximum values are similar to those observed for the Sudestada case and in the area of interest of this study are maxima at Playa Honda. The anomaly observed at this location in the upper estuary, suggests a larger extension to the north of the Paraná de las Palmas plume, also forced by the southwesterly winds. Time series of the tracers concentrations (Fig. 12) show that responses in the Pampero (Fig. 12b) and Sudestada (Fig. 12a) cases are somewhat different. Even for the Pampero the maximum sea surface elevation is observed on the northern coast, the maximum effect on tracers concentration is observed in the opposite side. This is a result of a combination of estuarine bathymetry and the tributaries plumes structure. In Playa Honda, the estuary is very shallow and, therefore, rapidly responds to winds. Consequently in Buenos Aires the signal rapidly grows during the onset of the storm. After the first 12 hours, even the storm relaxes, the signal on the tracers remains because the region is being re-occupied by the water that the storm had displaced northward.
After approximately 5 days, all signal of the storm has disappeared from this region. In La Plata these two time scales are even more clearly observed. During the first day an increment (reduction) in the concentration of the Paraná de las Palmas (Paraná Guazú-Bravo and Uruguay) waters is observed, which is a direct effect of the southwesterly winds, whereas the reciprocal is observed during the next days, as a result of the relaxation of the water that the storm accumulated on the northern coast. In Punta Piedras the effect is, as for the Sudestada, a reduction in the concentration of the three tracers as a result of sea water inflow from the south to compensate the northerly motion of estuarine waters induced by the storm. The lack of a significant signal along the Uruguayan coast can be attributed to the larger depths observed along it and the fact that there waters are always better mixed.
The tracer concentration fields (not shown) show that even though storms introduce deformations to those shown for mean winds (Fig. 4), the pattern and general features of the tributaries plumes are always preserved. Even though storms modify the relative composition of the estuarine waters, particularly along Argentinean coast, during the events, the signal is lost after approximately one week. Nevertheless, those changes could be important from a contamination point of view.
Mixing scales
The simulations discussed in the former sections also allow the estimation of several useful mixing time scales for the Río de la Plata estuary waters. The elapsed time to the arrival of the leading edge of the tracer cloud at a location can be related, for instance, with the time it would take to a contaminant spilled in the estuary head to reach that point. Values for this time scale for several coastal locations of the Río de la Plata estuary estimated from our simulations for diverse runoff and wind conditions are shown in Table 2.
Table 2: Elapsed time (in days) to the arrival of the leading edge of the tracer cloud of each of the main tributaries of the Río de la Plata at several coastal locations of the estuary. The position of the locations can be seen in figure 2.

This time scale obviously depends no only on the distance to the sources but also on the continental discharge; therefore, a significant reduction (increment) is observed for the high (low) runoff scenarios. Nevertheless, the scale does not significantly vary with the wind in the upper and central estuary, what is consistent with the formerly discussed results. It is interesting to note, also, that the Paraná de las Palmas waters do not reach intermediate points of the Uruguayan (northern) coast, except for low runoff conditions. For mean discharge conditions, the Paraná de las Palmas waters delay approximately 3 days in arriving to Buenos Aires, whereas those of the Uruguay and Paraná Guazú-Bravo need 7 and 5 days, respectively, to reach that location. For the intermediate estuary the time scale is of around 20 days.
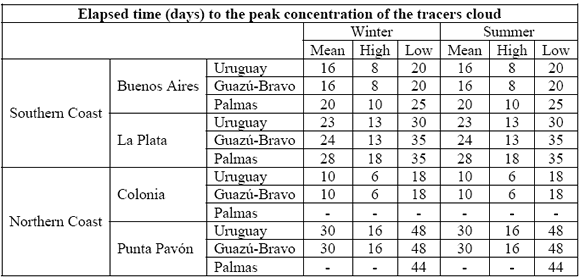
The elapsed time to the peak concentration of the tracer cloud is other useful time scale. This scale for several coastal locations, as estimated from our simulations, is shown in Table 3. Obviously, it becomes larger as the location is further away from the source and depends on the runoff. For a typical mean runoff scenario, for Buenos Aires it is of approximately 20 days.
Table 3: Elapsed time (in days) to the peak concentration of the tracer cloud of each of the main tributaries of the Río de la Plata at several coastal locations of the estuary. The position of the locations can be seen in figure 2.
The residence and flushing times of an estuary are two different concepts that are often confused. Flushing time is the time required for the freshwater inflow to equal the amount of freshwater originally present in the estuary. It is specific to freshwater (or materials dissolved in it) and represents the transit time through the system (e.g., from head to the mouth) (Sheldon and Albera 2002). Residence time is the average time particles take to escape the estuary. It can be calculated for any type of material and will vary depending on the starting location of the material. In the literature, the term residence time is often used to refer to the average freshwater transit time and is calculated as such (e.g. Bolin and Rhode 1973; Takeoka 1984; Zimmerman 1988; Monsen et al. 2003; Braunschweig et al. 2003). Hydrodynamic flushing feature in an estuary is a measure of its self-purification capability; it determines the renewal of fresh water and hence the water quality evolution. Conventionally, estuarine flushing time is computed by simplified approaches, such as the tidal prism or salt balance method (Ippen 1966; Fischer et al. 1979; Officer and Kester 1991). These methods typically assume full mixing and cannot account for spatial variations; they are also not applicable when no salinity data are available, or in bays with weak salinity gradients. More recently numerical tracer experiments in 3-D models have been used in different ways to calculate mixing scales (e.g. Burwell et al. 1999; Delhez et al. 2004; Banas and Hickey 2005).
As the concentrations of the tracers at the confluence of the tributaries to the estuary were set to 100%, values at every location represent percentage of waters of the corresponding tributary, at that position. Given that we initialized our simulations with zero concentration of tracers in the entire estuary, when the sum of their concentrations at a given point reaches 100, it means that the water has been completely renewed (either by water of a single tributary or by a combination of two or three of them) and represents, therefore, the flushing time (the time required for the freshwater inflow to equal the amount of freshwater originally present) according to the definition provided by Sheldon and Albera (2002). The portion of the estuary that reaches this condition after 10, 20, 30, 40, 50 and 60 days of simulation for a mean winter scenario is shown in figure 13. Results for the summer scenario resulted very similar and, therefore, are not shown. Figure 13 indicates that the flushing times of water in the intermediate estuary is of around 60 days for mean runoff conditions. For high discharge conditions (not shown) it can be reduced to 30 days, but it can increase to 90 days for low discharge conditions. The computed flushing time within the Río de la Plata Estuary for mean runoff conditions ranges from around 10 days in the inner estuary to 60 days in the outer part.

Figure 13: Flushing time contours every 10 days of the upper and intermediate Río de la Plata estuary for mean runoff conditions.
SUMMARY OF CONCLUSIONS AND DISCUSSION
The numerical solutions discussed in the previous sections show that for mean runoff conditions the waters of the major tributaries of the Río de la Plata flow through the estuary forming two main plumes. The Uruguay and Paraná Guazú Bravo waters mainly occupy the northern (Uruguayan) coast and the central part of the channel with abundant mixing between them, whereas the Paraná de las Palmas waters flow along the southern (Argentinean) coast. The occurrence and pattern of the plumes are controlled by the runoff and geometry and bathymetry of the estuary. Due to the much larger speed of the Paraná Guazú-Bravo River waters at its confluence with the Uruguay, the waters of this last river are pushed towards the opposite (eastern) coast and a lateral mixing layer is formed. After their confluence, the tidal trapping contributes to the formation of water lenses and the occurrence of a bend to the east and the varying geometry and bathymetry of the estuary favor further mixing. Those processes origin the northern plume formed by a mix of the waters of those two rivers, which continues flowing along the relatively deep Northern Channel on the Uruguayan coast. The relatively low discharge Paraná de las Palmas River waters, instead, occupy the shallow region of Playa Honda to the south of the upper estuary. Downstream Colonia, a change in the orientation of the coast line -that acquires an east to west orientation- and the presence of the Intermediate Channel, force the flow to concentrate in the central part of the estuary, favoring mixing between both plumes. The Earths rotation plays a role in favoring the separation of the Paraná de las Palmas plume from the southern coast of the estuary and its motion to the north and gives an elongated shape to the plumes.
SQUEMATIC REPRESENTARON OF THE PATH OF PLUMES
Numerical solutions indicate that whereas the occurrence of the above mentioned plumes is not essentially modified for low runoff conditions, they can result different if discharge is higher than normal. In this case, a change in the way in which the waters of the different tributaries flow in the upper estuary occurs. Due to the enormous volume of water discharged by the Uruguay and Paraná Guazú-Bravo in this condition, part of this last river waters flow south Oyarvide and Martín García islands. As a result, the northern part of the upper estuary is divided into two regions, one with a larger concentration of Uruguay waters northward the islands and along the coast and another with a larger concentration of Paraná Guazú-Bravo waters southward them. In this case there is a much larger influence of Uruguay waters along the northern coast, which might be enhanced if a peak runoff occurs for the Uruguay but not for the Paraná River. A scheme of the path of the plumes of the main tributaries to the Río de la Plata is displayed in figure 14, illustrating the ideas above discussed.

Figure 14: Schematic representation of the path of the plumes of the Río the la Plata estuary main tributaries. Whereas the Paraná de las Palmas waters flow to the south, following the southern coast, the waters of the Paraná Guazú-Bravo and Uruguay rivers mix after the confluence and flow along the northern coast. Part of the waters of the Paraná Guazú-Bravo River flows between the other two masses, particularly when the discharge of the Uruguay River is high.
Even though there are not direct observations that permit a validation of the former conclusions, our simulations are consistent with several indirect evidences. Firstly, our conclusions are qualitatively consistent with what can be inferred from the bottom sediments distribution. In effect, the left panel of figure 15 -adapted from Parker et al. 1987- shows that the bottom sediments associated to the Paraná de las Palmas (5 in the figure) have a distribution whose pattern is very similar to the plume for this tributary indicated by our simulations. Similarly, the shape and extension of the plume that according to Parker identifies the sediments related to the Uruguay and Paraná Guazú-Bravo rivers (4 in the figure) is very similar to the one provided by our simulations for the dies associated to those rivers. Moreover, quantitative consistency is also found. Parker et al. (1987) showed that the decantation time of the sediments characteristic of the Paraná de las Palmas is of around 12 days. A comparison of sediments distribution (Fig. 15, left panel) with our solution for this river after 12 days (Fig. 15, right panel) shows that the model properly captures the extension and pattern of the corresponding plume.

Figure 15: Left: Observed bottom sediments distribution at the upper and intermediate Río de la Plata estuary (adapted from Parker et al. 1987): (1) Mud; (2) Clay; (3) Sand; (4) Association of facies, of sand and clayey sand characteristic of the Uruguay and Paraná-Guazú rivers; (5) Fine textures with higher concentrations of carbon characteristic of the Luján and Paraná de las Palmas rivers. Right: Plume of the dye tracer characterizing the Paraná de las Palmas River after 12 days of simulation.
The occurrence of intense mixing in the northern portion of the estuary downstream Colonia indicated by our simulations is also consistent with what can be inferred from the conductivity field (Fig. 3a), which shows a plume of almost constant conductivity in that region, and is apparent in satellite images as well. Figure 16 (upper panel) shows a gray scale color image collected by the Moderate Resolution Imaging Spectroradiometer on board of Terra satellite (MODIS-TERRA, http://visibleearth.nasa.gov) in April 13th, 2003. During that period the discharges of the tributaries were comparable to their means (around 5,000 m3 s-1 for the Uruguay and 25,000 m3 s-1 for the Paraná). In this image clear waters, as those from the ocean and the Uruguay River look darker, whereas waters with high concentration of suspended matter, as those of the Paraná River, look lighter. The rapid and turbulent mixing of the Uruguay and Paraná Guazú-Bravo waters after their confluence is evident in the figure in good agreement with our simulations (Fig. 5). The lower panel of figure 15 shows another image collected on May 4th, 2002, a period when the discharge of the Uruguay River was very high (around 10,000 m3 s-1) and Paraná River runoff was normal (approximately 22,000 m3 s-1). A strong water color gradient transversal to the estuary can be observed in its northern portion, with the presence of eddies that suggest mixing zones. Even though unfortunately images do not allow for quantification, the main features described by our simulations are observed. In particular, the larger concentration of Uruguay River waters (darker) in the northern estuary is evident, so as the better differentiation of the Uruguay and Guazú-Bravo plumes after their confluence in the upper estuary. Also, the widening and mixing of the plumes downstream Colonia can be inferred. Similar features are observed in all the other images available.

Figure 16: Gray scale color images collected by the Moderate Resolution Imaging Spectroradiometer on board of Terra satellite (MODIS-TERRA) in April 13th, 2003 (upper panel) and May 4th, 2002 (lower panel). Figure shows typical images collected by the satellite for mean runoff and high Uruguay River runoff conditions, respectively. (From Visible Earth, http://visibleearth.nasa.gov).
The results of the simulations indicate that during the most frequent storm events (Sudestadas and Pamperos) the identity and general pattern of the plumes are preserved. Nevertheless during those events, due to its shallowness, Argentinean coast is significantly affected by advection and mixing. The persistence of the signal introduced by the storms depends on the location, but does not exceed one week.
The simulations also allowed for the estimation of several mixing scales for the estuary. Given that simulations were done for steady wind conditions they do not represent any particular situation. Nevertheless they provide a good approximation and constitute the first estimates for the Río de la Plata based on realistic simulations. At the upper and upper intermediate estuary mixing scales are mainly related to the runoff with scarce influence of the mean winds. Given the broad range of discharge conditions observed in the estuary, time scales can be 50% larger (lower) than the corresponding to mean conditions for low (high) discharge.
For mean runoff, the elapsed time to the arrival of the leading edge of the Paraná de las Palmas tracer cloud at Buenos Aires is of around 3 days, whereas those of the Uruguay and Paraná Guazú-Bravo are of 7 and 5 days, respectively. The elapsed time to the peak concentration of the tracer cloud for a typical mean runoff scenario is of around 20 days at Buenos Aires. For that condition, the flushing times of the upper and upper intermediate estuary range between 10 and 60 days. Compared to typical net algal growth rates of the order of 0.1 per day, the weak flushing would permit the accumulation of nutrients and algal blooms.
Acknowledgments. This paper is a contribution to the UNDP/GEF RLA/99/G31 Project Environmental Protection of the Río de la Plata and its Maritime Front, the PIP 112-200801-02599, and the UBA Grant I014 and the PICT 2005 7-32606. Satellite images were provided by Visible Earth, NASA Goddard Space Flight Center, http://visibleearth.nasa.gov.
REFERENCES
1. Acha, E. M. and G. J. Macchi. 2000. Spawning of Brazilian menhaden, Brevoortia aurea, in the Río de la Plata Estuary off Argentina and Uruguay. Fishery Bulletin 98: 227-235. [ Links ]
2. Acha, E. M., H. W. Mianzan, C. A. Lasta and R.A. Guerrero. 1999. Estuarine spawning of the whitemouth croaker Micropogonias furnieri (Pisces: Sciaenidae) in the Río de la Plata, Argentina. Marine and Freshwater Research 50: 57-65. [ Links ]
3. Allen-King, R. and C. K. Keller. 2001. Geochemical fingerprints aid non-point pollutant study. Washington Water Research Center Newsletter 4: 1-8. [ Links ]
4. Alvarez Fanjul, E. A., B. Pérez Gómez and I. Rodríguez Sanchez-Arévalo. 1997. A description of the tides in the Eastern North Atlantic. Progress in Oceanography 40: 217-244. [ Links ]
5. Backhaus, J. O. 1983. A semi-implicit scheme for the shallow water equations for application to shelf sea modelling. Continental Shelf Research 2(4): 243-254. [ Links ]
6. Backhaus, J. O. 1985. A three dimensional model for simulation of shelf sea dynamics. Deutsche Hydrographische Zeitschirft 38(H.4): 164-187. [ Links ]
7. Backhaus, J. O. and D. Hainbucher. 1985. A finite difference general circulation model for shelf sea and its applications to low frequency variability on the North European Shelf. In: Three dimensional model of marine and estuarine dynamics. J. C. Nihoul and B. M. Jamars, (Eds.) Elsevier Oceanographic Series. 45, Amsterdam, 221-244. [ Links ]
8. Balay, M.A. 1961. El Río de la Plata entre la atmósfera y el mar. Publicación. H-621. Buenos Aires: Servicio de Hidrografía Naval. Armada Argentina. 153 pp. [ Links ]
9. Banas, N. S. and B. M. Hickey. 2005. Mapping exchange and residence time in a model of Willapa Bay, Washington, a branching, macrotidal estuary. Journal of Geophysical Research, 110, C11011, doi:10.1029/2005JC002950. [ Links ]
10. Berasategui, A. D., E. M. Acha and N.C., Fernandez Araoz. 2004. Spatial patterns of ichthyoplankton assemblages in the Río de la Plata Estuary (Argentina-Uruguay). Estuarine Coastal and Shelf Science 60: 599-610. [ Links ]
11. Biron, P. M., A. S. Ramamurthy and S. Han. 2004. Three-Dimensional Numerical Modeling of Mixing at River Confluences. Journal of Hydraulic Engeneering 130(3): 243-253. [ Links ]
12. Bolin, B. and H. Rhode. 1973. A note on the concepts of age distribution and residence time in natural reservoirs. Tellus, 25: 58–62. [ Links ]
13. Booij, R. and J. Tukker. 2001. Integral model of shallow mixing layers. Journal of Hydraulic Research 39(2): 169-179. [ Links ]
14. Boxall, J.B., I. Guymer and A. Marion. 2003. Transverse mixing in sinuous natural open channel flows. Journal of Hydraulic Research 41(2): 153–165. [ Links ]
15. Braunschweig, F., F. Martins, P. Chambel and R. Neves. 2003. A methodology to estimate renewal 20 time scales in estuaries: the Tagus Estuary case. Ocean Dynamics 53(3): 137–145. [ Links ]
16. Burwell, D., M. Vincent, M. Luther and B. Galperin. 1999. Modeling Residence Times: Eulerian vs Lagrangian, Estuarine and Coastal Modeling, Proceedings of the Sixth International Conference, Nov. 3-5, 1999, New Orleans, Louisiana. [ Links ]
17. Consejo Federal de Inversiones. 1969. Los recursos hidráulicos de Argentina, análisis y programación tentativa de su desarrollo. Comisión Económica para América Latina, Vol. 2. [ Links ]
18. Courant, R., Friedrichs, K. and Lewy, H., 1928. Über die partiellen Differenzengleichungen der mathematischen Physik. Mathematische Annalen. 100(1): 32–74. [ Links ]
19. Delhez, E. J. M., A. W. Heemink and E. Deleersnijder. 2004. Residence time in a semi-enclosed domain from the solution of an adjoint problem, Estuarine Coastal and Shelf Science 61: 691–702. [ Links ]
20. Depetris, P. J and J. J. Griffin. 1968. Suspended load in the Río de la Plata drainage basin. Sedimentology 11: 53-60. [ Links ]
21. D'Onofrio, E., M. Fiore and S. Romero. 1999. Return periods of extreme water levels estimated for some vulnerable areas of Buenos Aires. Continental Shelf Research 19: 1681-1693. [ Links ]
22. Feurstein, D. L. and R. E. Selleck. 1963. Fluorescent tracers for dispersion measurements. American Society of Civil Engineers proceedings, Journal of the Hydraulics Division 90(SA3): 1-12. [ Links ]
23. Fischer, H. B., E. J. List, R. C. Y. Koh, J. Imberger and N. J. Brooks. 1979. Mixing in Inland and Coastal Waters, Academic Press, San Diego, California. [ Links ]
24. Framiñan, M. B., M. P. Etala, E. M. Acha, R. A. Guerrero, C. A. Lasta and O. B. Brown. 1999. Physical characteristics and processes of the Río de la Plata Estuary, in Estuaries of South America: Their morphology and dynamics. Edited by Perillo, G.M.E, M.C. Piccolo and M. Pino Quivira. Springer. Berlín, 161-194. [ Links ]
25. Guerrero, R. A., E. M. Acha, M. B. Framiñan and C. A. Lasta. 1997. Physical oceanography of the Río de la Plata Estuary, Argentina, Continental Shelf Research 17(7): 727-742. [ Links ]
26. Harms, I. 1997. Modeling the dispersion of 137Cs and 239Pu released from dumped waste in the Kara Sea. Journal of Marine Systems 13: 1-19. [ Links ]
27. Harms, I. and P. P. Povinec. 1999. The outflow of radionuclides from Novaya Zemlya bays - modeling and monitoring strategies. The Science of Total Envirnment 237/238: 193-201. [ Links ]
28. Hellweger, F. L., O. K. Scheible and E. Garland. 2003. Model for the Assessment and Remediation of Sediments (MARS Version 1.1 Beta) Users Manual and Technical Reference. Technical Report 1008884. Electric Power Research Institute (EPRI), Palo Alto, California. [ Links ]
29. Hellweger, F., A. F. Blumberg, P. Schlosser, D. Ho, T. Caplow, U. Lall and H. Li. 2004. Transport in the Hudson Estuary: A Modeling Study of Estuarine Circulation and Tidal Trapping. Estuaries, 27(3): 527-538. [ Links ]
30. Hellweger, F. 2005. Measuring and modeling large-scale pollutant dispersion in surface waters. Water Environment Federation Collection Systems 2005: 812-835. [ Links ]
31. Ippen, A.T. 1966. Estuary and Coastline Hydrodynamics. McGraw-Hill, New York. [ Links ]
32. Jaime, P., A. Menéndez and O. Natale. 2001. Balance y dinámica de nutrientes principales en el Río de la Plata interior. Proyecto INA 10.4. Informe 01. Instituto Nacional del Agua. Ezeiza, Sep. 2001. [ Links ]
33. Jaime, P., A. Menéndez, M. Uriburu Quirno and J. Torchio. 2002. Análisis del régimen hidrológico de los ríos Paraná y Uruguay. Informe LHA 05-216-02. [ Links ]
34. Jamali, M., G. A. Lawrence and K. Maloney. 2005. Dispersion in Varying-Geometry Rivers with Application to Methanol Releases. Journal of Hydraulic Engineering 131(5): 390-396. [ Links ]
35. Jobson, J. 1996. Prediction of Traveltime and Longitudinal Dispersion in Rivers and Streams. U.S. Geological Survey Water-Resources Investigations Report 96-4013, 69 p. [ Links ]
36. Kalnay, E. and Coauthors. 1996. The NCEP/NCAR 40-Year reanalisis project. Bulletin of the American Meteorological Society 77: 437-471. [ Links ]
37. Koutitonsky, V., T. Guyondet, A. St-Hilaire, S.C. Courtenay and A. Bohgen. 2004. Water renewal estimates for aquaculture developments in the Richibucto estuary, Canada. Estuaries 27(5): 839-850. [ Links ]
38. Liu, Z., H. Wei, G. Liu and J. Zhang. 2004. Simulation of water exchange in Jiaozhou Bay by average residence time approach. Estuarine Coastal and Shelf Science 61: 25-35. [ Links ]
39. López Laborde, J. 1987. Distribución de sedimentos superficiales de fondo en el Río de la Plata Exterior y Plataforma adyacente. Investigación en Oceanología 1: 19-30. [ Links ]
40. Macchi, G. J., E. M. Acha and C. A. Lasta. 1996. Desove y fecundidad de la corvina rubia (Micropogonias furnieri, Desmarest, 1826) en el estuario del Río de la Plata, Argentina. Bol. Inst. Esp. Oceanogr 12: 99-113. [ Links ]
41. Menéndez, A. N., P. Jaime and O. E. Natale. 2002. Nutrients Balance in the Río de la Plata River using Mathematical Modelling. 5th International Conference HydroInformatics, Cardiff, UK, July, 2002. [ Links ]
42. Monsen, N. E., J. E. Cloern and L.V. Lucas. 2003. A comment on the use of flushing time, residence time and age as transport time scales. Limnology and Oceanography 47(5): 1545–1553. [ Links ]
43. Nagy, G. J., C. M. Martinez, R. M. Caffera, G. Pedraloza, E. A. Forbes, A. C. Perdomo and J. L. Laborde. 1997. The hydrological and climatic setting of the Río de la Plata. In: The Río de la Plata, An Environmental Review, An EcoPlata Project Background Report. Dalhausie University, Halifax, Nova Scotia. 17-68. [ Links ]
44. Officer, C. B. and D. R. Kester. 1991. On estimating the non-advective tidal exchanges and advective gravitational circulation exchange in an estuary. Estuarine Coastal and Shelf Science 32: 99-103. [ Links ]
45. Okubo, A. 1973. Effect of shoreline irregularities on streamwise dispersion in estuaries and other embayments. Netherlands Journal of Sea Research, 6: 213–224. [ Links ]
46. Ottman, F. and C. M. Urien. 1965. La melange des eaux douces et marines dans le Río de la Plata. Cahiers Oceanographiques 17: 213-234. [ Links ]
47. Ottman, F. and C. M. Urien. 1966. Sur quelques problemes sedimentologiques dans le Río de la Plata. Revue de Géographie Physique et Géologie Dynamique 8: 209-224. [ Links ]
48. Overstreet, R. and J. A. Galt. 1995. Physical processes affecting the movement and spreading of oils in inland waters. NOAA / Hazardous Materials Response and Assessment Division, Seattle, Washington, HAZMAT Report 95-7, September 1995. [ Links ]
49. Parker, G., J. L. Cavalloto, S. Marcolini and R. Violante. 1986a. Los registros acústicos en la diferenciación de sedimentos subácueos actuales (Río de la Plata). 1er Reunión de Sedimentología Argentina, 32-44. [ Links ]
50. Parker, G., J. L. Cavalloto, S. Marcolini and R. Violante. 1986b. Transporte y dispersión de los sedimentos actuales del Río de la Plata (análisis de texturas). 1er Reunión de Sedimentología Argentina, 38-41. [ Links ]
51. Parker, G., S. Marcolini, J. Cavallo and R. Violante. 1987. Modelo esquemático de dispersión de sedimentos en el Río de La Plata. Ciencia y Tecnología del Agua 1(4): 68-80. [ Links ]
52. Pohlmann, T. 1996. Predicting the thermocline in a circulation model of the North Sea – Part I: model description, calibration and verification. Continental Shelf Research 16(2): 131-146. [ Links ]
53. Quirós, R. and H. Senone. 1985. Niveles de nutrientes y pigmentos fotosintéticos en el Rio de la Plata interior (55° - 59° W, 34° - 36° S). Informe Técnico No.1, Instituto Nacional de Investigación y Desarrollo Pesquero, Departamento de Aguas Continentales. [ Links ]
54. Rodrigues, K. A. 2005. Biología reproductiva de la saraquita, Ramnogaster arcuata del estuario del Río de la Plata. MS Thesis, University of Mar del Plata, Argentina, 40 pp. [ Links ]
55. Rodriguez, I. and E. Alvarez.1991. Modelo tridimensional de Corrientes. Condiciones de aplicación a las ostas españolas y análisis de resultados para el caso de un esquema de mallas anidadas. Clima Marítimo Report 42, 65 pp. [ Links ]
56. Rodriguez, I., E. Alvarez, E. Krohn and J. Backhaus. 1991. A mid-scale tidal analysis of waters around the north western corner of the Iberian Peninsula. Proceedings of a Computer Modelling in Ocean Engineering 91, Balkema, 568 pp. [ Links ]
57. Seluchi, M. E. and A. C. Saulo. 1996. Possible mechanisms yielding an explosive coastal cyclogenesis over South America: experiments using a limited area model. Australian Meteorological Magazine 47: 309-320. [ Links ]
58. Sheldon, J. E. and M. Albera. 2002. A Comparison of Residence Time Calculations Using Simple Compartment Models of the Altamaha River Estuary, Georgia. Estuaries, 25(6): 1304–1317. [ Links ]
59. Shen, J., J. D. Boon and A. Y Kuo. 1999. A Modeling Study of a Tidal Intrusion Front and Its Impact on Larval Dispersion in the James River Estuary, Virginia. Estuaries 22(3A): 661-692. [ Links ]
60. Shiklomanov, I.A. 1998. A summary of the monograph world water resources. A new appraisal and assessment for the 21st Century. UNEP: Society and Cultural Organization. [ Links ]
61. SHN. 1992. Acceso al Río de la Plata, Carta Náutica H1, 5th ed., Servicio de Hidrografia Naval, Armada Argentina. [ Links ]
62. SHN. 1999a. Río de la Plata Medio y Superior, Carta Náutica H116, 4th ed., Servicio de Hidrografia Naval, Armada Argentina. [ Links ]
63. SHN. 1999b. Río de la Plata Exterior, Carta Náutica H113, 2nd ed.,Servicio de Hidrografia Naval, Armada Argentina. [ Links ]
64. Simionato, C. G., M. N. Nuñez and M. Engel. 2001. The Salinity Front of the Río de la Plata - a numerical case study for winter and summer conditions. Geophysical Research Letters 28(13): 2641-2644. [ Links ]
65. Simionato, C. G., W. Dragani, M. N. Nuñez and M. Engel. 2004a. A set of 3-D nested models for tidal propagation from the Argentinean Continental Shelf to the Río de la Plata Estuary -Part I M2. Journal of Coastal Research 20: 893-912. [ Links ]
66. Simionato, C. G., W. Dragani, V. Meccia and M. N. Nuñez, 2004b. A numerical study of the barotropic circulation of the Río de La Plata Estuary: sensitivity to bathymetry, earth rotation and low frequency wind variability. Estuarine, Coastal and Shelf Science 61: 261-273. [ Links ]
67. Simionato, C. G., C. S. Vera and F. Siegismund. 2005. Surface wind variability on seasonal and interannual scales over Río de la Plata area. Journal of Coastal Research 21: 770-783. [ Links ]
68. Simionato, C. G., W. Dragani, V. Meccia and M. N. Nuñez. 2006. On the use of the NCEP/NCAR surface winds for modeling barotropic circulation in the Río de la Plata Estuary. Estuarine, Coastal and Shelf Science. In press. [ Links ]
69. Simmonds, I and K. Keay. 2000. Mean Southern Hemisphere extratropical cyclone behavior in the 40-year NCEP-NCAR Reanalysis. Journal of Climate, 13: 873-885. [ Links ]
70. Smart, P. L. and I. M. S. Laidlaw. 1977. An evaluation of some fluorescent dyes for water tracing. Water Resources Research 13(1): 15-33. [ Links ]
71. Stronach, J. A., J. Backhaus and T. S. Murty. 1993. An update on the numerical simulation of oceanographic processes in the waters between Vancouver Island and the mainland: the GF8 model. Oceanography and Marine Biology: An annual Review 31: 1-86. [ Links ]
72. Takeoka, H. 1984. Fundamental concepts of exchange and transport time scales in a coastal sea. Continental Shelf Research 3: 311–326. [ Links ]
73. Urien, C. M. 1966. Distribución de los sedimentos en el Río de la Plata Superior. Boletín Servicio de Hidrografía Naval 3: 197-203. [ Links ]
74. Urien, C. M. 1967 Los sedimentos modernos del Río de la Plata Exterior. Servicio de Hidrografía Naval, Argentina, Público H-106 4: 113-213. [ Links ]
75. Urien, C. M. 1972. Río de la Plata Estuary environments. Geol. Soc. of Amer.Memoirs 133: 213-234. [ Links ]
76. Vera, C. S., P. K. Vigliarolo and E. H. Berbery. 2002. Cold season synoptic scale waves over subtropical South America. Monthly Weather Review 130: 684-699. [ Links ]
77. Wanga, P., L. Linker, R. Batiuk and G. Shenk. 2000. Assessment of Impact of Storm on Point Source Pollutant Transport in Estuary by Dissolved Tracer Modeling. Water Quality and Ecosystems Modeling 1: 253-269. [ Links ]
78. Zimmerman, J. T. F. 1988. Estuarine residence times, in: Hydrodynamics of estuaries, edited by Kjerfve, B., Hydrodynamics of estuaries, CRC Press, 1: 75–84. [ Links ]














