Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Geoacta
versión On-line ISSN 1852-7744
Geoacta vol.35 no.2 Ciudad Autónoma de Buenos Aires ago./dic. 2010
ARTÍCULOS ORIGINALES
Respuesta de geófonos a campos electromagnéticos
Patricia M. Gauzellino1, Fabio I. Zyserman2 y Federico G. E. Späth3
1Depto. de Geofísica Aplicada, Fac. de Cs. Astro. y Geofísicas, UNLP.
2CONICET, Depto. de Geofísica Aplicada, Fac. de Cs. Astro. y Geofísicas, UNLP.
3Fac. de Cs. Astro. y Geofísicas, UNLP.
gauze@fcaglp.unlp.edu.ar
RESUMEN
La electro-ósmosis es el fenómeno físico por el cual una variación de potencial eléctrico, da lugar a una circulación de fluido. El fenómeno recíproco que genera una corriente eléctrica a partir de un gradiente de presión en el fluido, recibe el nombre de electro-filtración. La razón entre las variaciones de potencial y las variaciones de presión representa al coeficiente de acoplamiento electrocinético. Recién en 1999, se realizó una prueba de campo con propósitos exploratorios, donde las ondas sísmicas se generaron a partir de una fuente electromagnética. En el presente trabajo se explica el por qué de estos efectos electrosísmicos o sismoeléctricos, según sea la fuente de origen electromagnético o mecánico, respectivamente. Se presentan las ecuaciones de Maxwell y de Biot acopladas que gobiernan los fenómenos y se analizan los coeficientes de transporte que son la conductividad eléctrica, el coeficiente de acoplamiento electrocinético y la permeabilidad. Es posible hacer ciertas suposiciones que permiten resolver un conjunto de ecuaciones simplificadas donde las respuestas electromagnéticas y las respuestas poroviscoélasticas pueden determinarse unas de otras en forma independiente. En el tratamiento de las ecuaciones de Maxwell se sigue la forma usual de descomponer el campo eléctrico y el campo magnético en campos primarios (o principales) que se hallan analíticamente y campos secundarios, como perturbaciones de los primarios, que se calculan numéricamente. Trabajar en el dominio espacio-frecuencia, permite incorporar la naturaleza disipativa del medio poroso en la propagación de las ondas mecánicas, reemplazando los módulos elásticos reales por módulos complejos. Así mismo, se destaca la necesidad de establecer una grilla de cálculo adecuada para representar correctamente los gradientes de presión en el fluido a partir del skin-depth difusivo que se corresponde con la onda lenta de Biot. Ejemplos numéricos muestran la respuesta de los geófonos a partir de fuentes electromagnética y la posible identificación de contactos entre fluidos de reservorio.
Palabras clave: Electrosísmica; Ecuaciones de Maxwell; Ecuaciones de Biot; Medio Poroviscoelástico.
ABSTRACT
Electro-osmosis in saturated porous media is the physical phenomenon in which an electrical potential variation gives rise to fluid flow. The reciprocal phenomenon, called electro-filtration effect, is an electrical charge flux originated by pressure gradients in the pore fluid. The quotient between electrical potential and pressure gradient represents the electrokinetic coupling coefficient. In 1999 a proof field was performed, where seismic waves were generated by electromagnetic source. In this work it is explained why happen these phenomena. The equations that govern the coupled seismic and electromagnetic wavefields are presented and the transport coefficients (electrical conductivity, dynamic permeability and electrokinetic coupling coefficient) are analyzed. Some assumptions on the model allow solve a simplified set of equations where Maxwell's equations are decoupled from Biot's equations. For the Maxwell's equations it is possible to separate the electromagnetic fields in primary and secondary parts. The former can be found analytically, while to find the latter a numerical procedure is employed. Dissipative effects in porous media can be included by using complex viscoelastic moduli in space-frequency domain. Also, it is important notice that pressure gradients in the pore fluid are correctly represented if the grid points are calculated using diffusive skin depth of 55 the Biot slow wave. Numerical examples illustrate the capabilities of the modeling for detecting reservoir fluid contacts.
Keywords: Electroseismic; Maxwell Equations; Biot Equations; Poro-viscoelastic Medium
INTRODUCCIÓN
La electro-ósmosis es el fenómeno físico por el cual una variación de potencial eléctrico da lugar a una circulación de fluido en un medio poroso. El fenómeno recíproco que genera una corriente eléctrica a partir de un gradiente de presión en el fluido poral, recibe el nombre de electro-cinética. La ecuación de Helmholtz-Smoluchowski, relaciona ambos procesos y la razón entre las variaciones de potencial eléctrico y las variaciones de presión representa el coeficiente de acoplamiento electrocinético.
En sísmica de exploración, se conoce al fenómeno electro-cinético como fenómeno sismo-eléctrico (SE) y tiene lugar cuando una onda elástica se propaga en un medio poroso heterogéneo saturado por fluidos. En estos casos, la teoría de Biot, (Biot, 1956), predice las ondas clásicas compresional y de corte y, además, una onda compresional lenta que es una onda difusiva de presión en el fluido cuyo movimiento está en oposición de fase con el sólido. Esta última onda es la que induce un campo eléctrico variable en el tiempo. El proceso recíproco de la SE es el fenómeno electrosísmico (ES) que tiene lugar cuando se aplica un campo eléctrico variable en el tiempo generando un proceso de electroósmosis.
La superficie de contacto entre partículas sólidas y fluido del medio poroso da lugar a la llamada doble capa eléctrica, cuyo efecto se intensifica naturalmente en sistemas con gran desarrollo areal. En general, la carga superficial del sólido se considera negativa y el fluido como un conductor de segunda clase que conduce corriente eléctrica a través del movimiento de iones (electrolito ideal), es decir, los aniones del electrolito son adsorbidos químicamente a la superficie de los granos sólidos dejando un exceso neto de cationes distribuidos cerca del contacto entre el sólido y el fluido (Pride y Morgan, 1991). Esta doble capa, donde las cargas del electrolito se separan, se subdivide en una capa adsorbida o capa de Stern y una capa difusa (Fig. 1). En la capa de Stern las moléculas e iones están inmóviles. En la capa difusa existe una distribución de cationes móviles cuya posición está determinada por un balance entre la atracción electrostática de la capa adsorbida y la difusión hacia la zona neutra del electrolito. Asumiremos que la distribución difusa de cargas móviles es la única responsable del fenómeno electrocinético. La superficie que separa la capa difusa de la capa de Stern se denomina plano de corte y tiene un potencial eléctrico estático asociado llamado potencial ![]() .
.
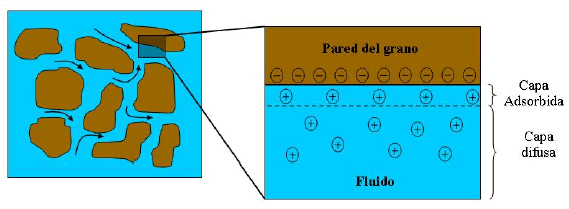
Figura 1. modelo de doble capa eléctrica.
Se observa que el espesor de la doble capa es mucho menor que el radio de curvatura de los granos sólidos y que al aumentar la concentración de iones este espesor disminuye, pues más serán los cationes en la capa de Stern y el potencial zeta disminuye. Esto explica la reducción del efecto electrosísmico en medios porosos con electrolitos de fuerte concentración y justifica considerar débiles concentraciones iónicas (Lorne et al., 1999).
El trabajo pionero de Blau y Statham en 1936, concluyó en la patente de un método de prospección sismoeléctrico (Blau y Statham, 1936). Años más tarde, Ivanov registró conversiones sismoeléctricas utilizando explosivos como fuente y antenas como receptores (Ivanov, 1939). También Thompson realizó experiencias de campo empleando el método de Blau y Statham, pero no se realiza la fundamentación teórica (Thompson, 1939). Desde estos primeros trabajos y hasta la fecha, son numerosos los autores que observaron conversiones sismoeléctricas e implementaron metodologías para detectar objetivos someros como acuíferos o nivel freático (Long y Rivers, 1975; Maxwell et al., 1992; Thompson y Gist, 1993; Butler et al., 1996). No ocurre lo mismo con las conversiones recíprocas, recién en 1999, se realizó una prueba de campo con propósitos exploratorios, donde las ondas sísmicas se generaron a partir de una fuente electromagnética (Thompson y Gist, 1999; Thompson, 2005; Thompson et al., 2007). El primer trabajo teórico que determina las ecuaciones macroscópicas que describen los fenómenos electrosísmico y sismoeléctrico corresponde a Pride (Pride, 1994).
El conjunto de ecuaciones de Pride se ha resuelto numéricamente mediante distintas aproximaciones, ver (Han y Wang, 2001; Pain et al., 2005; Haines y Pride, 2006; White, 2005; White y Zhou, 2006). En el presente trabajo estas ecuaciones serán resueltas mediante una técnica de descomposición de dominio combinada con elementos finitos no conformes y condiciones de borde absorbentes. Además, este procedimiento permite una implementación en paralelo del algoritmo, prácticamente directa y natural. Para mayores detalles y eficiencia computacional del mismo, aplicado al problema de Helmholtz, puede consultarse (Gauzellino et al., 2009; Zyserman y Gauzellino, 2005; Zyserman et al., 2003; Gauzellino et al., 2001).
ECUACIONES QUE GOBIERNAN LOS CAMPOS ACOPLADOS
Las ecuaciones en el dominio espacio-frecuencia que describen ambos fenómenos acoplados (SE y ES), (Pride, 1994), considerando una dependencia temporal del tipo ![]() , se expresan:
, se expresan:

Estas ecuaciones relacionan el campo eléctrico ![]() , el campo magnético
, el campo magnético ![]() , la inducción magnética
, la inducción magnética ![]() , el campo de desplazamiento
, el campo de desplazamiento ![]() y la densidad de corriente
y la densidad de corriente ![]() con los desplazamientos del sólido
con los desplazamientos del sólido ![]() y con los desplazamientos relativos grano-fluido
y con los desplazamientos relativos grano-fluido ![]() , donde
, donde ![]() es la porosidad de la roca.
es la porosidad de la roca.
La fuente sísmica externa está representada por ![]() y
y ![]() , en el medio sólido y fluido, respectivamente. La fuente electromagnética es la densidad de corriente
, en el medio sólido y fluido, respectivamente. La fuente electromagnética es la densidad de corriente ![]() La relación (3) es el balance total de las fuerzas actuantes y (5) es la ley de Darcy generalizada que es en sí misma un balance de fuerzas sobre el fluido desde un marco de referencia fijo sobre el esqueleto rocoso, siendo
La relación (3) es el balance total de las fuerzas actuantes y (5) es la ley de Darcy generalizada que es en sí misma un balance de fuerzas sobre el fluido desde un marco de referencia fijo sobre el esqueleto rocoso, siendo ![]() la velocidad de infiltración de Darcy. La densidad del medio poroso se indica por
la velocidad de infiltración de Darcy. La densidad del medio poroso se indica por ![]() . Las últimas ecuaciones (8) y (9) son ecuaciones constitutivas, siendo
. Las últimas ecuaciones (8) y (9) son ecuaciones constitutivas, siendo ![]() la presión del fluido y
la presión del fluido y ![]() el tensor de tensiones.
el tensor de tensiones.
El coeficiente de acoplamiento electrocinético, L, determina en SE la intensidad de flujo eléctrico inducido por flujo hídrico y en ES la intensidad de flujo hídrico engendrado por un flujo eléctrico. Con respecto a los coeficientes de las ecuaciones constitutivas (8) y (9), G es el módulo de corte de la matriz seca, C y M son los módulo de acoplamiento de Biot (Biot, 1962) y ![]() es el coeficiente que representa cuanto fluido puede acumularse en una muestra cuando la presión del fluido cambia y el tamaño de la muestra permanece constante. Por lo tanto, es el módulo elástico principalmente involucrado en difusión de la presión de fluido. En rocas naturales, G y las incompresibilidades C, M y
es el coeficiente que representa cuanto fluido puede acumularse en una muestra cuando la presión del fluido cambia y el tamaño de la muestra permanece constante. Por lo tanto, es el módulo elástico principalmente involucrado en difusión de la presión de fluido. En rocas naturales, G y las incompresibilidades C, M y ![]() son cantidades complejas y dependientes de la frecuencia debido a flujo mesoscópico y efecto"squirt". Sólo en el límite cuasi-estático (muy baja frecuencia), la presión del fluido se considera uniforme y los módulos poroelásticos pueden considerarse reales e independientes de la frecuencia. Las expresiones de los mismos en función del módulo de volumen de la matriz rocosa en ausencia de fluidos,
son cantidades complejas y dependientes de la frecuencia debido a flujo mesoscópico y efecto"squirt". Sólo en el límite cuasi-estático (muy baja frecuencia), la presión del fluido se considera uniforme y los módulos poroelásticos pueden considerarse reales e independientes de la frecuencia. Las expresiones de los mismos en función del módulo de volumen de la matriz rocosa en ausencia de fluidos, ![]() , y de los módulos de volumen del sólido,
, y de los módulos de volumen del sólido, ![]() y del fluido
y del fluido ![]() son:
son:

Siendo el parámetro adimensional Δ igual a:

El acoplamiento entre las ecuaciones de Biot y las de Maxwell está presente en las ecuaciones de transporte (4) y (5), y cuantificado por el coeficiente![]() .
.
Otros términos que intervienen en las ecuaciones son la viscosidad del fluido ![]() y la permeabilidad k.
y la permeabilidad k.
En las leyes constitutivas electromagnéticas, (6) y (7), resta definir la tortuosidad del medio ![]() , la permitividad eléctrica del vacío
, la permitividad eléctrica del vacío ![]() , la permeabilidad magnética del vacío
, la permeabilidad magnética del vacío ![]() y las constantes dieléctricas del sólido y del fluido,
y las constantes dieléctricas del sólido y del fluido, ![]() y
y ![]() , respectivamente.
, respectivamente.
CONSIDERACIONES SOBRE LOS COEFICIENTES DE TRANSPORTE
Una expresión para el coeficiente electrocinético en función de la frecuencia es dada por Pride en (Pride, 1994),

Donde ![]() es la frecuencia de transición:
es la frecuencia de transición:

Siendo ![]() el factor de formación eléctrico. Haciendo uso de la ley de Archie,
el factor de formación eléctrico. Haciendo uso de la ley de Archie, ![]() , (Archie, 1942),
, (Archie, 1942), ![]() es el exponente de cementación que se relaciona con la forma y distribución de los granos; por ejemplo,
es el exponente de cementación que se relaciona con la forma y distribución de los granos; por ejemplo,![]() varía entre 1.3 y 2.5 para la mayoría de las rocas sedimentarias,
varía entre 1.3 y 2.5 para la mayoría de las rocas sedimentarias,![]() en arenas limpias y
en arenas limpias y ![]() cuando la porosidad es del 100 %, que corresponde a una fractura abierta.
cuando la porosidad es del 100 %, que corresponde a una fractura abierta.
En la banda sísmica de frecuencias de exploración ![]() es seguro considerar:
es seguro considerar:

Donde ![]() es la permitividad del fluido,
es la permitividad del fluido, ![]() tiene dimensiones de longitud siendo una proporción pesada entre el volumen poral y la superficie poral con el peso favoreciendo a regiones angostas del espacio poral (gargantas), r es el radio poral y
tiene dimensiones de longitud siendo una proporción pesada entre el volumen poral y la superficie poral con el peso favoreciendo a regiones angostas del espacio poral (gargantas), r es el radio poral y ![]() es la longitud de Debye que mide el espesor de la doble capa. Algunos otros parámetros destacables que influyen sobre el valor de
es la longitud de Debye que mide el espesor de la doble capa. Algunos otros parámetros destacables que influyen sobre el valor de ![]() son la química del electrolito y el pH de la solución, ya que el potencial
son la química del electrolito y el pH de la solución, ya que el potencial ![]() puede expresarse como (Lorne et al., 1999; Revil, 1999; Pride y Garambois, 2001).
puede expresarse como (Lorne et al., 1999; Revil, 1999; Pride y Garambois, 2001).

La Figura 2 muestra la variación de la parte real del coeficiente de acoplamiento con la frecuencia para una concentración baja del electrolito, ![]() mol/litro.
mol/litro.

Figura 2. Variación de la parte real del coeficiente de acople ![]() con la frecuencia.
con la frecuencia. ![]() es la aproximación del coeficiente para bajas frecuencias.
es la aproximación del coeficiente para bajas frecuencias.
La permeabilidad dinámica ![]() es una cantidad compleja que depende de la frecuencia. El modelo propuesto en (Johnson, 1987) hecha mano de una función simple dependiente de la frecuencia que respeta condiciones de causalidad. En el límite de alta frecuencia, la capa viscosa de los bordes llega a ser muy delgada como para considerarse localmente plana en los granos curvos y la permeabilidad propuesta es
es una cantidad compleja que depende de la frecuencia. El modelo propuesto en (Johnson, 1987) hecha mano de una función simple dependiente de la frecuencia que respeta condiciones de causalidad. En el límite de alta frecuencia, la capa viscosa de los bordes llega a ser muy delgada como para considerarse localmente plana en los granos curvos y la permeabilidad propuesta es

(18)
Aunque m no es importante en la banda de frecuencias de exploración, éste se define como  . En arenas limpias, material no consolidado y poros tipo tubo
. En arenas limpias, material no consolidado y poros tipo tubo ![]() . Los valores de
. Los valores de ![]() dependerán del contenido de arcilla.
dependerán del contenido de arcilla.
En el límite de bajas frecuencias se tiene la permeabilidad hidráulica. Para ondas de frecuencia suficientemente bajas, la resistencia al movimiento, ![]() , es sólo resultado del corte viscoso asociado con el flujo.
, es sólo resultado del corte viscoso asociado con el flujo.
La conductividad ![]() del material, ver (Pride, 1994), puede definirse por:
del material, ver (Pride, 1994), puede definirse por:
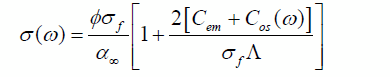
(19)
Donde ![]() es el exceso de conductancia asociada a la electromigración de iones de la doble capa y
es el exceso de conductancia asociada a la electromigración de iones de la doble capa y ![]() representa la conductancia debida a convección eléctrica inducida del exceso de iones en la doble capa. En el límite de las bajas frecuencias se puede considerar
representa la conductancia debida a convección eléctrica inducida del exceso de iones en la doble capa. En el límite de las bajas frecuencias se puede considerar

(20)
Un análisis análogo al realizado con ![]() , se llevó a cabo para los dos restantes coeficientes y dado que, la parte imaginaria de los mismos es un orden de magnitud menor, se estima suficiente considerarlos como valores reales para las frecuencias de interés. Consideraciones similares pueden
, se llevó a cabo para los dos restantes coeficientes y dado que, la parte imaginaria de los mismos es un orden de magnitud menor, se estima suficiente considerarlos como valores reales para las frecuencias de interés. Consideraciones similares pueden
encontrarse en (Han y Wang, 2001).
CONSIDERACIONES SOBRE LOS COEFICIENTES VISCOELÁSTICOS
Para considerar el comportamiento viscoelástico del subsuelo, puede usarse el principio de correspondencia establecido por Biot (Biot, 1956; Biot, 1962). Los módulos elásticos G, ![]() , y
, y ![]() se reemplazan por los respectivos módulos complejos dependientes de la frecuencia. Adoptando el modelo de viscoelasticidad lineal presentado por Liu (Liu et al., 1976), se obtiene para el módulo de corte:
se reemplazan por los respectivos módulos complejos dependientes de la frecuencia. Adoptando el modelo de viscoelasticidad lineal presentado por Liu (Liu et al., 1976), se obtiene para el módulo de corte:

(21)
Las funciones ![]() y
y ![]() caracterizan el comportamiento viscoelástico y están dadas por
caracterizan el comportamiento viscoelástico y están dadas por

Las variables del modelo  hacen que el factor de calidad
hacen que el factor de calidad ![]()

mantenga un valor constante ![]() , en el rango de frecuencias de interés. Valores clásicos de
, en el rango de frecuencias de interés. Valores clásicos de ![]() en rocas de la corteza están en el rango
en rocas de la corteza están en el rango ![]() correspondiendo las menores magnitudes a medios con mucha atenuación y dispersión.
correspondiendo las menores magnitudes a medios con mucha atenuación y dispersión.
CONSIDERACIONES SOBRE EL MODELO
Es posible realizar algunas simplificaciones a las ecuaciones acopladas de Pride, a saber:
a) Las corrientes de desplazamiento, ![]() , son cuatro órdenes de magnitud menor que las corrientes de conducción
, son cuatro órdenes de magnitud menor que las corrientes de conducción ![]() en el rango de bajas frecuencias; por lo tanto, pueden ignorarse.
en el rango de bajas frecuencias; por lo tanto, pueden ignorarse.
b) La realimentación por electrofiltración es despreciable. Cálculos propios y los realizados por Hainess y Pride (Hainess y Pride, 2006) arrojan un término de corrección menor a 10-5 para los medios que nos ocupan; luego, en la ecuación (4), el flujo de corriente eléctrica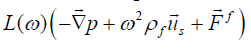 es muy pequeño comparado con
es muy pequeño comparado con ![]() .
.
c) Las fuentes sísmicas son nulas si se desea determinar la respuesta de receptores sísmicos a los campos electromagnéticos.
d) La Figura 3 muestra los dos modos de polarización posible, modo transverso eléctrico (TE) y modo transverso magnético (TM), en un modelo de subsuelo bidimensional.

Figura 3. a) modo Transverso Eléctrico y b) modo Transverso Magnético.
Para el modo TE, el esquema de la Figura 3, indica el campo eléctrico ![]() como la perturbación
como la perturbación
que origina una onda SH en el medio poroso. Mientras que para el modo TM, las componentes del
campo eléctrico ![]() y
y ![]() generan las ondas P y SV.
generan las ondas P y SV.
RESULTADOS NUMÉRICOS
Las ecuaciones (1-9) se resuelven numéricamente mediante el método de elementos finitos y una técnica iterativa de descomposición de dominio a nivel de las ecuaciones diferenciales. Además, es necesario establecer condiciones de borde tanto para el problema electromagnético como para el problema sísmico. En el subsuelo, se ha elegido condición de borde absorbente de primer orden y condición de superficie libre para la discontinuidad aire-tierra. Teniendo en cuenta la consideración b) mencionada previamente, es posible obtener la solución de las ecuaciones desacopladas; de forma tal, que primero se calcula el campo electromagnético y a partir del mismo se obtiene el campo de ondas sísmicas. Las condiciones de borde, existencia y unicidad de la solución se pueden ver en (Santos, 1998; Santos y Sheen, 2007). Detalles de la técnica de los elementos finitos empleados se muestran en (Zyserman et al., 2009).
En el primer ejemplo numérico, el modelo representa un rectángulo de 1100 m de profundidad y 2200 m en la dirección horizontal con cuatro capas de 500 m, 150 m, 150 m y 300 m de espesor, respectivamente; cuyas características están dadas en la Tabla 1. Cabe destacar que para modelar adecuadamente los gradientes de presión del fluido, se debe tener en cuenta la longitud de difusión (Pride y Garambois, 2001), relacionada con la longitud de onda que corresponde a la onda lenta de Biot.
Tabla 1. Parámetros empleados en el primer ejemplo numérico para la caracterización del modelo.

La fuente está ubicada en superficie y centrada con respecto al eje x. La dependencia temporal de la misma es una ondícula de Ricker de 20 Hz. En el modo TE, la misma queda representada por un cable infinito en la dirección del eje y, por el que circula una corriente eléctrica. En el modo TM, la fuente está caracterizada por un solenoide infinito en la dirección del eje y, por cuyas espiras circula la corriente eléctrica (dipolo magnético infinito).
Como ya se ha dicho, las ecuaciones de Maxwell y de Biot se resuelven en forma separada y para un conjunto finito de 100 frecuencias equiespaciadas entre 0 y 40 Hz. Con los resultados en el dominio de las frecuencias, la transformada de Fourier inversa permite obtener las respuestas en el dominio espacio-tiempo. Dado que el campo electromagnético aparece de manera instantánea en todo el dominio, la fuente sísmica está distribuida en todo el dominio también y "se enciende" donde hay contrastes del coeficiente de acoplamiento electrocinético, es decir, en los bordes de las diferentes capas. En la Figura 4 se muestra la respuesta en el modo TE, de los geófonos distribuidos en forma equiespaciada a lo largo de pozo, cuyo offset es nulo con respecto al centro del dominio.

Figura 4. Respuesta de geófonos equiespaciados en un pozo para el modo TE.
Las tres líneas horizontales en el eje de la profundidad indican las discontinuidades de subsuelo con el fin de ayudar a la interpretación de las señales resultantes. Para la identificación de los diferentes tipos de ondas sísmicas que registran los receptores se ha usado un conjunto de letras, tal que, A representa la onda generada por la fuente y reflejada en la superficie que no se atenúa debido a la condición de superficie libre. B es la reflexión en la interfaz a 500 m de profundidad. C, D y E dan cuenta de las señales sísmicas que se originan en las discontinuidades localizadas en 800 m, 650 m y 500 m, respectivamente y viajan hacia la superficie; observando que C tiene atenuación manifiesta. F y G se propagan hacia profundidades mayores, generándose a 800 m y 650 m, respectivamente.
El campo de ondas de receptores colocados en la superficie, puede observarse en la Figura 5. Aquí, las señales etiquetadas con A y B muestran la respuesta de los contactos entre la arenisca y la arcilita saturadas con agua muy poco salobre y el contacto entre la arcilita y la arenisca con gas. La figura 6 muestra la respuesta de los geófonos en un pozo desplazado lateralmente con respecto a la fuente para modo TM. En estas simulaciones participa la velocidad de onda P, los módulos de volumen de los granos sólidos y de los fluidos. Pueden identificarse: las ondas debidas a la fuente, sañaladas con A; las ondas que viajan hacia la superficie desde los 500 m y desde los 650 m, indicadas con C y B, respectivamente y las señales que se propagan hacia mayores profundidas, generadas a 500 m y 650 m llamadas F y D, respectivamente.

Figura 5. Respuesta de geófonos equiespaciados en la superficie para el modo TE.

Figura 6. Respuesta de geófonos equiespaciados en un pozo para el modo TM.
Como puede verse en estos ejemplos, la amplitud de las trazas es directamente proporcional al valor del campo eléctrico. En el caso TE, las mayores amplitudes están por debajo de la fuente electromagnética, mientras en el caso TM, los desplazamientos en la dirección de z, presentan las menores amplitudes. Por este motivo el pozo de la Figura 6 tiene offset no nulo con respecto a la fuente. Para comprender mejor las respuestas en el modo TM, presentamos los resultados de un segundo ejemplo numérico, donde el subsuelo está representado por una sola capa simple de 400 m de espesor, ubicada a 700 m de profundidad y en un entorno homogéneo (medio 1). La Tabla 2 indica los principales parámetros físicos de ambos medios. Los poros están saturados por agua. Se destaca que la componente x de la traza de la aceleración tiene su amplitud máxima por debajo de la fuente electromagnética y decae cuando los receptores se apartan de la fuente, hacia ambos laterales. La componente z de la traza de la aceleración tiene mínima amplitud a offset cero y para trazas con offset distintos de cero, incrementan sus amplitudes, cambiando de polaridad a izquierda y derecha de la fuente.
Tabla 2. Parámetros físicos principales para el modelo de una sola capa simple.


Figura 7. Trazas de aceleración en la superficie para modo TM con tres diferentes offset
CONCLUSIONES
En este trabajo se ha podido simular numéricamente la conversión de energía electromagnética a mecánica, que tiene lugar en un medio poroso saturado por fluidos. Se ha estudiado la implementación de dos tipos diferentes de fuentes electromagnéticas, conocidas como modo TE y modo TM. Las consideraciones realizadas sobre el modelo permiten resolver el conjunto de las ecuaciones de Pride de manera desacoplada, despreciando el término sismoeléctrico de realimentación al compararlo con las corrientes de conducción. El procedimiento numérico aplicado resuelve las ecuaciones en el dominio espacio-frecuencia, mediante un método de descomposición de dominio iterativo y elementos finitos no conformes. Estos algoritmos están especialmente pensados para máquinas con arquitecturas en paralelo y resultan ser eficientes para aplicaciones geofísicas. Del análisis de las simulaciones, se observa que los resultados obtenidos están de un todo en acuerdo con la respuesta física esperada y por lo tanto sirven para modelar estos fenómenos de la sísmica no convencional.
Agradecimientos: Este trabajo fue realizado gracias a los subsidios del programa de incentivos de la UNLP y al PIP (CONICET) 5126/04.
REFERENCIAS
1. Biot M. A., 1956a. Theory of propagation of elastic waves in a fluid-saturated porous solid. I. Low frequency range. J. Acoust. Soc. Amer., 28: 168-171. [ Links ]
2. Biot M. A., 1956b. Theory of propagation of elastic waves in a fluid-saturated porous solid. II. High frequency range. J. Acoust. Soc. Amer., 28: 179-191. [ Links ]
3. Biot M. A., 1962. Mechanics of deformation and acoustic propagation in porous media. J. Appl. Phys., 33: 1482-1498. [ Links ]
4. Blau L. W. y Statham L., 1936. Method and apparatus for seismic-electric prospecting, US Patent No 2: 054-067. [ Links ]
5. Butler K. E., Russell R. D., Kepic A. W. y Maxwell M., 1996. Measurement of the seismoelectric response from a shallow boundary, Geophysics, 61: 1769-1996. [ Links ]
6. Gassmann F., 1951. Über die elastizität poröser medien (On the elasticity of porous media). Vierteljahrsschrift der Naturforschenden Gessellschaft in Zurich, 96: 1-23. [ Links ]
7. Gauzellino P. M., Zyserman F. I. y Santos J. E., 2001. Análisis del comportamiento de algoritmos paralelos de elementos finitos con descomposición de dominio en aplicaciones geofísicas, Mecánica Computacional, 20: 474-481. 65 [ Links ]
8. Gauzellino P. M., Zyserman F. I. y Santos J. E., 2009. Nonconforming element methods for the three dimensional Helmholtz equation: iterative domian decomposition or global solution ?, J. Comp. Acoustic, 17 (2) (en prensa). [ Links ]
9. Haines S. H. y Pride S. R., 2006. Seismoelectric numerical modeling on a grid, Geophysics, 71 (6): 57-65. [ Links ]
10. Han Q. y Z. Wang Z., 2001. Time-domain simulation of SH-wave-induced electromagnetic field in heterogeneous porous media: A fast finite-element algorithm, 66 (2): 448-461. [ Links ]
11. Ivanov A., 1939. Effect of electrization of earth layers by elastic waves passing through them, Comptes Rendus (Doklady) de l'Academie des Sciences de L'URRS, 24:42-45. [ Links ]
12. Johnson D. L., Koplik J. y Dashen R.1987. Theory of dynamic permeability and tortuosity in fluidsaturated porous media,J. Fluid Mechanics, 176: 379-402. [ Links ]
13. Liu H. P., Anderson D. L. y Kanamori H., 1976. Velocity dispersion due to anelasticity; implications for seismology and mantle composition, Geophys. J. R. Astr. Soc., l47: 41-58. [ Links ]
14. Long L. T. y Rivers W. K., 1975. Field measurements of the electroseismic response, Geophysics, 40 (2): 233-245. [ Links ]
15. Lorne B., Perrier F. y Avouac J., 1999. Streaming Potential measurements 1. Properties of the electrical double layer from crushed rock samples, Journal Geophysical Research, 104: 17857- 17877. [ Links ]
16. Maxwell M., Russell R. D., Kepic A. W. y Butler K. E., 1992. Electromagnetic responses from seismically excited targets B: non-piezoelectric phenomena, Expl. Geophys., 23: 201-208. [ Links ]
17. Pain C., Saunders J., Worthington M., Singer J., Stuart-Bruges W., Mason G. y Goddard A., 2005. A mixed finite-element method for solving the poroelatic Biot equations with electrokinetic coupling, Geophys. J. Int., 160: 592-608. [ Links ]
18. Pride S. R. y Morgan F., 1991. Electrokinetic dissipation induced by seismic waves, Geophysics, 56: 914-925 [ Links ]
19. Pride S. R., 1994. Governing equations for the coupled electromagnetics and acoustics of porous media, Physical Review B, 50: 15678-15696. [ Links ]
20. Pride S. y Haartsen M., 1996. Electroseismic wave properties, J. Acoust. Soc. Amer., 100: 1301-1315. [ Links ]
21. Pride S. y Garambois S., 2001. The role of Biot slow waves in electroseismic wave phenomena, J. Acoust. Soc. Amer., 111: 697-706. [ Links ]
22. Revil A., Schwaeger H., Cathles III L. M. y Manhardt P., 1999. Streaming potential in porous media, 2. Theory and application to geothermal systems, Journal Geophysical Research, 104: 20033- 20048. [ Links ]
23. Santos J. E., 1998. Global and domain-decomposed mixed methods for the solution of Maxwell's equation with application to magnetotellurics, Num. Meth. For Partial Diff. Equations, 14: 263-280. [ Links ]
24. Santos J. E. y Sheen D., 2007. Finite element methods for the simulation of waves in composite saturated poroviscoelastic materials, SIAM, J. Numer. Anal., 45 (1): 389-420. [ Links ]
25. Thompson R. R., 1939. A note on the seismic-electric effect. Geophysics, 4: 102-105. [ Links ]
26. Thompson A. H. y Gist G., 1993. Geophysical applications of electrokinetic conversion, The Leading Edge, 12: 1169-1173. [ Links ]
27. Thompson A. H. y Gist G., 1999. Geophysical prospecting. US Patent No 5: 877-995. [ Links ]
28. Thompson A. H., 2005. Electromagnetic-to-seismic conversion: Successful developments suggest viable applications in exploration and production. 75th SEG Annual Meeting Expanded Abstracts, SEG, Houston, USA: 554. [ Links ]
29. Thompson A. H., Hornbostel S., Burns J., Murray T., Raschje R., Wride J., McCammon P., Sumner J., Haake G., Bixby M., Ross W., White B. S., Zhou M. y Peczak P, 2007. Field tests of electroseismic hydrocarbon detection, Geophysics, 72 (1): N1-N9. [ Links ]
30. White B. S., 2005. Asymptotic theory of electroseismic prospecting, SIAM J. Appl. Math., 65 (4): 1443-1462. [ Links ]
31. White B. S. y Zhou M., 2006. Electroseismic prospecting in layered media, SIAM J. Appl. Math.,67 (1): 69-98. [ Links ]
32. Zyserman F. I., Guarracino L. y Santos J. E., 1999. A hybridized mixed finite element domain decomposed method for two-dimensional magnetotelluric modelling, Earth, Planets and Space, 51: 297-306. [ Links ]
33. Zyserman F. I., Gauzellino P. M. y Santos, J. E., 2003. Dispersion analysis of a non-conforming finite element method for the Helmholtz and elastodynamic equations, Int. J. Numer. Meth. Engng., 58: 1381-1395. [ Links ]
34. Zyserman F. I. y Gauzellino P. M., 2005. Dispersion analysis of a nonconforming finite element method for the three dimensional scalar and elastic wave equations, Finite elements in analysis and design, 41: 1309-1326. [ Links ]
35. Zyserman F. I., Gauzellino P. M. y Santos, J. E., 2009. Finite element modeling of SHTE and PSVTM electroseismic, CCAM-2009-02-MATH, http://CCAM.math.purdue.edu/preprints. [ Links ]
Recibido: 24 de abril de 2009
Aceptado: 9 de junio de 2010














