Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Geoacta
versión On-line ISSN 1852-7744
Geoacta vol.37 no.1 Ciudad Autónoma de Buenos Aires ene./jun. 2012
TRABAJOS DE INVESTIGACIÓN
Inversión espectral prestack simultánea de ondas PP y PS para la caracterización cuantitativa de capas delgadas
Ramsis Guerrero(1), Danilo Velis(1)& J. Germán Rubino(2)
(1)Facultad de Ciencias Astronómicas y Geofísicas, Universidad Nacional de la Plata, y CONICET, Argentina.
(2)Institute of Geophysics, University of Lausanne, Suiza.
rguerrero@fcaglp.unlp.edu.ar, velis@fcaglp.unlp.edu.ar, German.Rubino@unil.ch
RESUMEN
En este trabajo extendemos un método de inversión espectral para determinar las propiedades de una capa delgada y de los medios que se encuentran por encima y por debajo de la misma, a partir del espectro de amplitud de la respuesta sísmica prestack, con aplicación a la caracterización de reservorios asociados a estructuras con espesores por debajo del tunning. Estas propiedades incluyen el espesor de la capa delgada como así también las velocidades de las ondas compresionales y de corte, y las densidades de cada uno de los tres medios. Se presentan numerosos ejemplos utilizando datos sintéticos con ruido gaussiano generados a partir de diversos modelos de capas delgadas representativos de reservorios de gas de unos pocos metros de espesor. Se demuestra que, bajo ciertas condiciones, es posible obtener estimaciones razonables de los diversos parámetros involucrados utilizando el dato sísmico prestack convencional (ondas PP). Se analiza asimismo el impacto del uso de la información adicional provista por las ondas de corte convertidas (ondas PS), demostrándose que éstas contribuyen a mejorar significativamente las calidad de los resultados y a relajar las condiciones requeridas por el uso de las ondas PP solamente. Por último, y con el objetivo de reducir los problemas de no-unicidad inherentes a este tipo de problema inverso, las soluciones son forzadas a satisfacer, dentro de cierta tolerancia, la posible correlación existente entre las velocidades de las ondas P y S, y entre la velocidad de la onda P y la densidad, información a priori con frecuencia disponible a partir de datos de pozo. Como consecuencia, la incerteza en la estimación del espesor, velocidades y densidad de la capa delgada se reduce significativamente, lo que permite obtener soluciones más precisas y confiables.
Palabras claves: Inversión; Simulated annealing; Capa delgada; Ondas de corte convertidas; AVO.
ABSTRACT
In this work, we extend a spectral inversion method for determining the properties of a thin bed and those of the media lying above and below it from prestack seismic data. These properties include the thickness of the thin layer as well as the compressional- and shear-wave velocities and densities of the three media. The estimation of the model parameters is carried out in the frequency domain, and can be applied to the characterization of geological formations with thicknesses below tuning. We apply the methodology to noisy synthetic data generated by considering different thin layers representative of gas reservoirs and having thicknesses of only a few meters. The corresponding results indicate that, under certain conditions, reasonable solutions can be obtained when using conventional prestack seismic data (PP waves). Moreover, we show that the additional information provided by the converted shear waves (PS waves) allows us to improve the quality of the results and, at the same time, it enables us to relax the constraints required when using PP waves only. Finally, in order to reduce the nonuniqueness difficulties typically arising in this kind of inverse problem, the solutions are forced to honor, within a certain tolerance, the potential correlations between P- and S-wave velocities, as well as between P-wave velocity and density, which constitutes valuable information often available from well log data. As a consequence, the uncertainties associated with the estimates of the thickness, wave velocities and density of the thin layer are significantly reduced, therefore allowing to obtain more accurate and reliable solutions.
Keywords: Inversion; Simulated annealing; Thin bed; Converted shear waves; AVO.
INTRODUCCIÓN
La determinación de los parámetros elásticos, densidades y espesores de las estructuras que componen el subsuelo a partir de datos sísmicos de superficie resulta clave para la caracterización de ambientes geológicos de interés. En exploración sísmica con frecuencia resulta necesaria la caracterización cuantitativa de reservorios de hidrocarburos con espesores por debajo del tunning, donde la determinación de los diversos parámetros que caracterizan estos ambientes es muy compleja. La principal dificultad reside en el hecho de que la información contenida en la sísmica de superficie poststack es insuficiente para brindar estimaciones confiables, sobre todo teniendo en cuenta que existen varios modelos posibles de capa delgada que explican la misma respuesta sísmica (Rubino y Velis, 2009). El problema es más notorio cuando no se cuenta con suficiente información sobre velocidades, densidades e incluso ondícula (sobre todo su fase) como para reducir este problema de ambigÜedad. El uso de la información adicional provista por datos prestack contribuye significativamente a mitigar estas limitaciones, pero aún así el problema inverso se vuelve muy complejo y los problemas de no-unicidad suelen persistir.
Varios autores han puesto énfasis en la estimación de los espesores de capas delgadas utilizando diversas estrategias. Partyka et al. (1999), por ejemplo, propusieron técnicas de descomposición espectral para obtener espesores temporales a partir de la posición de los notches que se observan en los espectros de amplitud de la respuesta sísmica de estas estructuras para incidencia normal. Hall (2006) propone en cambio el uso de una descomposición cepstral para predecir espesores temporales, lo que permitiría obtener una mayor resolución y precisión que utilizando la descomposición espectral. Otra estrategia consiste en utilizar una descomposición espectral cruzada (Nowak et al., 2008) valiéndose de la información adicional provista por datos AVA (amplitud versus ángulo). Esta alternativa permite resolver espesores temporales de hasta la mitad de los que se resuelven con la descomposición espectral convencional. No obstante, estas técnicas están limitadas por un lado a espesores que producen un notch dentro del ancho de banda efectivo del datos (o sea, espesores cercanos al de tunning o la mitad del mismo en el mejor de los casos), y por otro lado, a que este notch pueda ser determinado con cierta precisión en un contexto de baja relación señal-ruido.
Alternativamente, es posible obtener estimaciones de espesores mediante la inversión del dato, sin depender de la siempre difícil identificación de notches en los espectros. El método de optimización propuesto por Nowak et al. (2008) apunta en este sentido, valiéndose de la información contenida en el espectro de fase del dato, y obteniendo resoluciones muy superiores a los métodos mencionados en el párrafo anterior. Puryear y Castagna (2008), por otro lado, también desarrollaron técnicas para determinar espesores temporales pero a partir de la inversión espectral del dato para incidencia normal. Los resultados de estos métodos son excelentes y permiten obtener con cierta precisión espesores muy por debajo del tunning. No obstante, cabe resaltar que estas técnicas, además de asumir conocida la fase de la ondícula, están diseñadas para brindar espesores temporales solamente, y no permiten, en general, obtener espesores reales (o sea en metros), salvo que se conozca la velocidad sísmica del medio. En este contexto, el problema de ambigÜedad mencionado al principio de esta sección no ha sido abordado por estos autores.
Recientemente, Rubino y Velis (2009) presentaron un método de inversión espectral que permite obtener estimaciones de espesores reales, velocidades y densidades simultáneamente, para modelos de capas delgadas de unos pocos metros de espesor, y valiéndose únicamente de los espectros de amplitud de la respuesta sísmica prestack asociada a las ondas PP. Los resultados son muy alentadores a pesar de ciertas limitaciones de tipo prácticas, tales como la necesidad de contar con una respuesta sísmica susceptible de ser aislada del resto del dato sísmico y una buena calibración de amplitudes. Pero, por otro lado, la técnica presenta la ventaja de que no necesita ninguna corrección por NMO previa, por lo que el stretching asociado a este tipo de corrección no es un problema. Otra ventaja importante es que no se requiere información de fase de la ondícula, contrariamente a los métodos propuestos por Nowak et al (2008) y Puryear y Castagna (2008). Además, y a diferencia de estos trabajos, el método de inversión espectral prestack permite obtener las velocidades de las ondas P y S ( y ), y densidad , tanto de la capa delgada como de los medios que yacen por encima y por debajo de la misma. La incerteza en la determinación de algunos de los parámetros, que es producto de la no-unicidad del problema inverso planteado, puede ser sin embargo relativamente grande, excepto cuando se dispone de información adicional para acotar el valor de estos parámetros durante la inversión (Rubino y Velis, 2009).
El objetivo esencial de este trabajo consiste en extender el método de inversión propuesto por Rubino y Velis (2009) incluyendo información adicional que permita reducir significativamente los problemas de no-unicidad asociados a este tipo de problema inverso, y de esta manera mitigar las incertezas en la determinación de los diversos parámetros que caracterizan la capa delgada de interés. En este sentido, y gracias a los recientes avances en la adquisición y el procesamiento de datos sísmicos multi-componente, es posible incluir en el análisis sísmico la información proporcionada por las ondas convertidas PS. Son varios los autores que han analizado este tipo de ondas, obteniendo resultados satisfactorios en la estimación de , y por medio del análisis de AVO (amplitud versus offset) y diferentes técnicas de inversión (Duffaut et al., 2000; Jin et al., 2000; Mehdizadeh et al., 2005; Veire y Landrø, 2003, 2006; Khare y Rape, 2007; Rabben et al., 2008; Yang y Yu, 2009). Aunque no aplicados a capas delgadas, dichos estudios demostraron que la inversión simultánea de ondas PP y PS puede producir resultados más confiables que cuando se utilizan ondas PP y PS separadamente, permitiendo incrementar significativamente la capacidad de los métodos de inversión para la caracterización de reservorios.
Además de la información adicional que proporcionan las ondas PS, la información contenida en datos de pozos disponibles en la zona de interés puede resultar muy valiosa y debería ser tenida en cuenta para la inversión. En este sentido, resulta conveniente restringir las soluciones a aquellas que satisfacen, dentro de cierta tolerancia, las posibles correlaciones existentes entre y , y entre y de los medios involucrados. Castagna et al. (1985) y Xu y Bancroft (1998), por ejemplo, muestran cómo y pueden relacionarse empíricamente entre sí a partir de datos de pozo. Gardner et al. (1974), Dey y Stewart (1997) y Potter y Stewart (1998), por otro lado, encuentran expresiones empíricas para relacionar con P.
Con estas motivaciones, en este trabajo extendemos el procedimiento de inversión espectral prestack para caracterizar capas delgadas propuesto por Rubino y Velis (2009) incorporando la información adicional brindada por las ondas convertidas PS y la información a priori obtenida a partir de datos de pozo para restringir las soluciones estocásticamente. Asimismo, analizamos el impacto en los resultados que genera el uso de un mayor rango de ángulos de incidencia de ondas PP y PS durante la inversión. Aplicamos el método de inversión espectral a dos modelos de capa delgada representativos de reservorios conformados por areniscas con gas. El primer modelo está compuesto por una capa con velocidad mayor que la de las rocas que se encuentran por encima y por debajo de la misma. El otro modelo está compuesto por una capa de "baja" velocidad con los mismos medios en la parte superior e inferior que el modelo anterior. Realizamos un análisis numérico exhaustivo considerando varios espesores que van desde unos pocos metros hasta valores mayores al espesor de tunning. El análisis sugiere que la metodología propuesta permitiría obtener una mejora muy significativa con respecto al método presentado por Rubino y Velis (2009), tanto para la determinación del espesor de la capa como de las velocidades y densidades de los tres medios en cuestión. Los resultados muestran la importancia del uso de ondas PS y un rango extendido de datos prestack para reducir la incerteza de las soluciones. El uso de la información a priori obtenida a partir de datos de pozo permite asimismo mejorar significativamente la precisión y confiabilidad de los resultados, aún cuando las ondas PS no estuvieran disponibles.
TEORIA
Respuesta sísmica de una capa delgada
Para el modelado de la respuesta sísmica de la capa delgada seguimos el mismo procedimiento descripto por Rubino y Velis (2009). Consideramos una capa delgada horizontal elástica de espesor h ubicada entre dos semiespacios elásticos homogéneos, y una onda plana compresional de amplitud unitaria y frecuencia que incide con un ángulo (ver Figura 1). Luego, para cada frecuencia y cada ángulo de incidencia, determinamos las relaciones existentes entre los potenciales escalares y vectoriales asociados con los campos de ondas compresionales y de corte ascendentes y descendentes en cada uno de los tres medios. Requiriendo la continuidad de los desplazamientos de las partículas y de la tensión normal y la de corte en ambas interfases, se obtiene un sistema de ecuaciones lineales de 8x8 cuyas incógnitas son las amplitudes de los potenciales mencionados. Luego, realizando el producto de la transformada de Fourier de la fuente con las amplitudes de los potenciales asociados con las ondas ascendentes en el semi-espacio superior para diferentes ángulos de incidencia, se obtienen las respuestas sísmicas PP y PS de la capa delgada. Para más detalles ver el trabajo de Rubino y Velis (2009).
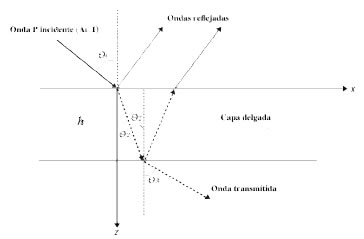
Figura 1. Diagrama del modelo de capa delgada y rayos transmitidos y reflejados. Por simplicidad no se muestran las ondas de corte generadas en las interfases, las cuales están incluidas en el modelado de la respuesta AVA.
Figure 1. Diagram of the thin bed model, and reflection and transmission waves. For simplicity, we do not show the shear waves generated at then interfases, which indeed are included in the AVA response calculations
Inversión espectral prestack
Con el fin de caracterizar cuantitativamente una dada capa delgada a partir de su respuesta sísmica definimos una función de costo que mide la discrepancia entre los datos observados y los calculados. Esta función depende de diez variables, que se corresponden con las propiedades elásticas de los tres medios, sus densidades y el espesor de la capa. En particular, dicha función mide la diferencia entre los espectros de amplitud de los datos prestack observados y y los calculados y , para cada frecuencia y ángulo de incidencia , tanto para las ondas compresionales como para las de corte. La función de costo queda definida mediante las siguientes expresiones:

son las contribuciones a la función de costo asociadas con las ondas PP y PS, y son el número de ángulos y M el número de frecuencias. La constante toma valores entre 0 y 1 y puede ser utilizada para asignar diferente peso relativo a cada uno de los términos de la ec. (1).
Debido a la alta no-linealidad de la expresión (1) que dificulta su minimización con respecto a los diez parámetros mencionados y a la posible presencia de mínimos locales, utilizamos el método de optimización global conocido como Very Fast Simulated Annealing (SA) (Ingber, 1989). Asimismo utilizamos en forma combinada con SA el método de optimización local de Powell (Press et al., 1992). Esta estrategia híbrida nos permite, por un lado, evitar los problemas de convergencia asociados a la dependencia de la solución con el modelo inicial, como ocurriría si solamente se utilizara un método basado en gradientes; y por otro lado, nos permite refinar la solución y acelerar la convergencia hacia el mínimo global cuando se está en las cercanías del mismo. El uso de un método de optimización estocástico como SA permite obtener, asimismo, un gran número de soluciones que se ajustan al dato dentro de cierta tolerancia, lo que permite a su vez calcular la incerteza de las soluciones.
En la práctica se estableció un número máximo de 500 iteraciones de SA a partir del cual se comenzó con el refinado de la solución mediante el método de Powell. El criterio adoptado para finalizar las iteraciones (además del número máximo de iteraciones) consistió en culminar el proceso iterativo cuando la función de costo sea menor que su valor esperado. En este caso, asumiendo ruido gaussiano, este valor resulta aproximadamente igual a la varianza del ruido aditivo agregado, como se desprende de las ecuaciones (2) y (3). En general, el valor esperado de ajuste fue alcanzado durante el proceso del SA, por lo que el refinado no fue necesario en varios de los ejemplos que se muestran en la sección de resultados. En el caso de no contar con el valor esperado (por ejemplo cuando se trabaja con datos reales), el criterio de corte se puede establecer como un número máximo de iteraciones o cuando la función de costo no varia significativamente durante un número determinado de iteraciones.
Correlación entre parámetros
Con el fin de reducir la no-unicidad del problema inverso planteado y mejorar la eficacia y rendimiento del proceso de optimización, asumimos que en cada uno de los tres medios y están correlacionadas y que dicha información está disponible a partir del análisis de registros de pozos cercanos. En este trabajo nos basamos en los estudios realizados por Castagna et al. (1985) y Xu y Bancroft (1998), de donde obtenemos parámetros para tales relaciones empíricas. Estas relaciones permiten escribir:
![]()
donde a y b son parámetros de ajuste determinados a partir de datos de pozo.
En el mismo sentido, se tomó en cuenta la posible relación empírica existente entre y para los medios involucrados (Gardner et al., 1974; Dey y Stewart, 1997; Potter y Stewart, 1998). A partir de una serie de estudios empíricos estos autores llegaron a la conclusión de que y pueden relacionarse mediante
![]()
donde c y d son también determinados a partir de datos de pozo.
En la práctica, cada uno de los diez parámetros incógnita que definen el modelo es generado, en cada iteración del SA, pseudo-aleatoriamente dentro de un cierto rango de búsqueda especificado por el usuario. Los rangos de búsqueda asociados al espesor y a las velocidades de las ondas compresionales en cada medio son asignados relativamente amplios de modo de no sesgar la solución hacia un valor determinado. En cambio, en el caso de las velocidades de las ondas de corte y las densidades, los rangos de búsqueda resultan acotados por las correlaciones mencionadas. Estas correlaciones se incorporan al proceso de inversión en forma estocástica considerando que para cada valor de generado en cada medio y en cada iteración, y tomarán valores dados por distribuciones gaussianas con medias y y con desviaciones estándar y , respectivamente, donde y se calculan a partir de las relaciones empíricas (4) y (5). Es decir,

En los ejemplos numéricos que siguen asignamos para a los valores 0.53, 0.6 y 0.55, y para b, 0.024, 0.044 y 0.032 para el medio superior, la capa intermedia y el medio inferior, respectivamente (Xu y Bancroft, 1998). En tanto que los valores de los parámetros c y d que utilizamos para determinar la densidad son 0.019 y 0.58, respectivamente, para los tres medios involucrados. Además, los valores que consideramos para las desviaciones estándar son y (Dey y Stewart, 1997). En todos los casos y están dadas en km/s y en g/cm3.
Es importante señalar que debido a que en la práctica las relaciones que se determinan entre los distintos parámetros son empíricas, los valores de y considerados en cada iteración no quedan unívocamente determinados para cada valor de generado. Por el contrario, el proceso de generación pseudo-aleatorio de parámetros descrito mediante las ecuaciones (6) y (7) implica que los rangos de búsqueda para estos parámetros son dinámicos y están acotados en intervalos relativamente angostos y centrados en los valores obtenidos con las relaciones empíricas. De esta manera, el número de incógnitas sigue siendo diez. No obstante, el uso de la información provista por las correlaciones permite reducir significativamente el tamaño del espacio del modelo y favorecer así una mejor convergencia y precisión de los resultados finales, como queda demostrado en los ejemplos numéricos que se muestran en la siguiente sección.
EXPERIMENTOS NUMÉRICOS
Datos utilizados
Para analizar el método de inversión se utilizaron registros sintéticos. Éstos fueron generados considerando un modelo simple de una capa delgada de arenisca. En las Tablas 1 y 2 se muestran los parámetros empleados para cada uno de los dos modelos considerados en este análisis. El primero pertenece a un modelo de alta velocidad y el segundo a un modelo de baja velocidad. Para realizar las simulaciones se utilizó una ondícula de Ricker de frecuencia central Hz. El tiempo de tuning para la ondicula de Ricker es , donde es la frecuencia dominante (Chung y Lawton, 1995). El tiempo de tuning para la ondícula utilizada es aproximadamente 13 ms, por lo que los espesores de tunning resultan igual a 26.5 m y 15.8 m para los modelos de alta y baja velocidad, respectivamente. Los modelos propuestos para ilustrar el método de inversión incluyen capas delgadas de entre 5 y 40 m de espesor.
Tabla 1. Parámetros utilizados para la creación del registro sintético correspondiente a un modelo de reservorio de gas asociado a una capa delgada de arenisca de alta velocidad.
Table 1. Parameters used to create the synthetic record corresponding to a sandstone gas reservoir model associated with a high-velocity thin bed.

Tabla 2. Parámetros utilizados para la creación del registro sintético correspondiente a un modelo de reservorio de gas asociado a una capa delgada de arenisca de baja velocidad.
Table 2. Parameters used to create the synthetic record corresponding to a sandstone gas reservoir model associated with a low-velocity thin bed.

La Figura 2 muestra registros sintéticos de ondas PP y PS correspondientes al modelo de alta velocidad (respuesta AVA), en tanto que la Figura 3 muestra sus respectivos espectros de amplitud, que constituyen los datos utilizados en la inversión. Los datos fueron contaminados con ruido aditivo gaussiano con una relación señal-ruido (S/N) de 10 (20dB) (en términos prácticos, la desviación estándar del ruido gaussiano fue igual al 10% de la amplitud máxima de la señal). En dichas figuras se puede observar una importante variación de la amplitud con el ángulo, que en este caso disminuye con el ángulo para las ondas PP y aumenta para las ondas PS. Son estas variaciones las que nos permiten caracterizar la capa delgada.
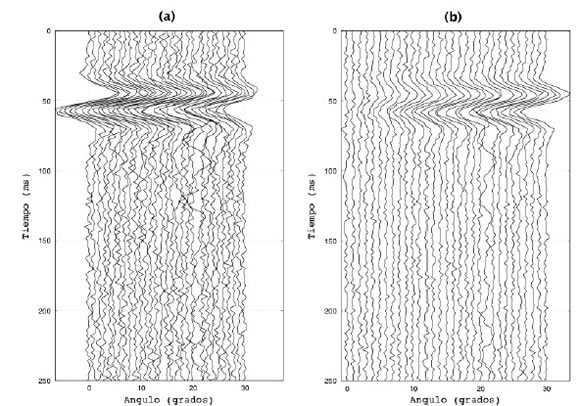
Figura 2. Respuesta AVA para el modelo de la Tabla 1. El espesor considerado es de 8 m y S/N=10 (20dB). (a) Ondas PP; (b) ondas PS.
Figure 2. AVA response for the model in Table 1. The thickness considered is 8 m and S/N=10 (20 dB). (a) PP waves (b) PS waves.

Figura 3. Espectros de amplitud correspondientes al modelo de la Tabla 1. El espesor considerado es de 8 m y S/N=10 (20dB). (a) Ondas PP; (b) ondas PS.
Figure 3. Amplitude spectra for the model in Table 1. The thickness considered is 8 m and S/N=10 (20dB). (a) PP waves (b) PS waves.
Impacto de las ondas PS en la función de costo
Con el fin de analizar el posible impacto generado por la información adicional provista por las ondas PS en el proceso de inversión, se calculó la función de costo utilizando los valores verdaderos de todos los parámetros correspondientes al modelo de alta velocidad de la Tabla 1, excepto el espesor h y correspondientes a la capa delgada. La Figura 4 muestra el logaritmo de la función de costo en función de y h utilizando las ondas PP y PS simultáneamente ( =0.5, Figura 4a) y utilizando solamente las ondas PP ( = 1.0, Figura 4b). Para el cálculo se utilizó una relación señal-ruido de 10, un espesor de 8 m y un rango de ángulos de incidencia de 0-30 grados, por lo que los espectros de frecuencia "observados" son los que se muestran en la Figura 3. Se puede observar en la Figura 4a que el mínimo de la función de costo es mucho más claro cuando se utiliza la información de los dos tipos de onda que cuando se utiliza sólo la información de las ondas compresionales (Figura 4b). Este análisis muestra que la función de costo es más sensible a y h de la capa delgada cuando se incorpora la información de la onda de corte, y, por consiguiente, la inversión resultará mejor condicionada. Por otro lado, la curva de nivel blanca que se muestra en la Figura 4 delimita la región del espacio del modelo donde el logaritmo de la función de costo es menor o igual al ajuste esperado, que en este caso es igual a la varianza del ruido gaussiano agregado, o sea log(0.024) -3.7. Luego, cualquier solución dentro de esta región ajusta al dato suficientemente bien, por lo que cualquiera de ellas constituye una solución posible. El agregado de información adicional a través de las ondas PS reduce el tamaño de esta región, y, por consiguiente, contribuye a disminuir la incerteza de las soluciones que se obtengan durante la inversión.
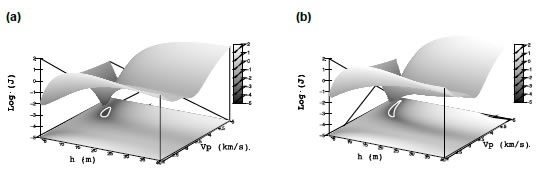
Figura 4. Log(J) en función de la velocidad de la onda P y espesor de la capa delgada utilizando: (a) ondas PP y PS ( =0.5) y (b) sólo ondas PP ( =1.0). La curva de nivel blanca delimita la región donde log(J) es menor o igual que el ajuste esperado, o sea log(0.024) -3.7.
Figure 4. Log (J) as a funtion of P-wave velocity and thickness of the thin bed using: (a) both PP and PS-waves ( =0.5) and (b) PP-waves only ( =1.0). The white contour line delimits the region where log (J) is less or equal than the expected misfit, i.e. log(0.024) -3.7.
Un resultado similar se muestra en la Figura 5. En este caso se comparan los valores de la función de costo cuando los parámetros desconocidos son y de la capa delgada. Nuevamente, la región de ajuste esperado es más pequeña, el mínimo de la función de costo es más claro y su comportamiento más adecuado para la inversión cuando se incorpora la información simultánea de las ondas compresionales y de corte (Figura 5a) que cuando se utiliza sólo la información de las ondas compresionales (Figura 5b).

Figura 5. Log(J) en función de la velocidad de la onda S y la densidad de la capa delgada utilizando: (a) ondas PP y PS (=0.5) y (b) sólo ondas PP ( =1.0). La curva de nivel blanca delimita la región donde log(J) es menor o igual que el ajuste esperado, o sea log(0.024) -3.7.
Figure 5. Log(J) as a function of S-ware velocity and density of the yhin bed using: (a) both PP and PS-waves ( =0.5) and (b) PP-waves only ( =1.0). The white contour line delimits the region where log(J) is less or equal than the expected misfit, i.e. log(0.024) -3.7.
La Figura 6 muestra la función de costo cuando se utilizan simultáneamente ondas PP y PS, pero extendiendo el rango de ángulos de incidencia hasta 50º. Como se puede apreciar, el tamaño de la región de ajuste esperado se reduce un poco más en relación a los casos anteriores, especialmente para el caso de y (Figura 6b). Esto contribuye a reducir la no-unicidad del problema inverso y por ende a aumentar la precisión y calidad de los resultados finales, como se demuestra en los ejemplos de la sección de resultados.
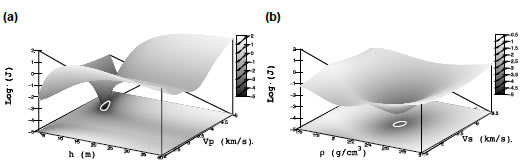
Figura 6. Log(J) utilizando ondas PP y PS ( =0.5) y un rango de ángulos de 0-50º, en función de: (a) la velocidad de la onda P y espesor de la capa delgada y (b) la velocidad de la onda S y la densidad de la capa delgada. La curva de nivel blanca delimita la región donde log(J) es menor o igual que el ajuste esperado, o sea log(0.024) -3.7.
Figure 6. Log (J) using PP and PS-waves ( =0.5) and a range of angles from 0 to 50 degrees as a function of (a) the P-wave velocity and thickness of the thin bed, and (b) the S-wave velocity and the density of the thin bed. The white contour line delimits the region where log(J) is less or equal than the expected misfit, i.e. log(0.024) -3.7.
Se analizó también el comportamiento de la función de costo frente a la variación de los otros parámetros que definen el modelo (velocidades y densidades de los semi-espacios superior e inferior), observándose resultados similares a los descriptos en las figuras anteriores.
Resultados de la inversión
Las Figuras 7, 8 y 9 muestran los principales resultados de la inversión espectral prestack para diferentes casos de capas delgadas con espesores que varían entre 5 y 40 m y para los parámetros definidos en las Tablas 1 y 2 y un rango de ángulos de incidencia de 0 a 30 grados. En dichas figuras se presentan los valores de los parámetros estimados para la capa delgada ( , , y h). Las líneas punteadas muestran el promedio de 100 inversiones para cada caso, en tanto que las regiones sombreadas representan las respectivas desviaciones estándar. La línea sólida indica el valor real de cada parámetro. Cada repetición representa el mismo dato pero diferente semilla para el proceso de optimización vía SA. En todos los casos se tomó una relación señal-ruido de 10. Para los parámetros asociados a la capa delgada se fijó un amplio rango de búsqueda, coincidente con los límites verticales indicados en las Figura 7, 8 y 9. El rango de búsqueda de los parámetros correspondientes a los semiespacios superior e inferior fue variable dependiendo del caso considerado, como se describe a continuación.
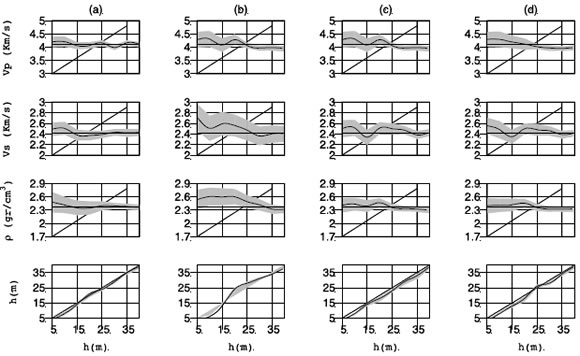
Figura 7. Inversión espectral prestack correspondiente al modelo de alta velocidad (S/N=10, 20dB) utilizando ondas compresionales solamente. (a) Los parámetros de los semi-espacios son conocidos. (b), (c) y (d) Los rangos de búsqueda de los parámetros de los semi-espacios son amplios. (b) Sin correlaciones. (c) Con correlaciones. (d) Con correlaciones y el rango de ángulos extendido de 0-30º a 0-50º. Notar que el espesor de tuning para este modelo es de 26.5 m.
Figure 7. Prestack spectral inversion in the high-velocity wedge model (S/N=10, 20dB) using compressional waves only. (a) The parameters of the semi-spaces are known. (b), (c) and (d) The search ranges of the parameters of the semi-spaces are wide. (b) Without correlations. (c) With correlations. (d) With correlations and the range of angles of incidence extended from 0-30° to 0-50°. Note that the tuning thickness for this model is 26.4 m.
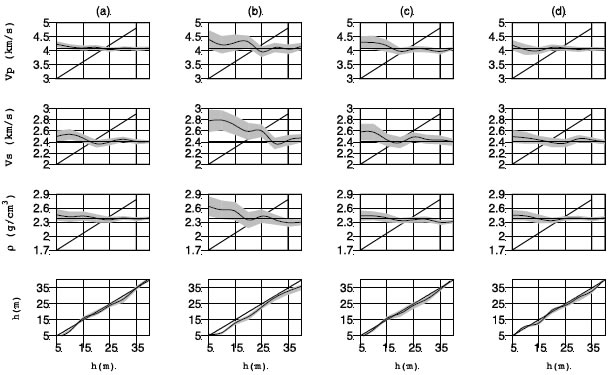
Figura 8. Inversión espectral prestack correspondiente al modelo de alta velocidad (S/N=10, 20dB) utilizando ondas compresionales y de corte simultáneamente. (a) Los parámetros de los semi-espacios son conocidos. (b), (c) y (d) Los rangos de búsqueda de los parámetros de los semi-espacios son amplios. (b) Sin correlaciones (c) Con correlaciones. (d) Con correlaciones y el rango de ángulos extendido de 0-30º a 0-50º. Notar que el espesor de tuning para este modelo es de 26.5m.
Figure 8. Prestack spectral inversion in the high-velocity wedge model (S/N = 10, 20dB) using both compressional and shear waves. (a) The parameters of the semi-spaces are known. (b), (c) and (d) The search ranges of the parameters of the semispaces are wide. (b) Without correlations. (c) With correlations. (d) With correlations and the range of angles of incidence extended from 0-30° to 0-50°. Note that the tuning thickness for this model is 26.5m.

Figura 9. Inversión espectral prestack correspondiente al modelo de baja velocidad (S/N=10, 20dB) incorporando las correlaciones VP -VS, y VP - . En los tres casos los rangos de búsqueda de todos los parámetros son escogidos relativamente amplios. (a) Utilizando ondas compresionales solamente. (b) Utilizando ondas compresionales y de corte simultáneamente. (c) Extendiendo el rango de ángulos de incidencia de las ondas de corte de 0-30º a 0-50º. Notar que el espesor de tuning para este modelo es de 15.8 m.
Figure 9. Prestack spectral inversion in the low-velocity wedge model (S/N=10, 20dB) the VP -VS, and VP - correlations are included. In all cases the search ranges of all parameters are chosen relatively wide. (a) Using compressional waves only. (b) Using both compressional and shear waves. (c) Extending the range of angles of incidence of the shear waves from 0-30° to 0-50 °. Note that the tuning thickness for this model is 15.8 m.
La Figura 7 muestra la inversión espectral prestack utilizando solamente ondas PP para el caso del modelo de alta velocidad (Tabla 1). En la Figura 7a los parámetros del tope y la base son conocidos. En consecuencia, los resultados de la inversión son muy precisos comparados con los obtenidos en la Figura 7b, donde los rangos de búsqueda de los parámetros de los dos semi-espacios fueron 2.0-4.0 km/s para , 1.0-2.0 km/s para y 1.7-2.9 g/cm3 para . En este caso, y como era de esperar, la incerteza en las estimaciones de los parámetros correspondientes a los semi-espacios desmejora los resultados significativamente. La principal razón no es numérica, sino netamente asociada a la no-unicidad intrínseca del problema inverso debido al mayor tamaño del espacio del modelo y de la región de ajuste esperado en relación al caso de la Figura 7a. Por consiguiente, las estimaciones de los diversos parámetros son menos precisas (aumenta la desviación estándar) y la calidad final de los resultados disminuye.
Estos resultados pueden mejorarse utilizando la información a priori de pozo mediante las correlaciones entre - y - . Efectivamente, la Figura 7c muestra que existe una disminución significativa en los valores de la desviación estándar, y además los valores medios de las estimaciones se acercan más a los valores reales cuando se introducen estas correlaciones, especialmente para los espesores menores, donde el impacto de la incerteza de los parámetros era más significativa.
En la Figura 7d se estudió el efecto de incorporar un mayor rango de ángulos de incidencia (0-50º en lugar de 0- 30º) para las ondas PP. En dicha figura no se observa una mejora significativa de los resultados, por lo que esta extensión de rango de ángulos de 30-50º no aportaría mayor información a la inversión. La Figura 8 corresponde a la inversión espectral prestack utilizando ondas PP y PS simultáneamente, también para el caso del modelo de alta velocidad. Se muestra cómo la desviación estándar decrece en cada caso (a,b,c) en comparación con la inversión que utiliza ondas PP solamente (Figura 7). Al igual que en la inversión de los datos PP, la inversión de los datos PP+PS converge muy bien cuando los parámetros del tope y la base son conocidos (Figura 8a). Al fijar un rango de búsqueda relativamente amplio para cada parámetro de los semiespacios, los resultados, como era de esperar, desmejoran significativamente (Figura 8b), aunque no en la misma medida que en el caso que se utilizaron solamente ondas PP (Figura 8b). Este inconveniente puede ser subsanado al introducir las correlaciones entre - y - , como se muestra en la Figura 8c.
Luego se examinó el efecto de introducir un mayor rango de ángulos de incidencia en los datos (0-50º en lugar de 0-30º) para las ondas PS. Al ampliar el rango de ángulos de incidencia de las ondas PS se observó una disminución significativa en la desviación estándar de las estimaciones, como se puede apreciar en la Figura 8d. Del mismo modo, se observó que los valores medios se aproximaron más a los valores verdaderos. Estos resultados están en concordancia con los observados en la Figura 6, cuando se analizó el comportamiento de la función de costo. Una disminución en el tamaño de la región de ajuste esperado contribuye a mitigar el problema de no-unicidad y por ende contribuye a reducir la incerteza de las soluciones. Notar que la calidad de estos resultados son comparables a los obtenidos en la Figura 8a, donde los parámetros de los semi-espacios son conocidos, lo que no representa una situación muy realista. La razón por la cual la extensión del rango de ángulos de las ondas PP no contribuye a mejorar los resultados reside en el hecho de que, para los modelos considerados, la variación de las amplitudes con el ángulo de incidencia es relativamente leve para ángulos de incidencia relativamente grandes. Esto se puede observar en la Figura 2a. Por lo tanto, el aporte de información adicional al pasar de 30 a 50º es poco significativo. Contrariamente, las amplitudes de las ondas PS, como se observa en la Figura 2b, poseen una variación notable con el ángulo de incidencia, que también se manifiesta más allá de los 30º. Cabe señalar que el potencial uso de datos PS asociados a ángulos de incidencia de hasta 50º no presenta mayores dificultades desde el punto de vista práctico. Como es bien sabido, debido a la asimetría del trazado de rayos y como consecuencia de la Ley de Snell para ondas convertidas, es más fácil registrar un rango amplio de ángulos de ondas PS que de ondas PP.
Por ejemplo, para un offset igual a dos veces la profundidad se podría obtener un ángulo de incidencia máximo para las ondas PP de unos 45º, pero de 57º para las ondas PS si se asume una relación / igual a 2 (Khare y Rape, 2007). Por ello, el uso de ondas PS en la inversión espectral prestack podría aprovecharse para mejorar significativamente la estimación de los diversos parámetros que caracterizan una capa delgada sin la necesidad de un offset extremadamente largo.
La Figura 9 es el resultado de la inversión espectral de los registros sintéticos creados a partir del modelo de baja velocidad (Tabla 2). En este caso, se establecieron los siguientes rangos de búsqueda: 2.5-4.5 km/s para de los dos semi-espacios, 1.5-2.5 km/s para del medio superior, 2.0-3.0 km/s para del medio inferior y 1.7-2.8 g/cm3 para de los dos semi-espacios. Asimismo, y en todos los casos considerados, se introdujeron las correlaciones entre - y - utilizando los mismos parámetros de ajuste empíricos que consideramos en el caso del modelo de alta velocidad. La Figura 9a corresponde a la inversión utilizando ondas compresionales solamente. Se observa que a pesar de la gran incertidumbre (rango de búsqueda) en los parámetros, la correlación impuesta entre los mismos contribuye a mejorar significativamente las estimaciones. Los resultados mejoran al incorporar la información de las ondas de corte (Figura 9b), notándose una disminución importante de las desviaciones estándar y un acercamiento de los valores medios de las estimaciones a los valores reales. Al aumentar el rango de ángulos de incidencia de las ondas de corte de 0-30º a 0-50º, se obtiene una mayor precisión (Figura 9c).
Impacto de la correlación entre parámetros en la convergencia
En esta sección analizamos el impacto de las correlaciones impuestas entre los diversos parámetros en la convergencia del proceso de inversión. La Figura 10 muestra algunos resultados parciales correspondientes a 10 inversiones independientes (modelo de baja velocidad). Los puntos grises representan los valores generados por el SA en cada iteración, en tanto que los puntos negros representan los valores aceptados (de acuerdo al criterio de Metrópolis (Metropolis et al,1953), como es usual en SA). Las líneas continuas indican las funciones empíricas que relacionan VP con VS (ecuación (4)) y VP con (ecuación (5)), correspondientes a la capa delgada. Finalmente, las líneas punteadas indican los valores verdaderos de los respectivos parámetros.

Figura 10. Valores de los parámetros generados por el SA luego de 500 iteraciones para 10 inversiones independientes sin correlación (paneles a y c) y con correlación entre los parámetros (paneles b y d). Los paneles (a) y (b) muestran los crossplots de versus , mientras que los paneles (c) y (d) muestran los crossplots versus .
Figure 10. Parameter values generated by the SA after 500 iterations for 10 independent inversions without parameter correlations (panels a and c) and with parameter correlation (panels b and d). The panels (a) and (b) show the - crossplots, while panels (c) and (d) show the - crossplots.
Los paneles a y b de la Figura 10 muestran los respectivos crossplots de VP versus VS cuando los rangos de búsqueda de los parámetros que definen el modelo son amplios y coincidentes con los límites de los ejes de coordenadas (Figura 10a), y cuando se utilizan las restricciones impuestas por las correlaciones (Figura 10b). Los paneles c y d de la Figura 10, en tanto, muestran los respectivos crossplots de VP versus para los mismos casos, es decir sin correlación (Figura 10c) y con correlación (Figura 10d). Cuando la inversión no incluye las correlaciones entre parámetros, se observa cómo el proceso iterativo genera valores pseudo-aleatorios que se distribuyen de manera relativamente uniforme en el espacio del modelo. Muchos de estos valores se encuentran en regiones muy alejadas de la solución, lo que perjudica la velocidad de convergencia del proceso iterativo (Figura 10a y c) y afecta naturalmente el costo computacional de todo el proceso de inversión. Por el contrario, cuando se introducen las correlaciones entre parámetros, los valores generados por el SA se concentran mayormente en las proximidades de las relaciones empíricas impuestas durante el proceso de inversión (Figura 10b y d), favoreciéndose de esta manera la convergencia hacia la solución correcta y contribuyendo a mitigar el problema de no-unicidad.
La Figura 11 muestra el logaritmo de la función de costo versus iteración para 10 inversiones independientes sin utilizar correlaciones (Figura 11a) y utilizando correlaciones (Figura 11b). Como se puede apreciar, en el segundo caso la convergencia al valor esperado de la función de costo (línea horizontal) se alcanza en menos iteraciones que en el primer caso, donde se puede observar una convergencia muy lenta para algunas de las realizaciones. Esto se debe a la reducción del tamaño del espacio del modelo, lo que contribuye a minimizar el problema de nounicidad y a la eficiencia del proceso de inversión. A su vez es posible observar en la Figura 11b, donde no se utilizan correlaciones, que en algunos casos no converge al valor esperado de la función costo, por lo que en estos casos fue necesario refinar la solución mediante el método de Powell. correlations.
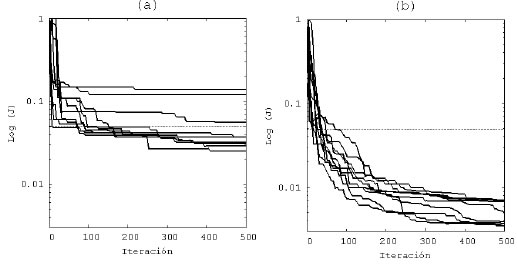
Figura 11. Logaritmo de la función de costo versus iteración sin correlación (a) y con correlación (b) entre los parámetros.
Figure 11. Logarithm of the cost function versus iteration (a) without parameter correlations and (b) with parameter.
Impacto de la conversión offset-ángulo
En la práctica los registros sísmicos son grabados en el dominio del offset, en tanto que la inversión requiere los datos en el dominio del ángulo de incidencia. Asumiendo un modelo de capas planas, horizontales y uniformes, existe una relación sencilla que vincula el offset con el ángulo para el caso de la reflexión en una interfase dada:

es el ángulo de incidencia, el offset, el tiempo ida y vuelta a incidencia normal, la velocidad intervalica por encima del reflector y la velocidad cuadrática media correspondiente a las capas que se encuentran por encima de la interfase (Yilmaz, 2001). Es fácil demostrar que para el caso de un modelo de una capa , entonces esta ecuación se puede reescribir como
![]()
Es posible observar que para realizar esta transformación es necesario tener conocimiento del valor de la velocidad del reflector, por lo que si no hay una buena estimación de las velocidades de los medios se puede generar errores al crear los registros AVA.
Para estudiar cómo impacta en la inversión los errores cometidos al transformar los registros del dominio del offset al dominio del ángulo, se generó un conjunto de trazas asociadas a ciertos ángulos de incidencia y se calcularon los offsets "verdaderos" a partir de la ecuación 10, asumiendo, por simplicidad, un modelo de una capa. Luego se procedió a recalcular los ángulos asumiendo un cierto error en la velocidad utilizada. Finalmente se realizó la inversión de las trazas originales utilizando estos ángulos erróneos.
Tabla 3. Impacto en la inversión de los parámetros de la capa delgada debido a la conversión offset-ángulo para diferentes errores en la velocidad.
Table 3. Impact on the inversion of the thin-bed parameters due to the offset-angle conversion for different errors in the velocity.
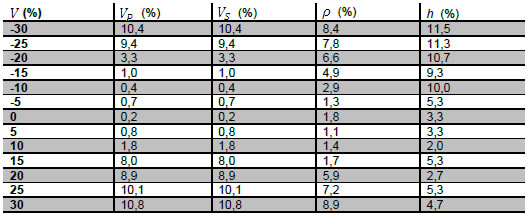
La muestra distintos porcentajes de error de la velocidad utilizada en el proceso de la conversión del offset al ángulo y el valor del error obtenido de los parámetros de la capa delgada luego de promediar 100 inversiones. El modelo utilizado fue el modelo de alta velocidad (Tabla 1), con =15m y S/N=10 (20dB). Sin perder generalidad, para la conversión se eligió =1 s y =3.62 km/s, una velocidad que es igual al promedio entre las velocidades del medio superior y de la capa delgada. Para la inversión se utilizó un rango de ángulos de incidencia de 0 a 30º, considerando tanto ondas PP como PS. Se incluyó, además, las correlaciones entre parámetros como se mostró en los ejemplos anteriores. Como se puede observar los errores introducidos no causan una variación significativa en la estimación de los parámetros de la capa delgada , y . En todos los casos el error en la estimación de los parámetros oscila en un máximo de 10%. Se realizó el mismo análisis para otros espesores y para el modelo de baja velocidad obteniéndose un comportamiento similar.
CONCLUSIONES
En este trabajo hemos extendido un método de inversión espectral prestack para capas delgadas recientemente publicado en la literatura con el fin de mitigar los problemas de no-unicidad inherentes al proceso de inversión. Se obtuvo una mejora significativa con respecto a ese trabajo en la precisión y exactitud de las estimaciones de los parámetros que sirven para caracterizar modelos de capas delgadas con espesores debajo del tunning. En particular, la nueva estrategia permite obtener estimaciones precisas de espesores, velocidades de ondas P y S y densidades a partir de datos sísmicos prestack. Esta mejora se logró al introducir, por un lado, la información adicional proporcionada por las ondas de corte convertidas (ondas PS), y por otro lado, la información a priori provista por datos de pozos cercanos. Esta información a priori consiste en tener en cuenta las posibles correlaciones empíricas existentes entre las velocidades de las ondas P y S y entre la velocidad de la onda P y la densidad, para cada uno de los tres medios que definen al modelo. La información se incorpora al método restringiendo estocásticamente, de acuerdo con las mencionadas correlaciones, las potenciales soluciones durante el proceso iterativo de inversión. Como resultado, y debido a que el espacio del modelo resulta más acotado, se obtuvo una mejora muy significativa en la velocidad de convergencia del proceso de inversión y una reducción en la incerteza de los diversos parámetros estimados. Asimismo se analizó el impacto que se obtiene al aumentar el rango de ángulos de incidencia de las ondas convertidas PS, observándose la importancia de contar con este tipo de información para mejorar la calidad de los resultados.
A partir del análisis de las soluciones de un gran número de problemas inversos utilizando datos sintéticos con ruido aditivo gaussiano, se concluye que los resultados son más precisos cuando se utilizan las ondas PP y PS simultáneamente que cuando se utilizan las ondas PP solamente. Además, cuando se incorpora la información a priori de pozos mediante restricciones de tipo estocásticas, se observa que la calidad de los resultados es equivalente al caso en que la inversión se realiza conociendo exactamente los parámetros del tope y la base del reservorio, incluso cuando se utilizan ondas PP solamente. Esto implica que, aún cuando no se dispone de ondas convertidas PS, es posible obtener estimaciones razonables si se cuenta con este tipo de información a priori obtenida a partir de datos de pozos cercanos.
A futuro, se planea validar la metodología con datos de campo.
Agradecimientos: Este trabajo fue parcialmente financiado por la Agencia Nacional de Promoción Científica y Tecnológica (PICT-2010-2129). Agradecemos también el apoyo de Dataseismic Geophysical Services.
REFERENCIAS
1. Castagna, J., Bazle M. and Eastwood, R., 1985. Relationships between compressional-wave and shear-wave velocities in clastic silicate rocks. Geophysics, 50, 571-581. [ Links ]
2. Chung, H. and Lawton, D., 1995. Frequency characteristics of seismic reflections from thin beds. Canadian Journal of Exploration Geophysics, 31, 32-37. [ Links ]
3. Dey, A. and Stewart, R., 1997. Predicting density using Vs and Gardner's relationship. CREWES Research Report, 9. [ Links ]
4. Duffaut, K., Alsos, T., Landrø, M., Rogno, H. and Al-Najjar, N., 2000. Shear-wave elastic impedance. The Leading Edge, 19, 1222-1229. [ Links ]
5. Gardner H., Gardner L. and Gregory A., 1974. Formation velocity and density. The diagnostic basics for stratigraphic traps. Geophysics, 74, 770-780. [ Links ]
6. Hall M., 2006. Predicting bed thickness with cepstral decomposition. The Leading Edge, 25, 199-204. [ Links ]
7. Ingber, L., 1989. Very fast re-annealing. Journal of Mathematical Computation and Modelling, 12, 967- 973. [ Links ]
8. Jin, S., Cambois, G. and Vuillermoz, C., 2000. Shear wave velocity and density estimation from PS- wave AVO analysis: Application to an OBS dataset from the North Sea. Geophysics, 65, 1446-1454. [ Links ]
9. Khare, V. and Rape T., 2007. Density inversion using joint PP/PS data: Sensivity to the angle range. 77th SEG Annual Meeting, Expanded Abstracts, 965-969. [ Links ]
10. Mehdizadeh, H., Landrø, M., Mythen, B., Vedanti, N. and Srivastava, R., 2005. Time lapse seismic analysis using long offset PS data. 75th SEG Annual Meeting, Expanded Abstracts, 3-7. [ Links ]
11. Metropolis, N., Rosenbluth, W., Rosenbluth, N., Teller, H., and Teller, E., 1953. Equations of State Calculations by Fast Computing Machines. Journal of Chemical Physics, 21, 1087-1092. [ Links ]
12. Nowak E., Swan H. and Lane D., 2008. Quantitative thickness estimates from the spectral response of AVO measurements. Geophysics ,73, C1-C6. [ Links ]
13. Partyka, G., J. Gridley, and J. Lopez, 1999. Interpretational applications of spectral decomposition in reservoir characterization. The Leading Edge, 18, 353-360. [ Links ]
14. Potter C. and Stewart R., 1998. Density predictions using Vp and Vs sonic logs. CREWES Research Report, 10. [ Links ]
15. Press W., Teukolsky S., Vetterling W. and Flannery, B., 1992. Numerical recipes in Fortran 77: The art of scientific computing. Second Edition. Cambridge University Press. [ Links ]
16. Puryear C. and Castagna J., 2008. Layer-thickness determination and stratigraphic interpretation using spectral inversion: Theory and application. Geophysics, 73, R37-R48. [ Links ]
17. Rabben, T., Tjelmeland H. And Ursin B., 2008. Non-linear Bayesian joint inversion of seismic reflection coefficients. Geophysical Journal International, 173, 265-280. [ Links ]
18. Rubino, J. and Velis D., 2009. Thin-bed prestack spectral inversion. Geophysics, 74, R49-R57. [ Links ]
19. Veire H. and Landrø M., 2003. Inversion of PP and PS seismic data. 65th EAGE Conference and Exhibition. Extended Abstracts, D14. [ Links ]
20. Veire H. and Landrø M., 2006. Simultaneous inversion of PP and PS seismic data. Geophysics, 71, R1-R10 [ Links ]
21. Yang W. and Yu J., 2009. Model-based PP-PS joint inversion - A sensitivity study on method, input data type, initial model and noise level. 71st EAGE Conference and Exhibition. Extended Abstracts, S024. [ Links ]
22. Xu, Y. and Bancroft, J., 1998. Statistical Vp-Vs relationships from well logs in Blackfoot. CREWES Research Report, 4. [ Links ]
23. Yilmaz, O., 2001. Seismic data analysis: Processing, inversión, and interpretation of seismic data: SEG Investigations in Geophysics Series No. 10. [ Links ]
Recibido: 2-3-2012
Aceptado: 28-5-2012














