ARTÍCULOS

EMPODERAMIENTO DOCENTE: LA PRÁCTICA DOCENTE MÁS ALLÁ DE LA DIDÁCTICA. ¿QUÉ PAPEL JUEGA EL SABER EN UNA TRANSFORMACIÓN EDUCATIVA?

 

Daniela Reyes-Gasperini y Ricardo Cantoral

Daniela Reyes-Gasperini*
Centro de Investigación y de Estudios Avanzados, México.
dreyes@cinvestav.mx

Ricardo Cantoral**
Centro de Investigación y de Estudios Avanzados, México.
rcantor@cinvestav.mx

* Profesora de Matemática por el Instituto Superior del Profesorado "Dr. Joaquín V. González", Ciudad Autónoma de Buenos Aires, Argentina. Maestra y Doctora en Ciencias especialidad en Matemática Educativa por el Centro de Investigación y de Estudios Avanzados del IPN (Cinvestav-IPN), Ciudad de México, México. Becaria Doctoral del Consejo Nacional de Ciencia y Tecnología (CONACYT). Miembro del Comité Latinoamericano de Matemática Educativa y de la Sociedad Argentina de Educación Matemática.

** Investigador titular 3D del Cinvestav IPN. Doctor en la especialidad de Matemática Educativa por el Cinvestav. Realizó un posdoctorado en la Université Paris VII. Investigador nacional del Sistema Nacional de Investigadores en su máximo nivel y miembro de la Academia Mexicana de Ciencias. Obtuvo la distinción de Profesor de Mérito del Ministerio de Educación Superior, La Habana y fue acreedor a la Medalla al Mérito 45 aniversario de la Universidad de Camagüey, CUBA. Fundador y presidente del Comité Latinoamericano de Matemática Educativa – CLAME. Director de la Revista Latinoamericana de Investigación en Matemática Educativa – Relime.

Recibido: 15/03/2016 Aceptado: 28/05/2016

---

Resumen

La Matemática Educativa, de origen latinoamericano y alcance mundial, concebida como disciplina científica que estudia fenómenos didácticos ligados al saber matemático, se encuentra en búsqueda continua de trayectos oportunos para la mejora en los procesos de enseñanza y de aprendizaje de las matemáticas. En este artículo compartimos uno de los más recientes estudios referente al desarrollo profesional docente desde la Teoría Socioepistemológica: el proceso de empoderamiento docente. Los lectores apreciarán cómo un fenómeno típicamente social, entrelazado con una mirada socioepistemológica de las matemáticas que pone en el centro a la problematización de la matemática escolar, promueve un cambio en la relación con el conocimiento matemático por parte del docente a fin de impulsar una transformación educativa.

Palabras clave: Empoderamiento; Socioepistemología; Problematización de la Matemática Escolar

Abstract

Mathematics teaching and learning are researched by Latin American Mathematics Education with global reach. This is a scientific discipline which studies didactic phenomena linked to mathematical knowledge. New and optimum learning and teaching paths are continuously investigated to better teach and learn mathematics. In this article we share one of the most recent studies on teachers professional development from the Socioepistemologic Theory: the teachers empowerment process. Readers will appreciate how a typically social phenomenon, interwoven with a socioepistemological gaze of mathematics, which puts in the center  the problematization of school mathematics, promotes a change in the relation between mathematical knowledge by the teacher in order to propel an education transformation.  

Keywords: Empowerment; Socioepistemology; Problematization of School Mathematics

---

Introducción

La investigación científica en Matemática Educativa se ocupa de brindar una respuesta ante situaciones específicas de la sociedad ligadas a las problemáticas propias de la dialéctica enseñanza–aprendizaje de las matemáticas.
Mientras que la pregunta best-seller de los años 90’s fue sin duda el cómo enseñar mediante diversas estrategias didácticas que pudieran hacer más accesible la comprensión de ciertos conocimientos matemáticos a los estudiantes de diferentes niveles educativos, la Teoría Socioepistemológica se planteó nuevos interrogantes: ¿qué es lo que estamos enseñando?, ¿qué es aquello que nuestros estudiantes están aprendiendo? Es decir, se propuso desde sus comienzos estudiar y discutir sobre la naturaleza del saber matemático y desde allí, reflexionar sobre el saber matemático escolar: el conocimiento puesto en uso en escenarios escolares.
Ahora bien, en cuanto a la práctica docente ¿qué se estudia en esta línea de investigación? He aquí la repetición de la historia: mientras que las corrientes clásicas analizan, con o sin el profesor, las tareas que los docentes usan en clase, las interacciones didácticas que tienen los estudiantes y sus profesores, la competencia puesta en juego para resolver problemas matemáticos, el conocimiento de los profesores sobre cómo los estudiantes piensan, conocen o aprenden un contenido matemático específico, entre muchas otras, la Socioepistemología se preguntó ¿cuál y cómo es la relación con el conocimiento matemático por parte del profesor de Matemáticas en una relación didáctica? Una vez más, como era de esperarse, el saber matemático adquirió mayor protagonismo en nuestro camino.
La Matemática Educativa se propone, desde sus inicios, un objetivo mayor e impostergable: alcanzar una democratización del aprendizaje de las matemáticas, esto es “que ningún ciudadano se quede atrás”. Uno de los medios para lograrlo consiste en aceptar un cambio de centración que va de la mirada platónica, focalizada en objetos abstractos ajenos a la realidad, a una visión socioepistemológica que asume a las prácticas sociales como la base misma de la construcción de significado en matemáticas (Cantoral, 2013a). Esto precisó de numerosas restructuraciones teóricas y prácticas al nivel del sistema educativo, una de ellas que consideramos fundamental y de la que tratamos intensamente en el presente escrito es el asunto del desarrollo profesional docente en el campo de las matemáticas. Nuestro eje de estudio considera una articulación indispensable entre tres elementos teóricos: la funcionalidad del saber matemático sobre la proporcionalidad (noción transversal en el sistema educativo y de alto valor práctico en la vida cotidiana), el constructo teórico de empoderamiento docente y la noción misma de espacio áulico que plantea la Socioepistemología (el aula extendida). Con base en dicha articulación, tejimos un entramado conceptual a fin de mostrar que el empoderamiento docente desde una visión socioepistemológica es un proceso que estudia a la profesionalización, problematizando la matemática escolar (anteriormente, denominada problematización del saber matemático). Este, es un cambio posible; pues lo mostró la propia experiencia de trabajar conjuntamente con docentes de educación secundaria (12 a 14 años) y nivel bachillerato (15 a 18 años) en el marco de un programa institucional mexicano. Nuestra misión entonces, como investigadores en activo, fue la de explicar teóricamente aquello que la empiria nos mostraba y que posteriormente reprodujimos en diversas regiones de México con más de 500 docentes en Oaxaca, Hidalgo, Puebla, Querétaro y Zacatecas.
Los lectores podrán encontrar en estas páginas elementos que facilitaron una reflexión profunda sobre el fenómeno de empoderamiento, enfatizando los caminos futuros. Se podrán encontrar ejemplos en detalle en (Reyes-Gasperini, 2011; Reyes-Gasperini y Cantoral, 2014; Reyes-Gasperini, Cantoral y Montiel, 2013), donde se explicita cómo el empoderamiento, a causa de un cambio de relación con el conocimiento matemático por parte del docente, le brinda la libertad de privilegiar la actividad situada del que aprende, su contexto de significación; le permite además el reconocer las distintas formas de argumentación que favorecen diversas racionalidades contextualizadas, y en ese sentido, propiciar la naturaleza funcional del saber, dotarlo de valor de uso. En síntesis, esto favorece un proceso de resignificación progresiva del que aprende inmerso en marcos referenciales diversos.
Invitamos a los lectores de este artículo a transitar por el camino recorrido por los autores, relativo al estudio de un fenómeno enmarcado en la línea del desarrollo profesional docente: el empoderamiento. ¿Por qué empoderar al docente? ¿En qué sentido se habla de empoderarlo? ¿Cuáles son los vínculos entre empoderamiento y saber matemático? ¿Cómo sabremos que está inmerso en un proceso de empoderamiento? Estas y otras preguntas son abordadas.

¿Por qué dar vuelta la mirada hacia el saber matemático?

Para la investigación es válido preguntarse cómo hacer más accesible un conocimiento matemático, ya sea poniendo el foco en los docentes en cuanto a las estrategias didácticas utilizadas para su enseñanza, o centrándonos en los estudiantes y el estudio de sus respuestas. Por tanto, la pregunta parece natural: ¿por qué esta vuelta de mirada y no continuar con la centración en las interacciones del docente con el estudiante?
Veamos esto mediante un ejemplo: si habláramos de la noción de función como un concepto difícil de asimilar, comprender y comunicar, también deberíamos reconocer las características específicas que tienen los diversos tipos de funciones. En particular en las funciones polinómicas (Alanís, 1996), las funciones periódicas (Buendía, 2004; Buendía y Cordero, 2005), las funciones trigonométricas (Montiel, 2011; Montiel, 2013), las funciones logarítmicas (Ferrari, 2010; Ferrari y Farfán, 2008), las funciones exponenciales (Lezama, 2003), es decir, lo que pareciera ser un “adjetivo” de las funciones, esconde un complejo conglomerado de niveles prácticos, funcionales, históricos y sociales que el sistema didáctico desconoce y aparece pura y exclusivamente expresado en la unidad temática: Funciones con distintos mecanismos de apropiación. Algo similar ocurre con las gráficas, las que en los libros de texto se muestran como ilustraciones acompañantes de la función, cuando en realidad son espacios donde se puede construir conocimiento (Cordero, Cen Che y Suárez, 2010; Arrieta, 2003; Cantoral y Montiel, 2003a, 2003b; Farfán, 2013). Del mismo modo, podríamos observar esto en el caso de la proporcionalidad (Cantoral y Reyes-Gasperini, 2012; Reyes-Gasperini, 2011; Reyes-Gasperini y Cantoral, 2014; Reyes-Gasperini, Cantoral y Montiel, 2014), siendo un tema de gran relevancia en la matemática escolar (Hart, 1988; Godino y Batanero, 2002; Oliveira, 2009) que es reducido, la mayoría de las veces, a la buena aplicación de la regla de tres simple, el valor unitario y la igualdad entre razones. Podríamos, también, focalizar nuestra atención en el Cálculo y verificar que la enseñanza se basa en la correcta aplicación de la regla de los cuatro pasos para obtener la derivada, lo cual cuestionamos, pero que en realidad, la derivada esconde un pensamiento y lenguaje variacional (Cantoral, 1990, 2013b; Caballero, 2012) que ha sido disminuido en el discurso didáctico que los manuales escolares transmiten.
Estos y otros ejemplos son los que nos hacen dar vuelta la mirada al saber matemático, pero insistimos: ¿por qué? Si partimos de la idea que señala que los problemas del aprendizaje en matemáticas residen en las acciones de los actores del sistema educativo, en particular los docentes, inevitablemente enfocaríamos nuestros análisis hacia cuestiones propiamente didáctico – pedagógicas a fin de contribuir en la mejora de las clases brindando mejores estrategias didácticas y hacer, de este modo, más accesible un saber matemático. Sin embargo, a contracorriente de lo que suele afirmarse, nuestra estrategia fue un tanto distinta; despersonificar dicha problemática y como hemos dicho, “dar vuelta la mirada” hacia aquello que hasta hace tres décadas no se cuestionaba: poner en discusión al propio objeto del aprendizaje, los contenidos y sus ideologías, digámoslo así, estudiar los efectos del discurso Matemático Escolar (dME) sobre los aprendizajes. Partimos entonces de la consideración de que éste es el causante de la mayor resistencia para el aprendizaje de las matemáticas. Si logramos el cuestionamiento del saber matemático podremos entonces, como consecuencia, discutir con los docentes la matemática escolar expresada, por ejemplo, en propuestas didácticas que nacen desde la investigación, o bien, entender y atender las reformas educativas que sufren los sistemas educativos continuamente.

Figura 1: Gráfica de una función de proporcionalidad.

Sólo como ejemplo: es habitual escuchar que para argumentar cuándo una función es de proporcionalidad directa o inversa se diga “es directa cuando uno aumenta y el otro aumenta”, y “es inversa cuando uno aumenta y el otro disminuye”. Éste es un estribillo en la matemática escolar que “ayuda” a los estudiantes a diferenciar una situación de otra. Ahora bien, dada esta “ayuda nemotécnica”, veamos la siguiente representación gráfica de una función (ver Figura 1): ¿Es de proporcionalidad directa o inversa? Más adelante veremos cuál es la respuesta matemáticamente correcta, mientras tanto, dejamos a los lectores pensando la respuesta (Reyes-Gasperini, Cantoral y Montiel, 2014).
Los docentes, en particular hacemos referencia a los mexicanos que hoy día dan clases de Matemáticas, fueron formados, ya sea en su formación inicial o en alguna formación afín que los llevó a la profesión docente, bajo una concepción de la Matemática basada en objetos abstractos y aislados de la realidad, considerados objetos anteriores a la praxis social y, en consecuencia, externos al individuo, siendo el profesor quien debe comunicar “verdades preexistentes” a sus alumnos, en donde la construcción social del conocimiento matemático queda sorteada (Cantoral, 2003). Entonces, ¿cómo podrían los docentes cuestionarse el conocimiento matemático escolar si en la mayoría de sus acercamientos a la matemática fue presentada como un cúmulo de conceptos que están “dados” y que su misión principal es que los estudiantes los “aprendan”, o quizás, “aprehendan”?
Aunado a las propuestas que se realizan sobre el desarrollo profesional del profesorado (Ponte, 2012), el proceso que se vive del análisis de la práctica al diseño de tareas matemáticas en la formación docente (Llinares, 2012), nosotros ponemos la lupa en el propio saber matemático y proponemos estudiar el desarrollo profesional docente a partir de la problematización de la matemática escolar, de suerte que esta acción les permita a los docentes hacerse dueños de su propia práctica a través del cambio de relación al conocimiento matemático, es decir, que transiten un proceso de empoderamiento. Entonces, dar vuelta la mirada al saber matemático refiere a problematizar el saber matemático (psm) de manera sistémica a partir de las cuatro dimensiones del saber: social, didáctica, epistemológica y cognitiva; para posteriormente, junto con los docentes, problematizar la matemática escolar (pme). Por tanto, replantearnos una transformación educativa respecto al desarrollo profesional docente amerita, a nuestro criterio, ampliar su mirada al saber matemático y, en particular, la matemática escolar puesta en juego en el aula.

¿Cuáles son los vínculos entre empoderamiento y saber matemático?

El empoderamiento es un fenómeno de carácter típicamente social que se ha estudiado en diversas disciplinas, por ejemplo, desde un enfoque psicosocial (Martín Mauri, 2011), social (Silva Dreyer y Martínez Guzmán, 2007), feminista (Camacho, 2003), desde la Psicología Comunitaria (Montero, 2006), o bien, desde un enfoque educativo (Howe & Stubbs, 1998, 2003; Stolk, de Jong, Bulte & Pilot, 2011). Si bien cada una de las disciplinas tiene una mirada particular hacia el fenómeno, todas coinciden en sus características principales que nosotros hemos sintetizado de la siguiente manera: se entiende como un proceso del individuo en colectivo (es necesaria la interacción en trabajo colectivo), que parte de la reflexión para consolidarse en la acción, que se produce desde el individuo sin la posibilidad de ser otorgado (el trabajo colaborativo será necesario pero no suficiente para garantizar el empoderamiento) y, por sobre todas las cosas, transforma la realidad del individuo y su contexto.
En particular, los proyectos que tienen como objetivo impulsar el empoderamiento docente (Howe & Stubbs, 1998, 2003; Stolk, de Jong, Bulte & Pilot, 2011) se focalizan en darle al docente herramientas para que realicen nuevas situaciones para el aula poniendo como punto importante la contextualización, ya sea mediante el conocimiento (conocer que existe) de nuevas investigaciones relacionadas con el tema a abordar, como así también, mediante la muestra de situaciones que brinden un contexto a lo que ellos ya conocen. Todo con el objetivo de que obtengan una actitud de liderazgo, confianza y mejora en sus prácticas para la enseñanza, enfatizando el hecho de que adquieran el poder de tomar las riendas de su propio crecimiento. Si bien nosotros coincidimos plenamente con los resultados que se esperan, consideramos que este tipo de análisis se reduce a una interpretación pedagógica.
Nuestra propuesta, dado el carácter socioepistemológico que se añade a este fenómeno social, incorpora las nociones de problematización del saber matemático (psm) y problematización de la matemática escolar (pme) como base para impulsar el empoderamiento docente. Ahora bien, ¿por qué diferenciamos psm y pme? La psm refiere al hecho de “hacer del saber un problema”, un objeto de análisis didáctico, localizando y analizando su uso y su razón de ser, es decir, refiere al estudio de la naturaleza de dicho saber matemático, por ejemplo relacionado con la proporcionalidad, sobre la base de preguntas del tipo: ¿qué problema llegaron a resolver las proporciones que no se podían resolver sin ellas? ¿Son más difíciles los problemas cuando las magnitudes son heterogéneas que cuando son homogéneas? ¿Por qué se trabajan problemas del cuarto valor faltante si allí no se representa la comparación, ni la construcción de una unidad de medida entre magnitudes? ¿Dónde aparecen las proporciones en la civilización? ¿Qué caracteriza a la relación de proporcionalidad? Entre muchas otras. El estudio socioepistemológico fundamentado en las dimensiones didáctica, epistemológica, social y cognitiva del saber permite confeccionar una unidad de análisis socioepistémica (uase) que provoca una singular simbiosis entre y desde las cuatro dimensiones, con el fin de generar una estructura teórica para cuestionar el saber matemático y posteriormente, consolidar estrategias para problematizar la matemática escolar.
En cambio, cuando trabajamos con la pme partimos de los conocimientos que para el sistema educativo son fundamentales dependiendo el nivel donde se realice el estudio. Con base en la uase se diseña una guía de actividades que confronte a las actividades didácticas típicas con el fin de poner en situación de aprendizaje al profesor y de esta manera generar espacios para que se realice la pme (Reyes-Gasperini, Cantoral y Montiel, 2014). Entendemos la pme como la acción que parte de la introspección, la mirada del que aprende y los usos que este saber posee en la cotidianeidad, apoyándose en las discusiones y reflexiones colectivas y en las investigaciones sobre dicho saber, o bien, siendo ellos mismos quienes se adentre a tal investigación. En particular, trabajar tareas donde se deban comparar magnitudes con el fin de construir una unidad de medida con la cual se permita conmensurar. Debemos retomar la idea de la constitución de proporciones como relaciones y no como una cuestión aritmética: pasar de lo aritmético a lo variacional, pues en este último, en la relación de magnitudes, se pone en juego lo proporcional.
Es necesario mencionar a esta altura que la Teoría Socioepistemológica descansa en cuatro principios fundamentales (Cantoral, 2011, 2013a): el principio normativo de la práctica social, el principio de la racionalidad contextualizada, el principio del relativismo epistemológico y el principio de resignificación progresiva o apropiación. Estos cuatro principios subyacen a la pme, pues esta problematización le permitirá al docente considerar que las prácticas sociales están en los cimientos de la construcción del conocimiento (normatividad de las prácticas sociales), y que el contexto determinará el tipo de racionalidad con la cual un individuo o grupo -como miembro de una cultura- construye conocimiento en tanto lo signifique y ponga en uso (racionalidad contextualizada). Una vez que este conocimiento es puesto en uso, es decir, se consolida como un saber, su validez será relativa al individuo o al grupo, ya que de ellos emergió su construcción y sus respectivas argumentaciones, lo cual dota a ese saber de un relativismo epistemológico. Así, a causa de la propia evolución de la vida del individuo o grupo y su interacción con los diversos contextos, se resignificarán esos saberes enriqueciéndolos de nuevos significados hasta el momento construidos (resignificación progresiva).
Por tanto, los vínculos entre empoderamiento y saber matemático están dados por la articulación del fenómeno típicamente social con el carácter socioepistemológico que subyace a su acción principal: la pme.

psm y psme: El caso de la proporcionalidad

La psm será la primera actividad por parte de los investigadores para construir las herramientas didácticas que se trabajarán a fin de realizar la pme conjuntamente con los profesores. En la uase, la dimensión social permite analizar los conocimientos matemáticos identificando la dimensión funcional, situacional e histórica, basada en la praxis, que está al nivel de la actividad y que es soslayada por el dME. La dimensión social, aunada a la dimensión epistemológica que estudia la naturaleza del saber, reconoce a la matemática como parte de una cultura producto de la actividad humana. Asimismo, bajo la mirada socioepistemológica, se concibe que los conocimientos se dotan de significados a través de su uso y su funcionalidad, por tanto se plantea la necesidad de que docentes y estudiantes, aunque inmersos en un sistema educativo, se relacionen con el saber matemático de una manera más activa con la intención de que construyan ideas fundamentales sobre dicho saber, más allá de las abstracciones, procedimientos y el aprendizaje propias de su aplicación. Es decir, la significación que construirá a partir de la actividad de relacionarse con el saber matemático (como aquel que es producto de la cultura), le permitirá entender aquellas nociones que las miradas platónicas consideran como “la matemática escolar”. Para poder hacer este análisis, el estudio de la dimensión didáctica ¹ del saber juega un papel central, pues será a través del estudio de libros de textos, programas de formación continua, notas y observaciones de clase, entre otros, que se podrá investigar cómo se manifiesta el discurso Matemático Escolar.
Asimismo, será a través del estudio de las prácticas en la construcción de casas, de la siembra, los estudios antropométricos, de la estimación de personas, que se estudiará cómo vive y se construye la proporcionalidad. ¿Cuáles son las prácticas asociadas a todas estas situaciones? La idea de comparar, aproximar, igualar, medir, son cuestiones fundamentales para desarrollar el pensamiento proporcional, distinto a la aplicación de la regla de tres simple (algoritmo aritmético). Conjuntamente con estos análisis, es a través del estudio de la dimensión cognitiva que se exploran los procesos de apropiación del saber matemático basado en el reconocimiento de que el paso del conocimiento al saber responde a procesos propios del desarrollo del pensamiento matemático, pues para el programa socioepistemológico, “la cognición es interpretada como la capacidad de hacer emerger el significado a partir de retroalimentaciones sucesivas de las acciones que las personas realizan sobre su medio ambiente próximo (tanto físico como cultural) y las interacciones de naturaleza dialéctica entre los actores” (Cantoral, 2013a, p. 61).
La construcción de la uase referente a la proporcionalidad nos ha llevado a estudiar, por ejemplo, la teoría de Piaget (1958, citado en Noelting, 1980; Inhelder & Piaget, 1972) en donde se considera a la proporcionalidad como el sello distintivo en el desarrollo de las operaciones formales, por tanto, dado que Piaget es un referente indiscutible dentro de la educación, nosotros nos preguntamos, ¿los estudiantes (o los profesores en nuestro caso), han desarrollado este tipo de pensamiento? La idea de pasar de una relación aditiva a una relación multiplicativa parece ser la idea fundamental que se ha perseguido en los estudios referentes a la proporcionalidad.
Si nos remontamos a los orígenes reportados de la proporcionalidad, nos encontramos con que si bien fue Eudoxo de Cnidos (390 A. N. E. – 337 A. N. E.), discípulo de Platón, quien trabajó con la teoría de proporciones, y se reconoce que fue Euclides quien reunió los aportes hechos por él, revisó, recapituló y transformó su teoría en su célebre Los Elementos (Guacaneme, 2012). Con el fin de comprender la proporcionalidad, hemos realizado un análisis axiomático de la teoría de proporciones abordada por Euclides en su Libro V. A la par del trabajo con Los Elementos, nos hemos puesto a trabajar con la inconmensurabilidad, por ejemplo la medida de la diagonal de un cuadrado. De allí nos surge el siguiente cuestionamiento: si no existe una medida común, ¿cómo se pueden medir estas magnitudes? El problema de medir fue sustituido, en la Teoría Euclidiana, por el problema de comparar. Esta es la pregunta fundamental que dio origen a la teoría de las proporciones entre magnitudes. Entonces, ¿será la condición provocada por la imposibilidad de medir lo que nos ha llevado a la necesidad de comparar, como la imposibilidad de adelantar el tiempo lo que nos ha llevado a predecir (Cantoral, 1990)? Es decir, ¿existe alguna práctica social subyacente? Estas preguntas son reflexiones que surgen a partir del análisis y que, de manera empírica, nos estamos acercando a su respuesta: encontrar una medida que conmensure a dos magnitudes inconmensurables es parte fundamental de lo proporcional, es decir, la constitución de la unidad de medida, que podría variar, según la referencia.
Al respecto, Guacaneme (2012) enuncia que dicha teoría emerge para atender dos problemas específicos de la época. Por un lado, ante el conflicto que había sufrido la teoría pitagórica respecto a la imposibilidad de asignar un número a la razón de dos magnitudes, los matemáticos griegos se replantearon la teoría de la proporción de tal suerte que “se pudiera hablar de razones y proporciones, sin necesidad de especificar si las magnitudes consideradas eran o no conmensurables” (Guacaneme, 2012, p. 104), en donde el mérito mayor de la teoría expuesta en el Libro V es la posibilidad de comparar magnitudes inconmensurables (Corry, 1994, citado en Guacaneme, 2012). Por otro lado, Los Elementos tienen el objetivo de presentar las teorías matemáticas bajo un esquema axiomático deductivo.
Ahora bien, si la Teoría de la proporcionalidad surge a partir de la posibilidad de comparar magnitudes inconmensurables, es lógico pensar que si la mayoría de problemas que aparecen en la literatura tienen que ver con el cuarto faltante, este tipo de problemas, no requiere siempre de un razonamiento proporcional (Lamon, 1999), pues no habría nada que comparar ya que las cantidades están dadas y sobre ellas hay que operar aritméticamente, aplicando, la mayoría de las veces, la regla de tres. Asimismo, pueden hacerse enunciados con la estructura del cuarto faltante, sin siquiera existir una relación proporcional entre las magnitudes, sin embargo, los estudiantes la resolverán dado que la característica que creen suficiente para aplicar la regla de tres simple es que ambas magnitudes aumenten (contraejemplo: el precio de un taxi y los kilómetros recorridos).
Continuando la psm, ahora desde el estudio de los funcionales de Cauchy (Roa, 2010), en particular, aquel que refiere a la función de proporcionalidad:

Este funcional nos ha dado luz para profundizar la diferencia entre el pensamiento aditivo y el multiplicativo. Asimismo, nos ha permitido analizar de manera profunda el ejemplo que hemos visto en la Figura 1, pues se articularon los razonamientos del modelo del pensamiento proporcional (Reyes-Gasperini, 2011; Reyes-Gasperini y Cantoral, 2014) con el funcional de Cauchy.
Retomemos la idea, ahora completa, de una de las actividades planteadas en los talleres para profesores con el fin de pme referido a la proporcionalidad y así, propiciar el proceso de empoderamiento.

Figura 2: Actividad 1 planteada en el taller a profesores.

Más del 80% de los profesores con los que hemos trabajado contesta que esa gráfica corresponde a una función de proporcionalidad inversa, pues “a medida que aumenta x, disminuye y”. Esta pregunta que pareciera trivial provoca una confrontación con la propia matemática escolar. Asimismo, preguntas del tipo “¿Qué significa

? ¿Qué es la proporcionalidad?”, que se construyen a partir de la uase basada en la noción de proporcionalidad, de alguna manera problematizan la matemática escolar, pues le hacen preguntas a las propias expresiones algebraicas y gráficas que aparecen en libros de texto y programas escolares.
Una argumentación posible para justificar que la gráfica corresponde a una función de proporcionalidad directa es que es una recta que pasa por el origen, siendo ésta, si se quiere, otro tipo de regla nemotécnica que, por sí sola, carece de argumentaciones.
Otra argumentación que podría darse, retomando el funcional de Cauchy

es la siguiente:

Figura 3: Argumentación visual con base en el funcional de Cauchy, que representa el razonamiento aditivo compuesto.

Asimismo, otras argumentaciones que se basan en los razonamientos del modelo del pensamiento proporcional son las siguientes:

Razonamiento aditivo simple: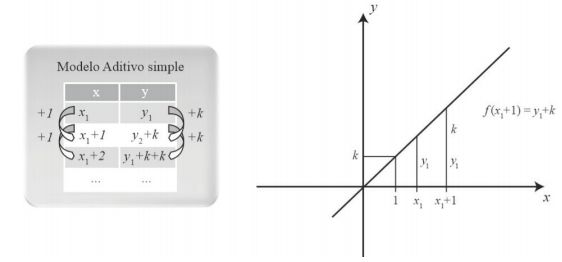

Figura 4: Razonamiento aditivo simple.

Razonamiento multiplicativo:

Figura 5: Razonamiento multiplicativo.

Razonamiento Inter:

Figura 6: Razonamiento inter.

Es decir, si el desarrollo del pensamiento proporcional pasa por los distintos razonamientos hasta llegar al intra que veremos a continuación, cualquiera de las argumentaciones anteriores, ya sea en la tabla de valores o en la gráfica, podrían ser válidas para justificar por qué la función planteada es de proporcionalidad directa. Sin embargo, la normatividad del dME provoca una respuesta matemáticamente errónea (a más-menos, entonces inversa), o bien, una respuesta memorística que, repetimos, por sí sola, carece de argumentaciones matemáticas (una recta que pasa por el origen).
Ahora bien, conjeturamos que el último de los pensamientos que radica en la idea de la razón entre las magnitudes resulta ser evidente si se estudia a través de la idea de un proceso variacional más que como una relación aritmética entre dos valores.
Analicemos por qué. En la gráfica no se puede observar a simple vista la relación entre las magnitudes. Sin embargo, es sabido que en las funciones de proporcionalidad directa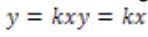

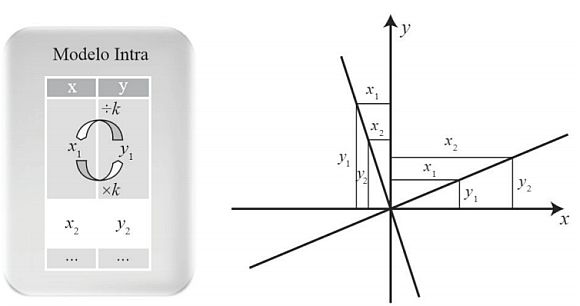
, la constante de proporcionalidad k, suele trabajarse como un simil con su pendiente:

.

Figura 7: Razonamiento intra.

Este último razonamiento es conflictual en tanto, puede expresarse, como se hace en el programa del ciclo escolar de secundaria de México, de la siguiente manera:

Razonamiento proporcional

El razonamiento proporcional en las matemáticas.
La noción de razón surge al comparar dos números o magnitudes a través de su cociente, mientras que las proporciones resultan de comparar los valores de dos listas de números o cantidades variables para ver si guardan siempre la misma razón entre sí. Si llamamos a y b a dos cantidades, su razón está dada por el cociente:

Y si denotamos por x los valores que puede tomar una cantidad variable y por y los valores correspondientes de la otra, decir que x e y son proporcionales significa que las dos cantidades están relacionadas por una expresión como la siguiente:

, donde k es la constante.
A pesar del aspecto tan sencillo de las fórmulas anteriores, las nociones de proporcionalidad y sus consecuencias son centrales en todas las matemáticas (Secretaría de Educación Pública, 2004, p. 88).
Al respecto nosotros nos preguntamos, ¿cuán sencillas serán para el estudiante estas fórmulas? Pues, demos el ejemplo de la siguiente tabla de valores, con valores sencillos, y “apliquemos” la fórmula planteada:

El hecho de que esa fórmula pueda ser aplicada es que subyace en ella un proceso variacional, por este motivo, es que conjeturamos que este tipo de pensamiento resulta ser evidente si se estudia a través de la idea de un proceso variacional más que como una relación aritmética entre dos valores, pues para decir que “en el caso de

la constante es -2”, deberíamos utilizar argumentaciones que podríamos construir, teniendo en cuenta la organización del Sistema Educativo, durante el bachiller, pues es en este momento cuando se estudia el Cálculo:
Dada

, siendo en nuestro caso particular

Entonces, la derivada de f en cero, es la constante negativa – 2,

. (Reyes-Gasperini, 2013).
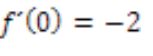
De aquí que, conjeturamos, cuando estamos trabajando con las funciones proporcionales dentro del Cálculo matemático, ya no se están comparando magnitudes inconmensurables de donde ha surgido la idea de proporcionalidad y el desarrollo del pensamiento proporcional, sino que éste se articula con un pensamiento variacional. Por tanto, el desarrollo del pensamiento proporcional amerita instancias previas a su articulación, con el pensamiento variacional.
Entonces, comenzamos a concluir este apartado sintetizando las siguientes preguntas: ¿cuál es la naturaleza de la proporcionalidad? ¿No será que el pensamiento humano tiene una estructura aditiva más que multiplicativa y el esfuerzo realizado por los individuos no es más que poner en funcionalidad sus herramientas tanto cognitivas, sociales como contextuales? ¿Qué se trabaja cuando se trabaja la noción de la proporcionalidad en la escuela? ¿Cuáles son las dificultades didácticas -en su formación- o bien, epistemológicas, que provocan que los individuos tengan este tipo de respuestas? ¿Cómo se podría rescatar la naturaleza del saber en situaciones de aprendizaje? ¿Qué rol jugarían estas situaciones en el aula? Como dijimos párrafos arriba ¿será la condición provocada por la imposibilidad de medir lo que nos ha llevado a la necesidad de comparar, como la imposibilidad de adelantar el tiempo lo que nos ha llevado a predecir (Cantoral, 1990)? Es decir, ¿existe alguna práctica social subyacente?
Dado el análisis realizado, podemos conjeturar que la proporcionalidad tiene un origen epistemológico como estrategia para atender a la imposibilidad de medir. Asimismo, con base en los estudios realizados a partir de una propiedad matemática

, se conoce que se construye la función proporcional. En términos de Vergnaud (1990), en el primer caso se precisa de estructuras multiplicativas (aquellas que requieren una multiplicación, división o combinación de ellas), mientras que en el segundo, de estructuras aditivas (aquellas que precisan una adición, sustracción o combinación de ellas). Hasta el momento, podemos postular que el pensamiento humano tiene una estructura aditiva más que multiplicativa y es por esto que en situaciones particulares en donde no se ponga en juego la comparación entre magnitudes, sino se solicite encontrar algún valor faltante, es decir, se enfatice en la cantidad más que en la relación, las respuestas llevarán a realizar procedimientos aditivos por encima de la comparación, y por tanto, por encima de la razón. Entonces, cabe estudiar qué tipo de actividades se trabajan a nivel escolar para detectar si son éstas las que obstaculizan el desarrollo deseado del pensamiento matemático escolar, pues están centradas en algoritmos para dar respuesta a preguntas concretas, más que en el desarrollo de un pensamiento proporcional que permita analizar y dar solución a problemáticas de estudio: comparar, igualar, medir.
Como se puede observar, la pregunta presentada en las Figuras 1 y 2, puede provocar la pme, en tanto confronta la forma tradicional de abordar los contenidos disponibles en el sistema didáctico con lo que le es propio al saber en juego. Pone en evidencia que aquello que se debe dominar de la proporcionalidad es insuficiente para analizar una situación de proporcionalidad. Actualmente estamos estudiando aspectos físicos, químicos, antropométricos, de construcción de viviendas, de siembra, de trueque, de Derecho, entre otros, para dar evidencia de la norma que subyace a la funcionalidad de la proporcionalidad como relación adecuada. La matemática escolar es concebida como un saber institucional intocable por y para el docente, sólo suelen aceptarse modificaciones en un proceso de reforma porque provienen de las instancias oficiales de educación. Sin embargo, con el tiempo se ha evidenciado que dichas modificaciones son, básicamente, a la cantidad de contenidos y al cómo son enseñados, no al qué se enseña con estos contenidos y estas formas pedagógicas.
En ese sentido es que reconocemos que cambios en la relación del docente con el conocimiento matemático escolar generan cambios en la práctica docente.

Reflexiones finales

Para hablar de las conclusiones, inevitablemente, recordemos las preguntas que nos hicimos al comienzo del capítulo: ¿Por qué empoderar al docente? ¿En qué sentido empoderarlo? ¿Cuáles son los vínculos entre el empoderamiento y el saber matemático? ¿Cómo sabremos que está inmerso en un proceso de empoderamiento?
Con la propuesta del empoderamiento docente estudiamos el desarrollo profesional docente desde la psm y despersonificamos el problema de investigación: no buscamos causas o responsables del fracaso, sino que ponemos el foco en el papel del propio saber matemático tanto al nivel de su significado como de su uso, y desde allí proporcionamos una alternativa viable. Nuestra propuesta entonces, no provee de manera explícita estrategias didácticas o reflexiones pedagógicas sobre la enseñanza de la matemática; sino más bien, hace del saber matemático escolar un problema y enmarca sobre él un conjunto de cuestionamientos que se trabajan con los docentes, quienes localizan y analizan los usos y razón de ser del saber matemático (en este caso de lo proporcional), con base en la uase construida.
Un docente que cuestione y analice los fundamentos y procesos matemáticos de donde se derivan los algoritmos, reconozca los diversos desarrollos del pensamiento que subyacen a su construcción, es decir, las distintas formas de argumentación, e incorpore la noción de aula extendida en tanto privilegie la vida misma del que aprende favoreciendo la aparición de diversas racionalidades contextualizadas y, así, el saber adquiera un estatus funcional, y sobre todas las cosas, que cambie su relación al conocimiento matemático, es un docente que está inmerso en un proceso de empoderamiento. ¿Qué significa “cambiar su relación al conocimiento matemático”? Que transite de una perspectiva platónica, centrada en objetos abstractos ajenos a la realidad, hacia una visión socioepistemológica, bajo la concepción de que las prácticas sociales son aquellas que norman intangiblemente la forma de construir conocimiento de los individuos en grupo, es decir, nos inducen a hacer lo que hacemos, y por tanto están en la base misma de toda construcción del conocimiento, mostrando como natural que en mayor o menor tiempo y medida, todos los individuos construyamos las nociones matemáticas basándonos en lo que en sus orígenes motivó su construcción.
Aunado a lo anterior, las actitudes de liderazgo que un docente desarrolle pasan a ser una parte importante de nuestra propuesta, pues el empoderamiento se compone de ambos elementos: problematización y apropiación del saber más la actitud de liderazgo que le permita innovar en su práctica docente, en tanto transformar su relación al conocimiento matemático. No puede haber el uno sin el otro: cuando nos refiramos al empoderamiento, no podemos hablar de la problematización de la matemática escolar sin las actitudes de liderazgo, ni bastarían las actitudes de liderazgo si no hay una verdadera apropiación del saber. Este hecho queda evidenciado en la incorporación de las interacciones con los estudiantes de manera autónoma, ya que cuando dialogamos con los docentes en los procesos de intervención, en ningún momento trabajamos la idea de llevarlo a la práctica, sino que esto surge como iniciativa propia. Aquí, es cuando el docente se vuelve agente activo.
La complementariedad entre saber matemático funcional, el constructo teórico de empoderamiento docente nos permiten postular una nueva manera de abordar la problemática de la profesionalización docente y así, atender a la exclusión que provoca el dME en los agentes del sistema educativo (Soto, 2010).
Por tanto, postulamos al empoderamiento como el proceso vivido por el docente, en conjunto con sus colegas (profesores e investigadores) con objeto de comprender, aceptar y participar de una propuesta novedosa sobre el aprendizaje centrado en prácticas y no en objetos abstractos. Ejemplo de ello, son profesores que incorporan, por ejemplo, las mezclas de colores en arte para hablar de proporciones: el color secundario es el invariante constante entre dos colores primarios. Incorporar nociones como aproximar, comparar, equivaler, medir, permitirán la significación mediante el uso del concepto de proporcionalidad directa, buscando mantener una relación adecuada entre las magnitudes que se comparan, por encima de encontrar un valor numérico per se que responde a la pregunta ¿cuánto?
Entonces, luego de haber transitado, por una síntesis del camino recorrido en el cual se explicó teóricamente aquello que la empiria nos dejaba ver, hemos caracterizado un fenómeno que de la propia realidad áulica ha emergido. Ahora podemos decir que hemos dado un nuevo paso en el objetivo de la democratización del aprendizaje, pues hemos postulado un mecanismo para estudiar al desarrollo profesional docente desde el propio saber matemático: el empoderamiento docente.
Nuestro próximo desafío será sistematizar los elementos a tener en cuenta en un diseño de intervención de desarrollo profesional docente que privilegie dicho empoderamiento. Para ello profundizaremos en la problematización del saber matemático con el fin de evidenciar la práctica social que permanece en el ámbito normativo humano y desde allí, continuar con la problematización de la matemática escolar, pues estamos convencidos de que el saber juega un papel fundamental en la transformación educativa.

Notas Bibliográficas

¹ Lo didáctico en este enfoque, no habrá de restringirse al ámbito escolar, pues se utiliza en un sentido extendido: como acción de construcción de significados compartidos, como acto de enseñanza. La dimensión didáctica está presente en toda clase de actividades humanas, escolares y no escolares, cuando se pretende enseñar ya sea en la escuela, en los oficios, en las tradiciones populares o en las prácticas (Cantoral, 2013a).

Referencias Bibliográficas

1. Alanís, J. (1996). Estudio para el rediseño del discurso didáctico del cálculo en las escuelas de ingeniería: Instalación y desarrollo de un lenguaje variacional (Tesis inédita de doctorado). D.F, México: Centro de Investigación y Estudios Avanzados del IPN.         [ Links ]

2. Arrieta, J. (2003). Las prácticas de modelación como proceso de matematización en el aula. (Tesis inédita de doctorado). D.F, México: Centro de Investigación y Estudios Avanzados del IPN.         [ Links ]

3. Buendía, G. (2004). Una epistemología de los aspectos periódicos de la función en un marco de prácticas sociales. (Tesis inédita de doctorado). D.F, México: Centro de Investigación y Estudios Avanzados del IPN.         [ Links ]

4. Buendía, G. & Cordero, F. (2005). Prediction and the Periodical Aspect as Generators of Knowledge in a Social Practice Framework: A Socioepistemological Study. Educational Studies in Mathematics, 58(3), 299-333. doi: 10.1007/s10649-005-2295-5        [ Links ]

5. Caballero, M. (2012). Un estudio de las dificultades en el desarrollo del lenguaje y pensamiento variacional en profesores de bachillerato (Tesis inédita de maestría). D.F, México: Centro de Investigación y Estudios Avanzados del IPN.         [ Links ]

6. Camacho de la O., A. L. (2003). Reflexiones preliminares en torno al empoderamiento. Recuperado el 20 de noviembre de 2010 de http://www.alforja.or.cr/centros/cep/documentos/poderyempoderamiento.pdf.         [ Links ]

7. Cantoral, R. (1990). Categorías Relativas a la apropiación de una base de significaciones para conceptos y procesos matemáticos de la Teoría elemental de las Funciones Analíticas. Simbiosis y Predación entre las nociones de “el Prædiciere” y “lo Analítico”. Tesis Doctoral. México: Departamento de Matemática Educativa – Cinvestav.

8. Cantoral, R. (2003). La aproximación socioepistemológica a la investigación en matemática educativa: una mirada emergente [CD–ROM]. XI Conferencia Interamericana de Educação Matemática (tema Educación Matemática & Desafíos y Perspectivas). Blumenau, Brazil: Universidad Regional de Blumenau.

9. Cantoral, R. (2011). Fundamentos y Métodos de la Socioepistemología. Simposio en Matemática Educativa, 22 – 26 agosto 2011. D. F., México: Centro de Investigación en Ciencia Aplicada y Tecnología Avanzada del IPN.

10. Cantoral, R. (2013a). Teoría Socioepistemológica de la Matemática Educativa. Estudios sobre construcción social del conocimiento. Barcelona, España: Gedisa.         [ Links ]

11. Cantoral, R. (2013b). Desarrollo del pensamiento y lenguaje variacional (Vol. 3). En R. Cantoral (Coord.). D.F., México: Secretaría de Educación Pública. ISBN: 978-607-9362-03-4. Disponible en: http://www.sems.gob.mx/work/models/sems/Resource/6586/1/images/desarrollo_del_pensamiento_y_leng_v_smc_baja.pdf        [ Links ]

12. Cantoral, R. & Reyes-Gasperini, D. (2012). Matemáticas y Práctica social: Construcción social del conocimiento matemático. Novedades educativas,261, 60-65.         [ Links ]

13. Cantoral, R. & Montiel, G. (2003a). Una presentación visual del polinomio de Lagrange. Números, 55, 3 – 22.

14. Cantoral, R. & Montiel, G. (2003b). Visualización y polinomios de interpolación. Enseñanza de la Matemática, 11(1), 24 – 38.

15. Cordero, F., Cen Che, C. & Suárez, L. (2010). Los funcionamientos y formas de las gráficas en los libros de texto: una práctica institucional en el bachillerato. Revista Latinoamericana de Investigación en Matemática Educativa, 13(2), 187-214.         [ Links ]

16. Farfán, R. (2013). Lenguaje gráfico de funciones. Elementos de Precálculo (Vol. 1). En R. Cantoral (Coord.). D.F., México: Secretaría de Educación Pública. ISBN: 978-607-9362-04-1. Disponible en: http://www.sems.gob.mx/work/models/sems/Resource/6586/1/images/lenguaje_grafico_de_funciones_baja.pdf        [ Links ]

17. Ferrari, M. (2010). Una socioepistemología de lo logarítmico. Revista Latinoamericana de Investigación en Matemática Educativa, 13(4), Número Especial, Tomo I, 53-68.         [ Links ]

18. Ferrari, M. & Farfán, R. M. (2008). Un estudio socioepistemológico de lo logarítmico: la construcción de una red de modelos. Revista Latinoamericana de Investigación en Matemática Educativa, 11(3), 309-354.         [ Links ]

19. Godino, J. D. & Batanero, C. (2002). Proporcionalidad y su didáctica para maestros. Granada, España: Proyecto de Investigación y Desarrollo del Ministerio de Ciencia y Tecnología.         [ Links ]

20. Guacaneme, É. A. (2012). Significados de los conceptos de razón y proporción en el Libro V de los Elementos. En O.L. León (Ed.), Pensamiento, epistemología y lenguaje matemático (pp. 99-135). Bogotá, Colombia: Fondo de Publicaciones Universidad Distrital Francisco José de Caldas.         [ Links ]

21. Hart, K. (1988). Ratio and Proportion. In J. Hiebert & M. Behr (Eds.), Number concepts and operations in the middle grades (pp.198-219). Reston, VA: National Council of Teachers of Mathematics.         [ Links ]

22. Howe, A. C. & Stubbs, H. S. (1998). Empowering Science Teachers: A Model for Professional Development. Journal of Science Teacher Education, 8(3), 167-182.         [ Links ]

23. Howe, A. C. & Stubbs, H. S. (2003). From Science Teacher to Teacher Leader: Leadership Development as Meaning Making in a Community of Practice. Science Teacher Education, 87(2), 281-297.         [ Links ]

24. Inhelder, B. & Piaget, J. (1972). “El equilibrio de la balanza”. En B. Inhelder y J. Piaget (Ed.), De la lógica del niño a la lógica del adolescente. Ensayo sobre la construcción de las estructuras operatorias formales (pp. 142-155). Buenos Aires, Argentina: Paidós.

25. Lamon, S. (1999). Reasoning Proportionally. In S. Lamon (Ed.), Teahcing fractions and rations for understanding (pp. 223-238). New Jersey: Lawrence Erlbaum Associates Publishers.         [ Links ]

26. Lezama, J. (2003). Un Estudio de reproducibilidad de situaciones didácticas. (Tesis doctoral no publicada). D.F, México: Centro de Investigación y Estudios Avanzados del IPN.         [ Links ]

27. Llinares, S. (2012). “Del análisis de la práctica al diseño de tareas matemáticas para la formación de maestros”. En N. Planas (Coord.), Teoría, Crítica y Práctica de la Educación Matemática (pp. 99-116). Barcelona, España: GRAÓ.

28. Martín Maruri, I. (2011). Empoderamiento para la innovación social. En Cibervoluntarios. org (Eds.), Innovación para el empoderamiento ciudadano a través de las TIC [Versió         [ Links ]n electrónica] (pp. 129-136). Recuperado el 20 de mayo de 2010 de http://www.mas-business.com/docs/Empoderamiento%20ciudadano.pdf

29. Montero, M. (2006). Teoría y práctica de la psicología comunitaria. La tensión entre comunidad y sociedad (3era ed.). Buenos Aires, Argentina: Paidós.         [ Links ]

30. Montiel, G. (2011). Construcción de conocimiento trigonométrico. Un estudio socioepistemológico. D.F., México: Díaz de Santos.         [ Links ]

31. Montiel, G. (2013). Desarrollo del pensamiento trigonométrico (Vol. 2). En R. Cantoral (Coord.). D.F., México: Secretaría de Educación Pública. ISBN: 978-607-9362-02-7. Disponible en: http://www.sems.gob.mx/work/models/sems/Resource/6586/1/images/desarrollo_del_pensamiento_trigonometrico_baja.pdf        [ Links ]

32. Noelting, G. (1980). The development of proportional reasoning and the ratio concept. Part I – Differentiation of stages. Educational Studies in Mathematics, 11, 217-253.

33. Oliveira, I. (2009). Proporcionalidade: estratégias utilizadas na Resolução de Problemas por alunos do Ensino Fundamental no Quebec. Boletim de Educação Matemática, 22(34), 57-80.         [ Links ]

34. Ponte, J. (2012). “Estudiando el conocimiento y el desarrollo profesional del profesor de matemáticas”. En N. Planas (Coord.), Teoría, Crítica y Práctica de la Educación Matemática (pp. 83-98). España: GRAÓ.

35. Reyes-Gasperini, D. (2011). Empoderamiento docente desde una visión Socioepistemológica: Estudio de los factores de cambio en las prácticas del profesor de matemáticas. (Tesis de maestría no publicada). D.F, México: Centro de Investigación y Estudios Avanzados del IPN.         [ Links ]

36. Reyes-Gasperini, D. (2013). La transversalidad de la proporcionalidad (Vol. 4). En R. Cantoral (Coord.). D.F., México: Secretaría de Educación Pública. ISBN: 978-607-9362-01-0. Disponible en: http://www.sems.gob.mx/work/models/sems/Resource/6586/1/images/transversalidad_smc_baja.pdf        [ Links ]

37. Reyes-Gasperini, D. & Cantoral, R. (2014). Socioepistemología y empoderamiento docente: acciones para un cambio educativo. Boletim de Educação Matemática, 28(48), 360-382. doi: 10.1590/1980-4415v28n48a14        [ Links ]

38. Reyes–Gasperini, D., Cantoral, R. y Montiel, G. (2013). “Profesionalización docente en Matemáticas. El empoderamiento docente: una mirada emergente”. En Dolores, C., J. Hernández, J., Sosa, L., García González, M. (Eds.), Matemática Educativa: la formación de profesores (pp. 153-172). México: Díaz de Santos. ISBN: 978–84–9969–664–5

39. Reyes-Gasperini, D., Cantoral, R. & Montiel, G. (2014). ‘Cuando una crece, la otra decrece’... ¿proporcionalidad inversa o directa? Premisa, 16(62), 3-15.

40. Roa, A. (2010). La ecuación funcional de Cauchy  y algunas aplicaciones (Tesis inédita de maestría). Universidad Nacional Abierta, Mérida, Colombia.         [ Links ]

41. Secretaría de Educación Pública (2004). Libro para el Maestro. Matemáticas. Educación secundaria. (2ª reimpresión) (pp. 88 – 105). México: Secretaría de Educación Pública.

42. Silva Dreyer, C. L. & Martínez Guzmán, M. L. (2007). Empoderamiento, Participación y Autoconcepto de Persona Socialmente Comprometida en Adolescentes Chilenos. Revista Interamericana de Psicología/Interamerican Journal of Psychology, 41(2), 129-138.         [ Links ]

43. Soto, D. (2010). El Discurso Matemático Escolar y la Exclusión. Una Visión Socioepistemológica. (Tesis inédita de maestría). D.F, México: Centro de Investigación y Estudios Avanzados del IPN.         [ Links ]

44. Stolk, M. J.; de Jong, O.; Bulte, A. M. W. & Pilot, A. (2011). Exploring a Framework for Professional Development in Curriculum Innovation: Empowering Teachers for Designing Context-Based Chemistry Education. Research in Science Education, 41(3), 369-388. doi: 10.1007/s11165-010- 9170-9        [ Links ]

45. Vergnaud, G. (1990). La teoría de los campos conceptuales. Recherchers en Didactiques des Mathématiques, 10(2), 133-170.         [ Links ]