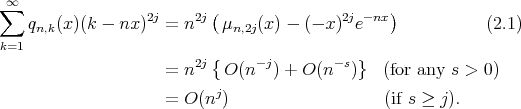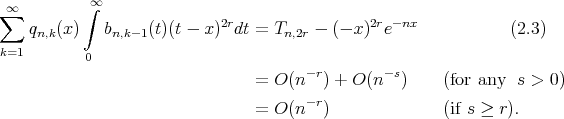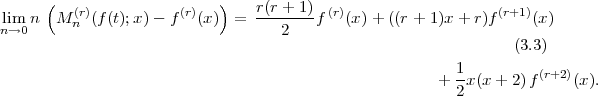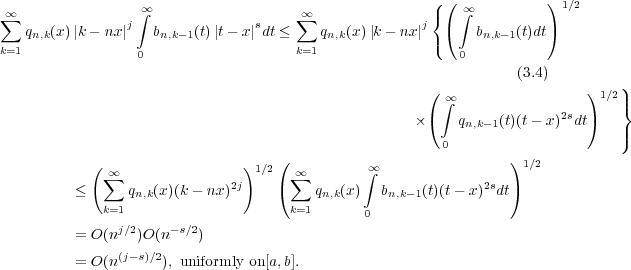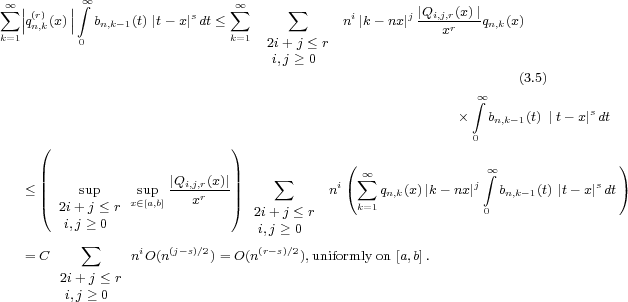Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Revista de la Unión Matemática Argentina
Print version ISSN 0041-6932
Rev. Unión Mat. Argent. vol.50 no.1 Bahía Blanca June 2009
Simultaneous approximation by a new sequence of Szãsz-beta type operators
Ali J. Mohammad and Amal K. Hassan
Abstract. In this paper, we study some direct results in simultaneous approximation for a new sequence of linear positive operators  of Szãsz-Beta type operators. First, we establish the basic pointwise convergence theorem and then proceed to discuss the Voronovaskaja-type asymptotic formula. Finally, we obtain an error estimate in terms of modulus of continuity of the function being approximated.
of Szãsz-Beta type operators. First, we establish the basic pointwise convergence theorem and then proceed to discuss the Voronovaskaja-type asymptotic formula. Finally, we obtain an error estimate in terms of modulus of continuity of the function being approximated.
Key words and phrases. Linear positive operators; Simultaneous approximation; Voronovaskaja-type asymptotic formula; Degree of approximation; Modulus of continuity.
In [3] Gupta and others studied some direct results in simultaneous approximation for the sequence:
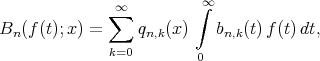
where 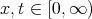 ,
, 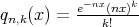 and
and 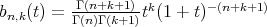 . After that, Agrawal and Thamer [1] applied the technique of linear combination introduced by May [4] and Rathore [5] for the sequence
. After that, Agrawal and Thamer [1] applied the technique of linear combination introduced by May [4] and Rathore [5] for the sequence  . Recently, Gupta and Lupas [2] studied some direct results for a sequence of mixed Beta-Szãsz type operator defined as
. Recently, Gupta and Lupas [2] studied some direct results for a sequence of mixed Beta-Szãsz type operator defined as 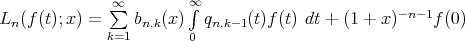 .
.
In this paper, we introduce a new sequence of linear positive operators 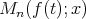 of Szãsz-Beta type operators to approximate a function
of Szãsz-Beta type operators to approximate a function  belongs to the space
belongs to the space 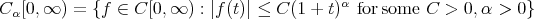 , as follows:
, as follows:
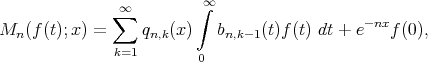 | (1.1) |
We may also write the operator (1.1) as 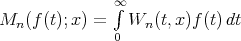 where
where 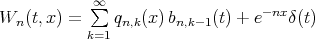 ,
, 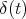 being the Dirac-delta function.
being the Dirac-delta function.
The space 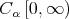 is normed by
is normed by  .
.
There are many sequences of linear positive operators with are approximate the space  . All of them (in general) have the same order of approximation
. All of them (in general) have the same order of approximation 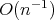 [6]. So, to know what is the different between our sequence and the other sequences, we need to check that by using the computer. This object is outside our study in this paper.
[6]. So, to know what is the different between our sequence and the other sequences, we need to check that by using the computer. This object is outside our study in this paper.
Throughout this paper, we assume that 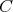 denotes a positive constant not necessarily the same at all occurrences, and
denotes a positive constant not necessarily the same at all occurrences, and ![[β ]](/img/revistas/ruma/v50n1/1a0419x.png) denotes the integer part of
denotes the integer part of 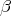 .
.
For 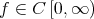 the Szãsz operators are defined as
the Szãsz operators are defined as  ,
,  and for
and for 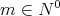 (the set of nonnegative integers), the
(the set of nonnegative integers), the 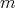 -th order moment of the Szãsz operators is defined as
-th order moment of the Szãsz operators is defined as 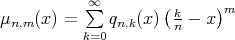 .
.
LEMMA 2.1. [3] For 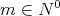 , the function
, the function 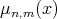 defined above, has the following properties:
defined above, has the following properties:
(i)  , and the recurrence relation is
, and the recurrence relation is
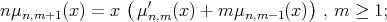
(ii) 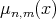 is a polynomial in
is a polynomial in 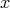 of degree at most
of degree at most ![[m ∕2]](/img/revistas/ruma/v50n1/1a0433x.png) ;
;
(iii) For every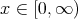 ,
,![( - [(m+1)∕2]) μn,m (x) = O n](/img/revistas/ruma/v50n1/1a0435x.png) .
.
From above lemma, we get
For 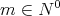 , the
, the 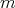 -th order moment
-th order moment 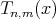 for the operators (1.1) is defined as:
for the operators (1.1) is defined as:
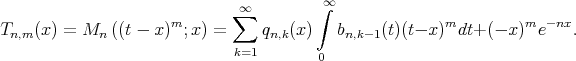
LEMMA 2.2.For the function 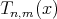 , we have
, we have 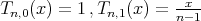 ,
, 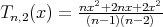 and there holds the recurrence relation:
and there holds the recurrence relation:
Further, we have the following consequences of 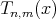 :
:
(i) 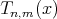 is a polynomial in
is a polynomial in 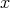 of degree exactly
of degree exactly  ;
;
(ii) For every ![x ∈ [0,∞ ) , T (x ) = O (n-[(m+1 )∕2]) n,m](/img/revistas/ruma/v50n1/1a0449x.png) .
.
Proof: By direct computation, we have 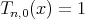 ,
, 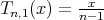 and
and  . Next, we prove (2.2). For
. Next, we prove (2.2). For  it clearly holds. For
it clearly holds. For 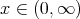 , we have
, we have
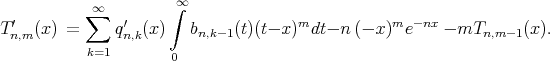
Using the relations  and
and 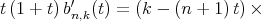
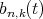 , we get:
, we get:

By using the identity 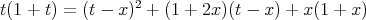 , we have
, we have
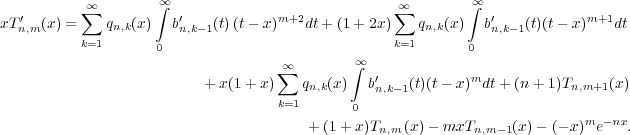
Integrating by parts, we get
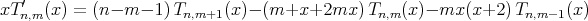
from which (2.2) is immediate.
From the values of 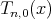 and
and 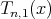 , it is clear that the consequences (i) and (ii) hold for
, it is clear that the consequences (i) and (ii) hold for 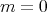 and
and  . By using (2.2) and the induction on
. By using (2.2) and the induction on  the proof of consequences (i) and (ii) follows, hence the details are omitted.
the proof of consequences (i) and (ii) follows, hence the details are omitted.
From the above lemma, we have
LEMMA 2.3. Let 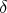 and
and 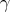 be any two positive real numbers and
be any two positive real numbers and ![[a,b] ⊂ (0,∞ )](/img/revistas/ruma/v50n1/1a0471x.png) . Then, for any
. Then, for any 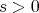 , we have
, we have
![∥∥ ∥∥ ∥∥ ∫ ∥∥ ∥ Wn (t,x)tγdt ∥ = O (n- s). ∥∥ ∥∥ |t-x|≥δ C[a,b]](/img/revistas/ruma/v50n1/1a0473x.png)
Making use of Schwarz inequality for integration and then for summation and (2.3), the proof of the lemma easily follows.
LEMMA 2.4. [3] There exist polynomials 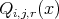 independent of
independent of  and
and  such that
such that
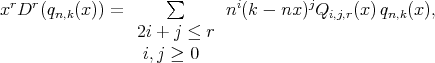 where
where 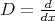 .
.
Firstly, we show that the derivative 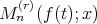 is an approximation process for
is an approximation process for 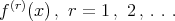 .
.
Theorem 3.1. If 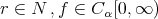 for some
for some 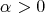 and
and 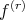 exists at a point
exists at a point 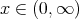 , then
, then
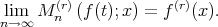 | (3.1) |
Further, if  exists and is continuous on
exists and is continuous on  , then (3.1) holds uniformly in
, then (3.1) holds uniformly in ![[a,b]](/img/revistas/ruma/v50n1/1a0488x.png) .
.
Proof: By Taylor's expansion of 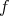 , we have
, we have
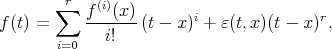
where, 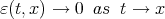 . Hence
. Hence
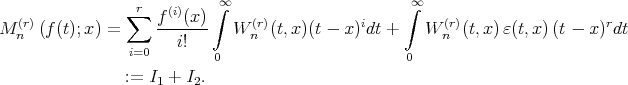
Now, using Lemma 2.2 we get that 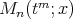 is a polynomial in
is a polynomial in  of degree exactly
of degree exactly
, for all 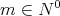 . Further , we can write it as:
. Further , we can write it as:
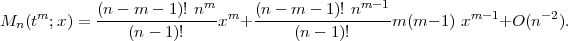 | (3.2) |
Therefore,
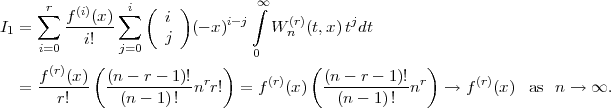
Next, making use of Lemma 2.4 we have
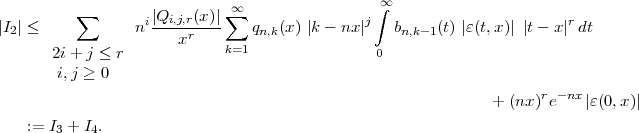
Since 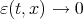 as
as 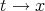 , then for a given
, then for a given 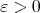 , there exists a
, there exists a  such that
such that 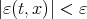 , whenever
, whenever  . For
. For 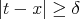 , there exists a constant
, there exists a constant 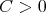 such that
such that 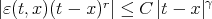 .
.
Now, since  . Hence,
. Hence,
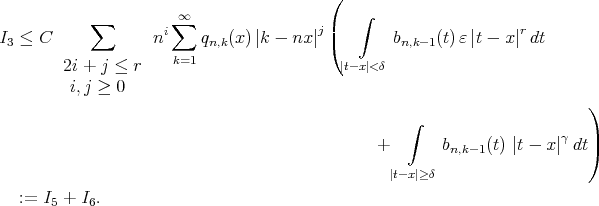
Now, applying Schwartz inequality for integration and then for summation, (2.1) and (2.3) we led to
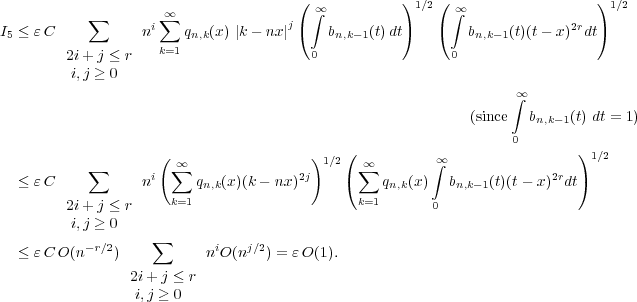
Again using Schwarz inequality for integration and then for summation, in view of (2.1) and Lemma 2.3, we have
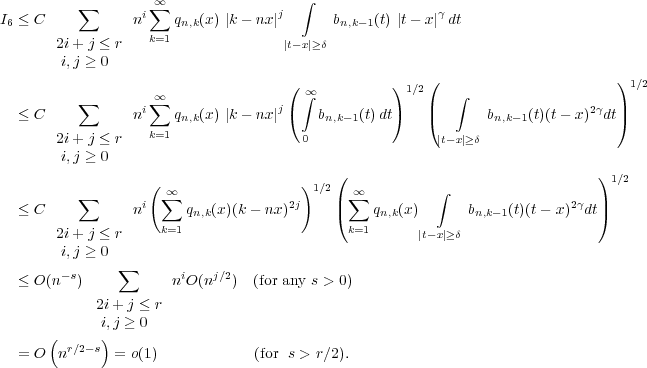
Now, since 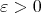 is arbitrary, it follows that
is arbitrary, it follows that 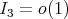 . Also,
. Also,  as
as 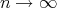 and hence
and hence  , combining the estimates of
, combining the estimates of 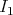 and
and 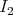 , we obtain (3.1).
, we obtain (3.1).
To prove the uniformity assertion, it sufficient to remark that 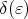 in above proof can be chosen to be independent of
in above proof can be chosen to be independent of ![x ∈ [a,b]](/img/revistas/ruma/v50n1/1a04120x.png) and also that the other estimates holds uniformly in
and also that the other estimates holds uniformly in ![[a,b]](/img/revistas/ruma/v50n1/1a04121x.png) .
.
Our next theorem is a Voronovaskaja-type asymptotic formula for the operators 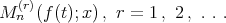 .
.
THEOREM 3.2. Let 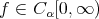 for some
for some 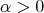 . If
. If 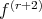 exists at a point
exists at a point  , then
, then
Further, if  exists and is continuous on the interval
exists and is continuous on the interval 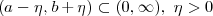 , then (3.3) holds uniformly on
, then (3.3) holds uniformly on ![[a,b]](/img/revistas/ruma/v50n1/1a04130x.png) .
.
Proof: By the Taylor's expansion of  , we get
, we get

where 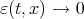 as
as 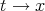 .
.
By Lemma 2.2 and (3.2), we have
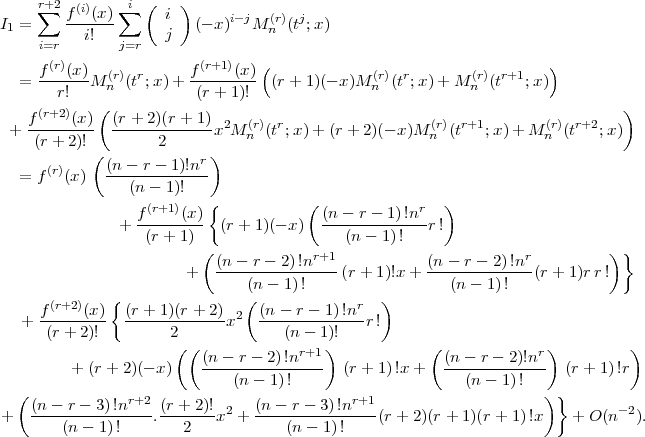
Hence in order to prove (3.3) it suffices to show that 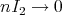 as
as 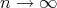 , which follows on proceeding along the lines of proof of
, which follows on proceeding along the lines of proof of 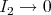 as
as  in Theorem 3.1.
in Theorem 3.1.
The uniformity assertion follows as in the proof of Theorem 3.1.
Finally, we present a theorem which gives as an estimate of the degree of approximation by  for smooth functions.
for smooth functions.
THEOREM 3.3. Let 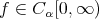 for some
for some 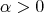 and
and 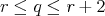 . If
. If 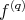 exists and is continuous on
exists and is continuous on 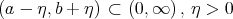 , then for sufficiently large
, then for sufficiently large 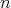 ,
,
![∥ ∥ ∑q ∥ ∥ ( ) ∥∥M (nr)(f(t);x) - f(r)(x)∥∥ ≤ C1n -1 ∥∥f(i)∥∥ +C2 n-1∕2ωf(q) n-1∕2 +O (n-2) C[a,b] i=r C[a,b]](/img/revistas/ruma/v50n1/1a04147x.png)
where  are constants independent of
are constants independent of 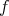 and
and  ,
, 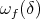 is the modulus of continuity of
is the modulus of continuity of 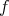 on
on 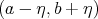 , and
, and ![∥ .∥C[a,b]](/img/revistas/ruma/v50n1/1a04154x.png) denotes the sup-norm on
denotes the sup-norm on ![[a,b]](/img/revistas/ruma/v50n1/1a04155x.png) .
.
Proof. By Taylor's expansion of 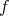 , we have
, we have
where  lies between
lies between  , and
, and 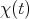 is the characteristic function of the interval
is the characteristic function of the interval 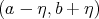 . Now,
. Now,
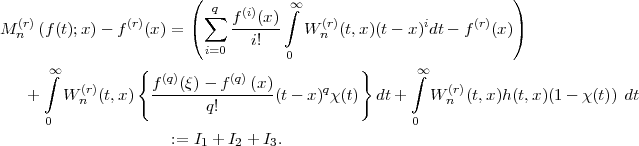
By using Lemma 2.2 and (3.2), we get
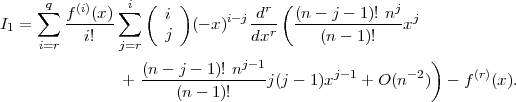
Consequently,
![( q ) - 1 ∑ ∥ (i)∥ -2 ∥I1∥C[a,b] ≤ C1n ∥f ∥C[a,b] + O (n ),uniformly on [a,b]. i=r](/img/revistas/ruma/v50n1/1a04164x.png)
To estimate  we proceed as follows:
we proceed as follows:
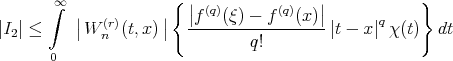
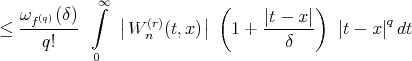
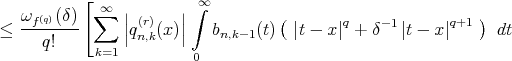
![] r - nx q - 1 q+1 + (- n )e (x + δ x ) , δ > 0.](/img/revistas/ruma/v50n1/1a04169x.png)
Now, for  , using Schwartz inequality for integration and then for summation, (2.1) and (2.3), we have
, using Schwartz inequality for integration and then for summation, (2.1) and (2.3), we have
Therefore, by Lemma 2.4 and (3.4), we get
(since ![Q (x) sup sup |i,jx,rr--|:= M(x) 2i+ j ≤ r x∈[a,b] i,j ≥ 0](/img/revistas/ruma/v50n1/1a04173x.png) but fixed )
but fixed )
Choosing 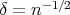 and applying (3.5), we are led to
and applying (3.5), we are led to

Since 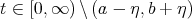 , we can choose
, we can choose  in such a way that
in such a way that 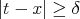 for all
for all ![x ∈ [a,b]](/img/revistas/ruma/v50n1/1a04179x.png) . Thus, by Lemmas 2.3 and 2.4 , we obtain
. Thus, by Lemmas 2.3 and 2.4 , we obtain
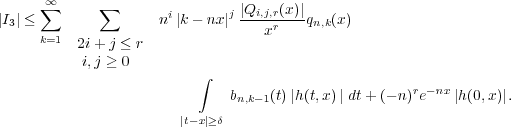
For 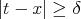 , we can find a constant
, we can find a constant  such that
such that 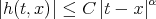 . Hence, using Schwarz inequality for integration and then for summation ,(2.1), (2.3), it easily follows that
. Hence, using Schwarz inequality for integration and then for summation ,(2.1), (2.3), it easily follows that 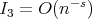 for any
for any 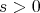 , uniformly on
, uniformly on ![[a,b]](/img/revistas/ruma/v50n1/1a04186x.png) .
.
Combining the estimates of 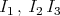 , the required result is immediate.
, the required result is immediate.
[1] P.N. Agrawal and Kareem J. Thamer. Linear combinations of Szãsz-Baskakov type operators, Demonstratio Math.,32(3) (1999), 575-580. [ Links ]
[2] Vijay Gupta and Alexandru Lupas. Direct results for mixed Beta-Szãsztype operators, General Mathematics 13(2), (2005), 83-94. [ Links ]
[3] Vijay Gupta, G.S. Servastava and A. Shahai. On simultaneous approximation by Szãsz-Beta operators, Soochow J. Math. 21, (1995), 1-11. [ Links ]
[4] C.P. May. Saturation and inverse theorems for combinations of a class of exponential- type operators, Canad. J. Math. 28 (1976), 1224-1250. [ Links ]
[5] R.K.S. Rathore. Linear Combinations of Linear Positive Operators and Generating Relations in Special Functions, Ph.D. Thesis, I.I.T. Delhi (India) 1973. [ Links ]
[6] E. Voronovskaja. Détermination de la forme asymptotique d'ápproximation des fonctions par les polynômes de S.N. Bernstein, C.R. Adad. Sci. USSR (1932), 79-85. [ Links ]
Ali J. Mohammad
University of Basrah,
College of Education,
Dept. of Mathematics,
Basrah, IRAQ.
alijasmoh@yahoo.com
Amal K. Hassan
University of Basrah,
College of Science,
Dept. of Mathematics,
Basrah, IRAQ.
Recibido: 8 de noviembre de 2006
Aceptado: 11 de marzo de 2008