Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Revista de la Unión Matemática Argentina
Print version ISSN 0041-6932
Rev. Unión Mat. Argent. vol.50 no.1 Bahía Blanca June 2009
Amalgamation Property in Quasi-Modal algebras
Sergio Arturo Celani
Abstract. In this paper we will give suitable notions of Amalgamation and Super-amalgamation properties for the class of quasi-modal algebras introduced by the author in his paper Quasi-Modal algebras.
2000 Mathematics Subject Classification. 06E25, 03G25.
Key words and phrases. Boolean algebras; Quasi-modal algebras; Amalgamation and Super-amalgamation properties.
1. Introduction and preliminaries
The class of quasi-modal algebras was introduced by the author in [2], as a generalization of the class of modal algebras. A quasi-modal algebra is a Boolean algebra  endowed with a map
endowed with a map  that sends each element
that sends each element 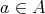 to an ideal
to an ideal 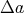 of
of 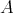 , and satisfies analogous conditions to the modal operator
, and satisfies analogous conditions to the modal operator  of modal algebras [3]. This type of maps, called quasi-modal operators, are not operations on the Boolean algebra, but have some similar properties to modal operators.
of modal algebras [3]. This type of maps, called quasi-modal operators, are not operations on the Boolean algebra, but have some similar properties to modal operators.
It is known that some varieties of modal algebras have the Amalgamation Property (AP) and Superamalgamation Property (SAP). These properties are connected with the Interpolation property in modal logic (see [3]). The aim of this paper is to introduce a generalization of these notions for the class of quasi-modal algebras, topological quasi-modal algebras, and monadic quasi-modal algebras.
We recall some concepts needed for the representation for quasi-modal algebras. For more details see [2] and [1].
Let 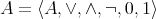 be a Boolean algebra. The set of all ultrafilters is denoted by
be a Boolean algebra. The set of all ultrafilters is denoted by  The ideal (filter) generated in
The ideal (filter) generated in  by some subset
by some subset  will be denoted by
will be denoted by 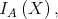
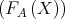 . The complement of a subset
. The complement of a subset 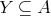 will be denoted by
will be denoted by  or
or 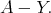 The lattice of ideals (filters) of
The lattice of ideals (filters) of 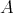 is denoted by
is denoted by  (
(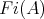 ).
).
Definition 1. Let 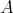 be a Boolean algebra. A quasi-modal operator defined on
be a Boolean algebra. A quasi-modal operator defined on  is a function
is a function 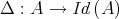 that verifies the following conditions for all
that verifies the following conditions for all 
-
Q1

-
Q2
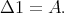
A quasi-modal algebra, or 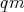 -algebra, is a pair
-algebra, is a pair 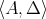 where
where 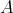 is a Boolean algebra and
is a Boolean algebra and  is a quasi-modal operator.
is a quasi-modal operator.
In every quasi-modal algebra we can define the dual operator 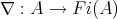 by
by 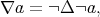 where
where 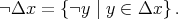 It is easy to see that the operator
It is easy to see that the operator 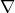 satisfies the conditions
satisfies the conditions
-
(1)
 , and
, and -
(2)
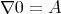 ,
,
for all 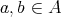 (see [2]). The class of
(see [2]). The class of  -algebras is denoted by
-algebras is denoted by 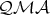 .
.
Let  be a
be a 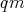 -algebra. For each
-algebra. For each 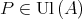 we define the set
we define the set

Lemma 2. [2] Let 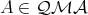 .
.
-
(1) For each
 ,
, 
-
(2)
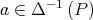 iff for all
iff for all 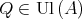 , if
, if 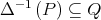 then
then 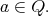
Let 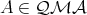 . We define on
. We define on 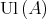 a binary relation
a binary relation 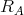 by
by

Throughout this paper, we will frequently work with Boolean subalgebras of a given Boolean algebra. In order to avoid any confusion, if  , then we will use the symbol
, then we will use the symbol 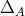 to denote the corresponding operation of
to denote the corresponding operation of 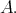 A function
A function 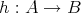 is an homomorphism of quasi-modal algebras, or a
is an homomorphism of quasi-modal algebras, or a 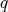 -homomorphism, if
-homomorphism, if  is an homomorphism of Boolean algebras, and
is an homomorphism of Boolean algebras, and
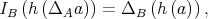
for any  A quasi-isomorphism is a Boolean isomorphism that is a q-homomor-phism.
A quasi-isomorphism is a Boolean isomorphism that is a q-homomor-phism.
Let 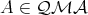 . Let us consider the relational structure
. Let us consider the relational structure
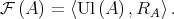
From the result given in [2] it follows that the Boolean algebra  endowed with the operator
endowed with the operator
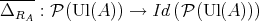
defined by
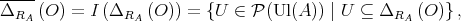
is a quasi-modal algebra. Moreover, the map  defined by
defined by 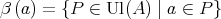 , for each
, for each 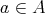 , is a
, is a  -homomorphism
-homomorphism i.e.
i.e. 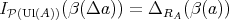 , for each
, for each  .
.
Let  Let
Let 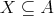 . Define the ideal
. Define the ideal 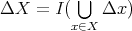 and the filter
and the filter 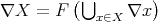 . For
. For 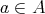 we define recursively
we define recursively 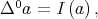 and
and 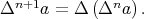
Theorem 3. [2] Let  . Then for all
. Then for all 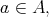 the following equivalences hold:
the following equivalences hold:
-
1.
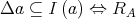 is reflexive.
is reflexive. -
2.
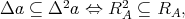 i.e.,
i.e., 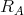 is transitive.
is transitive. -
3.
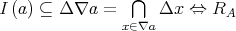 is symmetrical.
is symmetrical.
Let  We shall say that
We shall say that  is a topological quasi-modal algebra if for every
is a topological quasi-modal algebra if for every 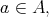
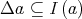 and
and  We shall say that
We shall say that 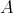 is a monadic quasi-modal algebra if it is a quasi-topological algebra and
is a monadic quasi-modal algebra if it is a quasi-topological algebra and  for every
for every 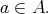 From the previous Theorem we get that a quasi-modal algebra
From the previous Theorem we get that a quasi-modal algebra  is quasi-topological algebra iff the relation
is quasi-topological algebra iff the relation 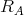 is reflexive and transitive. Similarly, a quasi-modal algebra
is reflexive and transitive. Similarly, a quasi-modal algebra  is a monadic quasi-modal algebra iff the relation
is a monadic quasi-modal algebra iff the relation 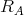 is an equivalence.
is an equivalence.
Let 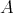 and
and 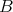 be two qm-algebras. We shall say that the structure
be two qm-algebras. We shall say that the structure 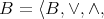
 is a quasi-modal subalgebra of
is a quasi-modal subalgebra of 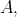 or qm-subalgebra for short, if
or qm-subalgebra for short, if 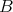 is a Boolean subalgebra of
is a Boolean subalgebra of 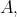 and for any
and for any 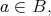
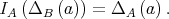
The following result is given in [1] for Quasi-modal lattices.
Lemma 4. Let 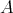 be a qm-algebra. Let
be a qm-algebra. Let 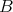 be a Boolean subalgebra of
be a Boolean subalgebra of 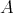 . Then the following conditions are equivalent
. Then the following conditions are equivalent
-
(1) There is a quasi-modal operator,
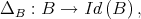 such that
such that 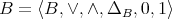 is a
is a 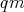 -subalgebra of
-subalgebra of 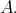
-
(2) For any
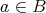 ,
, 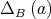 is defined to be
is defined to be 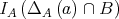 .
.
Remark 5. Let 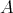 be a
be a  -algebra. Let
-algebra. Let 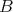 be a Boolean subalgebra of
be a Boolean subalgebra of 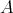 . If there is a quasi-modal operator
. If there is a quasi-modal operator 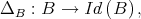 such that
such that  is a
is a 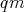 -subalgebra of
-subalgebra of 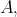 then
then 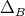 is unique. The proof of this fact is as follows: First, we note that if
is unique. The proof of this fact is as follows: First, we note that if 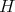 is an ideal of
is an ideal of 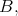 and
and 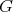 is a filter of
is a filter of 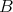 such that
such that  , then
, then 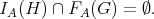 We suppose now that there exist two quasi-modal operators
We suppose now that there exist two quasi-modal operators 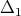 and
and 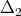 in
in 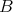 such that
such that 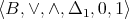 and
and 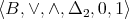 are two
are two 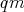 -subalgebras of
-subalgebras of  Then
Then

If 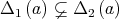 , there exists
, there exists  such that
such that 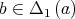 and
and 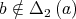 . Then
. Then 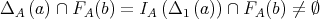 and
and 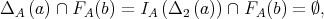 which is a contradiction.
which is a contradiction.
It is known that the variety of modal algebras has the Amalgamation Property (AP) and the Superamalgamation Property (SAP) (see [3] for these properties and the connection with the Interpolation property in modal logic). In this section we shall give a generalization of these notions and prove that the class  has these properties.
has these properties.
Definition 6. Let  be a class of quasi-modal algebras. We shall say that
be a class of quasi-modal algebras. We shall say that  has the AP if for any triple
has the AP if for any triple 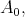
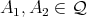 and injective quasi-homomorphisms
and injective quasi-homomorphisms 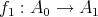 and
and 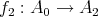 there exists
there exists 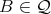 and injective quasi-homomorphisms
and injective quasi-homomorphisms  and
and 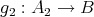 such that
such that  and
and 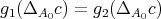 , for every
, for every 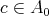 .
.
We shall say that  has the SAP if
has the SAP if  has the AP and in addition the maps
has the AP and in addition the maps 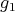 and
and 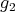 above have the following property:
above have the following property:
For all  such that
such that 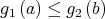 there exists
there exists 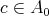 such that
such that 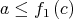 and
and 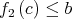 .
.
Let  be a class of quasi-modal algebras. Without losing generality, we can assume that in the above definition
be a class of quasi-modal algebras. Without losing generality, we can assume that in the above definition 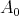 is a
is a 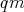 -subalgebra of
-subalgebra of 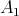 and
and  i.e., that
i.e., that  and
and 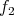 are the inclusion maps.
are the inclusion maps.
Theorem 7. The class 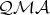 has the AP.
has the AP.
Proof. Let 
 such
such 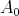 is a
is a  -subalgebra of
-subalgebra of 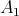 and
and  . Let us consider the relational structures
. Let us consider the relational structures 
 We shall define the set
We shall define the set
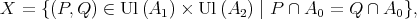
and the binary relation  in
in  as follows:
as follows:
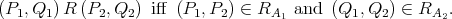
Let us consider the quasi-modal algebra  where the operator
where the operator

is defined by

We note that in this case 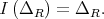
Let us define the maps 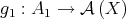 and
and 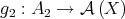 by
by
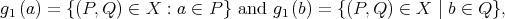
respectively. We prove that 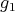 and
and  are injective q-homomorpshims.
are injective q-homomorpshims.
First of all let us check the following property:
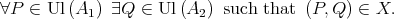 | (1) |
Let 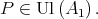 Since
Since 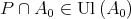 and
and  is a subalgebra of
is a subalgebra of  we get by known results on Boolean algebras that there exists
we get by known results on Boolean algebras that there exists 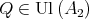 such that
such that  i.e.,
i.e., 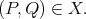
To see that 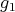 is injective, let
is injective, let  such that
such that 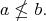 Then there exists
Then there exists 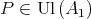 such that
such that 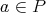 and
and 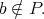 By (1), there exists
By (1), there exists  such that
such that  . So,
. So, 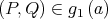 and
and 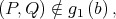 i.e.,
i.e., 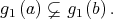 Thus,
Thus, 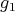 is injective. It is clear that
is injective. It is clear that 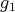 is a Boolean homomorphism.
is a Boolean homomorphism.
We prove next that 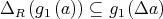 , for any
, for any  .
.
Let  Suppose that
Suppose that  i.e.,
i.e.,  From Lemma 2 there exists
From Lemma 2 there exists 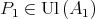 such that
such that  and
and  . By property (1), there exists
. By property (1), there exists 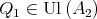 such that
such that  From the inclusion
From the inclusion 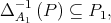 it is easy to see that
it is easy to see that 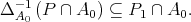 Thus,
Thus,
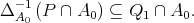
We prove that there exists 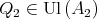 such that
such that 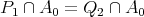 and
and 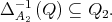 Let us consider the filter
Let us consider the filter
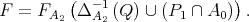
The filter 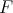 is proper, because otherwise there exist
is proper, because otherwise there exist  and
and 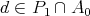 such that
such that 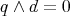 . So,
. So,  and since
and since 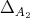 is increasing, we get
is increasing, we get  As
As  is a quasi-subalgebra of
is a quasi-subalgebra of 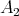 and
and  we get
we get
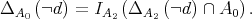
Thus,

So, there exists  and
and 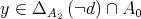 such that
such that  Since
Since 
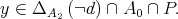 Then we have
Then we have 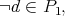 which is a contradiction. Therefore, there exists
which is a contradiction. Therefore, there exists 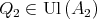 such that
such that
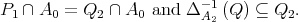
So, 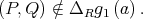 So, we have the inclusion
So, we have the inclusion 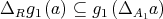 . The inclusion
. The inclusion  is easy and left to the reader. Thus,
is easy and left to the reader. Thus, 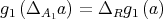 , and consequently we get
, and consequently we get
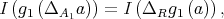
i.e.,  is an injective q-homomorphism.
is an injective q-homomorphism.
Similarly we can prove that  is an injective q-homomorphism. Moreover, it is easy to check that for all
is an injective q-homomorphism. Moreover, it is easy to check that for all 
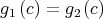 , and
, and 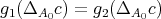 . Thus,
. Thus, 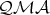 has the AP.
has the AP.
Lemma 8. Let 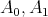 and
and 
 such that
such that 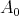 is a subalgebra of
is a subalgebra of 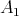 and
and 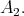 Let
Let 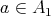 ,
,  and let us suppose that there exists no
and let us suppose that there exists no 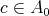 such that
such that 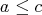 or
or 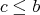 . Then there exist
. Then there exist 
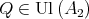 such that
such that

Proof. Let us consider the filter 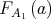 in
in  and the filter
and the filter 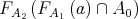 in
in  We note that
We note that
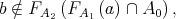
because in otherwise there exists 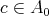 such that
such that 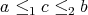 , which is a contradiction. Then by the Ultrafilter theorem, there exists
, which is a contradiction. Then by the Ultrafilter theorem, there exists  that such that
that such that
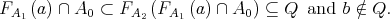
Let us consider in 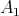 the filter
the filter  and the ideal
and the ideal 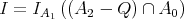 . We prove that
. We prove that
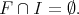
Suppose that there exist elements 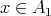 ,
, 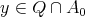 , and
, and  such that
such that 
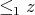 . This implies that
. This implies that
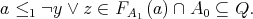
Thus, we get 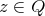 , which is a contradiction. So, there exists
, which is a contradiction. So, there exists 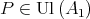 such that
such that
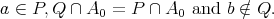
Theorem 9. The class  has the SAP.
has the SAP.
Proof. The proof of the SAP is actually analogous to the previous one. Let 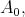
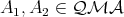 such that
such that  is a qm-subalgebra of
is a qm-subalgebra of 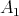 and of
and of 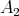 . Let us consider the set
. Let us consider the set 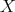 and the quasi-modal algebra
and the quasi-modal algebra 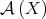 of the proof above.
of the proof above.
Let 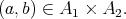 Suppose that there exists no
Suppose that there exists no 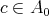 such that
such that 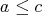 or
or  . By Lemma 8 there exists
. By Lemma 8 there exists 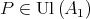 and there exists
and there exists 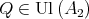 such that
such that

i.e., 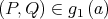 and
and 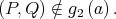 Thus,
Thus, 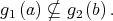 So,
So, 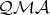 has the SAP.
has the SAP.
The results above can be applied to prove that other classes of quasi-modal algebras have the AP and SAP. For example, if 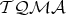 is the class of the topological quasi-modal algebras, then in the proof of Theorem 7 the binary relation
is the class of the topological quasi-modal algebras, then in the proof of Theorem 7 the binary relation 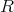 defined on the set
defined on the set 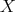 is reflexive and transitive. Consequently,
is reflexive and transitive. Consequently,  is a topological quasi-modal algebra and thus the class
is a topological quasi-modal algebra and thus the class  has the AP and the SAP. Similar considerations can be applied to the class
has the AP and the SAP. Similar considerations can be applied to the class  of monadic quasi-modal algebras.
of monadic quasi-modal algebras.
I would like to thank the referee for his observations and suggestions which have contributed to improve this paper.
[1] Castro, J. and Celani, S., Quasi-modal lattices, Order 21 (2004), 107-129. [ Links ]
[2] Celani, S. A., Quasi-Modal algebras, Mathematica Bohemica Vol. 126, No. 4 (2001), 721-736. [ Links ]
[3] Kracht. M., Tools and Techniques in Modal Logic, Studies in Logic and the Foundations of Mathematics, Vol. 142, Elsevier. [ Links ]
Sergio Arturo Celani
CONICET and Departamento de Matemáticas
Universidad Nacional del Centro
Pinto 399, 7000 Tandil, Argentina
scelani@exa.unicen.edu.ar
Recibido: 9 de marzo de 2007
Aceptado: 19 de septiembre de 2008














