Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista de la Unión Matemática Argentina
versión impresa ISSN 0041-6932
Rev. Unión Mat. Argent. vol.50 no.1 Bahía Blanca jun. 2009
Approximation degree for generalized integral operators
S. Jain and R. K. Gangwar
Abstract. Very recently Jain et al. [4] proposed generalized integrated Baskakov operators 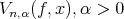 and estimated some approximation properties in simultaneous approximation. In the present paper we establish the rate of convergence of these operators and its Bezier variant, for functions which have derivatives of bounded variation.
and estimated some approximation properties in simultaneous approximation. In the present paper we establish the rate of convergence of these operators and its Bezier variant, for functions which have derivatives of bounded variation.
For 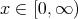 and
and 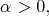 the general family of Baskakov type operators considered in [3] is defined as
the general family of Baskakov type operators considered in [3] is defined as
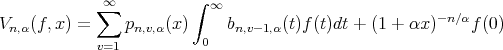 | (1) |
where

In the alternative form the above operators (1), can be defined as

where the kernel 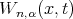 in terms of Dirac delta function
in terms of Dirac delta function  is given by
is given by
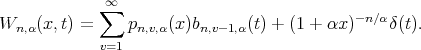
We define 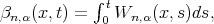 then as a special case we have
then as a special case we have 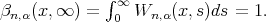 Let
Let 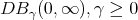 be the class of absolutely continuous functions
be the class of absolutely continuous functions 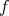 defined on
defined on 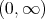 satisfying the growth condition
satisfying the growth condition  and having a derivative
and having a derivative 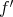 on the interval
on the interval 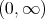 coinciding a.e. with a function which is of bounded variation on every finite subinterval of
coinciding a.e. with a function which is of bounded variation on every finite subinterval of 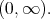 It can be observed that all functions
It can be observed that all functions  posses for each
posses for each 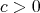 a representation
a representation

In [4] the authors studied some direct results in simultaneous approximation for the operators (1). Very recently the rate of convergence for bounded function for the operators 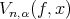 has been obtained by Gangwar and Jain [3]. For certain operators Bojanic and Khan [2] and Taberska [10] estimated the rate of convergence for functions having derivative of B.V. The analogous problem on the convergence rate for the Bernstein polynomials and certain other integral operators were studied in [1],[5], [6] and [8]. Very recently Ispir et al. [9] considered the Kantorovich process of a generalized sequence of linear positive operators and estimated the rate of convergence for absolutely continuous functions having a derivative coinciding a.e., with a function of bounded variation.
has been obtained by Gangwar and Jain [3]. For certain operators Bojanic and Khan [2] and Taberska [10] estimated the rate of convergence for functions having derivative of B.V. The analogous problem on the convergence rate for the Bernstein polynomials and certain other integral operators were studied in [1],[5], [6] and [8]. Very recently Ispir et al. [9] considered the Kantorovich process of a generalized sequence of linear positive operators and estimated the rate of convergence for absolutely continuous functions having a derivative coinciding a.e., with a function of bounded variation.
As the operators defined by (1) are the generalized operators, this motivated us to extend the studies and here we study the approximation properties of the operators 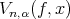 and its Bezier variant. We estimate the convergence rate for functions whose first derivative is of bounded variation.
and its Bezier variant. We estimate the convergence rate for functions whose first derivative is of bounded variation.
We shall use the following lemmas to prove our main theorem.
Lemma 1 [4]. Let the 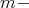 th order central moment be of the operators (1) be defined by
th order central moment be of the operators (1) be defined by
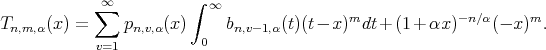
Then, we have
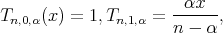
and

and for 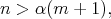 we have
we have

It is easily checked that for all 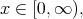 one has
one has
![Tn,m,α(x) = O (n-[(m+1 )∕2]).](/img/revistas/ruma/v50n1/1a0730x.png)
Remark 1. In particular given any number 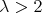 and
and 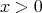 , by Lemma 1, we have for n sufficiently large one has
, by Lemma 1, we have for n sufficiently large one has
 | (2) |
Remark 2. In view of Remark 1, it can be observed by Holder's inequality that
![1∕2 ∘ -------------- Vn,α(| t - x |,x) ≤ [Tn,2,α(x )] ≤ λx (1 + αx )∕n.](/img/revistas/ruma/v50n1/1a0734x.png) | (3) |
Lemma 2. Let 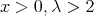 and the kernel
and the kernel  is defined by (1), then for
is defined by (1), then for 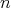 sufficiently large, we have
sufficiently large, we have
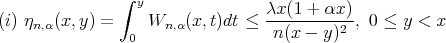
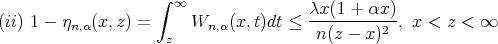
Proof. First we prove (i), by (2), we have
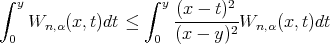

The proof of (ii) is similar, we omit the details.
In this section, we prove the following main theorem.
Theorem 1. Let 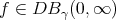 ,
,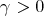 and
and  . Then for
. Then for 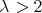 and for
and for 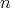 sufficiently large, we have
sufficiently large, we have
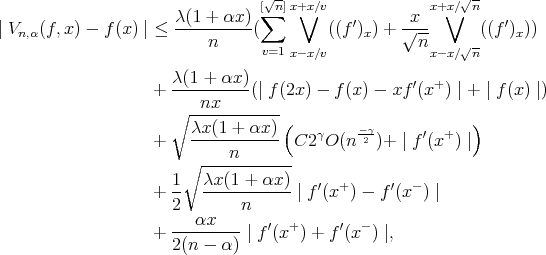
where 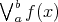 denotes the total variation of
denotes the total variation of 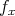 on
on ![[a, b],](/img/revistas/ruma/v50n1/1a0750x.png) and
and 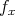 is defined by
is defined by
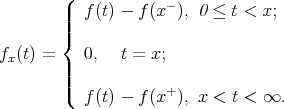
Proof. Using the fact that 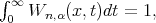 we can write
we can write

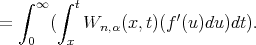
Also, we can write
![′ + ′ - ′ + ′ - f ′(u) = [f-(x-)-+-f-(x-)] + (f′)x(u ) + [f-(x--) --f-(x-)]sgn (u - x) 2 2](/img/revistas/ruma/v50n1/1a0756x.png)
![′ + ′ - +[f′(x) - [f(x--) +-f(x--)]]χx (u). 2](/img/revistas/ruma/v50n1/1a0757x.png)
Next, we have ![∫ ∫ ′ + ′ - ∞ ( tf ′(x) - [f(x-)+f-(x-)]χx (u )du))Wn,α(x, t)dt = 0, 0 x 2](/img/revistas/ruma/v50n1/1a0758x.png) thus
thus
![∫ ∫ ∞ t [f′(x+ ) + f′(x - )] ′ Vn,α(f,x )- f (x) = ( Wn (x,t)(--------2--------+ (f)x(u))du )dt 0 x](/img/revistas/ruma/v50n1/1a0759x.png)
![∫ ∞ ∫ t [f ′(x+ ) - f ′(x- )] ( Wn (x,t)-----------------sgn(u - x)du )dt. 0 x 2](/img/revistas/ruma/v50n1/1a0760x.png)
Also
![∫ ∞ ∫ t ′ + ′ - ′ + ′ - ( [f-(x--) --f-(x-)]sgn (u - x)du )Wn, α(x,t)dt = [f-(x--) --f-(x-)]Vn,α(| t- x |,x) 0 x 2 2](/img/revistas/ruma/v50n1/1a0761x.png)
and
![∫ ∞ ∫ t 1- ′ + ′ - 1- ′ + ′ - 0 ( x 2 [f (x ) + f (x )]du )Wn, α(x,t)dt = 2 [f (x )+f (x )]Vn,α((t- x),x ).](/img/revistas/ruma/v50n1/1a0762x.png)
Thus we can write
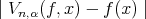

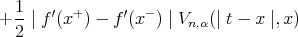
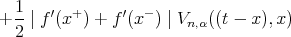

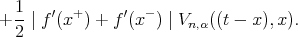 | (4) |
To complete the proof of the theorem it is sufficient to estimate the terms  and
and 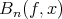 . Applying integration by parts, using Lemma 2 and taking
. Applying integration by parts, using Lemma 2 and taking 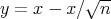 ,we have
,we have
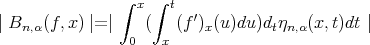

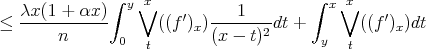

Let 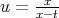 . Then we have
. Then we have
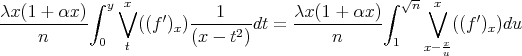
![√- [∑n] x∨ ≤ λ-(1-+-αx-) ((f ′)x). n v=1x- x u](/img/revistas/ruma/v50n1/1a0778x.png)
Thus
![[√n-] x x λ(1-+-αx-)∑ ∨ ′ -x-- ∨ ′ | Bn,α(f,x ) | ≤ n ((f )x) + √n- ((f )x). v=1 x- xu x-√xn-](/img/revistas/ruma/v50n1/1a0779x.png) | (5) |
On the other hand, we have
Next applying Holder's inequality, and Lemma 1, we proceed as follows for the estimation of the first two terms in the right hand side of (6):
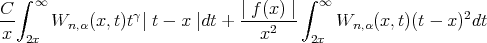
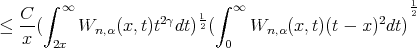
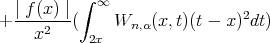
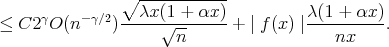 | (7) |
Also the third term of the right side of (6) is estimated as

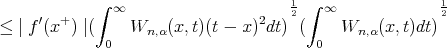
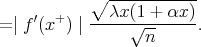
Collecting the estimates (4)-(7), we get the required result.
This completes the proof of Theorem 1.
For 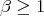 or
or  , the Bezier variant of the operators (1) can be defined as
, the Bezier variant of the operators (1) can be defined as
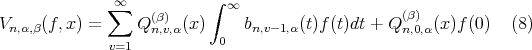
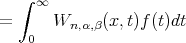
where 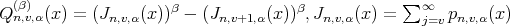 and the kernel is given by
and the kernel is given by
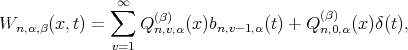
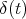 being Dirac delta function. In case
being Dirac delta function. In case  the operators defined by (8) reduce to the operators (1).
the operators defined by (8) reduce to the operators (1).
We define

Remark 3. By Lemma 2 for  we can write
we can write
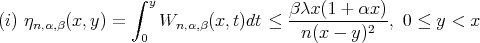
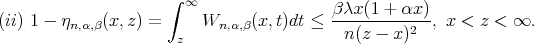
Remark 4. In view of Lemma 1 and Remark 1, for  it can be observed that
it can be observed that
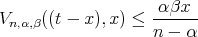
![∘ ------------- βλx (1 + αx) Vn,α,β (| t - x |,x) ≤ [βTn,2,α(x)]1∕2 ≤ ------------. n](/img/revistas/ruma/v50n1/1a07102x.png)
Our main result is stated as follows:
Theorem 2.Let 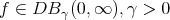 , also suppose
, also suppose  and
and 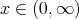 . Then for
. Then for 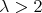 and
and 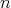 sufficiently large, we have
sufficiently large, we have
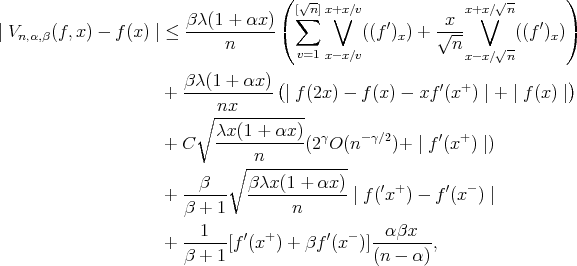
where 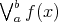 denotes the total variation of
denotes the total variation of 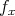 on
on ![[a,b]](/img/revistas/ruma/v50n1/1a07111x.png) and the auxiliary function
and the auxiliary function  is as given in Theorem 1.
is as given in Theorem 1.
Proof. Following the methods presented in [7], we can write
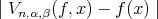
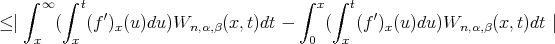
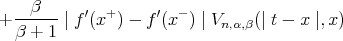
![+---1--[f′(x+ ) + βf′(x- )]V ((t - x),x) β + 1 n,α,β](/img/revistas/ruma/v50n1/1a07116x.png)

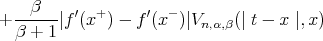
![+ --1---[f ′(x+ ) + βf ′(x - )]Vn,α,β((t - x),x ). β + 1](/img/revistas/ruma/v50n1/1a07119x.png)
Using Remark 4, we have

. (9)](/img/revistas/ruma/v50n1/1a07121x.png)
In order to complete the proof of the theorem, it is sufficient to estimate the terms 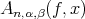 and
and 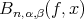 given in (9) above. Using Remark 3 and proceeding along the lines of proof of Theorem 1, we get the desired estimate. Here we omit the details.
given in (9) above. Using Remark 3 and proceeding along the lines of proof of Theorem 1, we get the desired estimate. Here we omit the details.
We are thankful to the referee for his critical review leading to overall improvement of the paper.
[1] R. Bojanic and F. Cheng, Rate of convergence of Bernstein polynomials for functions with derivatives of bounded variation, J. Math. Anal. Appl. 141 (1989), no. 1, 136-151. [ Links ]
[2] R. Bojanic and M. K. Khan, Rate of convergence of some operators of functions with derivatives of bounded variation, Atti. Sem. Mat. Fis. Univ. Modena (2)39 (1991), 495-512. [ Links ]
[3] R. K. Gangwar and V. K. Jain, Rate of approximation for certain generalized operators, General Math., to appear. [ Links ]
[4] S. Jain, R. K. Gangwar and D. K. Dubey, Convergence for certain Baskakov Durrmeyer type operators, Nonlinear Functional Anal. Appl.,to appear. [ Links ]
[5] V. Gupta, U. Abel and M. Ivan, Rate of convergence of Beta operators of second kind for functions with derivatives of bounded variation, Int. J. Math. Math. Sci. 2005(23) (2005), 3827-3833. [ Links ]
[6] V. Gupta and P. N. Agrawal, Rate of convergence for certain Baskakov Durrmeyer type operators, Anal. Univ. Ordea Fasc. Math. 14 (2007), 33-39. [ Links ]
[7] V. Gupta and H. Karsli, Rate of convergence for the Bezier variant of the MKZD operators, Georgian Math. J. 14 (2007), 651-659. [ Links ]
[8] V. Gupta, V. Vasishtha and M. K. Gupta, Rate of convergence of summation-integral type operators with derivatives of bounded variation, JIPAM. J. Inequal. Pure Appl. Math. 4(2) (2003), Art.34. [ Links ]
[9] N. Ispir, A. Aral and O. Dogru, On Kantorovich process of a sequence of the generalized linear positive operators, Numer. Funct. Anal. Optim., 29(5-6) (2008), 574-589. [ Links ]
[10] P. Pych Taberska, Pointwise approximation of absolutely continuous functions by certain linear operators, Funct. Approx. Comment. Math. 25 (1997), 67-76. [ Links ]
S. Jain
Guru Nanak Institute of Management
Road No. 75, Punjabi Bagh, New Delhi 110026, India
jainshipra11@rediffmail.com
Ravindra Kumar Gangwar
Department of Mathematics, Bareilly College
Bareilly 243001, India
ravindra1402@yahoo.co.in
Recibido: 6 de marzo de 2008
Aceptado: 7 de octubre de 2008















